Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise—An Aggregated Modelling Approach
Abstract
1. Introduction
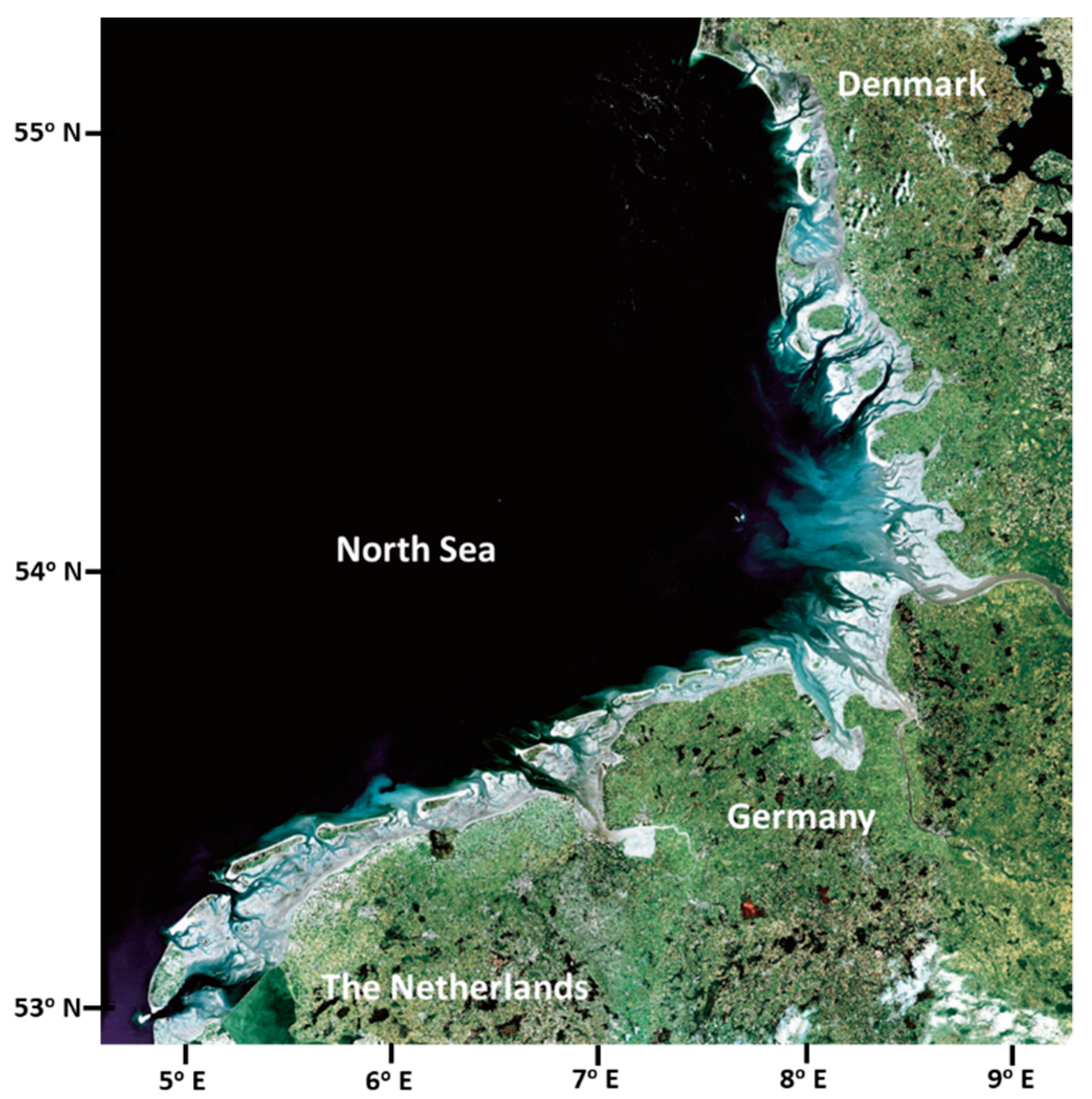
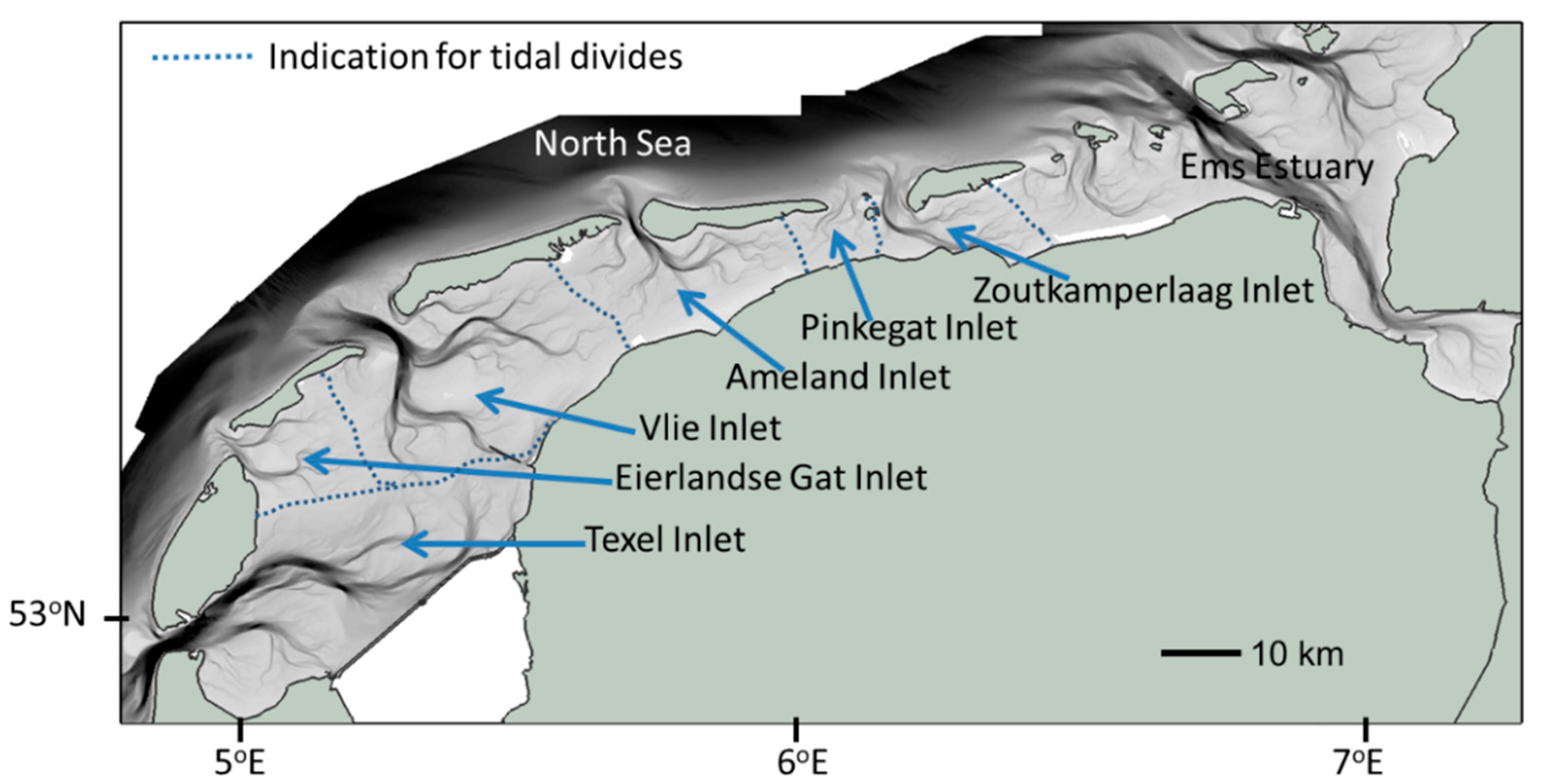
1.1. Study Area
1.2. Influence of Sea-Level Rise
1.3. Modelling the Response to Sea-Level Rise
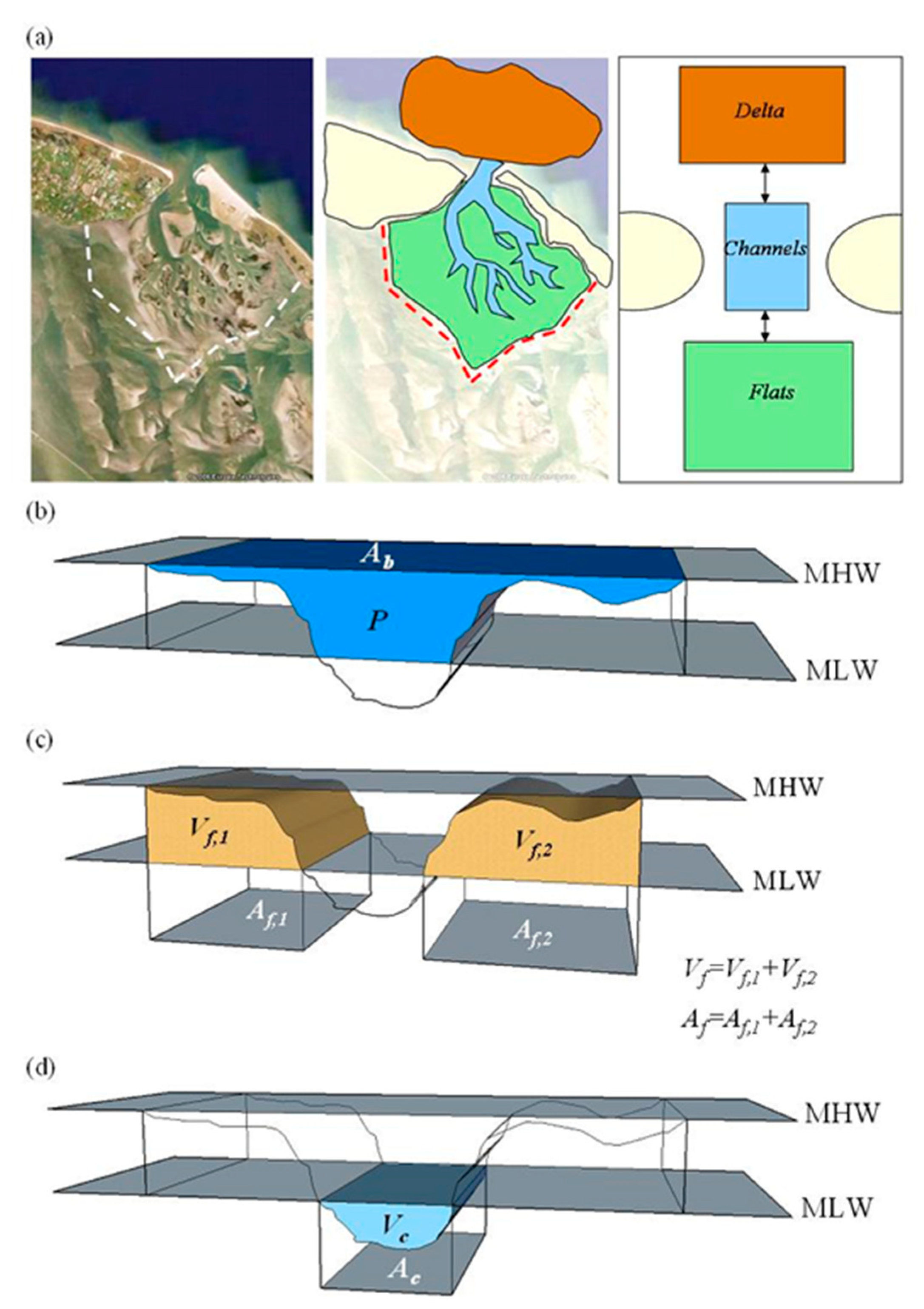
2. Modelling Approach—Aggregated Model ASMITA
- The ebb-tidal delta, with its state variable Vd = total excess sediment volume relative to an undisturbed coastal bed profile [L3];
- The inter-tidal flat area in the tidal basin, with its state variable Vf = total sediment volume between mean low water (MLW) and mean highwater (MHW) [L3];
- The channel area in the tidal basin, with its state variable Vc = total water volume below MLW [L3].
- t = time [T];
- w = vertical exchange coefficient [LT−1];
- δ = horizontal exchange coefficient [L3T−1];
- n = power in the formulation for the local equilibrium concentration [-];
- cE = overall equilibrium concentration [-];
- R = relative sea-level rise rate [LT−1].
3. Analysis and Modelling Results
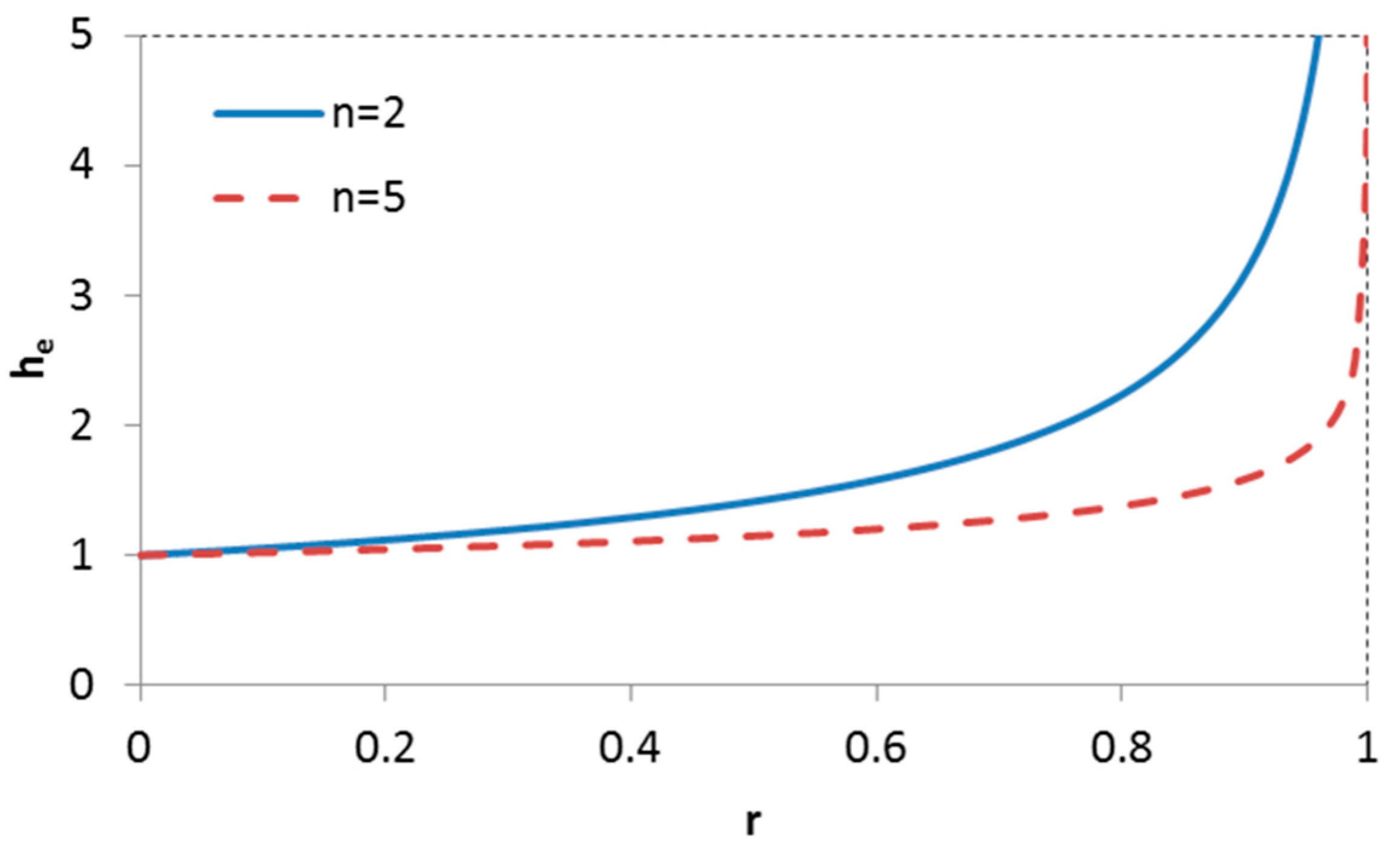
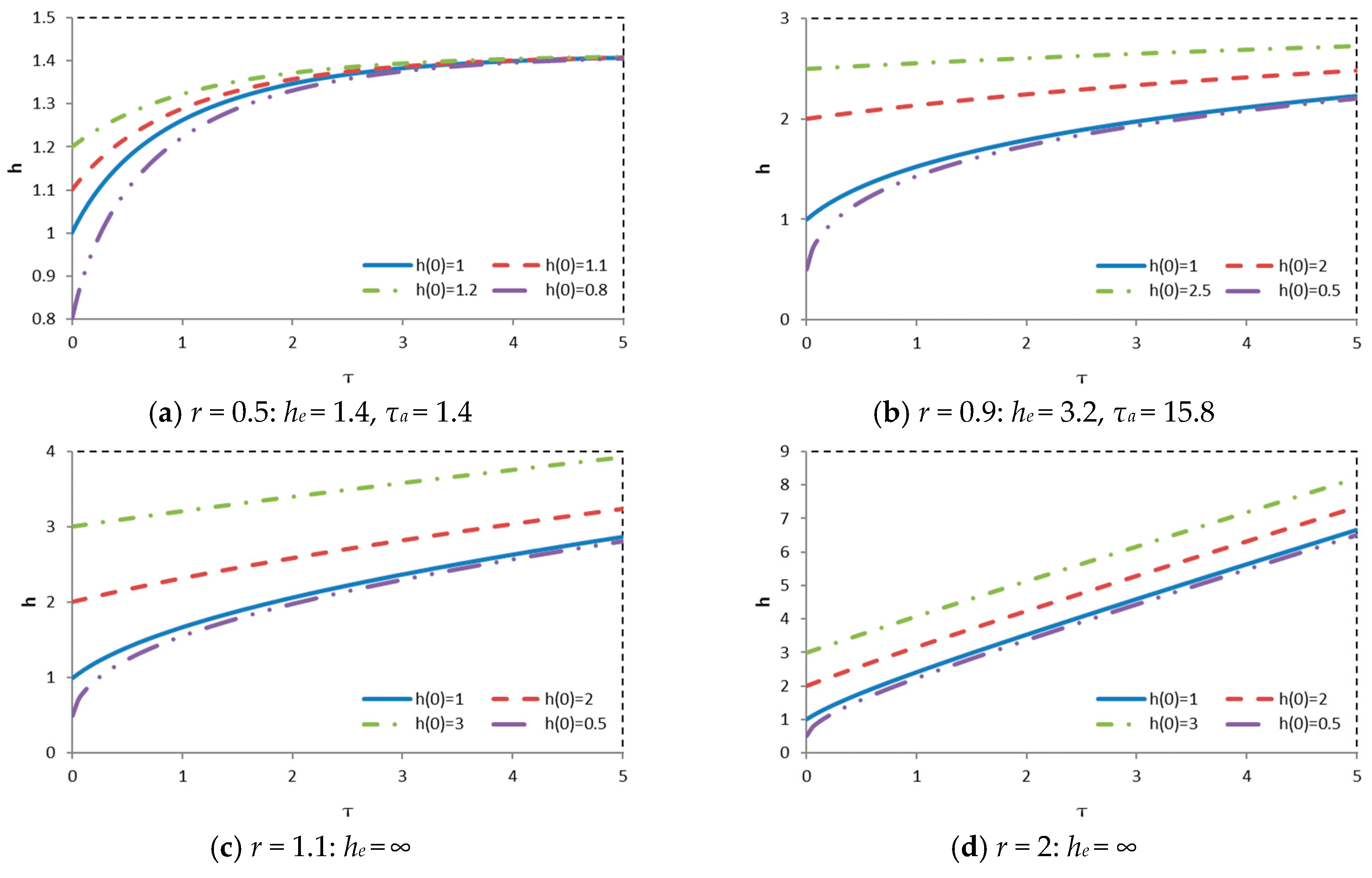
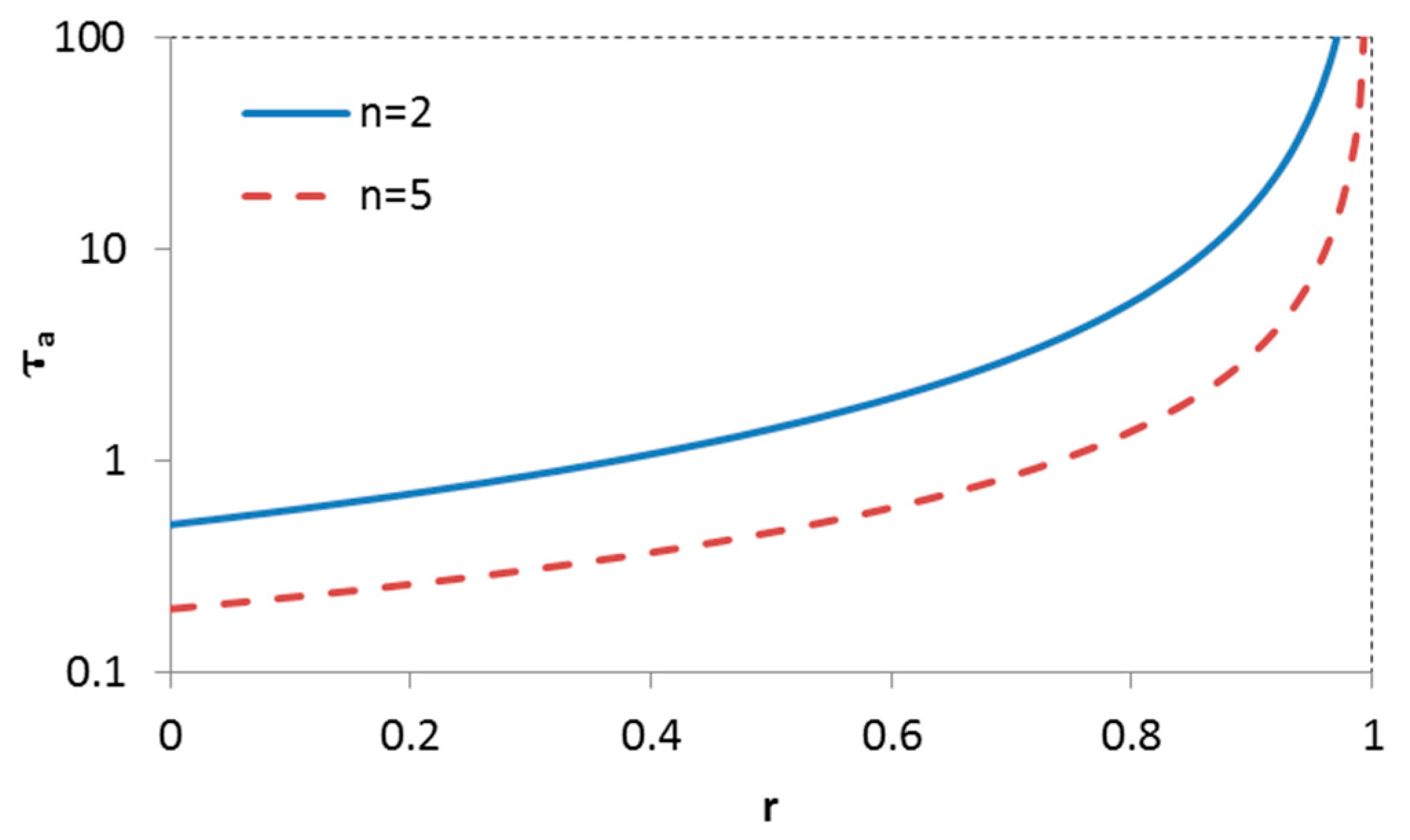
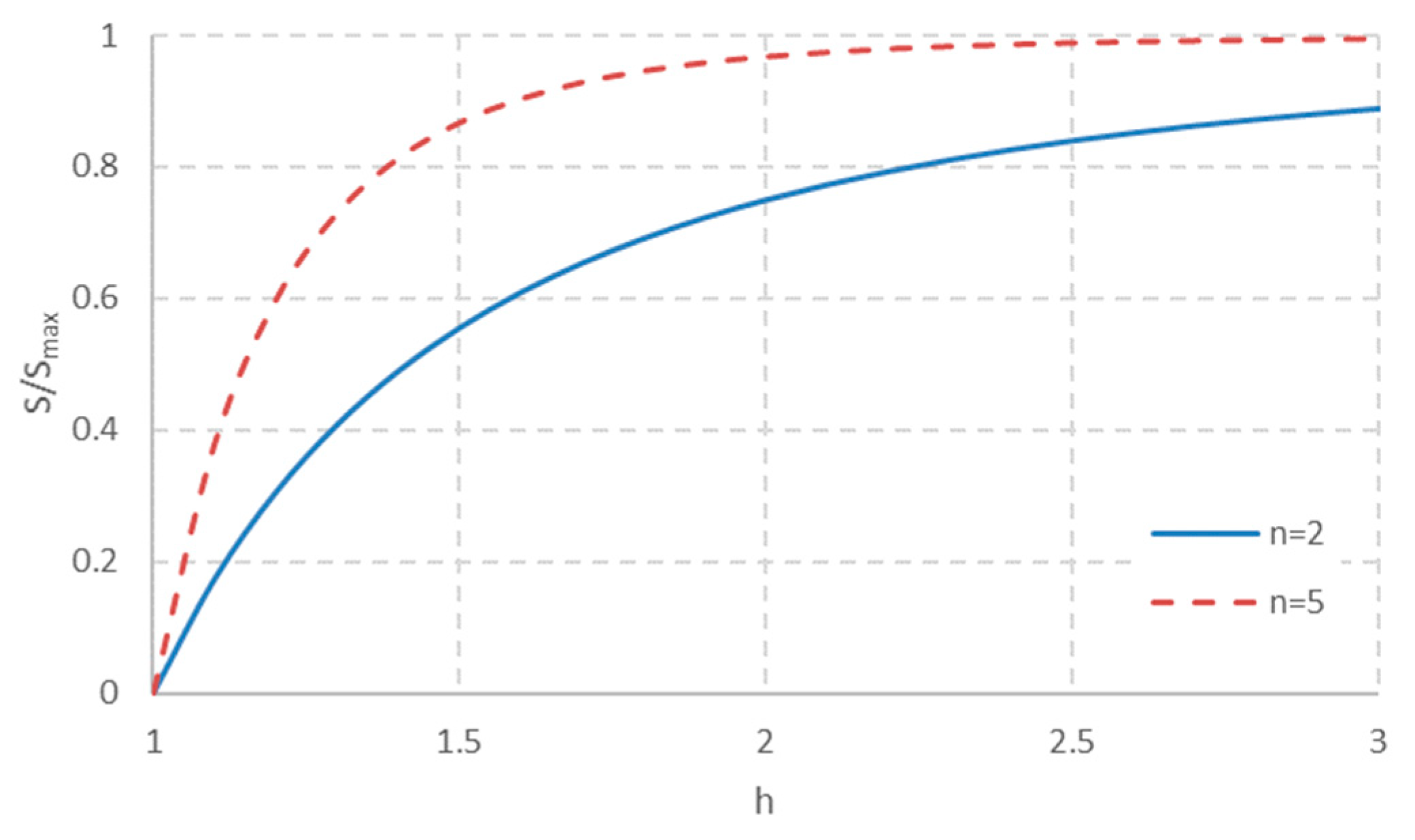
3.1. Dynamic Equilibrium and Critical SLR Rate
- Equation (15) for Rc revealed the importance of T. In this relation He is the equilibrium depth. Empirical relations [69] were available from which its value can be evaluated if the tidal amplitude a and the size of the tidal basin is known, He = F(Ab, a). Moreover, it was also connected to direct observations. For basins which are approximately in equilibrium, as, for example, when the basin has not been impacted by human interference for a long time, the equilibrium depth can be evaluated from the measured bathymetry. Note that a correction is necessary when it is in a dynamic equilibrium as it has been forced by sea-level rise with a constant rate for a long time (See Figure 4). An example within the Dutch Wadden Sea is the Ameland Inlet.
- Equation (15) can also be used for estimating the timescale T if Rc can be derived from observations. This is the case for the Texel Inlet, for example, in which a large sediment deficit arose after the closure of the Zuiderzee in 1932 [20,21]. The large sediment deficit (depth of the basin much larger than equilibrium depth, or h much larger than 1) in the basin has practically the same effect on sediment import as a ‘drowned’ system (see Figure 8), implying that the observed sedimentation rate is close to the critical sea-level rise rate.
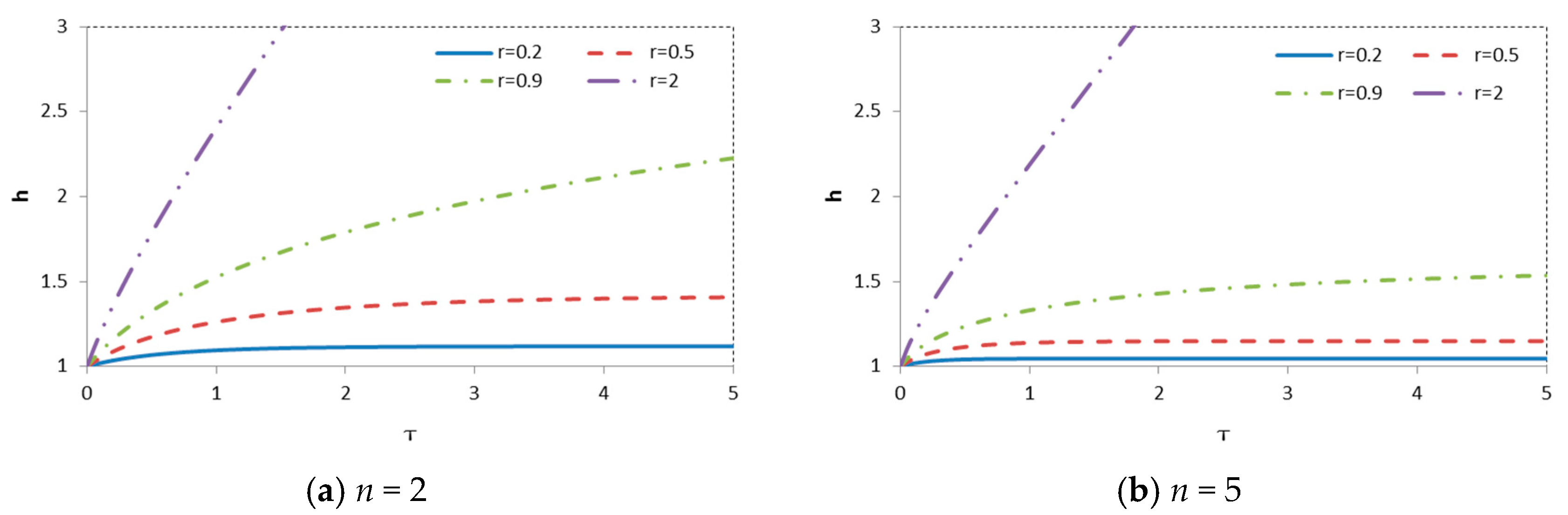
- The power n influences the morphological timescale, but not the critical sea-level rise rate. It does influence the dynamic equilibrium state.
3.2. Transient Development
3.3. Application to the Dutch Wadden Sea
4. Concluding Discussions
Author Contributions
Funding
Conflicts of Interest
References
- Duran-Matute, M.; Gerkema, T.; de Boer, G.J.; Nauw, J.J.; Gräwe, U. Residual circulation and freshwater transport in the Dutch Wadden Sea: A numerical modelling study. Ocean. Sci. 2014, 10, 611–632. [Google Scholar] [CrossRef]
- Van Prooijen, B.C.; Tissier, M.F.S.; de Wit, F.P.; Pearson, S.G.; Brakenhoff, L.B.; Van Maarseveen, M.C.G.; Van der Vegt, M.; Mol, J.W.; Kok, F.; Holzhauer, H.; et al. Measurements of Hydrodynamics, Sediment, Morphology and Benthos on Ameland Ebb-Tidal Delta and Lower Shore face. Earth Syst. Sci. Data 2019. Submitted. [Google Scholar]
- Van Weerdenburg, R.J.A. Exploring the relative importance of wind for exchange processes around a tidal inlet system: the case of Ameland Inlet. Msc. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Wang, Z.B.; Vroom, J.; Van Prooijen, B.C.; Labeur, R.J.; Stive, M.J.F. Movement of tidal watersheds in the Wadden Sea and its consequences on the morphological development. Int. J. Sediment. Res. 2013, 28, 162–171. [Google Scholar] [CrossRef]
- FitzGerald, D.M. Geomorphic variability and morphologic and sedimentologic controls on tidal inlets. J. Coast. Res. 1996, 23, 47–71. [Google Scholar]
- Van Straaten, L.M.J.U. Sedimentation in tidal flat areas. J. Alta. Soc. Pet. Geol. 1961, 9, 203–226. [Google Scholar]
- De Glopper, R.J. Over de Bodemgesteldheid Van Het Waddengebied; Van Zee tot Land 43. Tjeenk Willink: Zwolle, The Netherlands, 1984; 67p. [Google Scholar]
- Flemming, B.; Ziegler, K. High-resolution grain size distribution patterns and textural trends in the backbarrier environment of Spiekeroog Island (southern North Sea). Senckenbergiana Marit. 1995, 26, 1–24. [Google Scholar]
- Nyandwi, N. Sediment distribution patterns in the back-barrier areas of the Wadden Sea, Spiekeroog Island, Germany. In Tidalites: Processes and Products; Alexander, C., Davis, R.A., Jr., Henry, V.J., Eds.; SEPM (Society for Sedimentary Geology); Special Publication: Tulsa, OK, USA, 1998; Volume 61, pp. 15–22. [Google Scholar]
- Bartholomä, A.; Flemming, B.W. Progressive grain-size sorting along an intertidal energy gradient. Sediment. Geol. 2007, 202, 464–472. [Google Scholar] [CrossRef]
- Postma, H. Transport and accumulation of suspended matter in the Dutch Wadden Sea. Neth. J. Sea Res. 1961, 1, 148–190. [Google Scholar] [CrossRef]
- Van Straaten, L.M.J.U.; Kuenen, P.H. Accumulation of fine grained sediments in the Dutch Wadden Sea. Geologie en Mijnbouw 1957, 19, 329–354. [Google Scholar]
- Groen, P. On the residual transport of suspended matter by an alternating tidal current. Neth. J. Sea Res. 1967, 3, 564–574. [Google Scholar] [CrossRef]
- Gatto, V.M.; Van Prooijen, B.C.; Wang, Z.B. Net sediment transport in tidal basins: Quantifying the tidal barotropic mechanisms in a unified framework. Ocean. Dyn. 2017, 67, 1385–1406. [Google Scholar] [CrossRef]
- Davis, R.A.; Hayes, M.O. What is a wave-dominated coast? Mar. Geol. 1984, 60, 313–329. [Google Scholar] [CrossRef]
- Cleveringa, J.; Oost, A.P. The fractal geometry of tidal-channel systems in the Dutch Wadden Sea. Geol. en Mijnb. 1999, 78, 21–30. [Google Scholar] [CrossRef]
- Marciano, R.; Wang, Z.B.; Hibma, A.; De Vriend, H.J. Modeling of channel patterns in short tidal basins. J. Geophys. Res. 2005, 110, F01001. [Google Scholar] [CrossRef]
- Eysink, W.D. Morphological response of tidal basins to changes. In Coastal engineering 1990 Procding; Edge, B.L., Ed.; ASCE: New York, UY, USA, 1990; pp. 1948–1961. [Google Scholar]
- Van der Spek, A.J.F.; Beets, D.J. Mid-Holocene evolution of a tidal basin in the western Netherlands: A model for future changes in the northern Netherlands under conditions of accelerated sea-level rise? Sediment. Geol. 1992, 80, 185–197. [Google Scholar] [CrossRef]
- Elias, E.P.L.; Van der Spek, A.J.F.; Wang, Z.B.; De Ronde, J.G. Morphodynamic development and sediment budget of the Dutch Wadden Sea over the last century. Neth. J. Geosci. 2012, 91, 293–310. [Google Scholar] [CrossRef]
- Wang, Z.B.; Elias, E.P.L.; Van der Spek, A.J.F.; Lodder, Q.J. Sediment budget and morphological development of the Dutch Wadden Sea-impact of accelerated sea-level rise and subsidence until 2100. Neth. J. Geosci. 2018, 97, 183–214. [Google Scholar] [CrossRef]
- Nichols, M.M. Sediment accumulation rates and relative sea-level rise in lagoons. Mar. Geol. 1989, 88, 201–219. [Google Scholar] [CrossRef]
- Canon, D.R.; French, J.R.; Spencer, T.; Reed, D.; Möller, I. Vertical accretion versus elevation adjustment in UK saltmarshes: An evaluation of alternative methodologies. In Coastal and Estuarine Environments; Pye, K., Allen, J.R.L., Eds.; Geological Society Special Publications: London, UK, 2000; Volume 175, pp. 223–238. [Google Scholar]
- Morris, J.T.; Sundareshwar, P.V.; Nietch, C.T.; Kjerfve, B.; Canon, D.R. Responses of coastal wetlands to rising sea level. Ecology 2002, 83, 2869–2877. [Google Scholar] [CrossRef]
- Bartholdi, A.T.; Bartholdi, J.; Kroon, A. Salt marsh stability and patterns of sedimentation across a back-barrier platform. Mar. Geol. 2010, 278, 31–42. [Google Scholar] [CrossRef]
- Madsen, A.T.; Murray, A.S.; Andersen, T.J.; Pejrup, M. Temporal changes of accretion rates on an estuarine salt marsh during the late Holocene–reflection of local sea level changes? The Wadden Sea, Denmark. Mar. Geol. 2007, 242, 221–233. [Google Scholar] [CrossRef]
- Kentish, M.J. Coastal salt marsh systems in the U.S.: A review of anthropogenic impacts. J. Coastal Res. 2001, 17, 731–748. [Google Scholar]
- Van Wijnen, H.J.; Bakker, J.P. Long-term surface elevation change in salt marshes: A prediction of marsh response to future sea-level rise. Estuar. Coast. Shelf Sci. 2001, 52, 381–390. [Google Scholar] [CrossRef]
- Baart, F.; Rongen, G.; Hijma, M.; Kooi, H.; de Winter, R.; Nicolai, R. Zeespiegelmonitor 2018, De Stand Van Zaken Rond de Zeespiegelstijging Langs de Nederlandse Kust; Deltares en HKV rapport: Delft, The Netherlands, 2019. [Google Scholar]
- Deltacommissie, Rapport Deltacommissie. Dl. 1. Eindverslag en Interimadviezen; Staatsdrukkerij-en Uitgeverijbedrijf: Hague, The Netherlands, 1960. [Google Scholar]
- Deltacommissie. Working Together with Water, Report of Deltacommissie 2008; Deltacommissie: Hague, the Netherlands, 2008. [Google Scholar]
- Baart, F.; Van Gelder, P.H.; De Ronde, J.; Van Koningsveld, M.; Wouters, B. The effect of the 18.6-year lunar nodal cycle on regional sea-level rise estimates. J. Coast. Res. 2012, 28, 511–516. [Google Scholar] [CrossRef]
- Walton, T.D.; Adams, W.D. Capacity of inlet outer bars to store sand. In Proceedings of the Fifteenth Coastal Engineering Conference, Honlulu, HI, USA, 11–17 July 1976; American Society of Civil Engineers: Reston, VA, USA, 1976; pp. 1919–1936. [Google Scholar]
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Global climate projections. In Climate Change 2007, the Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 747–845. [Google Scholar]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S. Sea level change. In Climate Change 2013, the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 1137–1216. [Google Scholar]
- KNMI. Extreme Zeespiegelstijging in de 21e Eeuw. Koninklijk Nederlands Meteorologisch Instituut (KNMI). News Item, 6 April 2017. Available online: http://knmi.nl/ over-het-knmi/nieuws/extreme-zeespiegelstijging-in-de-21e-eeuw (accessed on 20 July 2019).
- Le Bars, D.; Drijfhout, S.; De Vries, H. A high-end sea level rise probabilistic projection including rapid Antarctic ice sheet mass loss. Environ. Res. Lett. 2017, 12, 044013. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Nicolai, M., Okem, A., Petzold, J., et al., Eds.; IPCC: Geneva, Switzerland, 2019; In Press. [Google Scholar]
- Vermeersen, L.L.A.; Slangen, A.B.A.; Gerkema, T.; Baart, F.; Cohen, K.M.; Dangendorf, S.; Duran-Matute, M.; Frederikse, T.; Grinsted, A.; Hijma, M.P.; et al. Sea level change in the Dutch Wadden Sea. Neth. J. Geosci. 2018, 97, 79–127. [Google Scholar] [CrossRef]
- De Waal, J.A.; Roest, J.P.A.; Fokker, P.A.; Kroon, I.C.; Muntendam-Bos, A.G.; Oost, A.P.; Van Wirdum, G. The effective subsidence capacity concept: How to assure that subsidence in the Wadden Sea remains within defined limits? Neth. J. Geosci./Geol. en Mijnb. 2012, 91, 385–399. [Google Scholar] [CrossRef]
- De Vriend, H.J. Mathematical modeling of meso-tidal barrier islands coasts. Part 1: Empirical and semi-empirical models. In Advances in Coastal and Ocean Engineering; Liu, P.L.F., Ed.; World Scientific Publishing Company: Singapore, 1996; pp. 115–149. [Google Scholar]
- De Vriend, H.J.; Ribberink, J.S. Mathematical modeling of meso-tidal barrier island coasts. Part II: Process-based simulation models. In Advances in Coastal and Ocean Engineering; Liu, P.L.F., Ed.; World Scientific Publishing Company: Singapore, 1996; pp. 151–197. [Google Scholar]
- Wang, Z.B.; Hoekstra, P.; Burchard, H.; Ridderinkhof, H.; De Swart, H.E.; Stive, M.J.F. Morphodynamics of the Wadden Sea and its barrier island system. Ocean. Coast. Manag. 2012, 68, 39–57. [Google Scholar] [CrossRef]
- Wang, Z.B.; Louters, T.; De Vriend, H.J. Morphodynamic modelling for a tidal inlet in the Wadden Sea. Mar. Geol. 1995, 126, 289–300. [Google Scholar] [CrossRef][Green Version]
- Lesser, G.R.; Roelvink, J.A.; Van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Elias, E.P.L. Morphodynamics of Texel Inlet. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006; p. 261. Available online: https://repository. tudelft.nl/islandora/object/uuid:92ad4ac0-9d54-4f5f-8536-80b7782a6aa6? collection=research (accessed on 3 July 2019).
- Lesser, G.R. An approach to medium-term coastal morphological modelling. Ph.D. Thesis, UNESCO-IHE, Delft, The Netherlands, 2009. [Google Scholar]
- Van der Wegen, M. Modeling Morphodynamic Evolution in Alluvial Estuaries. Ph.D. Thesis, UNESCO-IHE, Delft, The Netherlands, 2009. [Google Scholar]
- Elias, E.P.L.; Hansen, J. Understanding processes controlling sediment transports at the mouth of a highly energetic inlet system (San Francisco Bay, CA). Mar. Geol. 2012, 345, 207–220. [Google Scholar] [CrossRef]
- Hibma, A.; De Vriend, H.J.; Stive, M.J.F. Numerical modelling of shoal pattern formation in well-mixed elongated estuaries. Estuar. Coast. Shelf Sci. 2003, 57, 981–991. [Google Scholar] [CrossRef]
- Dastgheib, A.; Roelvink, J.A.; Wang, Z.B. Long-term process-based morphological modeling of the Marsdiep tidal basin. Mar. Geol. 2008, 256, 90–100. [Google Scholar] [CrossRef]
- Van der Wegen, M.; Roelvink, J.A. Long-term morphodynamic evolution of a tidal embayment using a two-dimensional, process-based model. J. Geophys. Res. 2008, 113, C03016. [Google Scholar] [CrossRef]
- Van der Wegen, M.; Wang, Z.B.; Savenije, H.H.G.; Roelvink, J.A. Long-term morphodynamic evolution and energy dissipation in a coastal plain, tidal embayment. J. Geophys. Res. 2008, 113, F03001. [Google Scholar] [CrossRef]
- Geleynse, N.; Storms, J.E.A.; Walstra, D.J.R.; Jagers, H.R.A.; Wang, Z.B.; Stive, M.J.F. Controls on river delta formation; insights from numerical modelling. Earth Planet. Sci. Lett. 2011, 302, 217–226. [Google Scholar] [CrossRef]
- Van Maanen, B.; Coco, G.; Bryan, K.R.; Friedrichs, C.T. Modeling the morphodynamic response of tidal embayments to sea-level rise. Ocean. Dyn. 2013, 63, 1249. [Google Scholar] [CrossRef]
- Gao, W.; Shao, D.; Wang, Z.B.; Nardin, W.; Yang, W.; Sun, T.; Cui, B. Combined effects of unsteady river discharges and wave conditions on river mouth bar morphodynamics. Geophys. Res. Lett. 2018, 45, 903–911. [Google Scholar] [CrossRef]
- Gao, W.; Shao, D.; Wang, Z.B.; Nardin, W.; Rajput, P.; Yang, W.; Sun, T.; Cui, B. Long-term cumulative effects of intra-annual variability of unsteady river discharge on the progradation of delta lobes: A modeling perspective. J. Geophys. Res. Earth Surf. 2019, 124, 960–973. [Google Scholar] [CrossRef]
- Tao, J.; Wang, Z.B.; Zhou, Z.; Xu, F.; Zhang, C.; Stive, M.J.F. A morphodynamic modeling study on the formation of the large-scale radial sand ridges in the Southern Yellow Sea. J. Geophys. Res. Earth Surf. 2019, 124, 1742–1761. [Google Scholar] [CrossRef]
- Van der Wegen, M. Numerical modeling of the impact of sea level rise on tidal basin morphodynamics. J. Geophys. Res. Earth Surf. 2013, 118, 447–460. [Google Scholar] [CrossRef]
- Elias, E.P.L.; Teske, R.; Van der Spek, A.; Lazar, M. Modeling tidal inlet morphodynamics on medium timescales. In The Proceedings of the Coastal Sediments 2015; Wang, P., Rosati, J.D., Cheng, J., Eds.; CD-ROM: San Diego, CA, USA, 2015; p. 14. [Google Scholar]
- Wang, Y.; Yu, Q.; Jiao, J.; Tonnon, P.K.; Wang, Z.B.; Gao, S. Coupling bedform roughness and sediment grain-size sorting in modelling of tidal inlet incision. Mar. Geol. 2016, 381, 128–141. [Google Scholar] [CrossRef]
- Dissanayake, D.M.P.K.; Ranasinghe, R.; Roelvink, J.A. The morphological response of large tidal inlet / basin systems to relative sea level rise. Clim. Chang. 2012, 113, 253–276. [Google Scholar] [CrossRef]
- Wang, Z.; Van der Spek, A. Importance of mud for morphological response of tidal basins to sea level rise. In The Proceedings of the Coastal Sediments 2015; Wang, P., Rosati, J.D., Cheng, J., Eds.; CD-ROM: San Diego, CA, USA, 2015; p. 10. [Google Scholar]
- Hofstede, J.L.A.; Becherer, J.; Burchard, H. Are Wadden Sea tidal systems with a higher tidal range more resilient against sea level rise? J. Coast. Conserv. 2018, 22, 71–78. [Google Scholar] [CrossRef]
- Becherer, J.; Hofstede, J.; Gräwe, U.; Purkiani, K.; Schulz, E.; Burchard, H. The Wadden Sea in transition–consequences of sea level rise. Ocean Dyn. 2018, 68, 131–151. [Google Scholar] [CrossRef]
- De Swart, H.E.; Zimmerman, J.T.F. Morphodynamics of tidal inlet systems. Ann. Rev. Fluid Mech. 2009, 41, 203–229. [Google Scholar] [CrossRef]
- Stive, M.J.F.; Capobianco, M.; Wang, Z.B.; Ruol, P.; Buijsman, M.C. Morphodynamics of a tidal lagoon and adjacent coast. In Physics of Estuaries and Coastal Seas, Proceedings of the 8th International Biennial Conference on Physics of Estuaries and Coastal Seas, the Hague, Netherlands, 9–12 September 1996; Dronkers, J., Scheffers, M.B.a.M., Eds.; CRC Press/ Balkema: Boca Raton, FL, USA, 1998; pp. 397–407. [Google Scholar]
- Stive, M.J.F.; Wang, Z.B. Morphodynamic modelling of tidal basins and coastal inlets. In Advances in Coastal Modelling; Lakkhan, C., Ed.; Elsevier Sciences: Amsterdam, The Netherlands, 2003; pp. 36–392. [Google Scholar]
- Townend, I.H.; Wang, Z.B.; Stive, M.J.F.; Zhou, Z. Development and extension of an aggregated scale model: Part 1 Background to ASMITA. China Ocean. Eng. 2016, 30, 483–504. [Google Scholar] [CrossRef]
- Townend, I.H.; Wang, Z.B.; Stive, M.J.F.; Zhou, Z. Development and extension of an aggregated scale model: Part 2 Extensions to ASMITA. China Ocean. Eng. 2016, 30, 651–670. [Google Scholar] [CrossRef]
- Van Goor, M.A.; Zitman, T.J.; Wang, Z.B.; Stive MJ, F. Impact of sea-level rise on the morphological equilibrium state of tidal inlets. Mar. Geol. 2003, 202, 211–227. [Google Scholar] [CrossRef]
- Wang, Z.B.; De Vriend, H.J.; Stive MJ, F.; Townend, I.H. On the parameter setting of semi-empirical long-term morphological models for estuaries and tidal lagoons. In River, Coastal and Estuarine Morphodynamics; Dohmen-Janssen, C.M., Hulscher SJ, M.H., Eds.; Taylor & Francis: Didcot, UK; London, UK; Abingdon, UK, 2008; pp. 103–111. [Google Scholar]
- Kragtwijk, N.G.; Stive MJ, F.; Wang, Z.B.; Zitman, T.J. Morphological response of tidal basins to human interventions. Coast. Eng. 2004, 51, 207–221. [Google Scholar] [CrossRef]
- Townend, I.H.; Wang, Z.B.; Rees, J.G. Millennial to annual volume changes in the Humber estuary. Proc. R. Soc. A 2007, 463, 837–854. [Google Scholar] [CrossRef]
- Wang, Z.B.; Townend, I.H. Influence of the nodal tide on the morphological response of estuaries. Mar. Geol. 2012, 291, 73–82. [Google Scholar] [CrossRef]
- de Vet, P.L.M.; van Prooijen, B.C.; Colosimo, I.; Steiner, N.; Ysebaert, T.; Herman, P.M.J.; Wang, Z.B. The Inhomogeneous Impact of Storm Events on Intertidal flat Eco-Morphodynamics. Sci. Rep. 2019. Submitted. [Google Scholar]
- Van der Wegen, M.; Jaffe, B.; Foxgrover, A.; Roelvink, D. Mudflat morphodynamics and the impact of sea level rise in South San Francisco Bay. Estuaries Coasts 2016, 40, 37–49. [Google Scholar] [CrossRef]
- Elmilady, H.; van der Wegen, M.; Roelvink, D.; Jaffe, B.E. Intertidal area disappears under sea level rise: 250 years of morphodynamic modeling in San Pablo Bay, California. J. Geophys. Res. Earth Surf. 2019, 124, 38–59. [Google Scholar] [CrossRef]
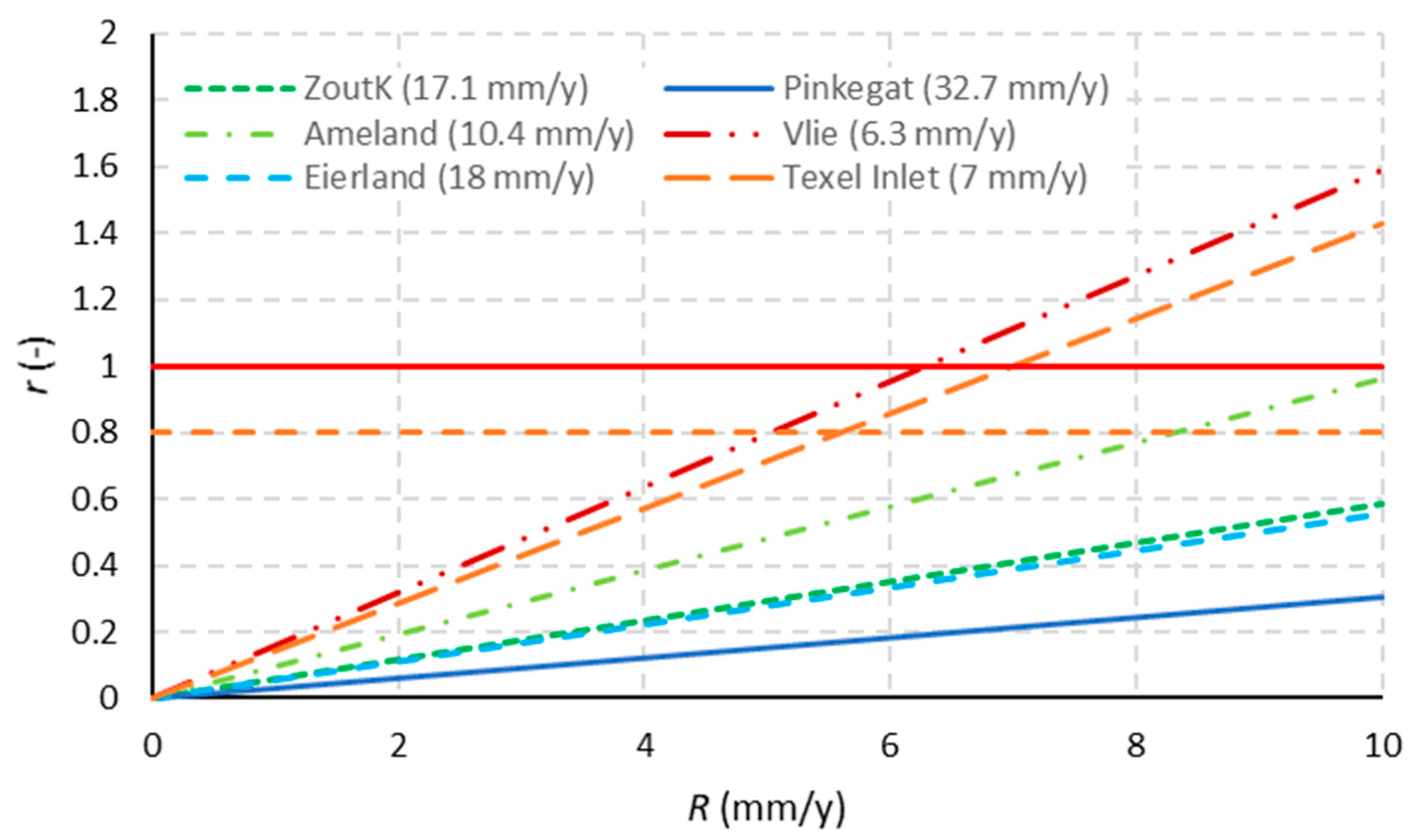
| Inlet | Ab (km2) | H (m) | He (m) | Rc (mm/y) | T (Year) | r for SLR Rate = | |||
|---|---|---|---|---|---|---|---|---|---|
| 2 mm/y | 4 mm/y | 6 mm/y | 8 mm/y | ||||||
| Texel | 655 | 1.65 | 2.8 | 7.00 | 400 | 0.29 | 0.57 | 0.86 | 1.14 |
| ELGT | 157.7 | 1.65 | 1.7 | 18.0 | 90 | 0.11 | 0.22 | 0.33 | 0.44 |
| Vlie | 715 | 1.9 | 3.5 | 6.30 | 560 | 0.32 | 0.63 | 0.95 | 1.27 |
| Amel | 276.3 | 2.15 | 2.7 | 10.4 | 260 | 0.19 | 0.38 | 0.58 | 0.77 |
| PinkeG | 49.6 | 2.15 | 1.7 | 32.7 | 55 | 0.06 | 0.12 | 0.18 | 0.24 |
| ZoutK | 105 | 2.25 | 2.1 | 17.1 | 125 | 0.12 | 0.23 | 0.35 | 0.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lodder, Q.J.; Wang, Z.B.; Elias, E.P.L.; van der Spek, A.J.F.; de Looff, H.; Townend, I.H. Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise—An Aggregated Modelling Approach. Water 2019, 11, 2198. https://doi.org/10.3390/w11102198
Lodder QJ, Wang ZB, Elias EPL, van der Spek AJF, de Looff H, Townend IH. Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise—An Aggregated Modelling Approach. Water. 2019; 11(10):2198. https://doi.org/10.3390/w11102198
Chicago/Turabian StyleLodder, Quirijn J., Zheng B. Wang, Edwin P.L. Elias, Ad J.F. van der Spek, Harry de Looff, and Ian H. Townend. 2019. "Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise—An Aggregated Modelling Approach" Water 11, no. 10: 2198. https://doi.org/10.3390/w11102198
APA StyleLodder, Q. J., Wang, Z. B., Elias, E. P. L., van der Spek, A. J. F., de Looff, H., & Townend, I. H. (2019). Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise—An Aggregated Modelling Approach. Water, 11(10), 2198. https://doi.org/10.3390/w11102198






