2D Numerical Modeling on the Transformation Mechanism of the Braided Channel
Abstract
1. Introduction
2. Numerical Model
2.1. Model Description
2.2. Consideration of the Riparian Vegetation Influence
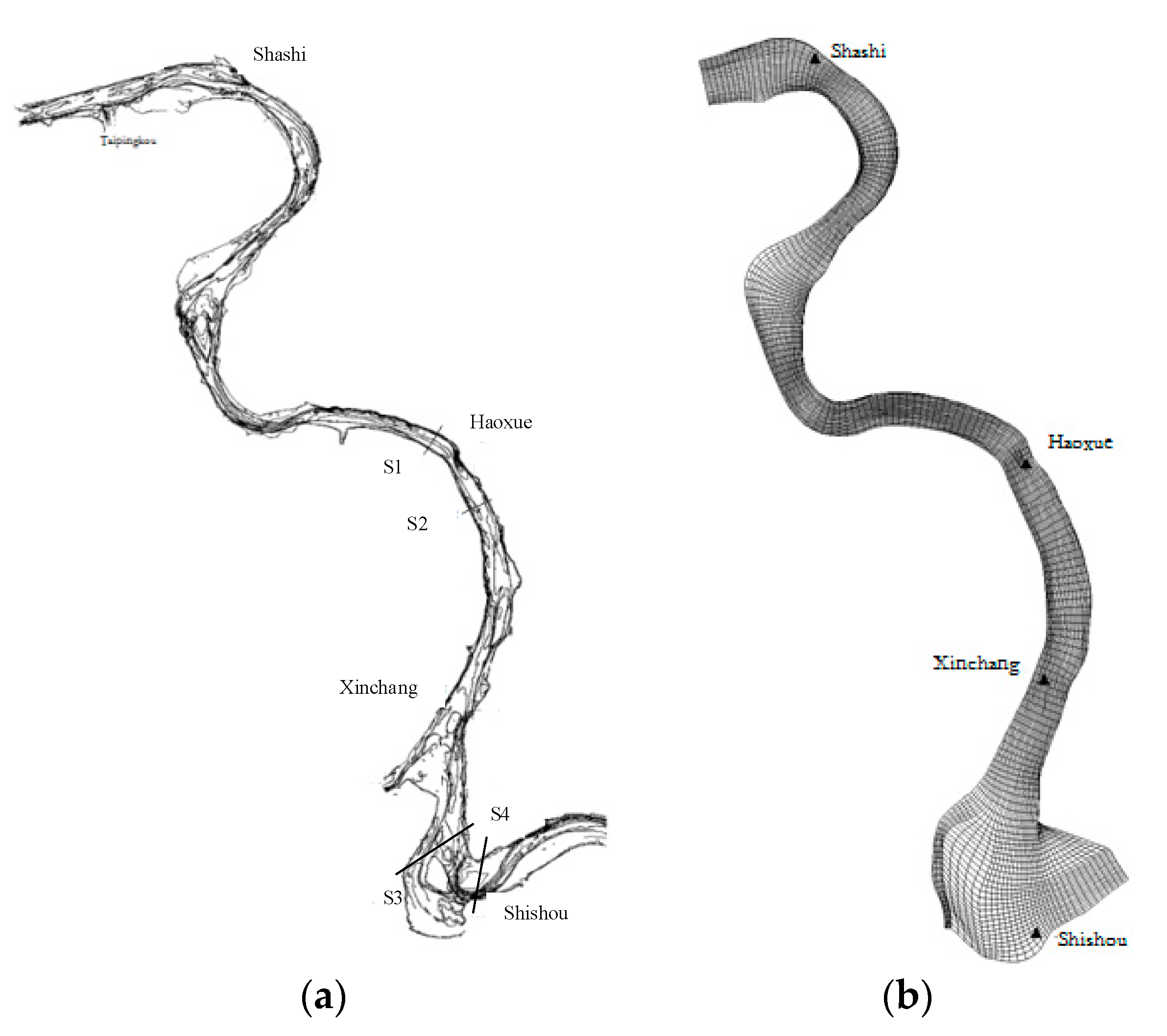
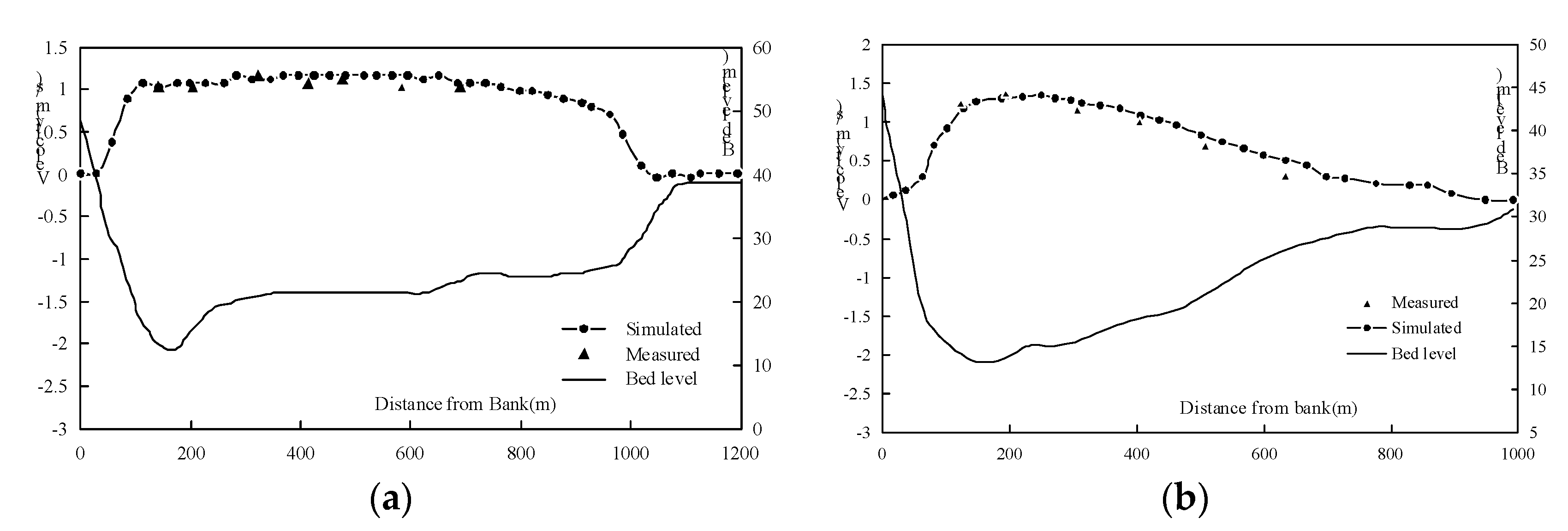
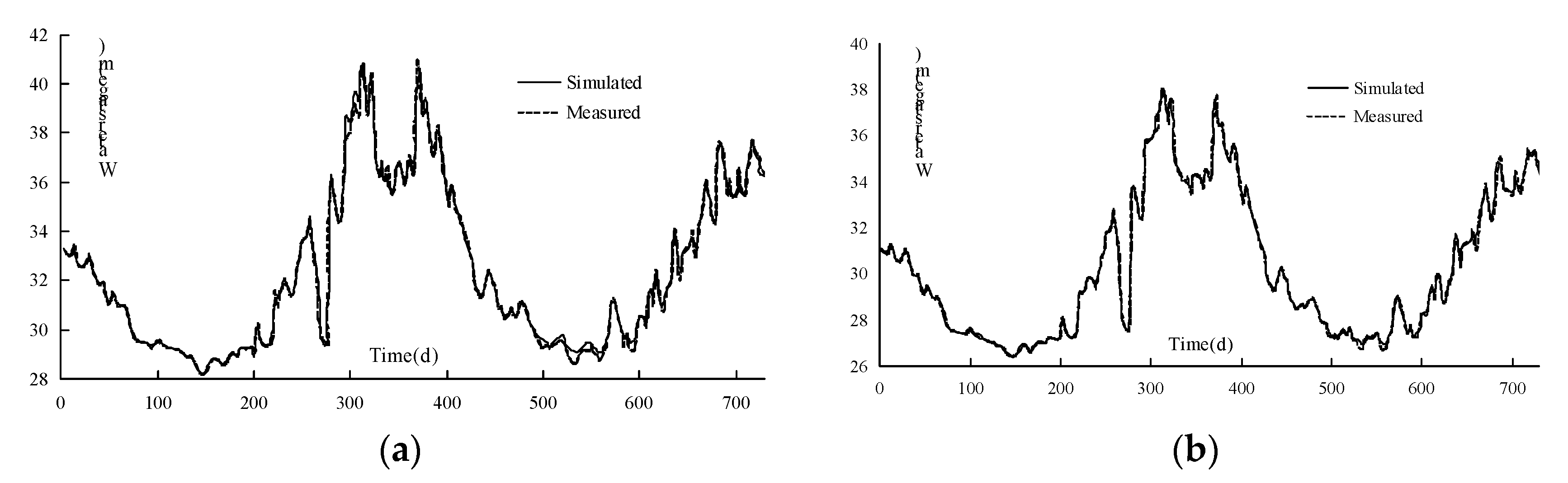
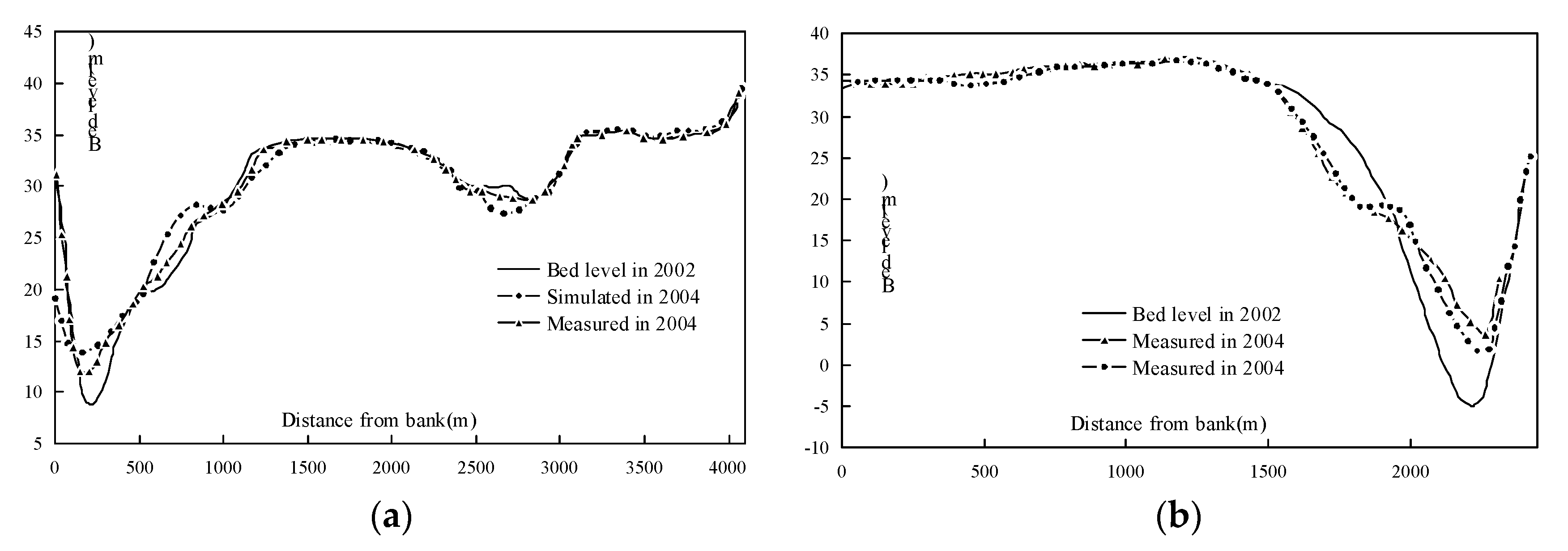
2.3. Verification
3. Numerical Modeling on the Transformation of Braided and Meandering Channel
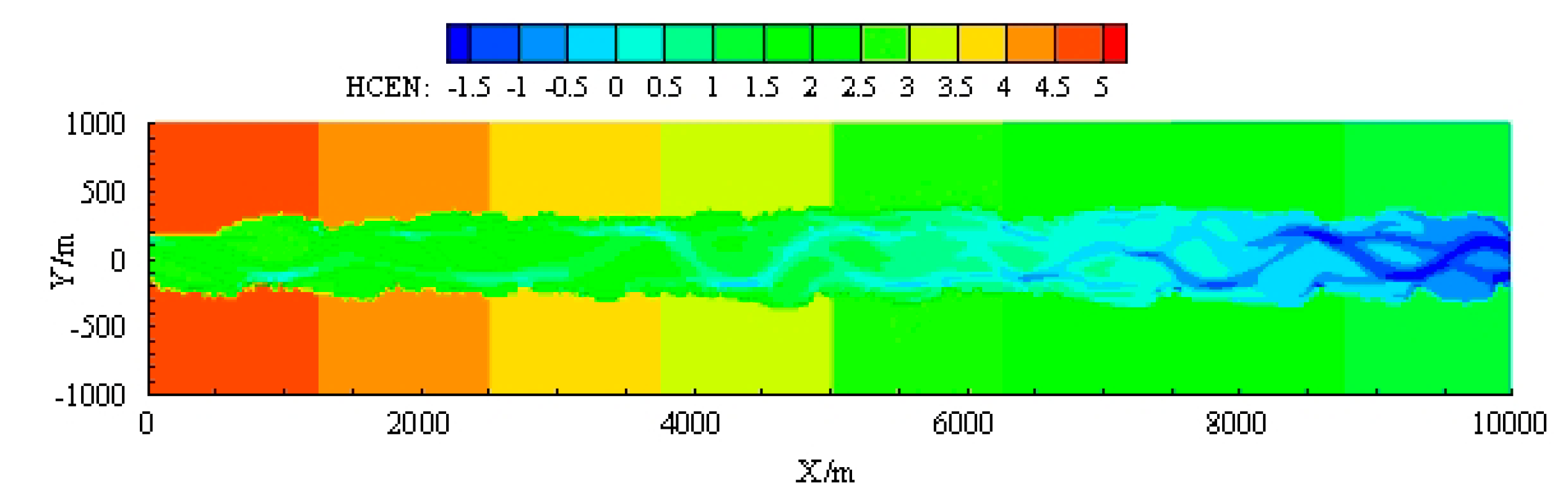
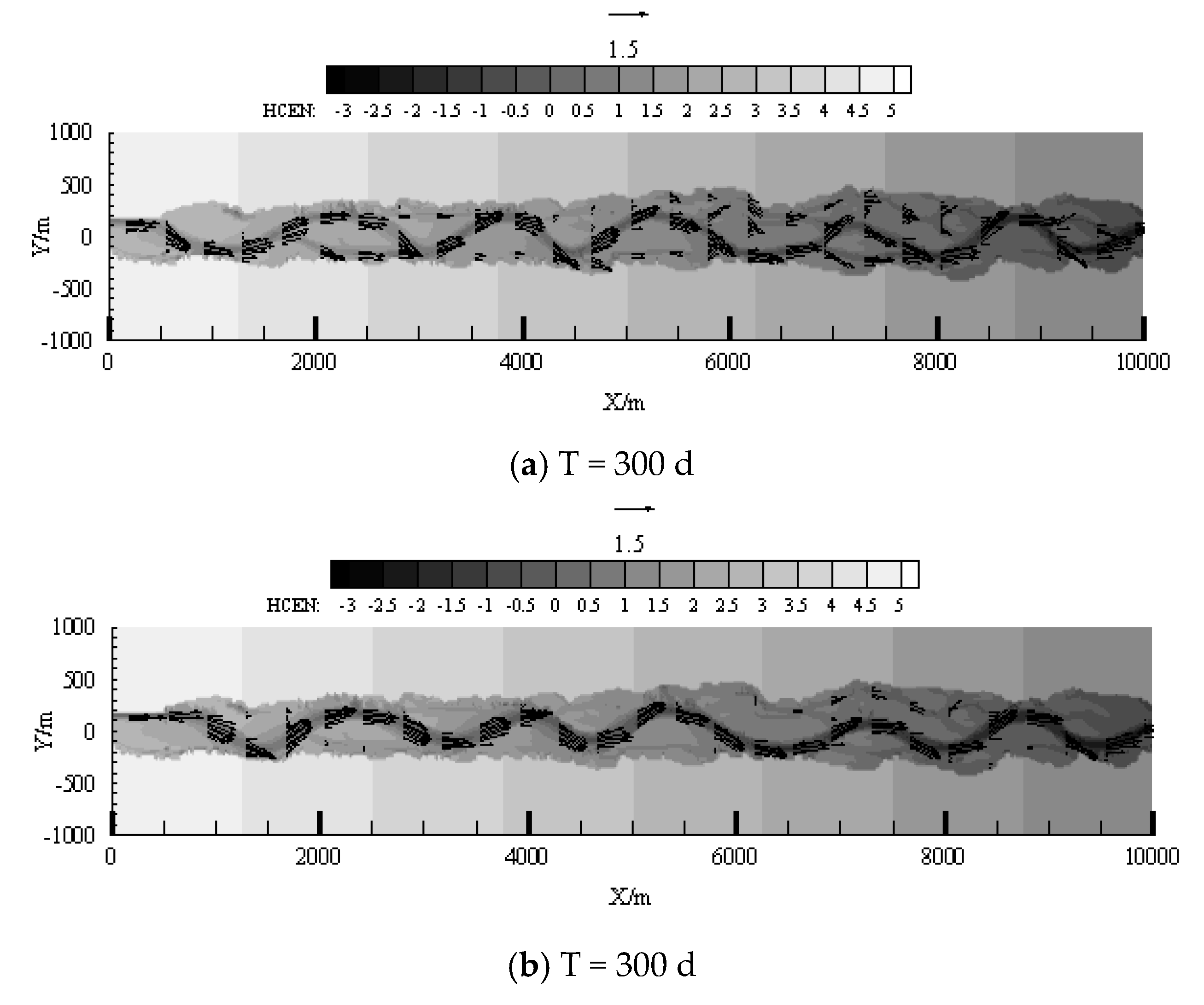
3.1. Formation of the Braided Channel
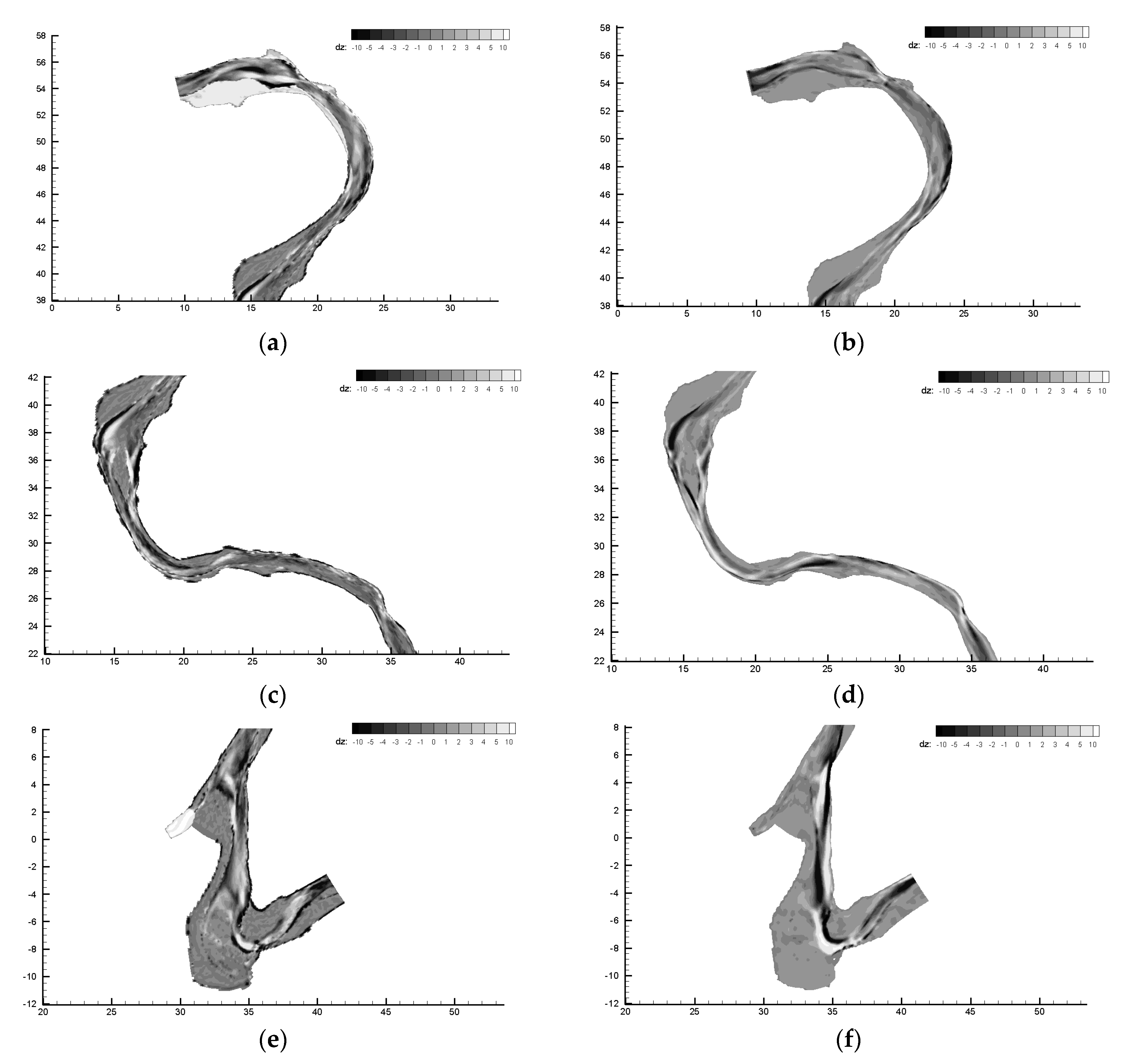
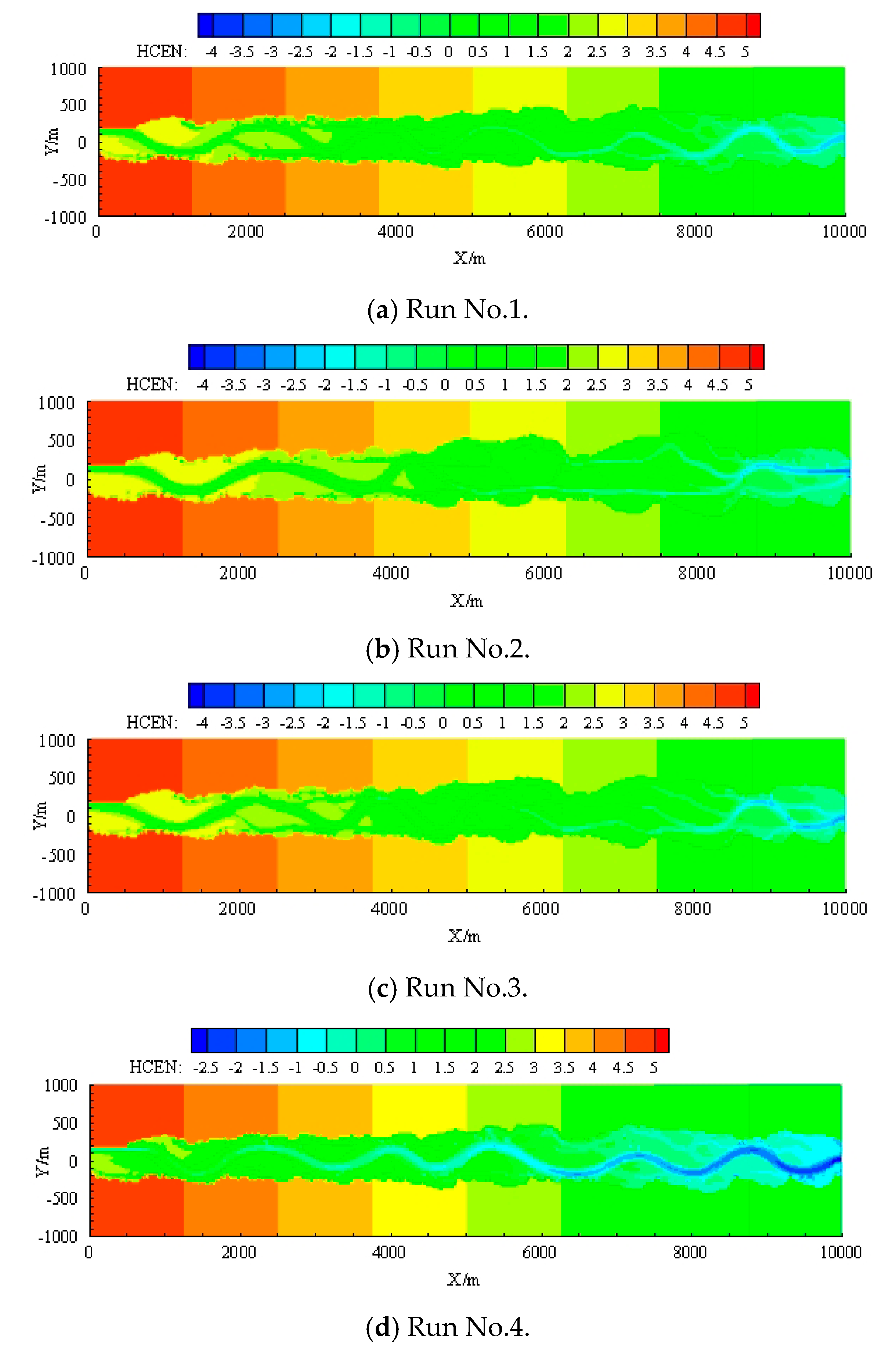
3.2. The Transformation of the Braided Channel under Control Variables
4. Discussion
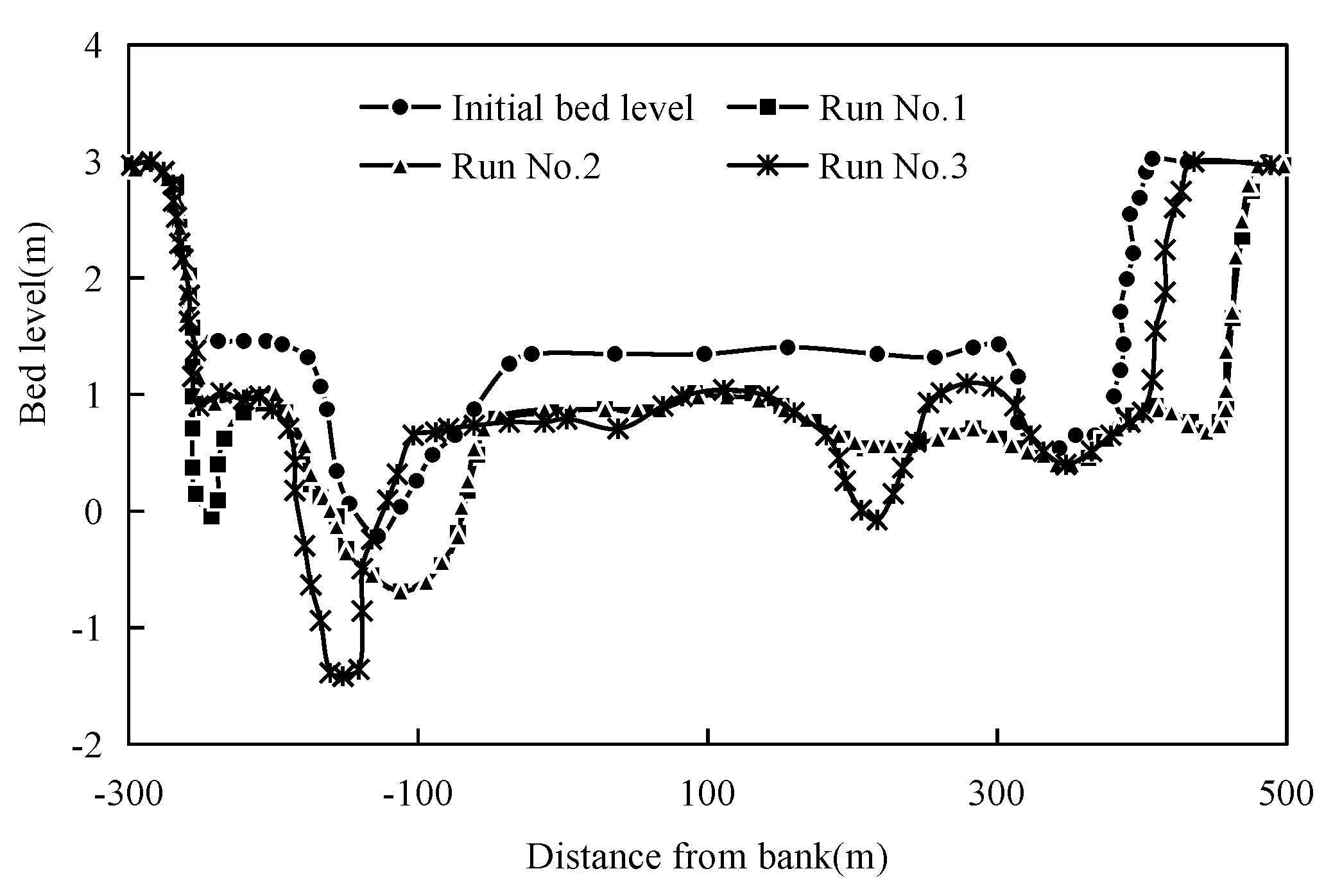
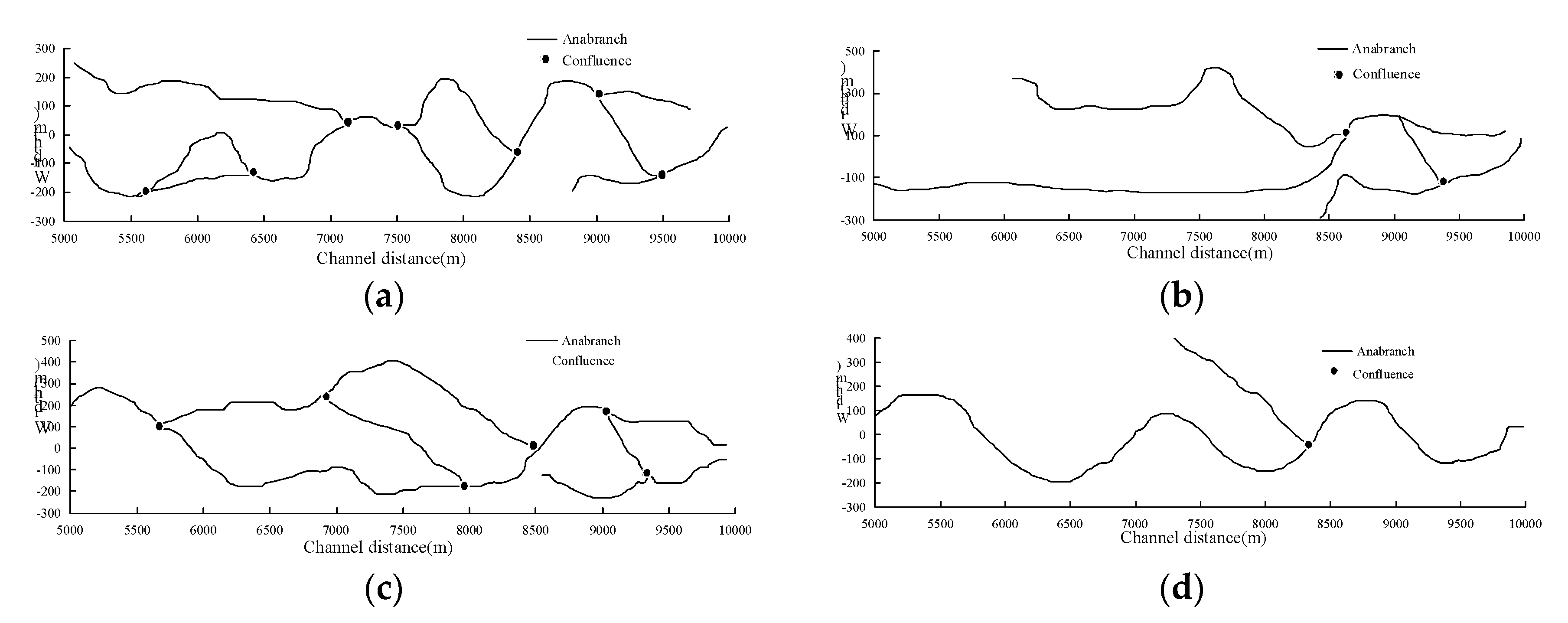
4.1. The Cross Section Change
4.2. The Channel Planform Change
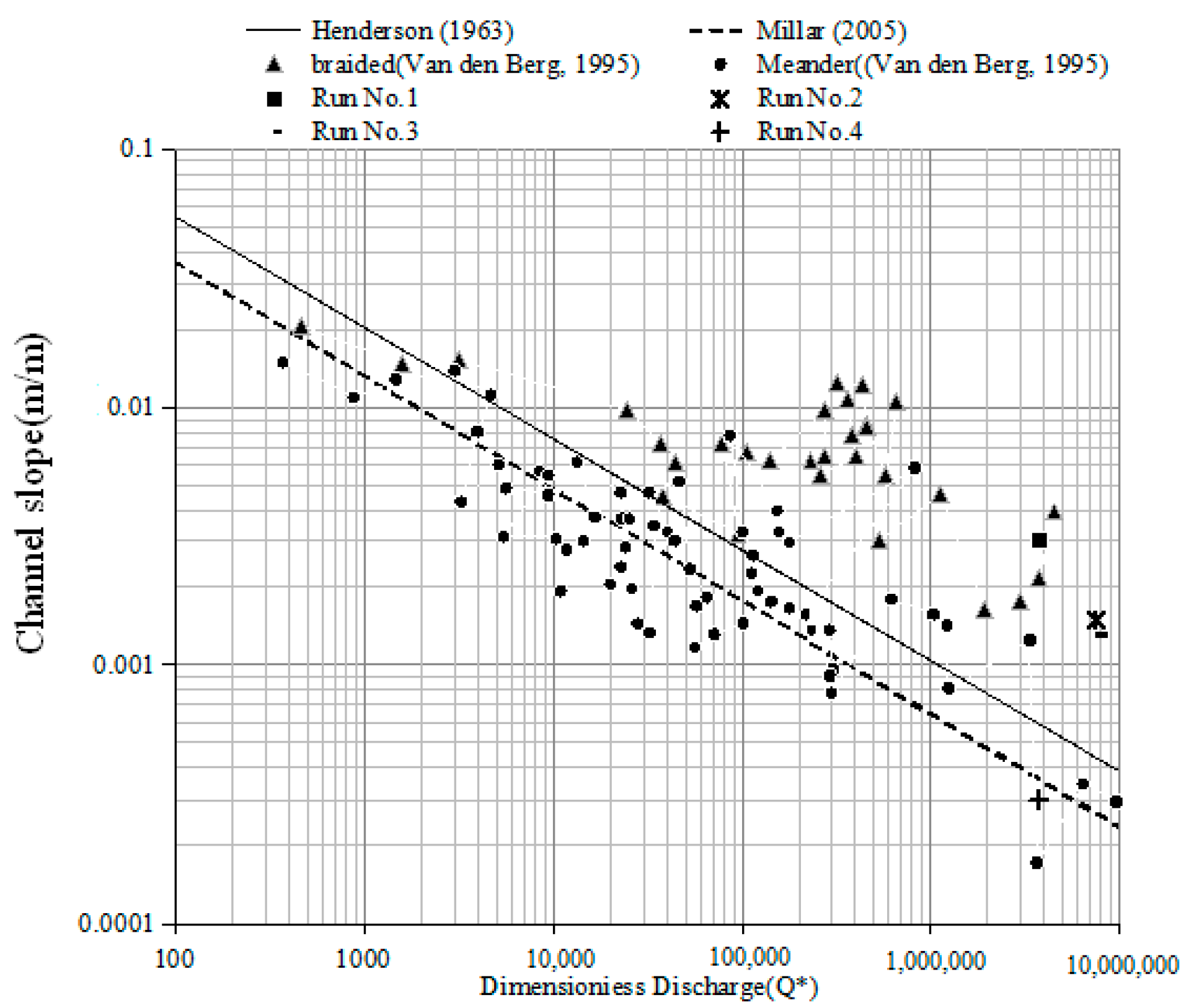
4.3. Comparison with the Empirical Dimensionless Braiding Criterion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| The shear-stress tensor | |
| The total shear stress near the river bank | |
| S | The slope of the water surface |
| u, v | The time-averaged flow velocity components in the Cartesian coordinate system |
| a | The vegetation density |
| lx, ly | The distance of vegetation in the longitudinal and transverse direction |
| ξ, η | The orthogonal curvilinear coordinates |
| h1, h2 | The Lamé coefficients |
| J | The Jacobian of the transformation J = h1h2 |
| Z | The water level relative to the reference plane |
| H | The averaged water depth |
| U, V | The depth-averaged velocity components in the ξ and η directions |
| β | The correction factor for the non-uniformity of the vertical velocity |
| f | The Coriolis parameter |
| g | The gravitational acceleration |
| C | The Chezy coefficient |
| The depth mean effective vortex viscosity | |
| D11, D12, D21, D22 | The depth-averaged dispersion stress terms |
| zs, zb | The dependent water levels for the water surface and channel bed |
| The inclination of the location | |
| The vegetation stress term | |
| k | von Karman constant |
| Δt | The time increment |
| B | The “braided-channel ratio” |
| Lctot | The sum of the mid-channel lengths of all the segments of primary channels in a reach |
| Lcmax | The mid-channel length of the same channel |
| S* | The meandering-braiding threshold slope |
| Q | The bankfull discharge |
| Q* | The dimensionless discharge |
| D50 | The median grain size |
References
- Richardson, W.R.; Thorne, C.R. Multiple thread flow and channel bifurcation in a braided river: Brahmaputra-jamuna river, Bangladesh. Geomorphology 2001, 38, 185–196. [Google Scholar] [CrossRef]
- Biedenharn, D.S.; Watson, C.C.; Thorne, C.R. Fundaments of fluvial geomorphology. In Sediment Engineering: Processes, Measurements. Modelling and Practice; Garcia, M.H., Ed.; ASCE: New York, NY, USA, 2008; pp. 355–386. [Google Scholar]
- Nicholas, A.P. Modelling bedload yield in braided gravel bed rivers. Geomorphology 2000, 36, 89–106. [Google Scholar] [CrossRef]
- Leopold Luna, B.; Wolman, M. Gordon. River Channel Patterns: Braided, Meandering and Straight; U.S. Government Printing Office: Washington, DC, USA, 1957.
- Acker, P.T.; Charlton, F.G. The geometry of small meandering streams. Proc. Inst. Civil Eng. 1971, 172, 289–317. [Google Scholar]
- Schumm, S.A.; Khan, H.R. Experimental study of channel patterns. Geol. Soc. Am. Bull. 1972, 83, 1755–1770. [Google Scholar] [CrossRef]
- Ikeda, H. A study of the formation of sand bars in an experimental flume. Geogr. Rev. Jpn. 1973, 46, 435–452. [Google Scholar] [CrossRef]
- Ikeda, H. On the bed configuration in alluvial channels; their types and condition of formation with reference to bars. Geogr. Rev. Jpn. 1975, 48, 712–730. [Google Scholar] [CrossRef]
- Ashmore, P.E. Laboratory modeling of gravel braided stream morphology. Earth Surf. Process. Landf. 1982, 7, 201–225. [Google Scholar] [CrossRef]
- Ashmore, P.E. How do gravel-bed rivers braid? Can. J. Earth Sci. 1991, 28, 326–341. [Google Scholar] [CrossRef]
- Gill, M.K. Erosion of sand beds around spur dikes. J. Hydraul. Div. 1972, 98, 1587–1602. [Google Scholar]
- Klingeman, P.C.; Kehe, S.M.; Owusu, Y.A. Steambank Erosion Protection and Channel Scour Manipulation Using Rockfill Dikes and Gabions; Technical Report; Water Resources Research Institute: Corvallis, OR, USA, 1984. [Google Scholar]
- Kuhnle, R.A.; Alonso, C.; Shields, F.D. Geometry of scour holes associated with 90 spur dikes. J. Hydraul. Eng. 1999, 125, 972–978. [Google Scholar] [CrossRef]
- Eaton, B.C.; Millar, R.G.; Davidson, S. Channel patterns: Braided, anabranching, and single-thread. Geomorphology 2010, 120, 353–364. [Google Scholar] [CrossRef]
- Van den Berg, J.H. Prediction of alluvial channel pattern of perennial rivers. Geomorphology 1995, 12, 259–279. [Google Scholar] [CrossRef]
- Alabyan, A.M.; Chalov, R.S. Types of river channel patterns and their natural controls. Earth Surf. Process. Landf. 1998, 23, 467–474. [Google Scholar] [CrossRef]
- Beechie, T.J.; Liermann, M.; Pollock, M.M.; Baker, S.; Davies, J. Channel pattern and river-floodplain dynamics in forested mountain river systems. Geomorphology 2006, 78, 124–141. [Google Scholar] [CrossRef]
- Ikeda, S.; Parker, G.; Sawai, K. Bend theory of river meanders, 1, Linear development. J. Fluid Mech. 1981, 112, 363–377. [Google Scholar] [CrossRef]
- Johannesson, H.; Parker, G. Linear theory of river meanders. Water Resour. Monogr. 1989, 12, 181–213. [Google Scholar]
- Zolezzi, G.; Seminara, G. Downstream and upstream influence in river meandering. Part1: General theory and application to overdeepening. J. Fluid Mech. 2001, 438, 183–211. [Google Scholar] [CrossRef]
- Crosato, A. Analysis and Modelling of River Meandering. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2008. [Google Scholar]
- Osman, A.M.; Thorne, C.R. Riverbank stability analysis, I: Theory. J. Hydraul. Eng. 1988, 114, 134–150. [Google Scholar] [CrossRef]
- Mosselman, E. Morphological modeling of rivers with erodible banks. Hydrol. Process. 1998, 12, 1357–1370. [Google Scholar] [CrossRef]
- Darby, S.E.; Alabyan, A.M.; Van de Wiel, M.J. Numerical simulation of bank erosion and channel migration in meandering rivers. Water Resour. Res. 2002, 38, 1–21. [Google Scholar] [CrossRef]
- Duan, J.G.; Julien, P.Y. Numerical simulation of meandering evolution. J. Hydrol. 2010, 391, 34–46. [Google Scholar] [CrossRef]
- Murray, A.B.; Paola, C. A cellular model of braided rivers. Nature 1994, 371, 54–57. [Google Scholar] [CrossRef]
- Murray, A.B.; Paola, C. Modelling the effect of vegetation on channel pattern in bedload rivers. Earth Surf. Proc. Land 2003, 2, 131–143. [Google Scholar] [CrossRef]
- Paola, C. Modelling stream braiding over a range of scales. In Gravel Bed Rivers; Mosley, M.P., Ed.; New Zealand Hydrological Society: Wellington, New Zealand, 2001; pp. 111–146. [Google Scholar]
- Thormas, R.; Nicholas, A.P. Simulation of braided river flow using a new cellular routing scheme. Geomorphology 2002, 43, 179–196. [Google Scholar] [CrossRef]
- Takebayashi, H.; Okabe, T. Numerical modeling of braided streams in unsteady flow. Water Manag. 2009, 162, 189–198. [Google Scholar]
- Bridge, J.S.; Lunt, I.A. Depositional models of braided rivers. In Braided Rivers: Process, Deposits, Ecology and Management; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Jang, C.L.; Shimizu, Y. Numerical analysis of braided rivers and alluvial fan deltas. Eng. Appl. Comput. Fluid Mech. 2009, 1, 390–395. [Google Scholar] [CrossRef][Green Version]
- Schuurman, F.; Kleinhans, M. Self-formed braided bar pattern in a numerical model. In River, Coastal and Estuarine Morphodynamics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lotsari, E.; Wainwright, D.; Corner, G.D.; Alho, P.; Kayhko, J. Surveyed and modeled one-year morphodynamics in the braided lower Tana River. Hydrol. Process. 2014, 28, 2685–2716. [Google Scholar] [CrossRef]
- Karmaker, T.; Dutta, S. Prediction of short-term morphological change in large braided river using 2D numerical model. J. Hydraul. Eng. 2016, 142, 04016039. [Google Scholar] [CrossRef]
- Crosato, A.; Mosselman, E. Simple physics-based predictor for the number of river bars and the transition between meandering and braiding. Water Resour. Res. 2009, 44, W03424. [Google Scholar] [CrossRef]
- Xiao, Y.; Shao, X.J.; Wang, H.; Zhou, H. Formation process of meandering channel by a 2D numerical simulation. Int. J. Sediment. Res. 2012, 3, 306–322. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, S.F.; Su, L. Fluvial sedimentation of the permanent backwater zone in the Three Gorges Reservoir, China. Lake Reserv. Manag. 2015, 31, 324–338. [Google Scholar] [CrossRef]
- Ikeda, S.; Izumi, N. Width and depth of self-formed straight gravel rivers with bank vegetation. Water Resour. Res. 1990, 26, 2353–2364. [Google Scholar] [CrossRef]
- CWRC. Hydrological data of Changjiang River Basin. Annual Hydrological Report of P. R. China; Changjiang Water Resources Commission: Beijing, China, 2004. [Google Scholar]
- Bridge, J.S. The Interaction between Channel Geometry, Water Flow, Sediment Transport and Deposition in Braided Rivers; Geological Society, Special Publications: London, UK, 1993; Volume V75, pp. 13–71. [Google Scholar]
- Friend, P.F.; Sinha, R. Braiding and meandering parameters. In Braided Rivers; Best, J.L., Bristow, C.S., Eds.; The Geological Society: London, UK, 1993; pp. 105–112. [Google Scholar]
- Henderson, F.M. Stability of alluvial channels. Trans. ASCE 1963, 128, 657–686. [Google Scholar]
- Parker, G. Hydraulic geometry of active gravel rivers. J. Hydraul. Div. ASCE 1979, 105, 1185–1201. [Google Scholar]
- Millar, R.G. Theoretical regime equations for mobile gravel-bed rivers with stable banks. Geomorphology 2005, 64, 207–220. [Google Scholar] [CrossRef]
- Eaton, B.C.; Giles, T.R. Assessing the effect of vegetation-related bank strength on channel morphology and stability in gravel bed streams using numerical models. Earth Surf. Process. Landf. 2009, 34, 712–714. [Google Scholar] [CrossRef]
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Size (mm) | 0.004 | 0.008 | 0.016 | 0.031 | 0.062 | 0.125 | 0.25 | 0.5 |
| Proportion | 30 | 12.7 | 13.4 | 14.6 | 13.1 | 8.2 | 6.5 | 1.5 |
| No. | Group Percentage of Bed Materials | D50 (mm) | Year | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.004 | 0.008 | 0.016 | 0.03 | 0.062 | 0.125 | 0.25 | 0.5 | 1 | |||
| % | 0 | 0 | 0 | 0.1 | 1.1 | 13.2 | 55.3 | 30 | 0.3 | 0.193 | 2002 |
| River Section | Total Distance (km) | Section Length (km) | Measured (106 m3) | Calculated (106 m3) |
|---|---|---|---|---|
| Taipingkou-Shashi | 8.47 | 8.47 | −827.26 | −1185.91 |
| Shashi-Haoxue | 58.65 | 50.19 | −1705.39 | −1730.82 |
| Haoxue-Xinchang | 73.62 | 14.96 | −1353.62 | −924.21 |
| Xinchang-Shishou | 93.38 | 19.76 | −1508.87 | −1719.86 |
| Time Period | Time (d) | Discharge (m3/s) | The Medium Grain Size (mm) | Sediment Supply (kg/m3) |
|---|---|---|---|---|
| 1 | 360 | 150 | 0.1 | 1 |
| 2 | 360 | 300 | 0.1 | 5 |
| No. | Flow Discharge (m3/s) | Sediment Supply (kg/m3) | Bank Vegetation | Time (d) |
|---|---|---|---|---|
| 1 | 150 | 5 | Yes | 600 |
| 2 | 300 | 1 | No | 600 |
| 3 | 300 | 5 | No | 600 |
| 4 | 150 | 1 | Yes | 600 |
| No. | Number of Breaches | Braided-Channel Ratio (B) | Sinuosity (P) |
|---|---|---|---|
| Run No. 1 | 6 | 2.11 | 1.06 |
| Run No. 2 | 5 | 1.9 | 1.00 |
| Run No. 3 | 4 | 1.97 | 1.01 |
| Run No. 4 | 2 | 1.22 | 1.35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Xiao, Y. 2D Numerical Modeling on the Transformation Mechanism of the Braided Channel. Water 2019, 11, 2030. https://doi.org/10.3390/w11102030
Yang S, Xiao Y. 2D Numerical Modeling on the Transformation Mechanism of the Braided Channel. Water. 2019; 11(10):2030. https://doi.org/10.3390/w11102030
Chicago/Turabian StyleYang, Shengfa, and Yi Xiao. 2019. "2D Numerical Modeling on the Transformation Mechanism of the Braided Channel" Water 11, no. 10: 2030. https://doi.org/10.3390/w11102030
APA StyleYang, S., & Xiao, Y. (2019). 2D Numerical Modeling on the Transformation Mechanism of the Braided Channel. Water, 11(10), 2030. https://doi.org/10.3390/w11102030




