Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity
Abstract
1. Introduction
2. Methodology
2.1. The Original GR4J Model and GR4J Model with Time-Varying Parameter
2.2. Model Calibration and Evaluation
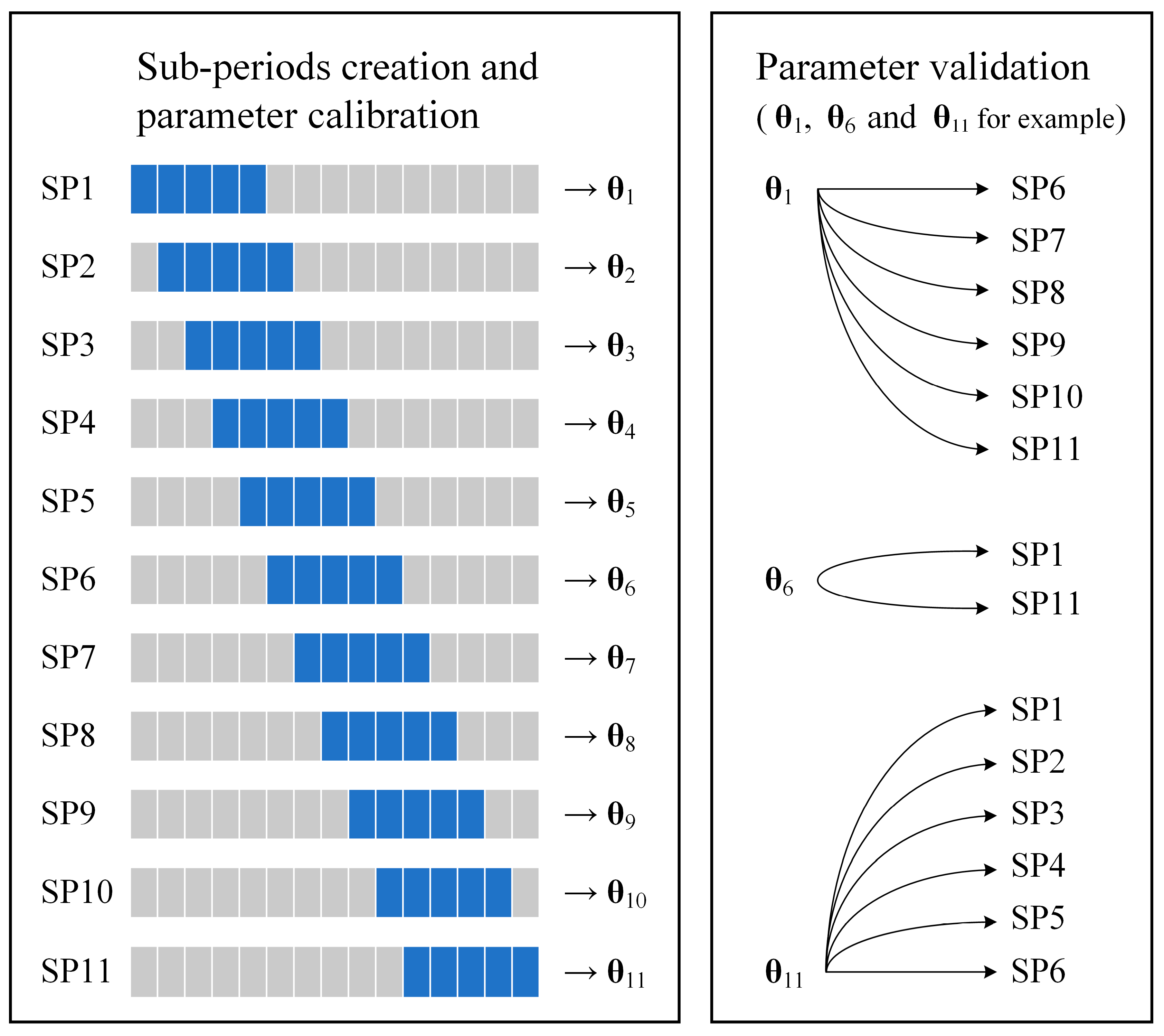
2.3. Temporal Transferability Test of Model Parameters
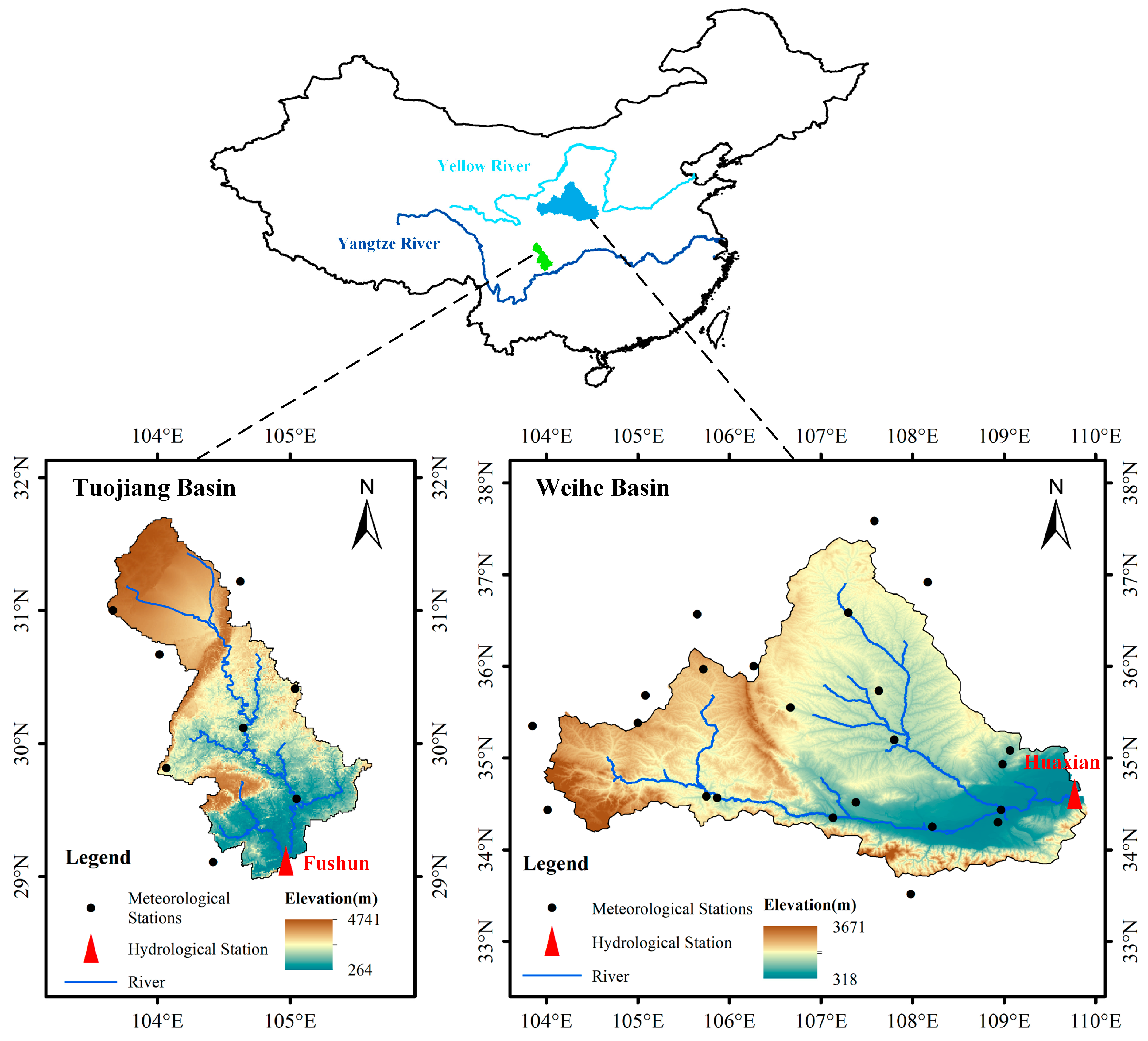
3. Study Data and Area
4. Results and Discussion
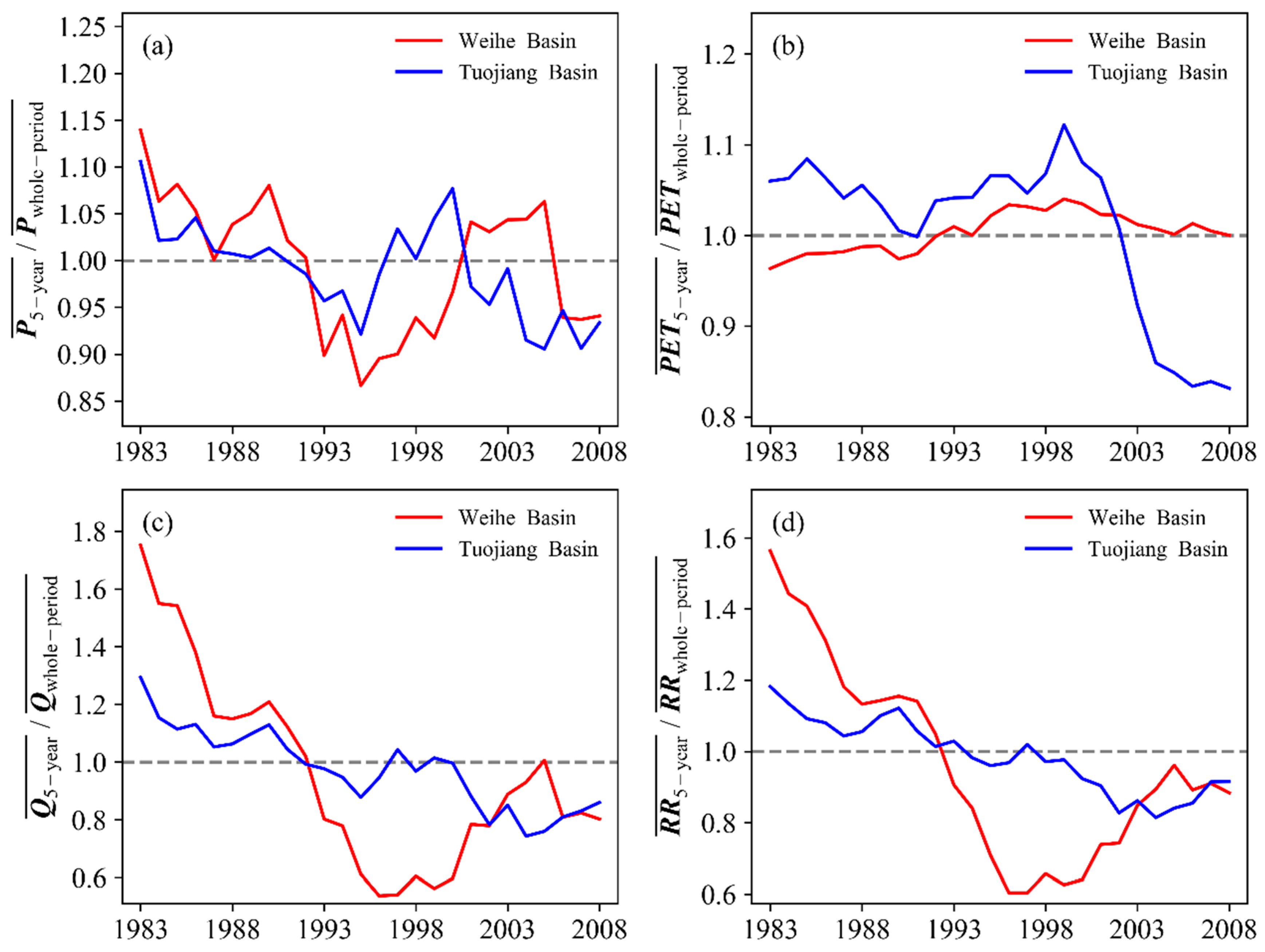
4.1. Diagnostics of Hydrological Nonstationarity
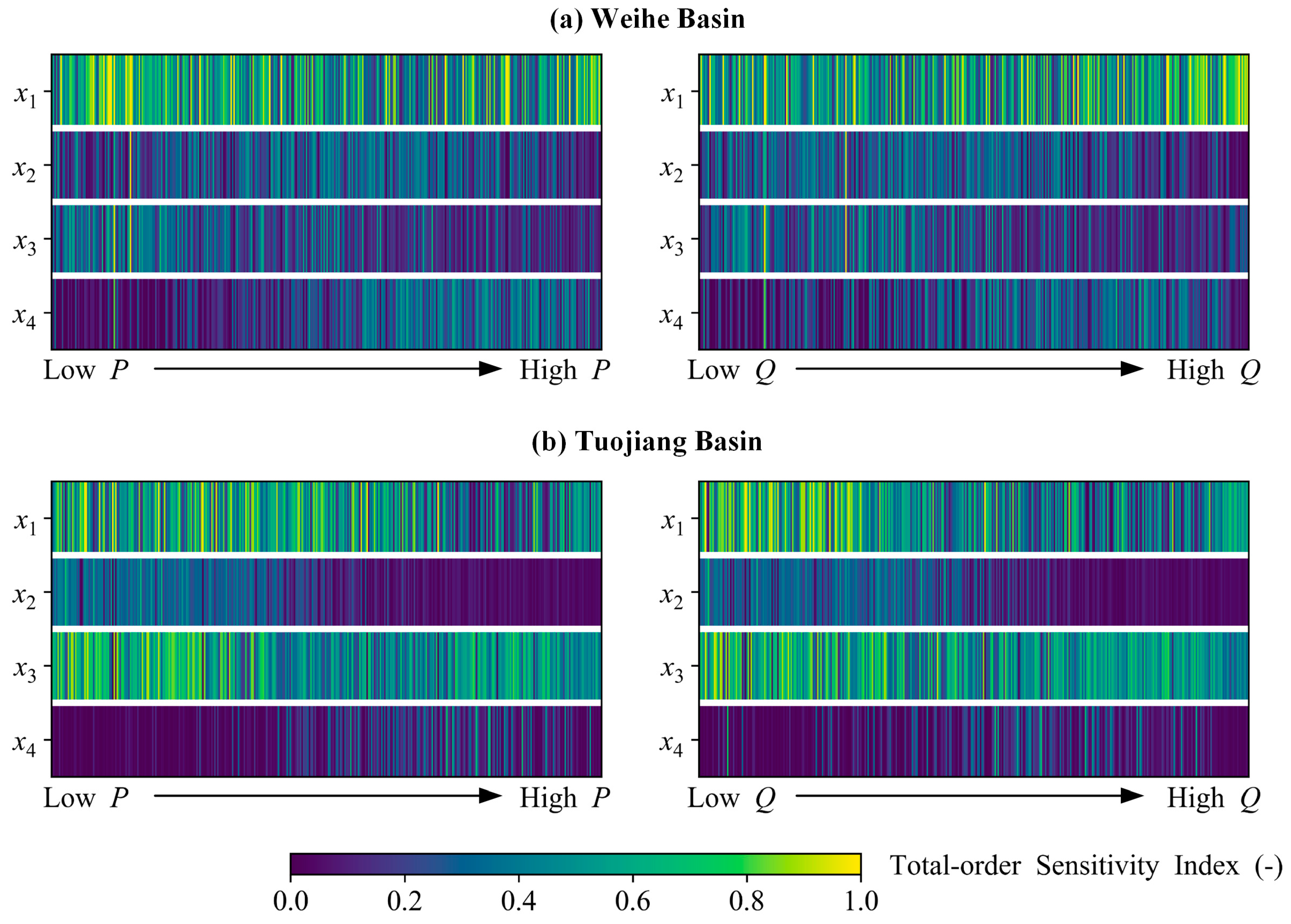
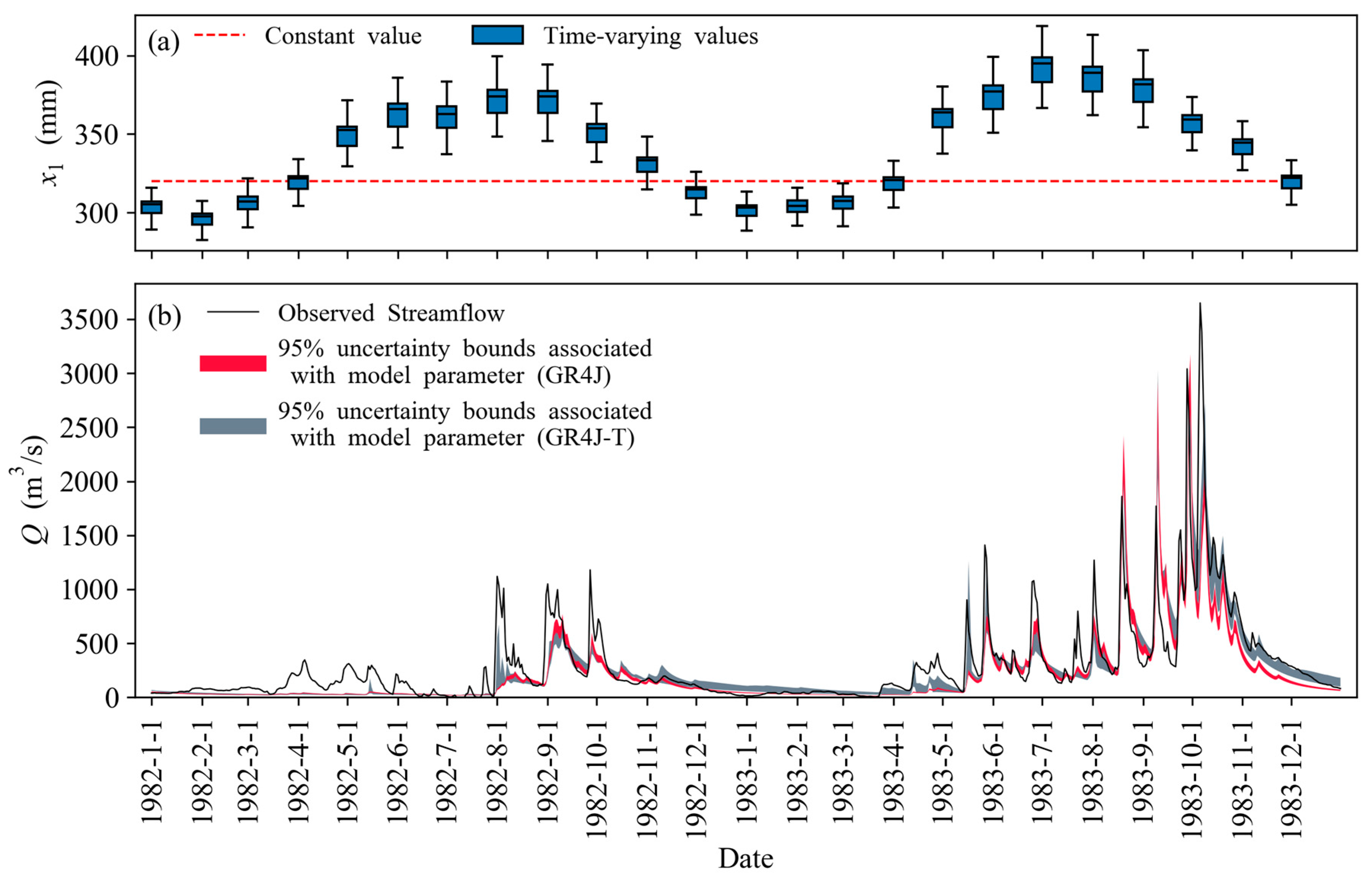
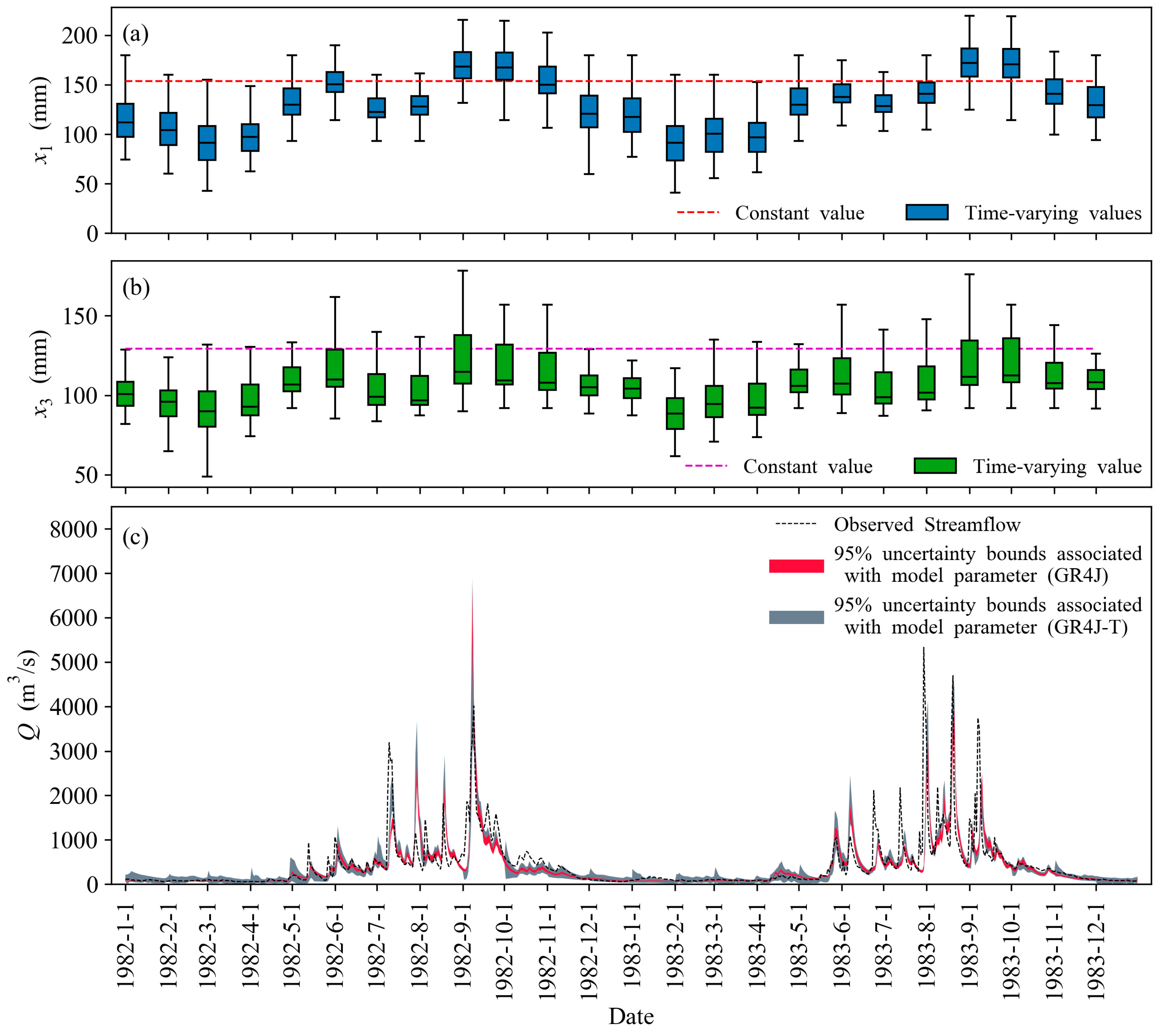
4.2. Parameter Estimation for the GR4J and GR4J-T Model
4.3. Streamflow Simulation Performance of the GR4J and GR4J-T Model
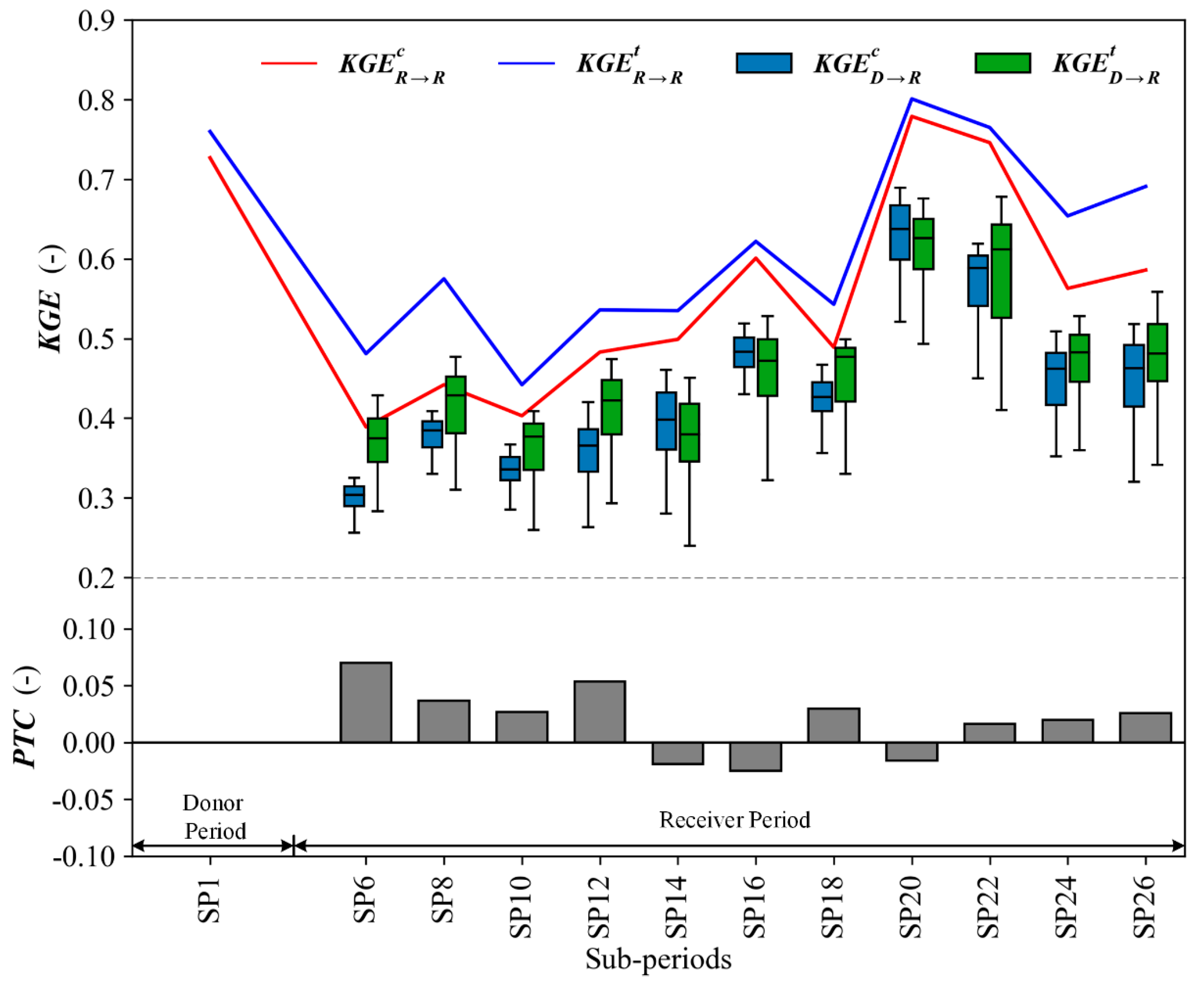
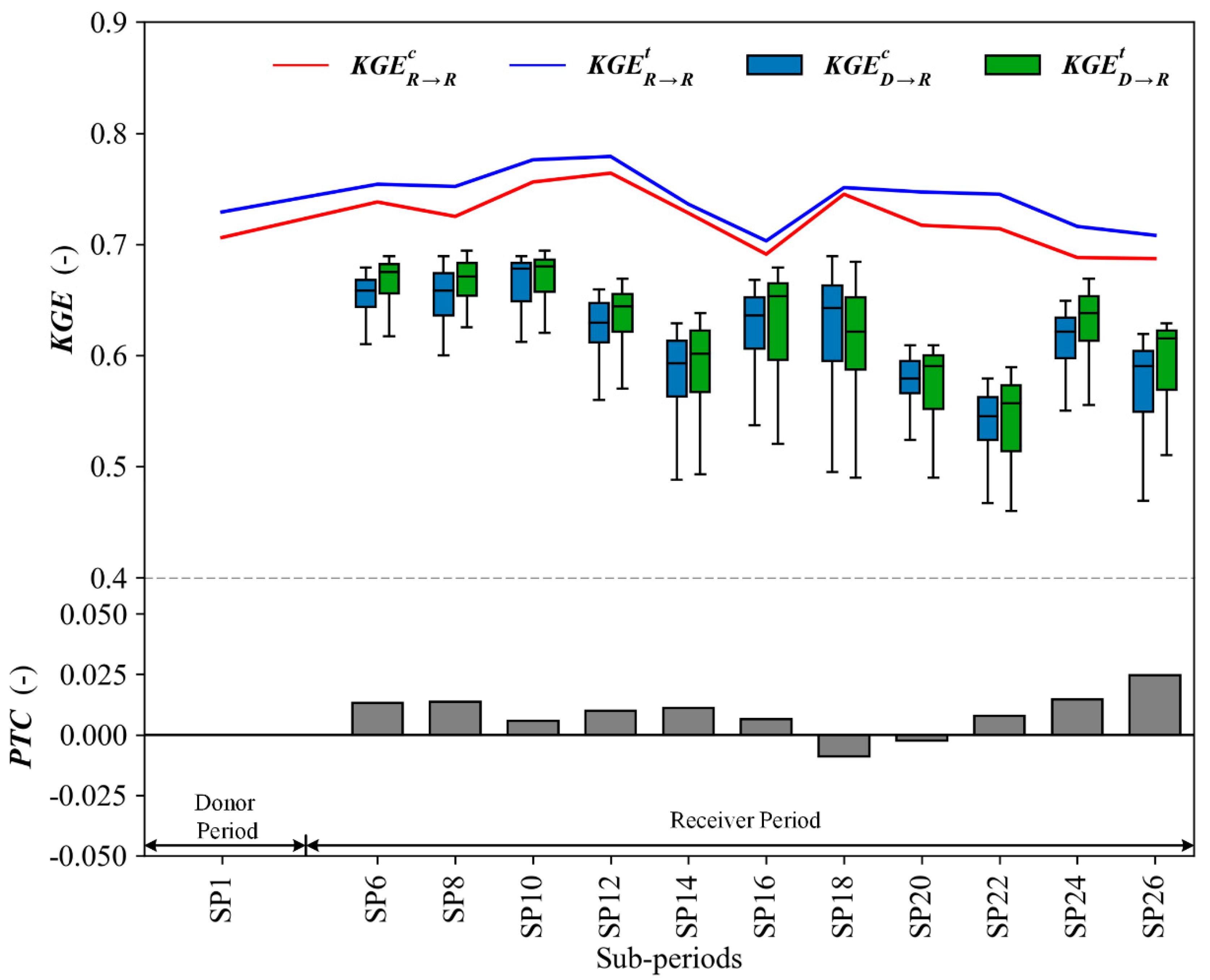
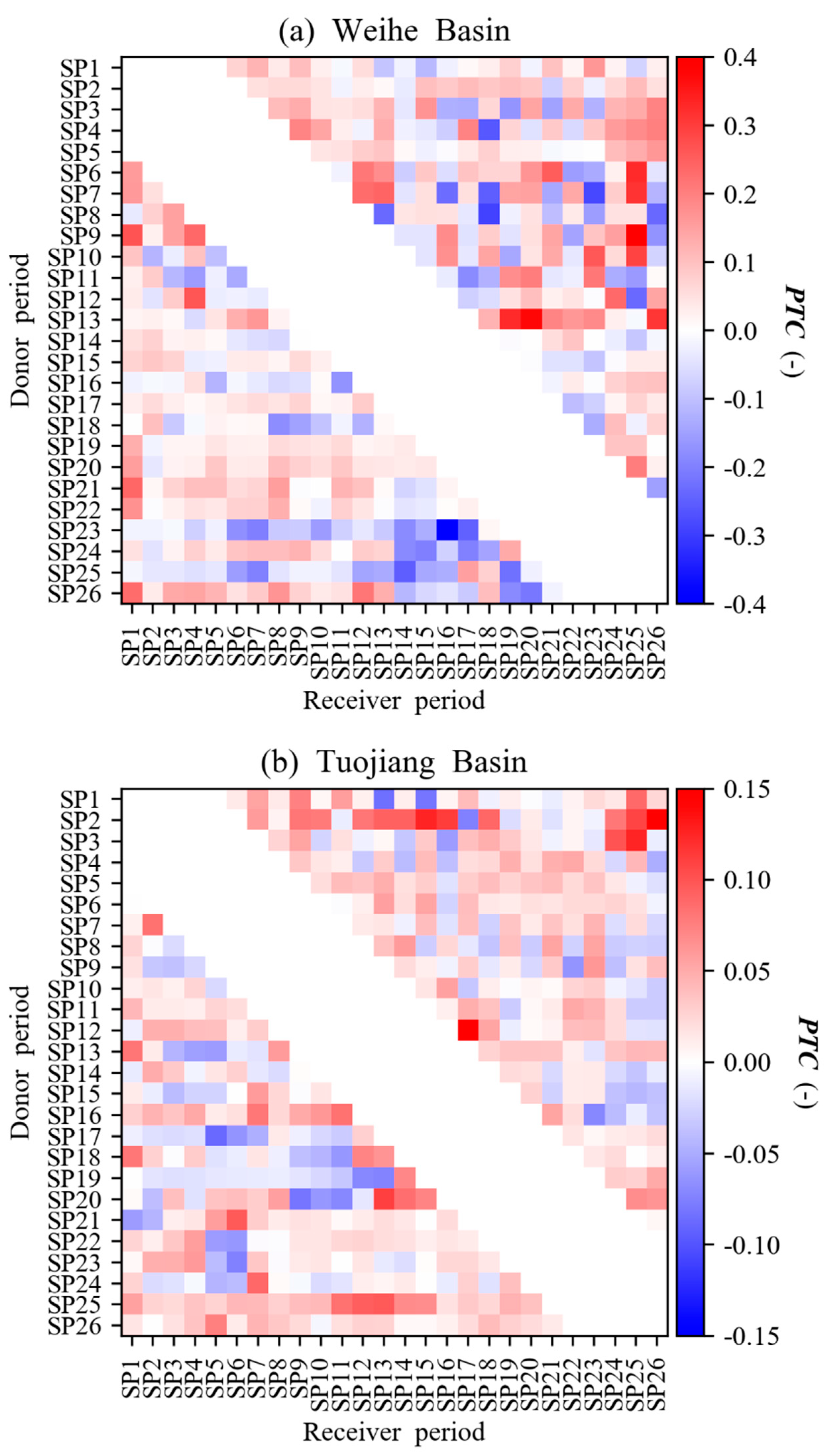
4.4. Parameter Transferability of the GR4J and GR4J-T Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Effective and efficient global optimization for conceptual rain-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1201. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is Dead: Whither Water Management. Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Ntegeka, V.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of hydrological model structures and calibration approaches in climate scenario impact projections. J. Hydrol. 2014, 519, 743–755. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time stability of catchment model parameters: Implications for climate impact analyses. Water Resour. Res. 2011, 47, w02531. [Google Scholar] [CrossRef]
- Saft, M.; Peel, M.C.; Western, A.W.; Perraud, J.; Zhang, L. Bias in streamflow projections due to climate-induced shifts in catchment response. Geophys. Res. Lett. 2016, 43, 1574–1581. [Google Scholar] [CrossRef]
- Xu, C.; Chen, H.; Guo, S. Hydrological Modeling in a Changing Environment: Issues and Challenges. J. Water Resour. Res. 2013, 2, 85–95. [Google Scholar] [CrossRef]
- Silberstein, R.P.; Aryal, S.K.; Braccia, M.; Durrant, J. Rainfall-runoff model performance suggests a change in flow regime and possible lack of catchment resilience. In Proceedings of the 20th International Congress on Modelling and Simulation (MODSIM2013), Adelaide, Australia, 1–6 December 2013; pp. 2409–2415. [Google Scholar]
- Omer, A.; Wang, W.G.; Basheer, A.K.; Yong, B. Integrated assessment of the impacts of climate variability and anthropogenic activities on river runoff: A case study in the Hutuo River Basin, China. Hydrol. Res. 2017, 48, 416–430. [Google Scholar] [CrossRef]
- Le Lay, M.; Galle, S.; Saulnier, G.M.; Braud, I. Exploring the relationship between hydroclimatic stationarity and rainfall-runoff model parameter stability: A case study in West Africa. Water Resour. Res. 2007, 43, 7. [Google Scholar] [CrossRef]
- Choi, H.T.; Beven, K. Multi-period and multi-criteria model conditioning to reduce prediction uncertainty in an application of TOPMODEL within the GLUE framework. J. Hydrol. 2007, 332, 316–336. [Google Scholar] [CrossRef]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of hydrological models and ensemble averaging methods between contrasting climatic periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef]
- Singh, R.; van Werkhoven, K.; Wagener, T. Hydrological impacts of climate change in gauged and ungauged watersheds of the Olifants basin: A trading-space-for-time approach. Hydrol. Sci. J. 2014, 59, 29–55. [Google Scholar] [CrossRef]
- Lacombe, G.; Ribolzi, O.; de Rouw, A.; Pierret, A.; Latsachak, K.; Silvera, N.; Pham Dinh, R.; Orange, D.; Janeau, J.; Soulileuth, B.; et al. Contradictory hydrological impacts of afforestation in the humid tropics evidenced by long-term field monitoring and simulation modelling. Hydrol. Earth Syst. Sci. 2016, 20, 2691–2704. [Google Scholar] [CrossRef]
- De Vos, N.J.; Rientjes, T.H.M.; Gupta, H.V. Diagnostic evaluation of conceptual rainfall-runoff models using temporal clustering. Hydrol. Process. 2010, 24, 2840–2850. [Google Scholar] [CrossRef]
- Gharari, S.; Hrachowitz, M.; Fenicia, F.; Savenije, H.H.G. An approach to identify time consistent model parameters: Sub-period calibration. Hydrol. Earth Syst. Sci. 2013, 17, 149–161. [Google Scholar] [CrossRef]
- Guo, D.; Johnson, F.; Marshall, L. Assessing the Potential Robustness of Conceptual Rainfall-Runoff Models Under a Changing Climate. Water Resour. Res. 2018, 54, 5030–5049. [Google Scholar] [CrossRef]
- Ekström, M.; Gutmann, E.D.; Wilby, R.L.; Tye, M.R.; Kirono, D.G.C. Robustness of hydroclimate metrics for climate change impact research. Wiley Interdiscip. Rev. Water 2018, 5, e1288. [Google Scholar] [CrossRef]
- Motavita, D.F.; Chow, R.; Guthke, A.; Nowak, W. The comprehensive differential split-sample test: A stress-test for hydrological model robustness under climate variability. J. Hydrol. 2019, 573, 501–515. [Google Scholar] [CrossRef]
- Fowler, K.; Coxon, G.; Freer, J.; Peel, M.; Wagener, T.; Western, A.; Woods, R.; Zhang, L. Simulating Runoff Under Changing Climatic Conditions: A Framework for Model Improvement. Water Resour. Res. 2018, 54, 9812–9832. [Google Scholar] [CrossRef]
- Vormoor, K.; Heistermann, M.; Bronstert, A.; Lawrence, D. Hydrological model parameter (in) stability-“crash testing” the HBV model under contrasting flood seasonality conditions. Hydrol. Sci. J. 2018, 63, 991–1007. [Google Scholar] [CrossRef]
- Kim, S.S.H.; Hughes, J.D.; Chen, J.; Dutta, D.; Vaze, J. Determining probability distributions of parameter performances for time-series model calibration: A river system trial. J. Hydrol. 2015, 530, 361–371. [Google Scholar] [CrossRef]
- Paik, K.; Kim, J.H.; Kim, H.S.; Lee, D.R. A conceptual rainfall-runoff model considering seasonal variation. Hydrol. Process. 2005, 19, 3837–3850. [Google Scholar] [CrossRef]
- Du, J.; Rui, H.; Zuo, T.; Li, Q.; Zheng, D.; Chen, A.; Xu, Y.; Xu, C.Y. Hydrological Simulation by SWAT Model with Fixed and Varied Parameterization Approaches Under Land Use Change. Water Resour. Manag. 2013, 27, 2823–2838. [Google Scholar] [CrossRef]
- Wallner, M.; Haberlandt, U. Non-stationary hydrological model parameters: A framework based on SOM-B. Hydrol. Process. 2015, 29, 3145–3161. [Google Scholar] [CrossRef]
- Pathiraja, S.; Marshall, L.; Sharma, A.; Moradkhani, H. Hydrologic modeling in dynamic catchments: A data assimilation approach. Water Resour. Res. 2016, 52, 3350–3372. [Google Scholar] [CrossRef]
- Westra, S.; Thyer, M.; Leonard, M.; Kavetski, D.; Lambert, M. A strategy for diagnosing and interpreting hydrological model nonstationarity. Water Resour. Res. 2014, 50, 5090–5113. [Google Scholar] [CrossRef]
- Deng, C.; Liu, P.; Wang, W.; Shao, Q.; Wang, D. Modelling time-variant parameters of a two-parameter monthly water balance model. J. Hydrol. 2019, 573, 918–936. [Google Scholar] [CrossRef]
- Sadegh, M.; AghaKouchak, A.; Flores, A.; Mallakpour, I.; Nikoo, M.R. A Multi-Model Nonstationary Rainfall-Runoff Modeling Framework: Analysis and Toolbox. Water Resour. Manag. 2019, 33, 3011–3024. [Google Scholar] [CrossRef]
- Pathiraja, S.; Anghileri, D.; Burlando, P.; Sharma, A.; Marshall, L.; Moradkhani, H. Time-varying parameter models for catchments with land use change: The importance of model structure. Hydrol. Earth Syst. Sci. 2018, 22, 2903–2919. [Google Scholar] [CrossRef]
- Xiong, M.; Liu, P.; Cheng, L.; Deng, C.; Gui, Z.; Zhang, X.; Liu, Y. Identifying time-varying hydrological model parameters to improve simulation efficiency by the ensemble Kalman filter: A joint assimilation of streamflow and actual evapotranspiration. J. Hydrol. 2019, 568, 758–768. [Google Scholar] [CrossRef]
- Rabassa, P.; Beck, C. Superstatistical analysis of sea-level fluctuations. Phys. A Stat. Mech. Its Appl. 2015, 417, 18–28. [Google Scholar] [CrossRef]
- Yalcin, G.C.; Rabassa, P.; Beck, C. Extreme event statistics of daily rainfall: Dynamical systems approach. J. Phys. A Math. Theor. 2016, 49, 154001. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Wagener, T. Time-varying sensitivity analysis clarifies the effects of watershed model formulation on model behavior. Water Resour. Res. 2013, 49, 1400–1414. [Google Scholar] [CrossRef]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.; Martel, J. The hazards of split-sample validation in hydrological model calibration. J. Hydrol. 2018, 566, 346–362. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Lerat, J.; Vaze, J.; Bourqui, M.; Hendrickx, F. Crash testing hydrological models in contrasted climate conditions: An experiment on 216 Australian catchments. Water Resour. Res. 2012, 48, w05552. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Bourqui, M.; Hendrickx, F. On the lack of robustness of hydrologic models regarding water balance simulation: A diagnostic approach applied to three models of increasing complexity on 20 mountainous catchments. Hydrol. Earth Syst. Sci. 2014, 18, 727–746. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Feyen, L.; Vrugt, J.A.; Nualláin, B.Ó.; van der Knijff, J.; De Roo, A. Parameter optimisation and uncertainty assessment for large-scale streamflow simulation with the LISFLOOD model. J. Hydrol. 2007, 332, 276–289. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications; Oxford University Press: Oxford, UK, 1970. [Google Scholar]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43, w01403. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Li, S.; Xiong, L.; Li, H.; Leung, L.R.; Demissie, Y. Attributing runoff changes to climate variability and human activities: Uncertainty analysis using four monthly water balance models. Stoch. Environ. Res. Risk Assess. 2015, 30, 251–269. [Google Scholar] [CrossRef]
- Xiong, L.; Du, T.; Xu, C.Y.; Guo, S.; Jiang, C.; Gippel, C.J. Non-Stationary Annual Maximum Flood Frequency Analysis Using the Norming Constants Method to Consider Non-Stationarity in the Annual Daily Flow Series. Water Resour. Manag. 2015, 29, 3615–3633. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C.Y. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Zou, L.; Xia, J.; She, D. Analysis of Impacts of Climate Change and Human Activities on Hydrological Drought: A Case Study in the Wei River Basin, China. Water Resour. Manag. 2018, 32, 1421–1438. [Google Scholar] [CrossRef]
- Su, X.L.; Kang, S.Z.; Wei, X.M.; Xing, D.W.; Cao, H. Impact of climate change and human activity on the runoff of Wei River basin to the Yellow River. J. Northwest A F Univ. (Nat. Sci. Ed.) 2007, 35, 153–159. [Google Scholar]
- Luan, X.; Wu, P.; Sun, S.; Li, X.; Wang, Y.; Gao, X. Impact of Land Use Change on Hydrologic Processes in a Large Plain Irrigation District. Water Resour. Manag. 2018, 32, 3203–3217. [Google Scholar] [CrossRef]
- National Meteorological Information Center of China. Available online: http://data.cma.cn/ (accessed on 30 July 2019).
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements, USDA Technical Bulletin 1275; US Department of Agriculture: Washington, DC, USA, 1962.
- Fensholt, R.; Rasmussen, K. Analysis of trends in the Sahelian ‘rain-use efficiency’ using GIMMS NDVI, RFE and GPCP rainfall data. Remote Sens. Environ. 2011, 115, 438–451. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long-term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Blasone, R.; Madsen, H.; Rosbjerg, D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J. Hydrol. 2008, 353, 18–32. [Google Scholar] [CrossRef]
| Parameter | Description | Unit | Feasible Range | |
|---|---|---|---|---|
| Lower Bound | Upper Bound | |||
| production storage capacity | mm | 20 | 1200 | |
| groundwater exchange coefficient | mm | −5 | 3 | |
| one day ahead maximum capacity of the routing store | mm | 20 | 500 | |
| time base of unit hydrograph | days | 1 | 5 | |
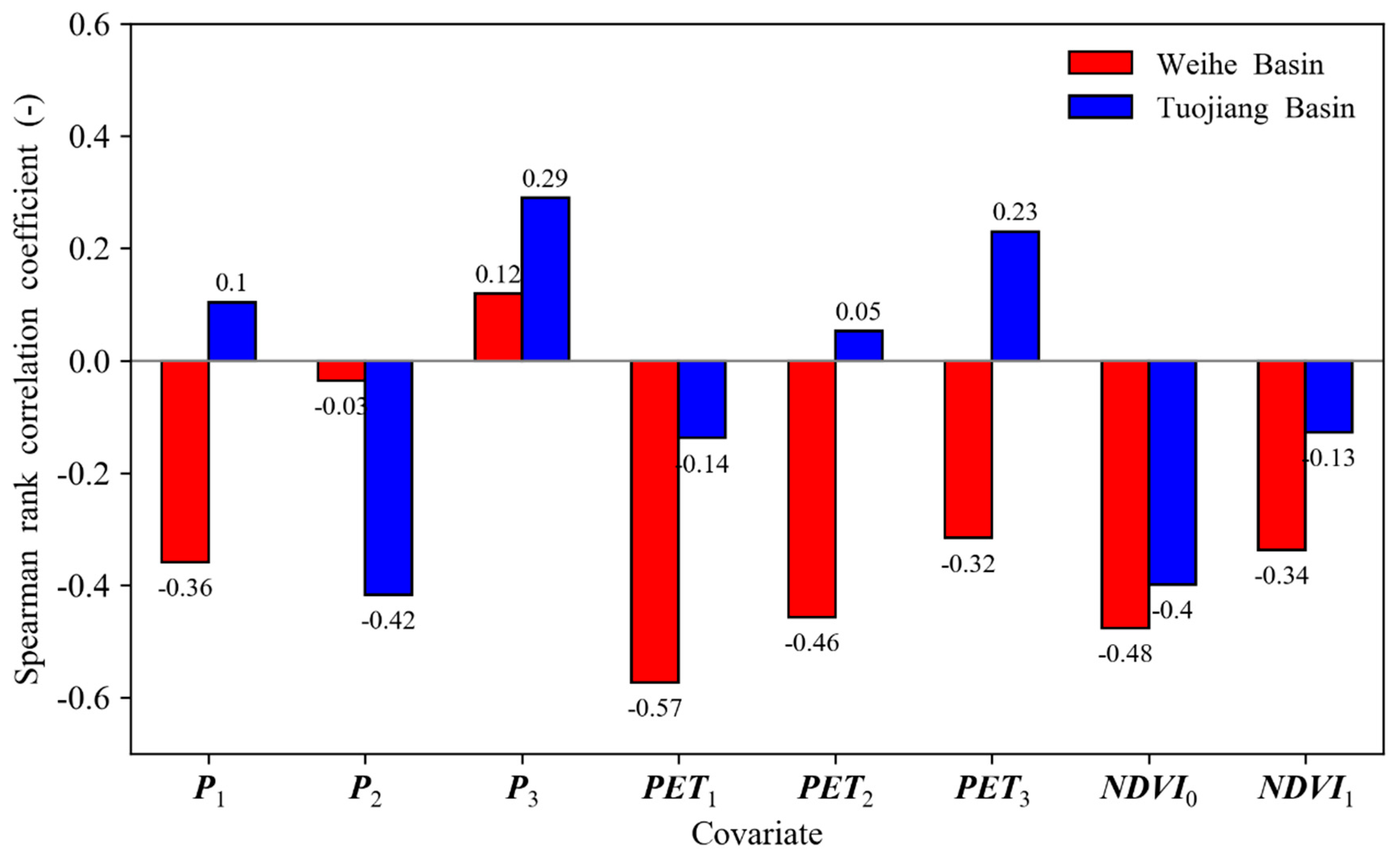
| Covariates | Unit | Description |
|---|---|---|
| P1 | mm | One-month antecedent monthly total precipitation |
| P2 | mm | Two-month antecedent monthly total precipitation |
| P3 | mm | Three-month antecedent monthly total precipitation |
| PET1 | mm | One-month antecedent monthly total potential evapotranspiration |
| PET2 | mm | Two-month antecedent monthly total potential evapotranspiration |
| PET3 | mm | Three-month antecedent monthly total potential evapotranspiration |
| NDVI0 | - | NDVI value for the current month |
| NDVI1 | - | NDVI value for the previous month |
| Basin | Data | Z statistic | Trend |
|---|---|---|---|
| Weihe Basin | Annual P | −1.22 | ↓ |
| Annual PET | 1.56 | ↑ | |
| Annual Q | −2.61 | ↓** | |
| Annual RR | −2.56 | ↓** | |
| Annual NDVI | 3.96 | ↑** | |
| Tuojiang Basin | Annual P | −1.32 | ↓ |
| Annual PET | −3.51 | ↓** | |
| Annual Q | −2.75 | ↓** | |
| Annual RR | −2.78 | ↓** | |
| Annual NDVI | 0.46 | ↑ |
| Case | Covariate | KGE (-) | BIAS (%) | |||
|---|---|---|---|---|---|---|
| C0 | 0.727 | −16.1 | ||||
| C1 | ✓ | 0.752 | −6.3 | |||
| C2 | ✓ | 0.749 | −8.1 | |||
| C3 | ✓ | 0.751 | −11.2 | |||
| C4 | ✓ | ✓ | 0.755 | −6.2 | ||
| C5 | ✓ | ✓ | 0.759 | −6.4 | ||
| C6 | ✓ | ✓ | 0.751 | −9.3 | ||
| C7 | ✓ | ✓ | ✓ | 0.761 | −6.1 | |
| Sub-Period | GR4J Model | GR4J-T Model | ||||
|---|---|---|---|---|---|---|
| KGE (-) | BIAS (%) | KGE (-) | BIAS (%) | |||
| SP1 | 320.1 | 0.727 | −16.1 | 0.761 | −6.1 | |
| SP2 | 443.2 | 0.617 | −17.3 | 0.631 | −14.5 | |
| SP3 | 324.1 | 0.571 | −19.1 | 0.572 | −11.6 | |
| SP4 | 263.5 | 0.509 | −26.2 | 0.591 | −20.2 | |
| SP5 | 447.3 | 0.611 | −16.2 | 0.635 | −13.2 | |
| SP6 | 375.5 | 0.389 | −22.2 | 0.481 | −20.3 | |
| SP7 | 367.4 | 0.392 | −22.9 | 0.514 | −27.9 | |
| SP8 | 300.9 | 0.442 | −25.7 | 0.575 | −26.4 | |
| SP9 | 256.3 | 0.341 | −23.3 | 0.504 | −19.6 | |
| SP10 | 414.5 | 0.403 | −18.1 | 0.442 | −15.2 | |
| SP11 | 417.6 | 0.392 | −26.4 | 0.438 | −26.6 | |
| SP12 | 244.1 | 0.483 | −25.2 | 0.536 | −19.7 | |
| SP13 | 182.4 | 0.230 | −42.9 | 0.432 | −40.3 | |
| SP14 | 340.4 | 0.499 | −23.6 | 0.535 | −17.9 | |
| SP15 | 424.1 | 0.659 | −13.7 | 0.713 | −7.8 | |
| SP16 | 208.1 | 0.601 | −28.2 | 0.622 | −26.4 | |
| SP17 | 295.5 | 0.582 | −18.4 | 0.639 | −10.1 | |
| SP18 | 315.3 | 0.489 | −24.5 | 0.543 | −17.5 | |
| SP19 | 378.7 | 0.734 | −23.3 | 0.763 | −16 | |
| SP20 | 429.1 | 0.779 | −21.5 | 0.801 | −17.4 | |
| SP21 | 339.5 | 0.732 | −4.6 | 0.771 | −1.5 | |
| SP22 | 460.1 | 0.746 | −4.7 | 0.765 | −3.2 | |
| SP23 | 382.8 | 0.729 | −15.3 | 0.772 | −13.8 | |
| SP24 | 334.5 | 0.563 | −24.6 | 0.654 | −10.6 | |
| SP25 | 223.1 | 0.522 | −37.5 | 0.583 | −22.3 | |
| SP26 | 426.5 | 0.586 | −18.7 | 0.691 | −13.8 | |
| Sub-Period | GR4J Model | GR4J-T Model | ||||
|---|---|---|---|---|---|---|
| KGE (-) | BIAS (%) | KGE (-) | BIAS (%) | |||
| SP1 | 0.706 | −4.7 | 0.729 | −3.8 | ||
| SP2 | 0.619 | −5.2 | 0.654 | −3.2 | ||
| SP3 | 0.677 | −4.4 | 0.701 | −4.2 | ||
| SP4 | 0.725 | −4.5 | 0.738 | −1.9 | ||
| SP5 | 0.696 | −4.9 | 0.702 | −6.3 | ||
| SP6 | 0.738 | −5.2 | 0.754 | −4.1 | ||
| SP7 | 0.724 | −2.2 | 0.743 | −0.7 | ||
| SP8 | x1 = 201.3 x3 = 281.2 | 0.725 | −2.5 | x1,t = 267.8 + 0.18PET1,t − 36.5NDVI0,t x3,t = 237.5 + 0.24P2,t − 0.31PET1,t − 18.9NDVI0,t | 0.752 | −4.4 |
| SP9 | x1 = 259.7 x3 = 115.8 | 0.771 | −3.5 | x1,t = 161.5 + 0.32PET1,t + 56.6NDVI0,t x3,t = 237.9 + 0.14P2,t − 0.28PET1,t − 45.7NDVI0,t | 0.792 | −0.1 |
| SP10 | x1 = 234.6 x3 = 122.7 | 0.756 | −5.1 | x1,t = 191.3 + 0.64PET1,t − 18.9NDVI0,t x3,t = 187.2 + 0.19P2,t − 72.1NDVI0,t | 0.776 | −4.8 |
| SP11 | x1 = 217.4 x3 = 220.8 | 0.759 | −2.3 | x1,t = 285.1 − 0.22P2,t − 24.3NDVI0,t x3,t = 188.2 + 0.12P2,t + 0.28PET1,t − 35.1NDVI0,t | 0.771 | −7.7 |
| SP12 | x1 = 137.3 x3 = 199.3 | 0.764 | −4.9 | x1,t = 216.5 + 0.36PET1,t − 62.7NDVI0,t x3,t = 244.7 + 0.34PET1,t − 46.8NDVI0,t | 0.779 | −8.6 |
| SP13 | x1 = 261.8 x3 = 161.6 | 0.726 | −7.5 | x1,t = 307.8 + 0.18P2,t − 0.42PET1,t − 42.9NDVI0,t x3,t = 155.8 + 0.52PET1,t − 29.1NDVI0,t | 0.739 | −10.1 |
| SP14 | x1 = 240.4 x3 = 152.5 | 0.728 | −2.1 | x1,t = 271.9 − 0.19PET1,t − 56.3NDVI0,t x3,t = 141.4 + 0.43PET1,t − 42.7NDVI0,t | 0.736 | −2.5 |
| SP15 | x1 = 240.1 x3 = 177.2 | 0.725 | −6.7 | 0.728 | −8.2 | |
| SP16 | 0.691 | 0.8 | 0.703 | 3.4 | ||
| SP17 | 0.721 | −3.7 | 0.727 | −2.3 | ||
| SP18 | 0.745 | −3.9 | 0.751 | −3.0 | ||
| SP19 | 0.728 | −9.1 | 0.739 | −9.9 | ||
| SP20 | 0.717 | −11.9 | 0.747 | −7.4 | ||
| SP21 | 0.795 | −7.1 | 0.812 | −5.2 | ||
| SP22 | 0.714 | −8.8 | 0.745 | −6.6 | ||
| SP23 | 0.749 | −6.6 | 0.766 | −7.1 | ||
| SP24 | 0.688 | −9.4 | 0.716 | −7.5 | ||
| SP25 | 0.678 | −9.4 | 0.681 | −6.9 | ||
| SP26 | 0.687 | −9.7 | 0.708 | −7.4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Xiong, L.; Liu, D.; Chen, J.; Kim, J.-S. Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity. Water 2019, 11, 2029. https://doi.org/10.3390/w11102029
Zeng L, Xiong L, Liu D, Chen J, Kim J-S. Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity. Water. 2019; 11(10):2029. https://doi.org/10.3390/w11102029
Chicago/Turabian StyleZeng, Ling, Lihua Xiong, Dedi Liu, Jie Chen, and Jong-Suk Kim. 2019. "Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity" Water 11, no. 10: 2029. https://doi.org/10.3390/w11102029
APA StyleZeng, L., Xiong, L., Liu, D., Chen, J., & Kim, J.-S. (2019). Improving Parameter Transferability of GR4J Model under Changing Environments Considering Nonstationarity. Water, 11(10), 2029. https://doi.org/10.3390/w11102029








