2.1. The Alcantara River Basin
The Alcantara River Basin (see
Figure 1) is located in North-Eastern Sicily (Italy), encompassing the north side of Etna Mountain, the tallest active volcano in Europe. The river basin has an extension of about 603 km
2. The headwater of the river is at 1400 m a.s.l in the Nebrodi Mountains, while the outlet in the Ionian Sea is reached after 50 km.
Table 1 lists the main morphometric and hydrologic characteristics of the entire river basin, as well as of its main sub-basin, at Moio Alcantara.
On the right-hand side of the river, the mountain area is characterized by volcanic rocks with a very high infiltration capacity and by the lack of a hydrographic network. Here, precipitation and snow melting supply a big aquifer whose groundwater springs at the mid/downstream of the river, mixing with surface water and contributing to feeding the river flow also during the dry season. The left side of the basin is characterized by sedimentary soils (heterogeneous marly clays complex with poor power water-bearing horizons in the rocky levels) where a dense hydrographic network was formed, and gives a seasonal contribution to the river flow, as it follows the rainfall annual variability typical of the Mediterranean climate.
The entire valley hosts many animal species, especially migrating birds. The rich vegetation changes in the different stretches of the river offering a great variety of plans along the way. All this area takes the name of Alcantara Fluvial Park, a wonderful nature reserve which includes a fluvial, a botanical and a geological park.
Groundwater resources, withdrawn in the upper part of the basin (over Moio Alcantara cross-section), are mainly used to supply agricultural areas (see
Figure 2) and all the municipalities inside the river basin through local aqueducts, as well as the villages along the Ionian coast, from the Alcantara basin itself up to the city of Messina, by the Alcantara aqueduct [
5]. In addition, an existing interconnection between the Alcantara aqueduct and the Messina water distribution system could be used to partially supply the city of Messina, in order to lighten other water sources in the near future. Surface water withdrawals, due to agricultural activities, are mainly concentrated at the downstream, from May to October. Industrial surface water demand is mainly related to paper factories, hydroelectric run-of-river power plants, and mineral extraction. Based on the water balance at the river mouth, about 15% of the annual rainfall recharges the aquifer, primarily during the winter season. The groundwater store has a peak during April-May and then gradually depletes over the summer-fall season until recharge occurs again in winter.
Beyond the prestigious environmental aspect aforementioned, the Alcantara river basin exhibits several environmental problems due to anthropogenic factors, i.e., urban pressure, industrial settlements (sometimes disused), problems related to flood and landslide defense, and water quality deterioration. Furthermore, following various research studies, climate change effects could exacerbate these criticalities. To this end, 13 municipalities within the Alcantara river basin have agreed upon a River Contract on 22 July 2016, with the aim to define and implement planning tools for the safeguard and the effective management of water resources, the appreciation of fluvial territories and the flood control, and to foster the socio-economic development of the area.
To this end, it is highly important to develop appropriate modeling tools able to simulate the basin’s hydrologic response by taking into account the complex aquifer-stream interactions.
2.2. The Modified IHACRES Model
The IHACRES rainfall-runoff model proposed by Jakeman and Homberger [
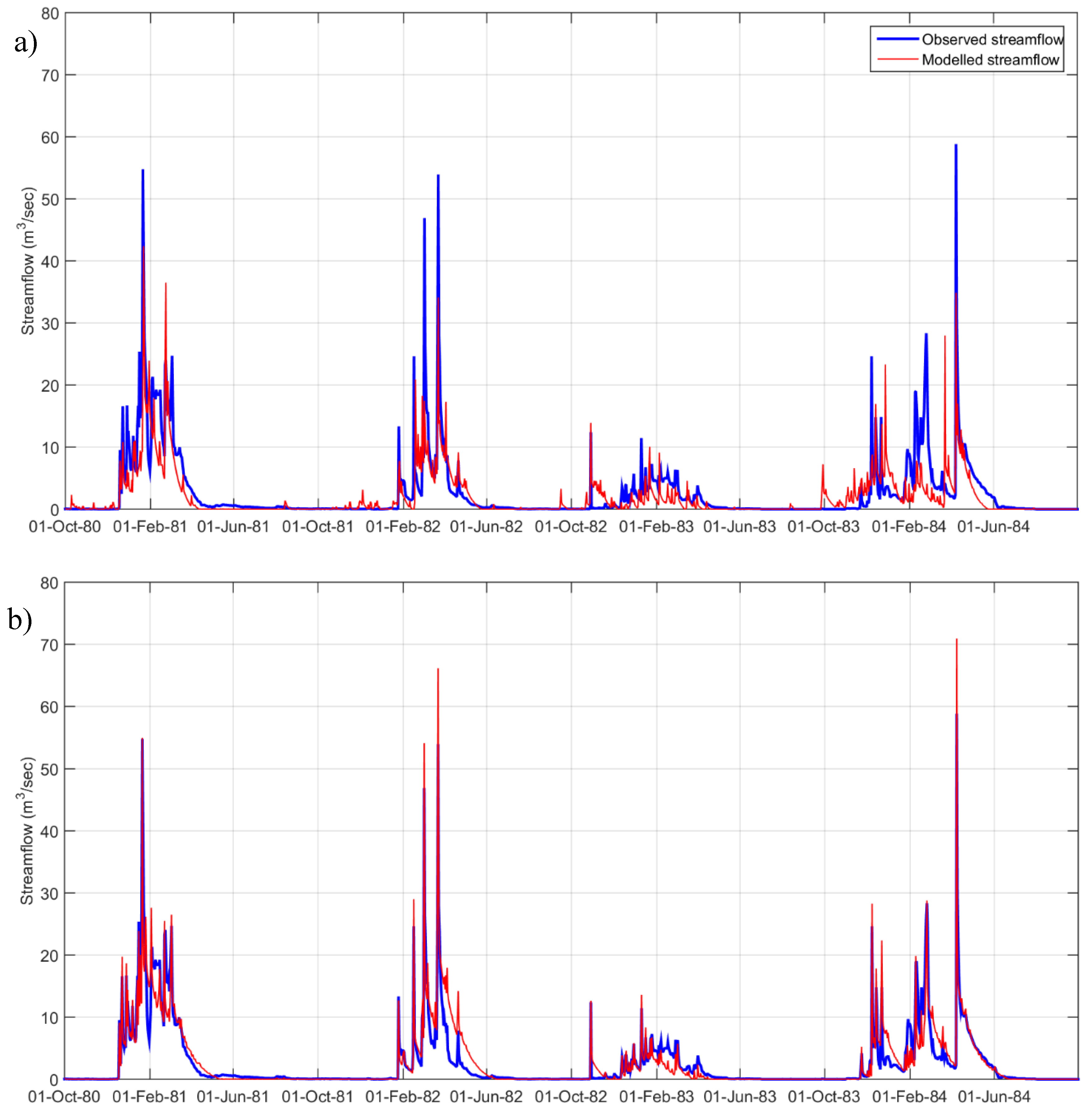
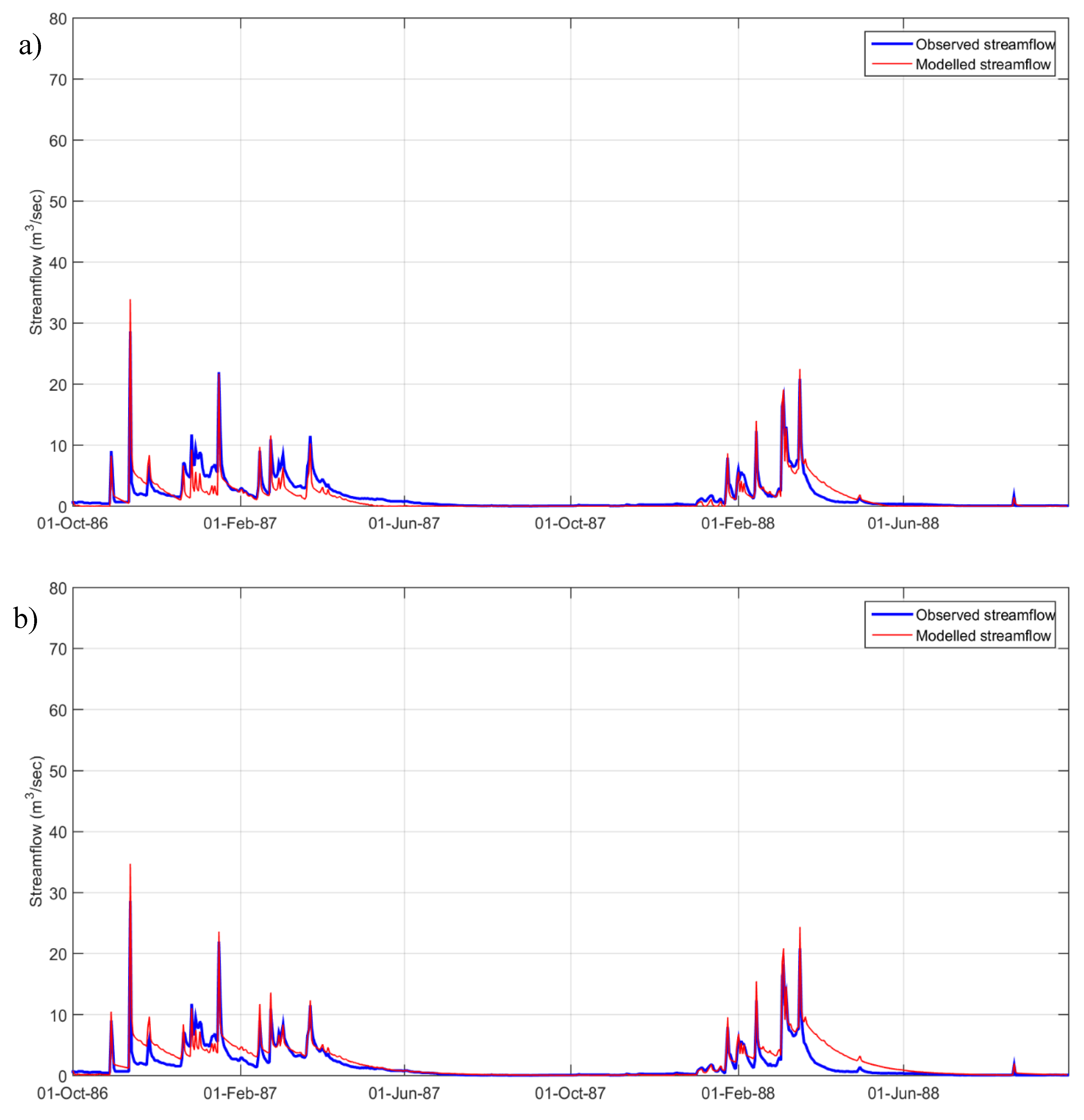
6], describes the basin’s behavior well in the case that the surface water is the primary component of the flow regime. It is a simple model designed to perform the identification of hydrographs and component flows purely from rainfall, evaporation, and streamflow data. In this model the rainfall-runoff processes are represented by two modules (see
Figure 3): A non-linear loss module that transforms precipitation to effective rainfall, considering the influence of temperature, followed by a linear module based on two parallel transfer functions, represented by exponential equations, which transform the effective rainfall into a quick flow and a slow flow component. The sum of the two components gives the modeled streamflow.
Extensions of the IHACRES model have been proposed by Croke et al. [
7], Ivkovic [
8], and Herron and Croke [
9] to take into account the role of the groundwater component in the hydrologic response of connected groundwater-surface water basins, by appropriately representing the effect of the change in groundwater storage and discharge, also due to water extraction.
Croke et al. [
7] integrated a parsimonious, lumped, and physically-based hillslope model, developed by Sloan [
10] for homogeneous aquifers, within the IHACRES rainfall-runoff model. The discharge formulation within the groundwater model is expressed as a series of exponential terms and is therefore similar to the commonly used form of the unit hydrograph approach implemented in streamflow models such as IHACRES.
Ivkovic [
8] proposed a simple coupled aquifer-river model, entitled IHACRES-GW, where the slow transfer function component of the IHACRES model has been modified by incorporating a groundwater storage module. The latter is conceptualized as a single reservoir, whose areal extent is the basin area upstream of a stream gauging station, considered as the basin outlet. The volume of water released from groundwater storage to the river system is represented by the baseflow component of streamflow. Groundwater extraction and other losses behave as additional outflows from the volume of water held in groundwater storage. The volume of water that recharges the groundwater storage is determined by the proportion of effective rainfall partitioned as slow flow. The remaining fraction of effective rainfall is apportioned to surface runoff. The model was developed for use in unregulated, gauged basins in narrow, semi-confined and narrow, shallow unconfined alluvial valleys with strong aquifer–river connectivity, where groundwater extractions predominantly occur upstream of the gauging station.
Herron and Croke [
9] formulated a three-store model (IHACRES-3S), where the slow flow pathway comprises two-layered stores able to capture non-linear hydrologic response better than the linear routing module of the IHACRES-GW model. The upper store receives the volume of effective rainfall partitioned as slow flow, discharges to the stream and recharges the lower store. Conceptually, it can be viewed as a perched water table which develops in response to rain and tends to be relatively short-lived. The lower store corresponds to the groundwater storage in IHACRES-GW.
Keeping in mind the non-linear response of the Moio Alcantara river basin, as well as the specific features of its aquifer system, we modify the original IHACRES model capitalizing on the works by Ivkovic [
8] and Herron and Croke [
9], in order to properly describe the groundwater discharge and extraction.
The structure of the modified IHACRES model is illustrated in
Figure 4. In particular, the routing module is formulated as a two-store model including an upper store to simulate the quick component of the runoff and a lower store that simulates the slow component of the runoff and the groundwater extraction and losses, which is recharged by the first store as well as by the proportion of effective rainfall partitioned as slow flow.
Recalling the IHACRES model, the non-linear loss module involves the calculation of an index of basin storage
s(
t) based upon an exponentially decreasing weighting of total rainfall
r(
t) and temperature
T(
t) conditions:
where
is the basin storage index, or basin wetness/soil moisture index at time
t, varying between 0 and 1,
is a time constant which is inversely related to the temperature declining rate,
is the value of
for a reference temperature fixed to a nominal value depending on the climate and usually equal to 20 °C for warmer climates [
11],
c (mm) is a conceptual total storage volume chosen to constrain the volume of effective rainfall to equal runoff, and
f (1/°C) is a temperature modulation factor.
The effective rainfall volume
is finally determined as:
where
A is the area of the river basin.
The model assumes that the partitioning of effective rainfall between the two stores is through the constant percentages
and
, respectively. Application of the mass balance equation to the upper store leads to:
where
is the volume of the upper store and
is the outflow volume at time
t, which is further portioned into the quick flow component
and the recharge component
through the constant percentages
and
.
Based on the property of linear reservoir, the following relationships between
and
hold:
where
is a dimensionless constant equivalent to the storage coefficient for the upper store.
Replacing Equation (5) into Equation (4) results in:
Multiplying Equation (6) by
allows determining for
a functional form similar to the classical exponential transfer function of the linear routing module in the IHACRES model. Thus, after some algebras, the following relation can be obtained:
where
the first parameter related to the rate of the flow recession and the second one related to the height of unit hydrograph peaks of the quick flow. It is worth reminding that
, being
the time constant describing the decay of the outflow from the upper store.
Similarly, the application of the mass balance equation to the lower store leads to:
where
is the volume of the lower store,
is the groundwater discharge to the stream and
accounts for both the groundwater extraction and natural losses at time
t.
In our formulation, the lower store is recharged by the upper store (i.e.,
) only when
and
, as well as it discharges to the stream (i.e.,
) only when
. Following the same line of reasoning as for the upper store, the following relationships between
and
can be considered:
where
is a dimensionless constant equivalent to the storage coefficient for the lower store.
Replacing Equation (10) into Equation (9) results in:
Once again, multiplying Equation (11) by
allows determining for
a functional form similar to the classical exponential transfer function for the slow component, although without the recharge and groundwater extraction and loss terms, with parameters:
the first parameter related to the rate of the flow recession and the second one related to the height of unit hydrograph peaks of the slow flow, with
, being
the time constant describing the slow flow decay from the lower store.
Finally, the streamflow discharge is given by: