Implementation of a Local Time Stepping Algorithm and Its Acceleration Effect on Two-Dimensional Hydrodynamic Models
Abstract
1. Introduction
2. Methods
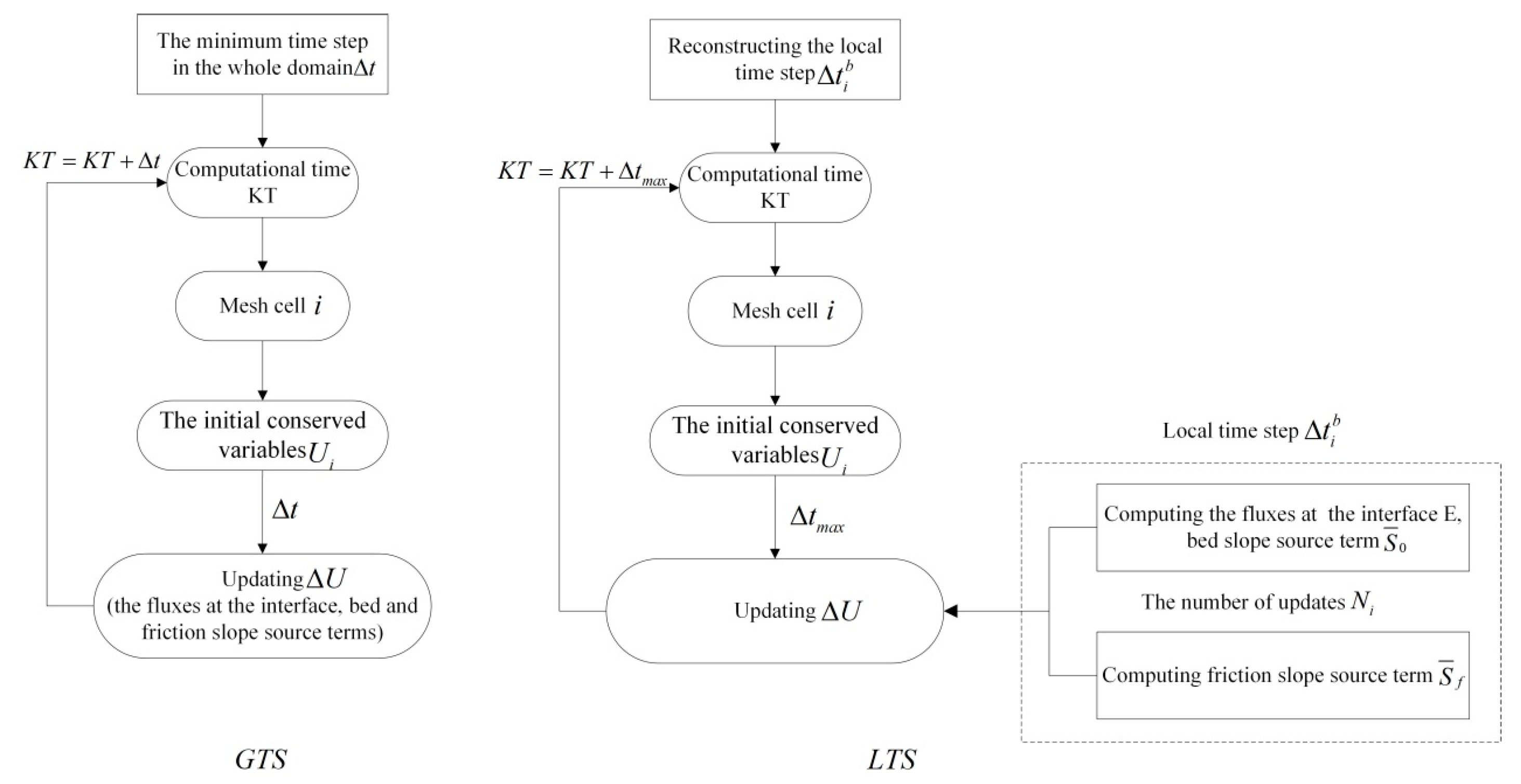
2.1. Global Time Stepping Scheme
2.1.1. Governing Equation
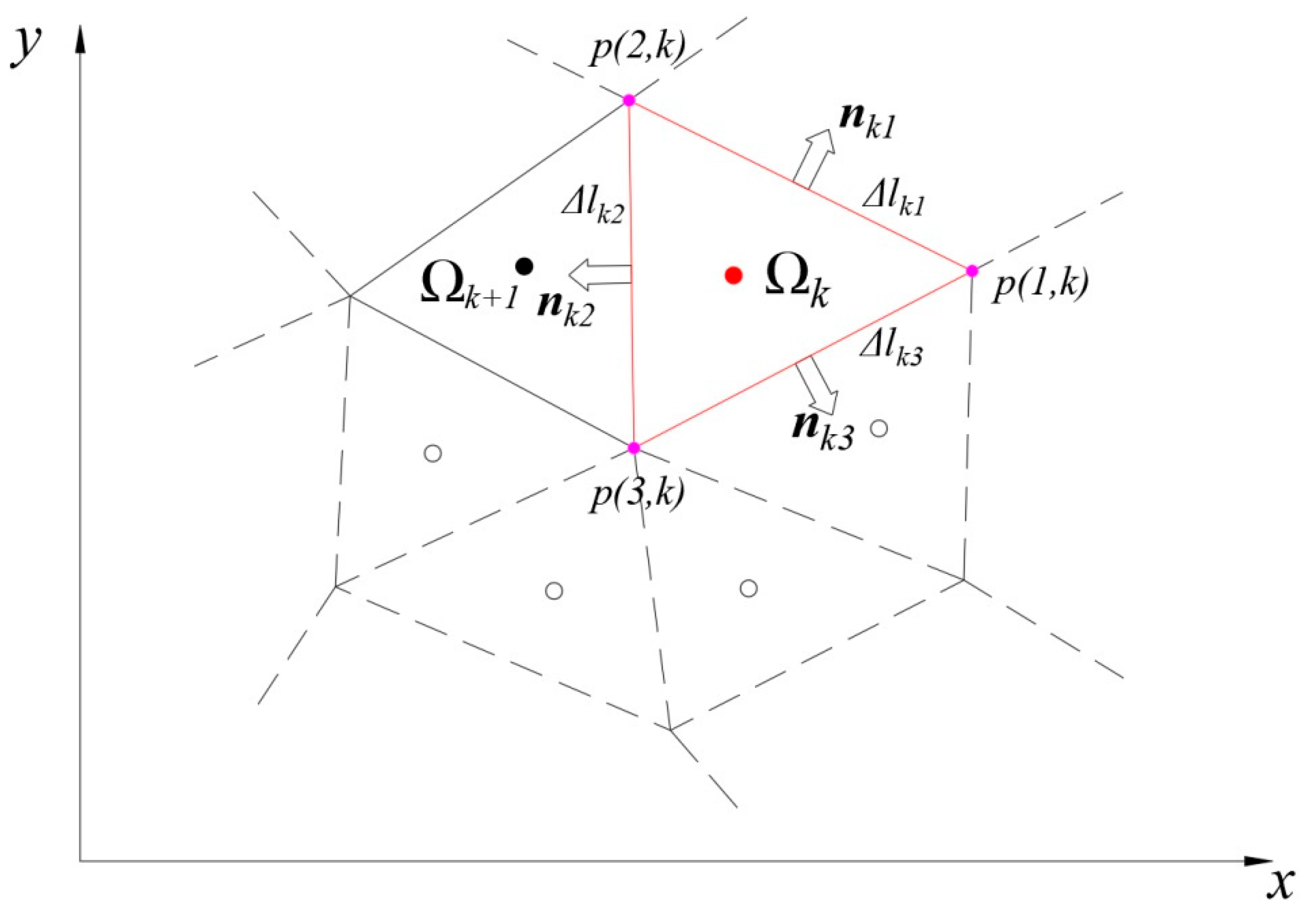
2.1.2. Numerical Technique
2.2. Local Time Stepping Scheme
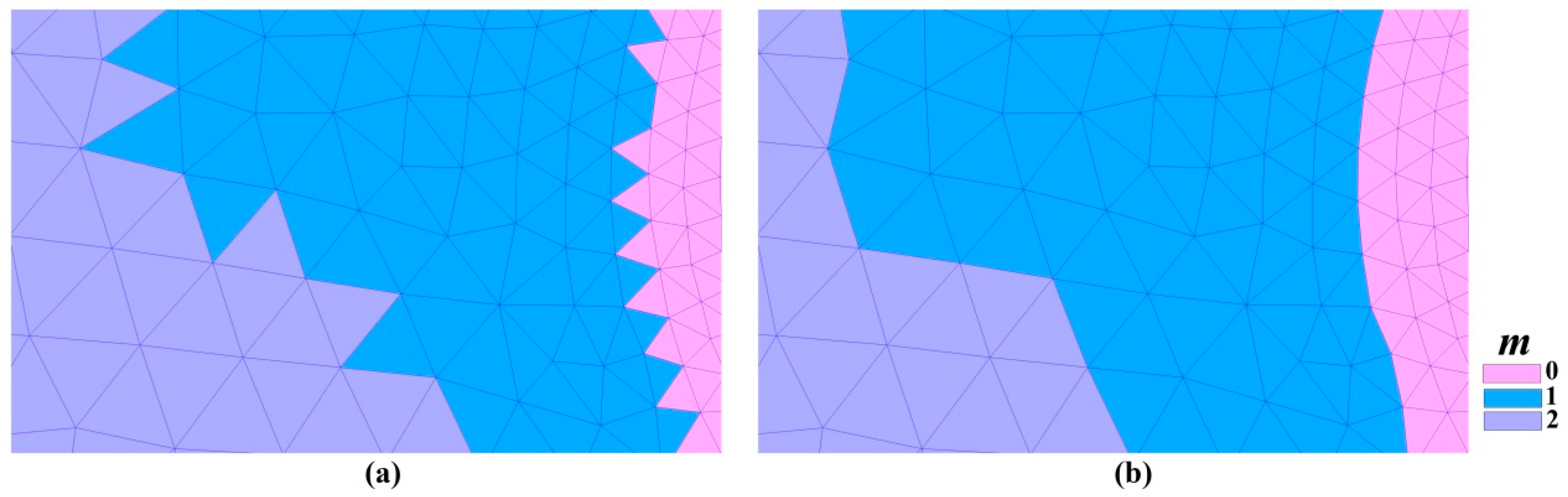
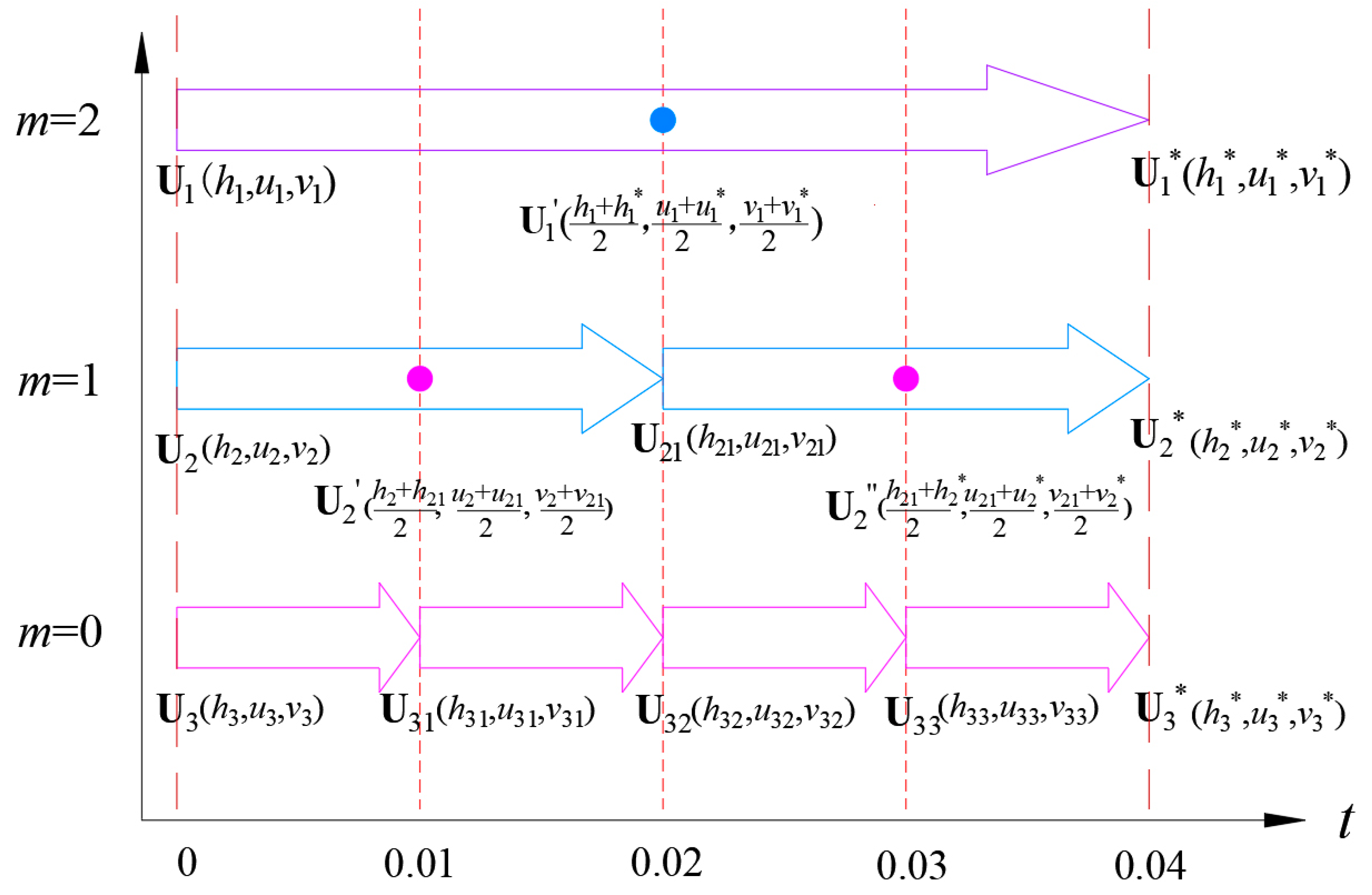
2.2.1. Reconstructing the Local Time Step of Each Cell
2.2.2. Calculation of Element Variables at the Interface
3. Numerical Tests
3.1. Anti-Symmetric Dam Break Case
3.2. Non-Flat Bottom Dam Break Case
3.3. Navigable Flow Simulation Case
4. Discussion
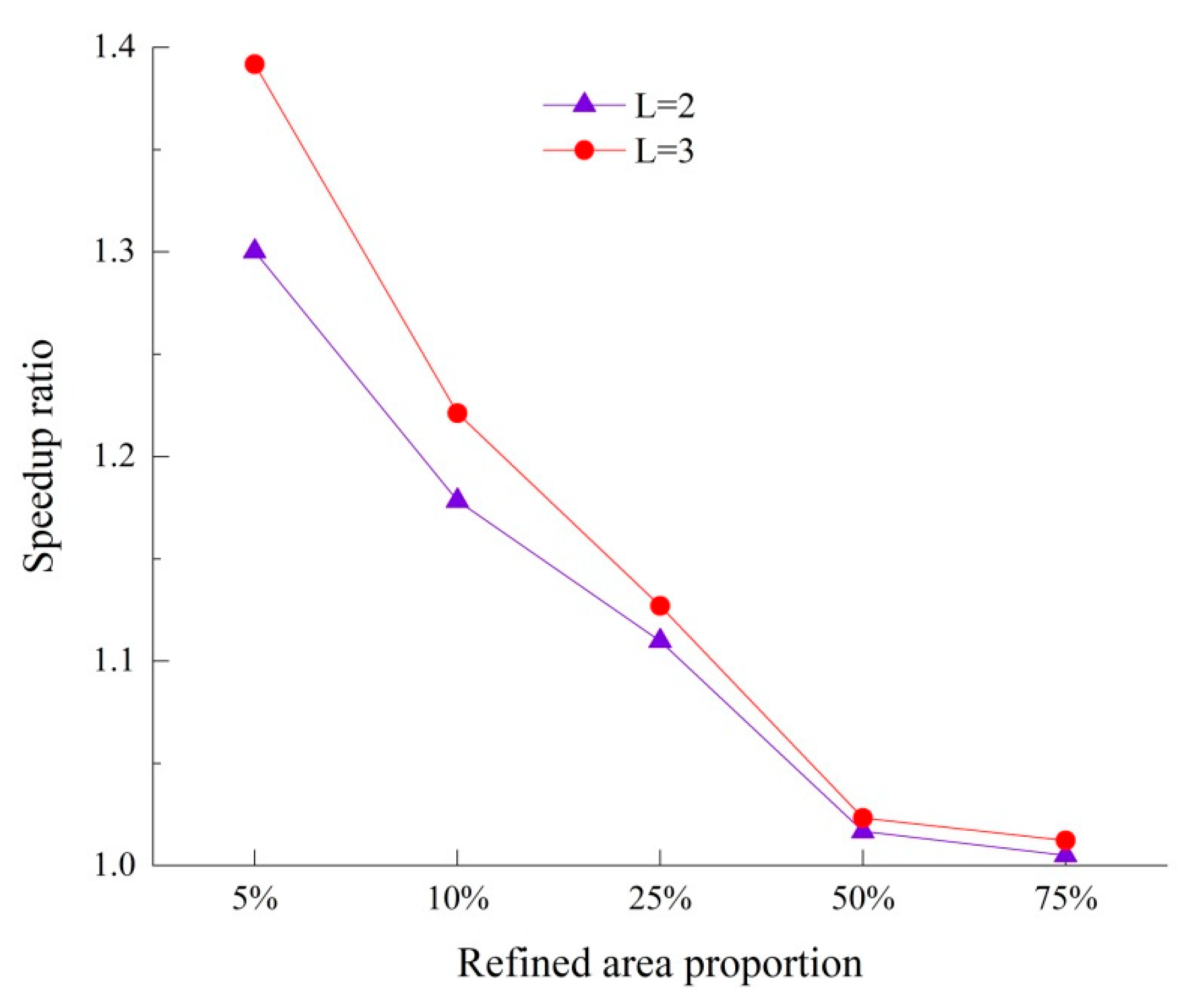
4.1. The Influence of the Proportion of Refined Mesh on the Acceleration Effect
4.2. The Impact of the Different Scale of the Mesh on Acceleration Effect
5. Conclusions
- (1)
- Based on the FVM for unstructured grids, an LTS algorithm was implemented that improved the computational efficiency of the model, while satisfying water conservation conditions. In the anti-symmetric dam break case, a speedup ratio of 2.1 was achieved, which saved 53% in execution time. The speedup ratio of the non-flat bottom dam break case was 1.3, which represented a shortening of 26% in the calculation time. The numerical simulation of the navigable flow of the river reach between the Three Gorges and Gezhouba Dams achieved a speedup ratio of 1.9, which represented a saving of 49% in modeling time.
- (2)
- The proportions of coarse to refined meshes on the acceleration effect of the LTS algorithm were noticeable. It was evident that a higher speedup ratio was obtained when the proportion of the refined mesh was minimized. When the proportion of the refined mesh was high, the acceleration effect was not significant. It is clear that the LTS algorithm is best suited to situations in which refinement is only required in small regions.
- (3)
- When using the LTS algorithm on non-uniform unstructured grids, the larger the grid scale difference, the more obvious the grid layering became. This led to increased acceleration effects. However, computational accuracy was slightly impaired by excessive differences in grid mesh size.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Gang, Y.; Jin, S. Numerical modeling of 2D shallow water flow with complicated geometry and topography. J. Hydraul. Eng. 2005, 36, 439–444. (In Chinese) [Google Scholar]
- Jin, H.; Jespersen, D.; Mehrotra, P.; Biswas, R.; Huang, L.; Chapman, B. High performance computing using MPI and OpenMP on multi-core parallel systems. Parallel Comput. 2011, 37, 562–575. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, Z.; Yuan, R.; Jiang, X. Parallel computation of a dam-break flow model using OpenMP on a multi-core computer. J. Hydrol. 2014, 512, 126–133. [Google Scholar] [CrossRef]
- Vacondio, R.; Dal Palù, A.; Ferrari, A.; Mignosa, P.; Aureli, F.; Dazzi, S. A non-uniform efficient grid type for GPU-parallel Shallow Water Equations models. Environ. Model. Softw. 2017, 88, 119–137. [Google Scholar] [CrossRef]
- Dawson, C. High Resolution Schemes For Conservation Laws With Locally Varying Time Steps. SIAM J. Sci. Comput. 2000, 22, 2256–2281. [Google Scholar] [CrossRef]
- Sanders, B.F. Integration of a shallow water model with a local time step. J. Hydraul. Res. 2008, 46, 466–475. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. RKDG2 shallow-water solver on non-uniform grids with local time steps: Application to 1D and 2D hydrodynamics. Appl. Math. Model. 2015, 39, 1317–1340. [Google Scholar] [CrossRef]
- Caboussat, A.; Boyaval, S.; Masserey, A. On the modeling and simulation of non-hydrostatic dam break flows. Comput. Vis. Sci. 2011, 14, 401–417. [Google Scholar] [CrossRef][Green Version]
- Li, D.; Zeng, Q.; Feng, H. A P-adaptive Discontinuous Galerkin Method Using Local Time-stepping Strategy Applied to the Shallow Water Equations. J. Inf. Comput. Sci. 2013, 10, 2199–2210. [Google Scholar] [CrossRef]
- Tirupathi, S.; Hesthaven, J.S.; Liang, Y.; Parmentier, M. Multilevel and local time-stepping discontinuous Galerkin methods for magma dynamics. Comput. Geosci. 2015, 19, 965–978. [Google Scholar] [CrossRef]
- Zhou, W.; Ouyang, J.; Wang, X.; Su, J.; Yang, B. Numerical simulation of viscoelastic fluid flows using a robust FVM framework on triangular grid. J. Non-Newton. Fluid Mech. 2016, 236, 18–34. [Google Scholar] [CrossRef]
- Cheng, L.; Hu, C. An adaptive multi-moment FVM approach for incompressible flows. J. Comput. Phys. 2018, 359, 239–262. [Google Scholar]
- Osher, S.; Sanders, R. Numerical approximations to nonlinear conservation laws with locally varying time and space grids. Math. Comput. 1983, 41, 321–336. [Google Scholar] [CrossRef]
- Tan, Z.; Huang, Y. An Adaptive Grid Method with Local Time Stepping for One Dimensional Conservation Laws. Nat. Sci. J. Xiangtan Univ. 2003, 25, 110–116. (In Chinese) [Google Scholar]
- Crossley, A.J.; Wright, N.G.; Whitlow, C.D. Local time stepping for modeling open channel flows. J. Hydraul. Eng. 2003, 129, 455–462. [Google Scholar] [CrossRef]
- Crossley, A.J.; Wright, N.G. Time accurate local time stepping for the unsteady shallow water equations. Int. J. Numer. Methods Fluids 2005, 48, 775–799. [Google Scholar] [CrossRef]
- Dazzi, S.; Maranzoni, A.; Mignosa, P. Local time stepping applied to mixed flow modelling. J. Hydraul. Res. 2016, 54, 145–157. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Dal Palù, A.; Mignosa, P. A local time stepping algorithm for GPU-accelerated 2D shallow water models. Adv. Water Resour. 2018, 111, 274–288. [Google Scholar] [CrossRef]
- Wu, D.; Yu, X.; Xu, Y. A Discontinuous Galerkin Method with Local Time Stepping for Euler Equations. Chin. J. Comput. Phys. 2016, 28, 1–9. (In Chinese) [Google Scholar]
- Trahan, C.J.; Dawson, C. Local time-stepping in Runge–Kutta discontinuous Galerkin finite element methods applied to the shallow-water equations. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 139–152. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.; Han, J.; Cao, Z.; Liu, H.; He, Z. Computationally efficient modeling of hydro–sediment-morphodynamic processes using a hybrid local time step/global maximum time step. Adv. Water Resour. 2019, 127, 26–38. [Google Scholar] [CrossRef]
- Baldauf, M. Local time stepping for a mass-consistent and time split advection scheme. R. Meteorol. Soc. 2019, 145, 337–346. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Thompson, J.F.; Warsi, Z.U.A.; Mastin, C.W. Numerical Grid Generation; North Holland: New York, NY, USA, 1985; Chapter 6; pp. 129–165. [Google Scholar]
- Pan, C. Advanced in numerical simulation of discontinuous shallow water flows. Adv. Sci. Technol. Water Resour. 2010, 30, 77–84. (In Chinese) [Google Scholar]
- Zhang, D.; Li, D.; Wang, X. Numerical modeling of dam-break water flow with wetting and drying change based on unstructured grids. J. Hydroelectr. Eng. 2008, 27, 98–102. (In Chinese) [Google Scholar]
- Murillo, J.; García-Navarro, P. Wave Riemann description of friction terms in unsteady shallow flows: Application to water and mud/debris floods. J. Comput. Phys. 2012, 231, 1963–2001. [Google Scholar] [CrossRef]
- Vacondio, R.; Dal Palù, A.; Mignosa, P. GPU-enhanced Finite Volume Shallow Water solver for fast flood simulations. Environ. Model. Softw. 2014, 57, 60–75. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; Morales-Hernández, M.; García-Navarro, P. Implicit finite volume simulation of 2D shallow water flows in flexible meshes. Comput. Methods Appl. Mech. Eng. 2018, 328, 1–25. [Google Scholar] [CrossRef]
- Brufau, P.; Vázquez-Cendón, M.E.; García-Navarro, P. A numerical model for the flooding and drying of irregular domains. Int. J. Numer. Methods Fluids 2002, 39, 247–275. [Google Scholar] [CrossRef]
- Lv, B.; Jin, S.; Ai, C. Well-balanced Roe-type scheme for 2D shallow water flow using unstructured grids. Hydro-Sci. Eng. 2010, 2, 39–44. (In Chinese) [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 87–114. [Google Scholar]
- Fennema, R.J.; Chaudhry, M.H. Explicit methods for 2-D transient free surface flows. J. Hydraul. Eng. 1990, 116, 1013–1034. [Google Scholar] [CrossRef]
- Wang, D. Computational Hydraulics: Theory and Application; Science Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Liu, H.; Zhou, J.G.; Burrows, R. Lattice Boltzmann simulations of the transient shallow water flows. Adv. Water Resour. 2010, 33, 387–396. [Google Scholar] [CrossRef]
- Baghlani, A. Simulation of dam-break problem by a robust flux-vector splitting approach in Cartesian grid. Sci. Iran. 2011, 18, 1061–1068. [Google Scholar] [CrossRef]
- Hu, P.; Han, J.; Lei, Y. Coupled modeling of sediment-laden flows based on local-time-step approach. J. Zhejiang Univ. (Eng. Sci.) 2019, 53, 743–752. (In Chinese) [Google Scholar]
- Kawahara, M.; Umetsu, T. Finite element method for moving boundary problems in river flow. Int. J. Numer. Methods Fluids 1986, 6, 365–386. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Bi, S.; Song, L.X. Two-dimensional shallow hydrodynamic model based on adaptive structured grid. Chin. J. Hydrodyn. 2012, 27, 667–678. (In Chinese) [Google Scholar]
- Yan, W.; Zhou, R.; Cheng, Z.; Yang, W.; Lu, H. Adaptation of fleets to the navigation discharge in the waterway between Three Gorges Project and Gezhouba Hydroproject. J. Yangtze River Sci. Res. Inst. 2013, 6, 33–37. (In Chinese) [Google Scholar]
- Zhang, S.; Jing, Z.; Li, W.; Wang, L.; Liu, D.; Wang, T. Navigation risk assessment method based on flow conditions: A case study of the river reach between the Three Gorges Dam and the Gezhouba Dam. Ocean Eng. 2019, 175, 71–79. [Google Scholar] [CrossRef]
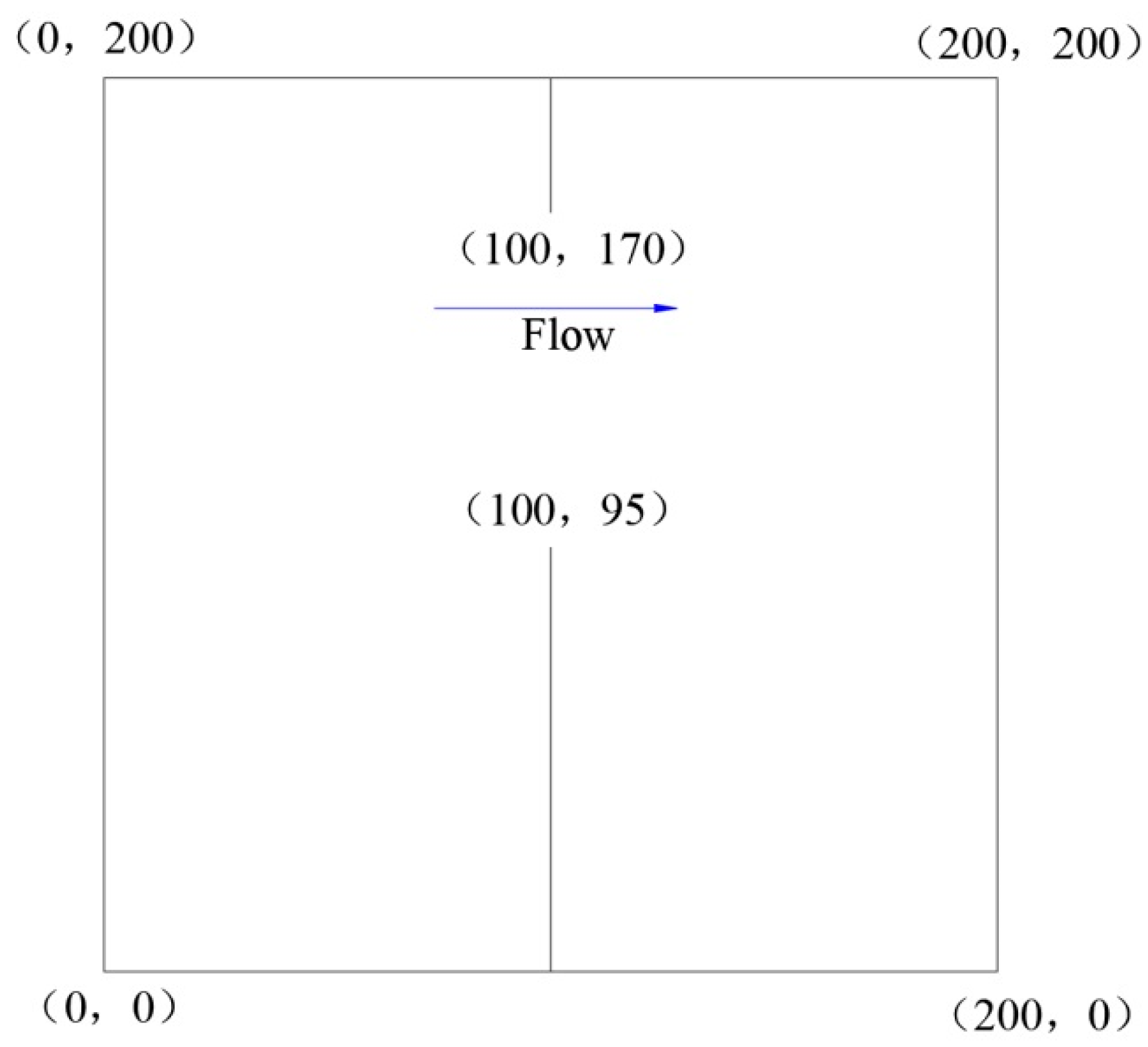

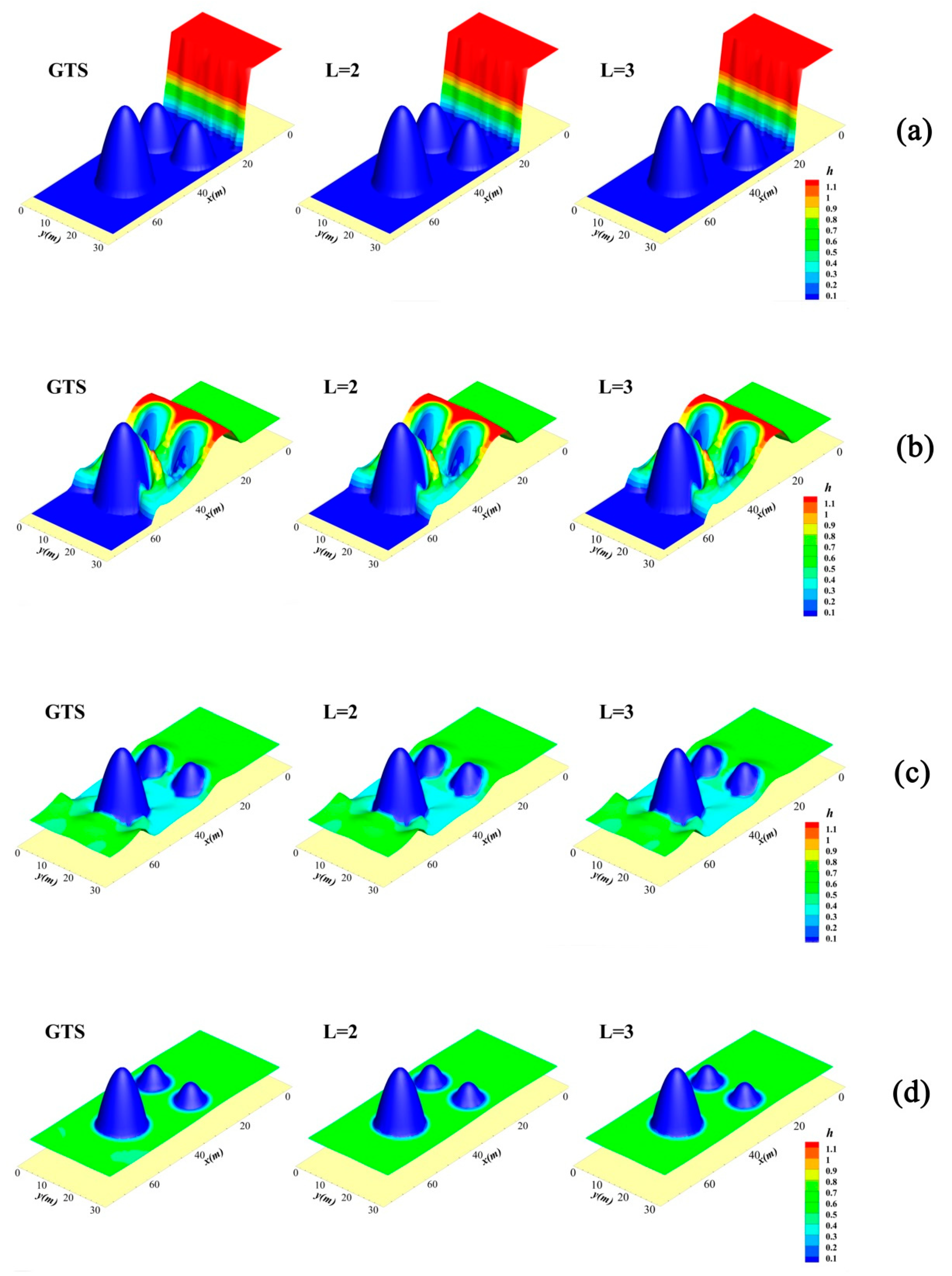
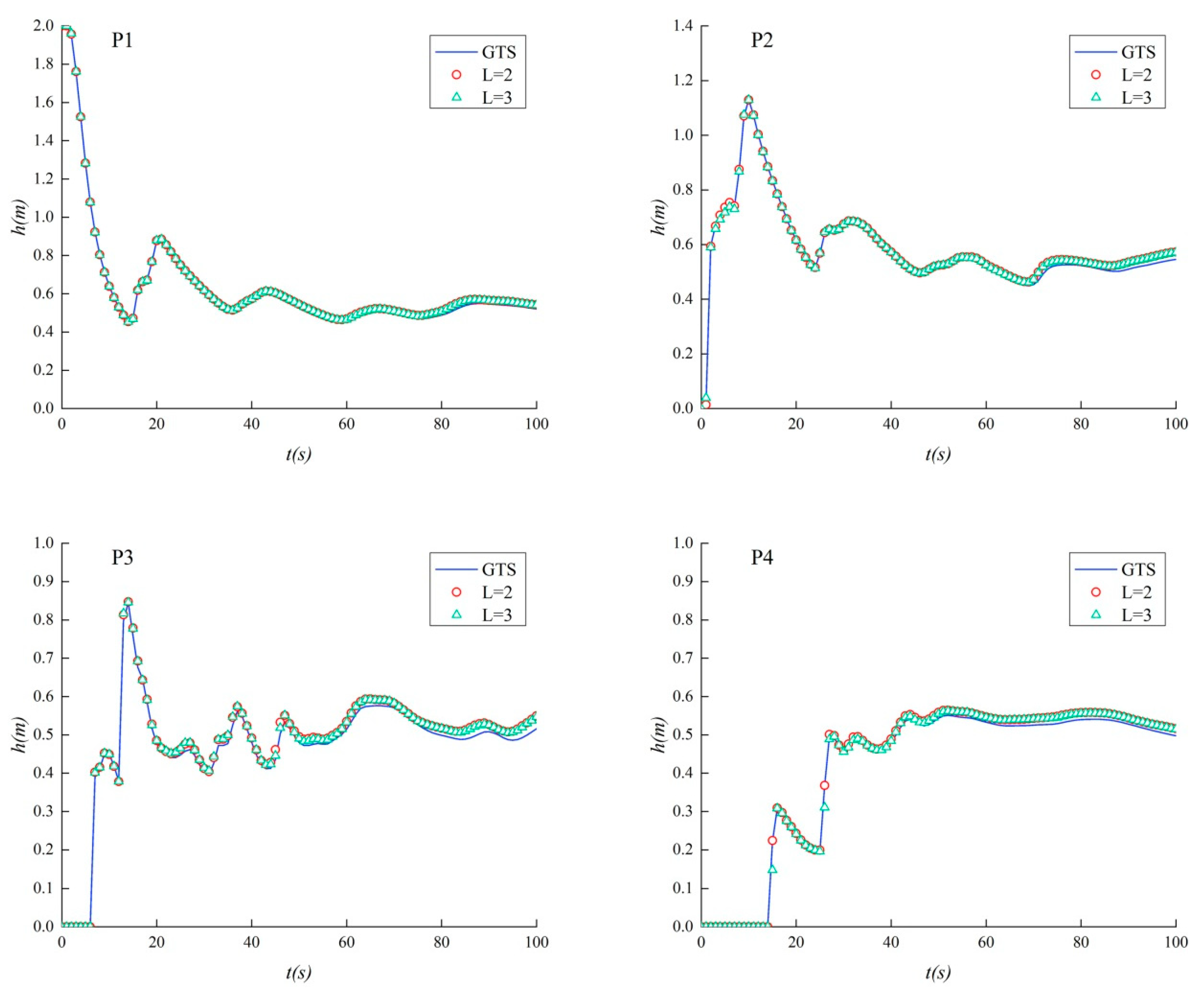

| t(s) | L = 2 | L = 3 | L = 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ls(u) × 10−2 | Ls(v) × 10−2 | Ls(h) × 10−2 | Ls(u) × 10−2 | Ls(v) × 10−2 | Ls(h) × 10−2 | Ls(u) × 10−2 | Ls(v) × 10−2 | Ls(h) × 10−2 | |
| 7.2 | 0.41 | 0.38 | 0.22 | 0.65 | 0.56 | 0.50 | 1.07 | 0.71 | 0.79 |
| 15.2 | 0.34 | 0.31 | 0.17 | 0.65 | 0.64 | 0.45 | 1.02 | 0.67 | 0.87 |
| 23.2 | 0.50 | 0.43 | 0.39 | 1.02 | 0.81 | 1.07 | 1.84 | 1.20 | 1.99 |
| 31.2 | 0.66 | 0.72 | 0.57 | 1.53 | 1.45 | 1.39 | 2.81 | 2.63 | 2.62 |
| 39.2 | 0.74 | 0.75 | 0.29 | 1.34 | 1.37 | 0.62 | 2.43 | 2.40 | 1.04 |
| 47.2 | 0.55 | 0.70 | 0.30 | 0.89 | 1.24 | 0.72 | 2.03 | 3.31 | 1.63 |
| 55.2 | 0.55 | 0.71 | 0.36 | 0.84 | 1.06 | 0.96 | 1.72 | 2.16 | 1.76 |
| 63.2 | 0.51 | 0.60 | 0.31 | 0.95 | 1.18 | 0.86 | 1.63 | 3.12 | 2.14 |
| 71.2 | 0.71 | 0.70 | 0.30 | 1.17 | 1.25 | 0.68 | 2.82 | 2.81 | 1.46 |
| 79.2 | 0.64 | 0.63 | 0.27 | 1.10 | 1.05 | 0.74 | 2.54 | 2.32 | 1.50 |
| 120 | 0.67 | 0.63 | 0.18 | 1.33 | 1.12 | 0.47 | 2.69 | 2.26 | 1.10 |
| 160 | 0.61 | 0.56 | 0.24 | 1.03 | 0.97 | 0.70 | 2.35 | 2.26 | 1.85 |
| average | 0.57 | 0.59 | 0.30 | 1.04 | 1.06 | 0.76 | 2.08 | 2.15 | 1.56 |
| Test | T | ||
|---|---|---|---|
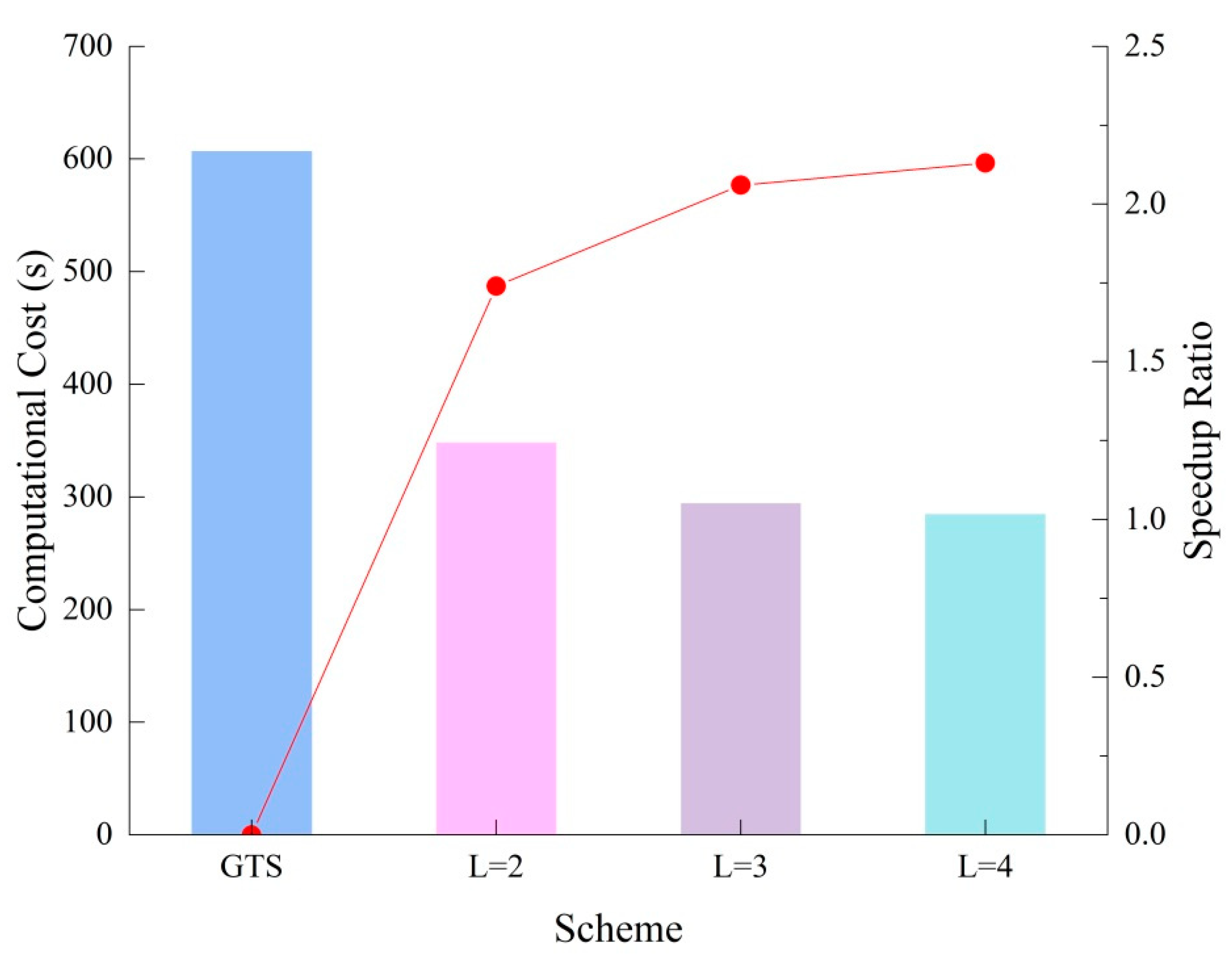
| GTS | 608 | - | - |
| L = 2 | 349 | 43 | 1.74 |
| L = 3 | 295 | 51 | 2.06 |
| L = 4 | 285 | 53 | 2.13 |
| Test | T | ||
|---|---|---|---|
| GTS | 148 | - | - |
| L = 2 | 115 | 22 | 1.28 |
| L = 3 | 110 | 26 | 1.34 |
| Data | River Reach | Water Level (m) | Flow Velocity (m/s) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Observation Time | Discharge (m3/s) | Measured | Calculated | Measured | Calculated | ||||||||||
| GTS | L = 2 | L = 3 | L = 4 | L = 5 | GTS | L = 2 | L = 3 | L = 4 | L = 5 | ||||||
| 2008.08.20 | 28,400 | Letianxi | Value | 68.32 | 68.39 | 68.39 | 68.39 | 68.39 | 68.39 | 1.56 | 1.63 | 1.63 | 1.63 | 1.63 | 1.63 |
| Deviation | - | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | - | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | |||
| 2008.08.20 | 29,700 | Liantuo | Value | 68.35 | 68.41 | 68.41 | 68.41 | 68.41 | 68.41 | 2.13 | 2.16 | 2.16 | 2.16 | 2.16 | 2.16 |
| Deviation | - | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | - | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | |||
| 2008.09.04 | 31,700 | Shipai | Value | 67.83 | 67.90 | 67.90 | 67.90 | 67.90 | 67.90 | 1.61 | 1.55 | 1.55 | 1.55 | 1.55 | 1.55 |
| Deviation | - | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | - | −0.06 | −0.06 | −0.06 | −0.06 | −0.06 | |||
| T | 6.65 | 3.86 | 3.56 | 3.45 | 3.39 | ||||||||||
| Tr | - | 41.96 | 46.47 | 48.06 | 48.96 | ||||||||||
| Sn | - | 1.72 | 1.87 | 1.93 | 1.96 | ||||||||||
| Refined Area Proportion | Refined Area (hm2) | Total Grid Number | Test | |||
|---|---|---|---|---|---|---|
| Index | GTS | L = 2 | L = 3 | |||
| 5% | 0.2 | 13,338 | T | 608 | 467 | 436 |
| - | 23% | 28% | ||||
| - | 1.30 | 1.39 | ||||
| 10% | 0.4 | 18,986 | T | 857 | 727 | 702 |
| - | 15% | 18% | ||||
| - | 1.18 | 1.22 | ||||
| 25% | 1 | 32,230 | T | 1474 | 1328 | 1308 |
| - | 9.8% | 11.3% | ||||
| - | 1.11 | 1.13 | ||||
| 50% | 2 | 48,622 | T | 2234 | 2197 | 2183 |
| - | 1.6% | 2.3% | ||||
| - | 1.01 | 1.02 | ||||
| 75% | 3 | 73,306 | T | 3393 | 3376 | 3352 |
| - | 0.5% | 0.5% | ||||
| - | 1.01 | 1.01 | ||||
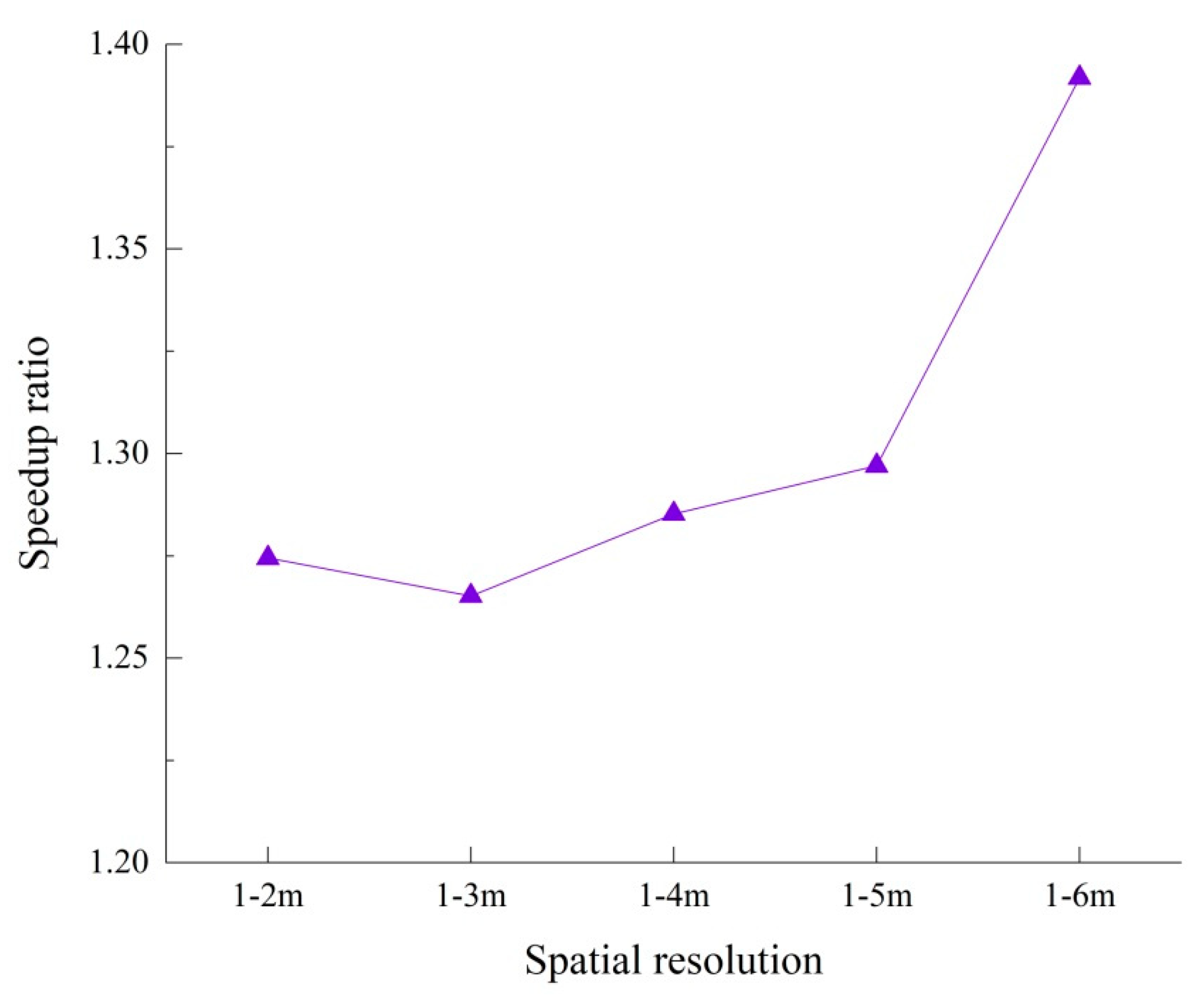
| Spatial Resolution | Grid Number | Test | ||
|---|---|---|---|---|
| Index | GTS | LTS | ||
| 1–2 m | 35,104 | T | 1558 | 1223 |
| - | 22% | |||
| - | 1.27 | |||
| 1–3 m | 22,084 | T | 973 | 769 |
| - | 21% | |||
| - | 1.26 | |||
| 1–4 m | 17,108 | T | 757 | 589 |
| - | 22% | |||
| - | 1.28 | |||
| 1–5 m | 14,380 | T | 641 | 494 |
| - | 23% | |||
| - | 1.30 | |||
| 1–6 m | 13,338 | T | 608 | 436 |
| - | 28% | |||
| - | 1.39 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; An, W.; Li, W.; Zhang, S. Implementation of a Local Time Stepping Algorithm and Its Acceleration Effect on Two-Dimensional Hydrodynamic Models. Water 2020, 12, 1148. https://doi.org/10.3390/w12041148
Yang X, An W, Li W, Zhang S. Implementation of a Local Time Stepping Algorithm and Its Acceleration Effect on Two-Dimensional Hydrodynamic Models. Water. 2020; 12(4):1148. https://doi.org/10.3390/w12041148
Chicago/Turabian StyleYang, Xiyan, Wenjie An, Wenda Li, and Shanghong Zhang. 2020. "Implementation of a Local Time Stepping Algorithm and Its Acceleration Effect on Two-Dimensional Hydrodynamic Models" Water 12, no. 4: 1148. https://doi.org/10.3390/w12041148
APA StyleYang, X., An, W., Li, W., & Zhang, S. (2020). Implementation of a Local Time Stepping Algorithm and Its Acceleration Effect on Two-Dimensional Hydrodynamic Models. Water, 12(4), 1148. https://doi.org/10.3390/w12041148




