Linear or Nonlinear Modeling for ENSO Dynamics?
Abstract
1. Non-Gaussian-Nonlinear Features of the ENSO Statistics
2. The Dynamics of the Components of the ENSO: The Recharge Oscillator Model
3. Is a Possible Internal Nonlinearity Relevant?
4. The Multiplicative Nature of the Forcing
5. The Fokker–Planck Equation Guiding the Statistics of the ROM
6. Inference of the Statistical Features of the ROM from Observations
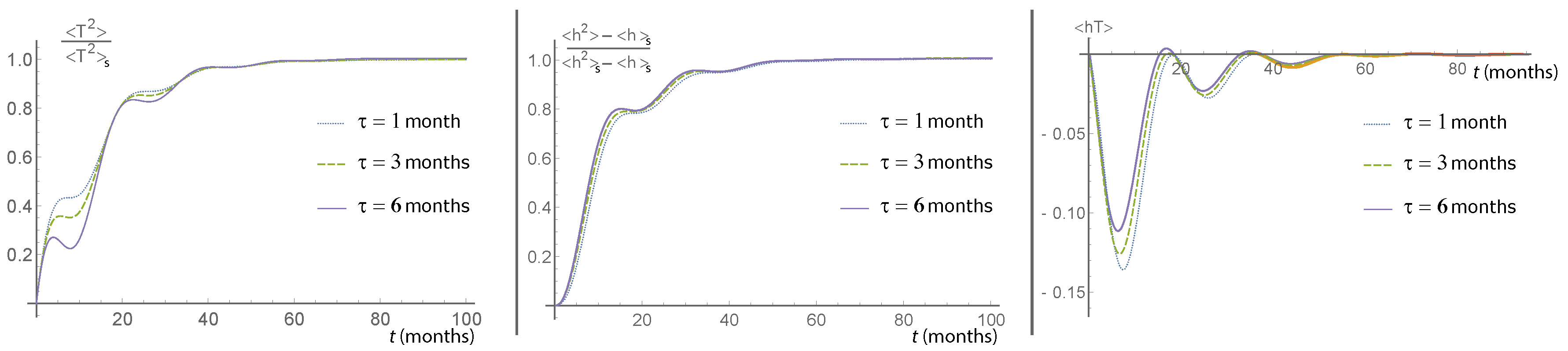
6.1. Linear Equation of Motion for the First Two Moments of the ROM and the White Noise Approximation
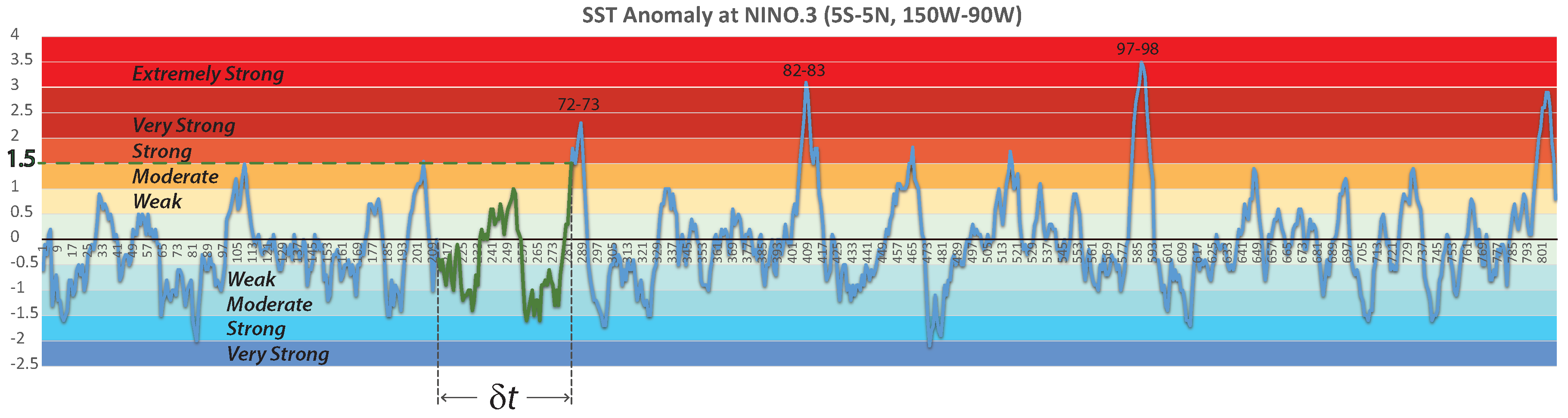
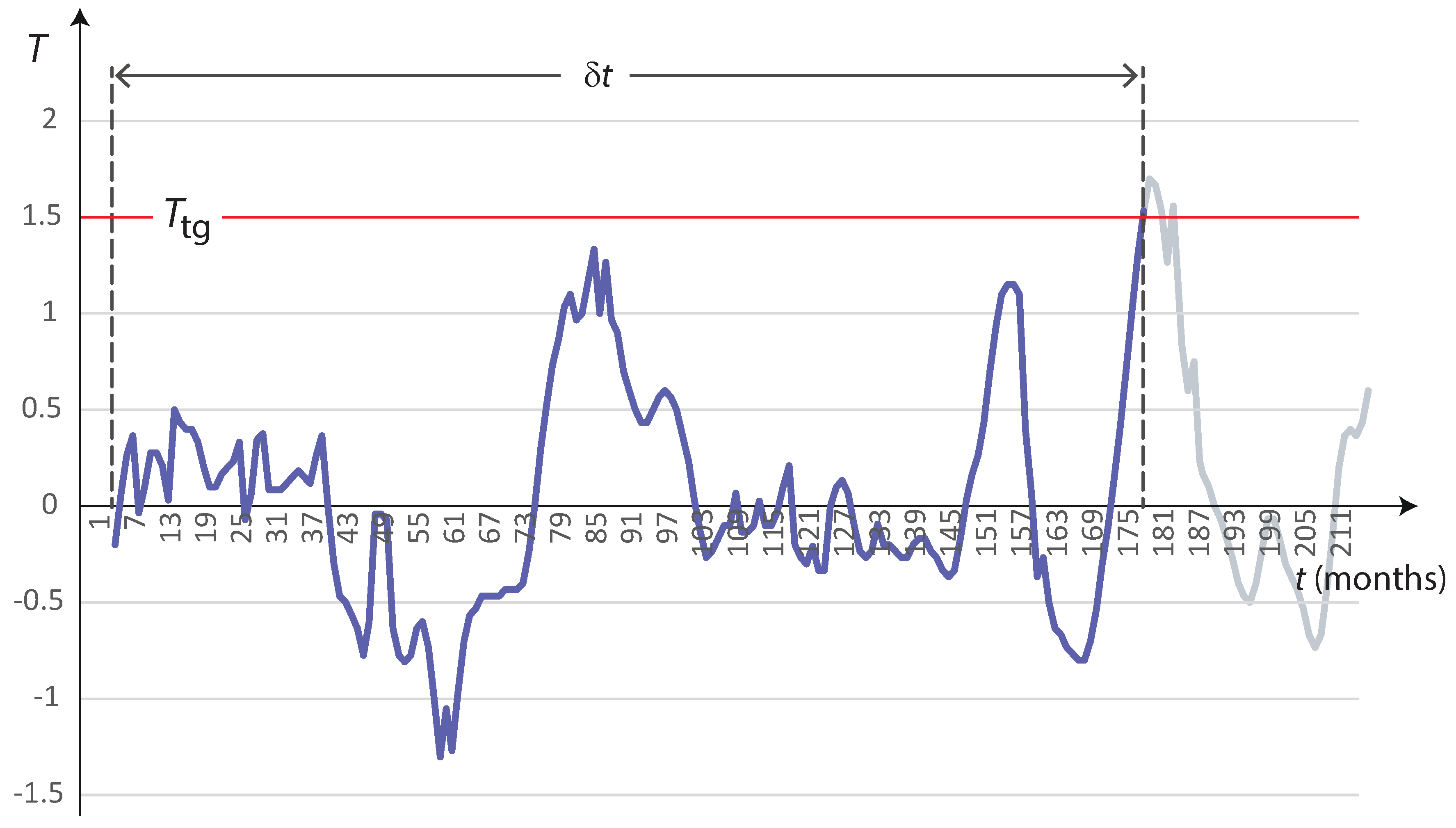
- analyzing only the first and second moments/cumulants/cross-correlation functions of the observations data, we cannot identify/detect the (possible) nonlinearity due to the interaction with the atmosphere, in the ENSO system;
- comparing the first and second moments/cumulants/cross-correlation functions, we obtain from the FPE of Equation (18) with observations, it would be really hard to determine how small the time scale of decaying of the correlation function of the effective noise perturbing the ROM is. On the other hand, as has been shown in [17], also for , the FPE of Equation (18) well accounts for the non-Gaussianity of the ENSO statistics. Thus, for the sake of simplicity, from now on, we shall use the FPE of Equation (17), which is the white noise limit of Equation (18), even if we are aware of the fact that the time scale separation between the dynamics of the averaged ROM and that of the fast atmosphere is not so “extreme”.
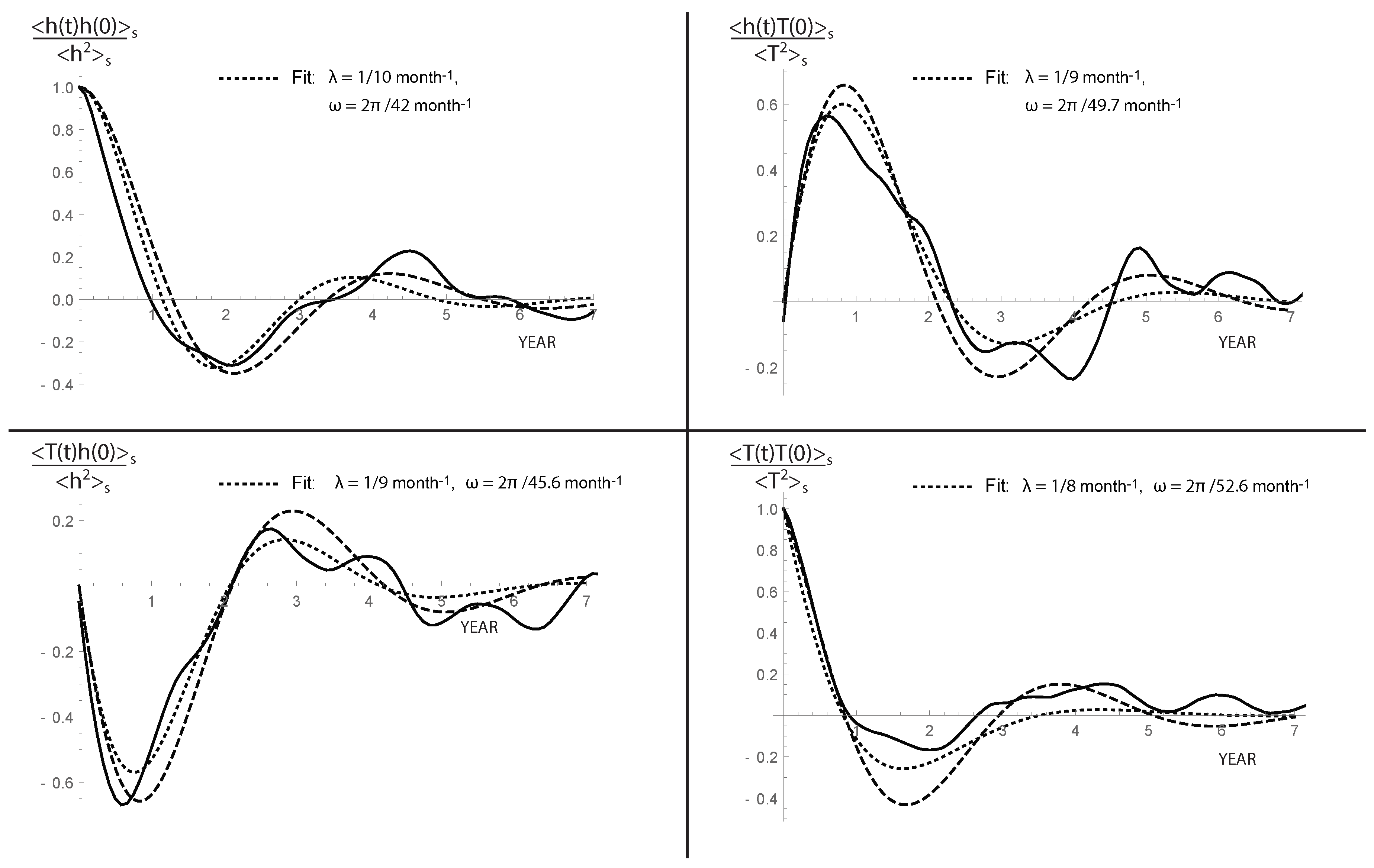
6.2. The Covariance Matrix of the ROM and the Comparison with the ENSO Data
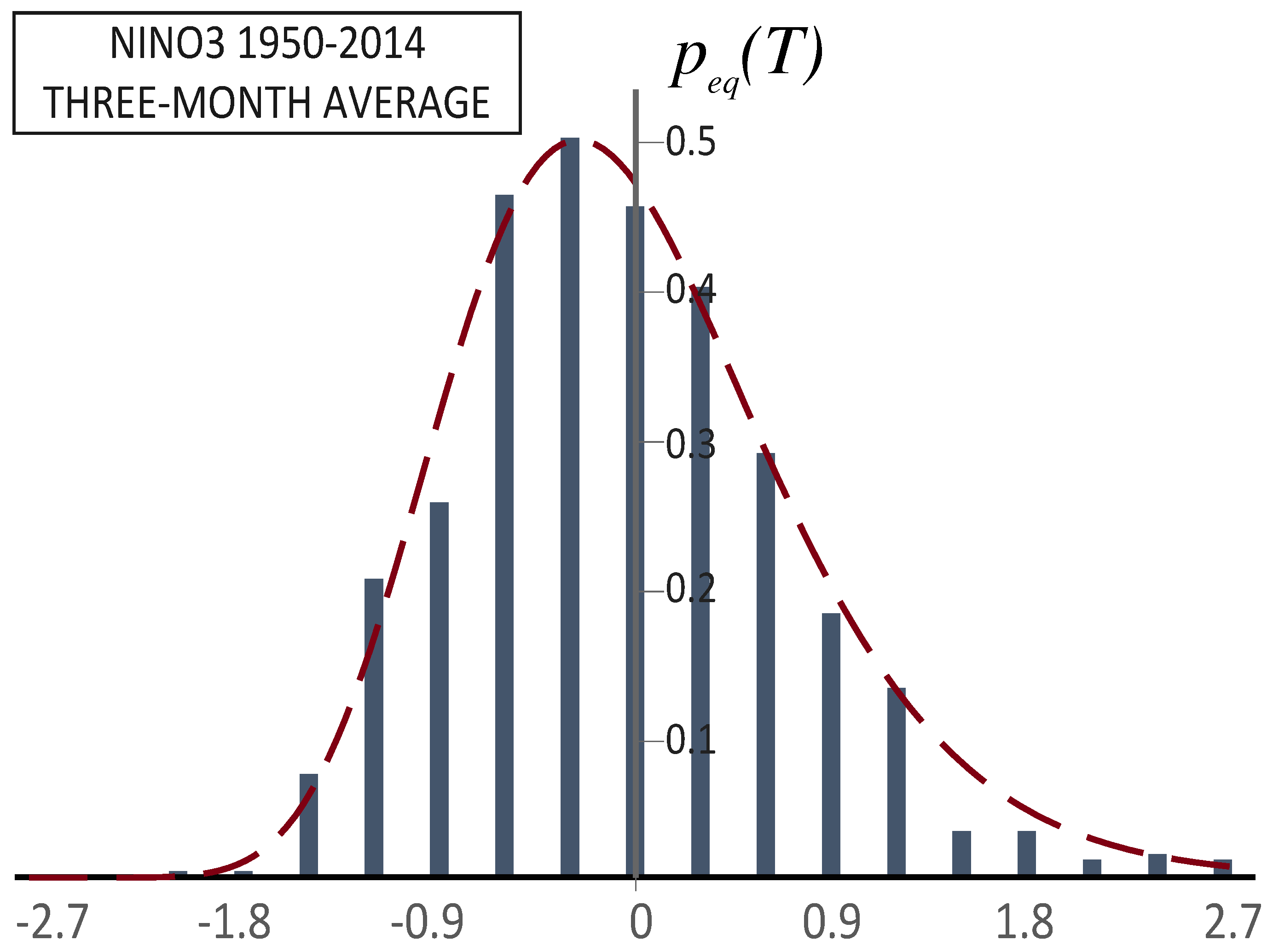
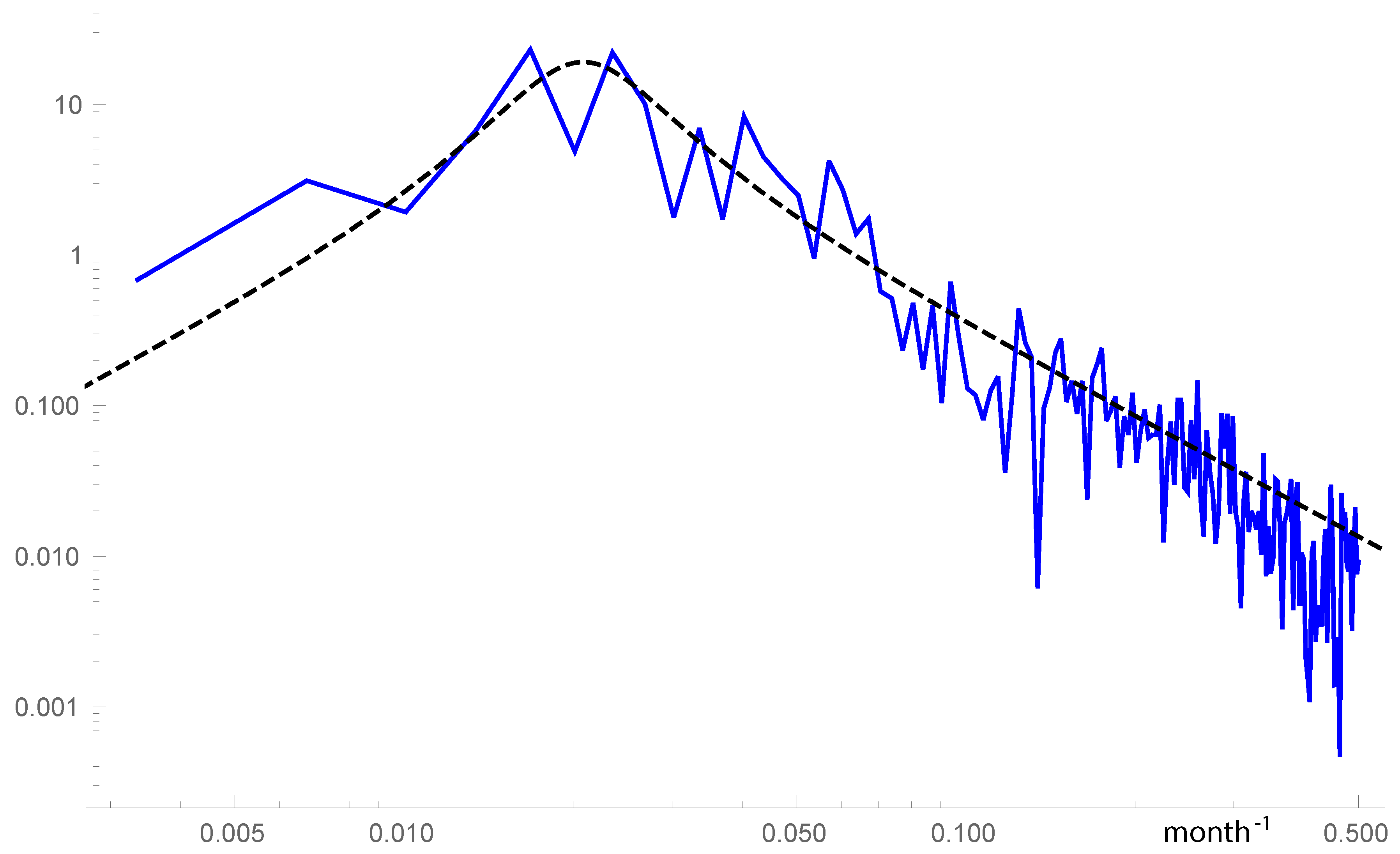
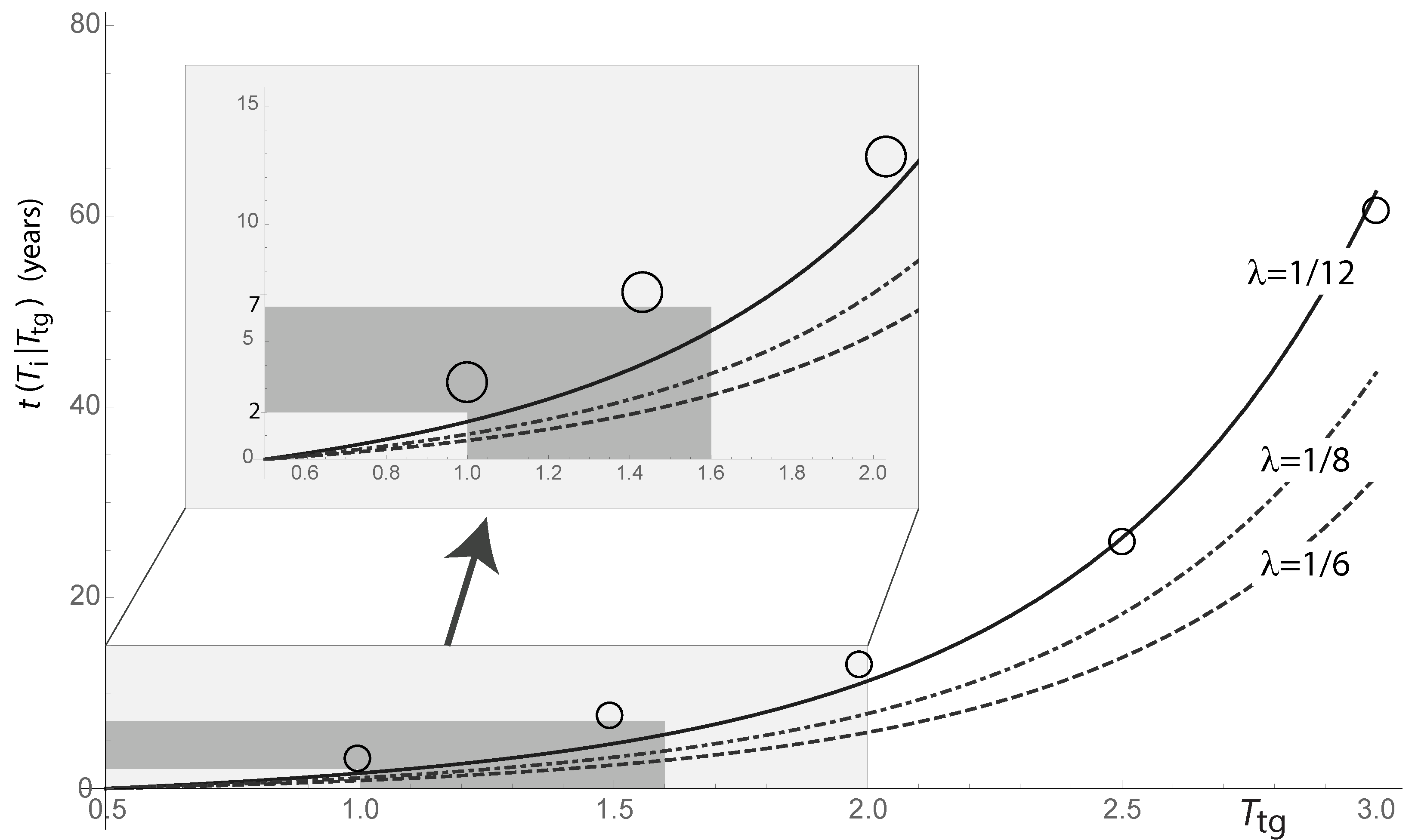
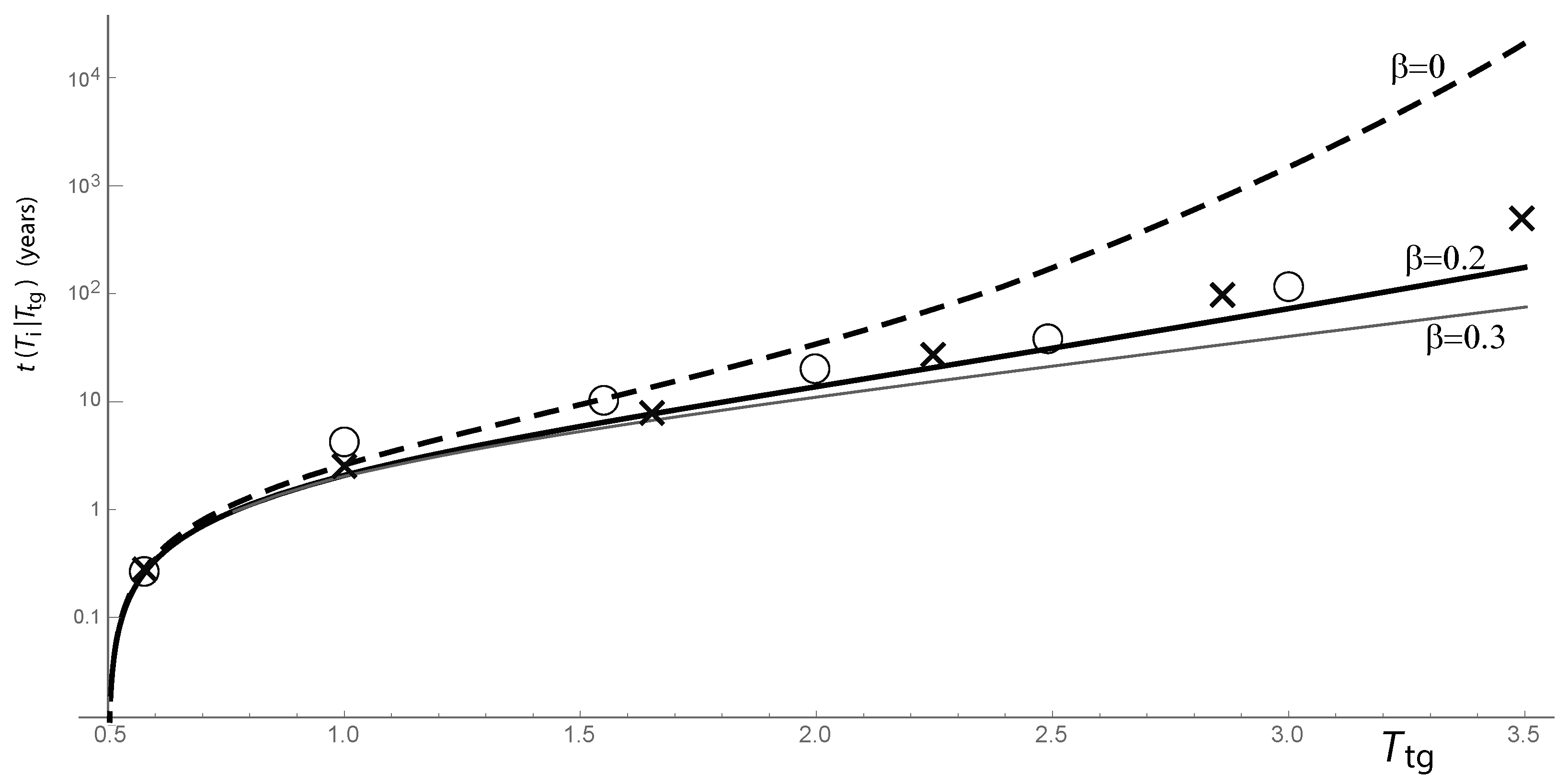
6.3. Signatures of a Nonlinear Perturbation: Skewed Stationary PDF and High Frequency of Strong Events
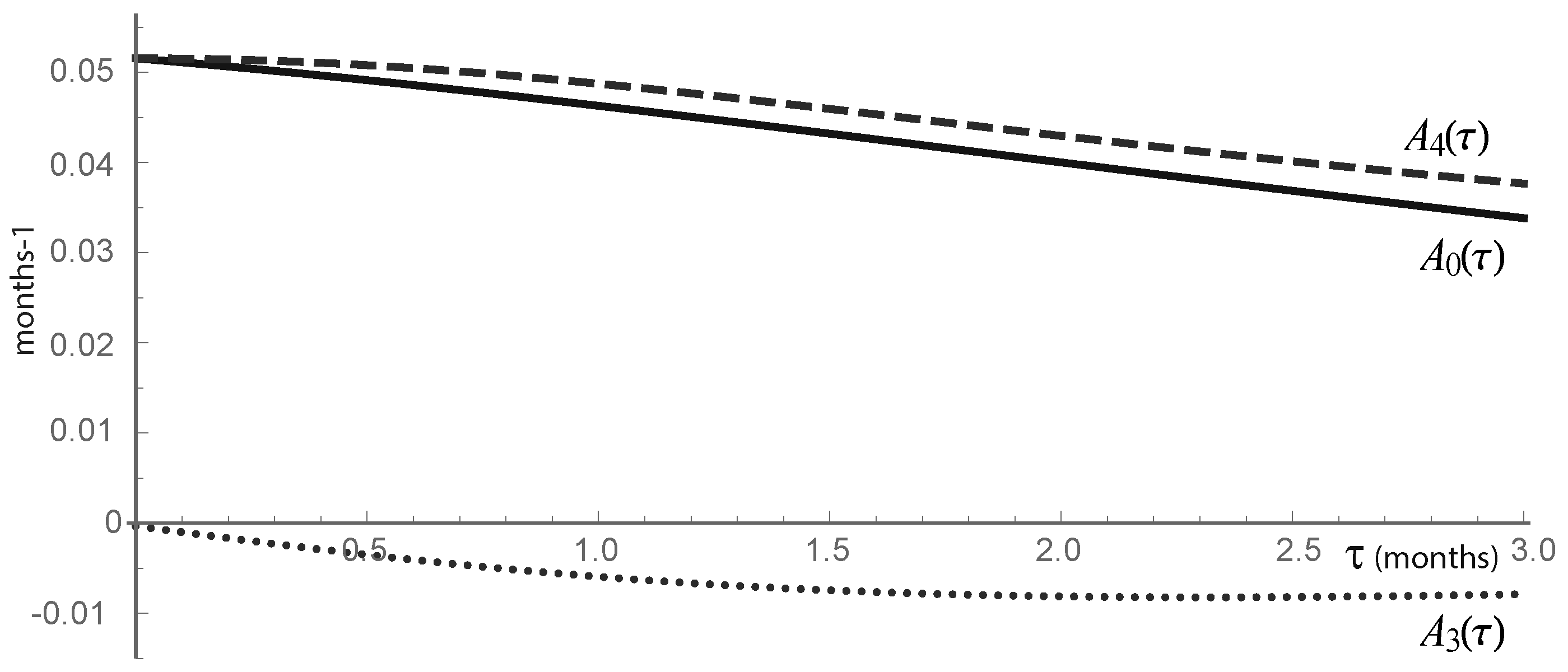
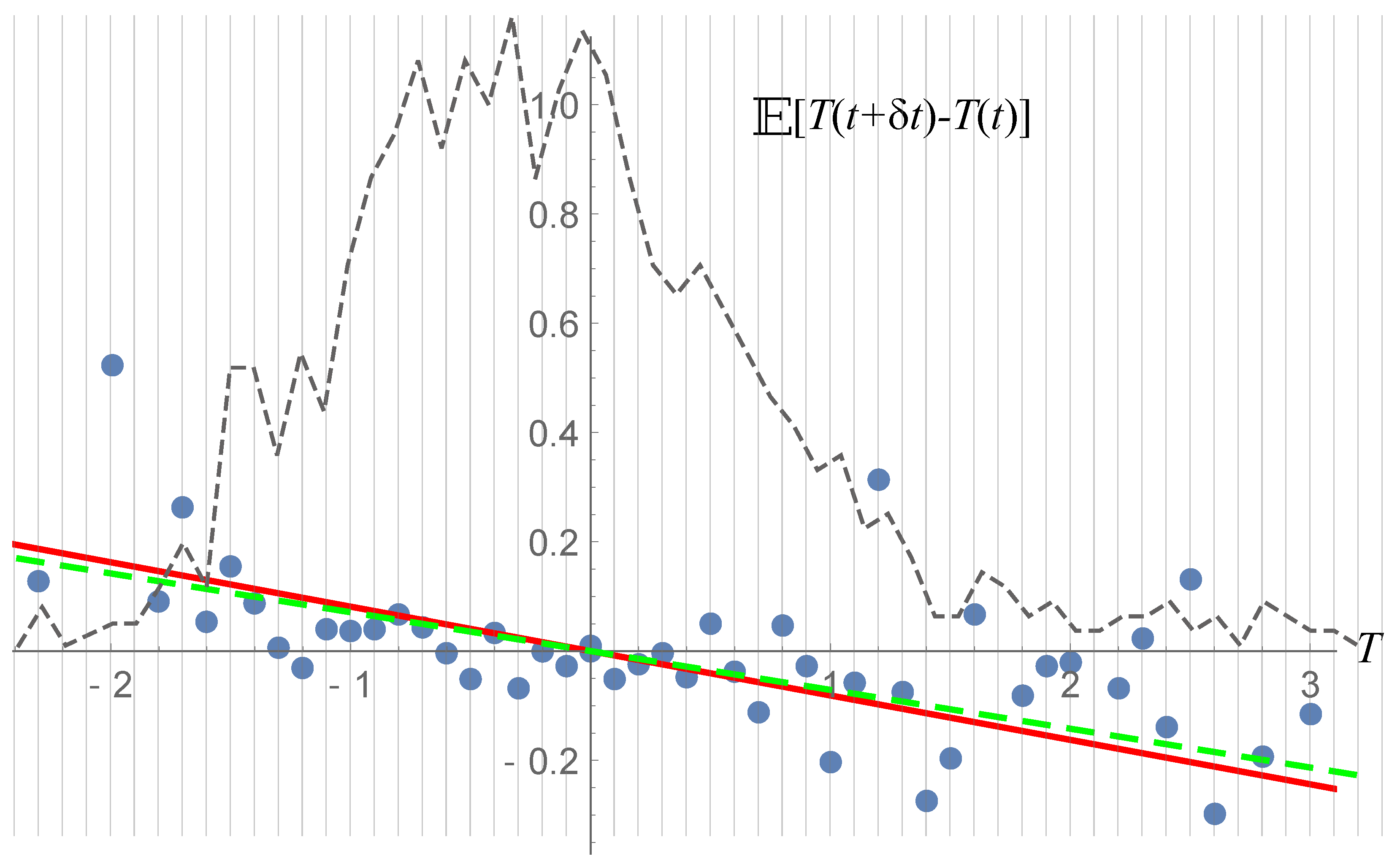
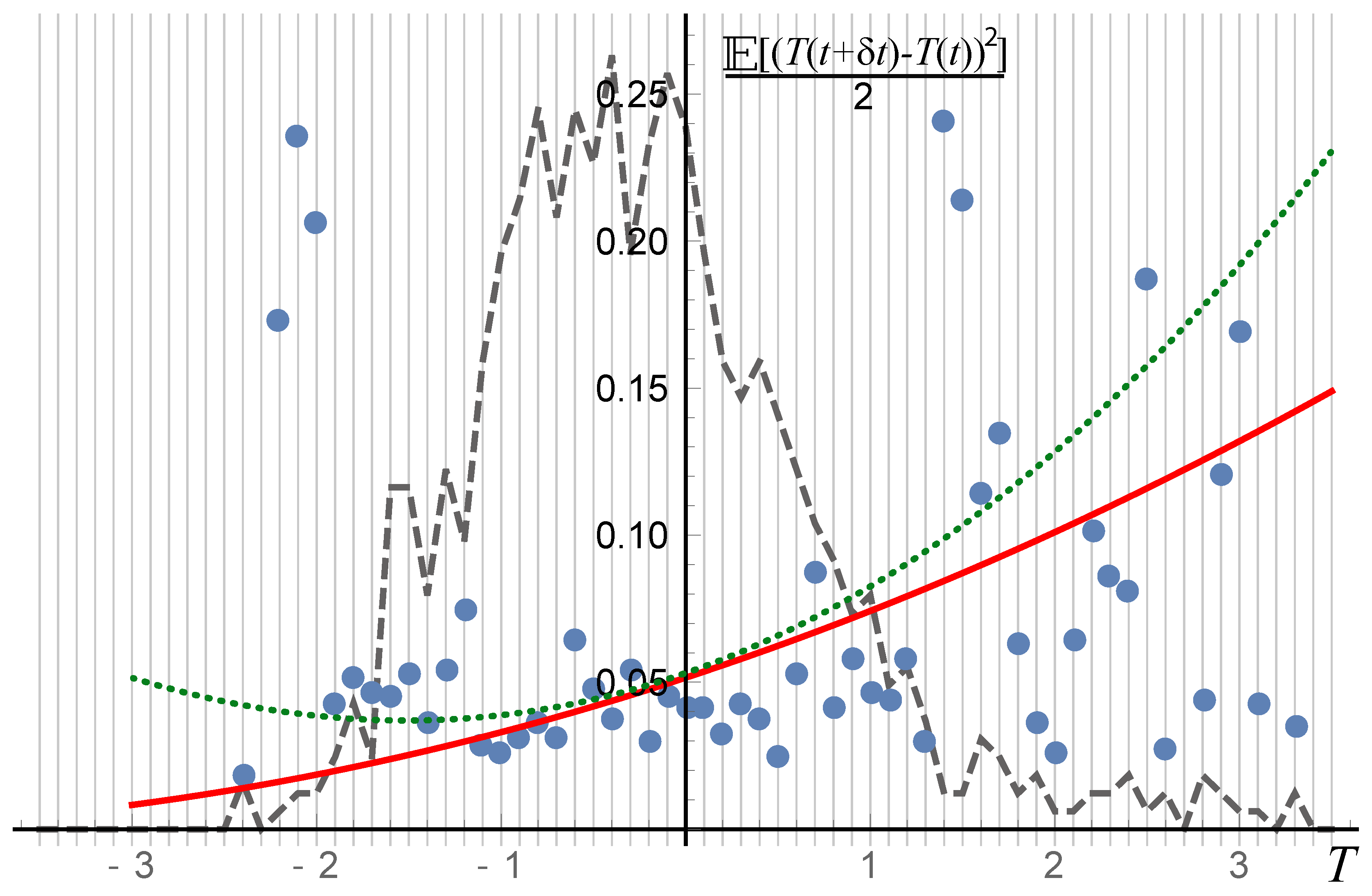
6.4. Inferring the FPE Coefficients from Data
7. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Validation of the Linear Relationship between the Wind Stress and TE
- (1)
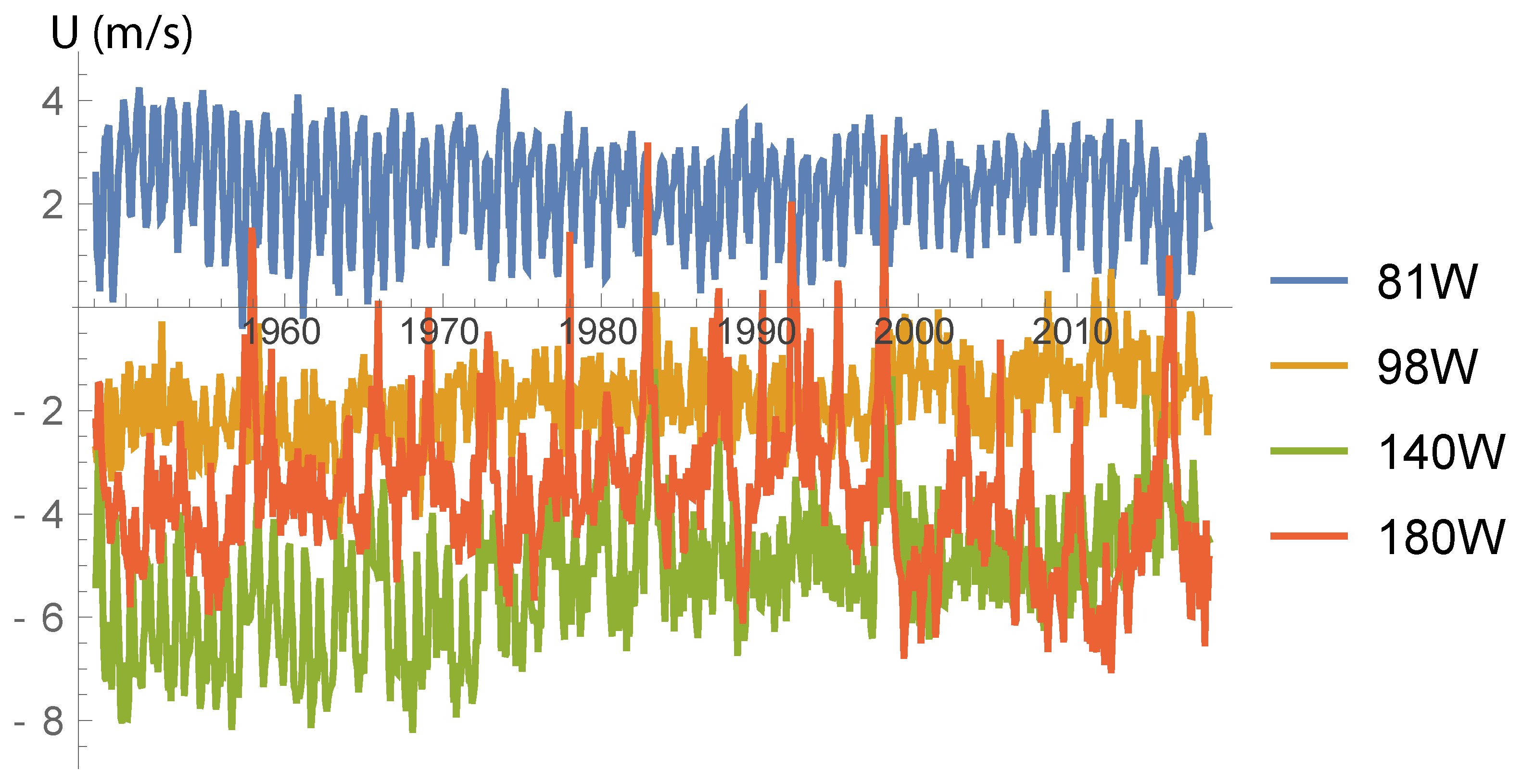
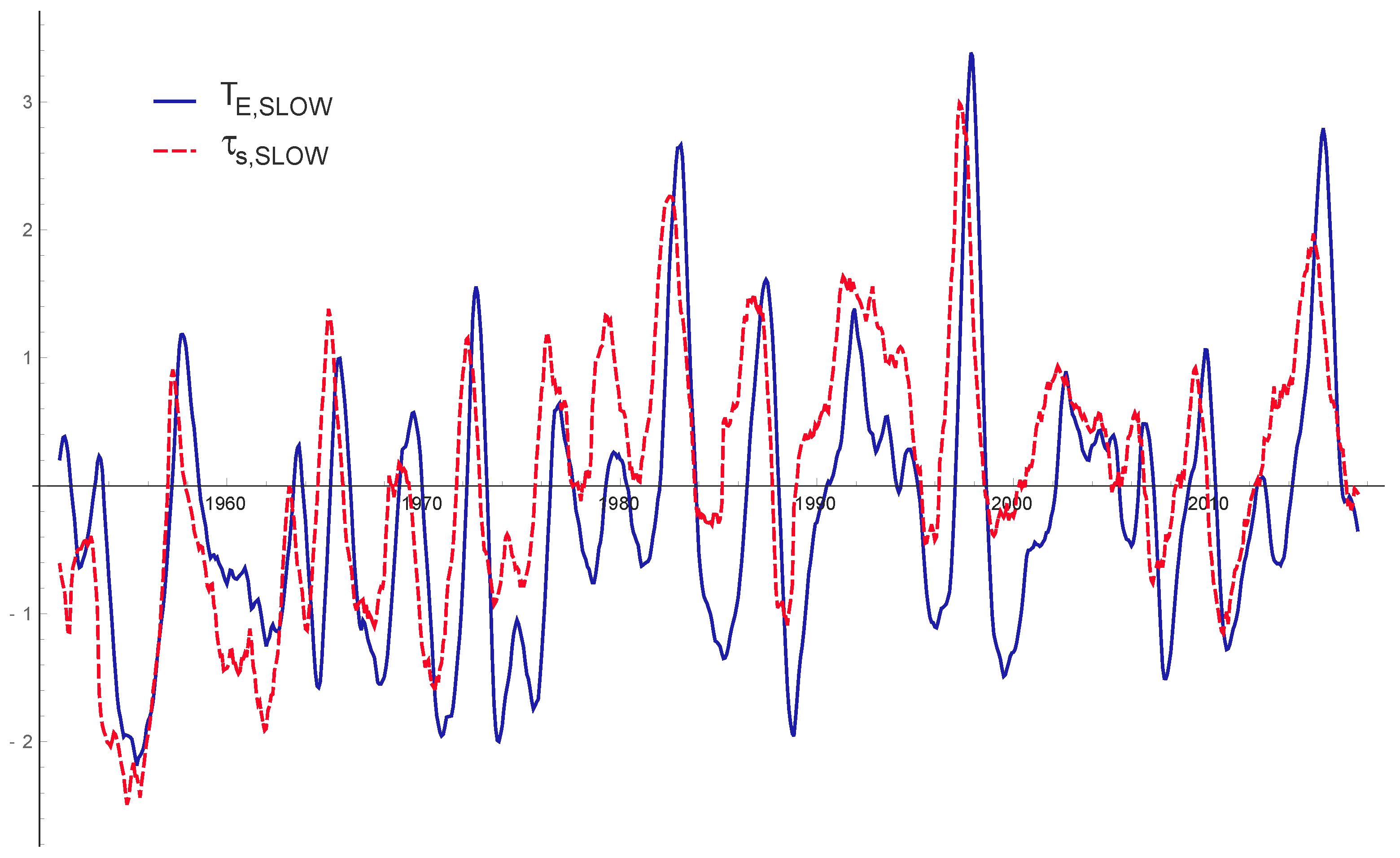
- From Figure A2, we clearly see that the time behaviors of and are similar (of course, some lag remains between the wind stress, which is a a forcing term, and the ocean reaction);
- (2)
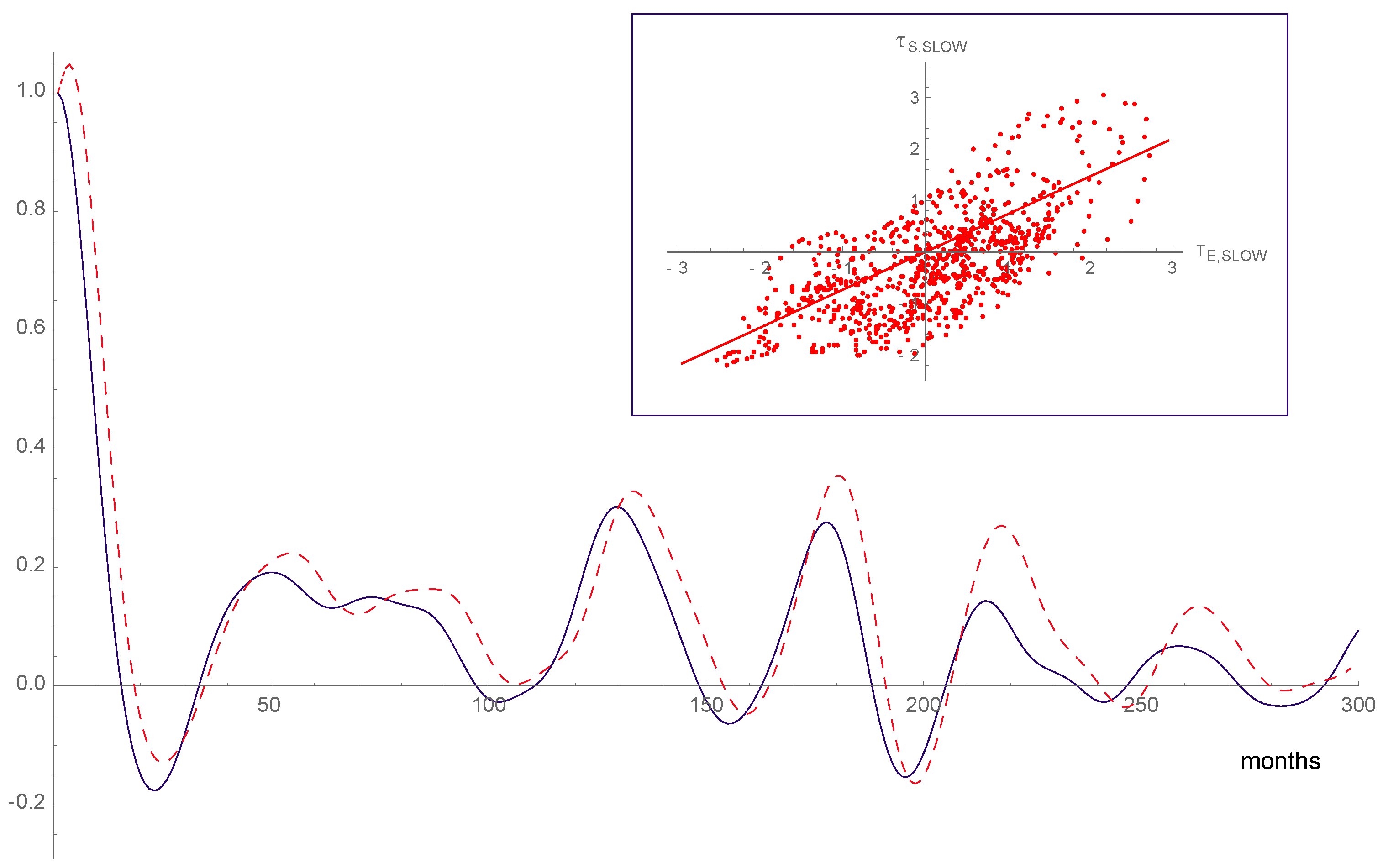
- From Figure A3, we see that the plot of the cross-correlation between and vs. time (in moths) is very similar to the plot of the autocorrelation of (notice the little time offset between these two plots, indicating the fact that the one-year time average has not completely hidden the cause-effect relationship between and ). Moreover, from the insert of the same figure, we see that the average relationship between and is mainly linear, with a small dispersion of the data around the linear fit (quantities are normalized by the standard deviation of the quantities from observations):
Appendix B. Very Short Review of the Projection Approach Applied to the ROM
Appendix C. The Ansatz and the Stationary PDF
References
- Larkin, N.K.; Harrison, D.E. ENSO Warm (El Niño) and Cold (La Niña) Event Life Cycles: Ocean Surface Anomaly Patterns, Their Symmetries, Asymmetries, and Implications. J. Clim. 2002, 15, 1118–1140. [Google Scholar] [CrossRef]
- Kug, J.S.; Ham, Y.G. Are there two types of La Nina? Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- An, S.I. Interdecadal changes in the El Nino-La Nina asymmetry. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- An, S.I.; Kim, J.W. Role of nonlinear ocean dynamic response to wind on the asymmetrical transition of El Niño and La Niña. Geophys. Res. Lett. 2017, 44, 393–400. [Google Scholar] [CrossRef]
- Dommenget, D.; Bayr, T.; Frauen, C. Analysis of the non-linearity in the pattern and time evolution of El Niño southern oscillation. Clim. Dyn. 2013, 40, 2825–2847. [Google Scholar] [CrossRef]
- Frauen, C.; Dommenget, D. El Niño and La Niña amplitude asymmetry caused by atmospheric feedbacks. Geophys. Res. Lett. 2010, 37, L18801. [Google Scholar] [CrossRef]
- Moore, A.M.; Kleeman, R. The dynamics of error growth and predictability in a coupled model of ENSO. Q. J. R. Meteorol. Soc. 1996, 122, 1405–1446. [Google Scholar] [CrossRef]
- Penland, C.; Sardeshmukh, P.D. The Optimal Growth of Tropical Sea Surface Temperature Anomalies. J. Clim. 1995, 8, 1999–2024. [Google Scholar] [CrossRef]
- Weiss, J.B. Fluctuation properties of steady-state Langevin systems. Phys. Rev. E 2007, 76, 061128. [Google Scholar] [CrossRef] [PubMed]
- Jin, F.F. An Equatorial Ocean Recharge Paradigm for ENSO. Part II: A Stripped-Down Coupled Model. J. Atmos. Sci. 1997, 54, 830–847. [Google Scholar] [CrossRef]
- Jin, F.F. An Equatorial Ocean Recharge Paradigm for ENSO. Part I: Conceptual Model. J. Atmos. Sci. 1997, 54, 811–829. [Google Scholar] [CrossRef]
- Burgers, G.; Jin, F.F.; van Oldenborgh, G.J. The simplest ENSO recharge oscillator. Geophys. Res. Lett. 2005, 32, L13706. [Google Scholar] [CrossRef]
- Capotondi, A.; Wittenberg, A.; Masina, S. Spatial and temporal structure of Tropical Pacific interannual variability in 20th century coupled simulations. Ocean Model. 2006, 15, 274–298. [Google Scholar] [CrossRef]
- Jin, F.F.; Lin, L.; Timmermann, A.; Zhao, J. Ensemble-mean dynamics of the ENSO recharge oscillator under state-dependent stochastic forcing. Geophys. Res. Lett. 2007, 34, L03807. [Google Scholar] [CrossRef]
- Levine, A.F.Z.; Jin, F.F. Noise-Induced Instability in the ENSO Recharge Oscillator. J. Atmos. Sci. 2010, 67, 529–542. [Google Scholar] [CrossRef]
- Ren, H.L.; Jin, F.F. Recharge Oscillator Mechanisms in Two Types of ENSO. J. Clim. 2013, 26, 6506–6523. [Google Scholar] [CrossRef]
- Bianucci, M. Analytical probability density function for the statistics of the ENSO phenomenon: Asymmetry and power law tail. Geophys. Res. Lett. 2016, 43, 386–394. [Google Scholar] [CrossRef]
- Battisti, D.S.; Hirst, A.C. Interannual variability in a tropical atmosphere-ocean model: Influence of the basic state, ocean geometry and nonlinearity. J. Atmos. Sci. 1989, 46, 1687–1712. [Google Scholar] [CrossRef]
- Mantua, N.J.; Battisti, D.S. Evidence for the Delayed Oscillator Mechanism for ENSO: The “Observed” Oceanic Kelvin Mode in the Far Western Pacific. J. Phys. Oceanogr. 1994, 24, 691–699. [Google Scholar] [CrossRef]
- Im, S.H.; An, S.I.; Kim, S.T.; Jin, F.F. Feedback processes responsible for El Niño-La Niña amplitude asymmetry. Geophys. Res. Lett. 2015, 42, 5556–5563. [Google Scholar] [CrossRef]
- Sardeshmukh, P.D.; Penland, C. Understanding the distinctively skewed and heavy tailed character of atmospheric and oceanic probability distributions. Chaos 2015, 25, 036410. [Google Scholar] [CrossRef] [PubMed]
- Sardeshmukh, P.D.; Sura, P. Reconciling Non-Gaussian Climate Statistics with Linear Dynamics. J. Clim. 2009, 22, 1193–1207. [Google Scholar] [CrossRef]
- Sura, P.; Sardeshmukh, P.D. A global view of air-sea thermal coupling and related non-Gaussian {SST} variability. Atmos. Res. 2009, 94, 140–149. [Google Scholar] [CrossRef]
- Sardeshmukh, P.D.; Compo, G.P.; Penland, C. Need for Caution in Interpreting Extreme Weather Statistics. J. Clim. 2015, 28, 9166–9187. [Google Scholar] [CrossRef]
- Penland, C.; Sardeshmukh, P.D. Alternative interpretations of power-law distributions found in nature. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023119. [Google Scholar] [CrossRef] [PubMed]
- Bianucci, M.; Merlino, S. Non Standard Fluctuation Dissipation Processes in Ocean-Atmosphere Interaction and for General Hamiltonian or Non Hamiltonian Phenomena: Analytical Results; Mathematics Research Developments, Nova Science Publisher: Hauppauge, NY, USA, 2017. [Google Scholar]
- Bianucci, M. On the correspondence between a large class of dynamical systems and stochastic processes described by the generalized Fokker Planck equation with state-dependent diffusion and drift coefficients. J. Stat. Mech. Theory Exp. 2015, 2015, P05016. [Google Scholar] [CrossRef]
- Dorfman, J.R. An Introduction to Chaos in Nonequilibrium Statistical Mechanics; Cambridge Lecture Notes in Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zwanzig, R. (Ed.) Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction and the Mori-Zwanzig representation of irreversible processes. Proc. Natl. Acad. Sci. USA 2000, 97, 2968–2973. [Google Scholar] [CrossRef] [PubMed]
- Grigolini, P.; Marchesoni, F. Basic Description of the Rules Leading to the Adiabatic Elimination of Fast Variables. In Advances in Chemical Physics: Memory Function Approaches to Stochastich Problems in Condensed Matter; Evans, M.W., Grigolini, P., Parravicini, G.P., Eds.; John Wiley & Sons: New York, NY, USA, 1985; Volume 62, p. 556. [Google Scholar]
- Bianucci, M. Using some results about the Lie evolution of differential operators to obtain the Fokker-Planck equation for non-Hamiltonian dynamical systems of interest. J. Math. Phys. 2018, 59, 053303. [Google Scholar] [CrossRef]
- Bianucci, M. Large Scale Emerging Properties from Non Hamiltonian Complex Systems. Entropy 2017, 19, 302. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Irregularity in the distribution of gaseous molecules and its influence. Boltzmann Festschr. 1904, 626–641. [Google Scholar]
- Smoluchowski, M.V. Theory of the Brownian movements. Bull. Acad. Sci. Crac. 1906, 577–602. [Google Scholar]
- Schadschneider, A.; Chowdhury, D.; Nishinari, K. (Eds.) Stochastic Transport in Complex Systems. From Molecules to Vehicles; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Kampen, N.V. (Ed.) Stochastic Processes in Physics and Chemistry, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Risken, H. The Fokker-Planck Equation. Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1996; Volume 18. [Google Scholar]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II. Nonequilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 1985; Volume 31. [Google Scholar]
- Ding, M.; Rangarajan, G. First Passage Time Problem: A Fokker-Planck Approach. In New Directions in Statistical Physics: Econophysics, Bioinformatics, and Pattern Recognition; Wille, L.T., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 31–46. [Google Scholar]
- Kramers, H. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Bianucci, M.; Grigolini, P.; Palleschi, V. Beyond the linear approximations of the conventional approaches to the theory of chemical relaxation. J. Chem. Phys. 1990, 92, 3427–3441. [Google Scholar] [CrossRef]
- Bianucci, M. Ordinary chemical reaction process induced by a unidimensional map. Phys. Rev. E 2004, 70, 026107. [Google Scholar] [CrossRef] [PubMed]
- Revelli, J.A.; Budde, C.E.; Wio, H.S. Diffusion in fluctuating media: First passage time problem. Phys. Lett. A 2002, 306, 104–109. [Google Scholar] [CrossRef]
- Kulkarni, V.G.; Tzenova, E. Mean first passage times in fluid queues. Oper. Res. Lett. 2002, 30, 308–318. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.; Ricciardi, L. Single neuron’s activity: On certain problems of modeling and interpretation. Biosystems 1997, 40, 65–74. [Google Scholar] [CrossRef]
- Tuckwell, H.C. (Ed.) Introduction to Theoretical Neurobiology; Cambridge Studies in Mathematical Biology; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kurzyński, M.; Chełminiak, P. Mean First-Passage Time in the Stochastic Theory of Biochemical Processes. Application to Actomyosin Molecular Motor. J. Stat. Phys. 2003, 110, 137–181. [Google Scholar] [CrossRef]
- Brics, M.; Kaupuzs, J.; Mahnke, R. How to solve Fokker-Planck equation treating mixed eigenvalue spectrum? Condens. Matter Phys. 2013, 16, 1–13. [Google Scholar] [CrossRef]
- NOAA Climate Prediction Center. Available online: https://www.cpc.ncep.noaa.gov/data/indices/ (accessed on 20 June 2018).
- Philander, S.G.H. The Response of Equatorial Oceans to a Relaxation of the Trade Winds. J. Phys. Oceanogr. 1981, 11, 176–189. [Google Scholar] [CrossRef]
- Jin, F.F.; Neelin, J.D. Modes of Interannual Tropical Ocean-Atmosphere Interaction—A Unified View. Part I: Numerical Results. J. Atmos. Sci. 1993, 50, 3477–3503. [Google Scholar] [CrossRef]
- Neelin, J.D.; Jin, F.F. Modes of Interannual Tropical Ocean-Atmosphere Interaction—A Unified View. Part II: Analytical Results in the Weak-Coupling Limit. J. Atmos. Sci. 1993, 50, 3504–3522. [Google Scholar] [CrossRef]
- Khas’minskii, R. A Limit Theorem for the Solutions of Differential Equations with Random Right-Hand Sides. Theory Probab. Appl. 1966, 11, 390–406. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in stationary states. J. Stat. Phys. 1995, 80, 931–970. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E.G.D. Dynamical Ensembles in Nonequilibrium Statistical Mechanics. Phys. Rev. Lett. 1995, 74, 2694–2697. [Google Scholar] [CrossRef] [PubMed]
- Terwiel, R. Projection operator method applied to stochastic linear differential equations. Physica 1974, 74, 248–265. [Google Scholar] [CrossRef]
- Da-jin, W.; Li, C.; Bo, Y. Probability Evolution and Mean First-Passage Time for Multidimensional Non-Markovian Processes. Commun. Theor. Phys. 1989, 11, 379. [Google Scholar] [CrossRef]
- Kampen, N.V. Elimination of fast variables. Phys. Rep. 1985, 124, 69–160. [Google Scholar] [CrossRef]
- Kim, S.T.; Jin, F.F. An ENSO stability analysis. Part II: Results from the twentieth and twenty-first century simulations of the CMIP3 models. Clim. Dyn. 2011, 36, 1609–1627. [Google Scholar] [CrossRef]
- NOAA ESRL, NCEP/NCAR Reanalysis Data. Available online: https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.derived.surfaceflux.html (accessed on 20 June 2018).
- Wen, C.; Kumar, A.; Xue, Y.; McPhaden, M.J. Changes in Tropical Pacific Thermocline Depth and Their Relationship to ENSO after 1999. J. Clim. 2014, 27, 7230–7249. [Google Scholar] [CrossRef]
- Bianucci, M. Nonconventional fluctuation dissipation process in non-Hamiltonian dynamical systems. Int. J. Mod. Phys. B 2015, 30, 1541004. [Google Scholar] [CrossRef]
- Grigolini, P. The projection approach to the Fokker-Planck equation: Applications to phenomenological stochastic equations with coloured noises. In Noise in Nonlinear Dynamical Systems; Moss, F., McClintock, P.V.E., Eds.; Cambridge University Press: Cambridge, UK, 1989; Volume 1, Chapter 5; p. 161. [Google Scholar]
- Bianucci, M.; Grigolini, P. Nonlinear and non Markovian fluctuation-dissipation processes: A Fokker-Planck treatment. J. Chem. Phys. 1992, 96, 6138–6148. [Google Scholar] [CrossRef]
- Bianucci, M.; Mannella, R.; West, B.J.; Grigolini, P. From dynamics to thermodynamics: Linear response and statistical mechanics. Phys. Rev. E 1995, 51, 3002–3022. [Google Scholar] [CrossRef]
- Hayashi, M.; Jin, F.F. Subsurface Nonlinear Dynamical Heating and ENSO Asymmetry. Geophys. Res. Lett. 2017, 44. [Google Scholar] [CrossRef]
- Kapur, A.; Zhang, C. Multiplicative MJO Forcing of ENSO. J. Clim. 2012, 25, 8132–8147. [Google Scholar] [CrossRef]
- Capotondi, A.; Sardeshmukh, P.D.; Ricciardulli, L. The Nature of the Stochastic Wind Forcing of ENSO. J. Clim. 2018, 31, 8081–8099. [Google Scholar] [CrossRef]
- Sura, P. On non-Gaussian SST variability in the Gulf Stream and other strong currents. Ocean Dyn. 2010, 60, 155–170. [Google Scholar] [CrossRef]
- Sura, P. A general perspective of extreme events in weather and climate. Atmos. Res. 2011, 101, 1–21. [Google Scholar] [CrossRef]
- Frankignoul, C. Sea surface temperature anomalies, planetary waves, and air-sea feedback in the middle latitudes. Rev. Geophys. 1985, 23, 357–390. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kohler, W. Asymptotic theory of mixing stochastic ordinary differential equations. Commun. Pure Appl. Math. 1974, 27, 641–668. [Google Scholar] [CrossRef]
- Gardiner, C. Stochastic Methods. A Handbook for the Natural and Social Sciences, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 13, pp. 18, 447. [Google Scholar]
- Prasad, P.; Ravindran, R. Partial Differential Equations; Wiley Eastern, Delhi and John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- IRI/LDEO Climate Data Library. Available online: http://iridl.ldeo.columbia.edu/ (accessed on 20 June 2018).
- Bianucci, M.; Capotondi, A.; Merlino, S.; Mannella, R. Estimate of the average timing for strong El Niño events using the recharge oscillator model with a multiplicative perturbation. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 103118. [Google Scholar] [CrossRef] [PubMed]
- Tokyo Climate Center. Available online: http://ds.data.jma.go.jp/tcc/tcc/ (accessed on 20 January 2018).
- Gardiner, C. Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 2009; Volume 20. [Google Scholar]
- Wang, M.C.; Uhlenbeck, G.E. On the Theory of the Brownian Motion II. Rev. Mod. Phys. 1945, 17, 323–342. [Google Scholar] [CrossRef]
- Siegert, A.J.F. On the First Passage Time probability problem. Phys. Rev. 1951, 81, 617–623. [Google Scholar] [CrossRef]
- Kampen, N.V. Chapter {VIII}—{THE} FOKKER–PLANCK {EQUATION}. In Stochastic Processes in Physics and Chemistry, 3rd ed.; Kampen, N.V., Ed.; North-Holland Personal Library, Elsevier: Amsterdam, The Netherlands, 2007; pp. 193–218. [Google Scholar]
- McGregor, S.; Timmermann, A.; Timm, O. A unified proxy for ENSO and PDO variability since 1650. Clim. Past 2010, 6, 1–17. [Google Scholar] [CrossRef]
- Bianucci, M.; Mannella, R.; Fan, X.; Grigolini, P.; West, B.J. Standard fluctuation-dissipation process from a deterministic mapping. Phys. Rev. E 1993, 47, 1510–1519. [Google Scholar] [CrossRef]
- Zhang, C.; Gottschalck, J. SST Anomalies of ENSO and the Madden-Julian Oscillation in the Equatorial Pacific. J. Clim. 2002, 15, 2429–2445. [Google Scholar] [CrossRef]
- Li, R.C.Y.; Zhou, W.; Chan, J.C.L.; Huang, P. Asymmetric Modulation of Western North Pacific Cyclogenesis by the Madden-Julian Oscillation under ENSO Conditions. J. Clim. 2012, 25, 5374–5385. [Google Scholar] [CrossRef]
- Zavala-Garay, J.; Zhang, C.; Moore, A.M.; Kleeman, R. The Linear Response of ENSO to the Madden-Julian Oscillation. J. Clim. 2005, 18, 2441–2459. [Google Scholar] [CrossRef]
- Hendon, H.H.; Wheeler, M.C.; Zhang, C. Seasonal Dependence of the MJO-ENSO Relationship. J. Clim. 2007, 20, 531–543. [Google Scholar] [CrossRef]
- Dijkstra, H.A.; Burgers, G. Fluid dynamics of el Niño variability. Annu. Rev. Fluid Mech. 2002, 34, 531–558. [Google Scholar] [CrossRef]
- Carmeli, B.; Nitzan, A. Non-Markovian theory of activated rate processes. I. Formalism. J. Chem. Phys. 1983, 79, 393–404. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianucci, M.; Capotondi, A.; Mannella, R.; Merlino, S. Linear or Nonlinear Modeling for ENSO Dynamics? Atmosphere 2018, 9, 435. https://doi.org/10.3390/atmos9110435
Bianucci M, Capotondi A, Mannella R, Merlino S. Linear or Nonlinear Modeling for ENSO Dynamics? Atmosphere. 2018; 9(11):435. https://doi.org/10.3390/atmos9110435
Chicago/Turabian StyleBianucci, Marco, Antonietta Capotondi, Riccardo Mannella, and Silvia Merlino. 2018. "Linear or Nonlinear Modeling for ENSO Dynamics?" Atmosphere 9, no. 11: 435. https://doi.org/10.3390/atmos9110435
APA StyleBianucci, M., Capotondi, A., Mannella, R., & Merlino, S. (2018). Linear or Nonlinear Modeling for ENSO Dynamics? Atmosphere, 9(11), 435. https://doi.org/10.3390/atmos9110435






