Abstract
With the increasing demand for near real-time atmospheric water vapor monitoring, this study evaluates the performance of the open-source PRIDE PPP-AR software (version 3.0.5) for retrieving Zenith Total Delay (ZTD) and Integrated Water Vapor (IWV) over the African continent over a one-year period. PRIDE PPP-AR is compared with established PPP-AR and PPP solutions, including CSRS-PPP, IGN-PPP, and NGL and using GipsyX, ERA5, and IGS products as references. A robust methodology combining time series processing and statistical evaluation was adopted. Multiple tools were leveraged to ensure a comprehensive performance analysis of GNSS data from seven stations in Africa, where such studies remain scarce. The results show that PRIDE PPP-AR achieves ZTD accuracy comparable to GipsyX (RMSE < 6 mm, R2 ≈ 0.99) and performs at a similar level to NGL and CSRS-PPP. Compared to the other solutions, PRIDE PPP-AR has an accuracy similar to CSRS-PPP and NGL, but slightly better than IGN-PPP, in line with ERA5 and IGS references. For IWV retrieval, comparisons with ERA5 indicate RMSE values of about 1.5 to 2.7 kg/m2, depending on station location and climatic conditions. IWV variability tends to increase towards the equator, where the recorded fluctuations are higher than in subtropical zones. In addition, collocated radiosonde (RS) measurements in Abidjan confirm good agreement, further validating the reliability of the software. This study highlights the potential of GNSS meteorology, in providing reliable spatiotemporal IWV monitoring and indicates that the PRIDE PPP-AR is ready for the high precision meteorological applications in African regions. These results offer promising prospects for spatiotemporal studies through African multi-GNSS networks and the PRIDE PPP-AR approach.
Keywords:
PPP-AR; zenith total delay; integrated water vapor; GNSS meteorology; PRIDE PPP-AR; ERA5; radiosonde; GNSS; GipsyX 1. Introduction
The study of the spatio-temporal distribution of tropospheric water vapor is a complex subject in meteorology. Tropospheric water vapor is highly variable in time and is an important factor in weather forecasting. Traditional tools for estimating its amount do not provide good temporal resolution and are extremely expensive. Global Navigation Satellite Systems (GNSS), initially applied for positioning and navigation concerns, are increasingly being exploited to estimate the amount of water vapor over stations. This technique, known as GNSS meteorology, was introduced by [1] and has developed in recent years with the enhancement of GNSS data processing algorithms. It offers a number of advantages due to its temporal resolution and its ability to perform observations regardless of meteorological conditions.
Electromagnetic waves are delayed by the troposphere. The original slant paths of the GNSS signals, which depend on the satellite’s elevation angle and azimuth position, are projected to the station’s zenith using mapping functions. The resulting zenith delay is called ZTD (Zenith Tropospheric Delay) and it consists of a wet part ZWD (Zenithal Wet Delay) and a neutral part ZHD (Zenithal Hydrostatic Delay). The ZHD is generally retrieved a priori by the model Saastamoinen’s model [2] and contributes to approximately 90% of the ZTD. The ZWD, on the other hand, is strongly linked to tropospheric water vapor [3]. According to [4], high accuracy in ZHD estimation is essential for high-precision applications, such as precise positioning and the retrieval of ZTD. Accurate estimation of tropospheric delays remains a complex task due to the dynamics of atmospheric gases, particularly water vapor [5].
Since the late 1990s, several studies have highlighted that ground-based GNSSs are a valuable tool for meteorological applications [6,7,8]. These results have been enhanced by the constant progress in processing algorithms, the availability of multi-GNSS correction products and the multiplication of ground-based GNSS networks. Indeed, water vapor content can be deduced from ZTD; after subtracting the recalculated ZHDs, the ZWDs are converted into integrated water vapor (IWV) using a conversion factor. Although instruments such as radiosondes (RS) and water vapor radiometers offer direct tropospheric delay measurements, the prohibitive cost of implementing them at each station limits their feasibility; the massive development of GNSS ground networks became a real alternative for water vapor sensing.
There are two primary methods for precise processing of GNSS data. Precise point positioning (PPP) processes undifferenced GNSS observations by incorporating precise satellite orbits and clock data to achieve high accuracy [9], whereas double difference (DD) relies on differencing observations from two receivers and two satellites to eliminate common errors such as satellite and ground receiver clock biases [10,11]. Studies have demonstrated that DD has a number of disadvantages and is more susceptible to induce errors than PPP in the estimation of ZTD [6,12]. In GNSS meteorology, numerous studies [13,14,15,16] have confirmed the reliability of this technique for estimating ZTD and deriving IWV. Moreover, in some parts of the world, such as Africa, where ground-based GNSS are sparsely distributed, PPP remains almost the only viable option in certain regions. PPP-AR differs from traditional PPP in that it improves accuracy by fixing phase ambiguities at integer values rather than floating value and reducing convergence time [17,18,19]. PPP-AR eliminates hardware biases from satellites and receivers. The development of AR products, such as those from Wuhan University (WHU), CNES/CLS, and CODE, has been a key driver in the advancement of PPP-AR. By providing essential phase bias corrections and enabling precise ambiguity resolution, these products have significantly improved the accuracy and reliability of PPP solutions, as highlighted in studies by [18,19,20]. Both PPP and PPP-AR strategies are implemented in a variety of open-source post-processing software packages, enabling advanced positioning techniques and the estimation of ZTD. Among the most well-known tools are GipsyX [21], PRIDE PPPAR [18], PPP-ARISEN [22], and GINS [23]. Additionally, free online solutions such as CSRS-PPP [24], IGN PPP [25], APPS [26], and PPP Wizard [27] also support these advanced positioning methods.
In this new era of (near) real-time water vapor retrieval services, the advancement of PPP-RTK [10,11,28,29,30,31], the interoperability of various products, the PPP-AR strategy are becoming increasingly relevant, particularly with software like Linux-based open-source PRIDE PPP-AR. It has been demonstrated that PRIDE PPP-AR delivers excellent performance in positioning [32,33,34]. However, its performance in ZTD retrieval deserves further investigation, especially in Africa, where few studies have been conducted [35]. Africa is highly vulnerable to climate change. Its latitudinal extent has a strong influence on its climate. It has seven climate zones, ranging from temperate to tropical. In the face of climate-related disasters in Africa, [35] point to the need to strengthen nowcasting capabilities in Africa. The lack of reliable, dense atmospheric information hinders adaptation strategies, particularly the understanding of water vapor variability. The poor spatial and temporal distribution of in situ radiosondes in Africa, as well as the technical issues surrounding data homogenization, as discussed by [36,37,38,39,40], are driving a growing interest in GNSS data on the continent. Refs. [41,42,43,44] have shown that the assimilation of ZTD GNSS data into weather prediction models can improve forecasts of heavy rainfall in Africa.
This study stands out from other comparative studies [45,46] due to its one-year analysis period capturing full seasonal cycles, the use of multiple independent data sources for comparison, and the validation of IWV from multiple PPP-AR approaches. It should be noted that [45] used several software packages to process GNSS data, but only for a few days and without incorporating other data sources into the comparisons.
The aim of this work is to evaluate the performance of the PPP-AR strategy with Linux-based open-source PRIDE PPP-AR software Version 3 in the retrieval of ZTD/IWV on the African continent over a whole year. The potential of ZTD from different PPP-AR approaches for tropospheric water vapor retrieval will be therefore investigated. The software will be evaluated with respect to other classical solutions such as the web-based service CSRS-PPP (Canadian Spatial Reference System precise point positioning service), IGN-PPP, Nevada Geodetic Laboratory (NGL), GipsyX Software (Version 2.2), IGS (International GNSS Services) products and the ERA5 Reanalysis model as references. After retrieving IWV values, data from a nearby Radiosonde (RS) station for Abidjan and ERA5 reanalysis data for all stations were also utilized for the IWV comparison.
The paper is organized as follows. Section 2 presents the dataset used, the GNSS data processing strategies, and the methodologies applied for the retrieval of ZTD and IWV. Section 3 is devoted to the results and discussion on the performance assessment of ZTD and IWV estimates derived from the PPP-AR strategy. Finally, conclusions and perspectives are drawn in the last section.
2. Datasets and Methods
2.1. GNSS ZTD Estimation and IWV Retrievals
The electromagnetic wave emitted by the satellite undergoes a non-dispersive delay as it crosses the troposphere. Code and phase measurements are affected by these delays because the troposphere is a non-dispersive medium for GNSS frequencies (≤15 GHz). The effects are more marked for low-elevation signals, which pass through a larger portion of the atmosphere, particularly in low-latitude areas [47,48]. The estimation of ZTD from GNSS data is based on fundamental equations that model the propagation of GNSS signals through the atmosphere. Pressure, temperature, and humidity are the main atmospheric parameters taken into account by these equations to model tropospheric delays.
The tropospheric path delay results from the integration of refractivity along the ray path S (Equation (1)). In the microwave spectrum, atmospheric refractivity (N) is related to key atmospheric properties through Equation (2).
where is the pressure of dry air, T is the temperature, e is the water vapor pressure, and and are the compressibility factors of dry air and water vapor, respectively. The refractivity coefficients determined empirically in laboratory are summarized in Table 1.

Table 1.
Values for Coefficients , , and .
Using mapping functions that depend on the elevation angle of the satellite above the horizon, the slant delay is projected onto the zenith to obtain the ZTD. The tropospheric path delay using the standard model and considering a symmetrical troposphere is expressed as follows [53]:
where ZHD and ZWD represent the zenith hydrostatic and zenith wet delays, E is the elevation angle, and and are the hydrostatic and wet mapping functions, respectively.
In order to consider azimuthal asymmetry of the troposphere delay, caused by horizontal variations in water vapor and atmospheric pressure, an extended model has been developed by incorporating a component dependent on tropospheric gradients. The tropospheric path delay in this extended model is defined as [53]
where and are the horizontal tropospheric gradients in the north and east directions, φ is the azimuth angle, and is the gradient mapping function.
In GNSS data analysis, regardless of the selected modeling approach, the ZHD is determined a priori using a climatological model, while the ZWD is estimated during the adjustment process. The total tropospheric delay (ZTD) is then expressed as
ZTD = ZHD + ZWD
Using the estimated ZTD, the procedure for converting them into IWVs is based firstly on calculating the ZHD. It is approximated by Saastamoinen’s model [2], which expresses the ZHD as a function of ground pressure (P, in hPa), receiver latitude (φ), and receiver altitude (H, in km) (Equation (6)):
ZWD = ZTD − ZHD
IWV can be derived from ZWD using a conversion factor Π, given by [5,54] (Equations (8) and (9)):
where and m is the ratio of the molar mass of water vapor and dry air. is the density of water, is the specific gas constant for water vapor in, and , and are constant based on laboratory estimates calculated [1,55]. is the water vapor weighted mean temperature of the atmosphere, as defined in [3]. The conventional method for determining is based on the following formula, derived from RS profiles:
where e is the water vapor pressure along the station’s vertical profile, h represents the geopotential altitude, and T is the absolute temperature along the vertical direction. In the absence of meteorological sensors at GNSS receiver sites, several studies [1,55,56,57] have established linear relationships between surface temperature and for use in GNSS meteorology. Additionally, some studies suggest estimating from climate models as an alternative approach. Appendix A (Table A1) provides the most commonly used linear model and the surface temperature ().
2.2. Description of Dataset
The benchmark dataset comprises the following data: GNSS observations and auxiliary products, IGS products, Nevada Geodetic Laboratory (NGL) products (https://geodesy.unr.edu/gps_timeseries/trop/ last access: 15 March 2025), TU Wien (TUV) products (https://vmf.geo.tuwien.ac.at/products.html last access: 22 March 2025), RS observations, ERA5 reanalysis data (https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=download last access: 22 March 2025), and MERRA-2 Precipitation Products (https://power.larc.nasa.gov/data-access-viewer/, last access: 24 March 2025). To evaluate the accuracy of ZTD estimation and IWV retrievals over Africa, based on the PPP-AR strategy, we selected data from the year 2022, obtained from 7 GNSS stations along the African coastline and surrounding regions. Despite several programs enabling the densification of ground-based GNSS networks, such as NIGNET CORS [58] and REGAT CORS [59], data collection and sharing remain limited. African IGS stations are sparsely distributed, and there are data gaps when compared with stations on other continents.
Thus, a limited selection of 7 stations was made based on the degree of data completeness throughout 2022, as well as climatic zones, which are also influenced by global factors such as the West African Monsoon [60] (WAM), the Inter-Tropical Convergence Zone (ITCZ), and the El Niño–Southern Oscillation [61] (ENSO).
These stations are situated in the main climate zones (tropical, arid, and temperate), as defined by the Mapping of Main Climatic Zones [62]. In the temperate zone, RABT was selected in the north, while in the arid zone, SUTH was selected. To ensure representativeness in the tropical zones, where few studies have been conducted, YKRO, ABJN, and MBAR were selected. The selection also includes two island stations in the Atlantic (CPVG) and Indian Oceans (MAYG). Our selection is also characterized by two high-altitude stations (≥1000 m).
The insights gained from this PPP-AR strategy evaluation study will be used to refine a larger study focusing on continuous water vapor retrieval in Africa and incorporating more stations. The IGS stations were obtained from the NASA CDDIS archive (https://cddis.nasa.gov/archive/gnss/data/daily/, last access: 11 March 2025). This selection ensures broad spatial coverage across various climatic zones while accounting for coastal influences in the Gulf of Guinea and beyond (Figure 1).
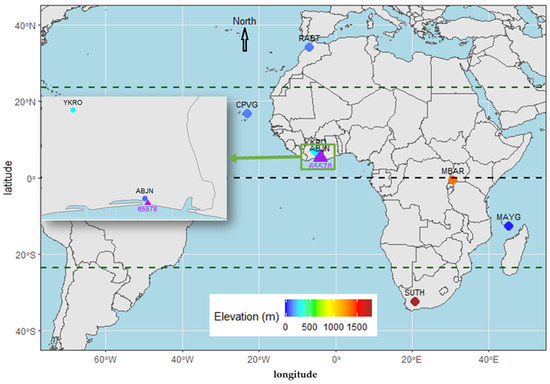
Figure 1.
Spatial distribution of 7 GNSS Stations (round circle) and one radiosonde station (triangle).
The geographical coordinates and elevation of each station are provided in Appendix B (Table A2). Additionally, RS data from station 65578 in Abidjan, operated by the Agency for the Safety of Air Navigation in Africa and Madagascar (ASECNA), were integrated for validation. This station is equipped with a German GRAW DFM17 probe. To further enhance the validation process, the non-IGS station ABJN was strategically located 10 km from RS Station WMO ID: 65578. The GNSS observations are provided in the RINEX (Receiver Independent Exchange Format) with a sampling interval of 30 s, while the RS observations are available at 12 h intervals (00:00 and 12:00 GMT).
2.3. Processing Strategy
The research was conducted using a two-stage data processing and analysis framework. In the first stage, GNSS data were processed with diverse solution strategies, and the resulting ZTD estimates were evaluated through comparative assessment. The common concept of GNSS Analysis Solutions is to model the ZHD with high accuracy using surface pressure derived from tropospheric models such as the Saastamoinen model [2], Hopfield model [63], or the UNB (University of New Brunswick) series model [64], Global Pressure and Temperature (GPT) models [65,66,67], or alternatively by interpolating meteorological variables from numerical weather reanalysis datasets. Following this ZHD modeling, ZWD is estimated in the GNSS solutions as a stochastic parameter at each epoch.
In the second stage, IWV, derived primarily from PPP-AR approaches, was rigorously validated using multiple independent tools and methods to establish accuracy and consistency.
GNSS raw data were processed with linux-based open-source PRIDE PPP-AR, de-veloped by the PRIDE Lab at Wuhan University (Wuhan, China) (WHU) (http://PRIDE.whu.edu.cn). PRIDE PPP-AR is an open-source software designed for PPP-AR. It features modularity, extensibility, and advanced integer ambiguity resolution using bootstrapping [18]. PPP-AR was used with three multi-GNSS processing strategies:
- VMF1 with First-Order Ionospheric Correction: This approach utilizes the VMF1 for modeling tropospheric delays.
- VMF3 with First-Order Ionospheric Correction: This method improves tropospheric delay estimation by employing VMF3, which offers higher temporal (hourly) and spatial (1° × 1°) resolution compared to VMF1 [68].
- VMF3 with Higher-Order Ionospheric Correction (HIONO): This advanced approach integrates VMF3 and also second- and third-order ionospheric corrections, significantly enhancing accuracy, particularly in tropical regions with high ionospheric activity. The higher-order ionospheric correction was applied using Global Ionosphere Maps (GIMs) products. These GIMs provide estimates of the Total Electron Content (TEC), derived from observations collected by hundreds of permanent GNSS stations worldwide [69].
The primary objective of this comparison is to assess the reliability of PPP-AR strategy for retrieving ZTD in these regions.
Three online free solutions are also used to position our PRIDE PPP-AR strategy in terms of accuracy: CSRS-PPP (Natural Resources Canada) [70] supports GPS and GLONASS data; IGN PPP (Institut National de l’Information Géographique et Forestière), Ref. [25], processes dual-frequency GNSS data using the Global Mapping Function (GMF); and NGL products [71] employ the VMF1 and provide tropospheric data at a 5 min frequency. Detailed characteristics of these strategies are summarized in Table 2.

Table 2.
Key characteristics of evaluated GNSS processing strategies.
For the calculation of accurate ZHD, surface pressure data were extracted from the ERA5 reanalysis dataset at an hourly resolution. ERA5, developed by the European Centre for Medium-Range Weather Forecasts (ECMWF), provides high-resolution atmospheric reanalysis with a spatial resolution of 0.25° × 0.25° and a temporal resolution of 1 h. Hourly pressure data were preferred over lower-resolution datasets to better capture diurnal variability, particularly critical in tropical regions [72]. Given the low-latitude positioning of the GNSS stations, was derived from the VMF1 grid provided by TU Wien (TUW). A bilinear interpolation method was applied to estimate values at each station location, with the associated uncertainty computed as the standard deviation of the four surrounding grid nodes, ranging between 0.2 and 1.8 K. We used the refractivity coefficients provided by Bock (2021) [16] (Table 1), which offer updated estimations compared to the classical values from Rüeger (2002) [52]. Following the determination of the ZWD using Equation (7), the IWV was finally derived for all GNSS stations.
2.4. References Data and Processing for Assessment
In this study, four different datasets are used as references to evaluate the accuracy of GNSS troposphere products. To establish ZTD accuracy metrics, we conducted comprehensive comparisons using the following:
- High-precision ZTD estimates obtained using GipsyX PPP-AR processing. Previous studies [12] have demonstrated that GipsyX provides reliable ZTD estimates.
- IGS ZTD products obtained from (https://cddis.nasa.gov/archive/gnss/products/troposphere/zpd/2022/, last access: 19 March 2025) with a resolution of 5 min.
- ZTDs computed from ERA5 reanalysis data by summing the ZHD and Zenith Wet ZWD. ZHD was adjusted to account for orthometric height differences, following the formulation proposed by [13].
For the evaluation of IWV derived from PPP-AR solutions, two reference datasets were considered:
- IWV from ERA5, available at an hourly resolution for all seven stations included in this study.
- IWV from RS 65578, located above 10 km from the ABJN station, used specifically for the validation of IWV estimates at this site. The launches are carried out at 12 h and 00 h UTC. The IWV_RS from RS is obtained by performing numerical integration of Equation (11), over altitude z using water vapor density provided in the radiosonde message.
IWV from GipsyX were included for comparative assessment. Due to elevation differences between GNSS antenna heights (H_GNSS), ERA5 model orography (H_ERA5), and RS launch sites (H_RS), we applied the altitude adjustment formula from [73]. We use geopotential heights referenced to mean sea level (MSL). The full details of the height conversion process, including equations and methodology, are provided in Appendix B.
Time series data are generated with outlier detection applied before proceeding to comparisons. Rainfall data from (https://power.larc.nasa.gov/data-access-viewer/, last access: 25 March 2025) are incorporated to investigate the relationship between ZTD variations and precipitation events. Additionally, time series analysis allows for a better understanding of seasonal influences in these tropical regions.
For IWV comparisons, the temporal resolution was adjusted to 1 h for consistency with ERA5 data. In the case of the comparison with IWV_RS in Abidjan, the Integrated water vapor from PRIDE PPP-AR (IWV_PPP-AR) at a 300 s resolution was averaged over the 45 min period preceding 00:00 and 12:00 UTC, aligning with radiosonde launch times to ensure comparability at the tropopause level. Figure 2 presents a flowchart summarizing the methodology for retrieving ZTD/IWV and assessing their accuracy. Automated processing workflows using Python version 3.13 facilitated the derivation of datasets from multiple platforms over a one-year period and the performance of statistical analyses.
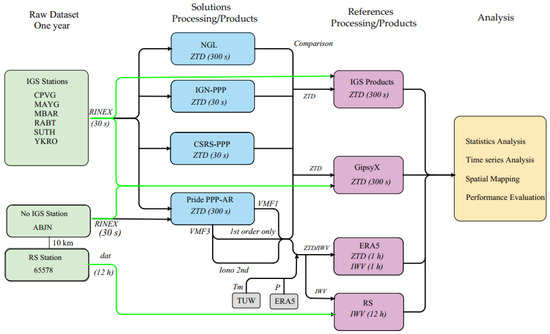
Figure 2.
Flowchart of the ZTD/IWV data retrieval and accuracy analysis.
3. Results and Discussions
In this section we present and discuss the ZTD and IWV assessments derived from the strategies.
3.1. Analysis and Assessment of the Quality of the Estimated ZTD
For brevity, we have limited the graphical representations to three of the seven stations analyzed in the rest of the document. These three stations were chosen according to these climatological criteria: YKRO is in the tropics, RABT is in a temperate zone, and SUTH is in an arid zone at a high altitude.
Figure 3 shows a marked seasonal variation, with high ZTD values of over 2.43 m between April and October, corresponding to the rainy season. Peak ZTD values of up to 2.63 m are closely correlated with peak rainfall. After an upward phase of ZTDs, characterized by higher rainfall values, a decrease in ZTDs and rainfall values is observed. The dry month of July, with little rain and low ZTDs, seems to divide the rainy season in two. This is characteristic of this climate zone, as described by Eldin M. [55]. It is also characterized by dense vegetation. In the weak dry season (January, February, March, November, and December), interspersed with a few rains, the ZTD values decrease. However, these values remain above 2.3 m due to the height of the troposphere in this zone. However, at SUTH, which is located at a low latitude and high altitude, the maximum ZTD values correlated with the rainfall peaks do not exceed 2.10 m (Figure 4). The ZTD varies only slightly over the year, ranging from 1.88 to 2.10 m. This is because water vapor decreases with altitude and the height of the troposphere is low at these latitudes.

Figure 3.
ZTD time series and daily rainfall (blue bars) of YKRO.
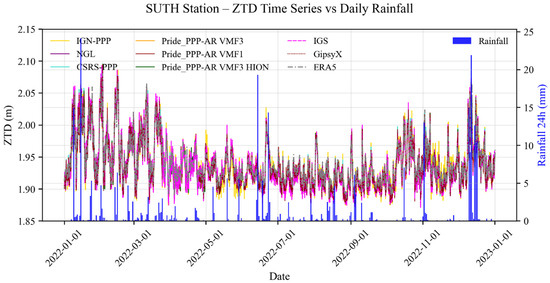
Figure 4.
Time series and daily rainfall (blue bars) of SUTH.
For the RABT station, the seasonal cycle is particularly influenced by the Azores anticyclone [56]. The wet season from October to April is characterized by heavy rainfall, which correlates with variations in ZTD. On the other hand, the dry season, with low rainfall but high ZTDs, could be driven by the Azores anticyclone, which produces moisture-laden sea breezes that can temporarily increase the water vapor content in the lower layers of the atmosphere without precipitation. In addition, the sea breeze typical of coastal regions can cause temporary additions of moisture, leading to fluctuations in the ZWD and hence the ZTD.
The time series for all stations shows that the PPP-AR solutions accurately capture the seasonal cycle. Post-precipitation ZTD baselines demonstrate effective atmospheric drying through rainout processes, showing a 5–9 mm decrease, relative to pre-event levels, particularly evident in the 72 h moving averages.
These results show that an increase in ZTD does not necessarily trigger rain. This is particularly important given that ZTD encompasses both the ZHD and ZWD components. While ZWD is directly related to atmospheric water vapor, ZHD is largely driven by surface pressure variations, which can exhibit slower temporal changes. Therefore, it is likely that some observed ZTD variations reflect pressure-induced fluctuations rather than changes in moisture content. Consequently, analyzing IWV derived from ZWD provides a more accurate and meteorologically relevant representation of atmospheric water vapor content, particularly in the context of climate and weather studies in Africa.
Analysis of the ZTD time series (Figure 3, Figure 4 and Figure 5) shows that the estimates obtained with PRIDE PPP-AR are globally consistent with those of the GipsyX, ERA5, and IGS references. The datasets show similar trends and patterns.
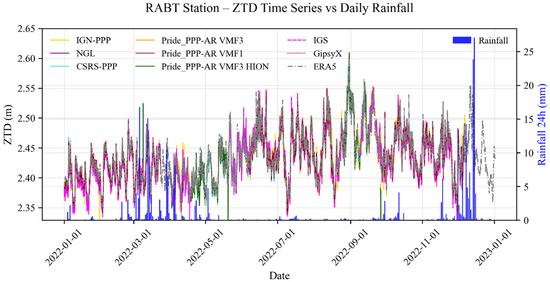
Figure 5.
ZTD time series and daily rainfall (blue bars) of RABT.
However, performance slightly varies depending on the PRIDE PPP-AR approaches used for tropospheric and ionospheric processing. The use of VMF3 (first order and H-Iono) in PRIDE PPP-AR slightly improves the results compared to VMF1, which is consistent with the conclusions of [74,75,76] on the importance of better tropospheric modeling. This improvement is due to the better spatio-temporal resolution of VMF3. The use of VMF3 generally reduces the RMSE by 0.8 mm to 3 mm compared to VMF1 using GipsyX as a reference. PRIDE PPP-AR with VMF3 (first-order iono) offers RMSEs between 2.9 and 6 mm (R2 = 0.99) compared to GipsyX references on most stations. However, its RMSE values increase when using IGS and ERA5 at 5–10 mm and 10–16 mm, respectively. This better agreement with GipsyX can be explained by the fact that GipsyX uses VMF3 for a priori ZHD estimation and VMF1 as the mapping function.
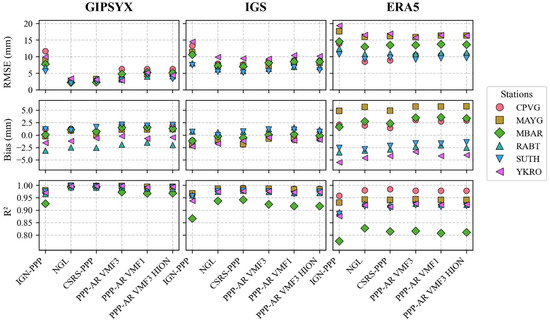
Figure 6.
ZTD retrieval performance (RMSE, Bias, R2) across GNSS processing solutions and reference datasets.
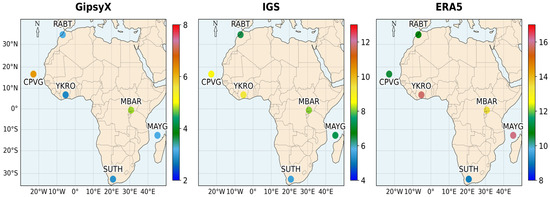
Figure 7.
Spatial distribution of the RMSE (mm) of the retrieved PPP-AR ZTDs compared to the reference (GipsyX, IGS, and ERA5).
- The comparison between CSRS-PPP, NGL solutions, and PRIDE PPP-AR solutions showed very similar results with typical biases ranging from −3 to 2.5 mm, typical RMSE ranging from 2 to 6 mm, and correlation coefficient above 0.99 when GipsyX is used as reference (Figure 6). While IGN-PPP shows higher errors that might be due to the lack of ambiguity resolution and gradients estimations (Table 2). These results are slightly better than when compared to the IGS final products and ERA5.
- Our analysis reveals distinct bias characteristics across the reference datasets (see Figure 6). The six GNSS solutions demonstrate consistent bias distributions. GipsyX shows a range of −3.0 to +2.5 mm, while IGS products exhibit slightly tighter constraints of −2.5 to +1.5 mm. By contrast, ERA5 shows significantly greater variability (−6.0 to +6.0 mm), consistent with known characteristics of GNSS (point measurements) versus ERA5 (gridded model) estimation methods.
- The use of the GMF mapping model by IGN-PPP seems to limit its accuracy compared to other strategies using VMF1 or VMF3.
- Figure 7 shows that the spatial distribution of RMSE indicates homogeneous performance of PRIDE PPP-AR, regardless of the station, when using GipsyX or IGS as references. However, when the ERA5 reference is considered, the results become heterogeneous and highlight a potential latitudinal dependence. Stations in temperate and arid zones (mid-latitudes) show RMSEs between 8 mm and 11 mm; these are similar to the results of [77]. However, RMSEs increase as we approach the equator. In YKRO, MBAR, and MAYG (tropical zones), RMSE values are around 13–17 mm, which is similar to the results of [78]. Figure 6 shows that the station MBAR (equator) has the lowest correlation (R2 ≈ 0.80). This may be due to greater atmospheric variability in these regions, including more pronounced ionospheric effects and tropospheric gradients dynamics [79] but a denser dataset could confirm this better.
- The non-alignment of points from one reference to another (Figure 6) shows that the choice of reference data has a significant influence on the RMSE values of the ZTDs. ERA5 tends to give higher RMSE values for all solutions, probably due to its systematic errors [61,80] in tropical areas. These discrepancies may also stem from the inherent scale mismatch between point-scale GNSS measurements and ERA5’s gridded data (0.25° resolution), which could smooth local moisture gradients.
3.2. Analysis of IWV Derived from ZTD Estimates
The evaluation of IWV with ERA5 and RS products has been carried out in accordance with the methodology described in Section 2. Higher annual mean IWV values are observed in tropical, low-altitude regions with dense vegetation cover, such as Abidjan (ABJN), Maygassa (MAYG), and Yamoussoukro (YKRO), where the average is between 40 and 47 kg·m−2. By contrast, the lowest values are recorded at Sutherland (SUTH), an arid, high-altitude site, with an annual mean of around 9 kg·m−2. The high altitude of MBAR in tropical zones influences its mean annual IWV above 30 kg·m−2. This spatial pattern highlights the latitudinal and altitudinal dependence of atmospheric water vapor over Africa, which is consistent with regional climatic gradients and vegetation density [14].
Time series analysis (Figure 8a and Figure 9a) confirms that IWV variations are strongly influenced by latitude and regional atmospheric circulation. CPVG, located in a tropical zone close to the equator, displays higher IWV values. In Cape Verde, IWV is notably higher from July to October, which correlates with increased rainfall. Figure 9a shows lower values observed from November to Juin. IWV follows the alternation between the African monsoon and the dry season, with peaks during the boreal summer (63 kg/m2) [81]. During the rainy season, the amplitude of IWV variations is very large, reaching 30–35 kg/m2 in just a few days. In dry periods, variations are small, while SUTH shows more moderate variability, in line with an arid climate. The amplitude of IWV fluctuations becomes more significant near the equator, surpassing those typical of subtropical areas [73].
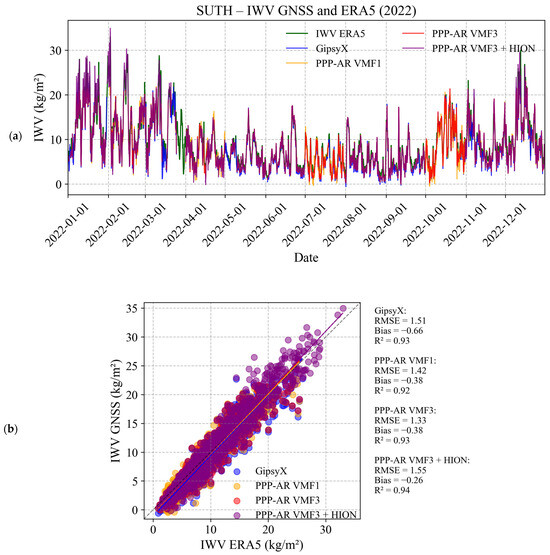
Figure 8.
(a) IWV time series and (b) regression with ERA5 for SUTH.
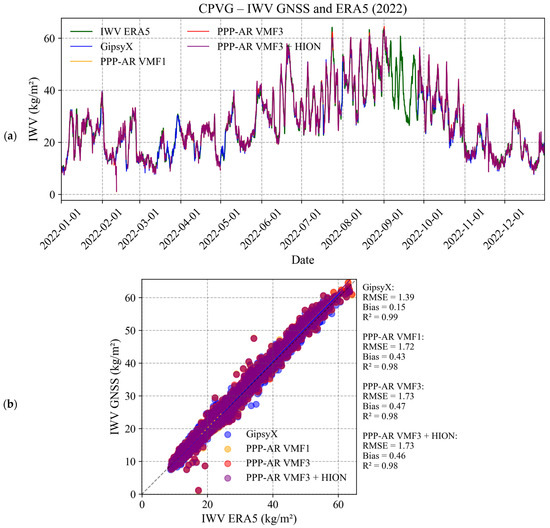
Figure 9.
(a) IWV time series and (b) regression with ERA5 for CPVG.
Cross plots (Figure 8b and Figure 9b) show a good relationship between ERA5 IWV and PRIDE PPP-AR IWV. However, discrepancies are noted for SUTH, which may be related to systematic errors and potential fluctuations in ERA5, especially at high altitudes.
All stations except ABJN show biases of less than 1 kg·m2 and RMSEs of less than 2.8 kg·m2 when comparing the results with the ERA5 IWVs obtained using different PPP-AR approaches (Figure 10).
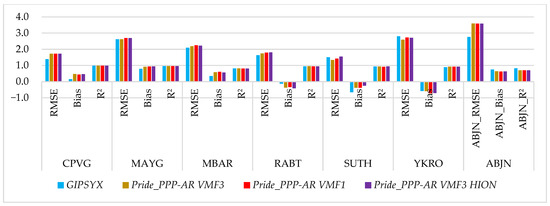
Figure 10.
Statistics of IWV differences with respect to ERA5.
The hypothesis that there would be an effect of the altitude factor in the comparison results between the GNSS and ERA5 solutions due to interpolations is not verified with our GNSS data sample (Figure 6). SUTH has one of the best RMSEs for the ZTD (9.1 mm), while the RMSE for MBAR is low (13.5 mm). For the IWV comparison, the RMSEs at these high-altitude stations are also quite small (Figure 10). We also found no altitude bias. This finding is consistent with the study of [82] in Ethiopia, which used a DD processing strategy with GAMIT. We have therefore investigated the relationship with the humidity of the area and the differences between the datasets.
Figure 11 shows a positive correlation (R2 = 0.74) between the annual mean IWV and the RMSE of the ZTD estimates with respect to ERA5, indicating a deterioration in accuracy in wetter regions. In fact, for areas with annual means above 35 kg/m2, the RMSE is greater than 2.5 kg/m2. This positive correlation could be explained by the limitations of ERA5 in very humid areas. These areas are often characterized by intense convection, high cloud cover, and rapid humidity variability [61]. These effects complicate remote sensing retrievals and reanalysis assimilation. Added to this is the limited number of RS or in situ measurements in the region, which could reduce the ability of ERA5 to constrain humidity profiles and amplify errors. These results appear to be consistent with those of [80].
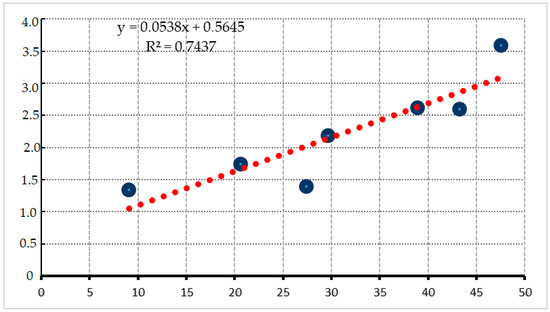
Figure 11.
Relationship between annual mean IWV and RMSE with ERA5. Higher humidity correlates with increased retrieval errors.
The retrieval of IWV from the different strategies also shows similar trends to the ZTD results (Figure 8, Figure 9, and Figure 11). RMSE errors of IWV for PRIDE PPP-AR are generally low (≈1.5 kg/m2) for stations with low annual mean IWV (MBAR, SUTH), but increase up to 2.76 kg/m2 in equatorial regions (YKRO, ABJN) (Figure 10). Average monthly deviations between PRIDE PPP-AR and GipsyX suggesting that PRIDE PPP-AR can be used for long-term trend studies. Figure 10 and the time series show a strong agreement between the IWV derived from GNSS and ERA5 across the selected stations, with a typical bias of less than 0.75 kg/m2. The RMSE results are similar to those of other recent studies, such as those of [83], in the tropical region. However, in our study, we noticed a smaller bias than in [83]. This can be explained by the use of Tm derived in VMF during the conversion process in these tropical regions. Using TUW VMF1 Tm rather than an empirical Tm (e.g., Bevis) minimizes discontinuities between models in these regions.
Figure 12 shows that the IWV_PPP-AR effectively describes the seasonal cycle in Abidjan with two rainy seasons from March to June and from September to November, separated by a dry season between July and August. The second dry season is from December to February. These time series agree well with the climatic study of [84]. The YKRO and ABJN time series clearly show the transition between the four seasons in southern Côte d’Ivoire and the two seasons in northern Côte d’Ivoire, with YKRO in the middle and low IWV values in July.
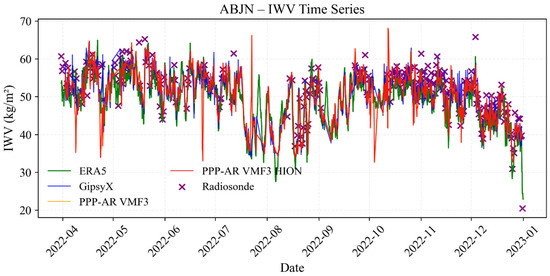
Figure 12.
IWV time series for ABJN with RS.
Evaluation of IWV with RS data at Abidjan shows good agreement with PRIDE PPP-AR, with an RMSE of 3.6 kg/m2 and R2 = 0.70, although GipsyX remains the closest reference with an RMSE of 2.94 kg/m2 and R2 = 0.82.
Finally, the correspondence analysis between water vapor peaks and precipitation events shows that the use of precipitation data at higher frequencies (6 h or 12 h) could improve the interpretation of IWV variations. Rainfall data with a frequency of 6 h or 12 h would be interesting in order to better detect correspondences between water vapor peaks and rainfall.
Although various GNSS processing strategies were employed, the proprietary nature of certain software packages limited our ability to fully investigate the implemented algorithms, which may have influenced the interpretation of the comparative performance.
4. Conclusions and Perspectives
Accurate ZTD and IWV estimation from GNSS is essential for high precision meteorology, climatology, and geodesy.
In this study, we use a limited sample of seven stations that are representative of Africa’s climatic regions and variety of topography. The results show that PRIDE PPP-AR provides competitive performance in ZTD and IWV estimation, especially when using VMF3 (first order) and VMF3 with high order ionospheric correction. RMSEs remain between 2.9 and 6 mm for most stations using GipsyX as a reference. Compared to the other solutions, PRIDE PPP-AR has a reliability similar to CSRS-PPP and NGL, but slightly better than IGN-PPP, in line with the ERA5 and IGS references. However, ERA5 seems to introduce greater variability, preventing RMSEs below 9 mm in some cases.
For IWV, PRIDE PPP-AR shows lower RMSEs (~1.5 kg/m2) for low humidity stations, but larger errors (2.76 kg/m2) in equatorial zones IWV_ERA5. Validation with RS from Abidjan confirms the reliability of PRIDE PPP-AR with an RMSE of 3.6 kg/m2, although GipsyX remains the reference, with an RMSE of 2.94 kg/m2.
In addition, the lack of tropospheric gradient estimation in IGN-PPP could explain its poorer performance. These results confirm the importance of taking gradients and ambiguity resolution into account to improve the accuracy of GNSS estimates. The very low RMSEs obtained in this study over an entire year demonstrate the robustness of this study with the advanced tools used.
This study allowed a detailed analysis of the seasonal cycles of the GNSS ZTDs to be conducted, revealing variations consistent with local weather patterns. The PPP-AR solutions show remarkable validity for monitoring these variations, with performances equivalent (RMSE < 5 mm, R2 > 0.98) to the best conventional GNSS solutions. These results confirm the suitability of PPP-AR techniques for high-precision characterization of water vapor variability, paving the way for their systematic use in atmospheric studies.
Tropospheric water vapor is the most abundant greenhouse gas and plays a crucial role in the hydrological cycle. Several studies have reported the difficulties in monitoring its short- and long-term changes due to the inhomogeneity of RS data and variations in observing systems [62,63,64]. In Africa, traditional techniques for observing water vapor are very limited in space and time. Their products are also very heterogeneous. GNSS meteorology would be a credible alternative to study the distribution of IWV in these regions, which are significantly affected by climate change [35]. The ERA5 reanalysis model shows some variations in very humid regions. The expansion of multi-GNSS stations, coupled with these convincing results for the performance of the PRIDE PPP-AR solution in Africa, offers good prospects for short and long term spatio-temporal distribution studies. The performance of near real-time water vapor retrieval in Africa could also be investigated to assess the potential of GNSS data assimilation in numerical weather prediction models.
The analysis of ZTDs in Section 3.1 for Rabat highlights the impact of ocean–land interactions on water vapor, a key element in understanding meteorological phenomena in coastal areas. The integration of shipborne GNSS, combined with land-based stations, offers a promising solution for refining climate models [35,85,86]. The use of PPP-AR techniques, particularly PRIDE PPP-AR, in shipborne campaigns deserves to be explored, as it could significantly enhance the study of extreme weather events along African coasts. A promising extension of this work would be to explore the integration of ZTD estimates from PRIDE PPP-AR into numerical weather prediction models to enhance short-term forecasting in tropical regions.
Author Contributions
Conceptualization, M.G.T. and P.B.; methodology, M.G.T. and P.B.; software, M.G.T., P.B., N.F., and L.J.-L.; validation, P.B., L.J.-L., and M.N.; formal analysis, M.G.T. and P.B.; investigation, M.G.T. and P.B.; resources, P.B. and L.J.-L.; data curation, P.B.; writing—original draft preparation, M.G.T.; writing—review and editing, M.G.T. and P.B.; visualization, M.G.T.; supervision, P.B.; project administration, P.B.; funding acquisition, P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on request.
Acknowledgments
The authors would like to thank the ASECNA, IGS, CORSAFOR for providing data and products.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Linear Models for the Determination of the Weighted Mean Temperature of the Atmosphere

Table A1.
Linear models for Tm in the literature.
Table A1.
Linear models for Tm in the literature.
| Reference | a | b | Model | Location |
|---|---|---|---|---|
| (Bevis., et al., 1992) [1] | 0.72 | 72 | Tm = 0.72 Ts + 70.2 | USA |
| (Song & Boutiouta, 2012) [87] | 0.96 | 14.79 | Tm = 0.96 Ts + 14.79 | Algeria |
| (Chen et al., 2017) [57] | 0.61 | 102.11 | Tm = 0.61 Ts + 102.11 | Guilin, China |
| (Liou et al., 2001) [88] | 1.07 | −31.5 | Tm = 1.07 Ts − 31.5 | Taipei |
| (Suresh Raju et al., 2007) [55] | 0.75 | 62.58 | Tm = 0.75 Ts + 62.58 | Indian |
| (L. Li et al., 2017) [89] | 0.65 | 87.08 | Tm = 0.65 Ts + 87.08 | Hunan, China |
| (Isioye et al., 2016) [56] | 0.57 | 116.60 | Tm = 0.57 Ts + 116.60 | West Africa |
| (D. Song et al., 2007) [90] | 1.01 | −12.35 | Tm = 1.01 Ts − 12.35 | South Korea |
Appendix B. Stations and Height Conversions

Table A2.
Basic information of stations used in this study.
Table A2.
Basic information of stations used in this study.
| Marker | Location | Country | Latitude (°) | Longitude (°) | Elevation (m) | Station |
|---|---|---|---|---|---|---|
| YKRO | Yamoussoukro | Ivory Coast | 6.871 | −5.24 | 270 | IGS |
| CPVG | Espargos | Cabo Verde | 16.732 | −22.935 | 94.089 | IGS |
| RABT | Rabat | Morocco | 33.998 | −6.854 | 90.1 | IGS |
| ABJN | Abidjan | Ivory Coast | 5.330 | −3.983 | 63.525 | No IGS |
| 65578 | Abidjan | Ivory Coast | 5.25 | −3.93 | 8.00 MSL | RS |
| SUTH | Sutherland | South Africa | −32.38 | 20.81 | 1799.766 | IGS |
| MAYG | Dzaoudzi | Mayotte | −12.782 | 45.258 | −16.35 | IGS |
| MBAR | Mbarara | Uganda | −0.601 | 30.738 | 1337.653 | IGS |
Appendix B.1. Ground-Based GNSS Height Conversion
The ellipsoidal height () obtained from GNSS processing (IGS14/GRS80) was converted to orthometric height () using the EGM2008 geoid model:
where N = geoid undulation (EGM2008).
Appendix B.2. IWV Reference Altitude Adjustment
For H_ERA5 or H_RS, we define a common reference height, denoted as , to standardize altitude adjustments across datasets. The correction is applied using the [73] formula
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. Geophys. Monogr. Ser. 1972, 15. [Google Scholar]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- A Two-Stage Tropospheric Correction Model Combining Data from GNSS and Numerical Weather Model|GPS Solutions. Available online: https://link.springer.com/article/10.1007/s10291-018-0742-x (accessed on 23 March 2025).
- Bevis, M.; Businger, S.; Chiswell, S. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. Climatol. 1994, 33, 379–386. Available online: https://journals.ametsoc.org/view/journals/apme/33/3/1520-0450_1994_033_0379_gmmzwd_2_0_co_2.xml (accessed on 27 August 2024). [CrossRef]
- Jones, J. An Assessment of the Quality of GPS Water Vapour Estimates and Their Use in Operational Meteorology and Climate Monitoring. Ph.D. Thesis, Institute of Engineering Surveying and Space Geodesy IESSG, Nottingham, UK, 2010. [Google Scholar]
- Panetier, A. Shipborne Global Navigation Satellite Systems for Offshore Atmospheric Water Vapor Monitoring. Ph.D. Thesis, ENSTA Bretagne—École Nationale Supérieure de Techniques Avancées Bretagne, Brest, France, 2023. [Google Scholar]
- Benevides, P.; Catalao, J.; Miranda, P. On the Inclusion of GPS Precipitable Water Vapour in the Nowcasting of Rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.; Jefferson, D.C.; Watkins, M.; Webb, F. Precise Point Positioning for the Efficient And Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Alkan, R.; Erol, S.; Ozulu, I.M.; ilçi, V. Accuracy Comparison of Post-Processed PPP and Real-Time Absolute Positioning Techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
- Dousa, J.; Vaclavovic, P.; Gyori, G.; Kostelecký, J. Development of Real-Time GNSS ZTD Products. Geophys. Res. Abstr. 2013, 15, 12698. [Google Scholar]
- Stępniak, K.; Bock, O.; Bosser, P.; Wielgosz, P. Outliers and Uncertainties in GNSS ZTD Estimates from Double-Difference Processing and Precise Point Positioning. GPS Solut. 2022, 26, 74. [Google Scholar] [CrossRef]
- Bosser, P.; Bock, O. IWV Retrieval from Ground GNSS Receivers during NAWDEX. Adv. Geosci. 2021, 55, 13–22. [Google Scholar] [CrossRef]
- Baldysz, Z.; Nykiel, G.; Latos, B.; Baranowski, D.B.; Figurski, M. Interannual Variability of the GNSS Precipitable Water Vapor in the Global Tropics. Atmosphere 2021, 12, 1698. [Google Scholar] [CrossRef]
- Ojegbile, B.M.; Okolie, C.J.; Omogunloye, O.J. The Dynamics of ERA5 and GNSS-Derived Precipitable Water Vapour in the Climatic Zones of Nigeria. Nig. J. Environ. Sci. Tech. 2023, 7, 372–394. Available online: https://mycoordinates.org/the-dynamics-of-era5-and-gnss-derived-precipitable-water-vapour-in-the-climatic-zones-of-nigeria/ (accessed on 23 March 2025).
- Bock, O.; Bosser, P.; Flamant, C.; Doerflinger, E.; Jansen, F.; Fages, R.; Bony, S.; Schnitt, S. Integrated Water Vapour Observations in the Caribbean Arc from a Network of Ground-Based GNSS Receivers during EUREC4A. Earth Syst. Sci. Data 2021, 13, 2407–2436. [Google Scholar] [CrossRef]
- Bezcioğlu, M.; Ucar, T.; Yiğit, C.Ö. Investigation of the Capability of Multi-GNSS PPP-AR Method in Detecting Permanent Displacements. Int. J. Eng. Geosci. 2023, 8, 251–261. [Google Scholar] [CrossRef]
- Geng, J.; Xingyu, C.; Pan, Y.; Mao, S.; Li, C.; Zhou, J.; Zhang, K. PRIDE PPP-AR: An Open-Source Software for GPS PPP Ambiguity Resolution. GPS Solut. 2019, 23. [Google Scholar] [CrossRef]
- Katsigianni, G.; Perosanz, F.; Loyer, S.; Gupta, M. Galileo Millimeter-Level Kinematic Precise Point Positioning with Ambiguity Resolution. Earth Planets Space 2019, 71, 76. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the Interoperability of IGS Products for Precise Point Positioning with Ambiguity Resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Bertiger, W.; Bar-Sever, Y.; Dorsey, A.; Haines, B.; Harvey, N.; Hemberger, D.; Heflin, M.; Lu, W.; Miller, M.; Moore, A.W.; et al. GipsyX/RTGx, a New Tool Set for Space Geodetic Operations and Research. Adv. Space Res. 2020, 66, 469–489. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, A.; Ni, S.; Xiao, G.; Xu, H. PPP-ARISEN: An Open-Source Precise Point Positioning Software with Ambiguity Resolution for Interdisciplinary Research of Seismology, Geodesy and Geodynamics. GPS Solut. 2022, 27, 45. [Google Scholar] [CrossRef]
- Marty, J.C.; Loyer, S.; Perosanz, F.; Mercier, F.; Bracher, G.; Legresy, B.; Portier, L.; Capdeville, H.; Fund, F.; Lemoine, J.M.; et al. GINS: The CNES/GRGS GNSS Scientific Software. Available online: https://ids-doris.org/images/documents/report/publications/GINS_GRGS_software-Marty-2011.pdf (accessed on 23 March 2025).
- Banville, S.; Donahue, B.; Farinaccio, J.; Hassen, E.; Lamothe, P. Updates to the CSRS-PPP Online Service. 2018. Available online: https://ostrnrcan-dostrncan.canada.ca/entities/publication/2fd0eaf8-c1bc-455f-a357-f5c7e938c58c (accessed on 21 March 2025).
- Calculs GNSS PPP En Ligne|RGP. Available online: https://rgp.ign.fr/SERVICES/ppp_online.php (accessed on 24 March 2025).
- Automatic Precise Positioning Service (APPS)—NASA Jet Propulsion Laboratory (JPL), GDGPS. Available online: https://pppx.gdgps.net/ (accessed on 29 March 2025).
- The PPP-Wizard Project—Positioning Service. Available online: http://www.ppp-wizard.net/upload.html (accessed on 29 March 2025).
- Du, S.; Shu, B.; Xie, W.; Huang, G.; Ge, Y.; Li, P. Evaluation of Real-Time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sens. 2022, 14, 4970. [Google Scholar] [CrossRef]
- Yao, Y.; Peng, W.; Xu, C.; Cheng, S. Enhancing Real-Time Precise Point Positioning with Zenith Troposphere Delay Products and the Determination of Corresponding Tropospheric Stochastic Models. Geophys. J. Int. 2017, 208, 1217–1230. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Li, Z. Real-Time Precise Point Positioning-Based Zenith Tropospheric Delay for Precipitation Forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef] [PubMed]
- Bosser, P.; Van Baelen, J.; Bousquet, O. Routine Measurement of Water Vapour Using GNSS in the Framework of the Map-Io Project. Atmosphere 2022, 13, 903. [Google Scholar] [CrossRef]
- Abd El- Naeim, A.E.; Elhatab, A.; Azzam, M.; Mosaad, R.; Elsharkawy, A. Assessment of GNSS Positioning Techniques In EGYPT. Port-Said Eng. Res. J. 2023, 28, 31–38. [Google Scholar] [CrossRef]
- Guo, Q. Precision Comparison and Analysis of Four Online Free PPP Services in Static Positioning and Tropospheric Delay Estimation. GPS Solut. 2015, 19, 537–544. [Google Scholar] [CrossRef]
- Vázquez-Ontiveros, J.R.; Padilla-Velazco, J.; Gaxiola-Camacho, J.R.; Vázquez-Becerra, G.E. Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode. Remote Sens. 2023, 15, 2034. [Google Scholar] [CrossRef]
- Tine, M.G.; Bosser, P.; Ndiaye, M. Tropospheric Water Vapor Retrievals by Ground-Based GNSS in Africa: A Systematic Review. Rep. Geod. Geoinform. 2025, 119, 71–84. [Google Scholar] [CrossRef]
- Pérez-Ramírez, D.; Whiteman, D.N.; Smirnov, A.; Lyamani, H.; Holben, B.N.; Pinker, R.; Andrade, M.; Alados-Arboledas, L. Evaluation of AERONET Precipitable Water Vapor versus Microwave Radiometry, GPS, and Radiosondes at ARM Sites. J. Geophys. Res. Atmos. 2014, 119, 9596–9613. [Google Scholar] [CrossRef]
- Ramella Pralungo, L.; Haimberger, L.; Stickler, A.; Brönnimann, S. A Global Radiosonde and Tracked Balloon Archive on 16 Pressure Levels (GRASP) Back to 1905 – Part 1: Merging and Interpolation to 00:00 and 12:00 GMT. Earth Syst. Sci. Data 2014, 6, 185–200. [Google Scholar] [CrossRef]
- van der Linden, R.; Knippertz, P.; Fink, A.H.; Ingleby, B.; Maranan, M.; Benedetti, A. The Influence of DACCIWA Radiosonde Data on the Quality of ECMWF Analyses and Forecasts over Southern West Africa. Q. J. R. Meteorol. Soc. 2020, 146, 1719–1739. [Google Scholar] [CrossRef]
- Dirksen, R.J.; Sommer, M.; Immler, F.J.; Hurst, D.F.; Kivi, R.; Vömel, H. Reference Quality Upper-Air Measurements: GRUAN Data Processing for the Vaisala RS92 Radiosonde. Atmos. Meas. Tech. 2014, 7, 4463–4490. [Google Scholar] [CrossRef]
- Ding, T.; Awange, J.L.; Scherllin-Pirscher, B.; Kuhn, M.; Khandu; Anyah, R.; Zerihun, A.; Bui, L.K. GNSS Radio Occultation Infilling of the African Radiosonde Data Gaps Reveals Drivers of Tropopause Climate Variability. J. Geophys. Res. Atmos. 2022, 127, e2022JD036648. [Google Scholar] [CrossRef]
- Suya, R.G. Advancing High-Resolution Weather Prediction Through Machine Learning and GNSS Techniques. In Proceedings of the Safe, Secure, Ethical, Responsible Technologies and Emerging Applications; Tchakounte, F., Atemkeng, M., Rajagopalan, R.P., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 175–189. [Google Scholar]
- Hdidou, F.Z.; Mordane, S.; Moll, P.; Mahfouf, J.-F.; Erraji, H.; Dahmane, Z. Impact of the Variational Assimilation of Ground-Based GNSS Zenith Total Delay into AROME-Morocco Model. Tellus A Dyn. Meteorol. Oceanogr. 2020, 72, 1–13. [Google Scholar] [CrossRef]
- El Ouardi, M. Quantification de La Vapeur d’eau Au MAROC à Travers Les Observations GPS Au Sol. Ph.D. Thesis, Hassan II University, Casablanca, Morocco, 2023. [Google Scholar]
- Drissi El Bouzaidi, R.; El Talibi, H.; El Moussaoui, S.; Mourabit, T. Estimating Atmospheric Precipitable Water Vapor in Northern Morocco: A Ground-Based GNSS Approach. Sci. Afr. 2025, 28, e02681. [Google Scholar] [CrossRef]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.-T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-Line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef]
- Performance Assessment of PPP-AR Positioning and Zenith. Available online: https://sciendo.com/fr/article/10.2478/arsa-2021-0003 (accessed on 23 March 2025).
- Hay, C.; Wong, J. Enhancing GPS Tropospheric Delay Prediction at Master Control Station. GPS World 2000, 11, 56–62. [Google Scholar]
- Path Delays in the Neutral Atmosphere|SpringerLink. Available online: https://link.springer.com/chapter/10.1007/978-3-642-36932-2_3 (accessed on 23 March 2025).
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Boudouris, G. On the Index of Refraction of Air, the Absorption and Dispersion of Centimeterwaves by Gases. J. Res. Natl. Bur. Stan. Sect. D Rad. Prop. 1963, 67, 631. [Google Scholar] [CrossRef]
- Thayer, G.D. An Improved Equation for the Radio Refractive Index of Air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Rüeger, J.M. Refractive Index Formulae for Radio Waves. 2022. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig_2002/Js28/JS28_rueger.pdf (accessed on 23 March 2025).
- Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Jones, J., Guerova, G., Douša, J., Dick, G., De Haan, S., Pottiaux, E., Bock, O., Pacione, R., Van Malderen, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-13900-1. [Google Scholar]
- Hogg, D.C.; Guiraud, F.O.; Decker, M.T. Measurement of Excess Radio Transmission Length on Earth-Space Paths. Astron. Astrophys. 1981, 95, 304–307. [Google Scholar]
- Suresh Raju, C.; Saha, K.; Thampi, B.V.; Parameswaran, K. Empirical Model for Mean Temperature for Indian Zone and Estimation of Precipitable Water Vapor from Ground Based GPS Measurements. Ann. Geophys. 2007, 25, 1935–1948. [Google Scholar] [CrossRef]
- Isioye, O.A.; Combrinck, L.; Botai, J. Modelling Weighted Mean Temperature in the West African Region: Implications for GNSS Meteorology: Weighted Mean Temperature in the West African Region. Met. App. 2016, 23, 614–632. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Liu, L.; Luo, G.; Mo, X. Model Establishment and Analysis of Weighted Mean Temperature in the Region of Guilin. In Proceedings of the China Satellite Navigation Conference (CSNC) 2017 Proceedings: Volume I; Sun, J., Liu, J., Yang, Y., Fan, S., Yu, W., Eds.; Springer: Singapore, 2017; pp. 199–207. [Google Scholar]
- Ayodele, E.; Okolie, C.J.; Ezeigbo, C.U.; Fajemirokun, F.A. Evaluating the Stability and Adequacy of NIGNET for the Definition of Nigerian Geodetic Reference Frame. Niger. J. Technol. Dev. 2020, 17, 1–12. [Google Scholar] [CrossRef]
- Koome, D.; Ogaja, C.; Rubino, E. Developing Africa One CORS at a Time. 2019. Available online: https://fig.net/resources/proceedings/fig_proceedings/fig2019/papers/fig03/FIG03_koome_ogaja_et_al_10022_abs.pdf (accessed on 25 March 2025).
- Basha, G.; Kishore, P.; Venkat Ratnam, M.; Ouarda, T.B.M.J.; Velicogna, I.; Sutterley, T. Vertical and Latitudinal Variation of the Intertropical Convergence Zone Derived Using GPS Radio Occultation Measurements. Remote Sens. Environ. 2015, 163, 262–269. [Google Scholar] [CrossRef]
- Johnston, B.R.; Randel, W.J.; Sjoberg, J.P. Evaluation of Tropospheric Moisture Characteristics Among COSMIC-2, ERA5 and MERRA-2 in the Tropics and Subtropics. Remote Sens. 2021, 13, 880. [Google Scholar] [CrossRef]
- Wang, R.; Wu, G.; Liu, Y.; Wang, R.; Fan, X.; Liu, Y. Significant Increase in African Water Vapor over 2001–2020. Remote Sens. 2024, 16, 2875. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Feng, P.; Li, F.; Yan, J.; Zhang, F.; Barriot, J.-P. Assessment of the Accuracy of the Saastamoinen Model and VMF1/VMF3 Mapping Functions with Respect to Ray-Tracing from Radiosonde Data in the Framework of GNSS Meteorology. Remote Sens. 2020, 12, 3337. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J. New Approaches in Global Ionospheric Determination Using Ground GPS Data. J. Atmos. Sol.-Terr. Phys. 1999, 61, 1237–1247. [Google Scholar] [CrossRef]
- Positionnement Ponctuel Précis. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php (accessed on 24 March 2025).
- Index of /Gps_timeseries/Trop. Available online: https://geodesy.unr.edu/gps_timeseries/trop/ (accessed on 24 March 2025).
- Bock, O. GNSS: Géodésie, Météorologie et Climat. Habilitation Thesis, Université Pierre et Marie Curie—Paris VI, Paris, France, 2012. Available online: https://theses.hal.science/tel-00851617v1 (accessed on 27 May 2025).
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV Trends and Variability in Atmospheric Reanalyses and GPS Observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef]
- Elsobeiey, M.; El-Diasty, M. Impact of Tropospheric Delay Gradients on Total Tropospheric Delay and Precise Point Positioning. Int. J. Geosci. 2016, 7, 645–654. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Li, Z.; Heinkelmann, R.; Nilsson, T.; Dick, G.; Ge, M.; Schuh, H. GNSS Tropospheric Gradients with High Temporal Resolution and Their Effect on Precise Positioning. J. Geophys. Res. Atmos. 2016, 121, 912–930. [Google Scholar] [CrossRef]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sens. 2019, 11, 674. [Google Scholar] [CrossRef]
- Ssenyunzi, R.C.; Andima, G.; Amabayo, E.B.; Kiroe, A.J. Assessment of ERA5 Derived Zenith Tropospheric Delay Data over East African Region. Adv. Space Res. 2024, 74, 695–710. [Google Scholar] [CrossRef]
- A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay. Available online: https://www.mdpi.com/2072-4292/15/13/3247 (accessed on 29 May 2025).
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J.T. GPS-Derived PWV for Rainfall Nowcasting in Tropical Region. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
- Ssenyunzi, R.C.; Oruru, B.; D’ujanga, F.M.; Realini, E.; Barindelli, S.; Tagliaferro, G.; von Engeln, A.; van de Giesen, N. Performance of ERA5 Data in Retrieving Precipitable Water Vapour over East African Tropical Region. Adv. Space Res. 2020, 65, 1877–1893. [Google Scholar] [CrossRef]
- Bock, O.; Bouin, M.N.; Doerflinger, E.; Collard, P.; Masson, F.; Meynadier, R.; Nahmani, S.; Koité, M.; Gaptia Lawan Balawan, K.; Didé, F.; et al. West African Monsoon Observed with Ground-Based GPS Receivers during African Monsoon Multidisciplinary Analysis (AMMA). J. Geophys. Res. Atmos. 2008, 113, D21105. [Google Scholar] [CrossRef]
- Koji, A.K.; Van Malderen, R.; Pottiaux, E.; Van Schaeybroeck, B. Understanding the Present-Day Spatiotemporal Variability of Precipitable Water Vapor over Ethiopia: A Comparative Study between ERA5 and GPS. Remote Sens. 2022, 14, 686. [Google Scholar] [CrossRef]
- Osah, S.; Acheampong, A.A.; Fosu, C.; Abukari, O.M.; Asiedu, S.B. Ground-Based GNSS for Meteorological Applications in Ghana 2024. Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2024/papers/ts05f/TS05F_osah_acheampong_et_al_12701_abs.pdf (accessed on 25 May 2025).
- ELDIN, M. Le Climat de La CÔte d’Ivoire. In Le Milieu Naturel de Côte d’Ivoire; Mémoire ORSTOM: Paris, France, 1971. [Google Scholar]
- Bosser, P.; Bock, O.; Flamant, C.; Bony, S.; Sabrina, S. Integrated Water Vapour Content Retrievals from Ship-Borne GNSS Receivers during EUREC4A. Earth Syst. Sci. Data 2021, 13, 1499–1517. [Google Scholar] [CrossRef]
- Boniface, K.; Champollion, C.; Chery, J.; Ducrocq, V.; Rocken, C.; Doerflinger, E.; Collard, P. Potential of Shipborne GPS Atmospheric Delay Data for Prediction of Mediterranean Intense Weather Events. Atmos. Sci. Lett. 2012, 13, 250–256. [Google Scholar] [CrossRef]
- Song, D.-S.; Boutiouta, S. Determination of Algerian Weighted Mean Temperature Model for Forthcoming GNSS Meteorology Application in Algeria. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2012, 30, 615–622. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Teng, Y.-T.; Hove, T.V.; Liljegren, J.C. Comparison of Precipitable Water Observations in the Near Tropics by GPS, Microwave Radiometer, and Radiosondes. Meteorol. Climatol. 2001, 40, 5–15. [Google Scholar] [CrossRef]
- Li, L.; Wu, S.; Wang, X.; Tian, Y.; He, C.; Zhang, K. Seasonal Multifactor Modelling of Weighted-Mean Temperature for Ground-Based GNSS Meteorology in Hunan, China. Adv. Meteorol. 2017, 2017, 3782687. [Google Scholar] [CrossRef]
- Song, D.-S.; Grejner-Brzezinska, D.A. Remote Sensing of Atmospheric Water Vapor Variation from GPS Measurements during a Severe Weather Event. Earth Planets Space 2009, 61, 1117–1125. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).