RANS and LES Simulations of Localized Pollutant Dispersion Around High-Rise Buildings Under Varying Temperature Stratifications
Abstract
1. Introduction
2. Research Methodology
2.1. RANS Method
2.2. LES Method
3. Numerical Techniques
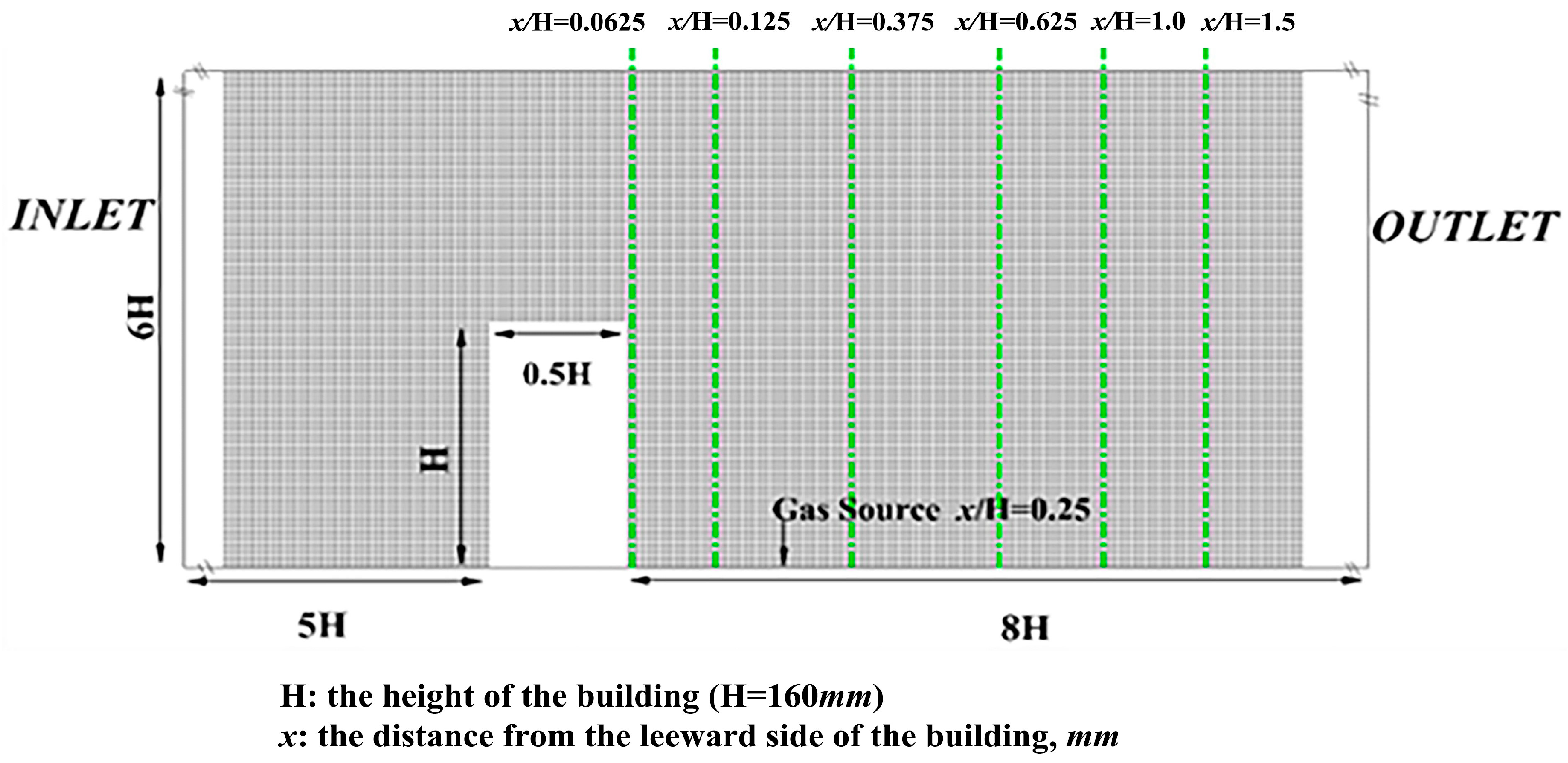
3.1. Numerical Model
3.2. Parameter Setting
3.3. Mesh Independence Analysis
4. Results and Discussion
4.1. Velocity Field
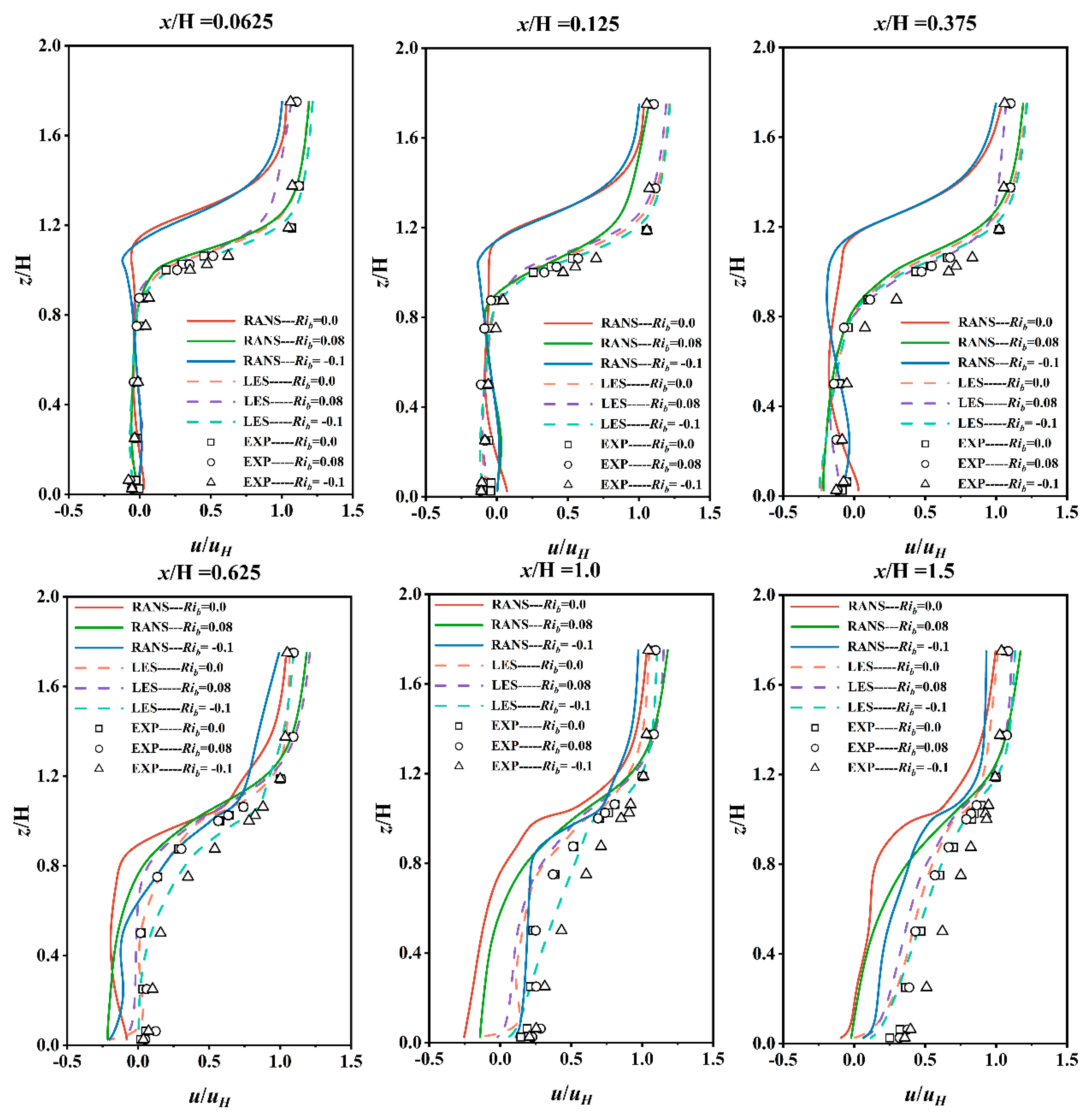
4.1.1. Mean Longitudinal Velocity
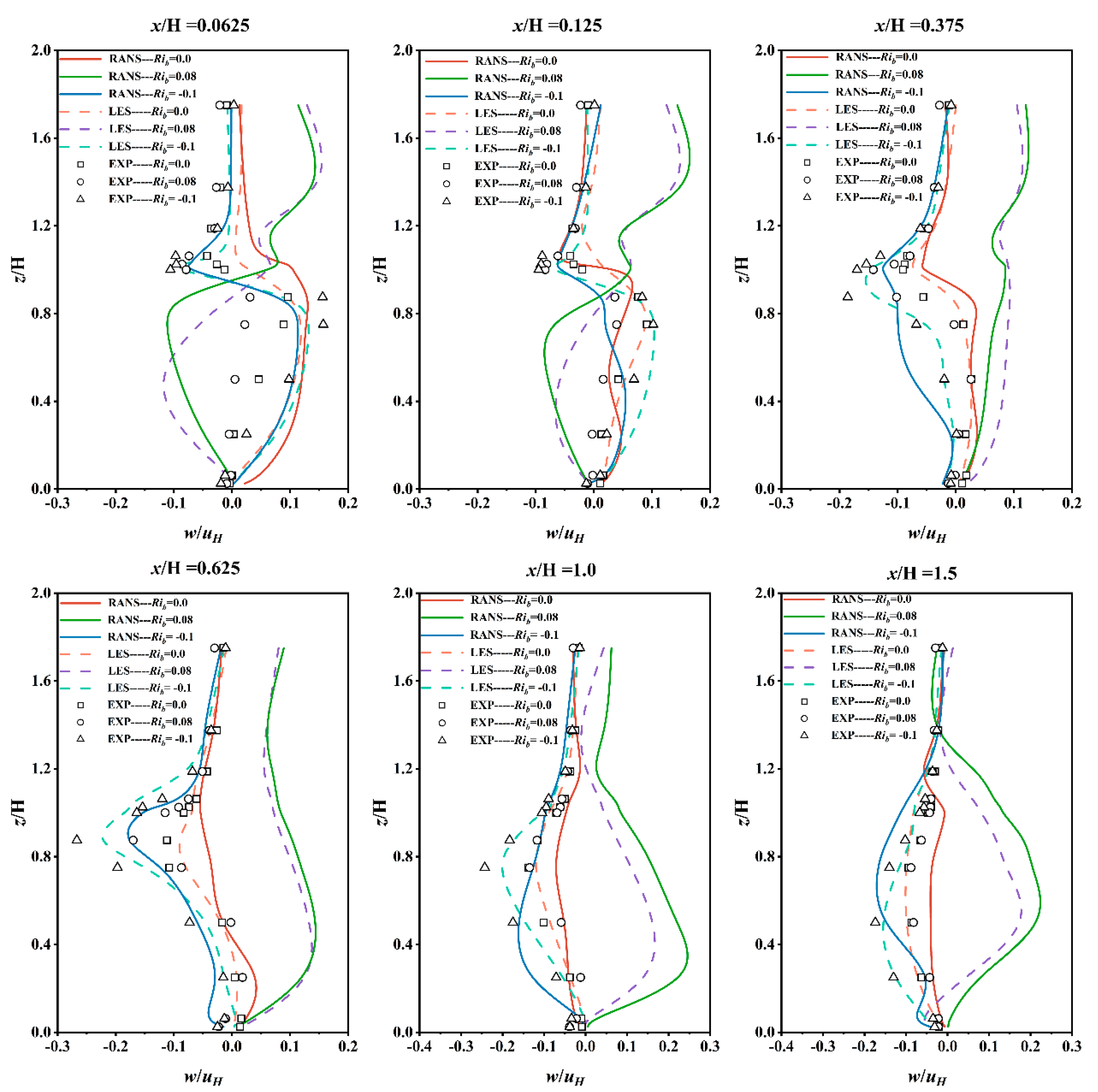
4.1.2. Mean Vertical Velocity
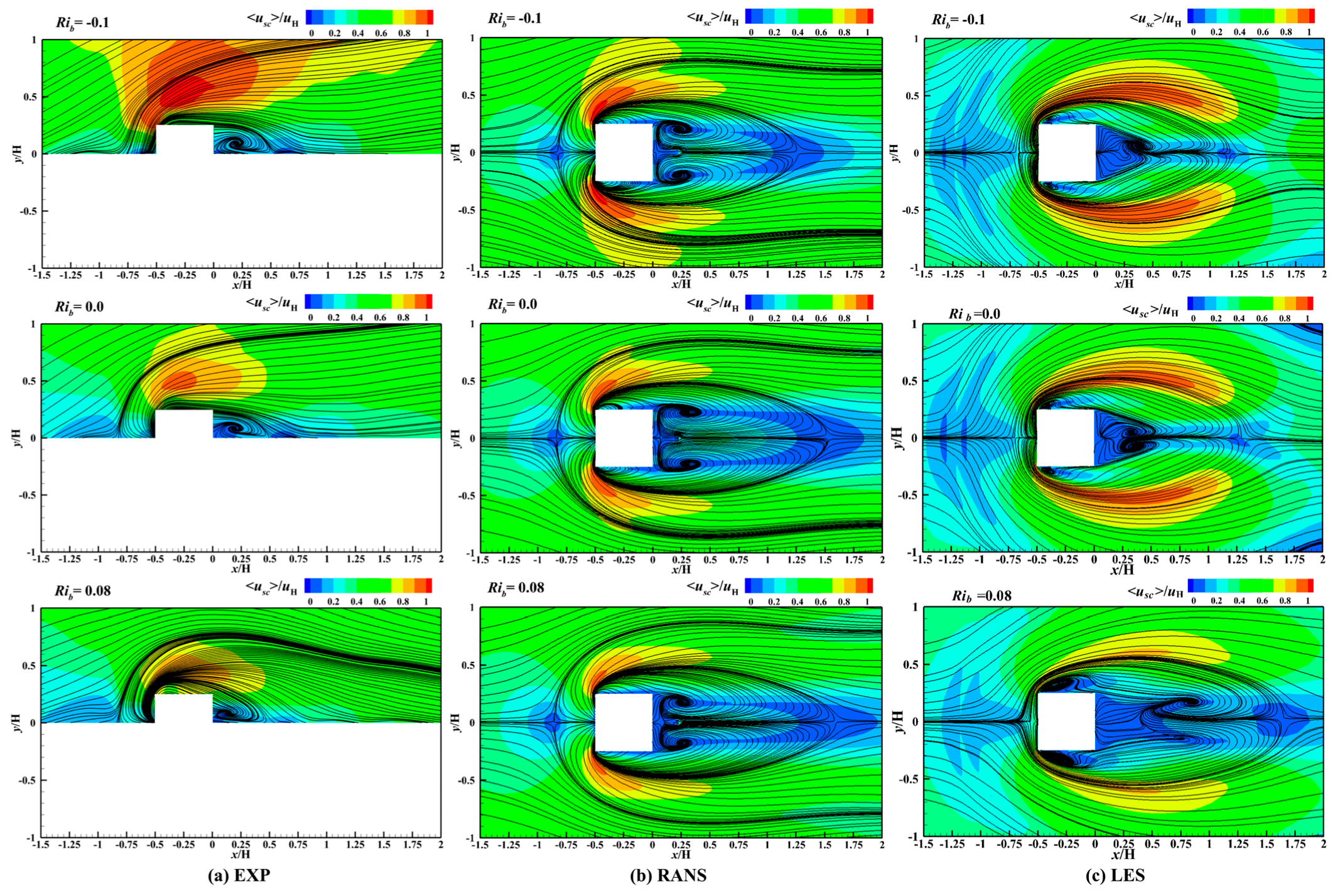
4.1.3. Flow Pattern
4.2. Concentration Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Träumner, K.; Damian, T.; Stawiarski, C.; Wieser, A. Turbulent Structures and Coherence in the Atmospheric Surface Layer. Bound.-Layer Meteorol. 2015, 154, 1–25. [Google Scholar] [CrossRef]
- Li, D. Turbulent Prandtl Number in the Atmospheric Boundary Layer—Where Are We Now? Atmos. Res. 2019, 216, 86–105. [Google Scholar] [CrossRef]
- Kanda, I.; Yamao, Y. Passive Scalar Diffusion in and above Urban-like Roughness under Weakly Stable and Unstable Thermal Stratification Conditions. J. Wind Eng. Ind. Aerodyn. 2016, 148, 18–33. [Google Scholar] [CrossRef]
- Yassin, M.F. A Wind Tunnel Study on the Effect of Thermal Stability on Flow and Dispersion of Rooftop Stack Emissions in the near Wake of a Building. Atmos. Environ. 2013, 65, 89–100. [Google Scholar] [CrossRef]
- Marucci, D.; Carpentieri, M. Dispersion in an Array of Buildings in Stable and Convective Atmospheric Conditions. Atmos. Environ. 2020, 222, 117100. [Google Scholar] [CrossRef]
- Marucci, D.; Carpentieri, M. Stable and Convective Boundary-Layer Flows in an Urban Array. J. Wind Eng. Ind. Aerodyn. 2020, 200, 104140. [Google Scholar] [CrossRef]
- Yan, B.; Li, Q.-S. Wind Tunnel Study of Interference Effects between Twin Super-Tall Buildings with Aerodynamic Modifications. J. Wind Eng. Ind. Aerodyn. 2016, 156, 129–145. [Google Scholar] [CrossRef]
- Zhou, X.; Ying, A.; Cong, B.; Kikumoto, H.; Ooka, R.; Kang, L.; Hu, H. Large Eddy Simulation of the Effect of Unstable Thermal Stratification on Airflow and Pollutant Dispersion around a Rectangular Building. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104526. [Google Scholar] [CrossRef]
- Jeong, S.J.; Kim, A.R. CFD Study on the Influence of Atmospheric Stability on Near-Field Pollutant Dispersion from Rooftop Emissions. Asian J. Atmos. Environ. 2018, 12, 47–58. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, K.; Cheng, J.; Xu, J.; He, J.; Kang, Y. Numerical Investigation of Building Gap Effects on Traffic Pollutant Dispersion in Urban Networks with Intersecting Streets. Atmos. Pollut. Res. 2025, 16, 102475. [Google Scholar] [CrossRef]
- Yassin, M.F.; Al-Rashidi, M.; Ohba, M. Experimental and Numerical Simulations of Air Quality in an Urban Canopy: Effects of Roof Shapes and Atmospheric Stability. Atmos. Pollut. Res. 2022, 13, 101618. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD Simulations of Near-Field Pollutant Dispersion with Different Plume Buoyancies. Build. Environ. 2018, 131, 128–139. [Google Scholar] [CrossRef]
- Guo, D.; Yang, F.; Shi, X.; Li, Y.; Yao, R. Numerical Simulation and Wind Tunnel Experiments on the Effect of a Cubic Building on the Flow and Pollutant Diffusion under Stable Stratification. Build. Environ. 2021, 205, 108222. [Google Scholar] [CrossRef]
- Guo, D.; Zhao, P.; Wang, R.; Yao, R.; Hu, J. Numerical Simulation Studies of the Effect of Atmospheric Stratification on the Dispersion of LNG Vapor Released from the Top of a Storage Tank. J. Loss Prev. Process Ind. 2019, 61, 275–286. [Google Scholar] [CrossRef]
- Madalozzo, D.M.S.; Braun, A.L.; Awruch, A.M.; Morsch, I.B. Numerical Simulation of Pollutant Dispersion in Street Canyons: Geometric and Thermal Effects. Appl. Math. Model. 2014, 38, 5883–5909. [Google Scholar] [CrossRef]
- Ghane-Tehrani, E.; Ziaei-Rad, M.; Seddighi, M. Detached Eddy Simulation of Traffic-Induced Air Pollution in an Urban Highway with Complex Surrounding Morphology. Atmos. Pollut. Res. 2025, 16, 102331. [Google Scholar] [CrossRef]
- Rao, A.N.; Zhang, J.; Minelli, G.; Basara, B.; Krajnović, S. An LES Investigation of the Near-Wake Flow Topology of a Simplified Heavy Vehicle. Flow Turbul. Combust. 2019, 102, 389–415. [Google Scholar] [CrossRef]
- Jiaxin, L.; Wang, J.; Yichen, Z.; Pan, C. Vortex Dynamics in the near Wake of a Surface-Mounted Hemisphere. Phys. Fluids 2024, 36, 013619. [Google Scholar] [CrossRef]
- Wang, F.; Lam, K.M. Wake of Elongated Low-Rise Building at Oblique Incidences. Atmosphere 2021, 12, 1579. [Google Scholar] [CrossRef]
- Martínez-Lera, P.; Izquierdo, S.; Fueyo, N. Lattice-Boltzmann LES of Vortex Shedding in the Wake of a Square Cylinder. In Complex Effects in Large Eddy Simulations; Kassinos, S.C., Langer, C.A., Iaccarino, G., Moin, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 203–217. [Google Scholar]
- Lin, C.; Ooka, R.; Kikumoto, H.; Flageul, C.; Kim, Y.; Wang, Y.; Maison, A.; Zhang, Y.; Sartelet, K. Large-Eddy Simulations on Pollutant Reduction Effects of Road-Center Hedge and Solid Barriers in an Idealized Street Canyon. Build. Environ. 2023, 241, 110464. [Google Scholar] [CrossRef]
- Lin, C.; Ooka, R.; Kikumoto, H.; Sato, T.; Arai, M. CFD Simulations on High-Buoyancy Gas Dispersion in the Wake of an Isolated Cubic Building Using Steady RANS Model and LES. Build. Environ. 2021, 188, 107478. [Google Scholar] [CrossRef]
- Chatzimichailidis, A.E.; Argyropoulos, C.D.; Assael, M.J.; Kakosimos, K.E. Qualitative and Quantitative Investigation of Multiple Large Eddy Simulation Aspects for Pollutant Dispersion in Street Canyons Using OpenFOAM. Atmosphere 2019, 10, 17. [Google Scholar] [CrossRef]
- Xie, Z.-T.; Hayden, P.; Wood, C.R. Large-Eddy Simulation of Approaching-Flow Stratification on Dispersion over Arrays of Buildings. Atmos. Environ. 2013, 71, 64–74. [Google Scholar] [CrossRef]
- Jiang, G.; Yoshie, R. Large-Eddy Simulation of Flow and Pollutant Dispersion in a 3D Urban Street Model Located in an Unstable Boundary Layer. Build. Environ. 2018, 142, 47–57. [Google Scholar] [CrossRef]
- Guo, D.; Zhao, J.; Zhang, Z.; Yang, G.; Li, Y.; Zhang, J.; Wang, X. Large Eddy Simulation of Flow Field and Pollutant Diffusion around Buildings with Different Thermal Stratifications. Process Saf. Environ. Prot. 2024, 190, 885–901. [Google Scholar] [CrossRef]
- Lopes, D.; Puga, H.; Teixeira, J.; Lima, R.; Grilo, J.; Dueñas-Pamplona, J.; Ferrera, C. Comparison of RANS and LES Turbulent Flow Models in a Real Stenosis. Int. J. Heat Fluid Flow 2024, 107, 109340. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Stathopoulos, T.; Heijst, G.J.F. CFD Simulation of Near-Field Pollutant Dispersion on a High-Resolution Grid: A Case Study by LES and RANS for a Building Group in Downtown Montreal. Atmos. Environ. 2011, 45, 428–438. [Google Scholar] [CrossRef]
- Salim, S.M.; Buccolieri, R.; Chan, A.; Sabatino, S.D. Numerical Simulation of Atmospheric Pollutant Dispersion in an Urban Street Canyon: Comparison between RANS and LES. J. Wind Eng. Ind. Aerodyn. 2011, 99, 103–113. [Google Scholar] [CrossRef]
- Yoshie, R.; Jiang, G.; Shirasawa, T.; Chung, J. CFD Simulations of Gas Dispersion around High-Rise Building in Non-Isothermal Boundary Layer. J. Wind Eng. Ind. Aerodyn. 2011, 99, 279–288. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Heijst, G.J.F. van Large-Eddy Simulation of Pollutant Dispersion around a Cubical Building: Analysis of the Turbulent Mass Transport Mechanism by Unsteady Concentration and Velocity Statistics. Environ. Pollut. 2012, 167, 47–57. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD Modeling of Pollution Dispersion in Building Array: Evaluation of Turbulent Scalar Flux Modeling in RANS Model Using LES Results. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 484–491. [Google Scholar] [CrossRef]
- Farzad Bazdidi-Tehrani, M.K.; Gholamalipour, P.; Kiamansouri, M.; Jadidi, M. Large Eddy Simulation of Thermal Stratification Effect on Convective and Turbulent Diffusion Fluxes Concerning, P. Gaseous Pollutant Dispersion around a High-Rise Model Building. J. Build. Perform. Simul. 2019, 12, 97–116. [Google Scholar] [CrossRef]
- Dai, Y.; Mak, C.M.; Ai, Z.; Hang, J. Evaluation of Computational and Physical Parameters Influencing CFD Simulations of Pollutant Dispersion in Building Arrays. Build. Environ. 2018, 137, 90–107. [Google Scholar] [CrossRef]
- Kikumoto, H.; Ooka, R. Large-Eddy Simulation of Pollutant Dispersion in a Cavity at Fine Grid Resolutions. Build. Environ. 2018, 127, 127–137. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in Building Simulation for Outdoor and Indoor Applications: A Foregone Conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Ishihara, T.; Qian, G.-W.; Qi, Y.-H. Numerical Study of Turbulent Flow Fields in Urban Areas Using Modified K−ε Model and Large Eddy Simulation. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104333. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical Simulation of Dispersion around an Isolated Cubic Building: Model Evaluation of RANS and LES. Build. Environ. 2010, 45, 2231–2239. [Google Scholar] [CrossRef]
- Argyropoulos, C.D.; Markatos, N.C. Recent Advances on the Numerical Modelling of Turbulent Flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- An, H.-B.; Park, S.-B. Assessing Urban Ventilation Using Large-Eddy Simulations. Build. Environ. 2024, 263, 111899. [Google Scholar] [CrossRef]
- Jiao, H.; Takemi, T. Investigating the Influence of Stepped Roofs on Wind Dynamics Using Large Eddy Simulation. Build. Environ. 2024, 262, 111819. [Google Scholar] [CrossRef]
- Foroutan, H.; Tang, W.; Heist, D.K.; Perry, S.G.; Brouwer, L.H.; Monbureau, E.M. Numerical Analysis of Pollutant Dispersion around Elongated Buildings: An Embedded Large Eddy Simulation Approach. Atmos. Environ. 2018, 187, 117–130. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Niu, J.; Du, Y.; Mak, C.M.; Zhang, Y. LES for Pedestrian Level Wind around an Idealized Building Array—Assessment of Sensitivity to Influencing Parameters. Sustain. Cities Soc. 2019, 44, 406–415. [Google Scholar] [CrossRef]
- Monbureau, E.M.; Heist, D.K.; Perry, S.G.; Brouwer, L.H.; Foroutan, H.; Tang, W. Enhancements to AERMOD’s Building Downwash Algorithms Based on Wind-Tunnel and Embedded-LES Modeling. Atmos. Environ. 2018, 179, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Pattnaik, P.; Jena, S.; Dei, A.; Sahu, G. Impact of Chemical Reaction on Micropolar Fluid Past a Stretching Sheet. JP J. Heat Mass Transf. 2019, 18, 207–223. [Google Scholar] [CrossRef]
- Pattnaik, P.; Moapatra, D.; Mishra, S.R. Influence of Velocity Slip on the MHD Flow of a Micropolar Fluid Over a Stretching Surface. In Recent Trends in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 307–321. ISBN 978-981-15-9816-6. [Google Scholar]
- Sosnowski, M.; Krzywanski, J.; Grabowska, K.; Gnatowska, R. Polyhedral Meshing in Numerical Analysis of Conjugate Heat Transfer. Int. Conf. Exp. Fluid Mech. (ICEFM) 2017, 180, 589–594. [Google Scholar] [CrossRef]
- Chew, L.W.; Glicksman, L.R.; Norford, L.K. Buoyant Flows in Street Canyons: Comparison of RANS and LES at Reduced and Full Scales. Build. Environ. 2018, 146, 77–87. [Google Scholar] [CrossRef]
- Jiang, G.; Yoshie, R.; Shirasawa, T.; Jin, X. Inflow Turbulence Generation for Large Eddy Simulation in Non-Isothermal Boundary Layers. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 369–378. [Google Scholar] [CrossRef]






| 0.09 | 1.0 | 1.22 | 0.9 | 0.9 | 1.44 | 1.92 | 1.44 | −0.33 | 0.419 | 9.0 |
| Stratifications | Rib | TH (K) | Tf (K) | △T (K) | uH(m/s) | Time Step (s) | Sampled Time (s) |
|---|---|---|---|---|---|---|---|
| Unstable | −0.1 | 284.3 | 318.3 | −34.0 | 1.37 | 0.0015 | 15.0–75.0 |
| Neutral | 0.0 | 294.35 | 294.35 | 0.0 | 1.4 | 0.0014 | 14.0–70.0 |
| Stable | 0.08 | 322.4 | 291.0 | 56.0 | 1.37 | 0.0015 | 15.0–75.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Guo, D.; Zhang, Z.; Guo, J.; Li, Y.; Zhang, J.; Wang, X. RANS and LES Simulations of Localized Pollutant Dispersion Around High-Rise Buildings Under Varying Temperature Stratifications. Atmosphere 2025, 16, 661. https://doi.org/10.3390/atmos16060661
Zhao J, Guo D, Zhang Z, Guo J, Li Y, Zhang J, Wang X. RANS and LES Simulations of Localized Pollutant Dispersion Around High-Rise Buildings Under Varying Temperature Stratifications. Atmosphere. 2025; 16(6):661. https://doi.org/10.3390/atmos16060661
Chicago/Turabian StyleZhao, Jinrong, Dongpeng Guo, Zhehai Zhang, Jiayi Guo, Yunpeng Li, Junfang Zhang, and Xiaofan Wang. 2025. "RANS and LES Simulations of Localized Pollutant Dispersion Around High-Rise Buildings Under Varying Temperature Stratifications" Atmosphere 16, no. 6: 661. https://doi.org/10.3390/atmos16060661
APA StyleZhao, J., Guo, D., Zhang, Z., Guo, J., Li, Y., Zhang, J., & Wang, X. (2025). RANS and LES Simulations of Localized Pollutant Dispersion Around High-Rise Buildings Under Varying Temperature Stratifications. Atmosphere, 16(6), 661. https://doi.org/10.3390/atmos16060661




