2.1. Theoretical Model of Rainfall Scavenging
Generally, the below-cloud scavenging process includes three mechanisms: Brownian diffusion, interception, and impaction [
8]. For fine particles with a particle size of 0.01–1 µm, the below-cloud scavenging process is mainly dominated by diffusion and interception mechanisms. According to the below-cloud rain-out theory proposed by Slinn et al. [
8], the basic governing equation for the scavenging of atmospheric aerosols by rainfall can be expressed as follows:
In the formula, c(t) represents the aerosol mass concentration at time t; Λ represents the rainfall scavenging coefficient.
If it is assumed that the rainfall scavenging coefficient Λ does not change with time, then the solution of Equation (1) is as follows:
In the formula, c0 is the aerosol mass concentration in the atmosphere at the start of rainfall scavenging; t is the scavenging time calculated from the start of rainfall scavenging.
However, from the perspective of the observation field, the scavenging coefficient of aerosols can be expressed by the rate of change of aerosol concentration [
9]:
In the formula, dp is the diameter of the aerosol particle; c0(dp) is the number concentration of aerosol particles at time t0; c1(dp) is the number concentration of aerosol particles at time t1.
The scavenging coefficient for aerosol particles with a particle size of
dp can be expressed as [
8]:
In the formula, Dp is the raindrop diameter; V(Dp) is the terminal settling velocity of raindrops; E(Dp,dp) is the coalescence coefficient, representing the capture efficiency of raindrop–aerosol particles through various physical mechanisms; N(Dp) is the raindrop size spectrum; Λ(dp) represents the scavenging coefficient of aerosol particles with a particle size of dp.
When studying the scavenging of aerosol particles within the full-scale range by rainfall, the average mass scavenging coefficient is usually used [
10]:
In the formula, Λm is the average mass scavenging coefficient; n(dp) is the aerosol size spectrum, representing the number concentration of aerosol particles with a particle size of dp per unit volume.
2.2. The Influence of Collision Efficiency on the Scavenging Coefficient
Since Langmuir [
11] and Greenfield [
12], many researchers have extensively studied the basic mechanisms of raindrop capture of aerosol particles at both the theoretical and experimental levels [
13,
14,
15]. In the latest research, Hua et al. [
16] studied how the turbulent effect affects the capture of aerosol particles by raindrops and introduced the collision probability. Gao et al. [
17] further studied this and gave the contribution rate of the turbulent effect to the capture of aerosols by raindrops.
Table 1 shows the contributions of various mechanisms to the collision efficiency. For the meanings of the symbols, see the Abbreviations.
If the raindrop size spectrum and raindrop settling velocity are given, then the scavenging coefficient of aerosol particles with a particle size of
dp depends on the collision efficiency. Slinn [
8] believed that Brownian diffusion, interception effect, and inertial impaction are the main mechanisms by which raindrops capture aerosol particles. Studies have found [
19,
20,
21] that the aerosol scavenging coefficients observed in the field are often from about two to three orders of magnitude higher than those calculated by only considering the three mechanisms of Brownian diffusion, interception effect, and inertial impaction.
Figure 1a shows the contributions of various mechanisms to the total collision efficiency. It is found that, for particles within the accumulation mode range, the collision efficiency considering the seven mechanisms is from two to ten times higher than the collision efficiency calculated by the currently commonly used Slinn formula (which only considers Brownian diffusion, interception effect, and inertial impaction). Brownian diffusion is the result of random collisions of aerosol particles by air molecules. The Brownian force decreases as the particle size increases; interception only takes into account the size of the particles while ignoring their mass. The particles are only captured when they move with the fluid to a position at a distance of
dp/2 from the raindrop; inertial collision, on the other hand, considers the mass of the particles while ignoring their size. Thermophoresis and diffusiophoresis drift [
22] are the results of temperature gradients and humidity gradients. The temperature gradient causes the particles to generate a thermophoretic force, moving from the high-temperature region to the low-temperature region; If the raindrop and the aerosol particles are charged, then a charge image force [
23] will be generated near the surface of the raindrop, causing the aerosol particles to be attracted when they are close to the raindrop and thus be captured. During the movement of particles along with the airflow on the windward side of raindrops, turbulent fluctuations will interfere with the movement trajectories of the particles. That is to say, a random effect (i.e., the additional transport effect generated by turbulent fluctuations) will be superimposed on the movement of the particles, thereby affecting the capture of aerosol particles by raindrops. For particles in the Aitken nucleus mode, the Brownian diffusion effect is dominant; for coarse-mode particles, the inertial collision mechanism is dominant. Accumulation-mode particles are the result of the joint action of various physical mechanisms. Therefore, in the accumulation mode, only considering Slinn’s three mechanisms significantly underestimates the collection efficiency of raindrops for aerosol particles.
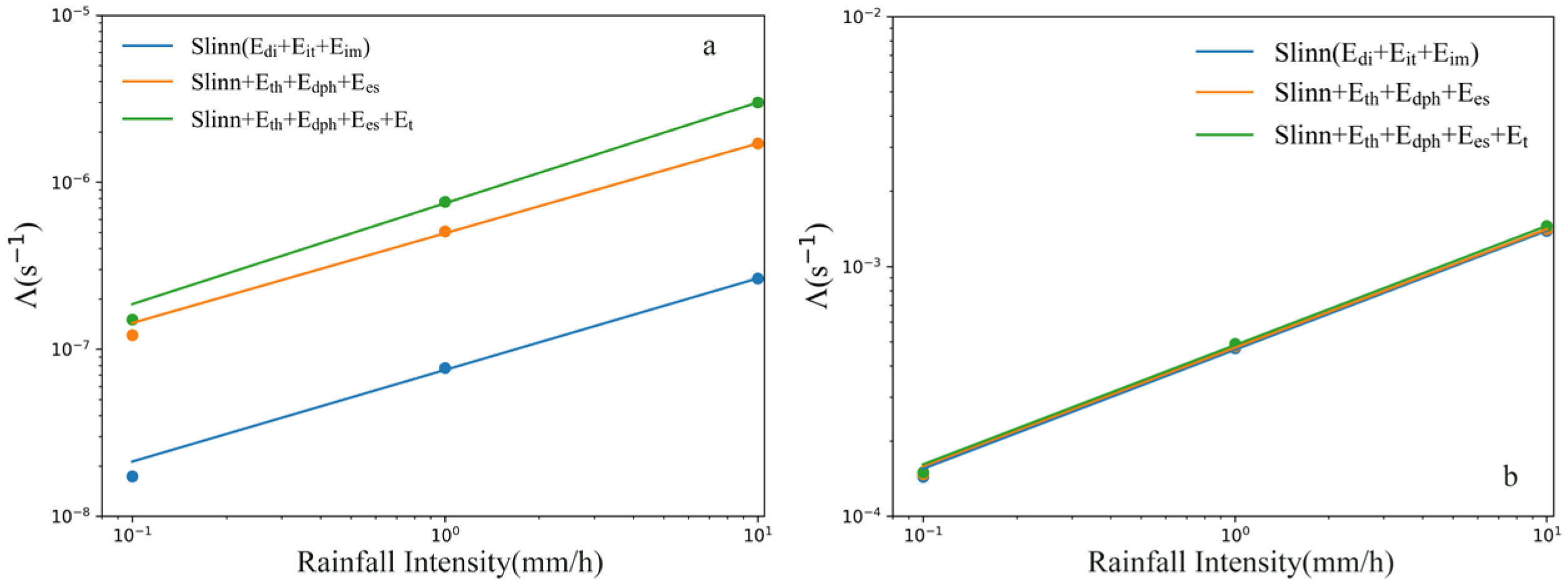
The relationship between the scavenging coefficient and the aerosol particle size is shown in
Figure 1b. It can be seen from Equation (4) that, when the raindrop spectrum and the terminal velocity of raindrops are determined, the monodisperse rainfall scavenging coefficient is related to the collision efficiency. As depicted in
Figure 1b, taking different collision mechanisms into account has a noticeable impact on the particles within the accumulation mode range. It is found that the scavenging coefficient of particles in the accumulation mode calculated by considering seven mechanisms simultaneously, namely, Brownian diffusion, interception effect, inertial impaction, thermophoresis, diffusiophoresis, electrostatic interaction, and turbulent effect, is from two to ten times higher than that calculated by the currently commonly used Slinn formula. This is approximately one order of magnitude higher than the theoretical value given by Slinn [
8], indicating that the scavenging coefficient is positively correlated with the collision efficiency. This also shows that thermophoresis, diffusiophoresis, electrostatic interaction, and turbulent effects have a significant enhancing effect on the capture of particles in the accumulation mode by raindrops. Therefore, when studying the rainfall scavenging coefficient, the three mechanisms proposed by Slinn cannot be the only factors to be considered.
In the study of rainfall scavenging, the scavenging coefficient is usually parameterized as a function of rainfall intensity I [
24]:
In the formula, A and B are parameters related to factors such as the raindrop size spectrum, aerosol size spectrum, and collision efficiency. Assuming that the raindrop size spectrum follows a log-normal distribution and the raindrop diameter ranges from 0.2 to 2 mm, the relationship between the scavenging coefficient of monodisperse aerosol particles with a diameter of 0.5 μm and the rainfall intensity is shown in
Figure 2a. The introduction of the thermophoresis mechanism, diffusiophoresis mechanism, electrostatic interaction mechanism, and turbulent effect mechanism makes the scavenging coefficient about seven times higher than that when only using the three mechanisms proposed by Slinn, which is nearly one order of magnitude higher. Therefore, when parameterizing the scavenging coefficient of monodisperse aerosol particles, especially for particles within the accumulation mode range, the influence of the collision efficiency needs to be carefully considered.
When studying the scavenging coefficient of aerosols within the full-scale range, the average mass scavenging coefficient is usually used. The average mass scavenging coefficient is related to the raindrop size spectrum, the aerosol size spectrum, the terminal settling velocity of raindrops, and the collision efficiency. When the raindrop size spectrum, the aerosol size spectrum, and the raindrop settling velocity are given, the scavenging coefficient of polydisperse aerosols is only related to the collision efficiency. Assuming that both the raindrop size spectrum and the aerosol size spectrum are distributed in the form of a log-normal function, the particle size distribution range of aerosols is from 0.001 to 10 μm, and the raindrop diameter distribution range is from 0.2 to 2 mm. The relationship between the average mass scavenging coefficient and the rainfall intensity is shown in
Figure 2b. The three lines almost overlap. It can be seen that, when considering rainfall scavenging within the full-scale range, the selection of the collision efficiency formula has little effect on the scavenging coefficient.
In conclusion, when studying the scavenging coefficient of monodisperse aerosols, especially for particles within the accumulation mode range, the collision efficiency formula should be carefully selected. However, when calculating the scavenging coefficient of aerosols within the full-scale range, the selection of the collision efficiency has little impact on the results. This is consistent with the research results of Peng Hong [
25] and Yao Keya et al. [
26].
2.3. The Influence of Raindrop Size Spectrum on the Scavenging Coefficient
The raindrop size spectrum refers to the number distribution of raindrops of different sizes in a unit volume. Clarifying the detailed information of the raindrop size spectrum is of great significance for the rainfall scavenging mechanism, estimating the scavenging coefficient, improving numerical weather models, and evaluating artificial rainfall enhancement [
4,
27]. Since Marshall and Palmer [
28] found in 1948 that the raindrop size spectrum could be approximated as an exponential distribution, some scholars have conducted in-depth research on this and found that the raindrop size spectrum can not only be regarded as an exponential distribution but also conforms to the Gamma distribution [
29] and the log-normal distribution [
30]. Among them, the exponential distribution is also known as the M-P distribution [
28]:
In the formula,
N0 = 8000 m
−3 mm
−1,
φ = 4.1 · I
−0.21 mm
−1, and I is the rainfall intensity in mm/h. Studies have shown [
31] that the M-P distribution is more suitable for stable stratiform cloud rainfall. For rainfall with large fluctuations in the cloud, it has large deviations in the range of small and large raindrops.
The Gamma distribution adds a new parameter based on the exponential distribution:
In the formula, when γ = 0, the Gamma distribution becomes the M-P distribution. When γ > 0, the curve bends upward, and vice versa. Therefore, raindrop size spectra of different shapes can be fitted by adjusting the parameter γ. Compared with the M-P distribution, the Gamma distribution improves the fitting accuracy in the range of small and large raindrops and is more universal.
The log-normal distribution is more complex than the previous two distribution forms, and its expression is as follows:
In the formula,
N is the initial total number concentration of raindrops, in m
−3;
Ddg is the average size of raindrops, in mm;
σ is the geometric standard deviation of raindrops. Among them, these three parameters are all functions of the rainfall intensity, as shown in
Table 2.
It is assumed that light rain, moderate rain, and heavy rain are defined by rainfall intensities of 0.1, 1, and 10 mm/h, respectively, and the three types of raindrop size spectra are shown in
Figure 3. The parameters used in the M-P exponential distribution are given by Marshall–Palmer [
28], the parameters of the Gamma distribution are given by Wolf [
33], and the log-normal distribution uses the parameters given by Feingold and Levin [
30] as well as Cerro et al. [
32].
As shown in
Figure 3a,b, the raindrop size spectrum increases rapidly with the increase of the raindrop diameter and then decreases with the further increase of the raindrop diameter after reaching the peak value. Light rain reaches the peak value first, followed by moderate rain, and heavy rain reaches the peak value last. With the increase in rainfall intensity, the peak value shifts to the right and the peak width becomes larger, indicating that, with the increase in rainfall intensity, the width of the raindrop size spectrum increases and the distribution range of raindrop sizes becomes larger. As shown in
Figure 3c,d, the raindrop size spectrum decreases with the increase of the raindrop diameter. This may be related to the influence of physical processes such as evaporation and fragmentation of raindrops during their fall. When the raindrop sizes are the same, the greater the rainfall intensity, and the greater the value of the raindrop size spectrum. This is because rainfall intensity indirectly indicates that precipitation is proportional to the raindrop diameter and the number concentration of raindrops. That is, when the rainfall intensity increases, if the raindrop diameters are the same, the number concentration of raindrops becomes larger.
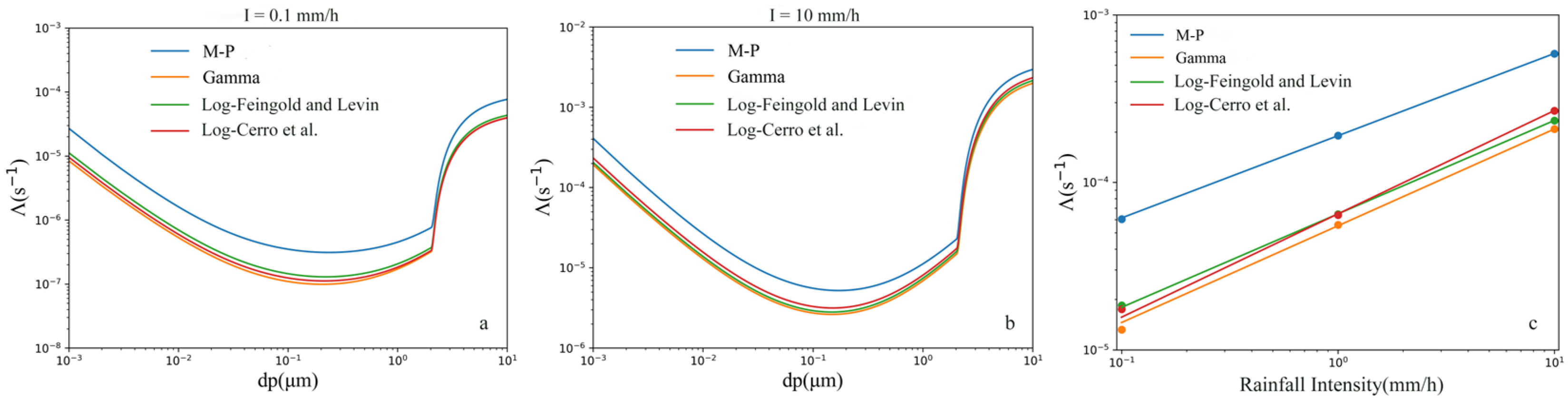
When the collision efficiency and the raindrop velocity are given, the value of the scavenging coefficient for monodisperse aerosol particles is only related to the raindrop size spectrum. The influence of three different types of raindrop size spectra under different rainfall intensities on the scavenging coefficient is shown in
Figure 4. It is found that the scavenging coefficient obtained when the raindrop size spectrum follows the M-P distribution is larger than that obtained from other types of raindrop size spectra. For a rainfall intensity of I = 10 mm/h, the scavenging coefficient calculated according to the M-P distribution is about twice as large as that calculated according to the Gamma distribution. For I = 0.1 mm/h, the scavenging coefficient of the M-P distribution is about three times that of the Gamma distribution. This may be because the M-P distribution has a higher number concentration of raindrops and a higher proportion of small raindrops. Also, the collision efficiency of small raindrops with aerosols is higher than that of large raindrops, which leads to a higher scavenging coefficient obtained from the M-P distribution. With the increase of the rainfall intensity, the differences in the scavenging coefficients calculated from various types of raindrop size spectra also decrease. This is because, as the rainfall intensity increases, the raindrop sizes also approach those of large raindrops.
When the aerosol size spectrum distribution, collision efficiency, and raindrop velocity are given, the average mass scavenging coefficient of polydisperse aerosols is only related to the raindrop size spectrum distribution function. Assuming that the aerosol size spectrum is distributed in the form of a log-normal function, the particle size distribution range of aerosols is from 0.001 to 10 μm, and the raindrop diameter distribution range is from 0.2 to 2 mm. For the different types of raindrop size spectra above, the relationship between the average mass scavenging coefficient and the rainfall intensity is shown in
Figure 4c. It can be seen that the scavenging coefficient calculated using the raindrop size spectrum of the M-P distribution is larger than that calculated using the raindrop size spectra of the Gamma distribution and the log-normal distribution, with a maximum difference of about 2.4 times. However, there is not much difference between the results of the Gamma distribution and the log-normal distribution.
A large number of studies have found [
31,
34,
35,
36] that the raindrop size spectra of rainfall in different cloud types, such as stratiform clouds, convective clouds, and mixed clouds, etc., vary greatly. Taking the study of Wang Fuzeng et al. [
36] as an example, the results show that, when fitting the three different types of rainfall situations above, it is found that the fitting result of the Gamma distribution is better than that of the M-P distribution. The fitting results are shown in
Table 3.
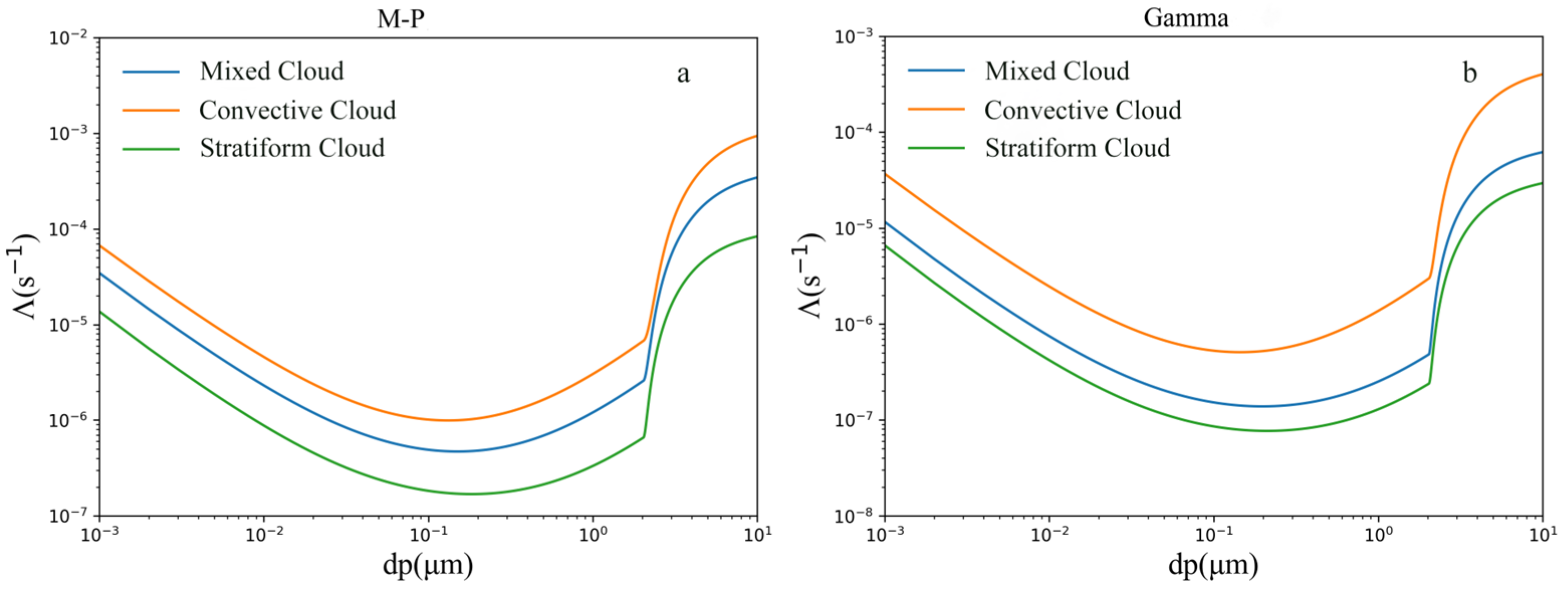
As shown in
Table 3, for rainfall in different cloud types, the raindrop size spectrum distributions vary significantly. For example, in the M-P distribution, the initial concentration
N0 of the raindrop size spectrum of stratiform clouds is larger than that of mixed clouds and convective clouds. However, the slope factor
φ is also larger than that of other cloud types. This will result in the number of small raindrops in stratiform clouds being higher than that in mixed clouds and convective clouds, while the number of large raindrops is lower than that in the other two cloud types.
Figure 5 shows the influence of the raindrop size spectra (including the M-P distribution and the Gamma distribution) of rainfall in three different cloud types, namely, mixed clouds, convective clouds, and stratiform clouds, on the scavenging coefficient. It can be seen that the rainfall in different cloud types has a significant impact on the scavenging coefficient. Whether it is the M-P distribution or the Gamma distribution, the calculation results of rainfall in convective clouds are larger than those in mixed clouds and stratiform clouds. This is because the average diameter and the dominant diameter of raindrops in stratiform cloud precipitation are relatively small. The average diameters of raindrops in convective cloud precipitation and mixed cloud precipitation are basically the same, but the dominant diameter of raindrops in convective cloud precipitation is larger than that in mixed cloud precipitation [
36]. The proportion of large particles in convective cloud precipitation is relatively large, and the contribution rate of precipitation is also large, which leads to a larger amount of convective cloud precipitation. Therefore, compared with other types, the scavenging coefficient of convective clouds is larger.
2.4. The Influence of Aerosol Spectrum on the Scavenging Coefficient
Atmospheric aerosol refers to a mixed system composed of the atmosphere and various solid- and liquid-phase particles in the atmosphere. In a narrow sense, it specifically refers to various solid-phase (dry) and liquid-phase (wet) particles [
37]. Aerosol particles can affect climate change by scattering and absorbing short-wave solar radiation, and can also affect cloud precipitation and thus indirectly affect the climate [
38]. Aerosol particles of different scales have significant differences in their optical, chemical compositional, and toxicological properties. Accurately describing the aerosol spectrum distribution is of great significance for research on the physical and chemical properties of aerosols. The scale of atmospheric aerosol particles can often span 5–6 orders of magnitude. Common functions used to describe the aerosol particle spectrum include the log-normal distribution, Gamma distribution, Junge distribution, etc. The log-normal distribution is a mathematical function with a physical basis. It can fit the distribution of the entire range of atmospheric aerosol scales and has good consistency in fitting the spectral distributions of number concentration, mass concentration, and surface area [
38]. Its expression is as follows:
In the formula,
n is the peak number of the aerosol particle size spectrum;
Ni represents the total number concentration of the i-th mode of aerosols, in cm
−3;
σi is the geometric standard deviation of the i-th mode;
Ri is the geometric mean diameter of the i-th mode, in μm. A log-normal distribution function curve can fit a unimodal particle size spectrum (
n = 1), and a multimodal particle size spectrum is composed of the superposition of log-normal distribution curves in multiple modes. The aerosol particle spectrum distributions of different modes have different characteristics, and the superimposed spectrum distribution can well reflect the state of the aerosol spectrum distribution. The selection of log-normal distribution simulation parameters for different regional types is from Jaenicke [
39], and the log-normal distribution parameters for different seasons in the same region are given by Cao Wei et al. [
38], as shown in
Table 4.
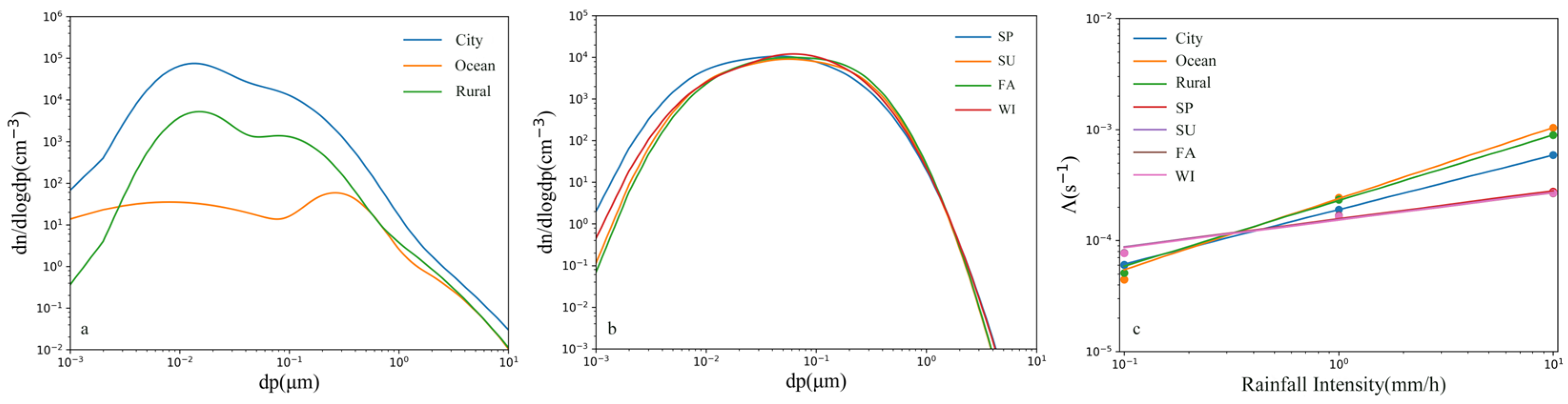
Figure 6 shows the aerosol spectrum distributions of different regional types and the aerosol spectrum distributions of different seasons in the same region. The aerosol spectrum distributions of different regional types vary significantly. Obviously, whether in urban, rural, or marine areas, the number concentration of the first mode is greater than that of the second and third modes. The geometric mean diameters of the three modes of urban aerosols are all within the Aitken mode range, so urban aerosols can be considered to be dominated by Aitken-mode particles. For rural aerosols, the second and third modes are both in the accumulation mode, but the number concentration is lower than that of the first mode. For marine aerosols, the first mode is in the Aitken mode, but the geometric standard deviation is relatively large, resulting in an expanded scale range of the aerosol spectrum distribution. For the aerosol spectrum distributions in different seasons in Beijing there is not much difference, but the number concentration is lower than that of urban aerosols.
When the raindrop size spectrum, raindrop settling velocity, and collision efficiency are given, the average mass scavenging coefficient of polydisperse aerosols is only related to the aerosol size spectrum. The particle size distribution range of aerosols is between 0.001 and 10 μm, and the raindrop size range is between 0.2 and 2 mm, as shown in
Figure 6c. For urban aerosols, when the aerosol size spectrum follows the log-normal distribution, there is a significant difference between the parameters given by Jaenicke and the measured results in Beijing, with a maximum difference of about 1.5 times, mainly in the range of high rainfall intensities. It can be seen that the aerosol size spectrum has a great influence on the scavenging coefficient. This indicates that, even if the same type of aerosol size spectrum is used, when there is a large difference between the empirical parameters and the measured parameters, the difference in the results of the scavenging coefficient will also increase, as happened in the case of the parameters given by Jaenicke and the measured results in Beijing. Therefore, when studying the rainfall scavenging coefficient, it is best to use the locally measured aerosol size spectrum to reduce the influence brought about by the aerosol size spectrum distribution. However, for the same region, the influence of the aerosol size spectrum distribution function on the scavenging coefficient under different seasonal conditions can be ignored. Therefore, the seasonal average aerosol size spectrum can be used to represent the local aerosol size spectrum.
2.5. The Influence of Raindrop Terminal Velocity on the Scavenging Coefficient
In the rainfall scavenging coefficient formula, the raindrop terminal settling velocity
V(
Dp) is an important parameter, which refers to the velocity of raindrops in the atmosphere. Under the action of gravity and resistance, the velocity of raindrops will gradually increase until it reaches a stable velocity. The terminal velocity of raindrops is determined by the raindrop diameter, atmospheric density, and viscosity. Since different rainfall forms may lead to different falling patterns, researchers have carried out a large number of observations and laboratory simulations to obtain data on the raindrop falling process, and have proposed corresponding calculation formulas, which are listed in
Table 5, where the unit of
Dp is m. In recent years, some scholars have studied the influence of turbulence on the terminal velocity of raindrops. Both in qualitative and quantitative studies, it has been found that the terminal falling velocity of raindrops decreases with the increase in turbulence intensity. Under turbulence of medium and low intensity, the actual measured values are closer to the terminal settling velocity of raindrops measured in the laboratory [
40,
41]. In the study by Zheng et al. [
41], under the condition of medium and low turbulence intensity with a turbulence dissipation rate of ε < ε
60%, the actually measured average falling velocity of raindrops is close to the velocity measured by Atlas et al. [
42] in the laboratory. However, under high-intensity turbulence, that is, ε > ε
80%, the actually measured values are slightly lower, but the standard deviation also increases accordingly. Therefore, considering the actual situation, we will use laboratory measurements instead of field measurements under turbulent conditions. The experimental data of Kinzer et al. have been fitted [
43], and the result is basically consistent with the velocity curve fitted by Atlas et al., as shown in
Figure 7a. In the subsequent content of this article, the Willis velocity formula will be used to calculate the raindrop terminal settling velocity.
The relationship between the raindrop terminal settling velocity distribution and the raindrop diameter is shown in
Figure 7a. Except for the velocity curves of Atlas (1977) [
46] and Kessler [
45], the velocity distributions of the others are basically the same, within the raindrop diameter range of 0–5 mm. When the raindrop size spectrum, the aerosol size spectrum, and the collision efficiency formula are given, the scavenging coefficient is related to the raindrop terminal settling velocity. As shown in
Figure 7b, it is found that the results calculated by the velocity formulas of Atlas (1977) [
46] and Kessler [
45] are relatively large, and the results calculated by other velocity formulas are similar. The scavenging coefficients calculated by the velocity formulas of Kessler [
45] and Atlas (1973) [
42] have a maximum difference of about 1.7 times, and the differences are mainly concentrated in the range of low rainfall intensities.