Optimizing Vertical Unidirectional Airflow in Cleanrooms: An Integrated Approach to Floor Perforation, Plenum, and Fan Filter Unit Configurations
Abstract
1. Introduction
2. Establishment of the Simulation Model and Evaluation Indicators
2.1. Energy, Mass, and Momentum Equations
- Incompressible Flow: Assumes the fluid density () remains constant throughout the domain. This is valid for cleanroom airflow as the flow speed is low (Mach number < 0.3), and compressibility effects are negligible.
- Newtonian Fluid: The fluid exhibits constant viscosity () with a linear stress–strain relationship.
- Steady-State Flow: Time-independent flow where all variables (e.g., velocity, pressure, temperature) remain constant with respect to time () from governing equations, assuming equilibrium conditions.
- No-Slip Boundary Condition: The velocity at solid surfaces (e.g., walls, doors) is zero relative to the surface (). This reflects physical reality, as air adheres to stationary surfaces due to viscous effects.
- Adiabatic Walls: Assumes no heat flux through walls.
- Negligible Radiation: Radiative heat transfer is ignored, assuming its contribution to the energy balance is insignificant compared to convective and conductive effects.
- Closed System: The cleanroom is modelled as sealed, with no air infiltration or leakage. This ensures that the airflow distribution is entirely governed by the internal supply and exhaust system.
2.2. Cleanroom Geometry Model and Mesh for Simulation
2.3. Evaluations of Air Flow Inclination
2.4. Model Validation
3. Results
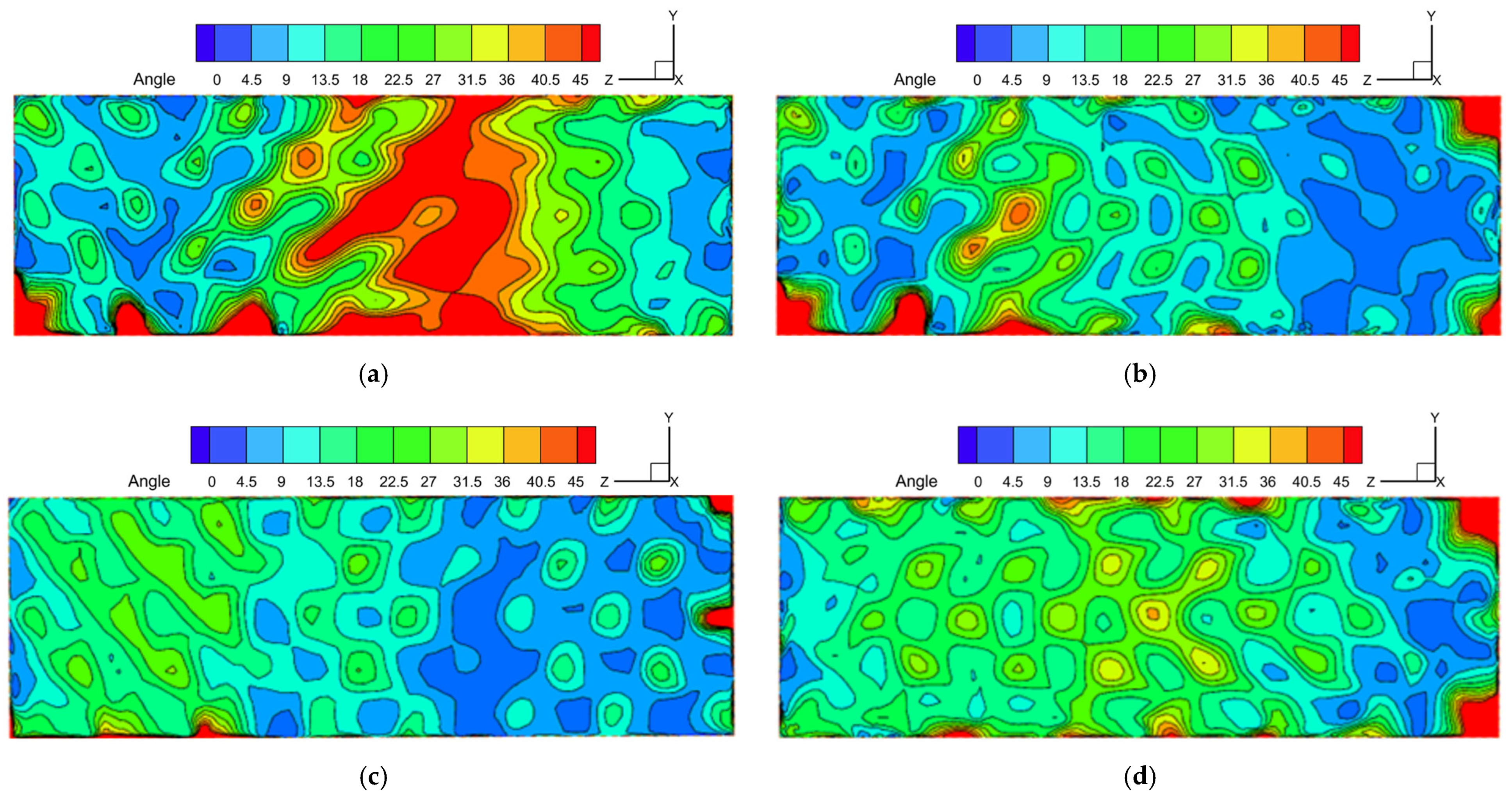
3.1. Impact of Uniform Perforated Plate Opening Ratios on Airflow
3.2. Impact of Non-Uniform Perforated Plate Opening Ratios Arrangements on Airflow
3.3. Impact of Plenum Height on Cleanroom Airflow Organization
3.4. Influence of FFU Arrangement Rates on Cleanroom Airflow Organisation
4. Conclusions
5. Limitations of Current Study and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACH | Air Change Rate per Hour |
| CFD | Computational Fluid Dynamics |
| DCC | Dry Cooling Coil |
| FFU | Fan Filter Unit |
| HVAC | Heating, Ventilation, and Air-Conditioning |
| ISO | International Standard of Organization |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equation |
| Fluid density | |
| Fluid velocity vector | |
| The vertical velocity component | |
| Static pressure | |
| Stress tensor | |
| Turbulent kinetic energy | |
| Turbulent dissipation rate | |
| Dynamic viscosity | |
| Turbulent viscosity | |
| Effective viscosity | |
| Effective thermal conductivity | |
| Specific heat capacity at constant pressure | |
| Temperature | |
| Gravitational acceleration | |
| Mass source term | |
| Heat source term | |
| Turbulent kinetic energy production term | |
| Turbulent Prandtl number for | |
| Turbulent Prandtl number for | |
| Empirical constants in turbulence models | |
| The inclination angle of the airflow streamline from the vertical direction |
References
- Al Beltagy, M.; El Morsi, M.; El Baz, A.; El Assy, A. Simulation of Radiant Cooling Systems in Cleanroom Applications Using Computational Fluid Dynamics. ASHRAE Trans. 2019, 61, 55–66. [Google Scholar]
- Jo, M.S.; Shin, J.H.; Kim, W.J.; Jeong, J.W. Energy-Saving Benefits of Adiabatic Humidification in the Air Conditioning Systems of Semiconductor Cleanrooms. Energies 2017, 10, 1774. [Google Scholar] [CrossRef]
- He, X.; Karra, S.; Pakseresht, P.; Apte, S.V.; Elghobashi, S. Effect of Heated-Air Blanket on the Dispersion of Squames in an Operating Room. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2960. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, T.; Kaga, A.; Kondo, A. Prediction Technique for Pressure Change in Rooms by Using an Equivalent Circuit Network. J. Environ. Eng. 2010, 5, 444–455. [Google Scholar] [CrossRef]
- Su, C.L.; Yu, K.T. Evaluation of Differential Pressure Setpoint of Chilled Water Pumps in Cleanroom HVAC Systems for Energy Savings in High-Tech Industries. In Proceedings of the 48th IEEE Industrial & Commercial Power Systems Conference, Louisville, KY, USA, 20–24 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Zhao, B. The ventilation needed to control thermal plume and particle dispersion from manikins in a unidirectional ventilated protective isolation room. In Building Simulation; Springer: Berlin/Heidelberg, Germany, 2015; Volume 8, pp. 551–565. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhou, L. Pressure Gradient Control and Energy-Saving Operation Strategy Study on a Multi-Zone Cleanroom. Procedia Eng. 2015, 121, 1998–2005. [Google Scholar] [CrossRef]
- Loomans, M.G.L.C.; Molenaar, P.C.A.; Kort, H.S.M.; Joosten, P.H. Energy Demand Reduction in Pharmaceutical Cleanrooms through Optimization of Ventilation. Energy Build. 2019, 202, 109346. [Google Scholar] [CrossRef]
- ISO 14644-1:2015; Cleanrooms and Associated Controlled Environments—Part 1: Classification of Air Cleanliness by Particle Concentration. International Organization for Standardization: Geneva, Switzerland, 2015.
- Lin, T.; Hu, S.C.; Xu, T. Developing an Innovative Fan Dry Coil Unit (FDCU) Return System To Improve Energy Efficiency of Environmental Control for Mission Critical Cleanrooms. Energy Build. 2015, 90, 94–105. [Google Scholar] [CrossRef]
- Lin, T.; Tung, Y.C.; Hu, S.C.; Lin, C.Y. Effects of the Removal of 0.1 µm Particles in Industrial Cleanrooms with a Fan Dry Coil Unit (FDCU) Return System. Aerosol Air Qual. Res. 2010, 10, 571–580. [Google Scholar] [CrossRef]
- Li, H.; Huang, C.; Yi, W.; Li, C. Analysis and Experiments on the Characteristics of Airflow and the Air Cleanliness Protection Region under Fan Filter Units in Cleanrooms. Sustainability 2023, 15, 13268. [Google Scholar] [CrossRef]
- Permana, I.; Agharid, A.P.; Singh, N.; Wang, F. Full-Scale Evaluation of FFU Configurations in an Optical Cleanroom Injection Molding for Improving Thermal Performance and Contaminant Removal. Case Stud. Therm. Eng. 2024, 61, 105076. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Tak, M.S.N.; Shoai-Naini, S.; Betz, F.; Mousavi, E. A Systematic Literature Review of Cleanroom Ventilation and Air Distribution Systems. Aerosol Air Qual. Res. 2023, 23, 220407. [Google Scholar] [CrossRef]
- Eslami, J.; Abbassi, A.; Saidi, M.H.; Bahrami, M. Effect of Supply/Exhaust Diffuser Configurations on the Contaminant Distribution in Ultra Clean Environments: Eulerian and Lagrangian Approaches. Energy Build. 2016, 127, 648–657. [Google Scholar] [CrossRef]
- Metwally, H.E.; Khalil, E.E.; Abou Dief, T.E.; AbouZeid, A.E. Air Quality and Flow Regimes at Clean Rooms. In Proceedings of the 2018 Joint Thermophysics and Heat Transfer Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3908. [Google Scholar] [CrossRef]
- Khoo, C.Y.; Lee, C.C.; Hu, S.C. An Experimental Study on the Influences of Air Change Rate and Free Area Ratio of Raised-Floor on Cleanroom Particle Concentrations. Build. Environ. 2012, 48, 84–88. [Google Scholar] [CrossRef]
- Permana, I.; Agharid, A.P.; Wang, F. Performance Improvement through CFD and Field Measurement in a Unidirectional Airflow Cleanroom for Wafer Manufacture. J. Build. Eng. 2024, 100, 111715. [Google Scholar] [CrossRef]
- Sofia, D.; Lotrecchiano, N.; Giuliano, A.; Barletta, D.; Poletto, M. Optimization of Number and Location of Sampling Points of an Air Quality Monitoring Network in an Urban Contest. Chem. Eng. Trans. 2019, 74, 277–282. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-Averaged Navier–Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
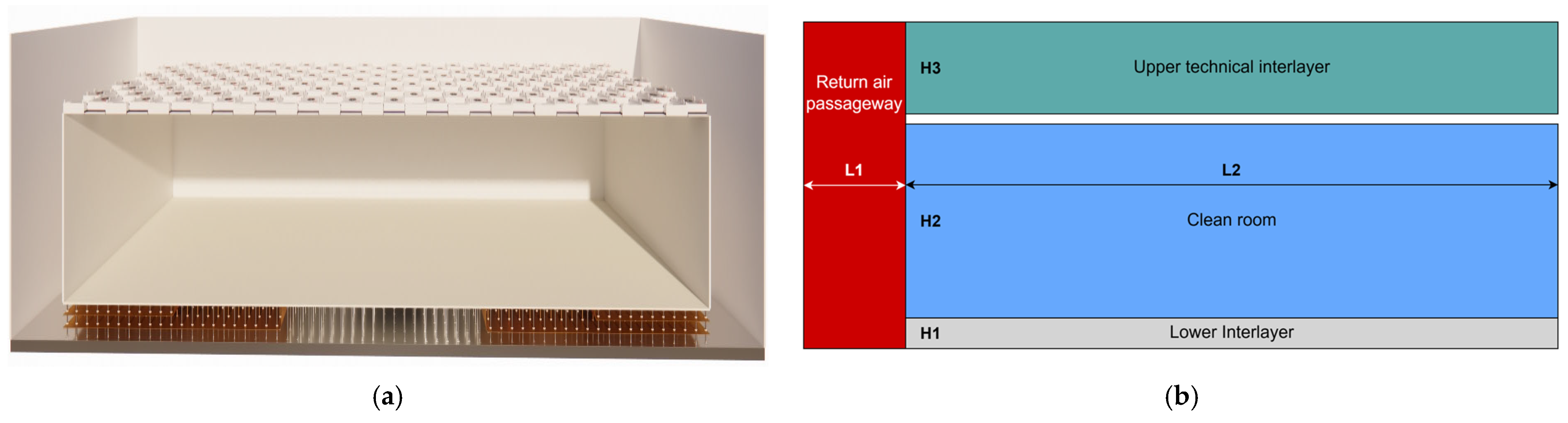



| Parameter | Type | Dimensions | Value |
|---|---|---|---|
| Supply Air (FFU) | Velocity Inlet | Unit area: 1200 mm × 600 mm | Temperature: 23 °C |
| Velocity: 2.76 m/s | |||
| FFU Arrangement Rate: 60% | |||
| Return Air | Pressure Outlet | Unit area: 600 mm × 600 mm | Temperature: 26 °C |
| Pressure: 25 Pa | |||
| Perforated Floor | Uniformly Perforated | Unit area: 600 mm × 600 mm | Perforated Ratio: 25% |
| Raised Floor | Wall | Height: 600 mm | - |
| Measurement Point 1 | Measurement Point 2 | Measurement Point 3 | Measurement Point 4 | Measurement Point 5 | NRMSE | |
|---|---|---|---|---|---|---|
| Experimental airflow velocity (m/s) | 2.56 | 2.51 | 2.51 | 2.39 | 2.11 | - |
| Simulation airflow velocity (m/s) | 2.74 | 2.67 | 2.52 | 2.35 | 2.16 | - |
| RMSE | 7.0% | 6.4% | 0.4% | 1.7% | 2.4% | 4.4% |
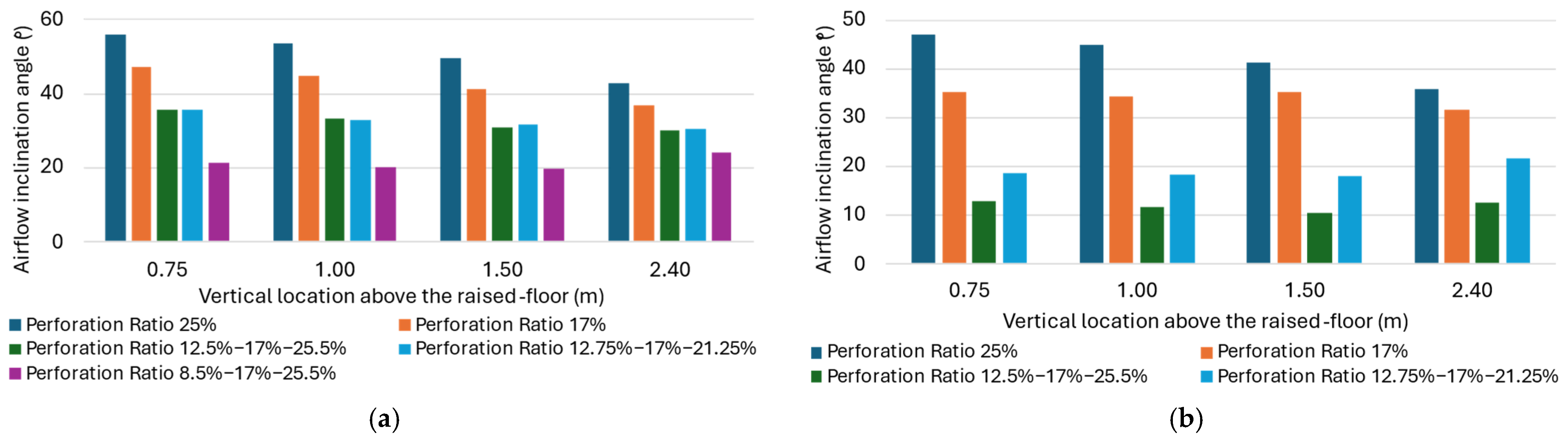
| Perforation Opening Ratio | Airflow Inclination Angle at the Vertical Location Above the Elevated Floor (m) | |||
|---|---|---|---|---|
| 0.75 m | 1 m | 1.5 m | 2.4 m | |
| 25% | 47.1° | 45.0° | 41.3° | 35.9° |
| 17% | 35.2° | 34.2° | 35.2° | 31.6° |
| 10% | 19.2° | 18.7° | 19.4° | 26.4° |
| Non-Uniform Perforated Plate Opening Ratio | Airflow Inclination Angle at the Vertical Location Above the Elevated Floor (m) | |||
|---|---|---|---|---|
| 0.75 m | 1 m | 1.5 m | 2.4 m | |
| 8% → 12% → 17% (Gentle gradients) | 25.0° | 23.9° | 22.9° | 25.8° |
| 8% → 17% → 25% (Steeper gradients) | 14.8° | 14.8° | 15.9° | 21.3° |
| 12% → 17% → 25% (Moderate gradients) | 13.0° | 11.5° | 10.4° | 12.6° |
| 12% → 17% → 21% (Moderate gradients) | 18.6° | 18.0° | 17.7° | 23.9° |
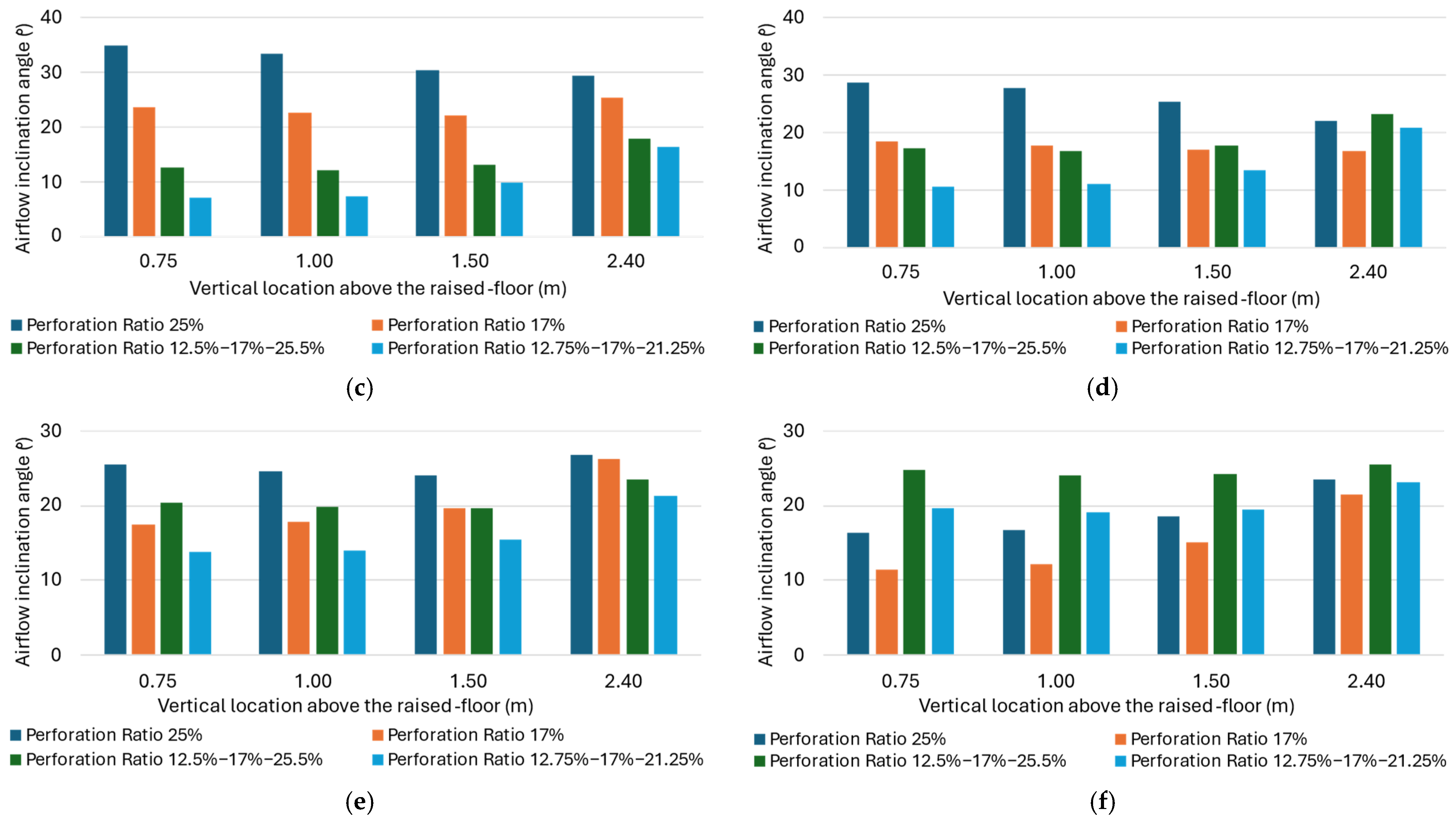
| Plenum Height (m) | Perforation Opening Ratio | Airflow Inclination Angle at the Vertical Location Above the Elevated Floor | K1 | |||
|---|---|---|---|---|---|---|
| 0.75 m | 1.0 m | 1.5 m | 2.4 m | |||
| 0.6 | 25% | 56.1° | 53.6° | 49.4° | 42.9° | 15.6 |
| 17% | 47.2° | 44.9° | 41.4° | 36.8° | 19.6 | |
| 12% → 17% → 25% | 35.3° | 33.4° | 31.0° | 29.9° | 22.9 | |
| 12% → 17% → 21% | 35.7° | 33.9° | 31.7° | 30.5° | 19.3 | |
| 8% → 17% → 25% | 21.1° | 20.2° | 19.6° | 24.2° | 24.5 | |
| 0.9 | 25% | 47.1° | 45.0° | 41.3° | 35.9° | 11.4 |
| 17% | 35.2° | 34.2° | 35.2° | 31.6° | 13.8 | |
| 12% → 17% → 25% | 12.9° | 11.5° | 10.4° | 12.6° | 14.0 | |
| 12% → 17% → 21% | 18.5° | 18.3° | 18.1° | 21.5° | 16.2 | |
| 1.3 | 25% | 34.8° | 33.3° | 30.4° | 29.3° | 8.2 |
| 17% | 23.5° | 22.7° | 22.2° | 25.3° | 9.4 | |
| 12% → 17% → 25% | 12.5° | 12.0° | 13.1° | 17.9° | 8.4 | |
| 12% → 17% → 21% | 7.1° | 7.2° | 9.8° | 16.3° | 9.4 | |
| 1.5 | 25% | 28.7° | 27.6° | 25.3° | 22.0° | 6.9 |
| 17% | 18.3° | 17.8° | 16.9° | 16.8° | 7.6 | |
| 12% → 17% → 25% | 17.3° | 16.8° | 17.6° | 23.1° | 6.9 | |
| 12% → 17% → 21% | 10.5° | 10.9° | 13.3° | 20.9° | 7.5 | |
| 1.8 | 25% | 25.5° | 24.7° | 24.1° | 26.8° | 5.5 |
| 17% | 17.5° | 17.9° | 19.7° | 26.2° | 6.0 | |
| 12% → 17% → 25% | 20.4° | 19.8° | 19.6° | 23.6° | 5.2 | |
| 12% → 17% → 21% | 13.9° | 14.0° | 15.5° | 21.3° | 5.6 | |
| 2.7 | 25% | 16.4° | 16.8° | 18.5° | 23.6° | 4.0 |
| 17% | 11.4° | 12.1° | 15.1° | 21.6° | 4.0 | |
| 12% → 17% → 25% | 24.8° | 24.0° | 24.2° | 25.6° | 3.3 | |
| 12% → 17% → 21% | 19.6° | 19.1° | 19.5° | 23.2° | 3.6 | |
| Plenum Heights | K1 | Design Suggestions |
|---|---|---|
| 0.6 m (low) | ≥9 | Use non-uniform perforation layouts with steep pressure gradients, such as 8.5%–17%–25.5%, to manage high velocity gradients and reduce airflow inclination. These layouts are essential to counteract the strong induced effects from the lower interlayer. |
| 1.3 m (medium) | 5–9 | Non-uniform layouts remain effective but are less critical as the interlayer velocity becomes more balanced. Both non-uniform arrangements and uniform plates with lower perforation rates can achieve acceptable verticality. |
| 2.7 m–3.6 m (high) | ≤5 | Uniform perforation layouts are sufficient and preferred. At these heights, airflow from the lower interlayer has minimal impact on cleanroom verticality, and uniform layouts ensure simplicity and energy efficiency without compromising performance. |
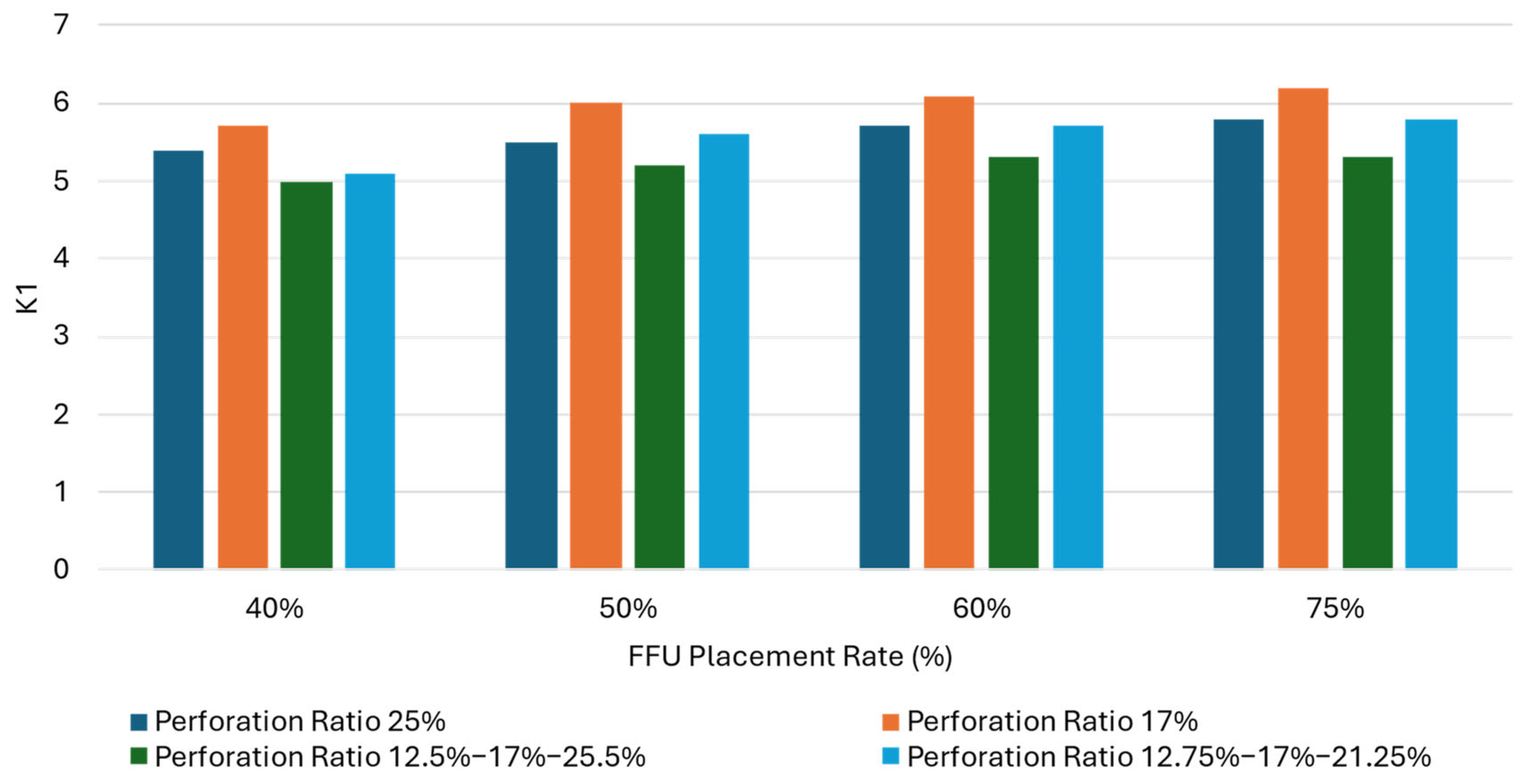
| FFU Arrangement Rates (%) | Perforation Opening Ratio | Airflow Inclination Angle at the Vertical Location Above the Elevated Floor | K1 | |||
|---|---|---|---|---|---|---|
| 0.75 m | 1.0 m | 1.5 m | 2.4 m | |||
| 40 | 25% | 34.9° | 34.7° | 34.6° | 38.9° | 5.4 |
| 17% | 30.7° | 30.9° | 31.7° | 38.6° | 5.7 | |
| 12% → 17% → 25% | 27.9° | 28.28° | 29.5° | 38.3° | 5.0 | |
| 12% → 17% → 21% | 23.2° | 24.6° | 28.9° | 39.6° | 5.1 | |
| 50 | 25% | 25.5° | 24.7° | 24.1° | 26.8° | 5.5 |
| 17% | 17.5° | 17.9° | 19.7° | 26.2° | 6.0 | |
| 12% → 17% → 25% | 20.4° | 19.8° | 19.6° | 23.6° | 5.2 | |
| 12% → 17% → 21% | 13.9° | 14.0° | 15.5° | 21.3° | 5.6 | |
| 60 | 25% | 24.8° | 23.7° | 22.1° | 21.7° | 5.7 |
| 17% | 15.6° | 15.1° | 15.1° | 19.3° | 6.1 | |
| 12% → 17% → 25% | 19.2° | 18.3° | 17.5° | 18.4° | 5.3 | |
| 12% → 17% → 21% | 13.1° | 12.6° | 12.9° | 15.9° | 5.7 | |
| 75 | 25% | 24.0° | 23.0° | 21.1° | 19.9° | 5.8 |
| 17% | 14.7° | 14.4° | 14.2° | 16.0° | 6.2 | |
| 12% → 17% → 25% | 18.7° | 17.8° | 16.6° | 16.6° | 5.3 | |
| 12% → 17% → 21% | 12.5° | 12.1° | 12.0° | 13.6° | 5.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Zeng, C.; Wang, Z.; Lu, J.; Xiang, Q.; Huo, X.; Tan, T.; Li, Y.; Feng, W.; Zhang, G. Optimizing Vertical Unidirectional Airflow in Cleanrooms: An Integrated Approach to Floor Perforation, Plenum, and Fan Filter Unit Configurations. Atmosphere 2025, 16, 632. https://doi.org/10.3390/atmos16060632
Huang Z, Zeng C, Wang Z, Lu J, Xiang Q, Huo X, Tan T, Li Y, Feng W, Zhang G. Optimizing Vertical Unidirectional Airflow in Cleanrooms: An Integrated Approach to Floor Perforation, Plenum, and Fan Filter Unit Configurations. Atmosphere. 2025; 16(6):632. https://doi.org/10.3390/atmos16060632
Chicago/Turabian StyleHuang, Zonghua, Cheng Zeng, Zhichu Wang, Jun Lu, Qian Xiang, Xingcheng Huo, Tingdong Tan, Yan Li, Wenmao Feng, and Guitao Zhang. 2025. "Optimizing Vertical Unidirectional Airflow in Cleanrooms: An Integrated Approach to Floor Perforation, Plenum, and Fan Filter Unit Configurations" Atmosphere 16, no. 6: 632. https://doi.org/10.3390/atmos16060632
APA StyleHuang, Z., Zeng, C., Wang, Z., Lu, J., Xiang, Q., Huo, X., Tan, T., Li, Y., Feng, W., & Zhang, G. (2025). Optimizing Vertical Unidirectional Airflow in Cleanrooms: An Integrated Approach to Floor Perforation, Plenum, and Fan Filter Unit Configurations. Atmosphere, 16(6), 632. https://doi.org/10.3390/atmos16060632







