Performance of the RadonEye Monitor
Abstract
1. Introduction
2. Materials and Methods
2.1. The RadonEye Monitor
Calibration
2.2. Parallel Exposure
2.3. Response to Thoron Exposure
2.4. Anomalies
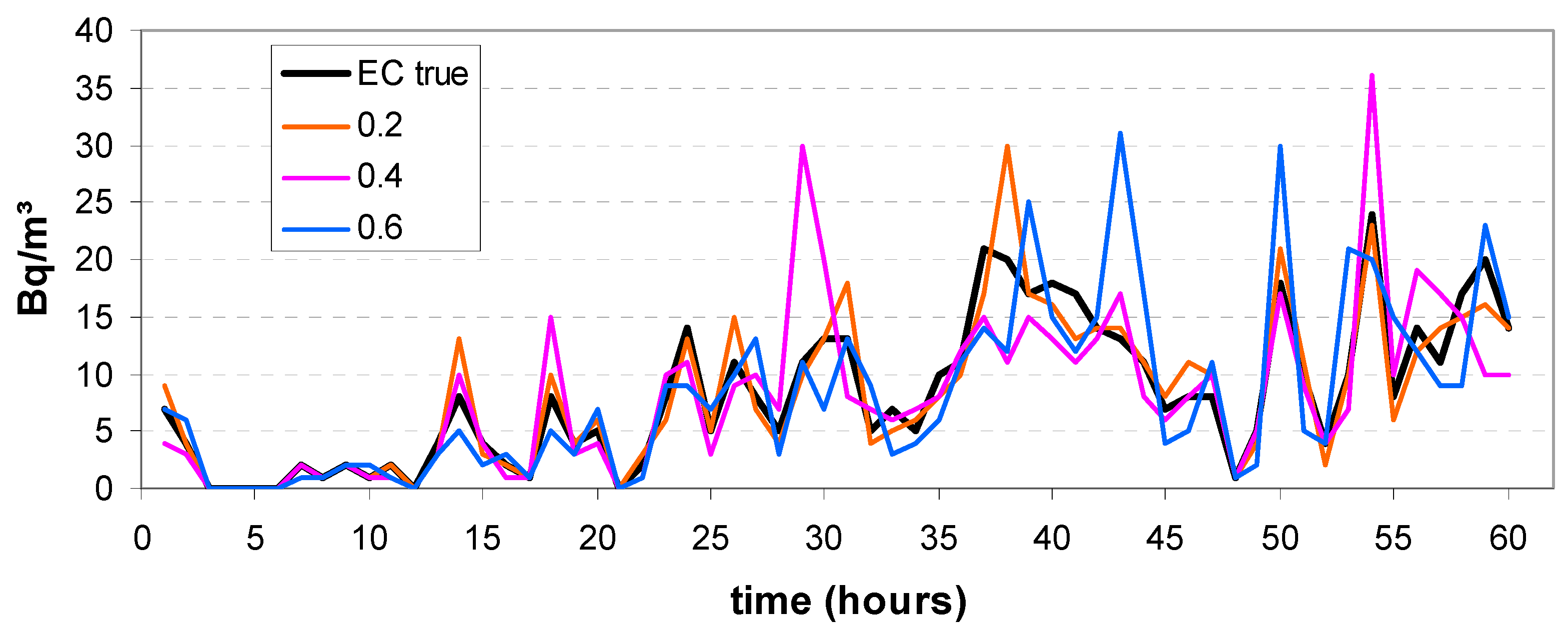
2.5. Correlation Between Parallel Time Series
2.6. Software
3. Results and Discussion
3.1. Deviation from Nominal Calibration
3.2. Effect of Thoron on the RadonEye
3.2.1. Experiments Tn-1 and Tn-2
3.2.2. Experiment Tn-3
3.3. Anomalies
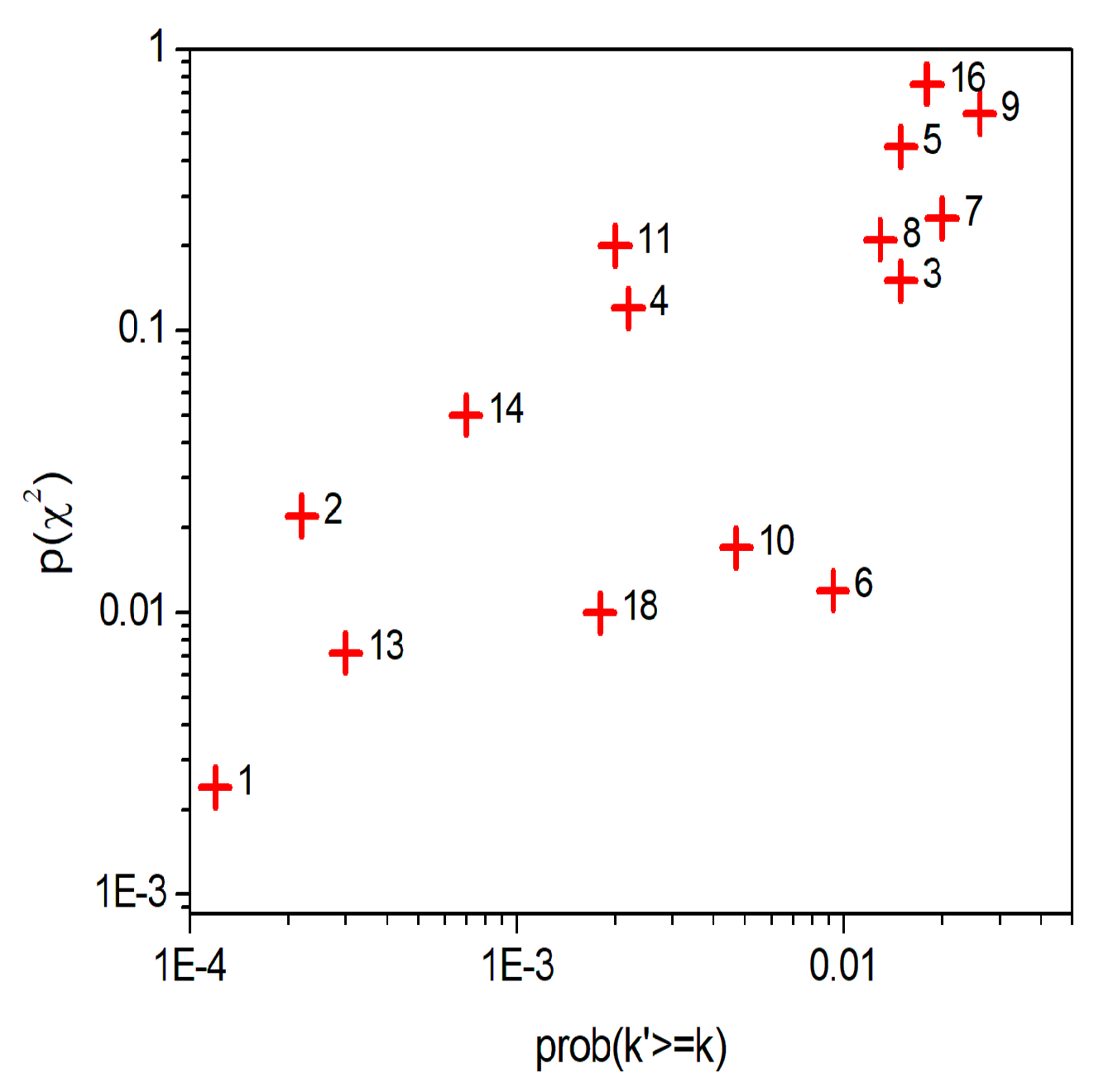
3.3.1. Series #1958
3.3.2. Series #0076
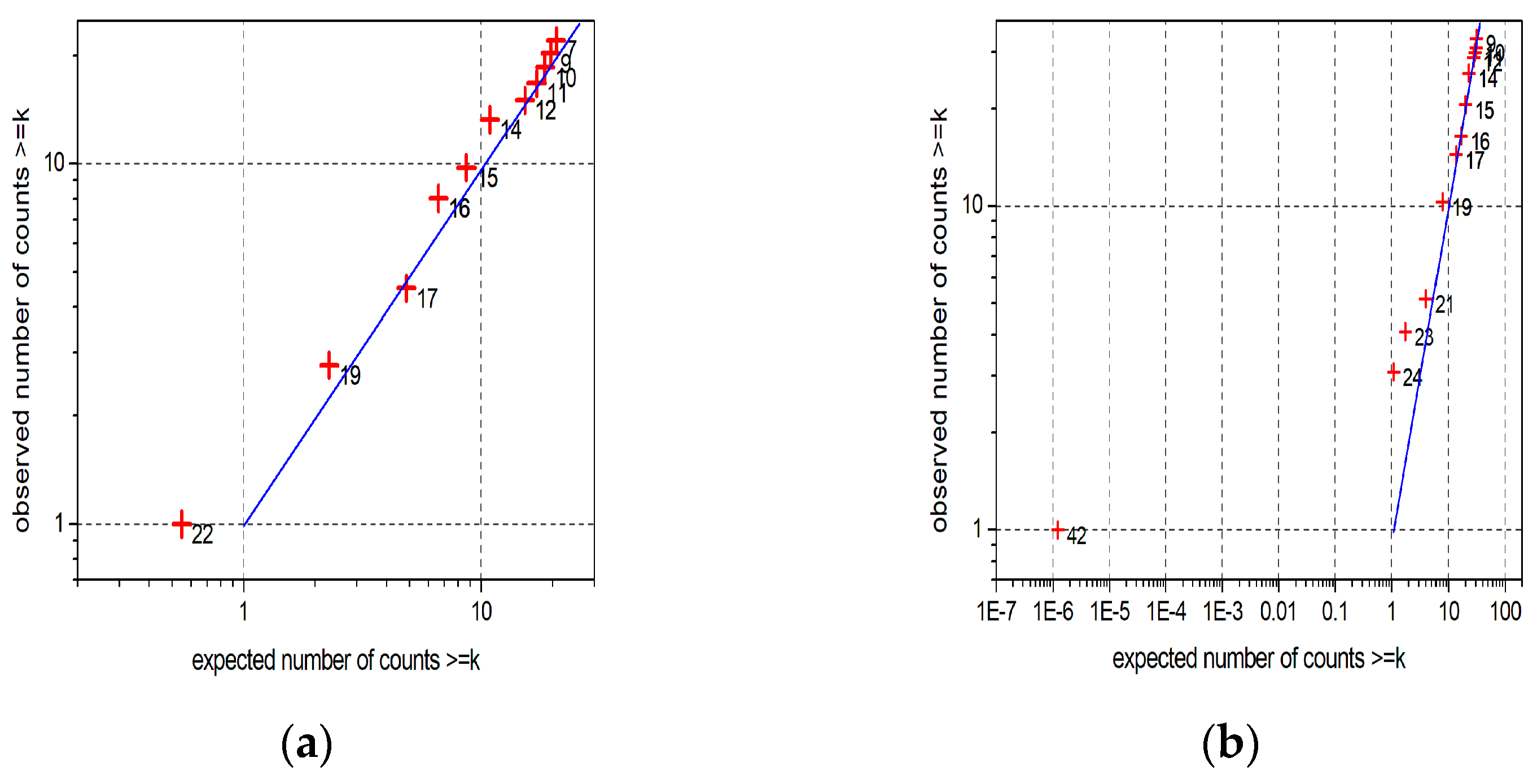
3.4. Missing Concentration Values
3.5. Correlation Between Parallel Time Series
3.5.1. Analysis 1
3.5.2. Analysis 2
4. Conclusions and Recommendations
4.1. Calibration Issues
4.2. Thoron
4.3. Anomalies
4.4. Statistical Issues and Missing Concentration Values
4.5. Citizen Science and Professional Use
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeeb, H.; Shannoun, F. (Eds.) WHO Handbook on Indoor Radon: A Public Health Perspective; WHO: Geneva, Switzerland, 2009; Available online: https://www.who.int/publications/i/item/9789241547673 (accessed on 14 January 2025).
- Vohland, K.; Landzandstra, A.; Ceccaroni, L.; Lemmens, R.; Perelló, J.; Ponti, M.; Samson, R.; Wagenknecht, K. (Eds.) The Science of Citizen Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Bossew, P.; Benà, E.; Chambers, S.; Janik, M. Analysis of outdoor and indoor radon concentration time series recorded with RadonEye monitors. Atmosphere 2024, 15, 1468. [Google Scholar] [CrossRef]
- Radon FTLab. Available online: http://radonftlab.com/ (accessed on 14 January 2025).
- Radon Eye Operation Manual, Model RD 200. Available online: https://merona.blob.core.windows.net/radonftlab-web/20220404_RadonEye_%EC%82%AC%EC%9A%A9%EC%9E%90%EC%84%A4%EB%AA%85%EC%84%9C(%EC%98%81%EB%AC%B8).pdf (accessed on 14 January 2025).
- Available online: https://www.radonshop.com/mediafiles/Anleitungen/Radon/FTLab_RadonEye-RD200/FTLab_RadonEye_ManualEN.pdf (accessed on 20 March 2025).
- Radon-220 (Thoron) Decay Chain. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/69157-radon-220-thoron-decay-chain (accessed on 11 January 2025).
- EPA, Radionuclide Decay Chain. Available online: https://epa-prgs.ornl.gov/cgi-bin/radionuclides/chain.pl (accessed on 21 January 2025).
- Bossew, P.; Kuča, P.; Helebrant, J. True and spurious anomalies in ambient dose rate monitoring. Radiat. Prot. Dosim. 2023, 199, 2183–2188. [Google Scholar] [CrossRef] [PubMed]
- Devroye, L. Discrete Univariate Distributions. 1986. Available online: http://luc.devroye.org/chapter_ten.pdf (accessed on 20 January 2025).
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeontol. Electron. 2024, 4. Available online: http://palaeo-electronica.org/2001_1/past/issue1_01.htm (accessed on 20 March 2025).
- Beck, T.; Foerster, E.; Biel, M.; Feige, S. Measurement Performance of Electronic Radon Monitors. Atmosphere 2024, 15, 1180. [Google Scholar] [CrossRef]
- Tsapalov, A.; Kovler, K.; Bossew, P. Strategy and Metrological Support for Indoor Radon Measurements Using Popular Low-Cost Active Monitors with High and Low Sensitivity. Sensors 2024, 24, 4764. [Google Scholar] [CrossRef] [PubMed]



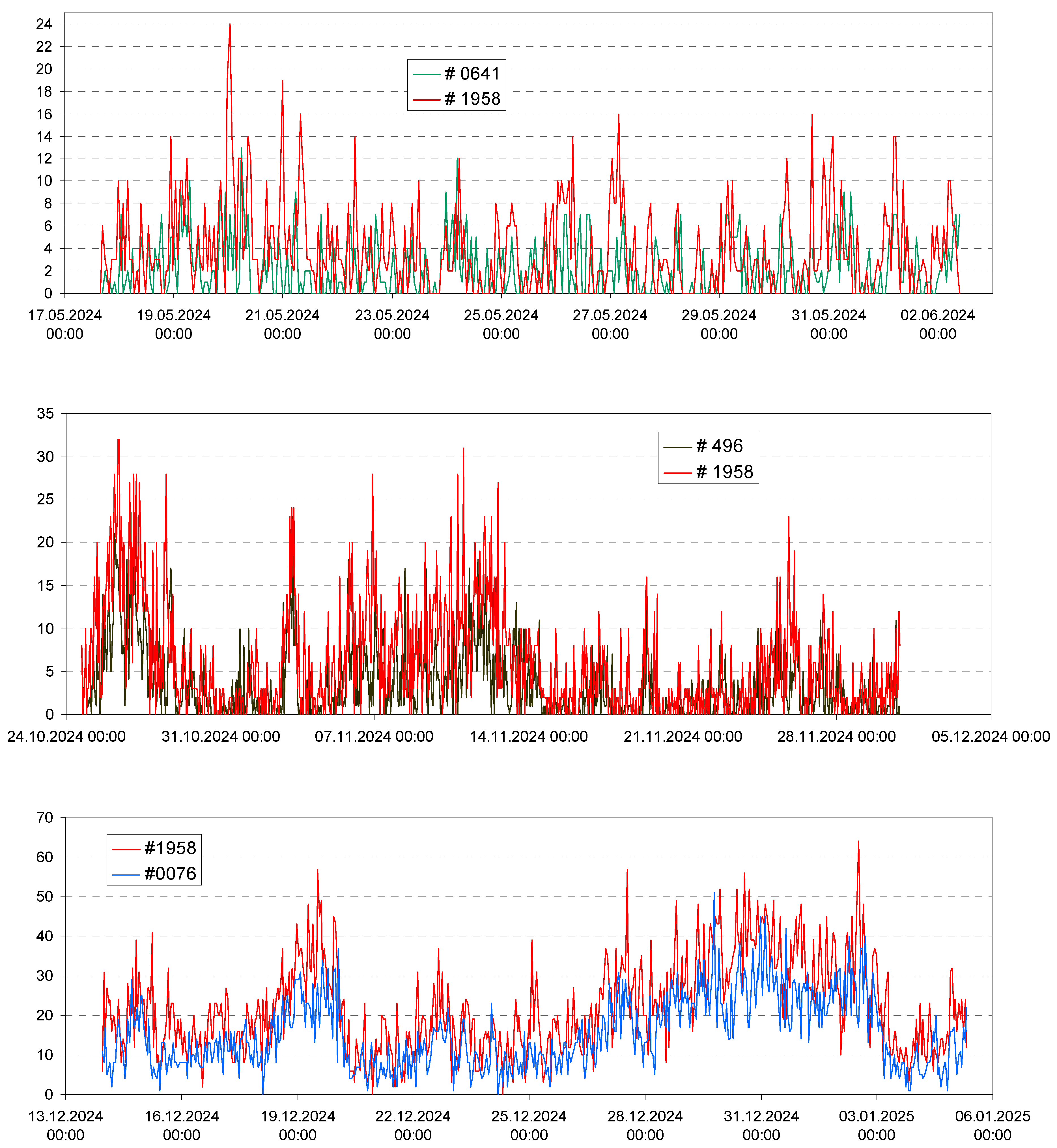
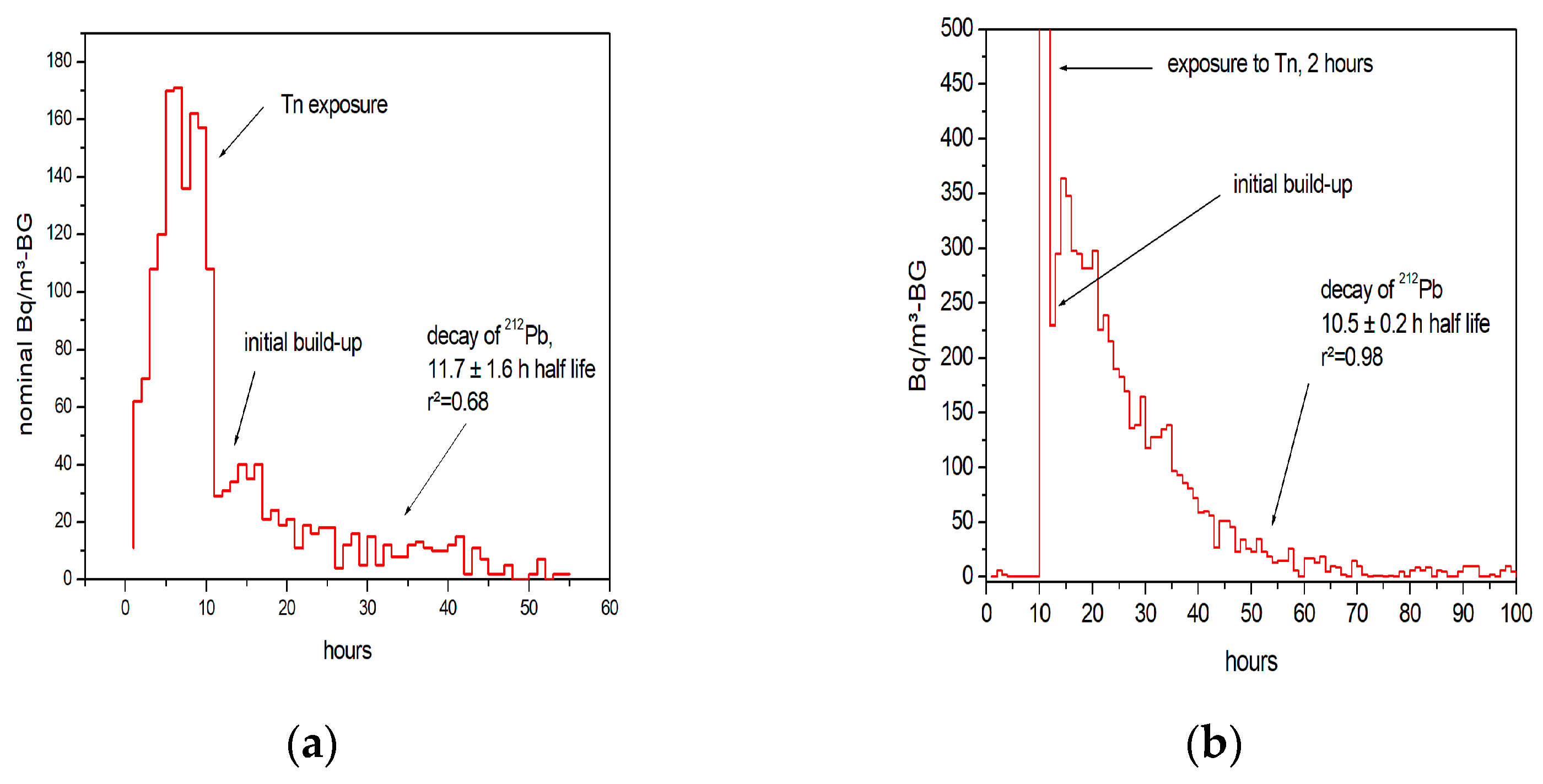
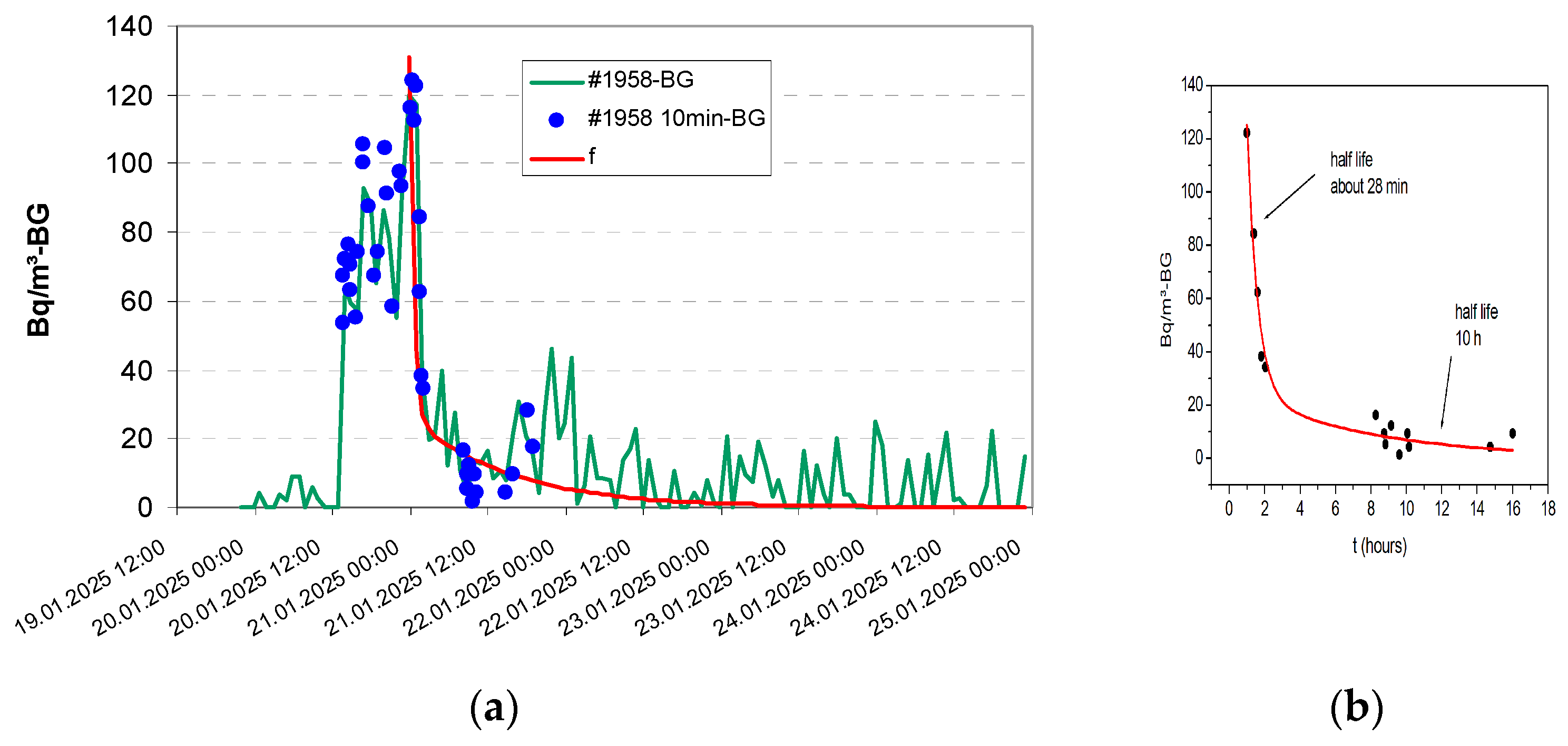
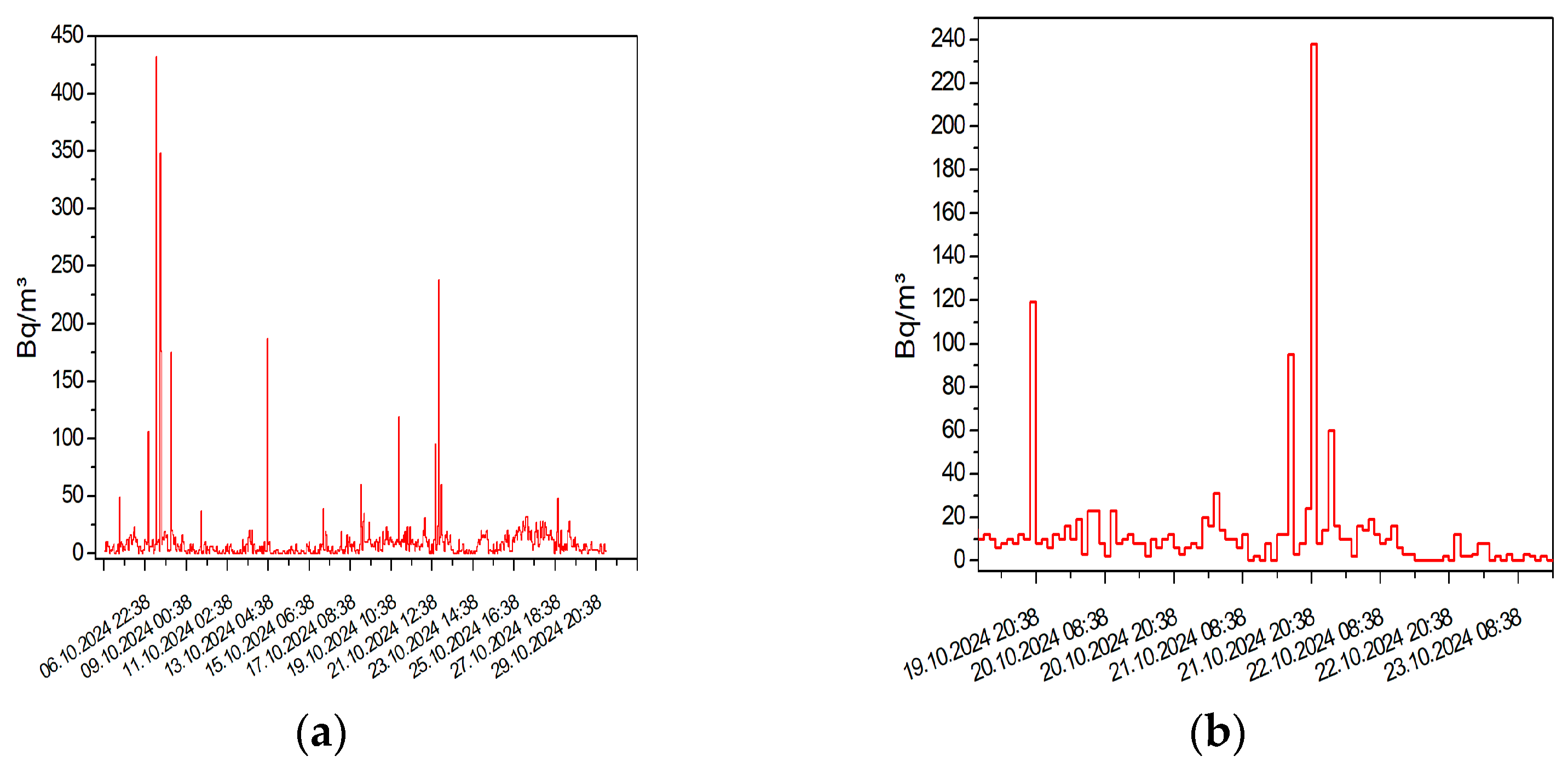



| Experiment | Par-1 | Par-2 | Par-3 | |||
| Device# | #1958 | #0641 | #1958 | #0496 | #1958 | #0076 |
| Date | 17 May–2 June 2024 | 24 October–3 November 2024 | 13 December 2024–5 January 2025 | |||
| n | 379 | 893 | 538 | |||
| AM (Bq/m3) | 3.8 | 2.4 | 5.8 | 3.5 | 22.1 | 15.4 |
| SD (Bq/m3) | 4.0 | 2.6 | 6.2 | 4.1 | 11.8 | 9.1 |
| SE (Bq/m3) | 0.20 | 0.13 | 0.21 | 0.14 | 0.51 | 0.39 |
| AM1/AM2 ± SE | 1.58 ± 0.12 | 1.66 ± 0.09 | 1.44 ± 0.05 | |||
| Paired test | ||||||
| t | 9.2 × 10−11 | 6.7 × 10−36 | 2.3 × 10−54 | |||
| Sign | 2.0 × 10−7 | 1.7 × 10−21 | 8.0 × 10−43 | |||
| Wilcoxon | 6.0 × 10−10 | 2.1 × 10−34 | 8.5 × 10−49 | |||
| Unpaired | ||||||
| t (uneq var) | 3.7 × 10−9 | 7.1 × 10−21 | 3.5 × 10−24 | |||
| M-W | 9.6 × 10−7 | 2.2 × 10−16 | 1.2 × 10−21 | |||
| F eq var | 6.9× 10−18 | 1.9 × 10−33 | 5.2 × 10−9 | |||
| K-S | 1.2 × 10−8 | 4.0 × 10−22 | 1.7 × 10−16 | |||
| A-D | 0 | 0 | 0 | |||
| Correlation | ||||||
| Pearson r | 0.22 | 0.51 | 0.67 | |||
| Spearman ρ | 0.20 | 0.48 | 0.68 | |||
| Event # | Date | Rn | cts k | BG (cts) | Prob (k’ ≥ k) | p (χ2) |
|---|---|---|---|---|---|---|
| 1 | 24.12., 0:48 | 23 | 19 | 6.94 | 1.2 × 10−4 | 0.0024 |
| 2 | 29.12., 18:48 | 51 | 42 | 22.93 | 2.2 × 10−4 | 0.022 |
| 3 | 30.12., 10:48 | 38 | 32 | 21.00 | 0.015 | 0.15 |
| 4 | 31.12., 15:48 | 42 | 35 | 20.50 | 0.0022 | 0.12 |
| 5 | 2.1., 6:48 | 40 | 33 | 21.82 | 0.015 | 0.45 |
| 6 | 2.1., 16:48 | 40 | 33 | 21.00 | 0.0093 | 0.012 |
| 7 | 2.1., 21:48 | 31 | 26 | 16.6 | 0.020 | 0.25 |
| 8 | 5.1., 7:48 | 22 | 19 | 10.67 | 0.013 | 0.21 |
| 9 | 6.1., 16:47 | 26 | 22 | 13.85 | 0.026 | 0.59 |
| 10 | 8.1., 5:47 | 26 | 22 | 11.74 | 0.0047 | 0.017 |
| 11 | 9.1., 22:47 | 32 | 27 | 14.41 | 0.0020 | 0.20 |
| 12 | 11.1., 18:47 | 26 | 22 | 8.09 | 3.9 × 10−5 | 6.0 × 10−6 |
| 13 | 12.1., 2:47 | 22 | 19 | 7.50 | 3.0 × 10−4 | 0.0072 |
| 14 | 15.1., 4:47 | 29 | 24 | 11.33 | 7.0 × 10−4 | 0.050 |
| 15 | 20.1., 16:47 | 37 | 31 | 10.22 | 1.3 × 10−7 | 1.8 × 10−5 |
| 16 | 23.1., 11:47 | 29 | 24 | 14.87 | 0.018 | 0.75 |
| 17 | 24.1., 9:47 | 51 | 42 | 15.87 | 3.8 × 10−8 | 1.2 × 10−4 |
| 18 | 26.1., 15:48 | 32 | 27 | 14.32 | 0.0018 | 0.010 |
| Device ID. | Missing Concentration Values (Bq/m3) |
|---|---|
| GJ17RE000076 | 3, 6, 9, 12, 15, 18, 21, 24, … |
| RE22207111958 | 1, 4, 5, 7, 9, 11, 13, 15, 17, 18, … |
| HG04RE000641 | 3, 6, 8, 11, 13, … |
| HK01RE000496 | 3, 6, 9, 12, 15, … |
| Experiment | Series | 〈r〉 ± SD | Empir. r |
|---|---|---|---|
| Par-1 | #0641 | 0.738 ± 0.0235 | 0.22 |
| #1958 | 0.735 ± 0.025 | ||
| Par-2 | #0496 | 0.851 ± 0.010 | 0.51 |
| #1958 | 0.821 ± 0.011 | ||
| Par-3 | #0076 | 0.860 ± 0.009 | 0.68 |
| #1958 | 0.829 ± 0.015 | ||
| rnd-1 | 0.514 ± 0.030 | ||
| rnd-2 | 0.703 ± 0.020 |
| Experiment | Series | σopt | Empir. r | |
|---|---|---|---|---|
| Model LN | Model SQR+, b = 0.5 | |||
| Par-1 | #0641 | 0.92 | 4.76 | 0.22 |
| #1958 | 0.92 | 4.89 | ||
| Par-2 | #0496 | 0.56 | 4.42 | 0.51 |
| #1958 | 0.52 | 3.80 | ||
| Par-3 | #0076 | 0.26 | 5.54 | 0.67 |
| #1958 | 0.22 | 4.58 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bossew, P. Performance of the RadonEye Monitor. Atmosphere 2025, 16, 525. https://doi.org/10.3390/atmos16050525
Bossew P. Performance of the RadonEye Monitor. Atmosphere. 2025; 16(5):525. https://doi.org/10.3390/atmos16050525
Chicago/Turabian StyleBossew, Peter. 2025. "Performance of the RadonEye Monitor" Atmosphere 16, no. 5: 525. https://doi.org/10.3390/atmos16050525
APA StyleBossew, P. (2025). Performance of the RadonEye Monitor. Atmosphere, 16(5), 525. https://doi.org/10.3390/atmos16050525






