Temporal Distribution of Extreme Precipitation in Barcelona (Spain) under Multi-Fractal n-Index with Breaking Point
Abstract
1. Introduction
1.1. Motivation
1.2. State of the Art
1.2.1. Maximum Averaged Intensities (MAI)
- A maximum mean reference intensity of any reference ,
- The duration of the rainfall event t,
- The variability of the intensity, according to the exponent n.
1.2.2. Intensity-Duration-Frequency (IDF) Curves
2. Data
Reference Observations
3. Methods
3.1. Climate Models
3.2. In Brief
3.3. Wet Spells and Return Periods
3.4. Multi-Fractal Models
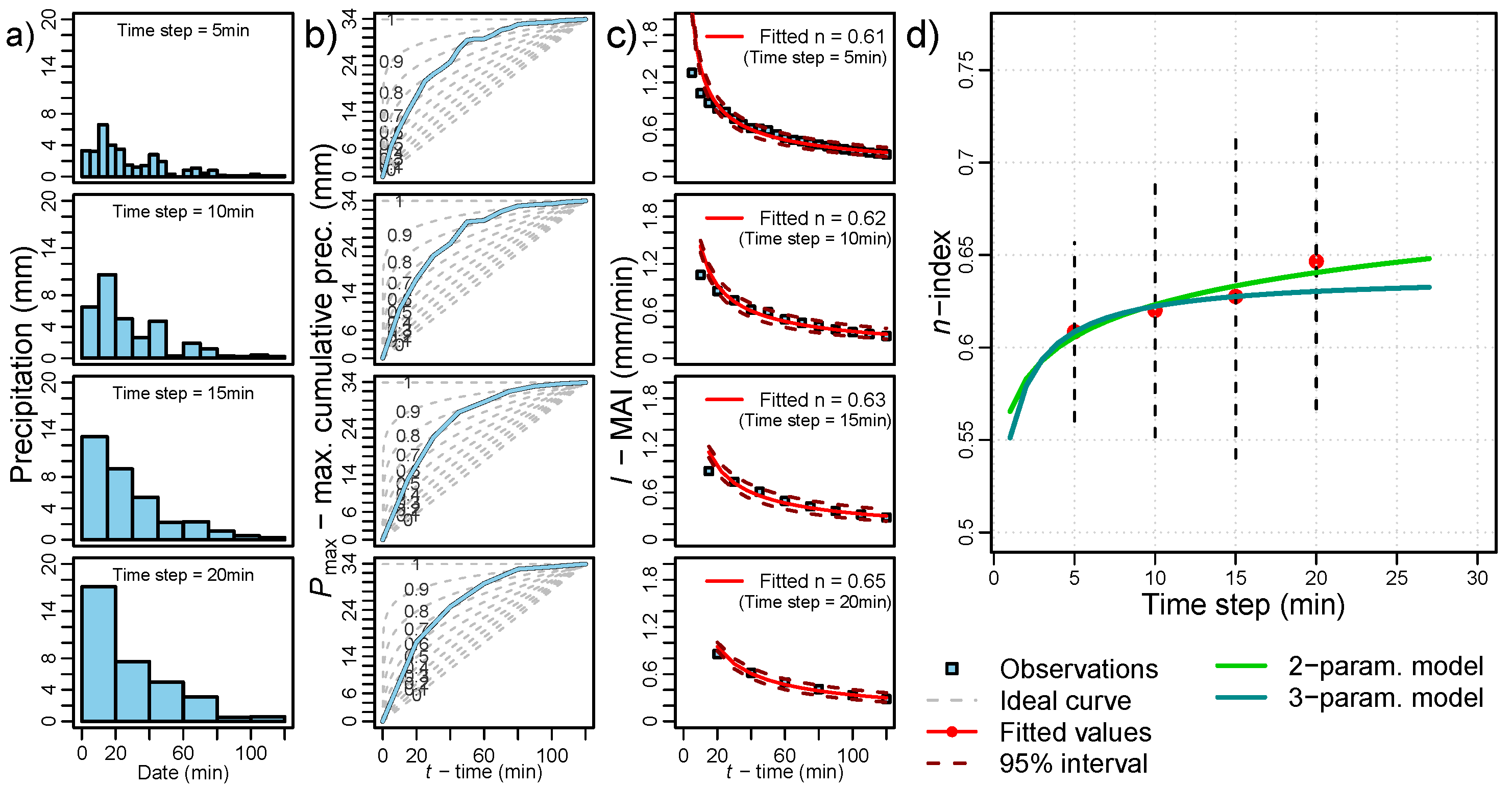
3.4.1. Temporal Resolution Models for n-Index
3.4.2. Temporal Resolution Models for Reference Intensity
4. Results
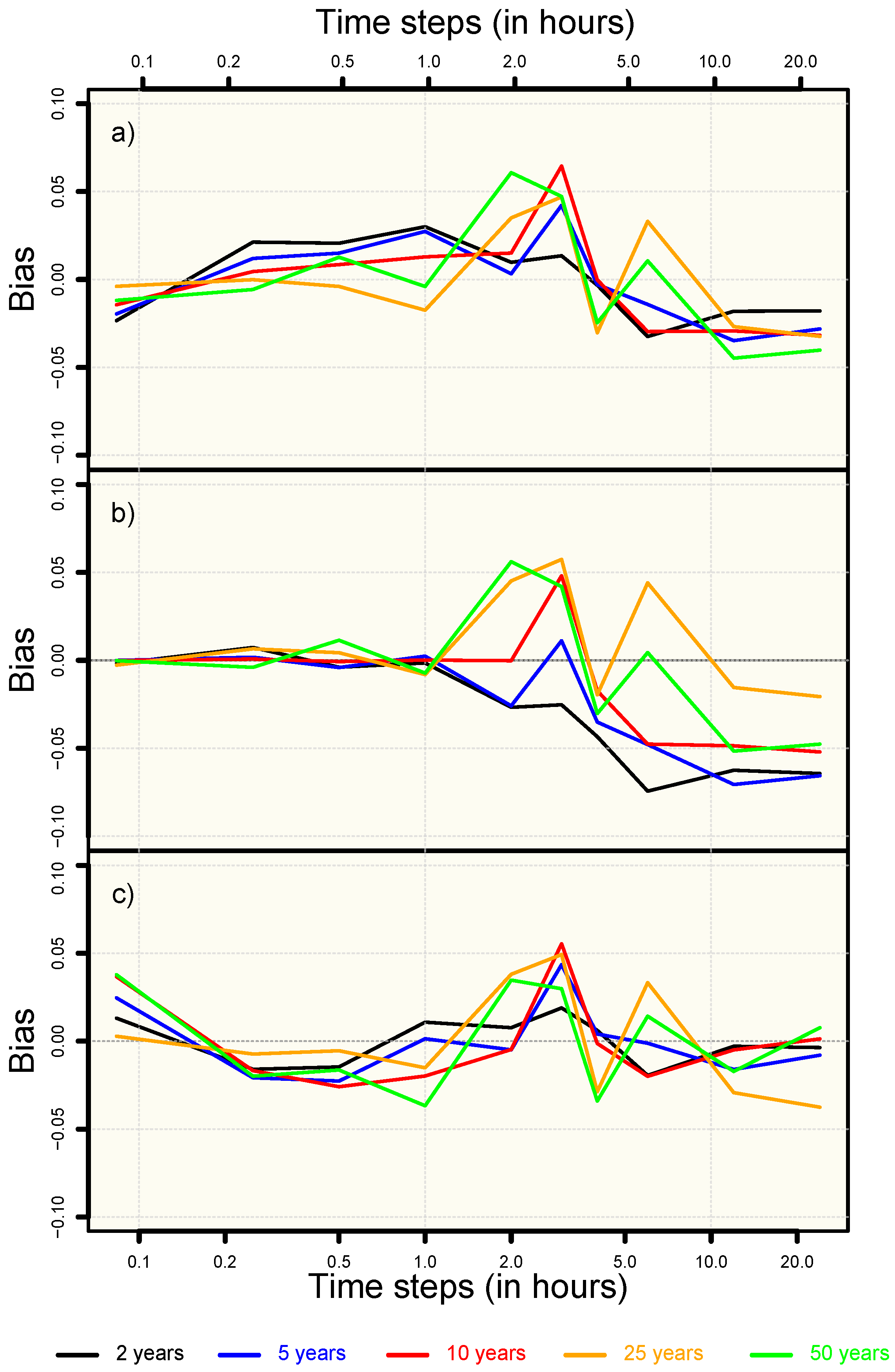
4.1. Multi-Fractal n-Index Models
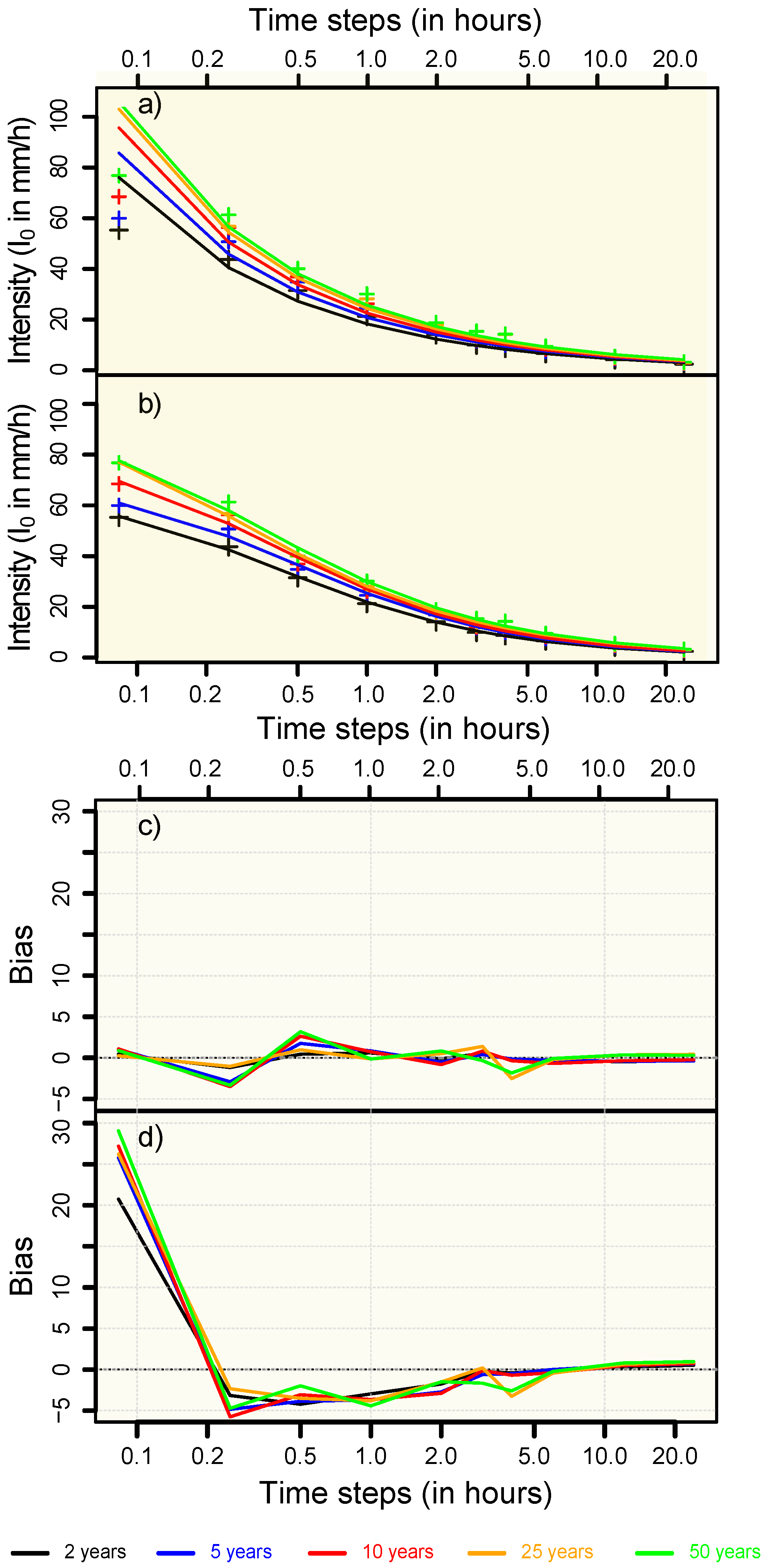
4.2. Multi-Fractal Reference Intensity Models
5. Discussion
5.1. Time Sensitivity of n-Index
5.2. Time Sensitivity of Reference Intensity
5.3. Climate Projections of Daily n-Index
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Fitted Parameters
Appendix A.1. Fitted Values and Score of the n-Index Regression Models
| Statistical | Return Periods p | ||||
|---|---|---|---|---|---|
| Scores | 2 | 5 | 10 | 25 | 50 |
| Two-parameter regression model on the full period (Figure 4a) | |||||
| p-value | |||||
| < | < | < | < | < | |
| k | < | < | |||
| Coefficient value | |||||
| 0.60 | 0.58 | 0.55 | 0.52 | 0.52 | |
| k | 0.44 | 0.4 | 0.32 | 0.25 | 0.27 |
| Two-parameter regression model for less than one hour (Figure 4b) | |||||
| p-value | |||||
| < | < | < | < | < | |
| k | 0.005 | < | < | 0.010 | 0.022 |
| Coefficient value | |||||
| 0.54 | 0.53 | 0.52 | 0.53 | 0.50 | |
| k | 0.30 | 0.28 | 0.25 | 0.28 | 0.23 |
| Three-parameter regression model (Figure 4c) * | |||||
| 0.342 [0.300,0.383] | 0.366 [0.303,0.428] | 0.394 [0.343,0.445] | 0.289 [0.000,0.652] | 0.398 [0.329,0.467] | |
| 0.563 [0.543,0.583] | 0.555 [0.510,0.600] | 0.552 [0.463,0.641] | 0.477 [0.446,0.507] | 0.567 [0.332,0.467] | |
| a | 0.026 [0.007,0.045] | 0.016 [0.001,0.043] | 0.006 [−0.008,0.020] | 0.136 [−0.417,0.689] | 0.002 [0.011,0.016] |
Appendix A.2. Fitted Values and Score of the Reference Intensity Regression Models
| Statistical | Return Periods p | ||||
|---|---|---|---|---|---|
| Scores | 2 | 5 | 10 | 25 | 50 |
| Two-parameter regressions on the full period (Figure 6a) | |||||
| p-value | |||||
| intercepts | < | < | < | < | < |
| < | < | < | < | < | |
| Coefficient value | |||||
| [mm/h] | 1.83 | 1.79 | 1.73 | 1.67 | 1.68 |
| n-index | 0.573 | 0.570 | 0.581 | 0.580 | 0.570 |
| Three-parameter regression (Figure 6b) * | |||||
| [mm/h] | 21.9 [21.3,22.4] | 25.4 [24.2,26.6] | 27.0 [25.5,28.5] | 28.1 [27.1,29.0] | 30.0 [28.4,31.5] |
| n | 0.802 [0.737,0.866] | 0.830 [0.691,0.967] | 0.802 [0.659,0.945] | 0.703 [0.630,0.775] | 0.719 [0.605,0.834] |
| [hr] | 0.331 [0.263,0.399] | 0.405 [0.244,0.566] | 0.323 [0.176,0.470] | 0.202 [0.137,0.268] | 0.249 [0.135,0.363] |
References
- Adloff, F.; Somot, S.; Sevault, F.; Jordà, G.; Aznar, R.; Déqué, M.; Herrmann, M.; Marcos, M.; Dubois, C.; Padorno, E.; et al. Mediterranean Sea Response to Climate Change in an Ensemble of Twenty First Century Scenarios; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Moncho, R.; Belda, F.; Caselles, V. Climatic study of the exponent “n” in IDF curves: Application for the Iberian. Tethys 2009, 6, 3–14. [Google Scholar] [CrossRef]
- Monjo, R. Measure of rainfall time structure using the dimensionless n-index. Clim. Res. 2016, 67, 71–86. [Google Scholar] [CrossRef]
- Monjo, R.; Locatelli, L.; Milligan, J.; Torres, L.; Velasco, M.; Gaitan, E.; Portoles, J.; Redolat, D.; Russo, B.; Ribalaygua, J. Estimation of future extreme rainfall in Barcelona (Spain) under monofractal hypothesis. Int. J. Climatol. 2023, 163, 4047–4068. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Negative fractal dimensions and multifractals. Phys. A Stat. Mech. Appl. 1990, 43, 306–315. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Barenblatt, G. Scaling; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Golitsyn, G. Laws of Random Walks Derived by A.N. Kolmogorov in 1934. Russ. Meteorol. Hydrol. 2018, 43, 135–142. [Google Scholar] [CrossRef]
- Barenblatt, G. Scaling, Self-Similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Monjo, R.; Royé, D.; Martin-Vide, J. Meteorological drought lacunarity around the world and its classification. Earth Syst. Sci. Data 2020, 12, 741–752. [Google Scholar] [CrossRef]
- Efstathiou, M.; Varotsos, C. Intrinsic properties of Sahel precipitation anomalies and rainfall. Theor. Appl. Climatol. 2012, 109. [Google Scholar] [CrossRef]
- Moncho, R.; Caselles, V.; Chust, G. Alternative model for precipitation probability distribution: Application to Spain. Clim. Res. 2009, 51, 23–33. [Google Scholar] [CrossRef]
- Monjo, R.; Gaitán, E.; Pórtoles, J.; Ribalaygua, J.; Torres, L. Changes in extreme precipitation over Spain using statistical downscaling of CMIP5 projections. Int. J. Climatol. 2016, 36, 757–769. [Google Scholar] [CrossRef]
- Russo, B.; De La Cruz Coronas, Á.; Leone, M.; Evans, B.; Brito, R.S.; Havlik, D.; Bügelmayer-Blaschek, M.; Pacheco, D.; Sfetsos, A. Improving Climate Resilience of Critical Assets: The ICARIA Project. Sustainability 2023, 15, 4090. [Google Scholar] [CrossRef]
- Llasat, M.C. An objective classification of rainfall events on the basis of their convective features: Application to rainfall intensity in the northeast of spain. Int. J. Climatol. 2001, 21, 1385–1400. [Google Scholar] [CrossRef]
- Rodríguez-Solà, R.; Casas-Castillo, M.C.; Navarro, X.; Redaño, Á. A study of the scaling properties of rainfall in spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Puigcerver, M.; Alonso, S.; Lorente, J.; Llasat, M.C.; Redaño, A.; Burgueno, A.; Vilar, E. Preliminary aspects of rainfall rates in the north east of Spain. Theor. Appl. Climatol. 1986, 37, 97–109. [Google Scholar] [CrossRef]
- Burgueño, A.; Codina, B.; Redaño, A.; Lorente, J. Basic statistical characteristics of hourly rainfall amounts in Barcelona (Spain). Theor. Appl. Climatol. 1994, 49, 175–181. [Google Scholar] [CrossRef]
- Llasat, M.C.; Puigcerver, M. Total rainfall and convective rainfall in Catalonia, Spain. Int. J. Climatol. 1997, 17, 1683–1695. [Google Scholar] [CrossRef]
- Casas, M.C.; Rodríguez, R.; Prohom, M.; Gázquez, A.; Redaño, A. Estimation of the probable maximum precipitation in Barcelona (Spain). Int. J. Climatol. 2011, 31, 1322–1327. [Google Scholar] [CrossRef]
- Rodríguez, R.; Casas, M.; Redaño, A. Multifractal analysis of the rainfall time distribution on the metropolitan area of Barcelona (Spain). Meteorol. Atmos. Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Martin-Vide, J. Spatial distribution of a daily precipitation concentration index in peninsular Spain. Int. J. Climatol. 2004, 24, 959–971. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Gan, Y.; Zhao, L.; Qin, W.; Ding, L. Rainfall erosivity index for monitoring global soil erosion. CATENA 2024, 234, 107593. [Google Scholar] [CrossRef]
- Dowdy, A.J.; Mills, G.A.; Finkele, K.; de Groot, W. Index sensitivity analysis applied to the Canadian Forest Fire Weather Index and the McArthur Forest Fire Danger Index. Meteorol. Appl. 2010, 17, 298–312. [Google Scholar] [CrossRef]
- Borzì, I. Evaluating Sustainability Improvement of Pressure Regime in Water Distribution Systems Due to Network Partitioning. Water 2022, 14, 1787. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Mizuki, C.; Kuzuha, Y. Frequency Analysis of Hydrological Data for Urban Floods—Review of Traditional Methods and Recent Developments, Especially an Introduction of Japanese Proper Methods. Water 2023, 15, 2490. [Google Scholar] [CrossRef]
- Sherman, C. Frequency and intensity of excessive rainfalls at Boston. Trans. Am. Soc. Civ. Eng. 1931, 95, 951–960. [Google Scholar] [CrossRef]
- Ribalaygua, J.; Torres, L.; Pórtoles, J.; Monjo, R.; Gaitán, E.; Pino, M. Description and validation of a two-step analogue/regression downscaling method. Theor. Appl. Climatol. 2013, 114, 253–269. [Google Scholar] [CrossRef]
- Ziehn, T.; Chamberlain, M.; Lenton, A.; Law, R.; Bodman, R.; Dix, M.; Mackallah, C.; Druken, K.; Ridzwan, S.M. CSIRO ACCESS-ESM1.5 Model Output Prepared for CMIP6 C4MIP; Earth System Grid Federation; 2023. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The main progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Jiao, Y.; et al. CCCma CanESM5 Model Output Prepared for CMIP6 FAFMIP; Earth System Grid Federation; 2023. [Google Scholar] [CrossRef]
- Cherchi, A.; Fogli, P.G.; Lovato, T.; Peano, D.; Iovino, D.; Gualdi, S.; Masina, S.; Scoccimarro, E.; Materia, S.; Bellucci, A.; et al. Global Mean Climate and Main Patterns of Variability in the CMCC-CM2 Coupled Model. J. Adv. Model. Earth Syst. 2019, 11, 185–209. [Google Scholar] [CrossRef]
- Voldoire, A.; Saint-Martin, D.; Sénési, S.; Decharme, B.; Alias, A.; Chevallier, M.; Colin, J.; Guérémy, J.F.; Michou, M.; Moine, M.P.; et al. Evaluation of CMIP6 DECK Experiments With CNRM-CM6-1. J. Adv. Model. Earth Syst. 2019, 11, 2177–2213. [Google Scholar] [CrossRef]
- Earth System Grid Federation. EC-Earth-Consortium EC-Earth3-CC Model Output Prepared for CMIP6 ScenarioMIP ssp245; Earth System Grid Federation; 2023. [Google Scholar] [CrossRef]
- Gutjahr, O.; Putrasahan, D.; Lohmann, K.; Jungclaus, J.H.; von Storch, J.S.; Brüggemann, N.; Haak, H.; Stössel, A. Max Planck Institute Earth System Model (MPI-ESM1.2) for the High-Resolution Model Intercomparison Project (HighResMIP). Geosci. Model Dev. 2019, 12, 3241–3281. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2.0: Description and Basic Evaluation of the Physical Component. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 931–965. [Google Scholar] [CrossRef]
- Bentsen, M.; Oliviè, D.J.L.; Seland, y.; Toniazzo, T.; Gjermundsen, A.; Graff, L.S.; Debernard, J.B.; Gupta, A.K.; He, Y.; Kirkevåg, A.; et al. NCC NorESM2-MM Model Output Prepared for CMIP6 CMIP Abrupt-4xCO2; Earth System Grid Federation; 2023. [Google Scholar] [CrossRef]
- Sellar, A.A.; Jones, C.G.; Mulcahy, J.P.; Tang, Y.; Yool, A.; Wiltshire, A.; O’Connor, F.M.; Stringer, M.; Hill, R.; Palmieri, J.; et al. UKESM1: Description and Evaluation of the U.K. Earth System Model. J. Adv. Model. Earth Syst. 2019, 11, 4513–4558. [Google Scholar] [CrossRef]
- Gutierrez-Lopez, A.; Jimenez Hernandez, S.; Escalante Sandoval, C. Physical Parameterization of IDF Curves Based on Short-Duration Storms. Earth Syst. Sci. Data 2019, 11, 1813. [Google Scholar] [CrossRef]
- Chen, J.; Dai, A.; Zhang, Y.; Rasmussen, K.L. Changes in convective available potential energy and convective inhibition under global warming. J. Clim. 2020, 33, 2025–2050. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Tzanis, C.; Cracknell, A.P. Precursory signals of the major El Niño Southern Oscillation events. Theor. Appl. Climatol. 2016, 15, 903–912. [Google Scholar] [CrossRef]
- Varotsos, C.; Sarlis, N.V.; Mazei, Y.; Saldaev, D.; Efstathiou, M. A Composite Tool for Forecasting El Niño: The Case of the 2023–2024 Event. Forecasting 2024, 6, 187–203. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.; et al. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC Summary for Policymakers; IPCC: Geneva, Switzerland, 2021. [Google Scholar]



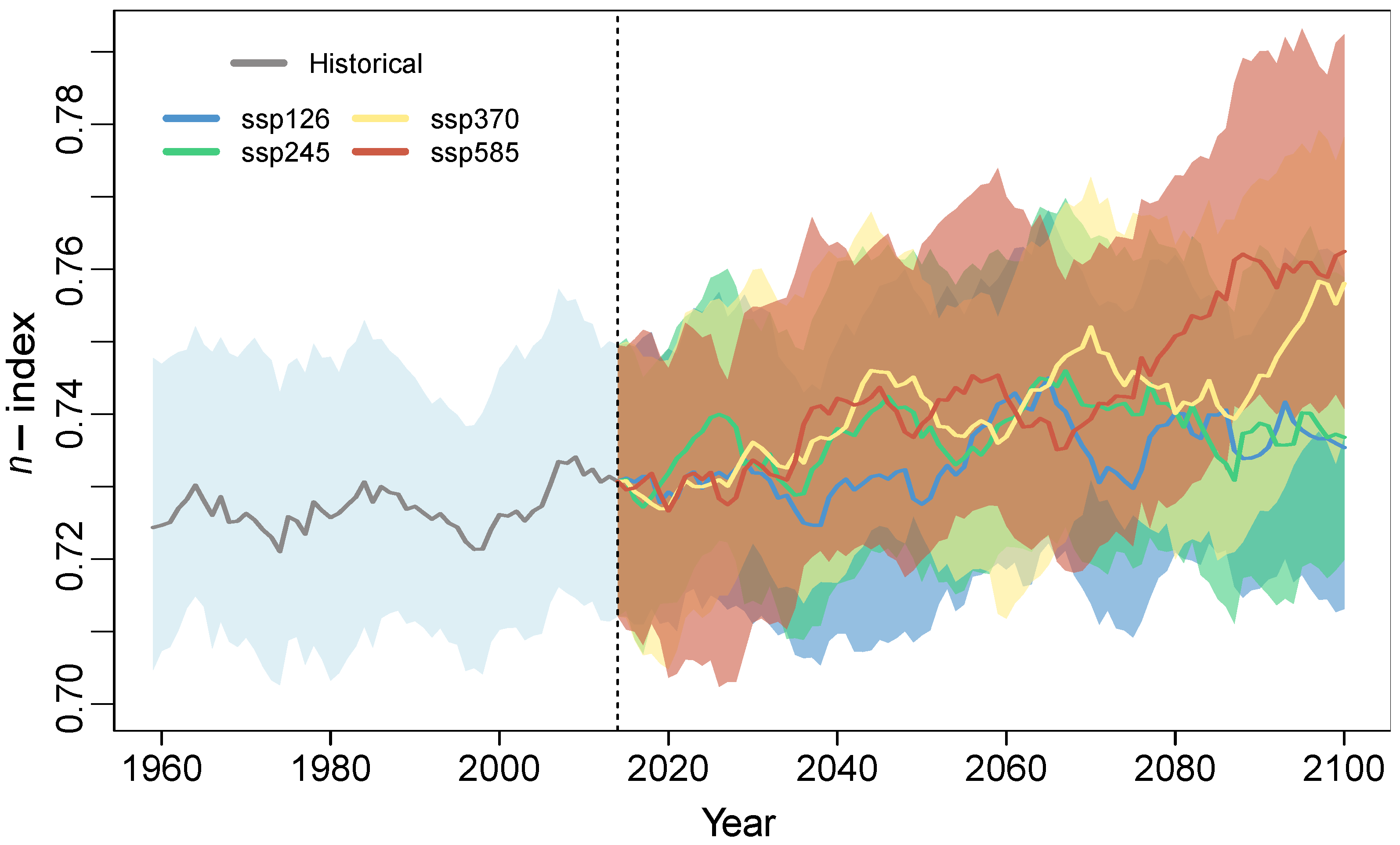
| Id | Lon | Lat | Altitude | Name | Resol. | Period |
|---|---|---|---|---|---|---|
| D5 | 2.12 | 41.42 | 411.00 | Barcelona-Obs. Fabra (main station) | 5 min | 1927–2016 |
| UF | 1.91 | 41.29 | 573.00 | PN del Garraf - el Rascler | 10 min | 1996–2020 |
| UG | 2.04 | 41.30 | 3.00 | Viladecans | 10 min | 1996–2020 |
| VT | 2.13 | 41.48 | 84.00 | Cerdanyola del Vallès | 10 min | 1996–2020 |
| Name | Institution | Released Year | Resolution Lon (°) × Lat (°) | Reference |
|---|---|---|---|---|
| ACCESS-CM2 | CSIRO-ARCCSS | 2019 | 1.9° × 1.3° | Ziehn et al. [31] |
| BCC-CSM2-HR | BCC | 2017 | 1.1° × 1.1° | Wu et al. [32] |
| CanESM5 | CCCma | 2019 | 2.8° × 2.8° | Swart et al. [33] |
| CMCC-ESM2 | CMCC | 2017 | 1.3° × 1.0° | Cherchi et al. [34] |
| CNRM-ESM2-1 | CNRM-CERFACS | 2017 | 1.4° × 1.4° | Voldoire et al. [35] |
| EC-Earth3 | EC-Earth-Consortium | 2019 | 0.7° × 0.7° | EC-Earth Con. [36] |
| MPI-ESM1-2-HR | MPI-M, DWD, DKRZ | 2017 | 0.9° × 0.9° | Gutjahr et al. [37] |
| MRI-ESM2-0 | MRI | 2017 | 1.1° × 1.1° | Yukimoto et al. [38] |
| NorESM2-MM | NCC | 2017 | 1.3° × 0.9° | Bentsen et al. [39] |
| UKESM1-0-LL | MOHC, NERC, NIMS, NIWA | 2018 | 1.9° × 1.3° | Sellar et al. [40] |
| p (Years) | Time Steps t (in Hours) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| d * | 1/12 | 1/4 | 1/2 | 1 | 2 | 3 | 4 | 6 | 12 | 24 | |
| 2 | 5.5 | 12.1 | 20.7 | 27.8 | 36.4 | 40.8 | 42.3 | 47.9 | 49.0 | 59.3 | 66.0 |
| 5 | 6.5 | 14.1 | 26.6 | 34.3 | 45.5 | 55.0 | 58.2 | 59.3 | 62.2 | 71.7 | 82.6 |
| 10 | 7.5 | 17.1 | 32.6 | 37.9 | 50.3 | 69.1 | 70.6 | 70.6 | 76.4 | 87.6 | 96.1 |
| 25 | 8.4 | 20.2 | 33.3 | 41.8 | 55.5 | 75.6 | 77.1 | 94.1 | 95.1 | 95.1 | 107.8 |
| 50 | 8.9 | 20.2 | 37.9 | 46.4 | 64.2 | 84.3 | 91.5 | 100.5 | 104.9 | 105.8 | 122.0 |
| Statistical | Return Periods p | ||||
|---|---|---|---|---|---|
| Scores | 2 | 5 | 10 | 25 | 50 |
| Two-parameter regression on the full period | |||||
| MAE | 0.0199 | 0.0199 | 0.0211 | 0.0230 | 0.0262 |
| 0.854 | 0.846 | 0.721 | 0.619 | 0.566 | |
| Two-parameter regression for less than one hour | |||||
| MAE | 0.0311 | 0.0264 | 0.0216 | 0.0224 | 0.0255 |
| 0.990 | 0.996 | 0.999 | 0.979 | 0.957 | |
| Three-parameter regression | |||||
| MAE | 0.0113 | 0.0147 | 0.0187 | 0.0247 | 0.0249 |
| 0.961 | 0.893 | 0.772 | 0.576 | 0.703 | |
| Statistical | Return Periods p | ||||
|---|---|---|---|---|---|
| Scores | 2 | 5 | 10 | 25 | 50 |
| Two-parameter regression | |||||
| MAE | 3.43 | 4.32 | 4.50 | 4.28 | 4.80 |
| 0.927 | 0.907 | 0.921 | 0.948 | 0.934 | |
| Three-parameter regression | |||||
| MAE | 0.458 | 0.872 | 1.12 | 0.782 | 1.13 |
| 0.999 | 0.996 | 0.995 | 0.998 | 0.995 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gacon, B.; Santuy, D.; Redolat, D. Temporal Distribution of Extreme Precipitation in Barcelona (Spain) under Multi-Fractal n-Index with Breaking Point. Atmosphere 2024, 15, 804. https://doi.org/10.3390/atmos15070804
Gacon B, Santuy D, Redolat D. Temporal Distribution of Extreme Precipitation in Barcelona (Spain) under Multi-Fractal n-Index with Breaking Point. Atmosphere. 2024; 15(7):804. https://doi.org/10.3390/atmos15070804
Chicago/Turabian StyleGacon, Benoît, David Santuy, and Darío Redolat. 2024. "Temporal Distribution of Extreme Precipitation in Barcelona (Spain) under Multi-Fractal n-Index with Breaking Point" Atmosphere 15, no. 7: 804. https://doi.org/10.3390/atmos15070804
APA StyleGacon, B., Santuy, D., & Redolat, D. (2024). Temporal Distribution of Extreme Precipitation in Barcelona (Spain) under Multi-Fractal n-Index with Breaking Point. Atmosphere, 15(7), 804. https://doi.org/10.3390/atmos15070804







