Abstract
This paper reviews current numerical developments for atmospheric modelling. Numerical atmospheric modelling now looks back to a history of about 70 years after the first successful numerical prediction. Currently, we face new challenges, such as variable and adaptive resolution and ultra-highly resolving global models of 1 km grid length. Large eddy simulation (LES), special applications like the numerical prediction of pollution and atmospheric contaminants belong to the current challenges of numerical developments. While pollution prediction is a standard part of numerical modelling in case of accidents, models currently being developed aim at modelling pollution at all scales from the global to the micro scale. The methods discussed in this paper are spectral elements and other versions of Local-Galerkin (L-Galerkin) methods. Classic numerical methods are also included in the presentation. For example, the rather popular second-order Arakawa C-grid method can be shown to result as a special case of an L-Galerkin method using low-order basis functions. Therefore, developments for Galerkin methods also apply to this classic C-grid method, and this is included in this paper. The new generation of highly parallel computers requires new numerical methods, as some of the classic methods are not well suited for a high degree of parallel computing. It will be shown that some numerical inaccuracies need to be resolved and this indicates a potential for improved results by going to a new generation of numerical methods. The methods considered here are mostly derived from basis functions. Such methods are known under the names of Galerkin, spectral, spectral element, finite element or L-Galerkin methods. Some of these new methods are already used in realistic models. The spectral method, though highly used in the 1990s, is currently replaced by the mentioned local L-Galerkin methods. All methods presented in this review have been tested in idealized numerical situations, the so-called toy models. Waypoints on the way to realistic models and their mathematical problems will be pointed out. Practical problems of informatics will be highlighted. Numerical error traps of some current numerical approaches will be pointed out. These are errors not occurring with highly idealized toy models. Such errors appear when the test situation becomes more realistic. For example, many tests are for regular resolution and results can become worse when the grid becomes irregular. On the sphere no regular grids exist, except for the five derived from Platonic solids. Practical problems beyond mathematics on the way to realistic applications will also be considered. A rather interesting and convenient development is the general availability of computer power. For example, the computational power available on a normal personal computer is comparable to that of a supercomputer in 2005. This means that interesting developments, such as the small sphere atmosphere with a resolution of 1 km and a spherical circumference between 180 and 360 km are available to the normal owner of a personal computer (PC). Besides the mathematical problems of new approaches, we will also consider the informatics challenges of using the new generation of models on mainframe computers and PCs.
1. Introduction
The potential merit of numerical procedures for weather prediction is obvious, and attempts in this direction were made even before the invention of the computer. While these early attempts were unsuccessful, the first successful numerical weather prediction was carried out by Charney [1] using a two-dimensional (2D) model with realistic data and one of the first programmable computers.
All such models use an approximation of the Navier–Stokes equation, and a recent development under the name of non-hydrostatic modelling uses the original form of these equations without approximations specific to the meteorological application. A review of the transition to non-hydrostatic models is given by given by [2], in future called St_Li.
Even though numerical weather prediction (NWP) has been around for 70 years, there are still new developments in the field of numerics. Until about the year 2000, most numerical procedures used the classic second to fourth-order differencing procedures as described by [3]. As an alternative to second to fourth-order methods, the highly accurate spectral method was used. This is a Galerkin procedure using harmonic or spherical harmonic basic functions and this method is also described by [3]. These methods have the objective to approximate the time derivatives of amplitudes, when the fields for a time level are given. To obtain a forecast, time integration must be performed. This means that the time derivatives computed at certain time levels are used to compute the fields at the desired times. This is normally carried out in rather small steps until the desired forecast time is reached. Durran (2010) [3] gives a rather complete description of possible time integration schemes. For the tests in this paper, we use the highly accurate four-step Runge Kutta method RK4 (see St_Li). Time integration is not the subject of this paper. It concentrates on spatial discretization beyond the classic methods as described by Durran (2010) [3]. The new methods are based on piecewise polynomial representations of dynamic fields. Current developments concentrate on the locality of procedures. Such locality is not necessarily present, even when using Galerkin methods with local basis functions.
Polynomials used with such piecewise polynomial representations are determined by grid-point values describing fields. They are used to compute spatial derivatives. Such interpolations can be different for use in different computational steps. An example is the fourth-order computation of the derivative at a point , This is most easily explained for the one-dimensional (1D) case, where the grid is . dx is the grid length which is assumed to be constant. An irregular grid is obtained when dx depends on i.
For one, two and three dimensions, such basis function representations and simple high-order differentiation are explained in [2]. hearafter cited as St_Li. Piecewise polynomial functions can be used to construct basis function methods. These are known under the names of Galerkin, spectral element, Local-Galerkin (L-Galerkin) methods or finite elements. These basis functions have local support. Basis functions with support over the whole modelling area are known as spectral methods and treated in [3]. In this paper, we outline the steps to be taken to go from the theoretical constructions described in St_Li to realistic models. Apart from the new mathematical methods outlined by St_Li, a realistic model contains many other features: the provision of realistic data, organizing the code to allow parallel execution on computers and the physical processes. Physical processes, such as radiation, turbulence and surface processes are normally programmed in such a way that clear interfaces to the dynamic model part allow their development to be independent of the other parts of a model. Therefore, they can easily be imported from other sources into a model.
The author obtained a personal impression of the difficulty of introducing L-Galerkin methods into a model. He spent one week with a specialist of the spectral element model HOMME (see [4]) and tried to modify the existing L-Galerkin procedures of HOMME. This was unsuccessful because we did not find a clear interface to the numeric part of this model. The shallow water version could be modified to use a sparse grid and this was possible because the author provided subroutines to the specifications of another HOMME model specialist (see St_Li, Figure of STLI page 2619). In order to make the application of L-Galerkin methods easier, an L-Galerkin compiler and IGEL-files were proposed in St_Li but this turned out to be still too complicated for transferring L-Galerkin methods from toy to realistic models. Section 4 gives an example of further simplifications using geometric files.
It is suggested to create realistic L-Galerkin models by modifying one of the existing models, called the background model. An example for such possible background models is the MPAS (Model for Prediction Across Scales, [5]) for global atmospheric prediction or Fluidity for pollution modelling [2,6]. In Section 2, a method will be outlined to allow a specialist of a background model to introduce high-order basis function methods without a detailed knowledge of such basis functions or high-order differentiation. The executive overview on spectral elements and other high-order methods given in this paper is sufficient to introduce such methods into a realistic background model. This will be done using geometric files, as introduced in St_Li.
For clarity, in particular for understanding the difference of polynomial interpolation and polynomial basis functions methods, the basics of polynomial algebra for models are outlined.
For each grid point, we assume the grid point values, or amplitudes of the dynamic field h to be given:
In Equation (1), are called grid-point values of the field . We want to compute the spatial derivative of the field and [7] gave a fourth-order approximation (KO formula) for :
As five points are used, we speak of a five-point stencil, the points having indices . As seen in Equation (2), the weight is 0, reducing this five-point stencil to four points. The Kreiss–Oliger formula as given in Equation (2) is applicable to regular grids (). Irregular grids, () dependent on , occur necessarily on the sphere. They require a replacement of Equation (2) by
The difference between Equations (3) and (2) is that the weights are dependent on the grid point . If the grid is irregular, the weight will be different from 0 and depend both on i and j.
Note that Equation (2) uses interpolating polynomials for the computation of the derivative and that these polynomials are different when the derivatives are computed at different points . There is not one polynomial to be used at every grid point. We speak of a piecewise polynomial representation with multiple polynomials. When following the arguments of Kreiss and Oliger (1994) [8], it turns out that also for one and the same point i more than one polynomial is used. This is illustrated in Figure 1.
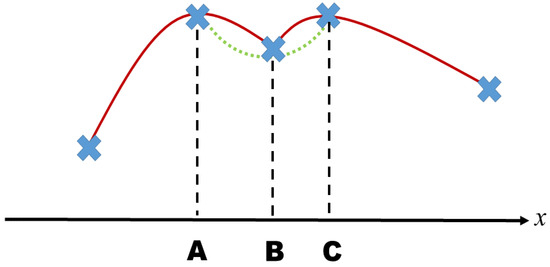
Figure 1.
Second-order differencing in the grid . The polynomials used for the differentiation of second approximation order at different grid points A, B, C. For second-order differencing at points A and C, the second-order polynomials are indicated as solid lines. The second-order differentiation at point B is carried out using the polynomial indicated as a dotted line. In contrast to this, a basis function method of second-order representation for h uses a unique interpolation, indicated as a solid line. It appears that direct differentiation is not possible at point B. The methods o2, spectral elements and the L-Galerkin method o2o2 use other means than direct differentiation to obtain time derivatives at such points. With spectral elements, points A and B are called inner collocation points and the time derivatives at such points are computed in the spectral representation (see St_Li). The objective of high-order differencing is to obtain an accuracy higher than second order, popular choices are third or fourth order. The construction of polynomials in higher than second order is similar as with second order, but more complicated. Basis function methods, such as spectral elements, o3o3 or o2o3, combine this with conservation properties, which are not present with classic o4. In addition, o3o3 and o2o3 support sparse grids, with the corresponding improvement of CPU times.
When for each point there is a unique polynomial used for interpolation, we speak of a basis function method.
For a basis function representation, we typically use discretization intervals involving more than one grid point. For second-order basis functions, we use amplitude points to describe the function values ; for this we use basis functions and the basis function representation is:
where are amplitudes, and basis functions. For local or finite element methods, we use basis functions with local support. This means that , when the distance of x and is large enough. The basis functions are piecewise polynomials with local support. For different intervals, these polynomials are different. Outside a few intervals near , are defined to be 0.
Equation (2) was derived using fourth-order polynomials. For demonstration purposes in Figure 1, second-order polynomials are used. With the fourth-order polynomials, this is more complicated but similar. There is an important point for an efficient introduction of the Kreiss–Oliger method [8] into atmospheric models. Many people apply Equation (2) without taking note of the polynomial algebra behind this. This is quite different for spectral or spectral element models. With such methods, the algebra of the basis functions is often implemented as part of the model and some modelers find this difficult to understand. In this paper, it is suggested that for spectral elements and other L-Galerkin models, the polynomial and basis function algebra is performed outside the model and the same concerns geometric relations of discretization cells. Geometric files are used to communicate such features. In this way, the transition to L-Galerkin methods in a meteorological model is not more difficult than programming centered differences.
The basis function representations are the same for the classic Galerkin method (finite elements), the spectral elements and the L-Galerkin methods (see St_Li). The required order and the demand of a minimum number of overlapping basis functions imply that the basis functions are polynomials (see St_Li). Details of the definition of the basis functions and the variants of the Galerkin method mentioned are given in St_Li. Here, we encourage the reader to implement such methods using geometric files from the internet and in Section 4 an example is given.
For classic fourth-order discretization in one dimension, Equation (2) is used for all points, and this results in a non-conserving high-order approximation of the homogeneous advection equation . For regular Cartesian grids, this readily extends to three dimensions.
Very few people will use and include the polynomial algebra leading in detail to the polynomial constructions leading to Equation (2) or (3) when creating a classic fourth-order model. In fact, it is not even necessary to understand this derivation, when creating a fourth-order model based on the classic fourth-order method. An example is the model of Kalnay [7]. The geometric files in this case consist of the . If the grid is irregular, we must use Equation (3) and the geometric file is larger, consisting of the needed to be used with irregular grids. i is the spatial index and j points to the different points of the stencil.
For the L-Galerkin method o3o3, for example, Equation (3) is the discretization formula at cell corner points. For the points on the edges, the formula is given in St_Li. They are as simple as Equation (2).
The more complicated cases of spectral elements and L-Galerkin methods involve sparse grids with triangular, rhomboidal and hexagonal grid cells, as described in St Li. In this paper, we go a step further and describe the work steps for a numerical discretization up to the point of creating a realistic model. Not only are the necessary numerical developments described, but problems of informatics also are considered. For numerical efficiency, sparse grids are used; these are most efficient in three dimensions and an example of a sparse grid is shown in Figure 2 for a cubic grid cell. The sparse grid has 7 points per cubic cell while the full grid has 27 points. A corresponding reduction in CPU time requirement is expected for a toy model exemplified in St_Li.
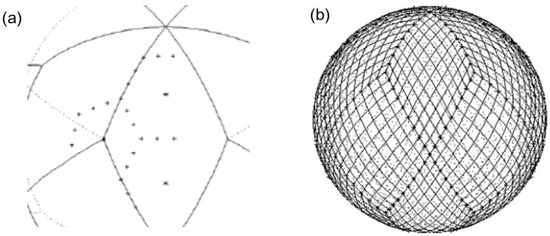
Figure 2.
Right (b): A rhomboidal cell grid in the T36/R18 solid. The T36 at the basic of this construction carries 18 rhomboidal basic spherical rhomboids, of which 6 are around the north pole and 6 around the south pole. The spherical rhomboids around the north and south poles are identical and regular. The six spherical rhomboids at the equator are also identical and regular, but not identical to the rhomboids around the poles. Therefore, the T36 is not a Platonic solid, but rather semi-Platonic. The cell structures derived from Platonic solids will be semi-Platonic, even when cubes or the icosahedron is taken as a basis. Therefore, it may be permitted to choose the basic rhomboidal structures to be semi-Platonic. Each spherical edge of a basic rhomboid is divided into nine grid intervals to obtain the cells. The left panel (a) shows a hexagonal cell structure. Triangular cells are obtained by dividing each rhomboidal cell into two triangles. For the sparse grids, the points are the corners and edges of the cells. The triangular grid is the full grid, containing all corner points of a cell structure, and this resolution is three times increased when introducing the points. Sparse grids are obtained by treating some of the points diagnostically. The right panel (b) shows a cell structure with a cell length of 1/3 of the edge of a basis rhomboid. The hexagonal grid has a reduced number of grid points, making the grid sparse. Grid points are on the edges or corners of the hexagons. The hexagonal centers do not carry amplitudes. The amplitude-carrying points in the right panel (b) are the crosses on the corners and edges of the hexagons. Only the points for one large rhomboid are shown. If the grid points for the other basic rhomboids are drawn, a full hexagonal sparse grid is created. This means that the points shown in the left panel (a) taken for all basic rhomboids of the basic solid form a compact set. The index of a point has four values, i, j, . is the index of the panel, i, j is the index of the hexagonal center and = 1, 2, 3, 4, 5, 6, 7, 8 indicates the position of the amplitude within each hexagon. h therefore has four indices: h, i, j, . The range of these indices is = (1, 2, …, 18), I = 1, …, ie, j = 1, …, ie). ie determines the resolution of the grid. In the left panel (a), we have = 1. Compact storage means that within the range of , i, j and , all values have amplitudes. Compact storage is convenient for all computers and necessary when a great deal of message passing is required.
The discretization on the sphere in this paper is carried out using the method of polygons inscribed into it and then projected to the sphere. This method is described in St_Li. Figure 2 gives an executive summary of this method. In this paper, we want to show the way to go from the grid definition towards a realistic application. This means a global or local model using realistic meteorological data.
All polygonal methods are applied using polygons inscribed into the sphere. Examples are the cubed sphere method, the icosahedral method and the T36 method. The first two are based on Platonic solids and the third, being used with the examples in this paper, is based on the T36 solid, which is semi-Platonic. When addressing a grid point, the first index is the large rhomboidal polygon which for the example of T36 is shown in Figure 2. It has a range of 1 to 18. This index is called the large rhomboid index. Each large rhomboid is divided into cells, which may be rhomboids, triangles or hexagons. Note that for a hexagonal cell structure on the sphere, there will be five pentagonal cells. While it is no problem to use unstructured cell grids, in this paper, we suggest a structured grid approach, as for a small team this is the easiest approach. In the rhomboidal approach indicated in Figure 2, the cells have indices , , both of a range , where is the number of grid points used in one direction. The sparse representations considered in this paper have grid points on the cell corners and edges. A system for indexing must be used which addresses each point only once. Using just one surface of the cell shown in Figure 3, it appears that in three dimensions there are seven points in a cell, one corner point and six edge points. It is seen from Figure 3 that the other corner and edge amplitudes in a rhomboid are defined with other cells. Therefore, the point index for the o3o3 method (see St_Li) has a range of = 0, 1, 2, 3, 4, 5, 6.
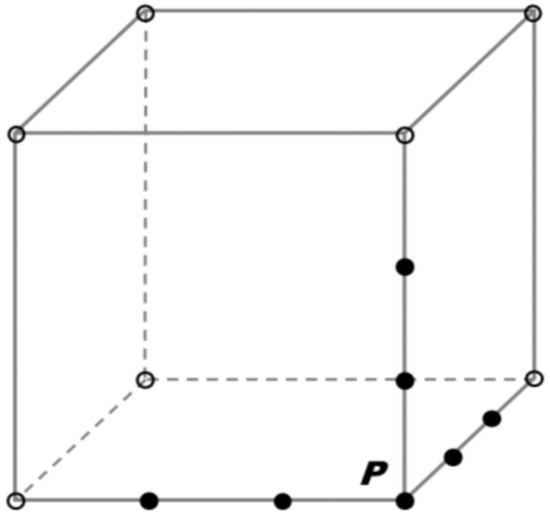
Figure 3.
A cell for 3D discretization. Each volume contains more than one grid point. The grid points form the collocation grid. A sparse grid is shown. The points for amplitude storage are indicated with black color. The white points also belong to this cell but are stored with other cells. There are 4 × 4 × 4 points in a cubic cell, some of them also belonging to other cubic cells. Of these, there are 3 × 3 × 3 = 27 independent points for amplitudes. The grid points shown for the sparse grids are only seven. Each cubic cell is indexed by i, j, k, and the points inside the cube are indexed by = 0, 1, 2, 3, 4, 5, 6. The total index is hi,j,k, . This representation provides a compact storage. This means that h is dimensioned by (0:ie, 0:je, 0:7). This is a compact storage, as all indices are used and carry amplitudes. An alternative is to dimension h by (0:3 × ie, 0:3 × je, 0:3 × ze). The figure above shows that for the second representation many points are unused. The second representation is therefore non-compact, and for computer representation, this is a severe disadvantage, as message passing may occur for points not carrying an amplitude.
, are local coordinates on the sphere. Their definition for a cell-based discretization is described in St_Li.
For a hexagonal cell structure in two dimensions, the indexing of h is similar, but the ranges of the parameters are different:
It can be seen that the different ranges of parameters in Equations (5) and (6) amount to a greater sparseness with hexagonal cells, potentially leading to more efficient methods.
The differentiation formula Equation (2) can be used when, at both sides of the target point, the grid points used in the stencil are on one straight line or great circle. For special points in the rhomboidal grid and for hexagonal corners, the differentiation stencil consists of lines meeting at a point, but not having a continuation beyond this point. In triangular grids, stencils with six legs may occur and at hexagonal corners we have three legs. Such problems will be highlighted in Section 2.
The introduction of a new numerical method into a meteorological model in the past often turned out to be difficult and took years of guest science visits at the institute running the model. The author experienced this for the example of introducing the Semi-Lagrange method into the ECMWF (European Centre for Medium-Range Weather Forecast) model in the 1980s. Faster was the introduction of the icosahedral grid into DWD’s (Deutscher Wetterdienst, Germany Weather Service) model around 2000 (the method of [9]). The latter project was fast because the icosahedral model was already prepared and the specialists of the target model (DWD) did the transfer themselves with the help of Baumgardner. In contrast to this, the adaptation of a new physics scheme into an existing model, such as a new radiation scheme, is often easier. The reason is that there is a clear interface and physics routines are often created as a subroutine, where all parameters used are calling parameters of the subroutine. To write a dynamics routine as such a subroutine is often difficult, as the dynamics is connected to the basic organization of a model, in particular, for calling all physics routines.
In this paper, it is suggested to make the import of L-Galerkin methods into a background model easier by using prepared geometric files and have all dynamics done by simple pieces of code, similar to Equation (2). For example, spectral models normally have large programs dealing with spectral transforms, etc. In polynomial approximations, the equivalent to spectral transforms is polynomial algebra, leading to the weights in Equation (2). So applying Equation (2) or (3) with pre-computed weights is a shortcut of introducing L-Galerkin methods. Corner point amplitudes are both grid point and spectral amplitudes. Equation (2) is the differentiation formula at corner points. It is suggested to make the introduction of a whole L-Galerkin model into a background model as easy as Equation (2). This is exemplified in Section 3. The working of a model using geometric files to create interfaces to a background model is explained for a simple example of cut cells in Section 4.
The L-Galerkin procedures are described in St_Li and a number of toy model tests are given there to validate them. For second-order approximations, all tools are given to go to realistic models. The scientific steps to be taken are outlined in Section 5. For third- and higher order basis functions, more fundamental problems need to be solved. These come from the spectral gap problem of spectral elements, which needs to be solved to have a proper performance. Rather similarly, another third-order L-Galerkin model, o3o3, suffers from the problem of a large 0-space. The scientific steps to solve such problems are described in Section 5. Another problem of current modelling is that new applications are envisaged. A model like Fluidity [10,11] is designed for pollution transport, but will also compute the corresponding wind fields. This is to be carried out for all scales, from the global to the micro scale, and so this model may double as a weather and climate forecast model, but also be used as an LES model. Currently, such general-purpose models do not exist, as many standard approaches for NWP models do not provide enough accuracy to be used for LES. This will be exemplified in Appendix B and Appendix D. Many numerical checks, such as the von Neumann analysis, use regular grids. If tests with irregular grids are avoided, there is a potential for overlooking model faults (see Appendix B). Section 6 suggests a simple test to be used on irregular grids. Some hints for the use of a PC for L-Galerkin numerical research are given in Appendix A. This paper explains some problems when going from highly idealized toy models on regular grids to realistic models. Appendix B explains second-order stencils and recommends a modification of the second-order stencils to remain second-order for irregular grids. This term is often neglected and this neglect results in first-order accuracy when the grid becomes irregular. Appendix D shows convergence experiments with the Fluidity model. This is one example for an almost universal neglect of this term. A notable exception is the model MPAS, which remains second- and even higher order by a special choice of the irregular grid. Appendix C shows that the classic Galerkin method loses fourth-order convergence on irregular grids.
2. Differentiation Stencils of Three, Four and Six Legs and Diagnostic Legs
The cell grid in Figure 2 has amplitudes at the corners and edges. Corners are the lines where two cell boundaries meet. The boundary lines are called edges. With grid cells, the legs of a stencil are edges and the center is a corner point. At corner points, Equation (2) can be used to compute derivatives, when the corners are inner points of a large rhomboid. By using derivatives along two different coordinate lines, divergences can be computed. These derivatives will be of first-order accuracy, because the grids along an edge line on the surface of the sphere will not be regularly divided. In this paper, we speak about lines, but the arguments are also valid for great circles.
In Figure 2, the reader is asked to imagine a triangular cell structure by dividing each rhomboidal cell into two triangles. It is seen that for such triangular cell structures, the corner points are in the center of a six-legged stencil. While such stencils have not yet been tested, there is no reason to assume that this would not work. However, the numerical expense of such six-legged stencils is double that of a three-legged stencil. Furthermore, a non-sparse or full grid would go with the six-legged stencil. This means that the standard triangular grid could be rather expensive. Comparing the right and left panels of Figure 2, we see that the dynamic points of the hexagonal grid are a small subset of the full triangular grid. Therefore, the full triangular grid carries a strong computational cost. This cost can be reduced if some of the legs of the stencils in Figure 2 are treated diagnostically. This means that the information contained in such legs is not needed for the forecast but rather is generated only at times of model output.
When considering Figure 2, it is seen that by treating some amplitudes on edges diagnostically, the rhomboidal and then the hexagonal grid are obtained, with very substantial numerical savings. Among the grids considered so far, the hexagon is the most economic to compute. The angles of the great circle forming the stencils in the hexagonal case have not been systematically explored and therefore it is not known if some stencils resemble the degenerated situation of Figure 4e, which would lead to considerable losses of computer economy by having to use small time steps. If this should be the case for some of the stencils, the solution would be to introduce diagnostic legs, shown in Figure 4 as dotted lines. In this way, potential degenerated stencils can be avoided.
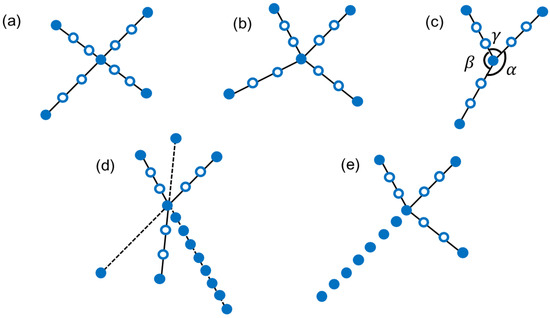
Figure 4.
Four- and three-legged stencils with corner points (black dots and edge points (+)). Some of the legs are extended by dotted lines to straight lines. (a) A 4-legged stencil where two pairs of legs extend to form two straight line stencils. For this situation, Equation (3) is directly applicable to form derivatives in the x and y directions. (b) Same as (a), but no leg aligns with another. (c) The angles , and of a three-legged stencil. These angles will determine the accuracy and stability of schemes based on such a three-legged stencil. The three angles may range from slightly above 0 to . Obviously, when one of the angles is near 0 or , the result for the derivative is very inaccurate. Until now, there exists no investigation of the accuracy and stability of derivatives taken from different stencils. Also, the distributions of such angles in hexagonal grids, as shown in Figure 2, has not yet been investigated. (d) shows as dotted lines additional diagnostic stencil lines which can be used to make the stencil a straight-line stencil and to improve the regularity of stencils such as shown in Figure 4. A three-legged stencil of the kind where extremely low accuracy is expected is shown in (e).
3. The Interface for the Connection of L-Galerkin Methods to a Background Model
This paper proposes the use of geometric files to the effect that the specialist of a background model needs to know only simple program statements, such as Equation (2), and no knowledge of geometry or L-Galerkin methods is necessary.
Grids which are totally irregular and unstructured can be used. The data management system used with such unstructured models can be used to formulate L-Galerkin methods on totally irregular grids. In this paper, the presentations are with structured grids, for simplicity. As will be pointed out in Section 5, the treatment of totally irregular grids has all scientific preliminaries performed when using second-order approximations. While three-point stencils are sufficient for this purpose, the second-order differences will use two points on each leg of the stencil. When testing this on data to produce a one-dimensional (1D) test and specialize this to two stencil legs being on a straight line, this line would contain five points. The increase in computational expense by such increase would be tiny, as each collocation point serves two corner points.
The steps to be taken to introduce a second-order L-Galerkin version of a given background model will be outlined. The procedure will for simplicity be described for a limited degree of parallelism of just 18 processors. It was shown in the introduction that h must have the cell index going from 0 to , where determines the resolution on the sphere. As with many other difference methods, we must introduce a halo of width , so that the cell index runs from to . The additional amplitudes must be obtained from other large rhomboids.
The Galerkin compiler will provide neighborhood lists and find the indices of points to be put into the halo. These lists are complicated to create, but the pieces of code to use this are not more complicated than Equation (2). Following St_Li, the interface to physics uses corner points only. This again can easily be programmed when the parameters to be used for a physics routine are contained in the data list of subroutines.
Output for plotting and archiving is obtained by transforming to a grid well known for plotting. Global maps are obtained by storing latitude and longitude at grid points. In this way, we obtain the rather popular global latitude–longitude plots of meteorological fields. For readers who want to use their own PC, Appendix A gives a short report on software needed.
For the vertical coordinate, it is planned to use the cut-cell method, even though terrain-following coordinates may also fit into the L-Galerkin framework. The spectral gap problem of spectral elements, or similarly the 0-space problem of the o3o3 L-Galerkin method, needs to be solved. The spectral gap means that the resolution is not fully usable. See more about this in Section 5.
When using rhomboidal or hexagonal cells with three independent points per edge, the cell structure shown in Figure 2 defines a grid on the earth of about 200 km. This resolution in the 1990s was a normal resolution for 10-day forecasts. At the time, this could only be achieved by supercomputers. It is assumed that such a model now fits into a normal PC. When running the same number of points on a planet with 1 km resolution, we obtain a small planet with a circumference of about 100 km. This small planet is assumed to be non-rotating and is large enough to have convection.
4. Cut Cells as an Example for the Use of Geometric Files
For an overview of the literature on cut cells, see St_Li. It is known that terrain-following coordinates have very large errors in the presence of steep mountains, and the reason is that the approximation conditions of terrain-following coordinates are very often not satisfied, and this means that, in most models, orography is parameterized rather than being discretized. Also, some versions of cut cells have not been free of errors. Steppeler and Klemp (2017) [12] showed that a cloud moving along a straight-line mountain of 45 degrees could produce large errors and this effect is named noise-producing smooth surfaces. The boundary produces small cells of irregular size and this makes some schemes less accurate. However, this is not all. The advection equation does not allow many boundary conditions. Only periodic and open boundaries are allowed. Any attempt to pose other boundary conditions with the advection equation will result in very noisy fields. In particular, the boundary conditions posed for fast waves will not be good when applied to advection. A model of passive advection using open boundary conditions is given by St_Li (Figure of STLI page 2619) and for a smooth curved boundary, the noise production of a smooth boundary is avoided. Realistic models have advection as well as fast waves. The advection must be approximated as proposed above. The open boundary condition is conserving, if the advection velocity on the surface points into the direction of this surface. Otherwise, mass may disappear or appear through the boundary.
A cut-cell model with advection and fast waves, such as shallow water or non-hydrostatic, needs a reflecting boundary in order to have the flow adapting to the surface. St_Li proposed to use the open boundary scheme for advection and for the fast waves a set of boundary conditions representing the reflective boundaries. Tests of such schemes have not been conducted, though a crude approximation of this procedure had good results concerning mountain-induced flows in a realistic model. This is an example of the difficulties to transfer cut cells to another model (Daniela Jacob GERICS, private communication). In spite of its simplicity, this seems to be a good example to see the power of geometric files for model construction. In Figure 5 for the uncut cells, the formula is as for C-grid discretization without orography. The boundary points (green) have amplitudes obtained by boundary conditions and these are different for fast waves and advection.

Figure 5.
Piecewise linear (a) and differentiable (b) lower boundaries and their effect on the cell boundaries. For the left panel, if u is a continuous function, then v must necessarily be discontinuous when requiring the velocity vector on the mountain to be in the direction of the mountain. Discontinuous basis functions are used in connection with the Arakawa C-grid. In the left panel, the white points are amplitudes for the definition of the density field h and + indicates definition points for the velocity points or . is piecewise constant in the y direction and linear in the direction, and vice versa for . is piecewise constant on the cell areas. Black points are node points of the orographic spline. The right panel shows a piecewise differentiable orographic spline. This is the discretization to be preferred with high-order L-Galerkin schemes, either spectral elements or o2o3. Dashed lines show the division of cut cells into triangles for the case. In the Fluidity model, corner amplitudes are indicated as white or green points (when they are on the orographic line). For the sake of numerical efficiency, some of the amplitudes may be treated diagnostically.
Geometric files will provide the positions of such boundary points and provide weights for differentiation and posing boundary conditions. A project is now under way to put such geometric files on a server, with the purpose that everybody can repeat cut cell experiments. In this case, it is for passive advection and later for a combination with fast waves. The grid for this first-order Arakawa C scheme with super-convergence to second order is shown in Figure 5a. An alternative to this linear basis function scheme is the right panel of Figure 5, which is suitable for high-order schemes such as o3o3 or o2o3. For this scheme, the orographic function must be a differentiable spline, here of third order. And it implies a curved lower boundary of some cells. This latter is an interesting option, but curved cell boundaries, to the knowledge of the author, have not been used.
5. Ten Scientific Project Steps towards a Realistic Forecast Model Based on Sparse L-Galerkin Method of Basis Function Orders Two, Three, and Four
This paper considers the implementation of L-Galerkin methods for realistic models. Even though, as with the Fluidity model, we want to cover all scales and applications, the 10 projects suggested here aim at a fully realistic model suitable for global forecasting. Scientific achievements, such as obtaining third and fourth order of convergence with totally irregular grids, are a sideline of this goal. Scientific steps to be taken are planned in what follows and allow to support scientific goals of the Fluidity model: pollution forecasts at small and medium scales and LES calculations. Appendix B gives an example of models not achieving more than second-order accuracy. So, as a first step, a second-order basis function approach is envisaged. The projects and improvements needed must only bring the scheme o2o2 towards the realistic case. We think of developing the L-Galerkin methods o2o2, o2o3, and o3o3. Note that until the solution of the 0-space problem, it is recommended to use o2o3 rather than o3o3, which reduces the benefits to be obtained from sparseness to a factor 4. At special points, such as the pentagonal points in Figure 2, interpolations are needed. To use such methods for totally irregular grids with interpolations would be computationally very expensive and complicated to program. Methods to do this simply by just using irregular stencils, as visualized in Figure 4, have been described in St_Li but have not yet been practically tested. The spectral element method is an L-Galerkin method which is already in practical use. Here, we concentrate on the methods mentioned above, which we want to bring to the same status of being practically applicable. The main advantage of the methods investigated here as compared to spectral elements is the use of sparse grids with the corresponding improvements of computer efficiency (see St_Li).
The following project steps serve the purpose of bringing L-Galerkin methods, such as spectral elements, o2o2, o2o3, o3o3, and o3o4, to practical use and provide the necessary tests. For descriptions of these methods, the reader is referred to St_Li. The successful completion of the following 10 projects would mean establishing the practical use of L-Galerkin methods of second and higher order, including spectral elements.
Besides global weather and climate prediction, this would open applications in pollution transport down to the micro scale and LES. Referring to St_Li, it is assumed that current global models have strong errors in the formulation of the lower boundary condition (the representation of mountains).
It was correctly pointed out by [10] in a lecture at MOW19 (The workshop of Mathematics of the Weather 2019, Bad Orb, Germany) that a basis function scheme would automatically produce a correct implementation of the lower boundary condition. In particular, the cut cells would be established. However, certain properties of the basis functions must be present for this to be true. There are two possibilities indicated in Figure 5. When the mountain is a piecewise linear spline (Figure 5a), the basis functions for velocities must be discontinuous. This follows from the fact that, at the surface, the velocity vector must be tangential to the mountain. If the velocity component u is represented by a continuous basis functions, the basis functions for the velocity component v must be discontinuous. This is necessary because, with a piecewise linear representation of the mountain, the velocity vector must make a jump at the surface.
According to St_Li, when representing the Arakawa C grid with basis functions, these are piecewise constant or linear. So the basis function representation of the Arakawa C-grid is suitable for use with mountain representations as piecewise linear splines. This is explained in Section 4. The purpose of this section is the program organization for dynamics using geometric files. The main aim of this paper is to go from second-order accuracy towards the higher (third- or fourth-) order basis functions. We will also support differentiable representations of mountains. These are shown in the right panel of Figure 5. It follows that cell boundaries are no longer straight lines, but polynomial curves. The author does not know any meteorological discretization using curved boundaries.
The suggested project steps are as follows:
- (1)
- Establish grid properties of polygonal models on the sphere in a systematic way: Polyhedral grids are based on the cube (cubed sphere), the icosahedron and the T36 solid (examples of this paper). The creation of such polyhedral models normally starts with the representation of a grid similar to that in Figure 2. When the creator is optically satisfied with its homogeneity, the program is created and the modeler hopes for sufficient stability and a reasonable CFL number. To the author’s knowledge, there exists no systematic evaluation of grid properties for the different grids based on the different polyhedral solids. It is highly desirable to create such systematic evaluations dependent on the resolution. Grid properties of interest are grid length, angles of stencils and homogeneity. The latter means the difference of good lengths in two different directions. This information can be used to get a priori information on the CFL, and badly designed stencils may be enhanced by a diagnostic stencil leg in order to enhance the CFL.
- (2)
- Solve the spectral gap/0-space problem for basis function representations of third order: The spectral element scheme has a small amplitude feature with negative group velocities at the 6 dx wave. The o3o3 has a large 0-space up to 4 dx. It seems likely that these two features are caused by the computation of the derivative at corner points. In fact, for o3o3, first experiments indicated that there is a large sensitivity of this phenomenon to different ways of computing the derivative at corner points. For o3o3, this means that the effective resolution is only that of the o2o3 scheme, still achieving a degree of sparseness and the corresponding saving of CPU time. For optimum efficiency of the two L-Galerkin schemes, it is desirable to solve these problems. There is no shortage of variants of these schemes which are worth trying. Without this achievement, it is still possible to go ahead with L-Galerkin schemes. The spectral element schemes are already in practical use (see St_Li for a review). For o3o3, it seems best to change to o2o3 currently and accept the smaller degree of sparseness. The totally irregular grid can be approached with o2o2. If the grid is formed by great circles, such as icosahedral grids, o2o3 or o3o3 can be applied. The spectral gap problem needs to be solved when a fourth- or third-order treatment is desired.
- (3)
- Approach the totally irregular grid for second-order methods. For test purposes, totally irregular grids can be approached as structured grids (see St_Li). Otherwise, a memory management scheme is necessary, as used, for example, with MPAS [5] or Fluidity [11,13]. In second-order approximation, this can be done using the tools provided in St_Li. While there is no doubt about the possibility of such applications, currently there exist no tests and these are necessary before going to applications such as Fluidity. As shown in Appendix B, the current schemes of Fluidity are somewhat below order two, and therefore second-order developments are still up to date. Due to the approximation order paradox (see St_Li), there is currently no benefit for forecast quality when going to third order with realistic models, even though toy models show such benefits very strongly. Even high-order models such as MPAS [5] are no exception due to problems of vertical discretization. Therefore, it is still interesting to improve second-order methods in practical modelling.
- (4)
- Test the 3:1 or 2:1 interface for physics interfaces. In St_Li, it was argued that with third-order methods, it would be appropriate to call the physical parameterizations only every third point. For second-order schemes, such as o2o2, and for o2o3, this would mean calling them every second grid point. Very simple 1D tests were given and it would be highly desirable to test this with realistic 3D models.
- (5)
- Test rhomboidal methods on the sphere. The Williamsson shallow water tests [13] should be conducted to gain confidence in the new L-Galerkin methods. With rhomboidal discretization, there is no problem to do this also for o3o3 or o2o3, keeping in mind the limitations of o3o3 due to the 0-space problem.
- (6)
- Test hexagonal methods on the sphere. Hexagons on the plane were tested. The program used there was so complicated that it was decided that further progress is not possible without a better compact storage for the amplitudes on the hexagon. The storage associated with the centers of the hexagonal cells is assumed to be suitable. Note that the center point stores the amplitudes but does not have an amplitude itself. The rather limited hexagonal tests given before are to be extended to the Williamsson tests.
- (7)
- Conduct 3D tests with the cut-cell scheme in second order. The quick and dirty scheme used earlier should be replaced by a conserving scheme such as that described in Section 4.
- (8)
- Extend Point (7) to third order and extend Point (5) to three dimensions on the sphere. This can be done using a resolution on the sphere of 200 km and it is expected that this would fit into a PC. For comparison, the non-conserving classic o4 method with terrain-following coordinates should be implemented and compared to the rhomboidal method for efficiency.
- (9)
- With a resolution of 5 km on the sphere, carry out one realistic case and evaluate meteorologically.
- (10)
- For the model of Point (9), carry out a series of 100 cases and evaluate statistically.
Points (1) to (8) can be performed on a PC. For some researchers, the demands on system/application programming would be a challenge. See Appendix A for some information.
Points (1) to (10) are a project plan to go to L-Galerkin applications with realistic weather prediction. Some features, considered to be nice to have, were left out, such as a realistic third-order hexagon discretization. Before Point (2) has a solution, we can have third order on the great circle horizontal grid, but the cut cells are limited to grids being formed by great circles. The benefit of computer time-saving using o2o3 in the horizontal without solving Point (2) would be limited. The same is true for cut cells, which in a first step should be approached in second order. The method o3o3 can easily be used and expected on structured spherical grids to be successful even without Point (2) finding a solution. Due to the 0-space problem, the resolution is not more than that of o2o2. For comparisons of resolutions, only the o2o2 resolution should be counted.
Still, a substantial increase in numerical efficiency is expected, which is estimated to be a factor of 4 for o2o2 on rhomboids and more with hexagons. This is also expected to be the efficiency increase compared to spectral elements.
After successfully completing Points (1) to (10), there is another benefit of a high approximation order, which could be explored together with Point (5) and then with Point (9), using artificial initial data. The purpose of a high-order approach, such as that followed with the L-Galerkin methods spectral and o2o3, is to compute a given field more accurately. Another question is how small a scale a feature of the initial value is allowed to be in order to create a reasonable forecast at all. For second order, 10 points to support a structure are often considered a good choice to create a minimum of accuracy.
It turned out in [14] that going from second order towards a third-order scheme does not only increase the prediction of a given feature, but also allows features of a smaller scale to be reasonably predicted. This essentially means that going towards a third order of accuracy should be similar as increasing the resolution. While toy models in [5] show this effect, it is consistently absent in realistic models. With all the improvements included in Points (1) to (10), it should be tested if this effect can be seen in a realistic model. In particular, the improvements introduced by cut cells could have an effect.
6. Simple Linear Tests to Be Used with Irregular Resolutions
New numerical schemes are normally tested using the von Neumann analysis. This computes the amplitudes and phases for predicted waves. It gives information on the accuracy of wave propagation and the stability of the wave as a function of wave number. This method is useful to give the critical CFL number. For irregular grids, it is suggested to add another test, also for linear propagation. Many rather popular numerical schemes show super-convergence (see Appendix C). For example, the centered differences using linear interpolation show quadratic accuracy. The classic Galerkin method with piecewise linear basis functions has fourth-order accuracy, which at the time led many researchers to believe that it is not necessary to go towards third-order basis functions. On the sphere, one particular great circle can be divided equally to obtain a regular grid. However, it is not possible to obtain a regular distribution of cells except for special cases. In particular, the rhomboidal cell structures (see Figure 2 for an example) have necessarily irregular edges. For efficient model construction, it is of great help that the gird points on rhomboidal edges line up on great circles. Such divisions of great circles on grids are necessarily irregular. So, for realistic models, irregular grids on some great circles have to be used.
For the two cases mentioned above, the super-convergence from order one to order two or order four exists on regular grids. On grids for realistic models, this super-convergence breaks down and the accuracy is less than the von Neumann analysis suggests. With linear basis functions, the loss of super-convergence means that the schemes go down in accuracy to first order. Experience has shown that much less than second-order accuracy is a disaster for practical model performance. St_Li gives an account of the literature and there are grids with a spectacular error production. If nothing is done, a typical error is that the borders of the large rhomboids in Figure 2 are seen in the results. Many researchers make the grid as near as possible to a regular grid. This procedure is called grid smoothing.
The classic o4 method of Kreiss and Oliger (see Equation (2)) can also be modified to be fourth-order for irregular grids. It was shown for the classic o4 method that no grid smoothing is necessary and when using the method in this version, Equation (3) did not result into any large errors near special points of the grid, such as the corners and edges of the large rhomboids.
Here, a test is suggested, which is still based on linear homogeneous advection, but suitable for irregular meshes. In this way, 1D, 2D and 3D tests are possible on realistic irregular grids. This test is explained in one dimension, as the extension to two and three dimensions is obvious. Tests for all scales are possible.
Let us assume that we have a discretization to compute at the grid points the time derivatives . We also need a time-marching procedure, for which, in the example given, we use the RK4 method. The grid is given as and we have . Define and let dx be the average of the . Then, we form the positive initial values:
where A is an amplitude. As the test equation is liner, the choice of A has no impact on the test result. For the test performed here, we choose 600 points for h. The homogeneous advection equation should be implemented with periodic boundary condition to allow very long forecast times.
In addition to Equation (7), we use another initial value called the point initial condition. The point initial condition is defined by having except for . The point initial value is the smallest scale initial value with only positive values. It is advisable to use for a large range of values. The author used values of = 2 , 4 , 8 and 16 . The choice of accuracy requirement is, to a degree, a question of preference. The experiments to test a second-order cut-cell scheme [12] used a value of = 8 dx for tests in two dimensions. This test can also be used in situations with boundaries, as was done by [12] where a second-order method was used with = 8 dx, which was the smallest scale to obtain reasonable results. In [14], the method was able to prove that, with the irregular resolution for cut cells near boundaries, the error dramatically increased to the effect that even a very smooth straight-line mountain generated noise and produced a “noise-generating surface”. Avoiding such noise-generating surfaces is a challenge for the construction of cut-cell schemes. Some more information on this is given in Section 4.
For third-order basis function methods, for example, already the point initial value produces meaningful results, as shown in Figure 6.

Figure 6.
Advection of the point initial condition by the o3o3 method. Left: plot of the point initial values. Right: plot after an advection over 400 grid intervals. For this very small-scale initial value, the 0-space shows as a structure remaining at the position of the initial condition and not being transported. This shows the 0-space. The non-transported feature is formed by the 0-space. Such non-transported parts of the solution vanish when the initial condition is smooth and involves more than one grid point, meaning initial values derived from Equation (7). The transported part of the solution, though showing strong dispersion and a loss of amplitude, has some forecast pow-er. (a) shows the initial values and (b) the forecasted field.7. Conclusions.
A review of the high-order basis function L-Galerkin methods was given. Arakawa methods can be seen as L-Galerkin methods using low-order and discontinuous basis functions. This scheme is included in our considerations. While the practical application of such schemes is well under way and shows advantages over classic schemes (see St_Li), a number of problems need to be solved to take full advantage of L-Galerkin schemes. For spectral elements, this is the spectral gap problem and for o3o3, it is the problem of a large 0-space. For o3o3, the 0-space problem can be solved by using o2o3 instead, which would reduce the numerical efficiency increase from sparse gridding. When a model aims to the full range of applications from the global to the micro scale, a totally irregular grid is desirable, as is done for Fluidity. L-Galerkin methods are easy to implement on grids of great circles. They can reach a third or fourth order of accuracy there, when there are only few points of irregularity, such as the edge lines of large rhomboids. For totally irregular grids, L-Galerkin methods of second-order basis functions are possible and efficient. Doing the same for third-order basis functions is possible when the large 0-space problem is solved. The small irregularities of grids arising from the curvature of the earth are no problem for either spectral elements or o3o3, for example. For triangular meshes, such as those used with Fluidity, sparseness, with potential CPU savings of up to a factor 20, can be realized by treating some of the edge amplitudes as diagnostic. Without diagnostic edges, triangular cells imply the full grid.
For the above considerations and methods on totally irregular grids, there is the possibility of using high-order interpolations to a regular stencil. This method is not elegant and seems very expensive. Such methods are not considered here.
Methods based on centered differences are still in use and often reduce to first approximation order when the grid becomes irregular. Grid smoothing is a way to make such deviations from the second order small. In this paper, it is suggested to go to genuinely third- or second-order methods, which do not need grid smoothing.
The representation of mountains is rather inaccurate with terrain-following methods, as the condition of the coordinate transformation is often not satisfied. It is true that methods using basis functions on cell structures naturally imply the cut-cell approximation. To represent the boundary condition on mountains correctly, either the basis functions for the velocity components need to be non-differentiable or the spline representing the orography must be differentiable. For the first method, an example was given in Section 4. Differentiable splines imply that cells bordering the mountains have curved boundaries, as shown in Figure 5. In meteorology, the author does not know about any use of such curved cell boundaries (not being straight lines), though such curved lines seem rather easy to handle. The earth without orography uses curved (great circle line) boundaries. However, such curvature disappears when using great circle distances as coordinates.
Funding
This research received no external funding.
Data Availability Statement
For the test cases shown, it is intended to put the geometric files on Huckert.com.
Acknowledgments
The author thanks Pu Gan and Jinxi Li for technical help with this paper. The plots in Appendix D about the accuracy of the Fluidity models in irregular grid situations were provided by Li and Gan. E. Huckert is thanked for information in connection with Appendix A and for the installation of programs on the author’s Apple computer as well as on the ECS server (see St_Li). The author thanks J. Klemp for his remarks on the proof in Appendix C. In particular, he followed the proof in detail and found it correct. This paper is a planning paper with the purpose of going to high order in practical modelling without falling into traps pointed out in this paper. This project is well prepared on the level of toy models (see St_Li). The author thanks Jinxi Li, Fangxin Fang and the other staff at the Institute of Atmospheric Physics, Chinese Academy of Sciences, and the Fluidity group of Imperial College London for their help so far.
Conflicts of Interest
The author owns a company with the purpose to create geometric files for discretization. Until now, however, all files were used for scientific purposes only and were provided free of charge.
Appendix A. Programs for Atmospheric Modelling on PCs
When giving overviews on NWP for larger audiences, every self-respecting lecturer points to the fact that most telephones and PCs have a computer power comparable to a supercomputer in the year 2005. It is another matter to try and install meteorological models on a PC. Let us consider a Fortran-based meteorological model running in a UNIX environment. A number of PC systems are UNIX-based and so it is easy to open a UNIX window on such computers.
The grid shown in Figure 2 (left panel) with three collocation points on each edge of cell has a resolution of 200 km, which in 1980 was considered a good resolution on a mainframe computer. Therefore, it seems appropriate to try modelling on a PC. Resolutions between 1 and 10 km can then be tested by transferring to a mainframe computer. Time on such computers may be available, if by means of tests on a PC, a model is already established.
The methods reviewed and suggested in this paper avoid fancy plotting. A minimum requirement for running models on a PC is as follows:
- -
- A Fortran compiler;
- -
- A plot routine drawing the line between two given points;
- -
- A plot routine to draw curves;
- -
- A plot routine for isolines.
The author used the Gnu compiler and Gnuplot. The plot program has many features beyond the above minimum requirements.
Many young scientists have no problems to install these programs. This appendix is not for them. The author was used to developing programs on mainframe computers, where the software was installed by IT departments. Such IT departments tend not to install software on private computers. For the non-specialist, the installation of such programs can lead to amazing problems.
It is intended to put some of the software needed for the examples described here on the server ECS (see St_Li) which is publicly available.
Appendix B. The Order of Approximation of Models Based on the Finite Volume Method
In the simplest case, a grid with a field in second order, we compute the derivative of h by
In Equation (A1), w can be computed according to St_Li or given by a geometric file. Testing this equation on any analytic test function will result into second-order convergence. The finite volume formula shows small differences to Equation (A1); the main purpose of such differences is to achieve conservation, in this case for mass. When using a regular grid , it turns out that . As many tests of numerical schemes are on regular grid, very often the middle term of Equation (A2) is omitted and it is used in the form:
For irregular meshes, Equation (A2) is wrong and the error can be large when the difference of to a regular grid is large. In St_Li, the literature is surveyed and there are examples of spectacular errors, which can be avoided by using Equation (A1) rather than Equation (A2).
A disadvantage is that for homogeneous advection, Equation (A1) does not lead to a formal conservation of mass. However, there are modifications, which make Equation (A1) conserving (see St_Li).
The use of Equation (A1) rather than Equation (A2) is highly recommended. This means that good results are achieved on all grids and grid smoothing is no longer necessary. For third- and fourth-order differencing, the situation is similar and it is recommended to switch to Equation (A1).
Appendix C. The Loss of Super-Convergence of the Classic Galerkin Finite Element Method with Irregular Resolution
The classic Galerkin method is known to converge in fourth order [15] with piecewise linear basis functions. This proof was obtained for regular resolution, as is the case for many tests. As realistic models necessarily use irregular resolution, there is the danger that realistic models are less accurate than indicated from regular resolution tests.
We investigate the approximation of the derivative of the function f. Without loss of generality, we assume , with i being the imaginary unit and k the wavenumber. We have and investigate the accuracy of approximations at the grid point , with neighboring points being and . We define and . For the definition of the finite volume and finite element approximations, we refer to St_Li. Supposing , we obtain the following:
- (1)
- The finite volume method is defined as:
- (2)
- The finite element classic Galerkin approximation of the derivative of a function f(x) uses functional approximations of f and where and . In the above expressions, is the piecewise linear hat function, being 1 at and 0 at all other grid points. The Galerkin approximation equation is:
Equation (A5) has no solution, but the weak form of Equation (A5) has a solution, being called the Galerkin equation. The weak form of Equation (A5) is obtained by multiplying with and integrating over x:
So the Galerkin approximation with linear basis functions is:
Considering the case of finite volume Equation (A4), for a regular grid () the cosine terms in Equation (A4) compensate to result into 0 and putting in the power series . We obtain from Equation (A3):
The first term is the analytic solution and the second term is proportional to . As is well known, this is a second-order error term which makes the scheme second-order-convergent. For irregular grids, assume , with the factor g indicating how irregular the grid is. For the results in this paper, we assume g = 1.5. Using the Taylor series for , which after division by becomes a first-order error term. We see that for the irregular case, super-convergence to second order is lost and the scheme becomes first-order.
First order is not considered accurate enough for meteorological modelling. Because the finite volumes are rather popular with models and on the sphere regular grids do not exist, much effort has gone into making grids on the sphere as regular as possible by means of grid smoothing [16].
The same analysis as performed for Equation (A3) can be performed for Equation (A7) for regular dx. After dividing through the factor on the left-hand side of Equation (A7), the function must be developed into a power series around . Then, the lowest error term is at least second-order. For irregular grids again, we get a first-order error term. The result is that for the classic Galerkin method, super-convergence to second order is lost in the same way as was the case with finite volumes.
Note that for the regular grid case: . The factor to be applied to the right-hand side of Equation (A7) is . When now developing the right-hand side of Equation (A7) into a power series and dividing through , we see that the second-error term in Equation (A7) is cancelled, making the scheme fourth-order-accurate [15]. This means that the classic Galerkin scheme with linear basis functions for regular grids has a better approximation order than centered differences. When the grid is irregular, the classic Galerkin method is not better than finite volumes in respect of convergence. This produces an inhomogeneous approximation order at internal and external boundaries when using linear basis functions. This unfortunate effect is of course absent when using third-order basis functions, which has been demonstrated for the slightly modified Local-Galerkin scheme “spectral elements”.
As finite elements on regular grids show super-convergence to fourth order, we have an inhomogeneous order of approximation (St_Li) going from fourth to first order at points where the resolution changes. This was shown in a practical way by [16]. This means that for irregular grids the fourth-order super-convergence does not apply. In order to see the practical effect, Figure A1 shows a convergence diagram for the case g = 1.5.
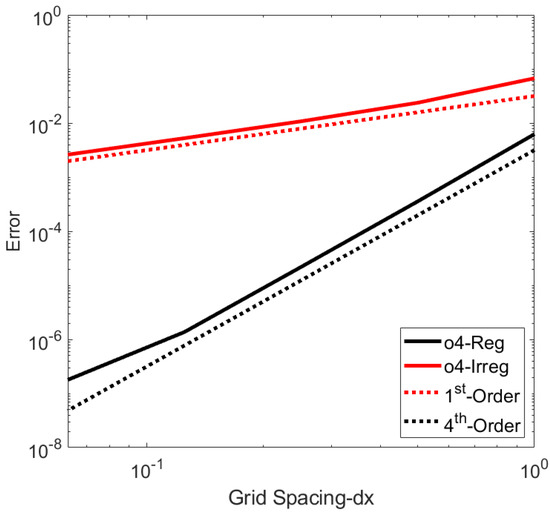
Figure A1.
Error of the computation of the derivative function of dx for the classic Galerkin method for regular and irregular grids. With regular resolution, we have super-convergence to fourth order and for irregular resolution, we have first-order convergence.
Appendix D. Convergence of Advection with an Irregular Mesh in the Model Fluidity
We have seen in Appendix B and Appendix C that for irregular grids the accuracy of some popular schemes goes down when the grid becomes irregular. We take the example of the model Fluidity. This model is intended for pollution transport. However, when the transporting velocities are computed in the same model, it may well be used for general predictions from the global to the micro scale. For applications in urban environments, the resolution may be very irregular, and therefore Fluidity supports triangular cell structures of total irregularity. If this is performed with high accuracy, there is no limit to the research opportunities using Fluidity, including LES calculations. Tests on regular grids for Fluidity result into fast convergence. Here, we choose a test which involves irregular triangular cells, such as those occurring with the cut-cell discretization.
As this model is constructed similarly to many others and uses linear basis functions, we expect a breakdown of approximation to first order with irregular meshes for all similar models. As a test, we use the advection of a structure along a mountain which is a straight line. The grid is regular nearly everywhere. Only at the lower surfaces is it irregular. Other models are expected to give similar results, as many are constructed in the same way. This demonstrates that further developments are necessary, as a convergence not much less than second order is necessary for models to be useful in practice. The straight-line mountain test was introduced by [12].
Fluidity has four numerical methods currently implemented and here we use the method called discontinuous Galerkin (DG), which produces best results. A circular 2D structure is advected along a straight mountain. The error goes down for smaller grid lengths, but this convergence is not larger than linear, according to Table A1. The error goes down for decreasing dx by a factor ½ not more than 1/2. For advection in the inside of the area, we have second-order convergence, meaning a decrease of error by 1/16 when the grid is reduced to 1/4. As LES calculations require fourth-order schemes, the numerics must be changed when aiming for LES applications. This means that the accuracy must be increased if LES computations are planned.
From Figure A2 and Table A1, it appears that the Fluidity model has a problem when the lower boundary condition is irregular. In this respect, Fluidity is not different to most other models. The reader is reminded that the Fluidity model, like many models of a similar kind, has been used for realistic applications in a grid setting where the grid boundaries are rectangular. A small irregularity of the lower boundary can be introduced by terrain-following coordinates. This approach is limited to rather smooth orography and not to steep mountains, as used in Figure A2. Realistic pollution transport applications using Fluidity in rectangular areas were described in St-Li. The terrain-following coordinate is known to be responsible for large errors including the occurrence of thunderstorms driven by numerical errors with a horizontally stratified stable dry atmosphere (see St-Li). Another practical application with the Fluidity model in a rectangular model area is given in Figure A3, where the development of a moisture-driven supercell is shown.

Table A1.
The error after 100 s for grid lengths 2, 4 and 8 m.
Table A1.
The error after 100 s for grid lengths 2, 4 and 8 m.
| 2 m | 4 m | 8 m |
|---|---|---|
| 0.049 | 0.072 | 0.111 |
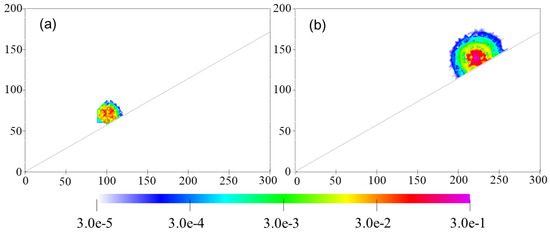
Figure A2.
The advection tests along a straight-line mountain using DG; the error at time 1 s and 100 s is shown. This error is concentrated near the position of the cloud, which for some of the less performing schemes of Fluidity is not the case. The interest of this test is the decrease in the error with increasing resolutions. This is shown in Table A1 and it shows linear convergence, where with regular grids (away from the surface) we see second-order convergence.
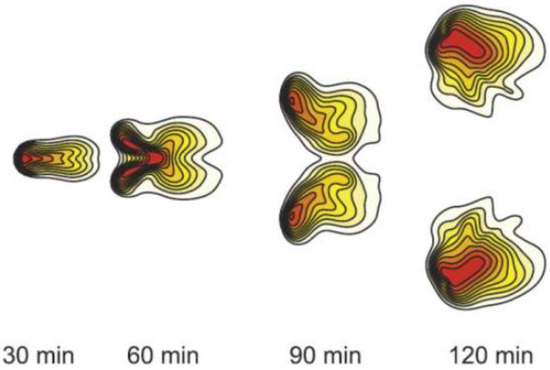
Figure A3.
A supercell simulation by the model Fluidity, showing relative moisture (red = 100%, white = 0%). A cross section at 500 m is shown.
The examples above show that the model Fluidity performs well in rectangular model areas but has problems in the presence of a steep lower boundary. This is similar for most models of this kind. Figure A2 shows that the problems occur even when the mountain is not curved.
The last result, given in Figure A4, shows that the method o2o2, using basis functions of piecewise second-order polynomials, is able to treat curved lower boundaries and is able to advect a cloud along such a boundary.
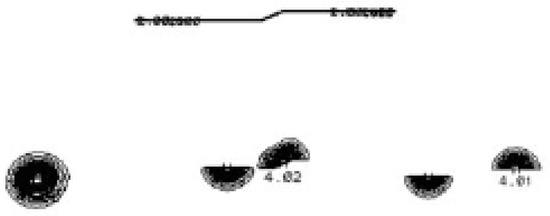
Figure A4.
Advection of a 2D cloud along a curved lower boundary. Note that we have the slip boundary, where the velocity is different from 0 at the boundary. The orography has the form of a ramp and the velocity at the surface is parallel to this ramp. The advection of the cloud follows this ramp. This indicates an error much smaller than that shown in Figure A2, even though the situation is more difficult, not being a straight line.
References
- Charney, J.G.; Fjortoft, R.; Von Neumann, J. Numerical integration of the barotropic vorticity equation. Tellus 1950, 2, 237–250. [Google Scholar] [CrossRef]
- Steppeler, J.; Li, J. Mathematics of the Weather, Springer Atmospheric Sciences; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Durran, D.R. Numerical Methods for Fluid Dynamics: With Applications to Geophysics, 2nd ed.; Springer: New York, NY, USA, 2010; pp. 35–146. [Google Scholar]
- Herrington, A.R.; Lauritzen, P.H.; Taylor, M.A.; Goldhaber, S.; Eaton, B.E.; Reed, K.A.; Ullrich, P.A. Physics-Dynamics coupling with Element based high order Galerkin methods. Mon. Weather Rev. 2019, 147, 69–84. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.B.; Duda, M.G.; Fowler, L.D.; Park, S.H.; Ringler, T.D.A. Multiscale Nonhydrostatic Atmospheric Model Using Centroidal Voronoi Tesselations and C-Grid Staggering. Mon. Weather Rev. 2012, 140, 3090–3105. [Google Scholar] [CrossRef]
- Zheng, J.; Fang, F.; Wang, Z.; Zhu, J.; Li, J.; Li, J.; Xiao, H.; Pain, C.C. A new anisotropic adaptive mesh photochemical model for ozone formation in power plant plumes. Atmos. Environ. 2020, 229, 117431. [Google Scholar] [CrossRef]
- Kalnay-Rivas, E.; Bayliss, A.; Storch, J. The fourth order GISS model of the global atmosphere. Beitr. Phys. Atmos. 1977, 50, 299–311. [Google Scholar]
- Kreiss, H.O.; Oliger, J. Comparison of accurate methods for the integration of hyperbolic equations. Tellus 1954, 24, 199–215. [Google Scholar] [CrossRef]
- Baumgardner, J.R.; Frederickson, P.O. Icosahedral discretization of the two-sphere. SIAM J. Numer. Anal. 1985, 22, 107–115. [Google Scholar] [CrossRef]
- Pain, C.C.; Umpleby, A.; Oliveria, C.R.E.; Goddard, A.J.H. Tetrahedral mesh optimisation and adaptivity for steady-state and transient finite element calculations. Comput. Method Appl. Mech. 2001, 190, 3771–3796. [Google Scholar] [CrossRef]
- Li, J.; Fang, F.; Steppeler, J.; Zhu, J.; Cheng, Y.; Wu, X. Demonstration of a threedimensional dynamically adaptive atmospheric dynamic framework for the simulation of mountain waves. Meteorol. Atmos. Phys. 2021, 133, 1627–1645. [Google Scholar] [CrossRef]
- Steppeler, J.; Klemp, J.B. Advection on cut-cell grids for an idealized mountain of constant slope. Mon. Weather Rev. 2017, 145, 1765–1777. [Google Scholar] [CrossRef]
- Williamson, D.L.; Drake, J.B.; Hack, J.J.; Jakob, R.; Swarztrauber, P.N. A standard test set for numerical approximations to the shallow water equations in spherical geometry. J. Comput. Phys. 1992, 102, 211–224. [Google Scholar] [CrossRef]
- Gassmannn, A. Numerische Verfahren in der Nichthydrostatischen Modellierung und Ihr Einfluss auf die Niederschlagvorsage; Berichte des Deutschen Wetterdienstes: Offenbach, Germany, 2002; Volume 221. [Google Scholar]
- Cullen, M.J.; Morton, K.W. Analysis of evolutionary error in finite element and other methods. J. Comput. Phys. 1980, 34, 245–267. [Google Scholar] [CrossRef]
- Tomita, H.; Tsugawa, M.; Satoh, M.; Goto, K. Shallow water model on a modified isosahedral geodesic grid by using spring dynamics. J. Comput. Phys. 2001, 174, 579–613. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).