1. Introduction
With the evident advancement in the development of autonomous vehicles (AVs), attention is being paid to the risks associated with their road operation [
1,
2]. Efforts have been made to increase the performance of existing navigation systems by improving the sensitivity of sensors and the accuracy of image recognition models. Moreover, research work in this field also focuses on enhancing the robustness of these systems and enabling their operation in various adverse weather conditions. Recent works have been dedicated to evaluating the performance of advanced driver-assistance system (ADAS) devices, such as RADAR, LiDAR, cameras, and ultrasonic sensors, exposed to adverse weather conditions, such as fog, heavy precipitation, sandstorms, and low light [
3,
4]. As cited by Vargas et al. [
5], raindrops, depending on their size, can attenuate electromagnetic signals emitted by navigation systems, generate false alarms, and mask real targets in front of sensors due to Mie scattering [
6]. In addition, snow can degrade the quality of images and videos by generating sharp variations in light levels, as camera-based recognition systems rely on the brightness of the surroundings to determine the intensity of the pixels. Despite these issues, there is a noticeable shortfall in research focusing specifically on snow accumulation on the surfaces of a moving vehicle, impacting the use of these systems. Work related to this topic has focused on the field of aviation, as icing has proved to be the cause of numerous incidents [
7]. Given the relative gap in studying snow accumulation on a moving vehicle’s surfaces, as well as the relation of accumulation with visibility, this type of research deserves attention. Recently, Jokela et al. [
8] conducted studies in Finland and Sweden to assess LiDAR functionality, especially regarding snow swirls generated by leading vehicles. Norouzian et al. [
9] explored the impact of snowfall on radar performance, observing increased signal attenuation with higher snowfall rates, particularly with wet snow, due to its greater water content and larger snowflake size. In a field study conducted by Hong et al. [
10], the RadarSLAM system’s outdoor trials aimed to evaluate its performance in adverse weather, such as fog and snow, and at night. The main objective was to test the system’s positional accuracy and its capacity to produce precise maps despite the environmental obstacles caused by bad weather. Based on the observations in this study, substantial snow accumulation was observed on cameras, LiDAR, and RADAR, which posed significant operational challenges.
These studies aimed to directly investigate the impacts of weather conditions (herein snow) on various navigation systems but did not attempt to model the driving parameters of the problem, which, in this case, is snow deposition. In order to generate such a model, precipitation measurements are needed in a pre-defined parametric space for the problem. Precipitation measurements may seem simple: water lands in a collector and the observer gauges the depth, volume, or weight, either manually or through automated methods. For rain, this is mostly accurate, barring minor errors like wetting loss and evaporation. However, gauging snowfall and snow depth is a far more complex process. The environment significantly influences snow measurements compared to rain. For instance, local wind conditions have a greater impact on the accuracy of snowfall sensors, as lighter, slower-falling snow hydrometers are more susceptible to wind-induced turbulence around the gauge, leading to significant systematic errors in the precipitation rate output. In addition, snow depth is subject to unique challenges due to factors such as redistribution, the transfer or displacement of snow from a specific location to another, and metamorphosis, i.e., the change in snow crystals or granules over time, in the measurement environment. These factors lead to significant variability both spatially and temporally [
11].
The density of freshly fallen snow is a crucial physical attribute of deposited snow, which undergoes changes upon reaching a surface. For windless conditions, the snowfall density is believed to be primarily influenced by hydrometeor types and dimensions. Snowpack moisture content determines the type of snow particle [
12,
13,
14,
15]. Characterized by a low density that seldom surpasses 100 kg/m
3, dry snow gathers under low-wind-speed conditions, generally below 2 m/s, and at sub-zero temperatures. In such circumstances, the fraction of liquid water is under 5%, and over 70% of the total volume consists of air bubbles. Typically, wet snow is produced when dry snowflakes, formed at below-freezing temperatures, undergo a swift transformation in supercooled clouds. This snowfall crosses the 0 °C isotherm, entering a layer of atmospheric air with a positive temperature. The longer these snowflakes remain in this warmer layer, the higher their stickiness becomes due to the water layer that is formed on their surface. In general, denser snow is more cohesive and sticks better to the underlying layers. Another variable that contributes to the adhesion force between a given surface and wet snow is the liquid water content (LWC), which refers to the percentage of the total weight of wet snow that is water. This has been the subject of various research works aimed at investigating snow morphology [
16,
17,
18,
19], forecasting wet snow avalanches, and predicting melt-water runoff. There is a lack of research into how the liquid water content in snow behaves on a moving car under different weather conditions. Snow density is also linked to other factors, like the structure of snowflakes. By understanding the LWC and density, among other factors, such as wind speed, hourly precipitation, temperature, and solar radiation, it is possible to predict, with some accuracy, the accumulation of snow on moving surfaces.
Over the past few decades, much work has been carried out on the numerical prediction of snow accretion. Many of these studies are oriented towards static bodies such as buildings and structures. Loading caused by snow on roofs was studied by Zhang et al. [
20] using data from experiments and numerical simulations. A numerical model for snow melt and accumulation was proposed using energy and mass balance principles [
21,
22]. Qiang et al. [
23] expanded upon this work by employing this numerical model for snow accumulation on steel roof structures subjected to snow loading using a probabilistic Monte Carlo approach. In CFD models, the amount of snow build-up is commonly calculated using dynamic mesh [
24,
25,
26,
27] or through surface contour plots [
28].
Models of snow accretion on structures generally aim to estimate ice loads that can be generated during storms. Most of these works focus primarily on modelling snow accumulation on power cables, as this is the major cause of structural problems observed on transmission towers [
29,
30,
31]. Because of this, the existing models deal with the issue exclusively on cylindrical geometries and calculate the total snow load per unit length [
32,
33]. Other studies used wind tunnel and in situ observations to understand the microphysics of wet snow and the thermodynamics of heat exchanges, as well as the mechanisms of snow accretion on cylindrical objects. Mohammadian et al. [
34] investigated wet snow accumulation on torsional rigid inclined cylinders, such as bridge cables, correlating the snow density and thickness of inclined cylindrical surfaces with outdoor weather conditions. Recently, Davalos et al. [
35] developed a model for predicting ice loads on power lines by combining wind and precipitation data from weather stations distributed across a mountainous region of British Columbia, Canada. To estimate ice accretion in locations not easily accessible, they drew correlations between data obtained at nearby stations using machine learning. For the spatial estimation of wind speed, they used an artificial neural network (ANN) model [
36], while K-Nearest Neighbour Imputation (KNNI) was employed for predictions of the precipitation rate [
37].
In order to design an analytical model for automotive applications, it is necessary to consider a larger range of parameters more in line with the operating conditions of autonomous vehicles, such as local particulate flux and varying relative wind direction, surface inclination, and surface roughness. Once such models are developed, they can be complemented with spatial and temporal correlation analysis to allow for snow accumulation predictions on various surfaces of a moving vehicle. Downstream, these models can be linked with visibility models predicting where and when sensors on AVs are affected in relation to driving safety criteria. Finally, these models need to be experimentally validated.
The challenge of simulating snow environments in wind tunnels, in contrast to rain, limits the controlled data support needed to drive the accretion models, restricting progress in this field [
3]. Snow accretion studies in wind tunnels are different from those under in situ conditions when a moving object is involved due to both particulate injection methods (ranging from snow guns to ice shaving methods) and the aerodynamic differences [
38].
Recent studies have concentrated on in situ snow conditions on moving car surfaces. Carvalho and Hangan [
39] developed a method based on unsupervised machine learning to classify snowfall events. The model clusters particle size distribution samples obtained from full-scale weather measurements in order to identify recurring precipitation patterns in southern Ontario. The proposed method enables realistic snowfall simulations both numerically and in climatic wind tunnels.
In conclusion, while snow accumulation on static bodies or surfaces with applications to buildings and structures has been widely studied over the years, there is still an important gap regarding this accumulation on moving bodies with applications to vehicles. This paper proposes an analytical model for snow accretion on moving surfaces, which can serve as the basis for a network of low-cost meteorological towers for monitoring the impact of heavy snowfall on autonomous vehicles on nearby roads. Some preliminary results are presented, and future validation is planned through both wind tunnel and full-scale measurements.
2. Snow Accretion Model
As observed by Kobayashi [
40], snow deposits occur under specific weather conditions. Dry snow, for example, represents a reduced risk in terms of accumulation, as the particles tend to bounce when they hit a surface. When accumulation occurs due to the low relative velocity between the given surface and the precipitation, there is no adhesion between the particles within the snow cover. To maintain cohesion between particles, they must be covered by a layer of water, as in the case of wet snow. Because of this, before estimating the snow cover growth rate, Makkonen [
30] defined criteria for wet snow formation, where the heat flux on the snow particles surface must be positive. The mathematical formulation is as follows:
The two major terms of the heat flux equation between the air and the snow particles are the convective heat,
and the evaporative heat,
where
h is the convective heat transfer coefficient,
is the air temperature and
is the snow surface temperature,
is the ratio of the molecular weights of water vapour and dry air,
is the latent heat of sublimation,
is the specific heat of air, and
p is the atmospheric pressure. The water vapour pressure in the air and at the surface of the snow particle is represented by
and
, respectively. Also, the relative humidity can be written as
. Therefore, by considering the temperature at the surface of the particles
and the melting temperature of the snow and inserting Equations (
2) and (
3) into Equation (
1), the condition for wet snow formation takes the form:
which means that the occurrence of wet snow can be described as a function of temperature and relative humidity. Wet snow forms at different temperatures according to different viewpoints. According to Admirat [
41], wet snow occurs only at temperatures between 0 °C and 2 °C. The heat transfer calculations of Makkonen [
30] have also shown that wet snow accumulates at wet bulb temperatures greater than zero. Afterward, he adapted his claim to values greater than −0.2 °C [
42]. Finstad [
43] proposed that wet snow occurs in conditions where the air temperature is in the range of −2 °C <
< 5 °C, which was later verified by Mohammadian et al. [
34], and a threshold percent relative humidity:
As wet snow presents higher density values than dry snow due to its water content, long-lasting wet snowstorms place a greater risk of collapse on structures such as electricity transmission lines and bridge cable supports. Wet snow is also critical for accumulation on moving body surfaces. It is therefore critical to establish a reliable criterion for the occurrence of wet snow based on real-time on-site weather data. From full-scale measurements conducted at GM’s McLaughlin Advanced Technology Track (MATT) in Oshawa, Canada, throughout the winter of 2021–2022, relative humidity and ambient temperature were assessed specifically for tests conducted under snow precipitation conditions to ascertain the above-mentioned wet snow criteria. This experiment was carried out using a test vehicle equipped with weather sensors, as described by Carvalho and Hangan [
39].
Figure 1 illustrates that the experimental data closely align with both criteria, most noticeably the one from Makkonen [
30]. The scatter of data points from the two test days differs, indicating that on March 15th, when temperatures were higher, the snow exhibited greater wetness compared to the snow on March 7th.
Once the criterion is met, the model describing the growth of the snow layer over the surface is a linear equation, as defined by Makkonen [
30]:
where
I is the growth rate of the snow mass,
is the sticking efficiency,
is the speed magnitude at which the particles reach the surface, and
W is the concentration of the snow mass in the air. When dealing with AVs, the values of the resulting particle speed vary as the vehicle modifies its trajectory and the wind speed and direction change. Because of this, Carvalho and Hangan [
44] proposed a model to estimate the rainfall/particulate intensity perceived by moving vehicles. The aim of the work was to analyze the level of precipitation on surfaces with different angles and nonlinear trajectories. For this, the flux of precipitation
, in kg/s, of precipitation particles with the velocity
on a given surface
S is computed:
Equation (
7)’s negative sign comes from flux equations of electromagnetism. The model is inspired by the work of Bocci [
45], who simulated rainfall levels on moving objects with complex geometries. In the adapted equation for rain flux,
is the water density in kg/m
−3,
is the concentration number with the unit m
−3, and
V is the total volume of the particles. These parameters quantify the mass of precipitation impacting the surface. The total volume can be approximated by considering the particles as spheres [
46], and the concentration number
can be obtained through disdrometer data [
47]:
where
is the number of particles of each diameter bin of the particle size distributions. The particles’ average velocity
can be computed from speed distributions also generated by optical disdrometers. The integral term contained in Equation (
7) represents the projection of the resulting particle speed, which is the sum of wind speed and particle terminal velocity, on the vector normal to the surface. For more details on the implementation of the precipitation flux model, see Carvalho and Hangan [
44]. A parallel between Equations (
6) and (
7) can be drawn, and the model for the snow cover growth rate, in kg/s, can be written as follows:
The
coefficient is introduced to model the effective growth rate of the snow layer and will be discussed next. In the case of snowfall, estimating the density of the particles is a more complex task, as it depends on their LWC [
16,
48]. For this reason, empirical models, such as the one proposed by Best [
49], have been established to assess the concentration of snow particles in the air:
with
W in kg/m
3 and
being the recorded precipitation rate in mm/h. Admirat [
41] proposed another concentration model based on the assumption that snow density is influenced by both the precipitation intensity at ground level and the terminal velocity of snowflakes.
where
P is the precipitation rate at the ground in mm/h of water equivalent, and
is the terminal velocity of snow in m/s. Another widespread model [
50] relates mass concentration to visibility, with
in meters:
In Equation (
9), since all parameters, except
, can be obtained experimentally, the challenge for predicting snow accretion on vehicles is to model the effective growth rate for different types of snow particles for surfaces with various angles and roughness. In order to adjust
more accurately to the interactions between the incoming snow particles and the formed snow layer, Makkonen [
51] expanded the coefficient into three new terms, denoted by
,
, and
, the values of which can vary between 0 and 1. The first one represents the collision efficiency between particles in the air and a given surface. Its value is obtained from the ratio of the flux density of particles hitting the object to the maximum flux density.
is the sticking efficiency, which represents the number of particles that remain stuck to the surface among those that have collided with it. A particle is considered to be aggregated if it remains in contact with the surface for long enough to affect the heat flux in the forming snow layer.
refers to the accretion efficiency, which is the ratio of the icing growth rate to the flux density of the aggregated particles. The work by Mohammadian et al. [
52] incorporated the coefficients into a model for predicting snow accumulation on a given flat surface
A. The new equation, which is derived from Equation (
6), takes the following form:
By combining Equations (
9) and (
13) to conform to the scenario of a moving referential, the model for snow accumulation on vehicles becomes
Next, the efficiency coefficients will be discussed individually in order to devise methods for modelling them based on a set of planned experiments.
2.1. Collision Efficiency ()
For the estimation of collision efficiency
, the dimensional analysis of an air flow over an inclined flat plate of length
l is adopted, in a similar approach to that used by Keith and Saunders [
53] and Makkonen [
51] for the case of the flow over a cylinder. The adaptation of the problem considers the impact of snow particles on the surface of the vehicle at low speed.
Figure 2 shows a representation of a snow particle within the boundary layer of a unidirectional air flow considered to be laminar and fully developed. As a starting point for identifying the main parameters of the problem, the equation for the velocity profile in the surface boundary layer is derived. It is assumed that the particle velocity is composed of the sum of the wind velocity
and the terminal velocity
. Making the simplifying assumptions of a steady-state regime and that the pressure drop due to the surface slope is negligible, the following equation can be obtained:
where
is the boundary layer thickness, and the air density and viscosity are represented by
and
, respectively. It is well known that the boundary layer thickness can be approximated by analytical equations and depends on the Reynolds number, even for inclined surfaces [
54,
55]. So far, it is assumed that the particles are small enough not to disturb the flow, as in the work of Böhm [
56,
57], who derived an analytical solution for atmospheric particle collision. However, their terminal velocity must be considered as they become larger. Estimating the terminal velocity of weather precipitation particles is challenging, but studies in controlled environments show that these values can be approximated through empirical equations that are functions of the diameter only [
58,
59].
It can be stated that the flow velocity within the boundary layer is a function of the surface angle
and the incoming air velocity
, as well as its density and viscosity. Also, the terminal velocity of the particles
varies with their diameter
D. With these assumptions made, the relation between the collision efficiency and the remaining parameters can be written as a function f using the Buckingham
theorem [
60]:
The dimensionless numbers show that depends on the Reynolds number , the surface angle, and the particle diameter and concentration, expressed by and , respectively. This leaves the function f to be defined through the interpolation of numerical and/or experimental simulations, which will be discussed later in this paper.
2.2. Sticking Efficiency ()
The interaction between snow particles in suspension and inside clouds has been studied for the purpose of modelling climatic precipitation at the atmospheric level [
61]. Analytical solutions for
, especially for the flat-plate problem, are, however, scarce due to the complexity of the problem. Makkonen [
51] discusses sticking efficiency values for different types of snow. Supercooled water droplets, for example, freeze when they come into contact with the surface and therefore do not bounce, leading to
. Snow particles, on the other hand, have a more varied range of behaviour. Dry snow effectively bounces off surfaces, so its sticking efficiency is very low. The opposite is true for wet snow due to the layer of water that forms in the contact zone. This effect favours the adhesion of particles, especially at low speeds and under suitable conditions of temperature and relative humidity. Despite the lack of theoretical models, empirical relationships based on wind speed observations provide a lead for implementing
in numerical snow accumulation models [
62]. A common practice is to consider wet snow as rime ice, with
, to prevent the growth of the snow layer from being underestimated. The need for more accurate models of sticking efficiency motivates work in this area. One of the limiting factors identified is the absence of consistent climate data so that correlations between
and temperature and relative humidity can be drawn. It is expected that a similar setup to the one that produced the data shown in
Figure 1 will be able to elucidate this issue.
2.3. Accretion Efficiency ()
The heat balance equation during the accumulation of snow on a given surface must be formulated so that the value of
can be determined. Makkonen [
51] and Poots and Sakamoto [
63] address this issue for power cables. The proposed models consist of the heat flux terms relevant to their respective applications, which is not necessarily the same for the case of AV sensing surfaces. Ohmic heating, for example, is included in the heat exchange equation of Poots and Sakamoto [
63] due to the electric current carried by the power lines. An adaptation of this model for the automotive context will therefore not account for this term. Makkonen [
51] includes air friction heating in his formulation, but he also states that this term can be negligible, as its values are only relevant to flow regimes encountered in aerospace. Although an equation for frictional heating is provided, it takes into account the recovery factor for the viscous heating of the body, which is known for cylinders but can vary drastically for flat surfaces. For simplification purposes, this term can also be overlooked at first glance. A heat flux equation of wet snow accretion appropriate to the topic under discussion can take the following form:
where
is the latent heat released by freezing at the ice–water interface:
where
is the flux density of water to the surface,
is the water’s latent heat of freezing, and
is the fraction of liquid in the snow layer.
is the sensible heat loss to the air:
which is a function of the convective heat transfer coefficient
h, the temperature of the icing surface
, and the air temperature
.
is the heat loss by evaporation:
where
denotes the ratio of the molecular weights of dry air and water vapour,
is the latent heat of vaporization,
is the saturation water vapour pressure over the accretion surface (
kPa),
is the ambient vapour pressure in the airstream, which is a function of temperature,
is the specific heat of air, and
p is the air pressure.
is the heat loss in heating the supercooled water to freezing temperature once it hits the surface:
with
as the specific heat of water and
representing the impacting droplets. Makkonen [
51] affirms that
can be assumed to be equal to
for supercooled raindrops. Finally,
is the heat loss due to radiation:
where
Wm
2 K
−4 is the Stefan–Boltzmann constant, and
K
3 is the radiation linearization constant. By entering the individual expressions of the heat exchange terms into Equation (
17) and assuming
,
can be derived as
The challenge in implementing this model remains the estimation of the liquid fraction
and the convective heat transfer coefficient
h. With respect to the former, previous work suggests that
is a good first approximation [
64,
65]. Nevertheless, new methods could be developed to assess this parameter.
Regarding the heat transfer coefficient, attempts were made to obtain a theoretical model, with reasonable results for cylindrical bodies [
29]. However, it was observed that values depend strongly on the shape and roughness of the icing surface. It is therefore agreed that the best approach to estimating h is to employ an empirical model based on observations of the configuration studied. The scope of the WoW project includes climate chamber tests using thermal cameras to analyze snow accretion on flat plates in order to feed Equation (
23) with suitable values for this parameter.
3. Model Architecture and Experimental Apparatus
Equation (
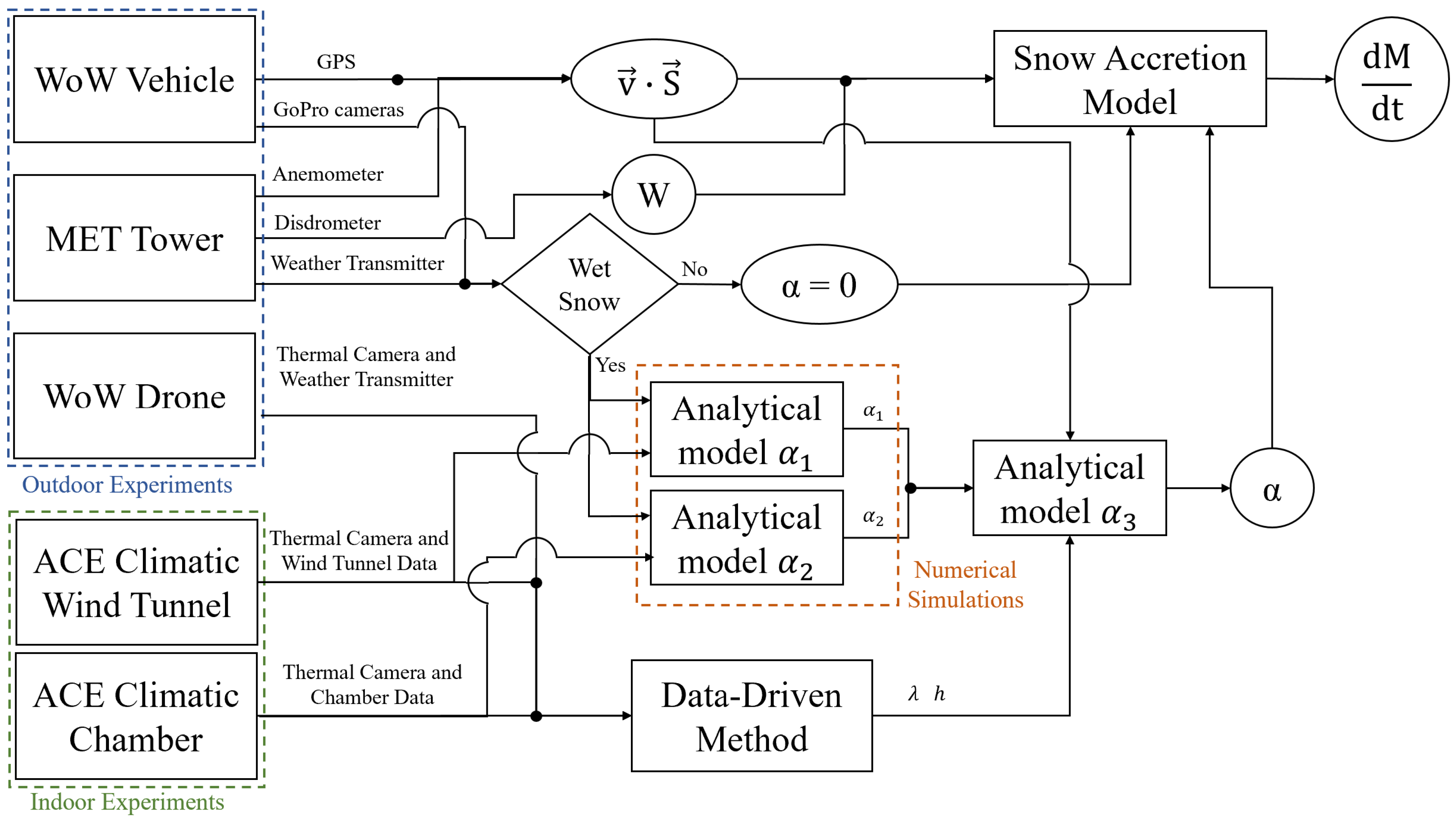
14) provides a potential analytical approach to quantifying the evolution of snow accumulation on moving surfaces with various orientations. The next stage in its implementation is to define an architecture that illustrates the procedure for obtaining the model parameters experimentally.
Figure 3 shows a flowchart summarizing the steps involved in the processing of sensor data to assess the rate of snow growth on a given surface. The experimental setup consists of three distinct modules for full-scale measurements. The first module consists of a test vehicle instrumented with a Vaisala WXT530 Weather Transmitter (Vaisala, Auckland, New Zealand), an Airmar WX220 weather station (Airmar, Milford, NH, USA), and two Laser Precipitation Monitors (LPM) from Thies Clima (Göttingen, Germany) oriented at 0° and 90°. The vehicle will record weather data as it travels along a track located at the Weather Farm land provided by Ontario Tech University in northern Oshawa, Ontario. In the vicinity of the course, two meteorological towers also equipped with Vaisala WXT530 transmitters and Thies LPM disdrometers, mounted at 0°, will serve as a static referential from which correlations between its measurements and those coming from the vehicle will be drawn. A Freefly Alta X drone (Freefly, Woodinville, WA, USA) adapted as a portable weather station will complement the database with measurements from an additional Vaisala WXT530 while it hovers still. By varying the geographical position of the drone, the coverage radius of the experimental setup can be defined. Correlation analysis between data obtained by the drone and the remaining static benchmarks will indicate the maximum distance at which the output of the instruments shows agreement and suggest a set of correlation coefficients to be used. The drone will also be equipped with a thermal camera for monitoring the layer of snow being formed on strategic surfaces of the vehicle during the experiments. In recent experimental campaigns, 3 GoPro cameras (Go Pro, San Mateo, CA, USA) were installed on distinct surfaces of the test vehicle to measure the thickness of the snow layer formed during the tests. The cameras were mounted so as to monitor the front and rear windshields and the hood of the vehicle.
Table 1 lists the experimental apparatus at the disposal of the WoW project, along with the data generated by the set of instruments.
Direct measurements allow the parameter
W of the analytical model of
to be obtained through Equations (
10)–(
12). However, new models are expected to be developed based on measurements of LWC and snow particle density for more accurate results. In addition, the vectors of the wind velocity and the displacement of the target surface, required for computing the integral of Equation (
14), can be obtained from the meteorological towers and GPS data, respectively. The projection of the particle velocity on the analyzed surface can be estimated by the scalar product between the wind velocity vector, obtained by the Vaisala WXT530 anemometer on the meteorological tower, and the moving surface vector of
S, represented by the vehicle velocity vector. The tower’s weather transmitter also plays an important role in evaluating the criterion presented by Equation (
4) for wet snow formation. In the event of dry snow, the
term is set to zero, as no accumulation takes place on moving surfaces. Otherwise, numerical methods should be employed, as experimentally obtaining the independent values of
,
, and
is challenging. The next sections of this paper will discuss strategies for this task currently being implemented in the full-scale data processing chain.
4. Perspectives and Preliminary Results
Experimental research on the snow accretion impact on vehicles is notably at an early stage of development, primarily due to the challenges in securing suitable test facilities and the inherent risks associated with vehicular navigation in snowy terrains. Alternatively, laboratory environments can substitute for outdoor field tests, offering more control on tested parameters. Given the challenges and high costs associated with testing in actual environments, a controlled setting such as an enclosed track or chamber equipped with machines capable of generating artificial rain, fog, or snow can closely replicate environmental conditions. Based on these benefits, the WoW project’s other scope aims to investigate how to enhance ADAS sensor performance and AV safety under adverse weather in the ACE climatic wind tunnel at Ontario Tech. This simulation aims to pinpoint adaptive control strategies that can mitigate the impact of Weather Design Cases (WDCs) on vehicles [
66]. In addition to outdoor climate measurement campaigns to define the WDCs, a series of indoor experiments have been designed to evaluate the performance of snow guns in replicating real snowfall. As input parameters that can be controlled within ACE’s facilities, air temperature and relative humidity, the flow rate of water sprays, and particle density and size can be cited.
To investigate the accumulation over a moving body subjected to various environmental conditions, a set of experiments was meticulously designed and conducted within the ACE Large Climatic Chamber, notably in the absence of wind, to isolate the effects of temperature and artificial snowfall. The experimental protocol was carefully crafted and focused on monitoring artificial snow build-up on a horizontal surface (zero degrees) while varying the temperature inside the chamber and the flow rate of the snow gun. For this, high-resolution IP cameras were strategically positioned to monitor the sample, enabling real-time documentation of snow accumulation under varying experimental conditions. The preliminary goal is to derive an effective value for alpha from this dataset. An initial analysis of the results points to
when the flow rate of the snow gun was set to 4 gallons per minute (GPM), and the room temperature was maintained at −10 °C. In addition, a second experimental campaign was carried out to investigate the accumulation of snow on inclined surfaces.
Figure 4 shows the experimental setup of the most recent campaign. As new results are generated, it is expected that the work will lead to progress in generating realistic snowfall indoors.
Following the tests, these experimental results will be used to calibrate numerical simulations aimed at determining all three alpha components for wide ranges of temperature and relative humidity. A CFD model based on a coupled solution between Ansys Fluent, for solving Navier–Stokes equations in a fluid medium, and Altair EDEM software, a Discrete Element Method (DEM) solver, has been identified as a promising strategy for snow accretion studies with automotive applications. The work by Xiong et al. [
67] used this method to investigate how dust accumulates over solar photovoltaic (PV) panels by simulating particle collisions against flat surfaces at various angles of inclination. A full DEM approach was presented by Sai Tanneru [
68] to study snow particle adhesion at different angles of repose. In this work, parameters like Young’s modulus, surface adhesion, and friction coefficients are used on granular snow particles to generate angle-of-repose values. The convective heat transfer coefficient is critical in determining
, following Equation (
23), and the surface convective heat transfer and its effect on accumulation can be observed in Ansys Fluent, potentially helping with an estimation of this quantity. Based on the numerical results, the estimated values of the alpha coefficients will be coupled to the precipitation flux model by Carvalho and Hangan [
44], which is designed to compute the precipitation rate on inclined surfaces in motion. As an illustration of what would be expected in terms of monitoring the growth rate of snow layers on vehicle surfaces, the preliminary effective value of
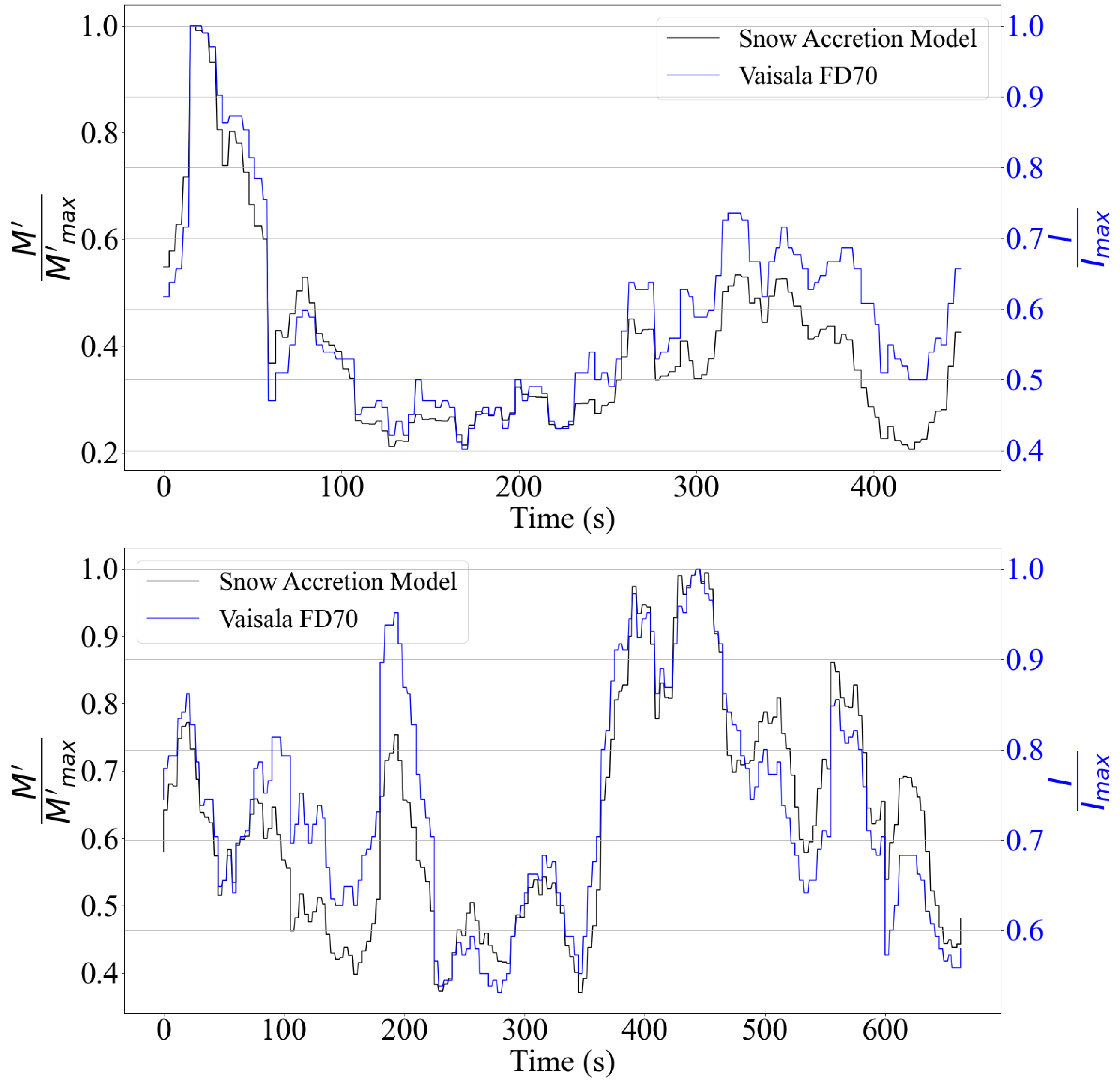
found in the indoor tests was used to generate synthetic values for
, as shown in
Figure 5. Outputs from the model in Equation (
14) fed with experimental data collected on March 7th 2022 at GM’s MATT test track showed good agreement when compared with direct precipitation rate readings from an FD70 disdrometer.
Table 2 shows the Pearson correlation coefficient [
69] values between the two results. Despite the high coefficients in both test cases, the correlation with the vehicle in motion is slightly lower. This might have been induced by aerodynamic forces linked to the flow around its structure, as the instrument was not designed as an embedded system for dynamic measurements. Despite this limitation in relation to the equipment, the overall performance of the model is considered satisfactory, as the model’s predictions and the disdrometer measurements show a correlation of more than 0.88 over 10 min of testing. This demonstrates the model’s responsiveness to variations in weather conditions. In terms of the mean absolute error (MAE), the static case showed a greater value compared to dynamic measurements. As can be seen in
Figure 5 (top), after 300 s of testing, when low levels of snowfall are encountered, the disparity between the signals increases. During this period, the maximum error between theoretical and experimental values reaches 60%. Given that the levels of precipitation recorded during this trial were on average 44% lower than in the case of 80 km/h, this error is likely due to the low measured values reaching the instrument’s resolution threshold. However, once the vehicle encountered higher snowfall (bottom of
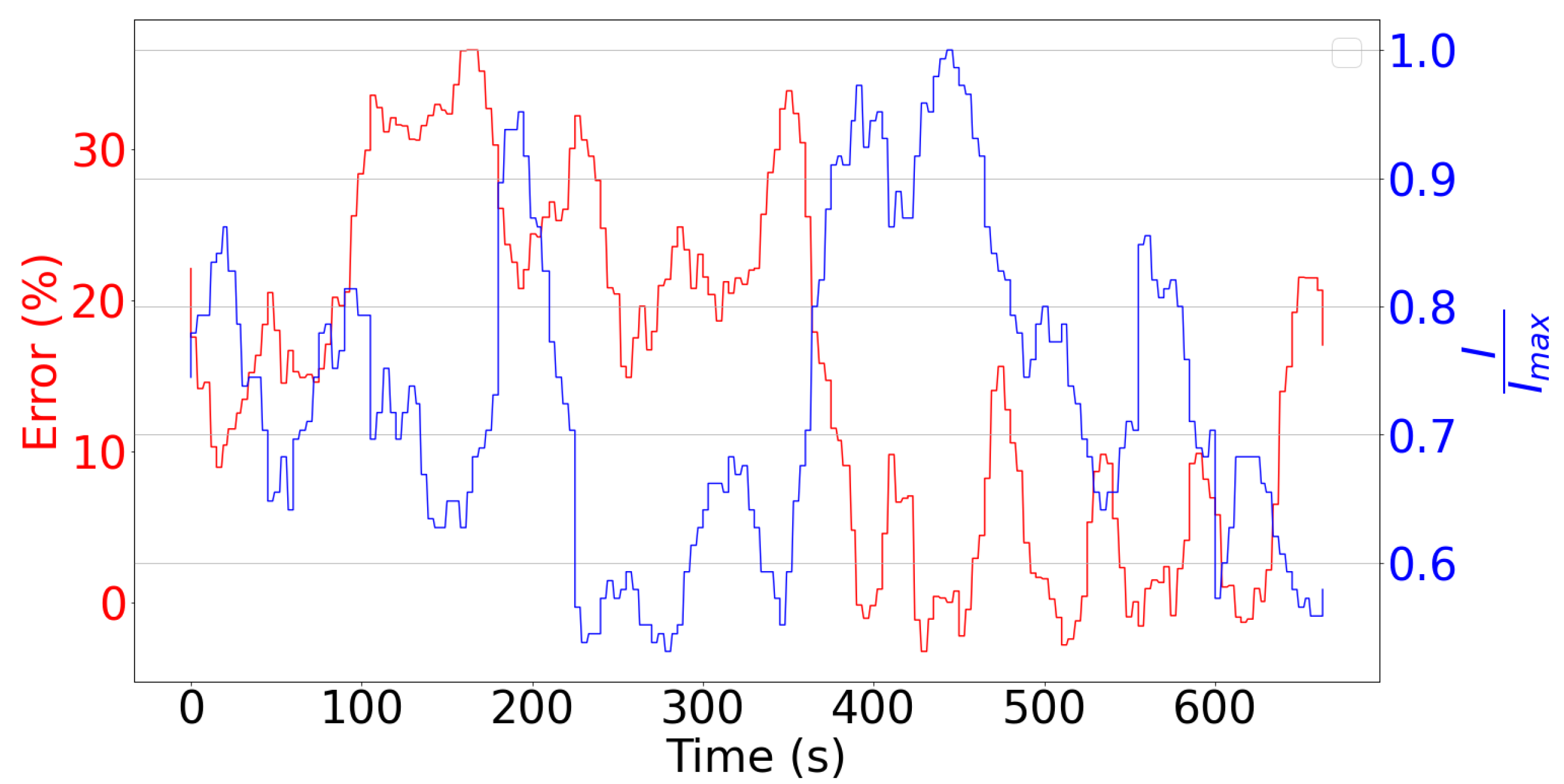
Figure 5), which is the critical case in terms of accumulation, the values generated by the model approach those obtained experimentally. This can be observed in
Figure 6, which shows the error between disdrometer readings and amounts predicted by the model over time throughout the dynamic test case. The values are plotted against the instrument output signal to highlight that the error is reduced when the precipitation rate is high. Other factors that can explain the divergence between the results may be associated with the hypothesis of the spherical shape of the particles, which directly influences the calculation of the total volume of snow encountered. To address this, characterization campaigns of the disdrometer combined with snow particle visualization techniques could provide elements to improve the accuracy of the model.
The final goal is to refine the snow accretion equation by setting accurate values for Makkonen’s coefficients through the numerical models calibrated by indoor experiments, which faithfully reproduce the events encountered outdoors. For this, the results will be cross-checked with a set of full-scale experiments presently running at Ontario Tech’s Weather Farm, where a test vehicle has been equipped with two disdrometers mounted with distinct orientations and cameras to monitor the growth of the snow layer, in addition to meteorological towers providing wind speed and direction data, as described in
Table 1. These sensors are capable of measuring the distribution and terminal velocity of snow particles, allowing for the calculation of precipitation amounts. These data will then be utilized to corroborate the analytical model. Additionally, the vehicle is equipped with three GoPro cameras to record snow accumulation on various critical surfaces of the vehicle in real time. This setup not only captures the total snow accumulation over a certain period but also provides data on the rate of snow accumulation. Other instruments on the vehicle, such as the Airmar WX220 weather station and Vaisala WXT530 weather transmitter sensors, measure wind speed in three components, temperature, vehicle positioning, relative humidity, and atmospheric pressure, offering a comprehensive analysis of environmental conditions, as can be seen in
Figure 7. Alongside this vehicle, there are two stationary towers equipped with the same types of sensors to measure identical properties. These will be used to compare results and determine the impact of movement on precipitation and accumulation.
The results generated throughout the Weather on Wheels project are expected to validate the proposed proof of concept, where a network of low-cost meteorological towers can be used to map, with high accuracy, the level of precipitation perceived by vehicles on nearby roads. In a future where most vehicles will have autonomous features, it is possible to imagine a means of communication between them and the nearest weather station. By combining measurements of wind and weather precipitation obtained by the tower with GPS data from the vehicles, the snow accretion model can be used to predict the level of build-up on the latter and set safety operational thresholds.