Unsteady and Inhomogeneous Turbulent Fluctuations around Isotropic Equilibrium
Abstract
1. Introduction
1.1. Perturbation Approaches
1.2. This Review
2. Equilibrium in Turbulence: Finding
3. Isotropic Turbulence: Deriving
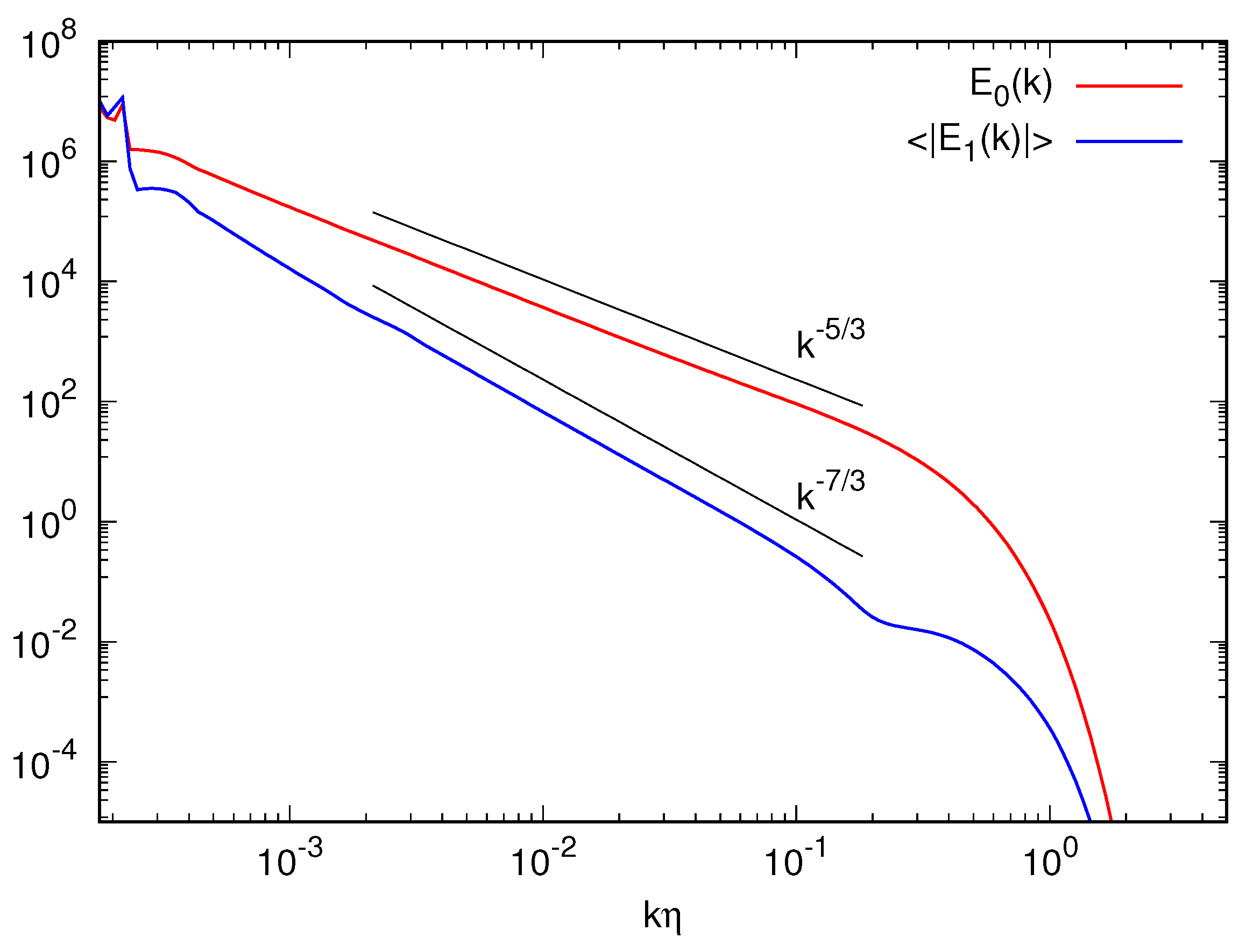
4. Temporal Perturbations to K41
5. Inhomogeneous Perturbations to K41
6. Mixing
7. Implications for the Large-Scale Statistics
8. Conclusions and Perspectives
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nayfeh, A.H. Perturbation Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Van Dyke, M. Perturbation methods in fluid mechanics/Annotated edition. NASA STI/Recon Tech. Rep. A 1975, 75, 46926. [Google Scholar]
- Yoshizawa, A. Nonequilibrium effect of the turbulent-energy-production process on the inertial-range energy spectrum. Phys. Rev. E 1994, 49, 4065. [Google Scholar] [CrossRef] [PubMed]
- Horiuti, K.; Ozawa, T. Multimode stretched spiral vortex and nonequilibrium energy spectrum in homogeneous shear flow turbulence. Phys. Fluids 2011, 23, 035107. [Google Scholar] [CrossRef]
- Araki, R.; Bos, W.J.T. Inertial range scaling of inhomogeneous turbulence. J. Fluid Mech. 2024, 978, A9. [Google Scholar] [CrossRef]
- Lee, T. On some statistical properties of hydrodynamical and magnetohydrodynamical fields. Q. Appl. Math. 1952, 10, 69. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Helical turbulence and absolute equilibrium. J. Fluid Mech. 1973, 59, 745. [Google Scholar] [CrossRef]
- Orszag, S. Statistical theory of turbulence. In Fluid Dynamics, Lecture Notes Les Houches; Oxford Academic: Oxford, UK, 1973; pp. 237–374. [Google Scholar]
- Cichowlas, C.; Bonaïti, P.; Debbasch, F.; Brachet, M. Effective Dissipation and Turbulence in Spectrally Truncated Euler Flows. Phys. Rev. Lett. 2005, 95, 264502. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 1941, 30, 301. [Google Scholar]
- Grant, H.L.; Stewart, R.W.; Moilliet, A. Turbulence spectra from a tidal channel. J. Fluid Mech. 1962, 12, 241. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. On the universality of the Kolmogorov constant. Phys. Fluids 1995, 7, 2778–2784. [Google Scholar] [CrossRef]
- Ishihara, T.; Gotoh, T.; Kaneda, Y. Study of high Reynolds number isotropic turbulence by Direct Numerical Simulation. Annu. Rev. Fluid Mech. 2009, 41, 65. [Google Scholar] [CrossRef]
- Alexakis, A.; Brachet, M.E. On the thermal equilibrium state of large-scale flows. J. Fluid Mech. 2019, 872, 594–625. [Google Scholar] [CrossRef]
- Bandak, D.; Goldenfeld, N.; Mailybaev, A.A.; Eyink, G. Dissipation-range fluid turbulence and thermal noise. Phys. Rev. E 2022, 105, 065113. [Google Scholar] [CrossRef] [PubMed]
- Lesieur, M. Turbulence in Fluids; Kluwer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Leith, C. Diffusion approximation to inertial energy transfer in isotropic turbulence. Phys. Fluids 1967, 10, 435–472. [Google Scholar] [CrossRef]
- Connaughton, C.; Nazarenko, S. Warm Cascades and Anomalous Scaling in a Diffusion Model of Turbulence. Phys. Rev. Lett. 2004, 92, 044501. [Google Scholar] [CrossRef] [PubMed]
- Bos, W.J.T.; Bertoglio, J.P. Dynamics of spectrally truncated inviscid turbulence. Phys. Fluids 2006, 18, 071701. [Google Scholar] [CrossRef]
- Qian, J. Inertial range and the finite Reynolds number effect of turbulence. Phys. Rev. E 1997, 55, 337. [Google Scholar] [CrossRef]
- Qian, J. Slow decay of the finite Reynolds number effect of turbulence. Phys. Rev. E 1999, 60, 3409. [Google Scholar] [CrossRef] [PubMed]
- Bos, W.J.T.; Chevillard, L.; Scott, J.F.; Rubinstein, R. Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 2012, 24, 015108. [Google Scholar] [CrossRef]
- Antonia, R.; Djenidi, L.; Danaila, L.; Tang, S. Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 2017, 29, 020715. [Google Scholar] [CrossRef]
- McComb, W.D.; Berera, A.; Yoffe, S.R.; Linkmann, M.F. Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E 2015, 91, 043013. [Google Scholar] [CrossRef] [PubMed]
- Gagne, Y.; Castaing, B.; Baudet, C.; Malécot, Y. Reynolds dependence of third-order velocity structure functions. Phys. Fluids 2004, 16, 482–485. [Google Scholar] [CrossRef][Green Version]
- Kolmogorov, A. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82. [Google Scholar] [CrossRef]
- Anselmet, F.; Gagne, Y.; Hopfinger, E.J.; Antonia, R.A. High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 1984, 140, 63. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence, the Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Taylor, G.I. Statistical theory of turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1935, 151, 421–444. [Google Scholar] [CrossRef]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- Millionschikov, M. On theory of homogeneous isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 615. [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics II; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Proudman, I.; Reid, W. On the Decay of a Normally Distributed and Homogeneous Turbulent Velocity Field. Philos. Trans. R. Soc. Lond. A 1954, 247, 163–189. [Google Scholar]
- Tatsumi, T. The Theory of Decay Process of Incompressible Isotropic Turbulence. Proc. R. Soc. Lond. A 1957, 239, 16. [Google Scholar]
- Ogura, Y. A consequence of the zero-fourth-cumulant approximation in the decay of isotropic turbulence. J. Fluid Mech. 1963, 16, 33–40. [Google Scholar]
- Kraichnan, R.H. Irreversible Statistical Mechanics of Incompressible Hydromagnetic Turbulence. Phys. Rev. 1958, 109, 1407. [Google Scholar] [CrossRef]
- Kraichnan, R.H. The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 1959, 5, 497–543. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Kolmogorov’s Hypotheses and Eulerian Turbulence Theory. Phys. Fluids 1964, 7, 1723. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Lagrangian-History Closure Approximation for Turbulence. Phys. Fluids 1965, 8, 575. [Google Scholar] [CrossRef]
- Kraichnan, R.H.; Herring, J. A strain-based Lagrangian-History turbulence theory. J. Fluid Mech. 1978, 88, 355–367. [Google Scholar] [CrossRef]
- Kaneda, Y. Renormalized expansions in the theory of turbulence with the use of the Lagrangian position function. J. Fluid Mech. 1981, 107, 131–145. [Google Scholar] [CrossRef]
- Kaneda, Y. Inertial range structure of turbulent velocity and scalar fields in a Lagrangian renormalized approximation. Phys. Fluids 1986, 29, 701–708. [Google Scholar] [CrossRef]
- Kida, S.; Goto, S. A Lagrangian direct-interaction approximation for homogeneous isotropic turbulence. J. Fluid Mech. 1997, 345, 307. [Google Scholar] [CrossRef]
- Orszag, S.A. Analytical theories of Turbulence. J. Fluid Mech. 1970, 41, 363. [Google Scholar] [CrossRef]
- Kraichnan, R.H. An almost-Markovian Galilean-invariant turbulence model. J. Fluid Mech. 1971, 47, 513. [Google Scholar] [CrossRef]
- Bos, W.J.T.; Bertoglio, J.P. A single-time two-point closure based on fluid particle displacements. Phys. Fluids 2006, 18, 031706. [Google Scholar] [CrossRef]
- Bos, W.J.T.; Bertoglio, J.P. Lagrangian Markovianized Field Approximation for turbulence. J. Turbul. 2013, 14, 99. [Google Scholar] [CrossRef]
- McComb, W. A local energy-transfer theory of isotropic turbulence. J. Phys. Math. Nucl. Gen. 1974, 7, 632. [Google Scholar] [CrossRef]
- McComb, W.; Yoffe, S. A formal derivation of the local energy transfer (LET) theory of homogeneous turbulence. J. Phys. A Math. Theor. 2017, 50, 375501. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur statistischen Theorie der Turbulenz. Z. Phys. 1948, 124, 628. [Google Scholar] [CrossRef]
- Rubinstein, R.; Clark, T. Reassessment of the Classical Turbulence Closures; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2022. [Google Scholar]
- Rubinstein, R.; Clark, T. A generalized Heisenberg model for turbulent spectral dynamics. Theor. Comput. Fluid Dyn. 2004, 17, 249. [Google Scholar] [CrossRef]
- Clark, T.; Rubinstein, R.; Weinstock, J. Reassessment of the classical turbulence closures: The Leith diffusion model. J. Turbul. 2009, 10, N35. [Google Scholar] [CrossRef]
- Kovaznay, L. Spectrum of locally isotropic turbulence. J. Aeronaut. Sci. 1948, 15, 745. [Google Scholar] [CrossRef]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 10. [Google Scholar]
- McComb, W.D. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures; OUP Oxford: Oxford, UK, 2014; Volume 162. [Google Scholar]
- Zhou, Y. Turbulence theories and statistical closure approaches. Phys. Rep. 2021, 935, 1–117. [Google Scholar]
- Rubinstein, R.; Clark, T.; Livescu, D.; Luo, L.S. Time-dependent isotropic turbulence. J. Turbul. 2004, 5, 011. [Google Scholar] [CrossRef]
- Woodruff, S.; Rubinstein, R. Multiple-scale perturbation analysis of slowly evolving turbulence. J. Fluid Mech. 2006, 565, 95. [Google Scholar] [CrossRef]
- Goto, S.; Vassilicos, J.C. Local equilibrium hypothesis and Taylor’s dissipation law. Fluid Dyn. Res. 2016, 48, 021402. [Google Scholar] [CrossRef]
- Rubinstein, R.; Clark, T.T. “Equilibrium” and “non-equilibrium” turbulence. Theor. Appl. Mech. Lett. 2017, 7, 301–305. [Google Scholar] [CrossRef]
- Fang, L.; Bos, W.J.T. An EDQNM study of the dissipation rate in isotropic non-equilibrium turbulence. J. Turbul. 2023, 24, 217–234. [Google Scholar] [CrossRef]
- Bos, W.J.T.; Clark, T.T.; Rubinstein, R. Small scale response and modeling of periodically forced turbulence. Phys. Fluids 2007, 19, 055107. [Google Scholar] [CrossRef]
- Horiuti, K.; Tamaki, T. Nonequilibrium energy spectrum in the subgrid-scale one-equation model in large-eddy simulation. Phys. Fluids 2013, 25, 125104. [Google Scholar] [CrossRef]
- Berti, S.; Boffetta, G.; Musacchio, S. Mean flow and fluctuations in the three-dimensional turbulent cellular flow. Phys. Rev. Fluids 2023, 8, 054601. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Test-field model for inhomogeneous turbulence. J. Fluid Mech. 1972, 56, 287–304. [Google Scholar] [CrossRef]
- Laporta, A. Etude Spectrale et Modélisation de la Turbulence Inhomogène. Ph.D. Thesis, Ecole Centrale de Lyon, Écully, France, 1995. [Google Scholar]
- Laporta, A.; Bertoglio, J.P. A model for inhomogeneous turbulence based on two-point correlations. In Advances in Turbulence V; Springer: Berlin/Heidelberg, Germany, 1995; pp. 286–297. [Google Scholar]
- Parpais, S. Développement d’un Modèle Spectral Pour la Turbulence Inhomogène. Résolution par une Méthode d’éléments Finis. Ph.D. Thesis, Ecole Centrale de Lyon, Écully, France, 1997. [Google Scholar]
- Besnard, D.; Harlow, F.; Rauenzahn, R.; Zemach, C. Spectral transport model for turbulence. Theor. Comput. Fluid Dyn. 1996, 8, 1–35. [Google Scholar] [CrossRef]
- Touil, H.; Bertoglio, J.P.; Shao, L. The decay of turbulence in a bounded domain. J. Turbul. 2002, 3, N49. [Google Scholar] [CrossRef]
- Touil, H.; Parpais, S.; Bertoglio, J.P. A spectral closure applied to anisotropic inhomogeneous turbulence. In Proceedings of the 8th European Turbulence Conference, Barcelona, Spain, 27–30 June 2000. [Google Scholar]
- De Karman, T.; Howarth, L. On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 164, 192–215. [Google Scholar] [CrossRef]
- Hill, R.J. Exact second-order structure-function relationships. J. Fluid Mech. 2002, 468, 317–326. [Google Scholar] [CrossRef]
- Cadiou, A.; Hanjalić, K.; Stawiarski, K. A two-scale second-moment turbulence closure based on weighted spectrum integration. Theor. Comput. Fluid Dyn. 2004, 18, 1–26. [Google Scholar] [CrossRef]
- Batchelor, G.K. Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 1959, 5, 113. [Google Scholar] [CrossRef]
- Obukhov, A. Structure of the temperature field in turbulent flows. Isv. Geogr. Geophys. Ser. 1949, 13, 58. [Google Scholar]
- Corrsin, S. On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 1951, 22, 469. [Google Scholar] [CrossRef]
- Roberts, P. Analytical theory of turbulent diffusion. J. Fluid Mech. 1961, 11, 257. [Google Scholar] [CrossRef]
- Newman, G.R.; Herring, J. A test field model of a passive scalar in isotropic turbulence. J. Fluid Mech. 1979, 94, 163. [Google Scholar] [CrossRef]
- Vignon, J.M.; Cambon, C. Thermal spectral calculation using eddy-damped quasi-normal Markovian theory. Phys. Fluids 1980, 23, 1935–1937. [Google Scholar] [CrossRef]
- Herring, J.; Schertzer, D.; Lesieur, M.; Newman, G.; Chollet, J.P.; Larcheveque, M. A comparative assessment of spectral closures as applied to passive scalar diffusion. J. Fluid Mech. 1982, 124, 411. [Google Scholar] [CrossRef]
- Rubinstein, R.; Clark, T.T. Reassessment of the classical closures for scalar turbulence. J. Turbul. 2013, 14, 71–98. [Google Scholar] [CrossRef]
- Bos, W.J.T.; Rubinstein, R. Dissipation in unsteady turbulence. Phys. Rev. Fluids 2017, 2, 022601. [Google Scholar] [CrossRef]
- Vassilicos, J.C. Dissipation in turbulent flows. Ann. Rev. Fluid Mech. 2015, 47, 95–114. [Google Scholar] [CrossRef]
- Goto, S.; Vassilicos, J.C. Energy dissipation and flux laws for unsteady turbulence. Phys. Lett. A 2015, 379, 1144–1148. [Google Scholar] [CrossRef]
- Hearst, R.J.; Lavoie, P. Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 2014, 741, 567–584. [Google Scholar] [CrossRef]
- Zheng, Y.; Nakamura, K.; Nagata, K.; Watanabe, T. Unsteady dissipation scaling in static-and active-grid turbulence. J. Fluid Mech. 2023, 956, A20. [Google Scholar] [CrossRef]
- Zheng, Y.; Koto, N.; Nagata, K.; Watanabe, T. Unsteady dissipation scaling of grid turbulence in the near-field region. Phys. Fluids 2023, 35, 095131. [Google Scholar] [CrossRef]
- Wacławczyk, M.; Nowak, J.L.; Siebert, H.; Malinowski, S.P. Detecting nonequilibrium states in atmospheric turbulence. J. Atmos. Sci. 2022, 79, 2757–2772. [Google Scholar] [CrossRef]
- Bos, W.J.T.; Rubinstein, R. Mixing in modulated turbulence. analytical results. Comput. Fluids 2017, 151, 102–107. [Google Scholar] [CrossRef][Green Version]
- Yang, Y.; Chahine, R.; Rubinstein, R.; Bos, W.J.T. Passive scalar mixing in modulated turbulence. Fluid Dyn. Res. 2019, 51, 045501. [Google Scholar] [CrossRef]
- Liu, F.; Lu, L.P.; Bos, W.J.T.; Fang, L. Assessing the nonequilibrium of decaying turbulence with reversed initial fields. Phys. Rev. Fluids 2019, 4, 084603. [Google Scholar] [CrossRef]
- Shao, X.; Fang, J.; Fang, L. Non-equilibrium dissipation laws in a minimal two-scale wake model. Phys. Fluids 2023, 35, 085105. [Google Scholar] [CrossRef]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Davidson, P.A. Turbulence in Rotating, Stratified and Electrically Conducting Fluids; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Lumley, J. Similarity and the turbulent energy spectrum. Phys. Fluids 1967, 10, 855. [Google Scholar] [CrossRef]
- Yoshida, K.; Ishihara, T.; Kaneda, Y. Anisotropic spectrum of homogeneous turbulent shear flow in a Lagrangian renormalized approximation. Phys. Fluids 2003, 15, 2385–2397. [Google Scholar] [CrossRef]
- Ishihara, T.; Yoshida, K.; Kaneda, Y. Anisotropic Velocity Correlation Spectrum at Small Scales in a Homogeneous Turbulent Shear Flow. Phys. Rev. Lett. 2002, 88, 154501. [Google Scholar] [CrossRef] [PubMed]
- Kaneda, Y.; Yoshida, K. Small-scale anisotropy in stably stratified turbulence. New J. Phys. 2004, 6, 34. [Google Scholar] [CrossRef][Green Version]
- Ishida, T.; Kaneda, Y. Small-scale anisotropy in magnetohydrodynamic turbulence under a strong uniform magnetic field. Phys. Fluids 2007, 19, 075104. [Google Scholar] [CrossRef]
- Kaneda, Y.; Yamamoto, Y.; Tsuji, Y. Linear response theory for one-point statistics in the inertial sublayer of wall-bounded turbulence. Phys. Rev. Lett. 2019, 122, 194502. [Google Scholar] [CrossRef] [PubMed]
- Kaneda, Y. Linear response theory of turbulence. J. Stat. Mech. Theory Exp. 2020, 2020, 034006. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and transitions in turbulent flows. Phys. Rep. 2018, 767–769, 1–101. [Google Scholar] [CrossRef]
- Marino, R.; Sorriso-Valvo, L. Scaling laws for the energy transfer in space plasma turbulence. Phys. Rep. 2023, 1006, 1–144. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S.; Elperin, T.; Kleeorin, N.; Rogachevskii, I. Energy-and flux-budget (EFB) turbulence closure model for stably stratified flows. Part I: Steady-state, homogeneous regimes. Bound.-Layer Meteorol. 2007, 125, 167–191. [Google Scholar] [CrossRef]
- Rogachevskii, I.; Kleeorin, N.; Zilitinkevich, S. Energy-and flux-budget theory for surface layers in atmospheric convective turbulence. Phys. Fluids 2022, 34, 116602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bos, W.J.T. Unsteady and Inhomogeneous Turbulent Fluctuations around Isotropic Equilibrium. Atmosphere 2024, 15, 547. https://doi.org/10.3390/atmos15050547
Bos WJT. Unsteady and Inhomogeneous Turbulent Fluctuations around Isotropic Equilibrium. Atmosphere. 2024; 15(5):547. https://doi.org/10.3390/atmos15050547
Chicago/Turabian StyleBos, Wouter J. T. 2024. "Unsteady and Inhomogeneous Turbulent Fluctuations around Isotropic Equilibrium" Atmosphere 15, no. 5: 547. https://doi.org/10.3390/atmos15050547
APA StyleBos, W. J. T. (2024). Unsteady and Inhomogeneous Turbulent Fluctuations around Isotropic Equilibrium. Atmosphere, 15(5), 547. https://doi.org/10.3390/atmos15050547






