Multiple-Win Effects and Beneficial Implications from Analyzing Long-Term Variations of Carbon Exchange in a Subtropical Coniferous Plantation in China
Abstract
1. Introduction
2. Instrumentation and Methods
2.1. Site Description
2.2. Instruments and Measurements
2.3. Processing and Usage of Flux Data
2.4. Applications of Empirical Models of GPP, Re, and NEP
3. Results
3.1. Model Simulations of GPP, Re, and NEP under All Sky Conditions from 2003–2017
3.1.1. Hourly Simulations of GPP, Re, and NEP
3.1.2. Daily Sum Simulations of GPP, Re, and NEP
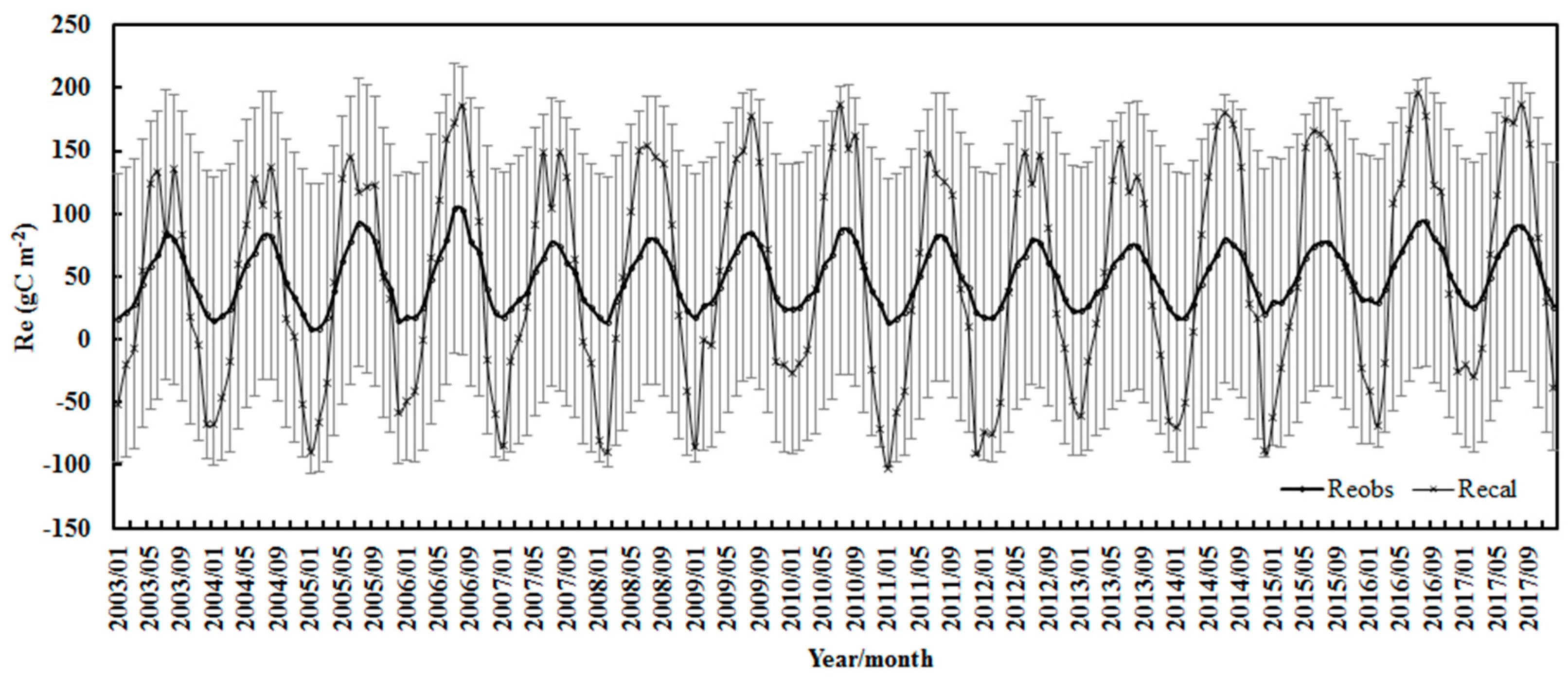
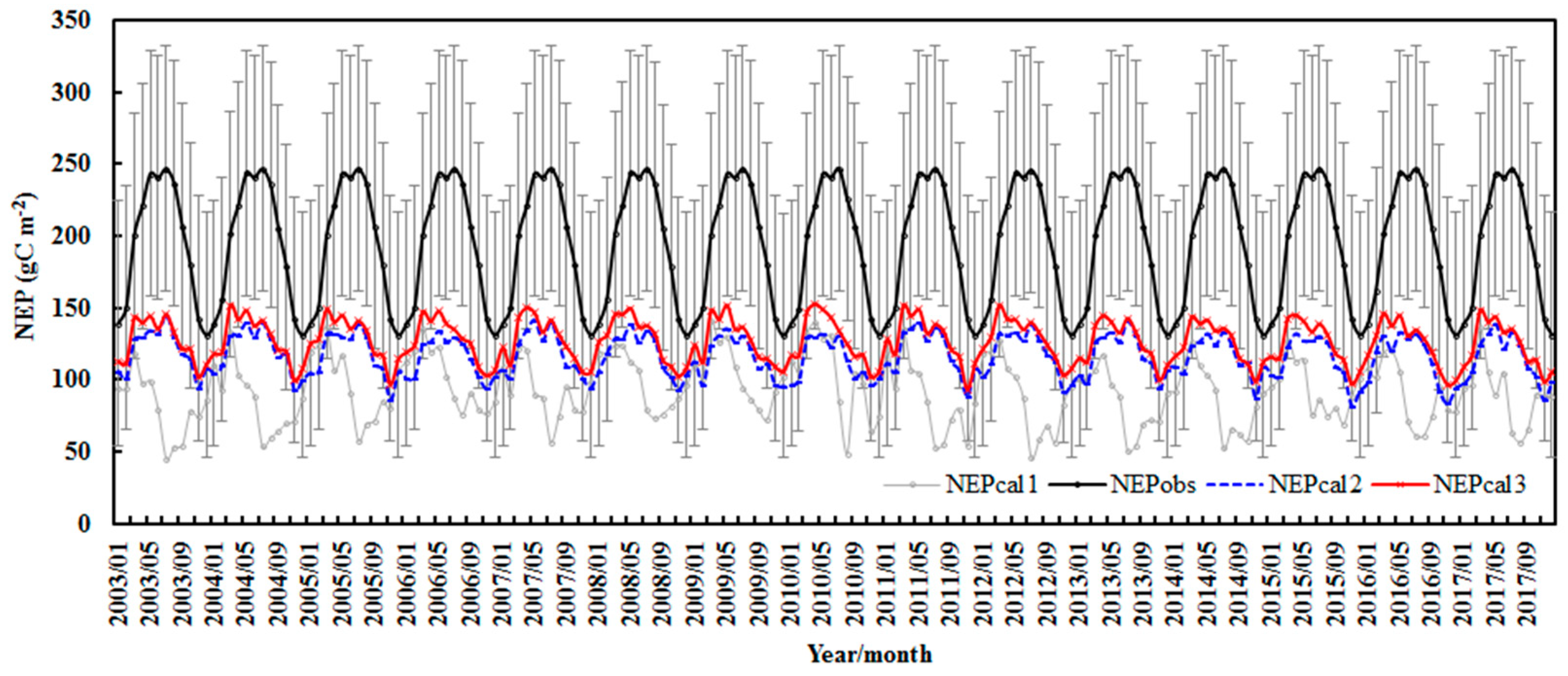
3.1.3. Monthly Sum Simulations of GPP, Re, and NEP
3.1.4. Annual Sum Simulations of GPP, Re, and NEP
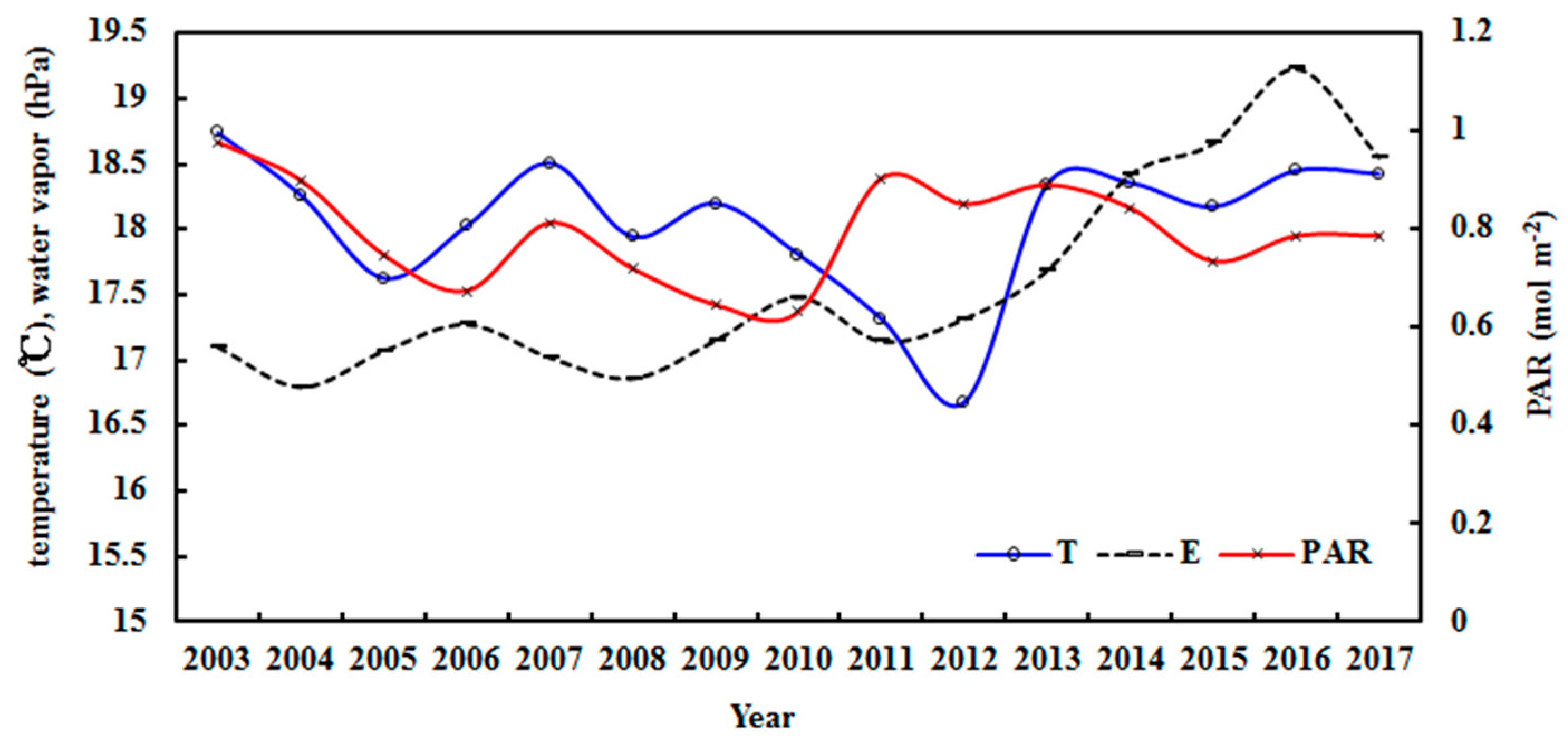
3.1.5. Long-Term Variations of Annual Sums of GPP, Re, and NEP
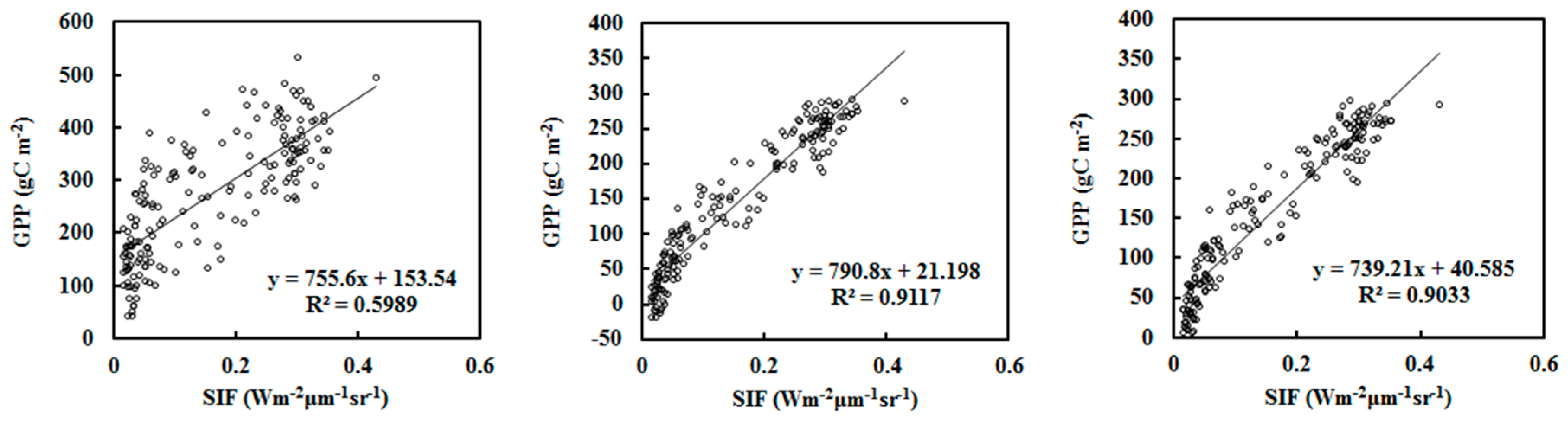
3.2. Relations between GPP and SIF and Its Application to Calculate GPP
4. Discussion
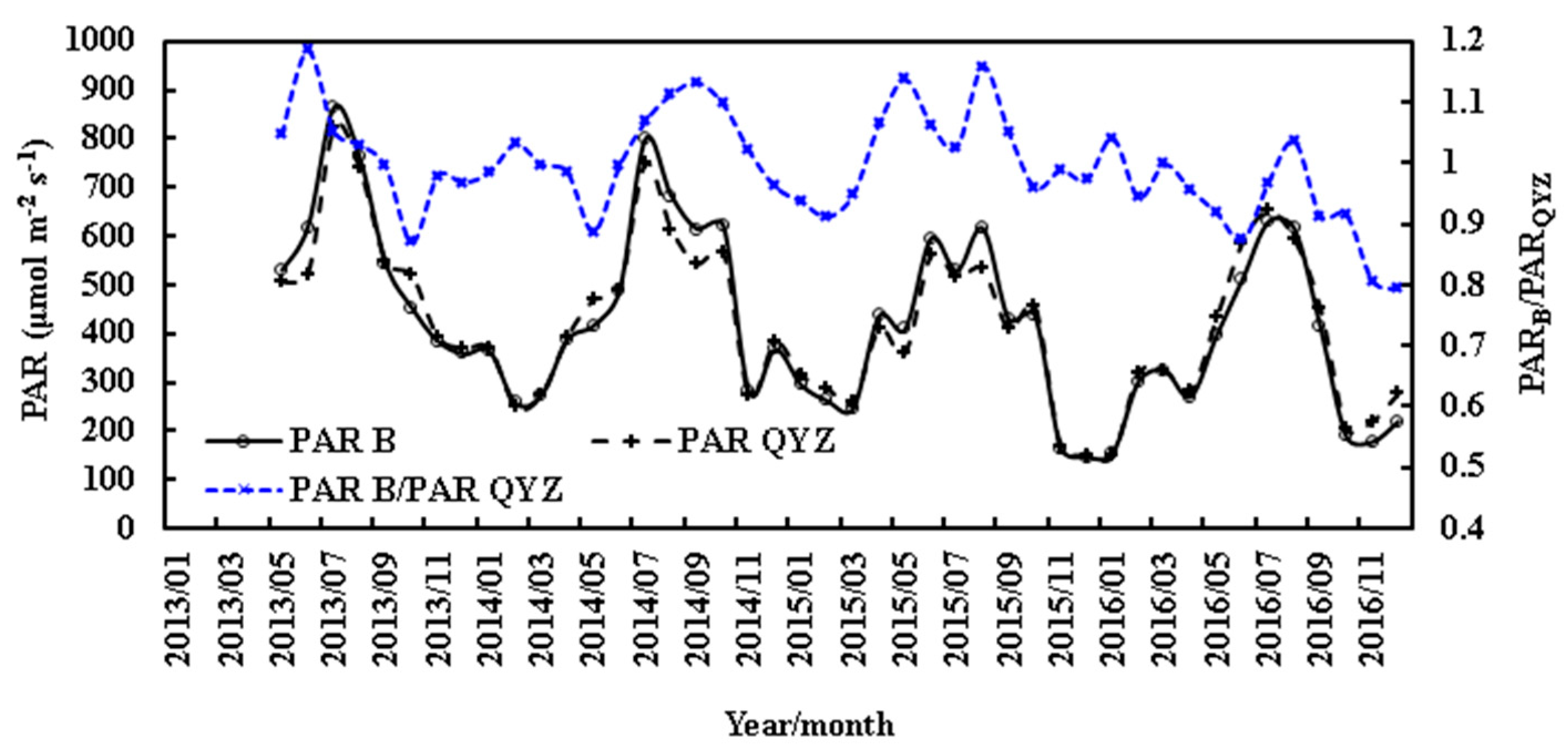
4.1. Possible Reasons for the Underestimations of NEP
4.2. Applications Potential of Empirical Models of GPP, Re, and NEP
4.3. Further Application of Respiration Model
4.4. Empirical Models of GPP, Re, and NEP
4.5. Some Issues Associated with the Empirical Models, GLPs, and Climate Warming
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural networks |
| BVOCs | Biogenic volatile organic compounds |
| CPRs | Chemical and photochemical reactions |
| DGVMs | Dynamic global vegetation models |
| EC | Eddycovariance |
| EMGPP, EMRe, EMNEP | Empirical models of GPP, Re, and NEP |
| GHG | Greenhouse gas |
| GIS | Geographic information system |
| GLP | Gas, liquid, and particle |
| GPP | Gross primary production |
| GOSIF | Multi-source-driven SIF product |
| MAD | Mean absolute deviations |
| MERRA-2 | Modern-Era Retrospective Analysis for Research and Applications |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NEE | Net ecosystem exchange |
| NEP | Net ecosystem productivity |
| NMSE | Normalized mean-square error |
| OCO-2 | Orbiting Carbon Observatory-2 |
| PAR | Photosynthetically active radiation |
| RE | Respiration |
| RMSE | Root mean-square errors |
| SIF | Satellite solar-induced fluorescence |
| SOA | Secondary organic aerosols |
| VOCs | Volatile organic compounds |
| XGBoost | Extreme gradient boosting |
| Q | Solar global radiation |
| D | Solar direct radiation |
| S | Solar diffuse radiation |
| T | Temperature |
| RH | Relative humidity |
| E | Water vapor pressure |
| R2 | Coefficient of determination |
References
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; King, J.C.; Mulvaney, R. Climate Change: Devil in the Detail. Science 2001, 293, 1777–1779. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; Parkinson, C.; Mulvaney, R.; Hodgson, D.A.; King, J.C.; Pudsey, C.J.; Turner, J. Recent rapid regional climate warming on the Antarctic Peninsula. Clim. Chang. 2003, 60, 243–274. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.C.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.; Dethloff, K.; Entekhabi, D.; Overland, J.; et al. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Hosking, J.S.; Bracegirdle, T.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st century warming on Antarctic Peninsula consistent with natural variability. Nature 2016, 535, 411–415. [Google Scholar] [CrossRef]
- Bai, J.; Zong, X.; Ma, Y.; Wang, B.; Zhao, C.; Yang, Y.; Guang, J.; Cong, Z.; Li, K.; Song, T. Long-term variations in global solar radiation and its interaction with atmospheric substances at Qomolangma. Int. J. Environ. Res. Public Health 2022, 19, 8906. [Google Scholar] [CrossRef]
- Zavalishin, N.N. Reasons for Modern Warming: Hypotheses and Facts. J. Atmos. Sci. Res. 2021, 5, 11–17. [Google Scholar] [CrossRef]
- Ahmed, M.; Khan, A.M.; Bibi, S.; Zakaria, M. Convergence of per capita CO2 emissions across the globe: Insights via wavelet analysis. Renew Sustain Energy Rev. 2017, 75, 86–97. [Google Scholar] [CrossRef]
- Stocker, T.; Qin, D.W.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M.; et al. (Eds.) IPCC 2013: Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef]
- Gurney, K.R.; Law, R.M.; Denning, A.S.; Rayner, P.J.; Baker, D.; Bousquet, P.; Bruhwiler, L.; Chen, Y.-H.; Ciais, P.; Fan, S.; et al. Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature 2002, 415, 626–630. [Google Scholar] [CrossRef]
- Wofsy, S.C.; Goulden, M.L.; Munger, J.W.; Fan, S.M.; Bakwin, P.S.; Daube, B.C.; Bassow, S.L.; Bazzaz, F.A. Net exchange of CO2 in a midlatitude forest. Science 1993, 260, 1314–1317. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Baldocchi, D. How eddy covariance flux measurements have contributed to our understanding of global change biology. Glob. Chang. Biol. 2020, 26, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, S.; Saigusa, N.; Gamo, M.; Fujinuma, Y.; Inoue, G.; Hirano, T. Findings through the AsiaFlux network and a view toward the future. J. Geogr. Sci. 2005, 15, 142–148. [Google Scholar] [CrossRef]
- Goulden, M.; Winston, G.; Cmillan, A.S.M.; Litvak, M.; Read, E.; Rocha, A.; Robelliot, J. An eddy covariance mesonet to measure the effect of forest age on land–atmosphere exchange. Glob. Chang. Biol. 2006, 12, 2146–2162. [Google Scholar] [CrossRef]
- Foken, T.; Aubinet, M.; Leuning, R. The eddy covariance method. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Aubinet, M., Vesala, T., Papale, D., Eds.; Springer Atmospheric Sciences: Berlin/Heidelberg, Germany, 2012; pp. 1–19. [Google Scholar]
- Yao, J.Y.; Gao, Z.M.; Huang, J.P.; Liu, H.P.; Wang, G.Y. Technical note: Uncertainties in eddy covariance CO2 fluxes in a semiarid sagebrush ecosystem caused by gap-filling approaches. Atmos. Chem. Phys. 2021, 21, 15589–15603. [Google Scholar] [CrossRef]
- Klosterhalfen, A.; Chi, J.; Kljun, N.; Lindroth, A.; Laudon, H.; Nilsson, M.B.; Peichl, M. Two-level eddy covariance measurements reduce bias in land-atmosphere exchange estimates over a heterogeneous boreal forest landscape. Agric. For. Meteorol. 2023, 339, 109523. [Google Scholar] [CrossRef]
- Liu, S.; Feng, Z.; Fang, S.; Liu, G.; Yuan, X.; Shang, B.; Xu, Y.S.; Fu, H.W.; Jin, Z.P.; Chen, Z.Y.; et al. Assessing the accuracy of eddy-covariance measurement at different source emission scenarios. J. Geophys. Res. Atmos. 2024, 129, e2023JD040701. [Google Scholar] [CrossRef]
- Van de Boer, A.; Moene, A.F.; Schuttemeyer, D.; Graf, A. Sensitivity and uncertainty of analytical footprint models according to a combined natural tracer and ensemble approach. Agric. For. Meteorol. 2013, 169, 1–11. [Google Scholar] [CrossRef]
- Lee, X. On micrometeorological observations of surface-air exchange over tall vegetation. Agric. For. Meteorol. 1998, 91, 39–49. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H. A re-evaluation of long-term flux measurement techniques part I: Averaging and coordinate rotation. Bound.-Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Twine, T.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Wesely, M. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 27–300. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Li, D.; Li, X. The effects of surface heterogeneity scale on the flux imbalance under free convection. J. Geophys. Res. Atmos. 2019, 124, 8424–8448. [Google Scholar] [CrossRef]
- Cao, M.K.; Prince, S.D.; Li, K.R.; Tao, B.; Small, J.; Shao, X.M. Response of terrestrial carbon uptake to climate interannual variability in China. Glob. Chang. Biol. 2003, 9, 536–546. [Google Scholar] [CrossRef]
- Cao, M.K.; Tao, B.; Li, K.R.; Shao, X.M.; Prience, S.D. Interannual variation in terrestrial ecosystem carbon fluxes in China from 1981 to 1998. Acta Bot. Sin. 2003, 45, 552–560. [Google Scholar]
- Zeng, N.; Mariotti, A.; Wetzel, P. Terrestrial mechanisms of interannual CO2 variability. Glob. Biogeochem. Cycles 2005, 19, Gb1016. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; Von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate-carbon cycle feedback analysis: Results from the (CMIP)-M-4 model intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Feng, X.; Liu, G.; Chen, J.M.; Chen, M.; Liu, J.; Ju, W.M.; Sun, R.; Zhou, W. Net primary productivity of China’s terrestrial ecosystems from a process model driven by remote sensing. J. Environ. Manag. 2007, 85, 563–573. [Google Scholar] [CrossRef]
- Li, X.L.; Liang, S.L.; Yu, G.R.; Yuan, W.P.; Cheng, X.; Xia, J.Z.; Zhao, T.B.; Feng, J.M.; Ma, Z.G.; Ma, M.G.; et al. Estimation of gross primary production over the terrestrial ecosystems in China. Ecol. Model. 2013, 261, 80–92. [Google Scholar] [CrossRef]
- Sitch, S.; Friedlingstein, P.; Gruber, N.; Jones, S.D.; Murray-Tortarolo, G.; Ahlström, A.; Doney, S.C.; Graven, H.; Heinze, C.; Huntingford, C.; et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 2015, 12, 653–679. [Google Scholar] [CrossRef]
- Wang, Q.F.; Zheng, H.; Zhu, X.J.; Yu, G.R. Primary estimation of Chinese terrestrial carbon sequestration during 2001–2010. Sci. Bull. 2015, 60, 577–590. [Google Scholar] [CrossRef]
- Xiao, J.F.; Zhou, Y.; Zhang, L. Contributions of natural and human factors to increases in vegetation productivity in China. Ecosphere 2015, 6, 1–20. [Google Scholar] [CrossRef]
- Li, X.R.; Zhu, Z.C.; Zeng, H.; Piao, S.L. Estimation of gross primary production in China (1982-2010) with multiple ecosystem models. Ecol. Model. 2016, 324, 33–44. [Google Scholar] [CrossRef]
- Mo, X.G.; Liu, S.X.; Chen, X.; Hu, S. Variability, tendencies, and climate controls of terrestrial evapotranspiration and gross primary productivity in the recent decade over China. Ecohydrology 2018, 11, e1951. [Google Scholar] [CrossRef]
- Yao, Y.T.; Li, Z.J.; Wang, T.; Chen, A.P.; Wang, X.H.; Du, M.Y.; Jia, G.S.; Li, Y.N.; Li, H.Q.; Luo, W.J.; et al. A new estimation of China’s net ecosystem productivity based on eddy covariance measurements and a model tree ensemble approach. Agric. For. Meteorol. 2018, 253, 84–93. [Google Scholar] [CrossRef]
- Yu, P.Y.; Zhang, Y.J.; Liu, P.R.; Zhang, J.S.; Xing, W.L.; Tong, X.J.; Zhang, J.R.; Meng, P. Regulation of biophysical drivers on carbon and water fluxes over a warm-temperate plantation in northern China. Sci. Total Environ. 2024, 907, 167408. [Google Scholar] [CrossRef]
- Wang, K.; Piao, S.; He, Y.; Liu, Y.; He, H. Spatial variations and mechanisms for the stability of terrestrial carbon sink in China. Sci. China Earth Sci. 2023, 66, 227–236. [Google Scholar] [CrossRef]
- Bai, J.H.; Yang, F.T.; Wang, H.M.; Xu, M.J. An empirical model of gross primary productivity (GPP) and relations between GPP and its driving factors, biogenic volatile organic compounds in a subtropical coniferous plantation in China. Atmosphere 2023, 14, 1046. [Google Scholar] [CrossRef]
- Bai, J.H.; Yang, F.T.; Xu, M.J.; Wang, H.M. Empirical models of respiration and net ecosystem productivity and their applications in a subtropical coniferous plantation in China. Atmosphere 2023, 14, 1557. [Google Scholar] [CrossRef]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, GB1015. [Google Scholar] [CrossRef]
- O’sullivan, M.; Friedlingstein, P.; Sitch, S.; Anthoni, P.; Arneth, A.; Arora, V.K.; Bastrikov, V.; Delire, C.; Goll, D.S.; Jain, A.; et al. Process-oriented analysis of dominant sources of uncertainty in the land carbon sink. Nat. Commun. 2022, 13, 4781. [Google Scholar] [CrossRef] [PubMed]
- Tans, P.P.; Fung, I.Y.; Takahashi, T. Observational constraints on the global atmospheric CO2 budget. Science 1990, 247, 1431–1438. [Google Scholar] [CrossRef] [PubMed]
- Denning, A.S.; Randall, D.A.; Collatz, G.J.; Sellers, P.J. Simulations of terrestrial carbon metabolism and atmospheric CO2 in a general circulation model. Tellus B 1996, 48, 543–567. [Google Scholar] [CrossRef][Green Version]
- Yao, Y.T.; Wang, X.H.; Li, Y.; Wang, T.; Shen, M.G.; Du, M.Y.; He, H.L.; Li, Y.N.; Luo, W.J.; Ma, M.G.; et al. Spatiotemporal pattern of gross primary productivity and its covariation with climate in China over the last thirty years. Glob. Chang. Biol. 2018, 24, 184–196. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, W.; Zhang, Y. The Change in Net Ecosystem Productivity and its Driving Mechanism in a Mountain Ecosystem of Arid Regions, Northwest China. Remote Sens. 2022, 14, 4046. [Google Scholar] [CrossRef]
- Gupta, S.; Burman, P.K.D.; Tiwari, Y.K.; Dumk, U.C.; Kumari, N.; Srivastava, A.; Raghubanshi, A.S. Understanding carbon sequestration trends using model and satellite data under different ecosystems in India. Sci. Total Environ. 2023, 897, 166381. [Google Scholar] [CrossRef]
- Granier, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Agric. For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Schmid, H.P.; Grimmond, C.S.; Cropley, F.; Offerle, B.; Su, H.B. Measurements of CO2 and energy fluxes over a mixed hardwood forest in the mid-n United States. Agric. For. Meteorol. 2000, 103, 357–374. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Loescher, H.W.; Law, B.E.; Mahrt, L.; Hollinger, D.Y.; Campbell, J.; Wofsy, S.C. Uncertainties in, and interpretation of, carbon flux estimates using the eddy covariance technique. J. Geophys. Res. 2006, 111, D21S90. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Gkritzalis, T.; Gregor, L.; Gruber, N.; Harris, I.; et al. Global carbon budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Dong, Y.X.; Yang, M.X.; Bakker, D.C.E.; Kitidis, V.; Bell, T.G. Uncertainties in eddy covariance air–sea CO2 flux measurements and implications for gas transfer velocity parameterisations. Atmos. Chem. Phys. 2021, 21, 8089–8110. [Google Scholar] [CrossRef]
- Nagy, L.; Bruce, R.F.; Paulo, A. (Eds.) Climate and the Amazonian Carbon Balance. In Ecological Studies 227; Springer Nature: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Robinson, J.M.; O’Neill, T.A.; Ryburn, J.; Liang, L.L.; Arcus, V.L.; Schipper, L.A. Rapid laboratory measurement of the temperature dependence of soil respiration and application to changes in three diverse soils through the year. Biogeochemistry 2017, 133, 101–112. [Google Scholar] [CrossRef]
- Remaud, M.; Chevallier, F.; Maignan, F.; Belviso, S.; Berchet, A.; Parouffe, A.; Abadie, C.; Bacour, C.; Lennartz, S.; Peylin, P. Plant gross primary production, plant respiration and carbonyl sulfide emissions over the globe inferred by atmospheric inverse modelling. Atmos. Chem. Phys. 2022, 22, 2525–2552. [Google Scholar] [CrossRef]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef]
- Fang, J.; Guo, Z.; Piao, S.; Chen, A. Terrestrial vegetation carbon sinks in China, 1981–2000. Sci. China Ser. D Earth Sci. 2007, 50, 1341–1350. [Google Scholar]
- Piao, S.; He, Y.; Wang, X.; Chen, F. Estimation of China’s terrestrial ecosystem carbon sink: Methods, progress and prospects. Sci. China Earth Sci. 2022, 65, 641–651. [Google Scholar] [CrossRef]
- Yu, G.R.; Chen, Z.; Piao, S.L.; Peng, C.H.; Ciais, P.; Wang, Q.F.; Li, X.R.; Zhu, X.J. High carbon dioxide uptake by subtropical forest ecosystems in the East Asian monsoon region. Proc. Natl. Acad. Sci. USA 2014, 111, 4910–4915. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Zhang, Y.; Wolf, S.; Zhou, S.; Joiner, J.; Guanter, L.; Verma, M.; Sun, Y.; Yang, X.; et al. On the Relationship between Sub-Daily Instantaneous and Daily Total Gross Primary Production: Implications for Interpreting Satellite-Based SIF Retrievals. Remote Sens. Environ. 2018, 205, 276–289. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, F.; Wang, H.; Qiu, B.; Wu, M.; He, W.; Ju, W.; Zhang, Y.; Chen, J.M.; Zhou, Y. Constraining Global Terrestrial Gross Primary Productivity in a Global Carbon Assimilation System with OCO-2 Chlorophyll Fluorescence Data. Agric. For. Meteorol. 2021, 304–305, 108424. [Google Scholar] [CrossRef]
- Pandiyan, S.; Navaneethan, C.; Vijayan, R.; Gunasekaran, G.; Khan, K.Y.; Guo, Y. Evaluation of Drought Using Satellite Solar-Induced Chlorophyll Fluorescence during Crop Development Stage over Xinjiang, China. Meas. J. Int. Meas. Confed. 2022, 187, 110327. [Google Scholar] [CrossRef]
- Jing, X.; Li, B.; Ye, Q.; Zou, Q.; Yan, J.; Du, K. Integrate the Canopy SIF and Its Derived Structural and Physiological Components for Wheat Stripe Rust Stress Monitoring. Remote Sens. 2022, 14, 3427. [Google Scholar] [CrossRef]
- Qiu, R.; Han, G.; Ma, X.; Xu, H.; Shi, T.; Zhang, M. A Comparison of OCO-2 SIF, MODIS GPP, and GOSIF Data from Gross Primary Production (GPP) Estimation and Seasonal Cycles in North America. Remote Sens. 2020, 12, 258. [Google Scholar] [CrossRef]
- Yu, G.R.; Wen, X.F.; Li, Q.K.; Zhang, L.M.; Ren, C.Y.; Liu, Y.F.; Guan, D.X. Seasonal patterns and environmental control of ecosystem respiration in subtropical and temperate forests in China. Sci. China Ser. D 2004, 34, 84–94. (In Chinese) [Google Scholar]
- Bai, J.H.; Duhl, T. A primary generalized empirical model of BVOC emissions for some typical forests in China. Atmos. Pollut. Res. 2021, 12, 101126. [Google Scholar] [CrossRef]
- Liu, Y.F.; Song, X.; Yu, G.R.; Sun, S.M.; Wen, X.F.; Chrn, Y.R. Seasonal dynamics of CO2 fluxes from subtropical plantation coniferous ecosystem. Sci. China Earth Sci. 2005, 48 (Suppl. I), 123–132. [Google Scholar]
- Xu, M.J.; Wang, H.M.; Wen, X.F.; Zhang, T.; Di, Y.B.; Wang, Y.D.; Wang, J.L.; Cheng, C.P.; Zhang, W.J. The full annual carbon balance of a subtropical coniferous plantation is highly sensitive to autumn precipitation. Sci. Rep. 2017, 1, 10025. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Sun, X.M.; Yu, G.R.; Wen, X.F.; Zhang, Y.P.; Han, S.J.; Yan, J.H.; Wang, H.M. Radiometers performance attenuation and data correction in long-term observation of total radiation and photosynthetically active radiation in typical forest ecosystems in China Chinese. J. Appl. Ecol. 2011, 22, 2954–2962. [Google Scholar]
- Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.; Chen, J.Y. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. Roy. Meteor. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the annual net carbon and water exchange of forests: The EUROFLUX methodology. Adv. Ecol. Res. 2000, 30, 113–175. [Google Scholar]
- Michaelis, L.; Menten, M.L. Die kinetik der invertinwirkung. Biochem 1913, 49, 333–369. [Google Scholar]
- Lloyd, J.; Taylor, J.A. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J. A Global, 0.05-Degree Product of Solar-Induced Chlorophyll Fluorescence Derived from OCO-2, MODIS, and Reanalysis Data. Remote Sens. 2019, 11, 517. [Google Scholar] [CrossRef]
- Yang, R.; Wang, M.; Zhao, M.; Feng, X. Synergic benefits of air pollutant reduction, CO2 emission abatement, and water saving under the goal of achieving carbon emission peak: The case of Tangshan city, China. Int. J. Environ. Res. Public Health. 2022, 19, 7145. [Google Scholar] [CrossRef]
- Yue, X.; Unger, N. Fire air pollution reduces global terrestrial productivity. Nat. Commun. 2018, 9, 5413. [Google Scholar] [CrossRef]
- Bai, J.H.; de Leeuw, G.; van der A, R.; Smedt, I.D.; Theys, N.; Van Roozendael, M.; Sogacheva, L.; Chai, W.H. Variations and photochemical transformations of atmospheric constituents in North China. Atmos. Environ. 2018, 189, 213–226. [Google Scholar] [CrossRef]
- Lee, J.D.; Drysdale, W.S.; Finch, D.P.; Wilde, S.E.; Palmer, P.I. UK surface NO2 levels dropped by 42% during the COVID-19 lockdown: Impact on surface O3. Atmos. Chem. Phys. 2020, 20, 15743–15759. [Google Scholar] [CrossRef]
- Weber, J.; King, J.A.; Abraham, N.L.; Grosvenor, D.P.; Smith, C.J.; Shin, Y.M.; Lawrence, P.; Roe, S.; Beerling, D.J.; Martin, M.V. Chemistry-albedo feedbacks offset up to a third of forestation’s CO2 removal benefits. Science 2024, 383, 860–864. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.H.; Wan, X.W.; Arslan, E.; Zong, X.M. Global solar radiation and its interactions with atmospheric substances, and their effects on air temperature change in Ankara Province. Climate 2024, 12, 35. [Google Scholar] [CrossRef]
- Liu, F.; Liu, H.Y.; Adalibieke, W.; Peng, Z.Y.; Liang, B.Y.; Feng, S.W.; Shi, L.; Zhu, X.R. Decline in stability of forest productivity in the tropics as determined by canopy water content. iScience 2023, 26, 107211. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Y.; Yun, H.; Wang, X.; Gong, X.; Duan, Y.; Liu, J. Variations in diurnal and seasonal net ecosystem carbon dioxide exchange in a semiarid sandy grassland ecosystem in China’s Horqin Sandy Land. Biogeosciences 2020, 17, 6309–6326. [Google Scholar] [CrossRef]
- Zhang, X.; Bi, J.; Zhu, D.; Meng, Z. Seasonal variation of net ecosystem carbon exchange and gross primary production over a Loess Plateau semi-arid grassland of northwest China. Sci. Rep. 2024, 14, 2916. [Google Scholar] [CrossRef]
- Magney, T.S.; Bowling, D.R.; Logan, B.A.; Grossmann, K.; Stutz, J.; Blanken, P.D.; Burns, S.P.; Cheng, R.; Garcia, M.A.; Kӧhler, P.; et al. Mechanistic evidence for tracking the seasonality of photosynthesis with solar-induced fluorescence. Proc. Natl. Acad. Sci. USA 2019, 116, 11640–11645. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, B.; Chen, J.; Zhou, J.; He, Q.Q.; Yu, H. Response of Vegetation Productivity to Greening and Drought in the Loess Plateau Based on VIs and SIF. Forests 2024, 15, 339. [Google Scholar] [CrossRef]
- Damm, A.; Elbers, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A.; et al. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.-E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Lee, J.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Yang, P.Q.; van der Tol, C. Linking canopy scattering of far-red Sun-induced chlorophyll fluorescence with reflectance. Remote Sens. Environ. 2018, 209, 456–467. [Google Scholar] [CrossRef]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2019, 231, 110772. [Google Scholar] [CrossRef]
- Wang, Y.N.; Wei, J.; Tang, X.G.; Hang, X.J.; Ma, M.G. Progress of using the chlorophyll fluorescence to estimate terrestrial gross primary production. Remote Sens. Technol. Appl. 2020, 35, 975–989. [Google Scholar]
- Qiu, B.; Guo, W.D. Progresses in solar-induced chlorophyll fluorescence and its applications in terrestrial ecosystem carbon cycling and land-atmosphere interaction. Trans. Atmos. Sci. 2022, 45, 801–814. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lv, Y.J.; Li, J.K. Spatial and temporal distribution characteristics of solar energy resources and and utilization in construction in Jiangxi Province. J. Henan Univ. Urban Constr. 2017, 26, 81–87. [Google Scholar] [CrossRef]
- Liu, M.; He, H.-L.; Yu, G.-R.; Sun, X.-M.; Zhu, X.-D.; Zhang, L.; Zhao, X.-Q.; Wang, H.-M.; Shi, P.-L.; Han, S.-J. Impacts of uncertainty in data processing on estimation of CO2 flux components. Chin. J. Appl. Ecol. 2010, 21, 2389–2396. [Google Scholar]
- Bai, J.H. A calibration method of solar radiometers. Atmos. Pollut. Res. 2019, 10, 1365–1373. [Google Scholar] [CrossRef]
- Wieckowski, A.; Vestin, P.; Ardö, J.; Roupsard, O.; Ndiaye, O.; Diatta, O.; Ba, S.; Agbohessou, Y.; Fensholt, R.; Verbruggen, W.; et al. Eddy covariance measurements reveal a decreased carbon sequestration strength 2010–2022 in an African semiarid savanna. Glob. Chang. Biol. 2024, 30, e17509. [Google Scholar] [CrossRef]
- Gu, L.H.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. 2002, 107, ACL 2-1–ACL 2-23. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014–1017. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, J.; Chen, M.; Xu, X.; Wang, Z.; Wang, B.; Wang, C.; Piao, S.; Lin, W.; Miao, G.; et al. Field evidences for the positive effects of aerosols on tree growth. Glob. Chang. Biol. 2018, 24, 4983–4992. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Zhang, L.; Chen, Z.; He, W.; Liu, Y.; Shen, Y. Modeling the effects of global and diffuse radiation on terrestrial gross primary productivity in china based on a two-leaf light use efficiency model. Remote Sens. 2020, 12, 3355. [Google Scholar] [CrossRef]
- Zhou, H.; Yue, X.; Lei, Y.; Zhang, T.; Tian, C.; Ma, Y.; Cao, Y. Responses of gross primary productivity to diffuse radiation at global FLUXNET sites. Atmos. Environ. 2021, 244, 117905. [Google Scholar] [CrossRef]
- Lowe, P.R. An approximating polynomial for computation of saturation vapor pressure. J. Appl. Meteorol. 1977, 16, 100–103. [Google Scholar] [CrossRef]
- Yu, Z.; Ciais, P.; Piao, S.; Houghton, R.A.; Lu, C.; Tian, H.; Agathokleous, E.; Kattel, G.R.; Sitch, S.; Goll, D.; et al. Forest expansion dominates China’s land carbon sink since 1980. Nat. Commun. 2022, 13, 5374. [Google Scholar] [CrossRef]
- Wu, D.; Shao, Q.; Li, J. Effects of afforestation on carbon storage in Boyang Lake Basin, China. Chin. Geogr. Sci. 2013, 23, 647–654. [Google Scholar] [CrossRef][Green Version]
- Li, S.P.; Matthews, J.; Sinha, A. Atmospheric hydroxyl radical production from electronically excited NO2 and H2O. Science 2008, 319, 1657–1660. [Google Scholar] [CrossRef]
- Rocha, A.V.; Su, H.B.; Vogel, C.S.; Schmid, H.P.; Curtis, P.S. Photosynthetic and water use efficiency responses to diffuse radiation by an aspen-dominated northern hardwood forest. For. Sci. 2004, 50, 793–801. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L. Exploring the link between clouds, radiation, and canopy productivity of tropical savannas. Agr. Forest Meteorol. 2013, 182, 304–313. [Google Scholar] [CrossRef]
- Cirino, G.G.; Souza, R.A.F.; Adams, D.K.; Artaxo, P. The effect of atmospheric aerosol particles and clouds on net ecosystem exchange in the Amazon. Atmos. Chem. Phys. 2014, 14, 6523–6543. [Google Scholar] [CrossRef]
- Bouvier-Brown, N.C.; Schade, G.W.; Misson, L.; Lee, A.; McKay, M.; Goldstein, A.H. A Contributions of biogenic volatile organic compounds to net ecosystem carbon flux in a ponderosa pine plantation. Atmos. Environ. 2012, 60, 527–533. [Google Scholar] [CrossRef]
- Cohan, D.S.; Xu, J.; Greenwald, R.; Bergin, M.H.; Chameides, W.L. Impact of atmospheric aerosol light scattering and absorption on terrestrial net primary productivity, Global Biogeochem. Cycles 2002, 16, 1090. [Google Scholar] [CrossRef]
- Knohl, A.; Baldocchi, D.D. Effects of diffuse radiation on canopy gas exchange processes in a forest ecosystem. J. Geophys. Res. 2008, 113, G02023. [Google Scholar] [CrossRef]
- Kesselmeier, J.; Ciccioli, P.; Kuhn, U.; Stefani, P.; Biesenthal, T.; Rottenberger, S.; Wolf, A.; Vitullo, M.; Valentini, R.; Nobre, A.; et al. Volatile organic compound emissions in relation to plant carbon fixation and the terrestrial carbon budget. Glob. Biogeochem. Cycles 2002, 16, 73-1–73-9. [Google Scholar] [CrossRef]
- Guenther, A. The contribution of reactive carbon emissions from vegetation to the carbon balance of terrestrial ecosystems. Chemosphere 2002, 49, 837–844. [Google Scholar] [CrossRef]
- Thais, M.R.; Sitch, S.; O’Sullivan, M.; Basso, L.S.; Wilson, C.; Silva, C.; Gloor, E.; Fawcett, D.; Heinrich, V.; Souza, J.G.; et al. Synthesis of the land carbon fluxes of the Amazon region between 2010 and 2020. Commun. Earth Environ. 2024, 5, 46. [Google Scholar]
- Chen, J.; Avise, J.; Guenther, A.; Wiedinmyer, C.; Salathe, E.; Jackson, R.B.; Lamb, B. Future land use and land cover influences on regional biogenic emissions and air quality in the United States. Atmos. Environ. 2009, 43, 5771–5780. [Google Scholar] [CrossRef]
- Xu, L.; He, N.P.; Li, M.X.; Cai, W.X.; Yu, G.R. Spatiotemporal dynamics of carbon sinks in China’s terrestrial ecosystems from 2010 to 2060. Resources. Conserv. Recycl. 2024, 203, 107457. [Google Scholar] [CrossRef]
- Wang, J.; Feng, L.; Palmer, P.I.; Liu, Y.; Fang, S.X.; Bösch, H.; W.O’Dell, C.; Tang, X.P.; Yang, D.X.; Liu, L.X.; et al. Large Chinese land carbon sink estimated from atmospheric carbon dioxide data. Nature 2020, 586, 720–723. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.H. UV extinction in the atmosphere and its spatial variation in North China. Atmos. Environ. 2017, 154, 318–330. [Google Scholar] [CrossRef]
- Bai, J.H.; Wan, X.W.; Chai, W.H.; Wu, Y.M.; Li, K.L.; Song, T. Study on the importance of the observational data and their accuracies. Adv. Geosci. 2024, 14, 722–732. (In Chinese) [Google Scholar] [CrossRef]








| RMSE | MAD | σobs | σcal | NMSE | R3 | R2 | R1 | obs | cal3 | cal2 | cal1 | Model | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (mgCO2 m− 2 s−1) | (%) | (mgCO2 m−2 s−1) | |||||||||||
| 69.51 | 0.301 | 52.75 | 0.228 | 0.299 | 0.333 | 0.434 | 1.114 | 1.035 | 1.931 | 0.433 | 0.482 | 0.447 | 0.835 | EMGPP |
| 174.98 | 0.367 | 141.04 | 0.215 | 0.073 | 0.320 | 2.888 | 1.060 | 0.592 | 3.611 | 0.153 | 0.162 | 0.090 | 0.551 | EMRe |
| 41.58 | 0.247 | 35.85 | 0.213 | 0.259 | 0.155 | 0.265 | 0.651 | 0.598 | 0.472 | 0.998 | 0.761 | 0.727 | 0.761 | EMNEP |
| RMSE | MAD | σobs | σcal | NMSE | R3 | R2 | R1 | obs | cal3 | cal2 | cal1 | Model | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (mgCO2 m− 2 s−1) | (%) | (mgCO2 m−2 s−1) | |||||||||||
| 55.81 | 2.643 | 42.82 | 2.028 | 2.372 | 3.338 | 0.280 | 1.114 | 1.035 | 1.931 | 4.736 | 5.276 | 4.901 | 9.144 | EMGPP |
| 151.01 | 2.533 | 126.42 | 2.121 | 0.801 | 3.192 | 2.159 | 1.056 | 0.592 | 3.611 | 1.678 | 1.771 | 0.993 | 6.058 | EMRe |
| 39.06 | 2.547 | 34.99 | 2.282 | 1.411 | 0.608 | 0.235 | 0.650 | 0.599 | 0.473 | 6.522 | 4.240 | 3.906 | 3.084 | EMNEP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Yang, F.; Wang, H.; Yao, L.; Xu, M. Multiple-Win Effects and Beneficial Implications from Analyzing Long-Term Variations of Carbon Exchange in a Subtropical Coniferous Plantation in China. Atmosphere 2024, 15, 1218. https://doi.org/10.3390/atmos15101218
Bai J, Yang F, Wang H, Yao L, Xu M. Multiple-Win Effects and Beneficial Implications from Analyzing Long-Term Variations of Carbon Exchange in a Subtropical Coniferous Plantation in China. Atmosphere. 2024; 15(10):1218. https://doi.org/10.3390/atmos15101218
Chicago/Turabian StyleBai, Jianhui, Fengting Yang, Huimin Wang, Lu Yao, and Mingjie Xu. 2024. "Multiple-Win Effects and Beneficial Implications from Analyzing Long-Term Variations of Carbon Exchange in a Subtropical Coniferous Plantation in China" Atmosphere 15, no. 10: 1218. https://doi.org/10.3390/atmos15101218
APA StyleBai, J., Yang, F., Wang, H., Yao, L., & Xu, M. (2024). Multiple-Win Effects and Beneficial Implications from Analyzing Long-Term Variations of Carbon Exchange in a Subtropical Coniferous Plantation in China. Atmosphere, 15(10), 1218. https://doi.org/10.3390/atmos15101218








