Stochastic Parameterization of Moist Physics Using Probabilistic Diffusion Model
Abstract
1. Introduction
2. Methodology
2.1. Training Data Preprocessing
2.2. DIFF-MP, Inference Acceleration, and Classifier-Free Guidance
2.2.1. DIFF-MP
2.2.2. Inference Acceleration of DIFF-MP
| Algorithm 1. The training algorithm of DIFF-MP with inference acceleration. |
| Require: a fixed noise schedule |
| 1: repeat |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: take gradient descent step on |
| 7: until converged |
| Algorithm 2. The sampling algorithm of DIFF-MP with inference acceleration. |
| Require: denoising steps T |
| Require: noise level function |
| 1: get denoising schedule from |
| 2: |
| 3: for do |
| 4: if , else |
| 5: |
| 6: end for |
| 7: return |
2.2.3. Classifier-Free Guidance of DIFF-MP
| Algorithm 3. The training algorithm of DIFF-MP with classifier-free guidance and inference acceleration. |
| Require: a fixed noise schedule |
| Require: probability of unconditional training |
| 1: repeat |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: with probability |
| 7: take gradient descent step on |
| 8: until converged |
| Algorithm 4. The sampling algorithm of DIFF-MP with classifier-free guidance and inference acceleration. |
| Require: denoising steps |
| Require: noise level function |
| Require: guidance strength |
| 1: get denoising schedule from |
| 2: |
| 3: for do |
| 4: if , else |
| 5: |
| 6: |
| 7: end for |
| 8: return |
3. Results
3.1. Baseline Models and Their Trainings
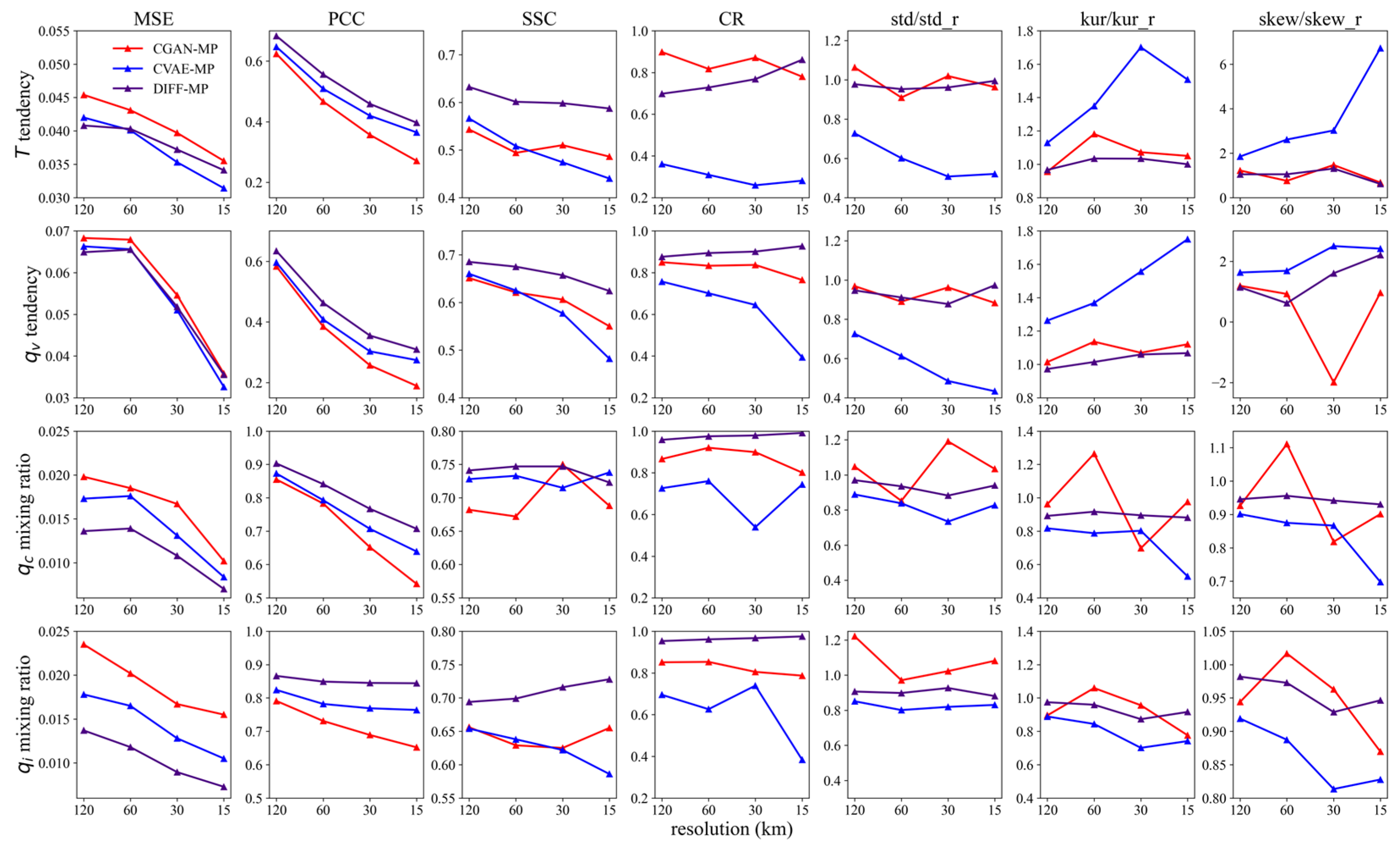
3.2. Performance Comparison between Models
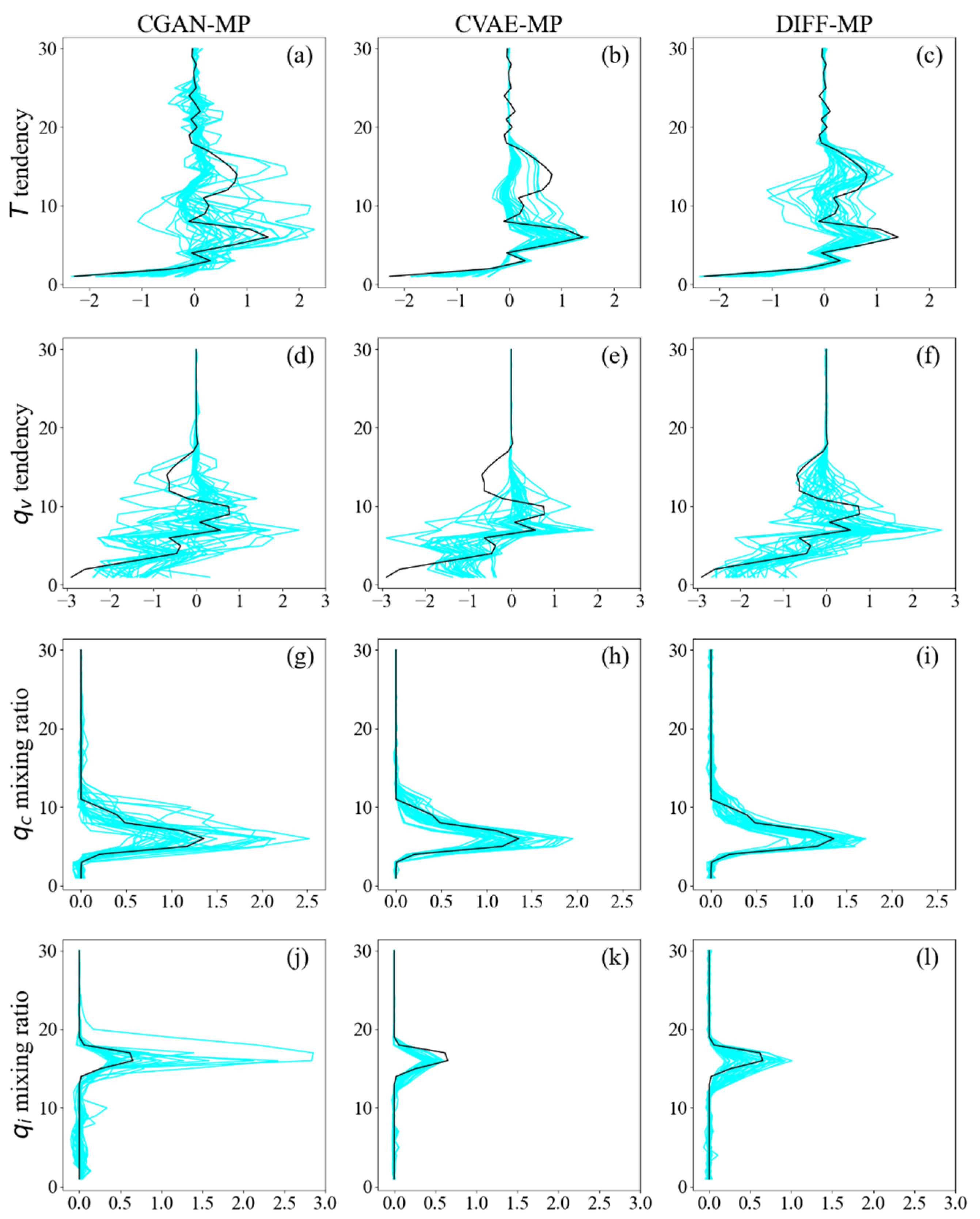
3.3. Interpretability of DIFF-MP
4. Conclusions and Discussions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Daleu, C.L.; Plant, R.S.; Woolnough, S.J.; Sessions, S.; Herman, M.J.; Sobel, A.; Wang, S.; Kim, D.; Cheng, A.; Bellon, G.; et al. Intercomparison of methods of coupling between convection and large-scale circulation: 1. Comparison over uniform surface conditions. J. Adv. Model. Earth Syst. 2015, 7, 1576–1601. [Google Scholar] [CrossRef] [PubMed]
- Daleu, C.L.; Plant, R.S.; Woolnough, S.J.; Sessions, S.; Herman, M.J.; Sobel, A.; Wang, S.; Kim, D.; Cheng, A.; Bellon, G.; et al. Intercomparison of methods of coupling between convection and large-scale circulation: 2. Comparison over nonuniform surface conditions. J. Adv. Model. Earth Syst. 2016, 8, 387–405. [Google Scholar] [CrossRef]
- Arnold, N.P.; Branson, M.; Burt, M.A.; Abbot, D.S.; Kuang, Z.; Randall, D.A.; Tziperman, E. Effects of explicit atmospheric convection at high CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 10943–10948. [Google Scholar] [CrossRef]
- Hohenegger, C.; Stevens, B. Coupled radiative convective equilibrium simulations with explicit and parameterized convection. J. Adv. Model. Earth Syst. 2016, 8, 1468–1482. [Google Scholar] [CrossRef]
- Bony, S.; Stevens, B.; Frierson, D.M.W.; Jakob, C.; Kageyama, M.; Pincus, R.; Shepherd, T.G.; Sherwood, S.C.; Pier Siebesma, A.; Sobel, A.H.; et al. Clouds, circulation, and climate sensitivity. Nat. Geosci. 2015, 8, 261–268. [Google Scholar] [CrossRef]
- Coppin, D.; Bony, S. Physical mechanisms controlling the initiation of convective self-aggregation in a general circulation model. J. Adv. Model. Earth Syst. 2015, 7, 2060–2078. [Google Scholar] [CrossRef]
- Nie, J.; Shaevitz, D.A.; Sobel, A.H. Forcings and feedbacks on convection in the 2010 Pakistan flood: Modeling extreme precipitation with interactive large-scale ascent. J. Adv. Model. Earth Syst. 2016, 8, 1055–1072. [Google Scholar] [CrossRef]
- Brenowitz, N.D.; Bretherton, C.S. Prognostic validation of a neural network unified physics parameterization. Geophys. Res. Lett. 2018, 45, 6289–6298. [Google Scholar] [CrossRef]
- Gentine, P.; Pritchard, M.; Rasp, S.; Reinaudi, G.; Yacalis, G. Could machine learning break the convection parameterization deadlock? Geophys. Res. Lett. 2018, 45, 5742–5751. [Google Scholar] [CrossRef]
- Beucler, T.; Gentine, P.; Yuval, J.; Gupta, A.; Peng, L.; Lin, J.; Yu, S.; Rasp, S.; Ahmed, F.; O’Gorman, P.A.; et al. Climate-invariant machine learning. Sci. Adv. 2024, 10, eadj7250. [Google Scholar] [CrossRef]
- Brenowitz, N.D.; Bretherton, C.S. Spatially extended tests of a neural network parametrization trained by coarse-graining. J. Adv. Model. Earth Syst. 2019, 11, 2728–2744. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, G.J.; Huang, X.; Wang, Y. A moist physics parameterization based on deep learning. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002076. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, G.J.; Wang, Y. An ensemble of neural networks for moist physics processes, its generalizability and stable integration. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003508. [Google Scholar] [CrossRef]
- Lin, J.; Yu, S.; Peng, L.; Beucler, T.; Wong-Toi, E.; Hu, Z.; Gentine, P.; Geleta, M.; Pritchard, M. Sampling Hybrid Climate Simulation at Scale to Reliably Improve Machine Learning Parameterization. arXiv 2024, arXiv:2309.16177. [Google Scholar]
- Mooers, G.; Pritchard, M.; Beucler, T.; Ott, J.; Yacalis, G.; Baldi, P.; Gentine, P. Assessing the potential of deep learning for emulating cloud superparameterization in climate models with real-geography boundary conditions. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002385. [Google Scholar] [CrossRef]
- Rasp, S.; Pritchard, M.S.; Gentine, P. Deep learning to represent subgrid processes in climate models. Proc. Natl. Acad. Sci. USA 2018, 115, 9684–9689. [Google Scholar] [CrossRef]
- Wang, X.; Han, Y.; Xue, W.; Yang, G.; Zhang, G.J. Stable climate simulations using a realistic general circulation model with neural network parameterizations for atmospheric moist physics and radiation processes. Geosci. Model. Dev. 2022, 15, 3923–3940. [Google Scholar] [CrossRef]
- Watt-Meyer, O.; Brenowitz, N.D.; Clark, S.K.; Henn, B.; Kwa, A.; McGibbon, J.; Perkins, W.A.; Harris, L.; Bretherton, C.S. Neural network parameterization of subgrid-scale physics from a realistic geography global storm-resolving simulation. J. Adv. Model. Earth Syst. 2024, 16, e2023MS003668. [Google Scholar] [CrossRef]
- Yuval, J.; O’Gorman, P.A. Stable machine-learning parameterization of subgrid processes for climate modeling at a range of resolutions. Nat. Commun. 2020, 11, 3295. [Google Scholar] [CrossRef]
- Yuval, J.; O’Gorman, P.A.; Hill, C.N. Use of neural networks for stable, accurate and physically consistent parameterization of subgrid atmospheric processes with good performance at reduced precision. Geophys. Res. Lett. 2021, 48, e2020GL091363. [Google Scholar] [CrossRef]
- Buizza, R.; Miller, M.; Palmer, T.N. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 1999, 125, 2887–2908. [Google Scholar] [CrossRef]
- Christensen, H.M.; Berner, J.; Coleman, D.; Palmer, T.N. Stochastic parametrisation and the El Niño-Southern oscillation. J. Clim. 2017, 30, 17–38. [Google Scholar] [CrossRef]
- Weisheimer, A.; Corti, S.; Palmer, T. Addressing model error through atmospheric stochastic physical parametrizations: Impact on the coupled ECMWF seasonal forecasting system. Phil. Trans. R. Soc. A 2014, 372, 20130290. [Google Scholar] [CrossRef]
- Kingma, D.; Welling, M. Auto-encoding variational Bayes. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Alcala, J.; Timofeyev, I. Subgrid-scale parametrization of unresolved scales in forced Burgers equation using generative adversarial networks (GAN). Theor. Comp. Fluid. Dyn. 2021, 35, 875–894. [Google Scholar] [CrossRef]
- Bhouri, M.A.; Gentine, P. History-Based, Bayesian, Closure for Stochastic Parameterization: Application to Lorenz’ 96. arXiv 2022, arXiv:2210.14488. [Google Scholar]
- Crommelin, D.; Edeling, W. Resampling with neural networks for stochastic parameterization in multiscale systems. Phys. D Nonlinear Phenom. 2021, 422, 132894. [Google Scholar] [CrossRef]
- Gagne, D.J.; Christensen, H.; Subramanian, A.; Monahan, A.H. Machine learning for stochastic parameterization: Generative adversarial networks in the lorenz’ 96 model. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001896. [Google Scholar] [CrossRef]
- Nadiga, B.T.; Sun, X.; Nash, C. Stochastic parameterization of column physics using generative adversarial networks. Environ. Data Sci. 2022, 1, e22. [Google Scholar] [CrossRef]
- Parthipan, R.; Christensen, H.M.; Hosking, J.S.; Wischik, D.J. Using probabilistic machine learning to better model temporal patterns in parameterizations: A case study with the Lorenz 96 model. Geosci. Model. Dev. 2023, 16, 4501–4519. [Google Scholar] [CrossRef]
- Perezhogin, P.; Zanna, L.; Fernandez-Granda, C. Generative data-driven approaches for stochastic subgrid parameterizations in an idealized ocean model. J. Adv. Model. Earth Syst. 2023, 15, e2023MS003681. [Google Scholar] [CrossRef]
- Bao, J.; Chen, D.; Wen, F.; Li, H.; Hua, G. CVAE-GAN: Fine-grained image generation through asymmetric training. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ichikawa, Y.; Hukushima, K. Learning Dynamics in Linear VAE: Posterior Collapse Threshold, Superfluous Latent Space Pitfalls, and Speedup with KL Annealing. In Proceedings of the 27th International Conference on Artificial Intelligence and Statistics, PMLR, València, Spain, 2–4 May 2024. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Huang, H.; Li, Z.; He, R.; Sun, Z.; Tan, T. IntroVAE: Introspective variational autoencoders for photographic image synthesis. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Kim, T.; Cha, M.; Kim, H.; Lee, J.K.; Kim, J. Learning to discover cross-domain relations with generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the 34th Annual Conference on Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Esser, P.; Kulal, S.; Blattmann, A.; Entezari, R.; Müller, J.; Saini, H.; Levi, Y.; Lorenz, D.; Sauer, A.; Boesel, F.; et al. Scaling rectified flow transformers for high-resolution image synthesis. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Luo, C. Understanding diffusion models: A unified perspective. arXiv 2022, arXiv:2208.11970. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Online, 18–24 July 2021. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. In Proceedings of the 35th Annual Conference on Neural Information Processing Systems, Online, 6–14 December 2021. [Google Scholar]
- Chen, N.; Zhang, Y.; Zen, H.; Weiss, R.J.; Norouzi, M.; Chan, W. Wavegrad: Estimating gradients for waveform generation. arXiv 2020, arXiv:2009.00713. [Google Scholar]
- Ho, J.; Salimans, T. Classifier-free diffusion guidance. arXiv 2022, arXiv:2207.12598. [Google Scholar]
- Zhang, Y.; Li, J.; Yu, R.; Zhang, S.; Liu, Z.; Huang, J.; Zhou, Y. A layer-averaged nonhydrostatic dynamical framework on an unstructured mesh for global and regional atmospheric modeling: Model description, baseline evaluation, and sensitivity exploration. J. Adv. Model. Earth Syst. 2019, 11, 1685–1714. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Yu, R.; Liu, Z.; Zhou, Y.; Li, X.; Huang, X. A multiscale dynamical model in a dry-mass coordinate for weather and climate modeling: Moist dynamics and its coupling to physics. Mon. Weather Rev. 2020, 148, 2671–2699. [Google Scholar] [CrossRef]
- Heikes, R.; Randall, D.A. Numerical integration of the shallow-water equations on a twisted icosahedral grid. Part II. A detailed description of the grid and an analysis of numerical accuracy. Mon. Weather Rev. 1995, 123, 1881–1887. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). Asia-Pac. J. Atmos. Sci. 2006, 42, 129–151. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Bińkowski, M.; Donahue, J.; Dieleman, S.; Clark, A.; Elsen, E.; Casagrande, N.; Cubo, L.C.; Simonyan, K. High fidelity speech synthesis with adversarial networks. arXiv 2019, arXiv:1909.11646. [Google Scholar]
- Park, T.; Liu, M.Y.; Wang, T.C.; Zhu, J.Y. Semantic image synthesis with spatially-adaptive normalization. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 10 September 2024).
- Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. In Proceedings of the 33rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Song, Y.; Ermon, S. Improved techniques for training score-based generative models. In Proceedings of the 34th Annual Conference on Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Wang, L.-Y.; Tan, Z.-M. Deep learning parameterization of the tropical cyclone boundary layer. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003034. [Google Scholar] [CrossRef]
- McGibbon, J.; Brenowitz, N.D.; Cheeseman, M.; Clark, S.K.; Dahm, J.P.; Davis, E.C.; Elbert, O.D.; George, R.C.; Harris, L.M.; Henn, B.; et al. fv3gfs-wrapper: A Python wrapper of the FV3GFS atmospheric model. Geosci. Model. Dev. 2021, 14, 4401–4409. [Google Scholar] [CrossRef]
- Pietrini, R.; Paolanti, M.; Frontoni, E. Bridging Eras: Transforming Fortran legacies into Python with the power of large language models. In Proceedings of the 2024 IEEE 3rd International Conference on Computing and Machine Intelligence, Mount Pleasant, MI, USA, 16–17 March 2024. [Google Scholar]
- Zhou, A.; Hawkins, L.; Gentine, P. Proof-of-concept: Using ChatGPT to Translate and Modernize an Earth System Model from Fortran to Python/JAX. arXiv 2024, arXiv:2405.00018. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]









| Conditional Input | Level Number | Output | Level Number |
|---|---|---|---|
| Temperature | 30 | Subgrid tendencies for | 30 |
| Water vapor mixing ratio | 30 | Subgrid tendencies for | 30 |
| Surface pressure | 1 | Cloud water mixing ratio | 30 |
| Sensible heat flux | 1 | Cloud ice mixing ratio | 30 |
| Latent heat flux | 1 | ||
| Shortwave radiation at surface | 1 |
| 120 km | 60 km | 30 km | 15 km | |
|---|---|---|---|---|
| 0.5 | 0.6 | 0.6 | 0.8 | |
| 0.5 | 0.6 | 0.6 | 1.0 | |
| 0.0 | 0.0 | 0.0 | 0.3 | |
| 0.0 | 0.0 | 0.0 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, Y.; Hu, X.; Wang, H.; Zhou, R. Stochastic Parameterization of Moist Physics Using Probabilistic Diffusion Model. Atmosphere 2024, 15, 1219. https://doi.org/10.3390/atmos15101219
Wang L, Wang Y, Hu X, Wang H, Zhou R. Stochastic Parameterization of Moist Physics Using Probabilistic Diffusion Model. Atmosphere. 2024; 15(10):1219. https://doi.org/10.3390/atmos15101219
Chicago/Turabian StyleWang, Leyi, Yiming Wang, Xiaoyu Hu, Hui Wang, and Ruilin Zhou. 2024. "Stochastic Parameterization of Moist Physics Using Probabilistic Diffusion Model" Atmosphere 15, no. 10: 1219. https://doi.org/10.3390/atmos15101219
APA StyleWang, L., Wang, Y., Hu, X., Wang, H., & Zhou, R. (2024). Stochastic Parameterization of Moist Physics Using Probabilistic Diffusion Model. Atmosphere, 15(10), 1219. https://doi.org/10.3390/atmos15101219








