Nonlinear Calibration and Temperature Sensitivity of Makrofol Solid-State Nuclear Track Detectors for Radon Measurement
Abstract
1. Introduction
2. Materials and Methods
2.1. SSNTD
2.2. Radon Exposures
2.3. Calibration
2.4. Postal Background and Detection Limits
2.5. Uncertainty Budget
3. Results
3.1. Detector Background
3.2. Track Densities of the Exposed Detectors
3.3. Fitting the Calibration Function
3.4. Calibration at Cold Temperature
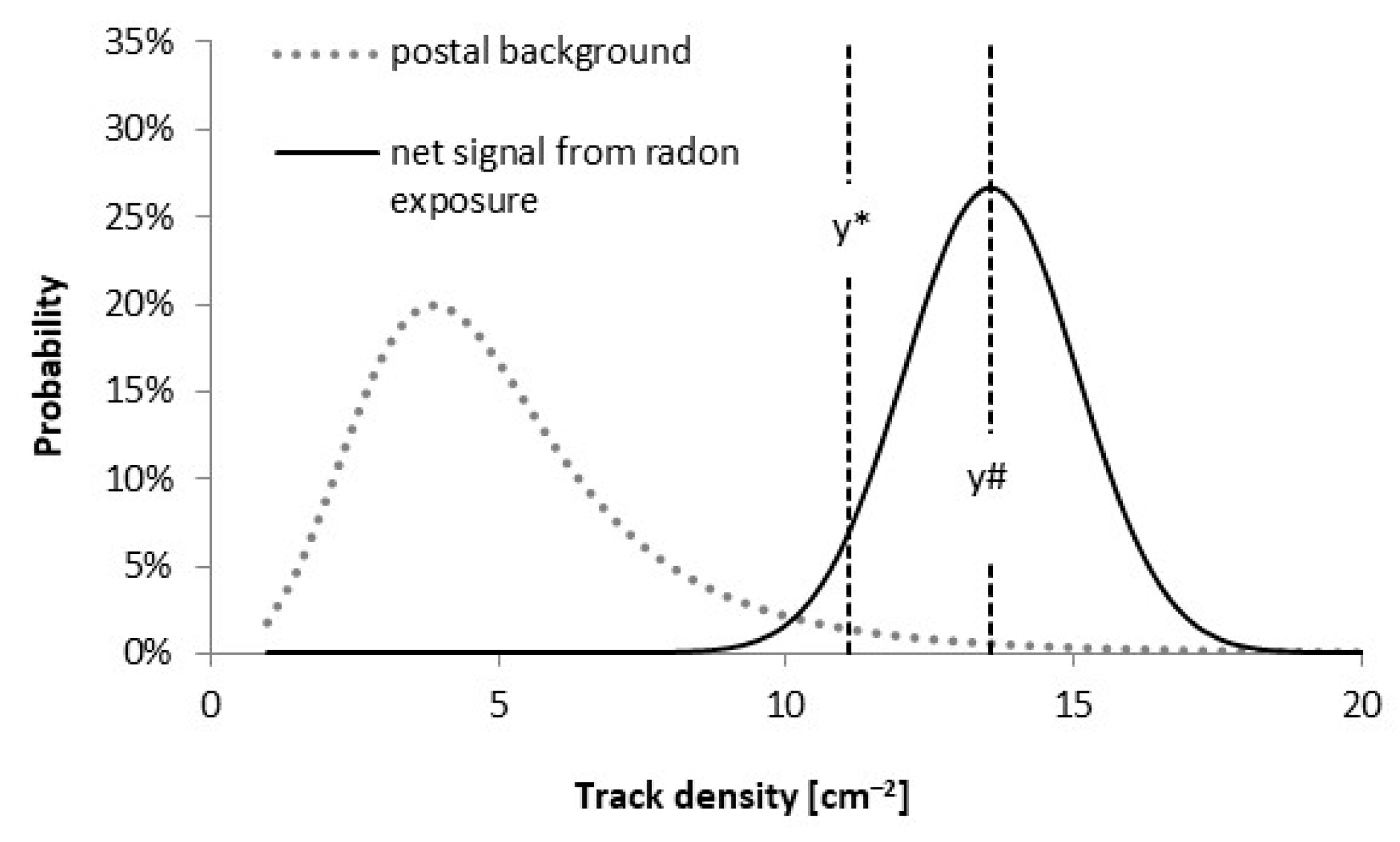
3.5. Postal Background and Minimum Detectable Exposure
3.6. Maximum Detectable Concentration
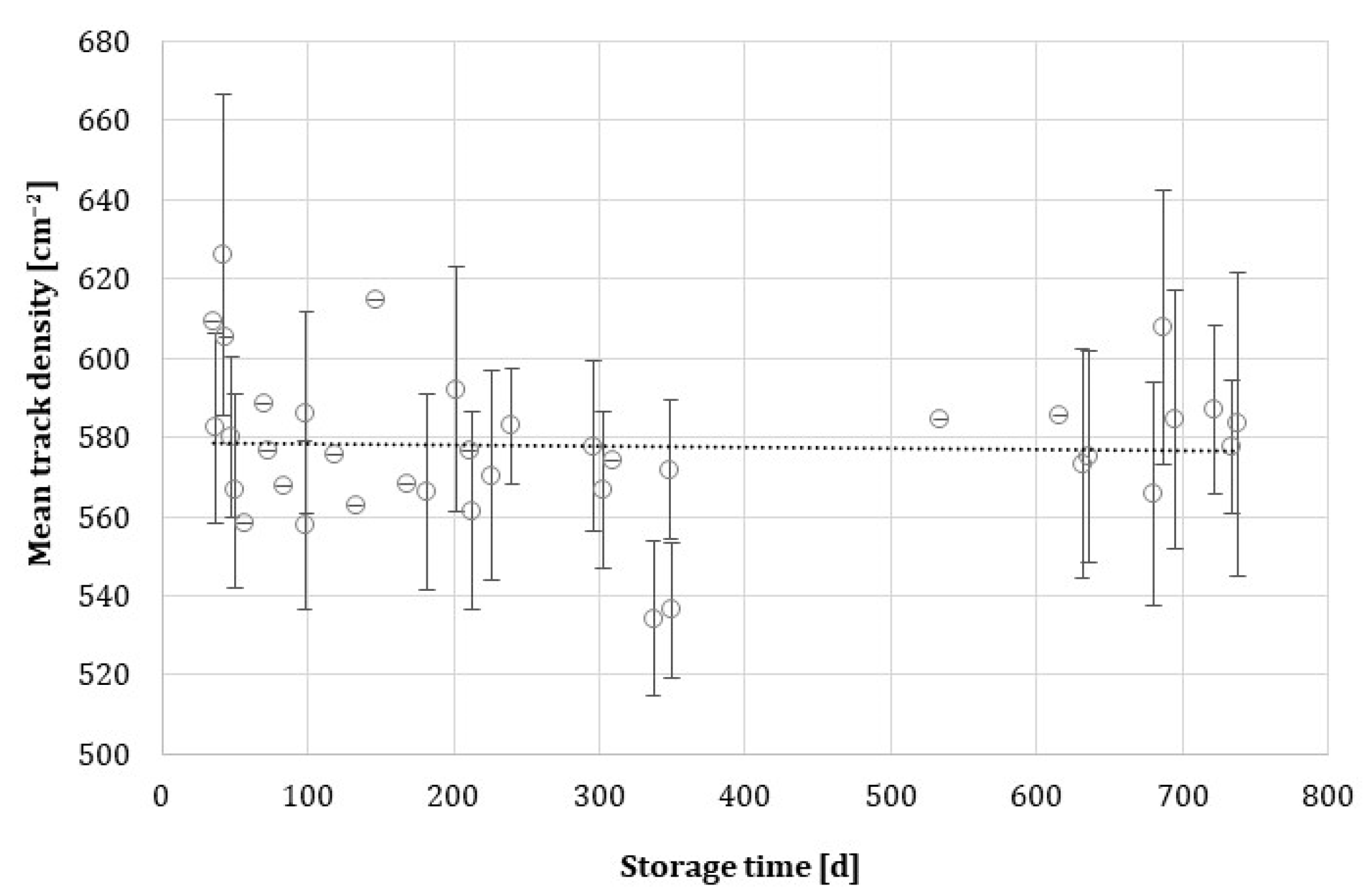
3.7. Thermal Fading of Latent Tracks
3.8. Uncertainty of Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Durrani, S.A. Alpha Particle Etched Track Detectors. In Radon Measurements by Etched Track Detectors; Durrani, S.A., Ilić, R., Eds.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1997; pp. 75–101. [Google Scholar]
- ICRP—The International Commission on Radiological Protection. Radiological Protection against Radon Exposure; ICRP Publication 126; ICRP: Ottawa, ON, Canada, 2014. [Google Scholar]
- López-Coto, I.; Bolívar, J.P. A theoretical model for the overlapping effect in solid state nuclear track detectors. Nucl. Instrum. Methods Phys. Res. 2011, A 652, 550–553. [Google Scholar] [CrossRef]
- Miles, J.J.H. Calibration and Standardisation of Etched Track Detectors. In Radon Measurements by Etched Track Detectors; Durrani, S.A., Ilić, R., Eds.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1997; pp. 143–154. [Google Scholar]
- STUK—Radiation and Nuclear Safety Authority. Radiation and Nuclear Safety Authority Regulation on Practices that Cause Exposure to Natural Radiation. Regulation STUK S/6/2022; STUK: Helsinki, Finland, 2022; pp. 1–11. Available online: https://www.stuklex.fi/en/maarays/stuk-s-6-2022 (accessed on 5 September 2024).
- Turtiainen, T.; Kojo, K.; Laine, J.-P.; Holmgren, O.; Kurttio, P. Improving the assessment of occupational exposure to radon in above-ground workplaces. Radiat. Prot. Dosim. 2021, 196, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Pressyanov, D.; Buysse, J.; Poffijn, A.; Van Deynse, A.; Meesen, G. Integrated measurements of 222Rn by absorption in Makrofol. Nucl. Instrum. Methods Phys. Res. 2004, 516, 203–208. [Google Scholar] [CrossRef]
- El-Sersy, A.; Mansy, M.; Hussein, A. Effect of environmental conditions on radon concentration—Track density calibration factor of solid-state nuclear track detectors. Pramana 2004, 62, 861–867. [Google Scholar] [CrossRef]
- Pressyanov, D.; Mitev, K.; Dimitrova, I.; Georgiev, S.; Dutsov, C.; Michielsen, N.; Bondiguel, S.; Malet, J.; Cassette, P.; Sabot, B.; et al. Report on the Influence of Thoron on Radon Monitors Used in Europe Including (i) Procedures for Checking Their Sensitivity to Thoron, (ii) Recommendations on the Construction of Radon Monitors That Are Not Sensitive to Thoron and (iii) Technical Approaches Aimed at Reducing Thoron-Related Bias in the Radon Signal in Existing Monitor; Sofiiski Universitet Sveti Kliment Ohridski (SUBG): Sofia, Bulgaria, 2020; Available online: http://metroradon.eu/wp-content/uploads/2017/06/D2_accepted.pdf (accessed on 5 September 2024).
- IEC 61577-4; International Standard Radiation Protection Instrumentation—Radon and Radon Decay Product Measuring Instruments—Part 4: Equipment for the Production of Reference Atmospheres Containing Radon Isotopes and Their Decay Products (STAR). 1st ed. The International Electrotechnical Commission (IEC): Geneve, Switzerland, 2009.
- Durrani, S.A.; Bull, R.K. Solid State Nuclear Track Detection, 1st ed.; Pergamon Press: Exeter, UK, 1987; pp. 96–113. [Google Scholar]
- Mateus, A.; Caeiro, F. Improved Shape Parameter Estimation for the Three-Parameter Log-Logistic Distribution. Comput. Math. Methods 2022, 2022, 8400130. [Google Scholar] [CrossRef]
- ISO 11929-3; Determination of the Characteristic Limits (Decision Threshold, Detection Limit and Limits of the Coverage Interval) for Measurements of Ionizing Radiation—Fundamentals and Application—Part 3: Applications to Unfolding Methods. 2nd ed. ISO: Geneva, Switzerland, 2019; pp. 1–39.
- ISO 11665-4; Measurement of Radioactivity in the Environment—Air: Radon-222—Part 4: Integrated Measurement Method for Determining Average Activity Concentration Using Passive Sampling and Delayed Analysis. 3rd ed. ISO: Geneva, Switzerland, 2021; pp. 1–31.
- Miller, C.A. Results of the 2023 Intercomparison of Passive Radon Detectors; Report RCE-DSD-04-2024; UK Health Security Agency: London, UK, 2024; pp. 1–38. Available online: https://www.ukradon.org/cms/assets/gfx/content/resource_5548csd10ddbe86f.pdf (accessed on 6 September 2024).
- FINAS—Finnish Accreditation Service. Decision T167/A25/2023. Available online: https://www.finas.fi/Documents/T167_A25_2023.pdf (accessed on 6 September 2024).

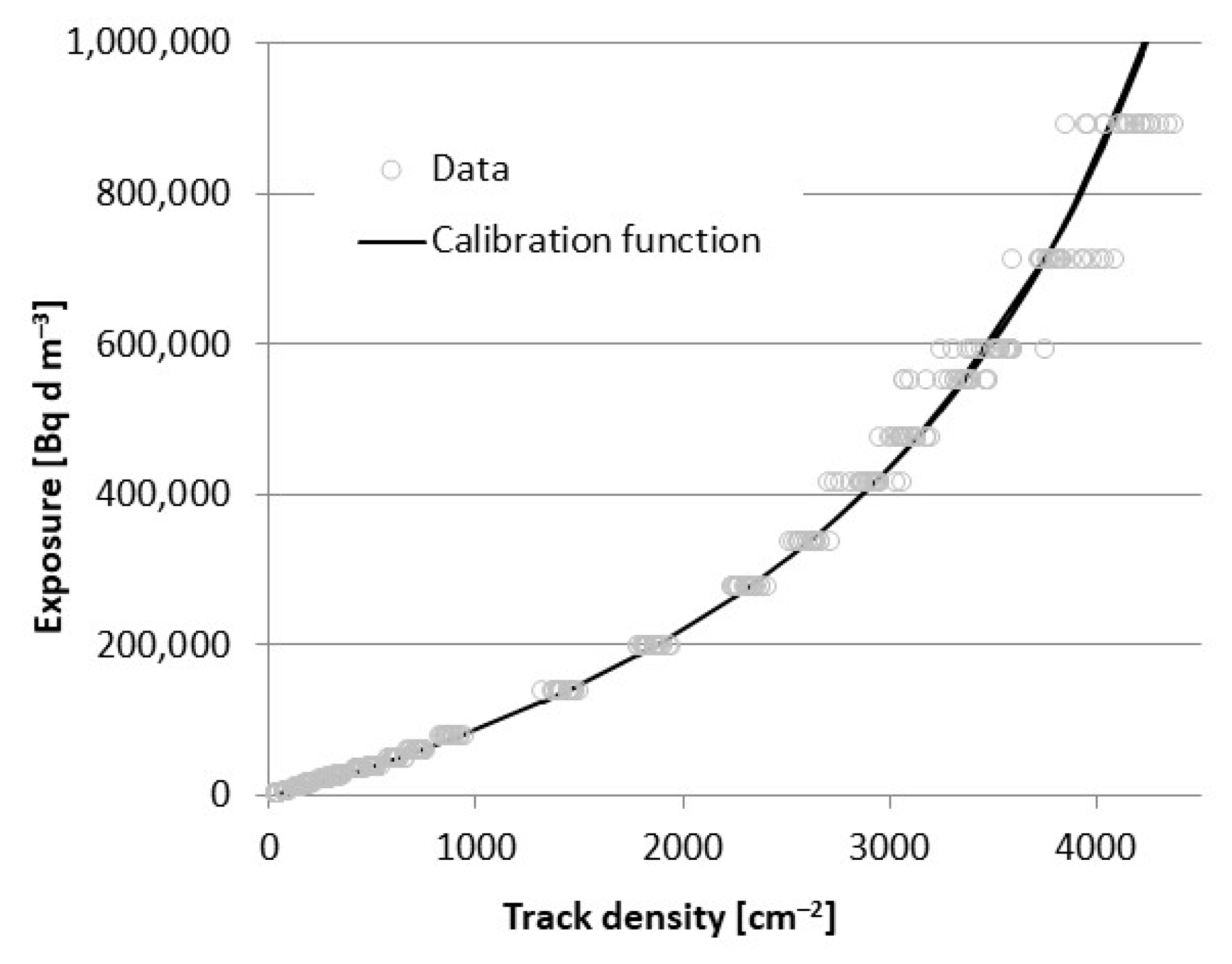
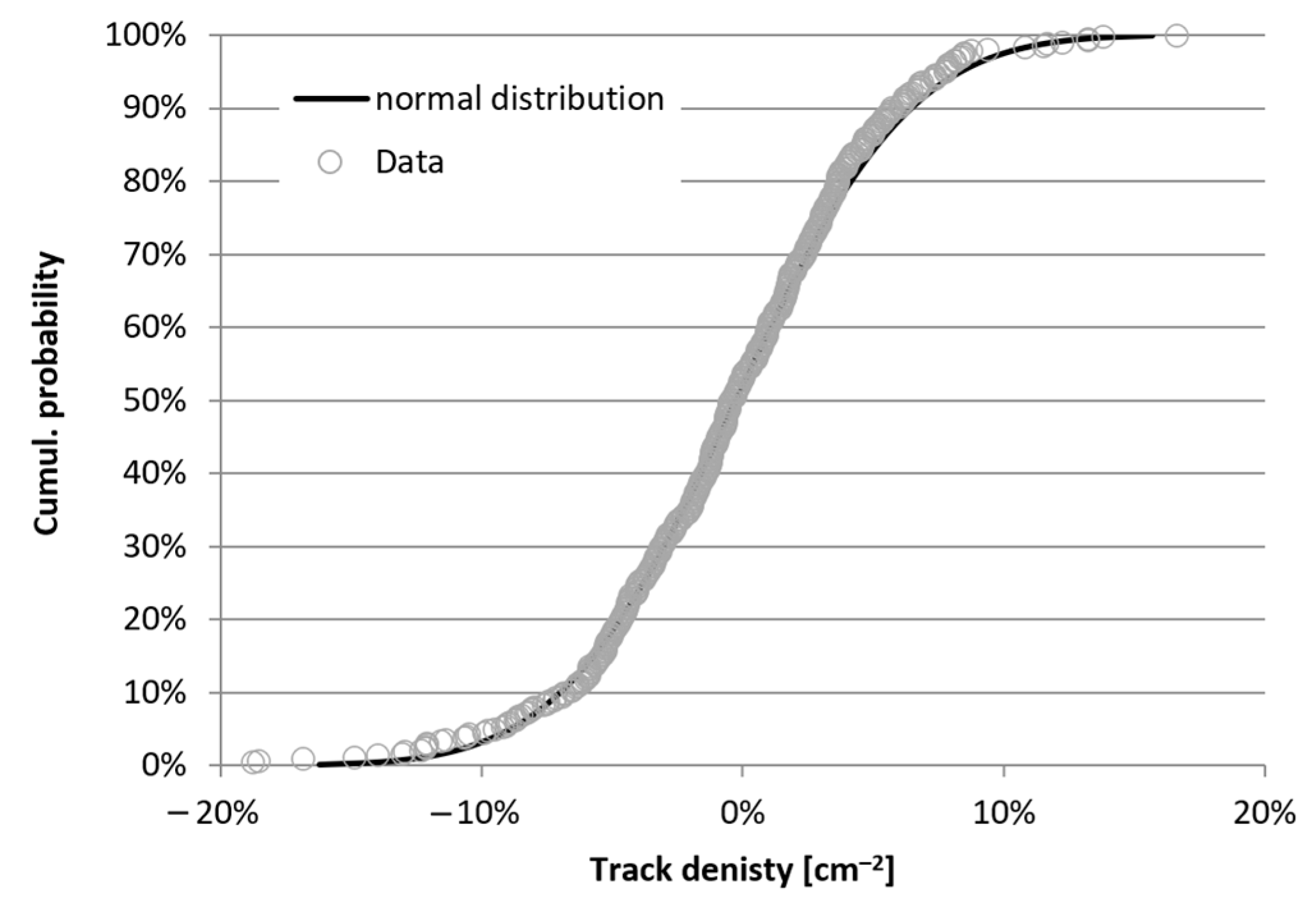
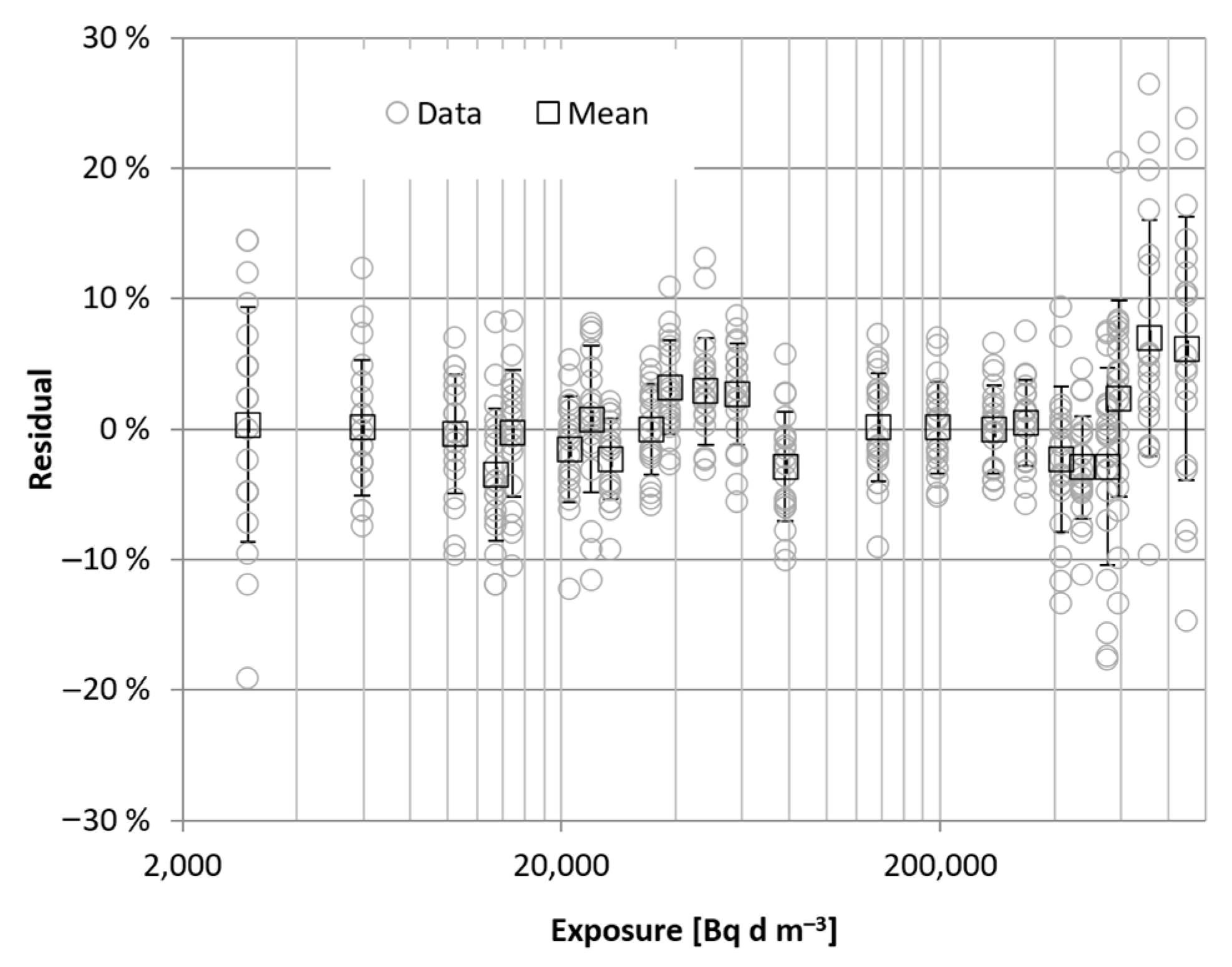
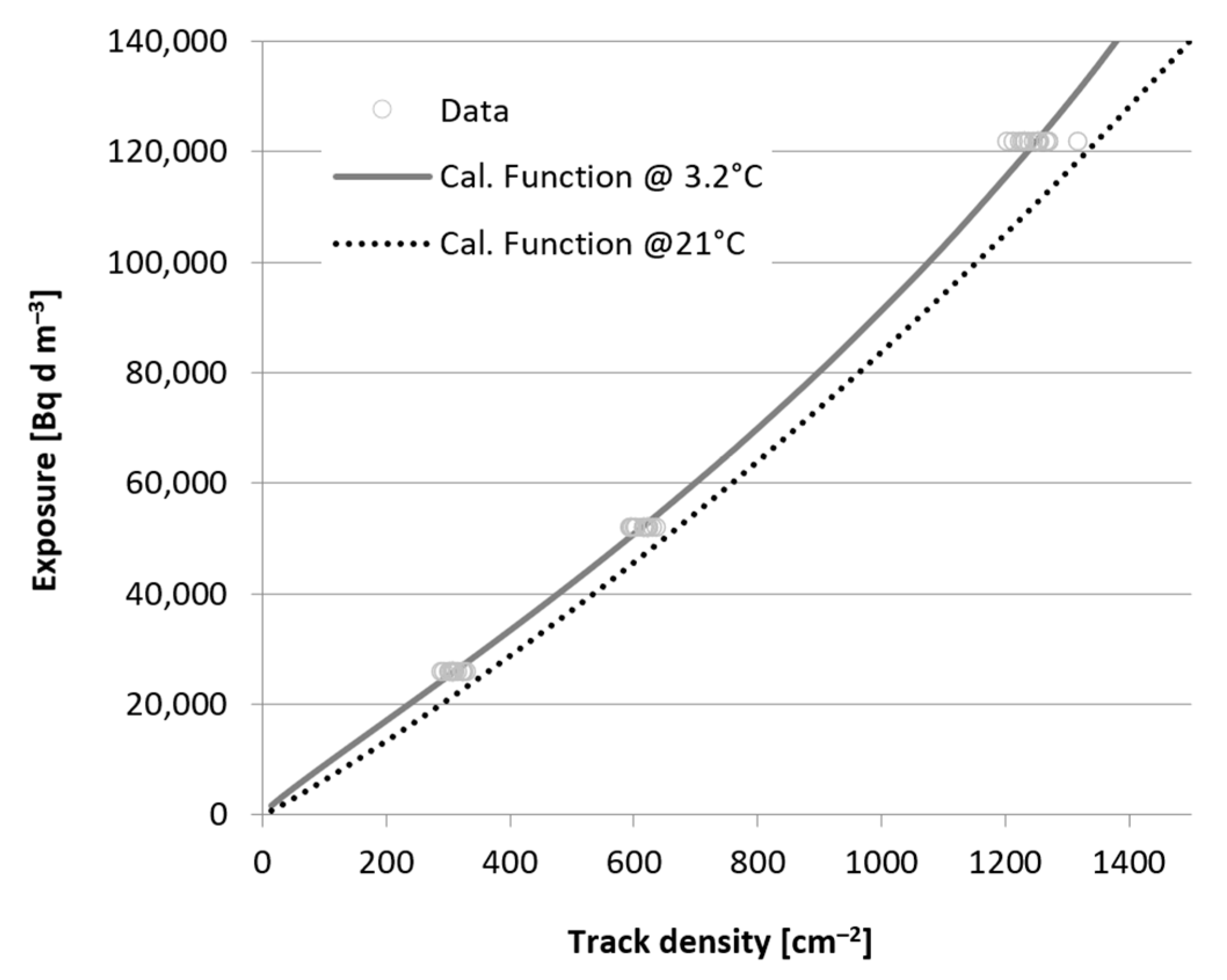
| Exposure (Bq·d·m−3) | N | Mean Track Density (cm−2) | Median Track Density (cm−2) | Standard Deviation (cm−2) | Coeff. of Variation (%) |
|---|---|---|---|---|---|
| 2983 | 20 | 45 | 46 | 4 | 8.3 |
| 5959 | 20 | 86 | 85 | 4 | 4.9 |
| 10,460 | 20 | 146 | 146 | 6 | 4.3 |
| 13,403 | 20 | 179 | 178 | 9 | 4.9 |
| 14,900 | 20 | 204 | 205 | 9 | 4.6 |
| 20,987 | 20 | 277 | 280 | 11 | 3.8 |
| 23,980 | 20 | 321 | 322 | 17 | 5.2 |
| 27,017 | 20 | 348 | 351 | 10 | 2.9 |
| 34,558 | 20 | 445 | 446 | 14 | 3.2 |
| 38,660 | 20 | 505 | 503 | 16 | 3.1 |
| 48,066 | 20 | 615 | 611 | 22 | 3.5 |
| 58,254 | 20 | 724 | 726 | 24 | 3.3 |
| 77,952 | 20 | 885 | 888 | 32 | 3.6 |
| 137,489 | 20 | 1429 | 1418 | 45 | 3.2 |
| 196,989 | 20 | 1855 | 1853 | 45 | 2.4 |
| 276,374 | 20 | 2316 | 2319 | 48 | 2.1 |
| 336,173 | 20 | 2611 | 2619 | 49 | 1.9 |
| 416,223 | 20 | 2892 | 2902 | 88 | 3.1 |
| 474,580 | 20 | 3086 | 3080 | 62 | 2.0 |
| 553,126 | 20 | 2982 | 3363 | 125 | 4.2 |
| 592,106 | 20 | 3507 | 3536 | 114 | 3.2 |
| 711,168 | 20 | 3820 | 3830 | 123 | 3.2 |
| 891,460 | 20 | 4161 | 4178 | 136 | 3.3 |
| Calibration Parameter | Value | Radon Concentration in 60-Day Measurement (Bq·m−3) | Expanded Uncertainty |
|---|---|---|---|
| m | 6335 cm−2 | 20 | 47% |
| h | 485,763 Bq·d·m−3 | 30 | 34% |
| b | −0.9793 | 60 | 28% |
| dbg | 5.4 cm−2 | 100 | 19% |
| u(dbg) | 3.6 cm−2 | 200 | 16% |
| u(dg,res) | 0.289 cm−2 | 300 | 15% |
| urel(s) | −0.28% | ||
| urel(m) | 5.15% | ||
| urel(ω) | 3.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turtiainen, T.; Laine, J.-P.; Rantanen, S.; Oinas, T. Nonlinear Calibration and Temperature Sensitivity of Makrofol Solid-State Nuclear Track Detectors for Radon Measurement. Atmosphere 2024, 15, 1179. https://doi.org/10.3390/atmos15101179
Turtiainen T, Laine J-P, Rantanen S, Oinas T. Nonlinear Calibration and Temperature Sensitivity of Makrofol Solid-State Nuclear Track Detectors for Radon Measurement. Atmosphere. 2024; 15(10):1179. https://doi.org/10.3390/atmos15101179
Chicago/Turabian StyleTurtiainen, Tuukka, Jussi-Pekka Laine, Salla Rantanen, and Tiina Oinas. 2024. "Nonlinear Calibration and Temperature Sensitivity of Makrofol Solid-State Nuclear Track Detectors for Radon Measurement" Atmosphere 15, no. 10: 1179. https://doi.org/10.3390/atmos15101179
APA StyleTurtiainen, T., Laine, J.-P., Rantanen, S., & Oinas, T. (2024). Nonlinear Calibration and Temperature Sensitivity of Makrofol Solid-State Nuclear Track Detectors for Radon Measurement. Atmosphere, 15(10), 1179. https://doi.org/10.3390/atmos15101179






