Abstract
General circulation models (GCMs) run at regional resolution or at a continental scale. Therefore, these results cannot be used directly for local temperatures and precipitation prediction. Downscaling techniques are required to calibrate GCMs. Statistical downscaling models (SDSM) are the most widely used for bias correction of GCMs. However, few studies have compared SDSM with multi-layer perceptron artificial neural networks and in most of these studies, results indicate that SDSM outperform other approaches. This paper investigates an alternative architecture of neural networks, namely the long-short-term memory (LSTM), to forecast two critical climate variables, namely temperature and precipitation, with an application to five climate gauging stations in the Lake Chad Basin. Lake Chad is a data scarce area which has been impacted by severe drought, where water resources have been influenced by climate change and recent agricultural expansion. SDSM was used as the benchmark in this paper for temperature and precipitation downscaling for monthly time–scales weather prediction, using grid resolution GCM output at a 5 degrees latitude × 5 degrees longitude global grid. Three performance indicators were used in this study, namely the root mean square error (RMSE), to measure the sensitivity of the model to outliers, the mean absolute percentage error (MAPE), to estimate the overall performance of the predictions, as well as the Nash Sutcliffe Efficiency (NSE), which is a standard measure used in the field of climate forecasting. Results on the validation set for SDSM and test set for LSTM indicated that LSTM produced better accuracy on average compared to SDSM. For precipitation forecasting, the average RMSE and MAPE for LSTM were 33.21 mm and 24.82% respectively, while the average RMSE and MAPE for SDSM were 53.32 mm and 34.62% respectively. In terms of three year ahead minimum temperature forecasts, LSTM presents an average RMSE of 4.96 degree celsius and an average MAPE of 27.16%, while SDSM presents an average RMSE of 8.58 degree celsius and an average MAPE of 12.83%. For maximum temperatures forecast, LSTM presents an average RMSE of 4.27 degree celsius and an average MAPE of 11.09 percent, while SDSM presents an average RMSE of 9.93 degree celsius and an average RMSE of 12.07%. Given the results, LSTM may be a suitable alternative approach to downscale global climate simulation models’ output, to improve water management and long-term temperature and precipitations forecasting at local level.
Keywords:
comparison; forecasting; gridded data; Lake Chad Basin; LSTM; precipitation; SDSM; temperature 1. Introduction
The climate system is highly complex, dynamic and multi-dimensional, with no single steady state. Models that attempt to predict the expected state of the system are therefore not intended to be an exact representation of the system, or able to reproduce all aspects of the system perfectly. However, partial representations and predictions are still useful in understanding certain phenomena, as well as in financial and infrastructure planning and adapting to climatic change, which has long been recognised as being crucial in society and the environment [1]. Where we may not be able to perfectly predict the climate system, we can attempt to improve our prediction methods for small parts of the system to better support decision making, especially for regional or local-level analyses [2]. Considerable efforts have been devoted to improving long-term weather forecasting. General circulation models (GCMs) also known as global climate models are established techniques for these types of assessments [3,4,5]. GCMs use the Navier–Stokes equations of thermodynamics, to understand climate patterns, given various energy sources such as radiation and latent heat [6,7]. GCMs produce large scale forecasts which are generally too coarse in resolution and do not consider processes on a small scale for localized use. To make GCM output more useful on a regional or local level, downscaling methods of GCM output have been developed that is either dynamic and based on regional climate models [8], or statistical, or a combination of both [9]. In this article, the focus is on statistical methods of downscaling.
Wilby [10] developed the Statistical Downscaling Model (SDSM), which has since been widely applied to temperature and precipitations forecasting [11,12,13]. Statistical downscaling is the process of using GCM atmospheric output, to estimate precipitations, maximum temperatures as well as minimum temperatures at local level [14]. Different techniques for statistical downscaling have since been developed and are described in several textbooks and review publications [9,15,16,17]. In recent years, statistical downscaling and bias correction have become standard tools in climate impact studies. The growing field of machine learning has also received increasing attention in geoscientific studies [18,19]. Harphan and Wilby [20] compared SDSM to multi-layer perceptron (MLP) neural network for precipitations forecasting, with an application to precipitation gauging stations in England. Contrasting results were found between stations. A number of other studies comparing both the MLP as well as the recurrent neural network (RNN) with SDSM were recorded [21,22,23]. In all these cases, SDSM outperformed both MLP and RNN in downscaling precipitation, minimum and maximum temperatures forecasting.
Long-Short-Term-Memory (LSTM) was proposed by Hochreiter and Schmidhuber [24] in 1997 and has been shown superior in learning long-term dependencies between inputs and outputs as compared to MLP and RNN, given its specific architecture, which consists of a set of recurrently connected subnets, known as memory blocks [25]. Bengio [26] shows that it is difficult for RNN to remember a sequence of more than 10 lags. Grave [25] shows in contrast that each LSTM block contains one or more self-connected memory cells and three multiplicative units, namely the input, output and forget gates, which allow longer memory. However, very few cases are reported in literature where LSTM is applied to hydrology and climate studies [27,28]. Given the superior performance of LSTM in learning long-term dependencies compared to MLP and RNN, the aim of this article is to compare LSTM prediction performances for long-term precipitation, minimum and maximum temperature forecasting, against SDSM, to establish whether LSTM can outperform SDSM, in contrast to the cases of MLP and RNN. In addition, given the limited applications of LSTM to hydrological and climate-related studies in literature, this study contributes to literature by establishing the relevance of LSTM within the given context, as an alternative to the widely used SDSM. Furthermore, by using the Lake Chad Basin as a case study, our approach specifically test SDSM and LSTM performances for climate stations with significant differences in Mean Annual Precipitation (MAP: 510–1160 mm/yr) and average monthly temperatures (24.5 to 41 °C) and investigate the drivers of these differences. The catchment has a high spatial variability in precipitation, ranging from 150 mm/yr in the north to over 1500 mm/yr in the South [29]. Likewise, monthly average temperature ranges from 40.8 °C in the north to 24.5 °C in the south [30].
The main objective of this study is therefore to compare the performances of SDSM and LSTM in downscaling monthly precipitation, minimum and maximum temperatures for selected gauging stations in the Lake Chad Basin. In order to compare SDSM and LSTM performances, the root mean square error (RMSE) as well as the mean absolute percentage error (MAPE) and the Nash Sutcliffe Efficiency (NSE) are used as performance indicators. The interest of using all three resides in the fact that the RMSE measures the ability of the model to avoid large errors between the prediction and the actual values, the MAPE provides an idea on the overall error percentage in the prediction, and the NSE is a standard measure used in the field of climate forecasting and hydrology for comparison [31]. The presented approach provides an enhanced downscaled GCM product, as well as the modelling framework needed to develop better local predictions of precipitation and temperature from GCMs, considering data and computing limitations.
2. Study Area and Data
2.1. Study Area
The Lake Chad Basin is a trans-boundary basin, situated between Cameroon, Chad, Niger and Nigeria. It is one of the largest interior basins in the world, with an estimated catchment area of 2,500,000 km. The lake itself supports 37 million people with water resources which are needed for agriculture, fishing and domestic use [32]. It contains two rivers upstream, namely the Logone and Chari, and a lake downstream called Lake Chad. On the northern catchment, the Kumadugu-Yobe river is considered as a marginal water contributor in the basin, with only one percent contribution, due to its divertion in Nigeria for national food production. Water for agriculture and domestic water use is typically taken directly from the lake, its main feeding tributaries, but also from a highly productive unconfined quaternary aquifer [29]. The southern catchment provides food and income for riparians living in cities like Ndjamena, through irrigated agriculture and fishing activities. Food security in this region requires a sustainable management of available water resources. This is especially important, considering the fact that the Lake Chad is in a water scarce region.
In the last half century, the lake’s surface area has decreased from 24,000 km in the 1950s to 1700 km currently. Inconsistent trends between precipitation and the lake’s water level remain, particularly during dry periods [33], but significant trends have been associated between the lake’s water level recovery and the occurrence of wet periods from 2012–2014 [34]. The increasing use of irrigation and abstraction from the lake itself are additional major threats contributing to the lake’s decline and vulnerability to climate change [35]. Being able to forecast temperature and precipitation, two critical climate variables are required for improving water management, to forecast oncoming dry or wet periods but also reduce the over allocation of water.
For our study, only five out of nine gauging stations are considered, given data availability and quality. The five stations considered in the study are presented in Figure 1 and enumerated from upstream to downstream as follows: Sarh, Doba, Lai, Bongor and Ndjamena. The MAP for the locations Sarh, Doba, Lai, Bongor and Ndjamena is 1160 mm/yr, 1381 mm/yr, 1100 mm/yr, 1018 mm/yr and 510 mm/yr. The average monthly temperature for these locations are 30.4 °C, 39.0 °C, 33.4 °C, 39.4 °C, and 40.8 °C for Sarh, Doba, Lai, Bongor and Ndjamena.
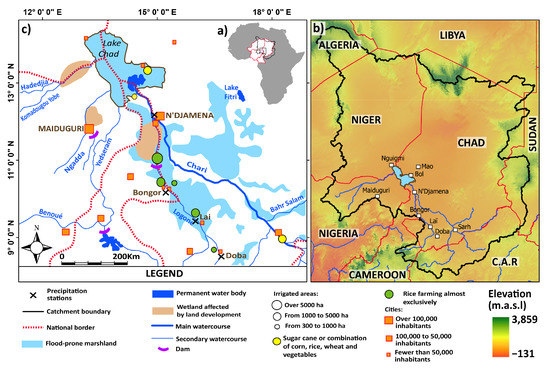
Figure 1.
(a) Location of Lake Chad within Niger, Nigeria, Cameroon, Chad and their position in relation to Africa. (b) The zoomed LCB with riparian countries, where C.A.R stands for the Central African Republic. (c) The major and secondary water courses that feed lake Chad, neighbouring permanent water bodies and dams used for irrigation/domestic supply, local city names and locations with over 100,000 inhabitants (location only for cities with fewer than 100,000 inhabitants), irrigation areas and relative field sizes as well as common agricultural crops grown in the region, as well as the precipitation gauges considered in the study.
2.2. Data
The data used in this paper are divided in two sets, namely: (1) The large-scale atmospheric data used as independent variables [36]; as well as (2) the precipitations, maximum and minimum temperatures, observed at-site, collected by the Lake Chad Basin Commission (LCBC) [30]. The latter are used as dependent variables [30] in the SDSM and LSTM models.The atmospheric data are 57 years (1950–2007) of monthly atmospheric parameters collected from the national centre for environmental prediction (NCEP), for each gauging station, using longitude and latitude coordinates for Sarh (9.14 N 18.36 E), Doba (8.67 N 16.85 E), Lai (9.39 N 16.3 E), Bongor (10.27 N 15.37 E) and Ndjamena (12.13 N 15.05 E). The data from the LCBC are 57 years (1950–2007) of monthly data recorded at each gauging station. For the SDSM implementation, the calibration set consists of 70.2 percent of the original dataset, and the validation set 29.8 percent. For the LSTM implementations, the training, validation and test sets consist of , and percent of the data, respectively (see Table 1). For the purpose of clearer comparison between SDSM and LSTM, the SDSM was re-implemented using only the last three years of the SDSM validation, to correspond with the test set of the LSTM implementation (see Table 1).

Table 1.
Data subsets for the purpose of comparison between SDSM and LSTM implementation in the Lake Chad Basin. The validation set of the SDSM implementation correspond to the test set of the LSTM subset.
For the chosen training, validation and test subsets, there is a consistent statistically significant difference in variance between the calibration and validation sets in the five gauging stations. This significant difference in variance may be explained by the fact that the validation set coincides with a set of extreme values, caused by the drought that happened between 2006 and 2007.
3. Methods
3.1. Statistical Downscaling Model
SDSM developed by Wilby [10] is a hybrid of multiple linear regression (MLR) and the stochastic weather generator (SWG). SDSM is presented in the literature as the easiest to implement, with low computational requirement and yet satisfactory accuracy. MLR designs the econometric relationship between the NCEP data and the at-site predictants, while SWG on the other hand uses the MLR parameters to generate up to 20 climate scenarios, over a period of 3 years. The SDSM approach is summarised in four steps: (1) screening, (2) calibration, (3) validation, (4) climate scenarios simulation.
The screening step consists of selecting the atmospheric data presenting the highest correlation with the variables to predict. A correlation matrix is used to filter the 31 independent variables (atmospheric data), such that only the predictors with correlation greater than 30 percent with at-site dependent variables and presenting very little paired correlation between each other are used for downscaling purposes. Predictors selected are presented in Table 2 along with the corresponding models where they are used. The precipitation forecasting model is denoted by (a), the minimum temperature model is represented by (b) and the maximum temperature forecast model is denoted by (c). The selected variables are used in SDSM4.2 [36] to predict precipitations, minimum and maximum temperatures three years ahead.

Table 2.
Definition of variable names, their units and corresponding models. °N denotes North direction, mm denotes Millimeter, and * denotes dimensionless Z-score. (a) denotes monthly precipitation model, (b) denotes monthly minimum temperatures and (c) denotes monthly maximum temperatures model.
The calibration step consists of finding the suitable parameters that explain the causal relationship between the selected predictors (see Table 2) and each predictant, namely precipitations, minimum temperatures and maximum temperatures. The calibration principle in the SDSM software (SDSM4.2) consists of splitting the dataset into calibration and validation, and then splitting the calibration set into k subsets, , such that subsets are used for calibration and the subset for internal validation. With such configuration, k calibrated models are built, and the average parameters are considered for prediction purposes. SDSM4.2 allows up to folds. This study therefore performs 20 calibrations and internal validation.
The calibration robustness is given by the average coefficient of determination () from the 20 calibrated models; the model accuracy is given by the average standard error (SE) from the 20 internal validation subsets. The residual autocorrelation test is performed on each of the 20 calibrated models to check that the residuals are white noise and therefore there is absence of lag one residuals autocorrelation, in the models used to predict precipitations, minimum temperatures as well as maximum temperatures. The Durbin-Watson test is used to check the residuals for autocorrelation [37]. The parameters stability test is also performed to check whether the parameters obtained do not vary significantly with sample change. The Chow tests is performed for the parameter stability check [38]. Once the tests are successfully performed on the calibration set, the average regression parameters explaining the causal relationship between the atmospheric data and each dependent variable, namely precipitations, minimum and maximum temperatures, are applied to the validation set. The aim is to check the capacity of the model to predict unseen data with accuracy. This is investigated by comparing the observed values with the model output. The validation tests include the Levene test for variance comparison and the Student paired t-test test for mean comparison. The simulation scenarios use the validated model and generate up to 20 scenarios of future precipitations or temperatures.
The above mentioned procedure is performed to show that SDSM results were obtained through a rigourous process, and can therefore be compared with results from LSTM without bias.
3.2. Long-Short-Term Memory Network
In this paper, three implementations of LSTM to forecast precipitations, minimum temperatures and maximum temperatures, respectively, are presented. The following sections provide details on (1) the architecture, (2) the feedforward propagation, (3) the loss function and (4) the backpropagation and weights update used in the three different implementations.
3.2.1. LSTM Architecture and Feedforward
Figure 2 presents a classical hidden layer node with an activation function (A) and a single cell LSTM memory block with forget gate, input gate and output gate. In the figure, denotes the cell state that contains all previous values of atmospheric data, such that:
where is the general term of the ith predictor at time , with and . It is worthwhile to note that I is the set of predictors and T is the length of time of a specific predictor. In this case study, the number of predictors is for precipitations, maximum and minimum temperatures respectively (see number of predictors for model (a), (b), (c) in Table 2).
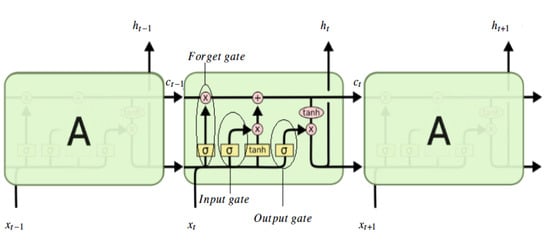
Figure 2.
Contrast between a classical reccurrent neural network cell equipped with an activation function (A) and a memory block for LSTM artificial neural network [39].
An effective use of the information contained in the cell state for actual prediction at time t is performed through three types of decisions which are taken at three gates in the LSTM architecture, namely the forget gate, the input gate and the output gate.
Forget gate: This gate is used to decide on the atmospheric data points to throw away from the cell state in the estimation process of the target value . A sigmoid function () is used for the purpose, with
In Equation (1), is a vector with values in the range (0,1), the matrix of the learnable coefficients associated with the vector of predictor inputs (atmospheric predictors at time t), is the hidden layer vectors , representing all matrix of predictors value up to (atmospheric predictors before time t) and is the matrix of biased coefficients associated to each hidden layer, at the forget gate f. At time step , the hidden layer is given by a null vector of length I, and the potential cell state vector denoted by , given that there is no previous information in the network. For , , such that is a vector with values between , , and are another set of learnable parameters.
Input gate: This gate decides on what new information from atmospheric data should be used to replace the information removed from the cell state at the forget gate. It uses both a sigmoid function to decide which values to update, and a hyperbolic tangent function (), to create a vector of new cell state candidate values, denoted by . The computation used at the input gate to update the cell state is given by
where is a vector with values in range (0,1), , and are learnable parameters defined for the input gate.
The cell state update from to is finally given by
Output gate: The output gate controls the information flow from to the next hidden layer such that
where is a vector with values in the range (0,1), , and are learnable parameters for the output gate. A new hidden state is computed for the next prediction, such that
The single output neuron at the last time step (), which computes either the precipitation, the maximum or minimum temperatures, is given by the last layer of the LSTM, denoted the dense layer, such that
where is the matrix of the learnable weights of the dense layer, is the biased term. The computation of is followed by the computation of the error function.
3.2.2. Error Function
The output of the activation function at the last layer is compared to the target solution, given in historical data. The error function at the kth iteration (), is the average deviation obtained for each sample , as given by
Here, the objective is to find a linear combination of weights and inputs, that minimises the error function.
Backpropagation is used to determine the contribution of each neuron per layer to the error function. It allows weight update, in order to increase forecasting accuracy.
3.2.3. The Backpropagation in LSTM
This study uses the mini batch gradient descent, as it updates weights for every mini-batch of m training examples (, ), and ensures more stable convergence to the minimised error function. Mini-batch is a good trade-off optimisation algorithm for error function minimisation [40]. This study uses mini batch sizes of and 10 (see Table 3).

Table 3.
Architectures and hyperparameters investigated for monthly precipitation and temperatures forecasting.
In order to minimise the error function in Equation (7), partial derivatives with respect to the parameters of the weight matrices () are computed. Previous weights are updated according to both the sign of the derivative, and the learning rate (), given as input to the network, in order to speed up the convergence in the optimisation direction.
A summary of the implementation process of the LSTM methodology is presented in Algorithm 1. Python 3.5 [41], Pandas [42], Keras [43] and tensorFlow [44] libraries are used for the implementation.
| Algorithm 1 Steps to implement LSTM in Python |
|
3.2.4. LSTM Setup
In this work, we developed a basic neural network model based on the LSTM framework. The model contains 3 layers (Figure 3). LSTM layers with 576 and 216 neurons were set as the input layer, for precipitations and temperatures forecasting, respectively. A dropout rate of was set on the LSTM layer. A fully connected layer was then set up as the output layer which yields three time series, namely precipitations, minimum and maximum temperatures.
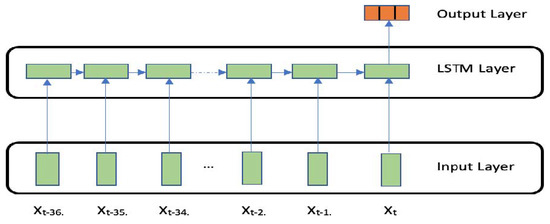
Figure 3.
The general architecture of the proposed LSTM networks implemented for both the precipitations and temperatures forecasting.
3.2.5. Tuning Procedure for LSTM Window Size and Hyperparameters
A proper setting of the window size is important for good model performances. In this study, monthly window sizes, of 1, 2, …, 12, 24, and 36 months, were explored (see Table 3). The window size of 36 months, that produce the best forecasting accuracy were then selected for each forecasting task. Hyperparameter optimization or tuning is the process used to find a tuple of hyperparameters that yields a model which minimize the loss function on the given data [45]. The mean-square-error was used in this study as the loss function for hyperparameter optimization [27].
In this study, after investigating five options of optimisers (see Table 3), we chose the efficient adam version of stochastic gradient descent [46]. The epoch, which is generally defined as one pass over the entire dataset in neural network, is used to separate training into distinct phases. Training for too long will lead the model to be overfitted, learning patterns that only exist in the training dataset. Whereas training for too short will lead the model to be underfitted, which means the model has not learned the relevant patterns in the training data [45]. In this study, the training epochs were first set to 200 [27] and the highest NSE were achieved after 2500, and 3000 epochs (see Table 4 and Figure 4), in the five gauging stations, for precipitations and temperature forecasting. Consequently, we used the number of 2500, and 3000 epochs for the final training of the model. These number of epochs were selected after a continuous stability of the training and validation loss, over more than 1500 iterations, after an unstable learning stage that occurred between 0 to 1000 iterations, represented with an oscillating validation loss function, as observed in Doba and Bongor (see Figure 4).

Table 4.
The chosen LSTM architectures for precipitation, minimum and maximum temperature forecasting in the five gauging stations after hyperparameter tuning.
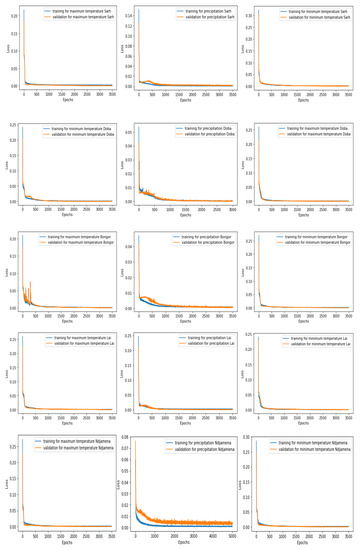
Figure 4.
The training and validation loss function plots for the maximum and minimum temperature and precipitation forecasting for the five gauging stations.
The best network architecture per gauging station for precipitation is given in Table 4. They indicate heterogenous architectures per gauging stations. These architectures were obtained after trials and errors of multiple configurations. The window size of 36 months was investigated for all stations, with one hidden layer and adam optimiser. Twenty nodes were found suitable for Sarh and Doba, while fifteen nodes were found suitable for Bongor, Lai and Ndjamena. An identical number of epochs were found to produce best results for all stations, except for Doba, where fewer epochs were used. Different dropout and batch size strategies were found for each gauging station. The ensemble method was implemented for twenty simulations per stations. The LSTM architectures for minimum and maximum temperatures are also given in Table 4. Almost identical architectures were implemented for both minimum and maximum temperatures forecasting. A fewer number of epochs (2500) were considered in Lai for minimum temperature forecasting. A fewer number of epochs in both Doba and Lai (2500 epochs), for maximum temperatures forecasting, and a fewer number of batch size in Doba (5 batch size).
3.3. Models Comparison
The results from the three LSTM models for precipitation, minimum and maximum temperatures forecasting are compared with results from the SDSM using the root mean squared Error (RMSE) as well as the mean absolute percentage error (MAPE), and the Nash Sutcliffe Efficiency (NSE). The corresponding mathematical formulations are given by
where is the observed data, is the generated data, and N is the length of the dataset.
The model with the smallest MAPE, RMSE or the highest NSE was considered as the most accurate, and was adopted for precipitations and temperatures forecasting in the given gauging station.
4. Results
4.1. SDSM Results
The SDSM models’ performances on the training and validation precipitation subsets are presented in Figure 5. The mean RMSE, the mean MAPE, the mean NSE, as well as the mean coefficients of determination () for 20-folds precipitations forecasting are given for each of the five gauging stations. There is a contrast between both the high NSE and , on the calibration set, and the low NSE and , on the validation set, in the five gauging stations (NSE = 0.70 versus NSE = 0.51; and versus ). This is an indication of the weak robustness of the SDSM precipitation forecasting models. This may be explained by a number of aspects, including a consistent statistically significant difference in variance between the calibration and validation sets in the five gauging stations (see Table 5). This significant difference in variance may be explained by the fact that the validation set coincides with a set of extreme values, caused by the drought that happened between 2006 and 2007, and which has as consequence to increase the bias of the calibrated model toward unseen data. This is a common issue encountered in the process of implementing a regression based model like the SDSM. Nevertheless, the values of NSE show that the models may be useful. In addition, the performances obtained are comparable with results generally observed in the literature [10,11,13,31,47]. For example, the average RMSE of the recorded literature survey is millimeters, which is greater than the average RMSE of millimeters, observed in each of the five gauging station considered in this case study.
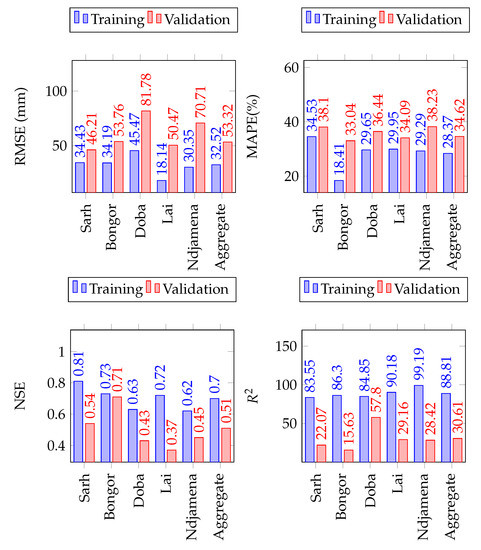
Figure 5.
Comparison of SDSM performance on the training and validation sets for monthly precipitations forecast in the Lake Chad Basin.

Table 5.
The statistical difference of the mean and variance estimation for the five gauging stations between the training, validation and test sets. p-values are given in brackets.
The prediction performances of SDSM for minimum and maximum temperatures at the five gauging stations are given in Figure 6 and Figure 7, respectively. The performances obtained suggest an average RMSE of degree celsius, a MAPE of percent, a NSE of 0.64 as well as a coefficient of determination of percent on the validation set, for minimum temperatures forecast. For maximum temperatures, the results suggest an average RMSE of degree celsius, a mean MAPE of percent, a NSE of 0.47 and a coefficient of determination of percent on the validation set. These results are indicators of the robustness of the calibrated model developed for minimum and maximum temperatures forecast and fall within the threshold of what is generally encountered in the literature [13,20,48,49].
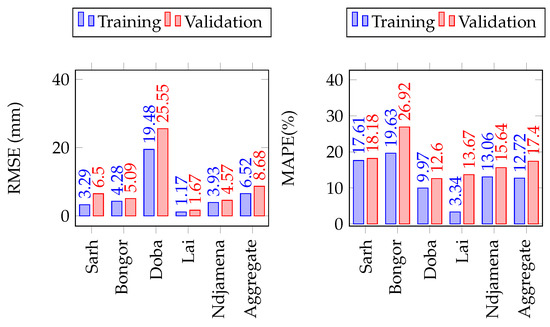
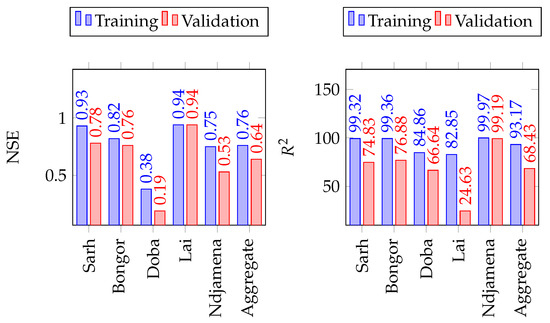
Figure 6.
Comparison of SDSM performance on the training and validation sets for monthly minimum temperature forecast in the Lake Chad Basin.
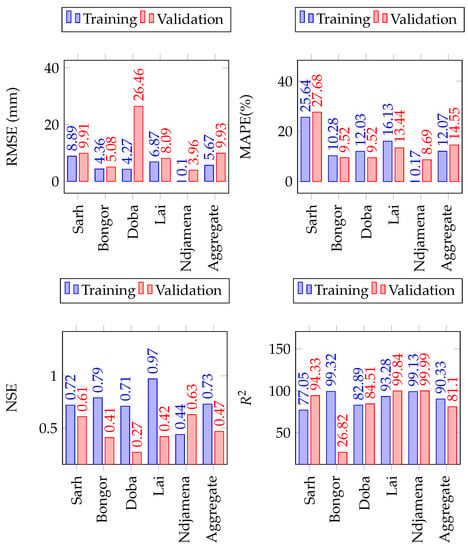
Figure 7.
Comparison of SDSM performance on the training and validation sets for monthly maximum temperature forecast in the Lake Chad Basin.
Nevertheless, it is worthwhile to note the descrepency of the model performances, between the calibration and the validation sets. This may be due to both the difference in the variance between the calibration and the validation sets (see Table 5), as well as the structural difference of the data, in the two subsets, as shown by the boxplot, in Figure 8. Additionally, this may suggest that SDSM is sensitive to temporal heterogeneity in the dataset.
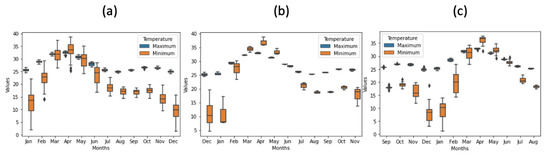
Figure 8.
Boxplot of monthly minimum and maximum temperatures data, displaying the heterogeneous spread in (a) the training, (b) the validation and (c) the test sets.
4.2. LSTM Results
The LSTM performances for the five gauging stations, as well as the average prediction performance in the LCB are presented in Figure 9, for precipitation. The performances obtained suggest an average RMSE of , an average MAPE of percent and an average NSE of on the test set, and which shows reliable forecasting. This observation is consistent for each of the five (05) gauge station considered in the study. The minimum NSE is observed in Lai (NSE = 0.71), and its maximum value is recorded in Sarh (NSE = 0.98). The loss function plot shown in Figure 4, indicate that there is no overfitting in the LSTM models trained for precipitation forecasting, and the above performances show that reanalysis data are suitable predictors for precipitations forecasting.
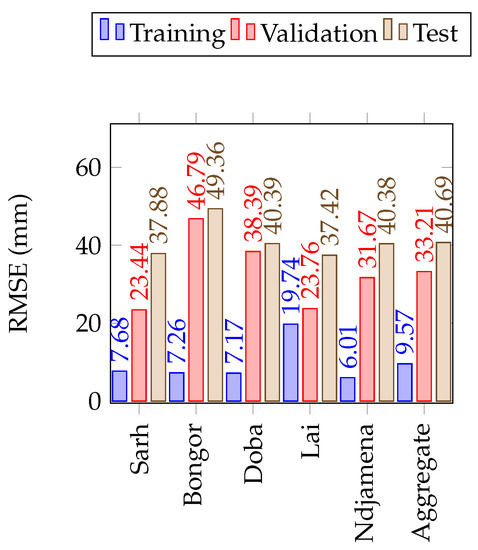
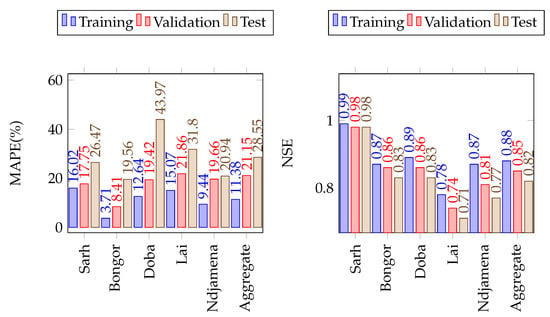
Figure 9.
The LSTM model performance on the training, validation and test sets of precipitation in the Lake Chad Basin. The number of simulations run were 20 in all cases.
The prediction performances for each station as well as the average performances in the Lake Chad Basin, for minimum and maximum temperatures, are presented in Figure 10 and Figure 11, exhibit a mean RMSE of degree celsius for minimum temperatures and degree celsius for maximum temperatures. The average MAPE informs that the prediction errors are percent for minimum temperatures and percent for maximum temperatures. In addition, the average NSE (0.95 and 0.97 for minimum and maximum temperature respectively), indicate that the LSTM models trained for minimum and maximum temperature forecasting are very suitable for practical use. Finally, the loss function plots shown in Figure 4, indicate that there is no overfitting in the LSTM models, trained for temperature forecasting. These results show that reanalysis data are suitable predictors for temperatures forecasting.
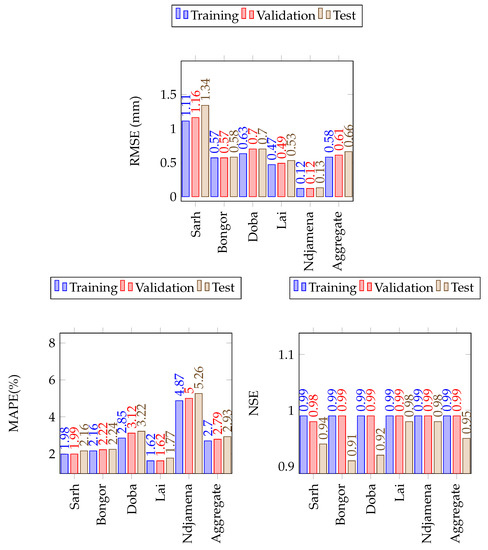
Figure 10.
The LSTM model performance on the training, validation and test sets of minimum temperature in the Lake Chad Basin. The number of simulations run were 20 in all cases.
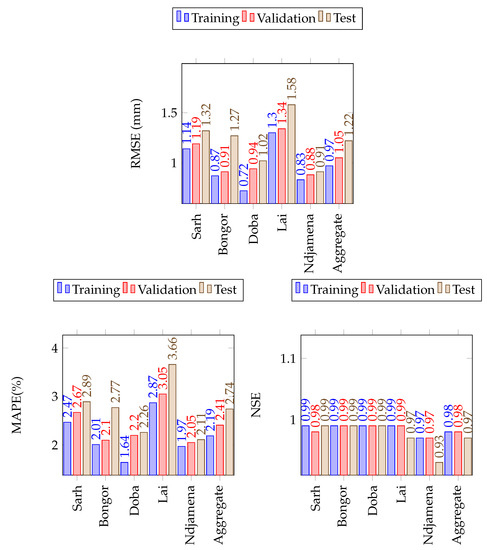
Figure 11.
The LSTM model performance on the training, validation and test sets of maximum temperature in the Lake Chad Basin. The number of simulations run were 20 in all cases.
4.3. Forecasting Comparison
A sample of the actual and predicted precipitation values on the test set for Ndjamena are given in Figure 12. A sample of the actual and observed temperatures for Ndjamena are given in Figure 13 and Figure 14. The monthly prediction biases (errors), as well as the correlations between predicted and observed values are provided in Table 6. The monthly prediction errors, indicate a tendency of underestimation in the LSTM predictions in March, April, May, September, November and December, and a tendency of overestimation, for the months of January, February, June, July, August, and October for precipitations. With regards, to the minimum temperature, LSTM predictions are underestimated in April, May, June and July, and overestimated in the other months. Maximum temperatures are underestimated in August, and overestimated elsewhere. In addition, the correlation between the observed and the predicted values of temperatures and precipitation show that both are highly related, especially for the prediction obtained with LSTM.
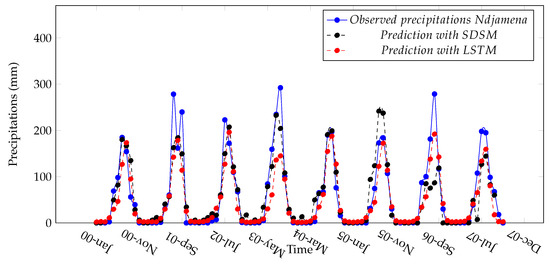
Figure 12.
Observed and predicted precipitation in Ndjamena.
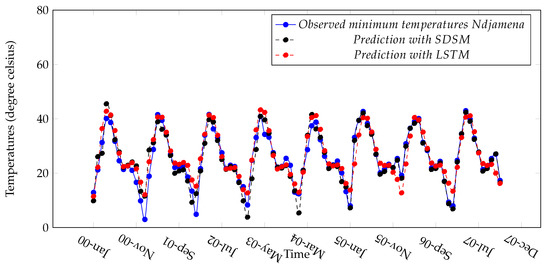
Figure 13.
Observed and predicted minimum temperature in Ndjamena.
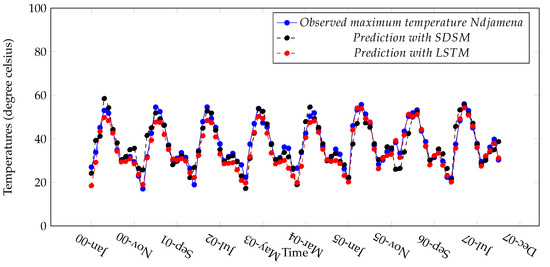
Figure 14.
Observed and predicted maximum temperature in Ndjamena.

Table 6.
Monthly predictions biases and monthly correlations between observed and predicted values.
5. Discussion
5.1. Performance of LTSM vs. SDSM
The multivariate LSTM for precipitations forecasting presents both the smallest RMSE, MAPE, and the highest NSE (see Figure 15). Therefore, LSTM may be a better prediction tool for long-term precipitations in the Lake Chad Basin.
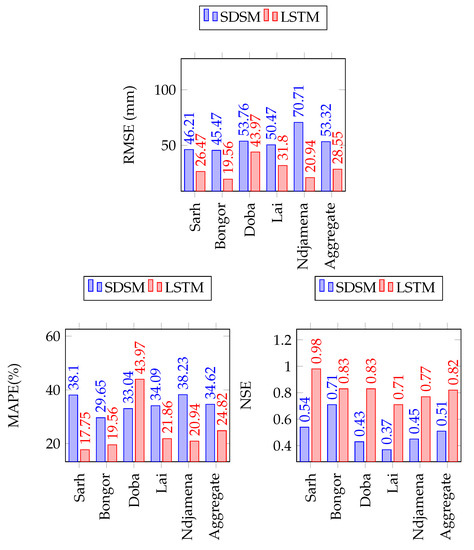
Figure 15.
Comparison of SDSM & LSTM for monthly precipitations forecast in the Lake Chad Basin.
A comparison of SDSM and LSTM for minimum and maximum temperatures forecasting per gauging station (see Figure 16 and Figure 17) indicate that LSTM produces better performances in all five gauging stations, with the smaller values of RMSE and MAPE, and the higher values of NSE, for all the five gauging stations (see Figure 16 and Figure 17).
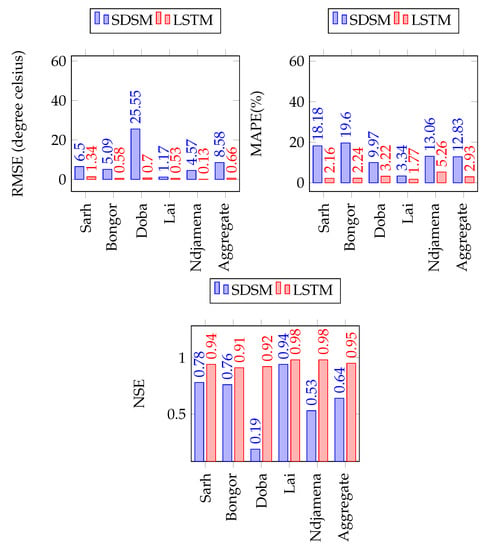
Figure 16.
SDSM and LSTM forecasting performance comparison for monthly minimum temperature forecast.
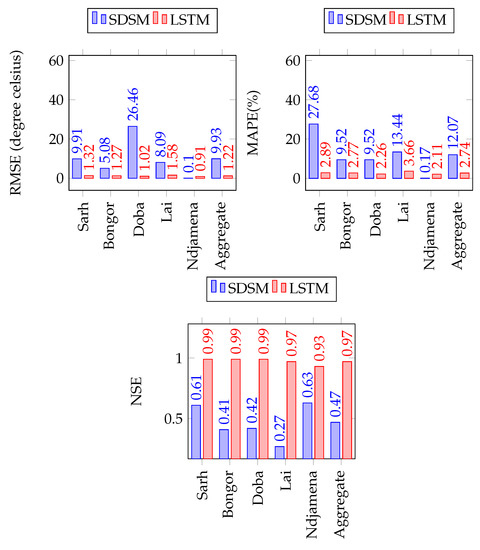
Figure 17.
SDSM and LSTM forecasting performance comparison for monthly maximum temperature forecast.
In terms of maximum temperature, LSTM outperforms SDSM in the five gauging stations, showing smaller values of RMSE, MAPE as well as the higher values of NSE.
The RMSE results shows the better abilities of LSTM to handle outliers as compared to SDSM, and NSE results indicates better reliability of LSTM forecasting outputs, for practical use, related to water ressources management and other hydrological purposes.
The better performances of neural networks in comparison to SDSM for precipitations, and temperatures forecasting observed in this study, do not align well with the results reported by Harphan and Wilby [20]. They compared the performances of RNN and SDSM in some gauging stations in England. Results of previous research still establish SDSM as the benchmark approach. This paper presents an exception. The tendency of LSTM to outperform SDSM in the Lake Chad Basin case may suggests LSTM as a good alternative to SDSM. The broader literature also suggest that LSTM architectures generally present an additional advantage in the forecasting of time series [50,51]. Moreover, LSTM performances can be improved through an automated hyperparameters search, with an advanced algorithms such as grid search or Bayesian optimisation, which are not investigated in this paper.
5.2. The Spatial and Temporal Heterogeneity of Microclimates in Forecasting Precipitation and Temperature
This study has shown the performance of SDSM and LSTM to be dependent on the local microclimates within the Lake Chad Basin. This application showed that SDSM had a higher NSE for stations with a higher overall MAP (Ndjamena 500–750 mm/yr) compared to stations with a lower MAP (Sarh, Doba, Bongor, Lai: 1000–1500 mm/yr).
For LSTM the largest NSE was less dependent on stations’ MAP. In the minimum and maximum monthly temperature forecasts, SDSM tended to perform worse for Doba in terms of NSE, where this station had a lower average monthly temperature (25–27.5 degree celsius) compared to stations in Sarh, Bongor, Lai and Ndjamena (27.5–30.3 degree celsius). In contrast, LSTM performance was less biased by the overall average temperature and was less dependent on local microclimate in this study. From the above observations, LSTM may present better abilities to handle the spatial heterogeneity of microclimates in forecasting precipitation and temperature, in the Lake Chad Basin. To fully evaluate the advantage of LSTM over SDSM for conditions with higher local microclimate variability, catchments with more in-situ data need to be selected. The application of LSTM has potential relevance for forecasting temperature and precipitation in regions with known high microclimatic variability, such as the Berg River in the Western Cape of South Africa [52], but also a region experiencing localised droughts [53]. Forecasting and the bias correction of GCM products using LSTM has the potential to be useful where recent data has shown spatial precipitation shifts and where other approaches tend to be more bias for local microclimates.
6. Conclusions
The aim of this paper was to compare the performances of SDSM and LSTM for monthly time–scales precipitations and temperatures forecasting in the Lake Chad basin, using grid resolution GCM output at a 5 degrees latitude × 5 degrees longitude global grid. This was motivated by the absence of such comparison in the literature. MLP and classical RNN were previously investigated in the literature, and results still confirmed SDSM as benchmark method for monthly precipitations and temperatures forecasting. From the results obtained in this study, the following conclusions can be made:
- LSTM provides more accurate monthly precipitations and temperatures forecasting outputs than SDSM, both in terms of sensitivity to outliers, with smaller RMSE, or in terms of forecasting reliability, with higher NSE coefficients;
- SDSM monthly precipitations and temperatures forecasting outputs are subject to the spatial heterogeneity of microclimates. This leads to less accurate forecasting outputs, in stations with higher MAP. Yet LSTM is capable to consider those variability, in the forecasting process;
- The comparison of LSTM with SDSM show that LSTM has high potential for monthly forecasting and the bias correction of GCM products, where recent data has shown spatial precipitation shifts and where other approaches tend to be more biased for local microclimates.
- The performances of LSTM could be enhanced by adding hyperparameter optimisation methods, such as grid search, and Bayesian optimisation. This may contribute further to establish LSTM as a benchmark for monthly climate forecasting.
Author Contributions
Conceptualization, N.C.F.M., L.P. and J.H.N.; methodology, N.C.F.M., L.P. and J.H.N.; software, N.C.F.M.; validation, N.C.F.M., L.P. and J.H.N.; data curation, N.C.F.M.; writing—original draft preparation, N.C.F.M.; writing—review and editing, L.P., N.C.F.M., J.H.N. and A.W.; visualization, N.C.F.M. and A.W.; supervision, L.P. and J.H.N.; funding acquisition, L.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Graduate School of Economics and Management at Stellenbosch University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hewitson, B.; Daron, J.; Crane, R.; Zermoglio, M.; Jack, C. Interrogating empirical-statistical downscaling. Clim. Chang. 2013, 122, 539–554. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M.; Gutiérrez, J.; Kotlarski, S.; Chandler, R.; Hertig, E.; Wibig, J.; Huth, R.; Wilcke, R. VALUE: A framework to validate downscaling approaches for climate change studies. Earth’s Future 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Wilby, R.; Wigley, T. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Madec, G.; Delecluse, P.; Imbard, M.; Levy, C. Ocean general circulation model reference manual. In Note du Pôle de Modélisation; CNRS-Université Pierre et Marie Curie-Université Versailles-Saint-Quentin CEA-ORSTOM-Ecole Normale Supérieure-Ecole Polytechnique: Paris, France, 1997. [Google Scholar]
- Richmond, A.; Ridley, E.; Roble, R. A thermosphere/ionosphere general circulation model with coupled electrodynamics. Geophys. Res. Lett. 1992, 19, 601–604. [Google Scholar] [CrossRef]
- Vallis, G.K. Geophysical fluid dynamics: Whence, whither and why? Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 201–601. [Google Scholar]
- Petersen, A.C. Philosophy of climate science. Bull. Am. Meteorol. Soc. 2000, 81, 265–272. [Google Scholar] [CrossRef]
- Rummukainen, M. State-of-the-art with regional climate models. WIREs Clim. Chang. 2010, 1, 82–96. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, 2009RG000314. [Google Scholar] [CrossRef]
- Wilby, R.; Dawson, C.; Barrow, E. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Gagnon, S.; Singh, B.; Rousselle, J.; Roy, L. An application of the statistical downscaling model (SDSM) to simulate climatic data for streamflow modelling in Québec. Can. Water Resour. J. 2005, 30, 297–314. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M. Future changes in extreme temperature events using the statistical downscaling model (SDSM) in the trans-boundary region of the Jhelum river basin. Weather. Clim. Extrem. 2014, 5, 56–66. [Google Scholar] [CrossRef]
- Hussain, M.; Yusof, K.; Mustafa, M.; Afshar, N. Application of statistical downscaling model (SDSM) for long term prediction of rainfall in Sarawak, Malaysia. Water Resour. Manag. 2015, 8, 269. [Google Scholar]
- Laflamme, E.; Linder, E.; Pan, Y. Statistical downscaling of regional climate model output to achieve projections of precipitation extremes. Weather. Clim. Extrem. 2016, 12, 15–23. [Google Scholar] [CrossRef]
- Benestad, R.; Hanssen-Bauer, I.; Chen, D. Empirical-Statistical Downscaling; World Scientific Publication: Singapore, 2008. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Tabari, H.; Paz, S.; Buekenhout, D.; Willems, P. Comparison of statistical downscaling methods for climate change impact analysis on precipitation-driven drought. Hydrol. Earth Syst. Sci. 2021, 25, 3493–3517. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Dehghani, M.; Várkonyi-Koćzy, A. Deep learning and machine learning in hydrological processes climate change and earth systems a systematic review. In Proceedings of the International Conference on Global Research and Education, Balatonfured, Hungary, 4–7 September 2019; pp. 52–62. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Harpham, C.; Wilby, R. Multi-site downscaling of heavy daily precipitation occurrence and amounts. J. Hydrol. 2005, 312, 235–255. [Google Scholar] [CrossRef]
- Khan, M.; Coulibaly, P.; Dibike, Y. Uncertainty analysis of statistical downscaling methods. J. Hydrol. 2006, 319, 357–382. [Google Scholar] [CrossRef]
- Samadi, S.; Wilson, C.; Moradkhani, H. Uncertainty analysis of statistical downscaling models using Hadley Centre Coupled Model. Theor. Appl. Climatol. 2013, 114, 673–690. [Google Scholar] [CrossRef]
- Samadi, S.; Carbone, G.; Mahdavi, M.; Sharifi, F.; Bihamta, M. Statistical downscaling of river runoff in a semi arid catchment. Water Resour. Manag. 2013, 27, 117–136. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A. Supervised sequence labelling. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–13. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-Runoff modelling using Long-Short-Term-Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Zaytar, M.; Amrani, C.E. Sequence to sequence weather forecasting with long short term memory recurrent neural networks. Int. J. Comput. Appl. 2016, 143, 7–11. [Google Scholar]
- Mahamat, N.; Hunea, F.; Ali, M.; Saleh, H.; Mahamat, H.; Boum-Nkot, S.; Nlend, B.; Djebebe-Ndjiguim, C.; Foto, E.; Sanoussi, R.; et al. Shallow Quaternary groundwater in the Lake Chad basin is resilient to climate change but requires sustainable management strategy: Results of isotopic investigation. Sci. Total. Environ. 2022, 851, 158152. [Google Scholar] [CrossRef]
- Lemoalle, J.; Magrin, G.; Ngaressem, G.; Ngounou, N.; Raimond, C.; Issa, S.; Amadou, B.; Djoret, D.; Favreau, G.; Goni, I.; et al. Le développement du Lac Tchad: Situation Actuelle et Futurs Possibles: Expertise Collégiale Réalisée par l’IRD à la Demande de la Commission du Lac Tchad. Contributions intégrales des Experts; IRD éditions; Institut de Recherche pour le Développement: Paris, France, 2014. [Google Scholar]
- Abudu, S.; Chun-liang, C.; King, J.; Kaiser, A. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River, China. Water Sci. Eng. 2010, 3, 269–281. [Google Scholar]
- Coe, M.; Birkett, C. Calculation of river discharge and prediction of lake height from satellite radar altimetry: Example for the Lake Chad basin. Water Resour. Res. 2004, 40, 1–12. [Google Scholar] [CrossRef]
- Okonkwo, C.; Demoz, B.; Gebremariam, S. Characteristics of Lake Chad level variability and links to ENSO, precipitation, and river discharge. Sci. World J. 2014, 2014, 145893. [Google Scholar] [CrossRef]
- Ndehedehe, C.; Agutu, N.; Okwuashi, O.; Ferreira, V. Spatio-temporal variability of droughts and terrestrial water storage over Lake Chad Basin using independent component analysis. J. Hydrol. 2016, 540, 106–128. [Google Scholar] [CrossRef]
- Lemoalle, J.; Bader, J.; Leblanc, M.; Sedick, A. Recent changes in Lake Chad: Observations, simulations and management options (1973–2011). Glob. Planet. Chang. 2012, 80, 247–254. [Google Scholar] [CrossRef]
- Sachindra, D.; Khandakar, A.; Rashid, M.M.; Shahid, S.; Perera, B. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- White, K. The Durbin-Watson test for autocorrelation in nonlinear models. Rev. Econ. Stat. 1992, 74, 370–373. [Google Scholar] [CrossRef]
- Hansen, B. Testing for parameter instability in linear models. J. Policy Model. 1992, 14, 517–533. [Google Scholar] [CrossRef]
- Olah, C. Understanding lstm Networks. 2015. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Rossum, V.G.; Drake, J.F.L. Python Tutorial; Centrum Voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 51–56. [Google Scholar]
- Chollet, F. Deep Learning mit Python und Keras: Das Praxis-Handbuch vom Entwickler der Keras-Bibliothek; MITP-Verlags GmbH & Co. KG: Bonn, Germany, 2018. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chu, J.; Xia, J.; Xu, C.; Singh, V. Statistical downscaling of daily mean temperature, pan evaporation and precipitation for climate change scenarios in Haihe River, China. Theor. Appl. Climatol. 2010, 99, 149–161. [Google Scholar] [CrossRef]
- Karamouz, M.; Falahi, M.; Nazif, S.; Rahimi, F. Long lead rainfall prediction using statistical downscaling and artificial neural network modeling. Sci. Iranica 2009, 16, 165–172. [Google Scholar]
- Kazmi, D.; Li, J.; Ruan, C.; Zhao, S.; Li, Y. A statistical downscaling model for summer rainfall over Pakistan. Clim. Dyn. 2016, 47, 2653–2666. [Google Scholar] [CrossRef]
- Zeroual, A.; Harrou, F.; Dairi, A.; Sun, Y. Deep learning methods for forecasting COVID-19 time-Series data: A Comparative study. Chaos Solitons Fractals 2020, 140, 110121. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
- Watson, A.; Kralisch, S.; Künne, A.; Fink, M.; Miller, J. Impact of precipitation data density and duration on simulated flow dynamics and implications for ecohydrological modelling of semi-arid catchments of Southern Africa. J. Hydrol. 2020, 590, 125280. [Google Scholar] [CrossRef]
- Watson, A.; Miller, J.; Künne, A.; Kralisch, S. Using soil-moisture drought indices to evaluate key indicators of agricultural drought in semi-arid Mediterranean Southern Africa. Sci. Total. Environ. 2022, 812, 152464. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
