Abstract
There are several attempts to model rainfall time series which have been explored by members of the hydrological research communities. Rainfall, being one of the defining factors for a flooding event, is rarely modeled singularly in deep learning, as it is usually performed in multivariate analysis. This study will attempt to explore a time series modeling method in four subcatchments located in Samar, Philippines. In this study, the rainfall time series was treated as a signal and was reconstructed into a combination of a ‘smoothened’ or ‘denoised’ signal, and a ‘detailed’ or noise signal. The discrete wavelet transform (DWT) method was used as a reconstruction technique, in combination with the univariate long short-term memory (LSTM) network method. The combination of the two methods showed consistently high values of performance indicators, such as Nash–Sutcliffe efficiency (NSE), correlation coefficient (CC), Kling–Gupta efficiency (KGE), index of agreement (IA), and Legates–McCabe index (LMI), with mean average percentage error (MAPE) values at almost zero, and consistently low values for both residual mean square error (RMSE) and RMSE-observations standard deviation ratio (RSR). The authors believe that the proposed method can give efficient, time-bound results to flood-prone countries such as the Philippines, where hydrological data are deficient.
1. Introduction
Mathematical models are key to understanding the dynamics of natural systems. Hence, the use of multivariate analysis [1], correlation and principal component analysis (PCA), as well as stream flow reconstruction [2] were used by researchers for hydrological models. The challenging area of disaster and water resources management drives scientists to arrive at more accurate and, most of the time, consolidated approaches.
The LSTM networks of [3], a type of DL, are developed for prolonged retention of information in order to train more successfully across datasets composed of consecutive samples. As a consequence of a series of activations and operations, LSTM neurons produce two distinct values as opposed to an activation function, which produces one output and transmits it to immediate neurons in the same layer, as well as those in the layer above. Although both outputs are kept in the LSTM layer, one is shifted to the next layer to maintain track of the lessons from the previous part of the sequence.
Necesito et al. (2021) [4] subsequently used DWT and univariate LSTM to visualize dengue surges. The authors of [5], on the other hand, used DWT and SVM to predict monthly rainfall in China. Choi et al. (2019) [6] subsequently used CNN and DWT to forecast rainfall in Malaysia. DWT has been a well-tested decomposition technique and was proven effective, as emphasized by [4].
LSTM is an established method of modeling in hydrological research. In fact, Chong et al. (2020) [7] estimated daily runoff using an LSTM model that used meteorological data. The results outperformed those of the Sacramento soil moisture accounting model (SAC-SMA) snow-17, a well-known physical model. Kratzert et al. (2019) [8] showed that the LSTM model outperforms hydrological models, such as the calibrated SAC-SMA and the national water model, when applied to ungauged watersheds. They achieved this by utilizing k-fold cross-validation to apply the LSTM model to 531 U.S. watersheds.
Many studies have proven how LSTM surpasses other hydrological models. Using climatic data and the current day’s stream flow, Damavandi et al. (2019) [9] developed an LSTM model on a Texas watershed to forecast the daily stream flow the next day. Their findings demonstrated that LSTM outperforms the CaMa-Flood model. Zhang et al. (2018) [10] used an LSTM model to forecast monthly reservoir inflow and outflow on an hourly, daily, and monthly basis, and outperformed backpropagation neural networks and support vector machines in their analysis.
Kumar et al. (2019) [11] employed RNN and LSTM models, and it was shown that LSTM gave better results. Qin et al. (2019) [12] projected stream flow using LSTM and compared it to the AR model. An LSTM model was employed by [13] to calculate the reservoir’s daily overflow. The use of ENN in a real-time 3 h flood forecast by [14] was equally successful.
Other studies have used LSTM with spatiotemporal attention (STA) for an interpretable AI flood forecasting [15]. Song et al. (2019) [16] used T multivariate single-step LSTM networks, which receives inputs related to the geographical and temporal dynamics of actual and modeled precipitation and runoff. However, some research concentrated on the pretreatment of the data, such as the breakdown of runoff and rainfall before using deep learning models. He at al. (2019) [17] developed a DNN model for prediction of daily stream flow, with stream flow series inputs broken down into a number of intrinsic mode functions (IMF) using variational mode decomposition (VMD).
Rainfall modeling has been a subject of different studies in the field of hydrology. In fact, Scopus (https://www.scopus.com, accessed on 6 December 2022) recorded a total of 148,859 journal articles that are related to rainfall models from 1969 to 2022. These studies used different methods in modeling rainfall, which vary from conventional mathematics to the 20th century machine learning techniques. The table below shows the different approaches in rainfall modeling used by other scientists.
Table 1 shows how rainfall has been modeled by several scientists from the field of hydrology. The variables used vary from single rainfall to multiple hydrological variables such as temperature, wind speed, and humidity, among others. Performance indicators also vary between each study, with RMSE or MSE being the most common. The techniques also showed that some studies tried to model rainfall through conventional mathematical techniques, such as regression and ARIMA, to various machine learning approaches.

Table 1.
Some Rainfall Models used by Other Research Scientists.
There are studies which have used discrete wavelet transform (DWT) in combination with neural networks. However, unlike in this study, the whole raw data were preprocessed by DWT and the results were all transmitted to the neural network, including the base signal [23,31,34]. Interestingly, Choi et al. (2019) [32] modeled the rain damage and model residuals separately using several machine learning techniques, but without using DWT. On the other hand, Wu et al. (2021) [33] separated the noise from the raw data and used LSTM for the residuals and the remainder using ARIMA.
DWT is often applied in signal processing to transform signals into a frequency [36]. DWT was used in surveillance or tracking of moving objects [37], and in disease classification [38]. Shmueli (2013) [39] and Alimohamadi et al. (2020) [40] investigated the use of DWT to detect outbreaks using biosurveillance systems, while the latter author focused on pertussis aberrations. Essentially, DWT transforms the signal into a different frequency [36]. Hence, DWT is simply a derivation of the theory of spectral decomposition, which states that any time series can be decayed into multiple statistically independent time series.
Time series data analysis for rainfall model is rarely performed singularly in deep learning, as it is usually performed in multivariate analysis. There are also several attempts to model rainfall which have been explored by members of the hydrological research communities. Some researchers used data-driven techniques such as regression methods [41,42,43], while others used physical-based models, in which the latter (physical-based models) was found to be less accurate than the former (data-driven techniques) [44,45].
Some studies have associated rainfall with several climatological factors. However, many studies have also used univariate modeling techniques in analyzing rainfall [30,46,47]. In fact, Ray and Chattopadhyay (2021) [48] emphasized that the “steady state probabilities indicate that a month with high surface air temperature is most likely to be preceded by another warm month but less likely lead to a low surface air temperature in the subsequent month.” Thus, according to Ray and Chattopadhyay (2021) [48], surface air temperature may have an effect on rainfall, but its impact on summer monsoon rainfall cannot be explained through a time-domain approach, but on a frequency-domain approach, hence, the authors used DWT in this study.
Several research studies have investigated the use of DWT in surveillance or tracking of moving objects [37], damage detection in building structures [49], and disease classification [38]. Based on the authors’ knowledge, only a handful of research investigated the use of DWT in series with univariate LSTM to model rainfall, and none have focused on the Philippines region. In addition, none have considered noise modeling of rainfall using univariate LSTM.
2. Discrete Wavelet Transform
The continuous wavelet transform (CWT) can be expressed as [50]:
where is the complex conjugate of the base signal,
However, CWT’s scale parameter’s dyadic discretization, which is the DWT, has a linear connection to the shift parameter’s step size.
which makes Equations (1) and (2) become
Using the Mallat algorithm, Equations (4) and (5) are further simplified to
where
where are the high-frequency coefficients, are the low-frequency coefficients, and are the high- and low-pass filters, respectively, expressed as:
where
Denoising signals make use of orthogonal wavelets as a scaling function or basis for DWT. Daubechies wavelet four is a common and ideal scaling function for denoising [51,52]. Figure 1 shows the DWT mechanism.
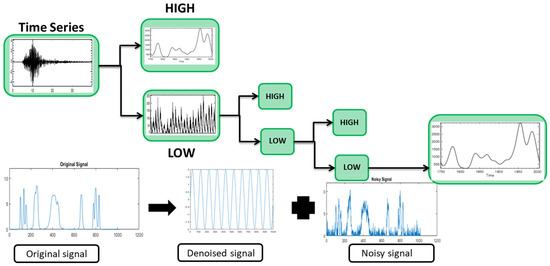
Figure 1.
Mechanism of Discrete Wavelet Transform (DWT).
For DWT with Daubechies wavelet four as the scaling function, the following matrix applies [53]:
where a are the low-frequency coefficients, y is the raw signal, s and d are the transformed signal, which can also be calculated as:
For more details regarding Daubechies wavelet four and other types of wavelets, the authors suggest to refer to [54].
DWT can either be calculated manually or by using pywavelets in python.
3. Long Short-Term Memory Network
LSTM neural networks were first introduced by Hochreiter and Schmidhuber (1997) [3]. As emphasized by Qashwai et al. (2021) [55], LSTM, just like other recurrent neural networks (RNN), is a blackbox method. It is a special type of RNN which is capable of identifying long-term dependencies. LSTMs are designed specifically to avoid the long-term dependence problem. They do not work hard to learn; instead, it comes naturally to them to retain information for a long time. All recurrent neural networks have the form of an array of repeating neural network modules. Although it too has a chain-like architecture, the repeating module of LSTMs is organized differently. Instead of just one, there are three layers in the neural network, and they interact significantly differently.
LSTM has three main layers: the input layer, the recurrent hidden layer, and the output layer. LSTM does not simply have memory blocks which memorize the temporal state, but it also has gating units which adapt and control the flow of information. LSTM has shown efficiency in capturing time series dependencies, most particularly in dealing with longer periods [56]. One can imagine the LSTM gates as controls, and the LSTM network as a set or series of LSTM units with each unit having four main controls or gates. One is the forget control (ft), which allows the network to either keep or forget the memory in transit. Next is the new memory control, which allows new memories to pass through and later on merge with the memories that passed through the forget control. The merging of these memories will happen with the help of the merged control. On the other hand, a set of new memories is being processed by another neural network. Eventually, these new memories will join the first two memories through the merged control. The last control is the output control, which checks how much memory should be produced as an output to the next LSTM unit (Figure 2).
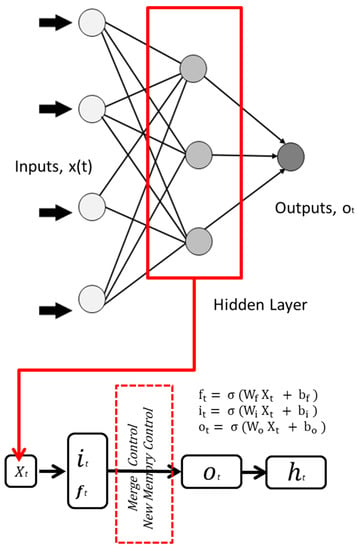
Figure 2.
LSTM Diagram [4].
Where W represent weights, b is the bias, σ are nonlinear activated functions, and Xt is the input. Rectified linear activation function (ReLU), σ, which allows the LSTM network to approximate not just a linear function (if it exists), but also accounts for the nonlinearity of the time series, is represented by the formula:
which returns 0 if it receives negative input, and the value is retained if it is positive. The adaptive moment estimation (Adam) optimizer, which handles bias estimation and weights, is used in this study (algorithm can be found in the paper of [57]).
In this study the following LSTM structure was used: five units (nodes) for the hidden layer, and one unit (node) for the output layer.
4. Model Performance Indicators
The authors used several metrics for evaluation, one of which is RMSE. The discrepancy between the values that were modeled and those that were actually observed is known as the residual mean square error, or RMSE. RMSE is a measurement of the amount of error between the projected and simulated outcomes and the actual rainfall (mm). In addition to comparing the highest and lowest values of the simulated and the observed values, we also used the Nash–Sutcliffe efficiency (NSE), correlation coefficient (CC), Kling–Gupta efficiency (KGE), index of agreement (IA), Legates–McCabe index (LMI), mean average percentage error (MAPE), percent (%) bias (PBIAS), and RMSE-observations standard deviation ratio (RSR) to assess the performance of the univariate LSTM and DWT rainfall model.
RMSE is commonly used for verification of experimental results in forecasting and regression analysis. It is essentially a standard deviation of the model residuals, which could tell us how concentrated the data around the line of best fit. Thus, lower values of RMSE mean a better model fit.
The following is the formula for RMSE:
where is the simulated output, is the observed sample, and n denotes the number of data points. By convention, the lower the value of these metrics, the better the forecasted model.
NSE is a measure of how well simulated and real data fit on a 1:1 line in a graphic. This metric’s values vary, with positive values indicating the opposite of the message, and negative values indicating bad simulation. Positive values, on the other hand, are almost identical to the observations. The efficiency of how well the modeling technique could model the resultants were studied through the use of various indicators. Nash–Sutcliffe efficiency, NSE, can be evaluated using:
where X and Y are the observed and simulated variables, while is the mean of the simulated variable in the model.
CC values illustrate the degree of statistical association between the variables. Its values range from negative one to one. Such values determine either a positive or a negative correlation among the datasets. Moreover, a CC value of zero indicates no linear correlation. CC is a performance indicator of statistical association between the variables. To calculate CC, the following formula should be used:
where is the mean of the observed variable.
Originally proposed by [58], Kling–Gupta efficiency has been used in various fields. The bias, α (see Equation (20)), is calculated by dividing the standard deviation of the simulated variable by the standard deviation of the observed variable. Another bias, β (see Equation (21)), is calculated by dividing the mean of the simulated variable by the mean of the observed variable. The Pearson correlation coefficient, CCKGE (see Equation (22)), of the simulated and observed variables together with the two aforementioned biases, were the input values in the KGE, as shown in Equation (23):
On the other hand, to measure the relative magnitude of the residual variance to the variance of errors of the model, IA, is also calculated. The following formula applies:
The ratio of the mean square error (MSE) to the potential error (PE), multiplied by the number of observations, is how [59] defines the index of agreement (IA). Then, one is deducted from this figure. The range of IA values is zero to one, with higher index values indicating better agreement between observed and simulated values.
Legates–McCabe index (LMI) is another metric used in this study.
In the equations stated above, n represents the number of data points, represents the observed values, represents the simulated values, and is the mean of the observed values.
On the other hand, KGE assesses the skill of the model simulation by optimizing the bias and the variability of the datasets. KGE values range from −∞ to 1, and as with the other indicators, a value of 1 is preferred.
Another metric used is mean absolute percentage error (MAPE, %), which is calculated as follows:
The smaller the MAPE value, the better the simulated value.
Percent (%) bias (PBIAS) is also used in this study. A lower value of PBIAS means better simulation. If the value is positive, it means model overestimation bias, and if the value is negative, it means the model has underestimation bias. The optimal value of this metrics is 0.0.
The last metric is RMSE-observations standard deviation ratio (RSR). As implied by its name, it utilizes the standard deviation of the observed values to compare the models. This metric is calculated as follows:
where the RSR optimum value is 0.0, thus, the lower the value obtained means the better the performance of the model.
5. Study Area
The Philippines, which is known to be consistently rampaged by typhoons, has been prone to excessive flooding, causing a huge number of fatalities each year. Samar, which is located in the Visayas region, has always been subject to heavy rainfall, which took a heavy toll on the province’s facilities and infrastructure. In January 2021, more than a thousand people were displaced in the 13 upstream barangays of Oras, Eastern Samar.
This study will focus on four subcatchments in Samar, Philippines (see Figure 3). The extents of the subcatchments, which will be named as S-7, S-8, S-9, and S-10, are shown in Figure 4. The four subcatchments (S-7, S-8, S-9, and S-10) were chosen simply based on data availability. Some stations failed to record rainfall amounts due to broken rain gauges, which were caused by several factors, both man-made and natural. The study area is harsh and steep, and enveloped with thick rainforest. However, the catchment area is also drained by diverse bodies of water. The area has several mountain ranges and summits as well. Table 2 shows the stations and date range used in this study. The time-scale used for the entire study is daily.
Figure 3.
Location of subcatchments in Samar, Philippines.
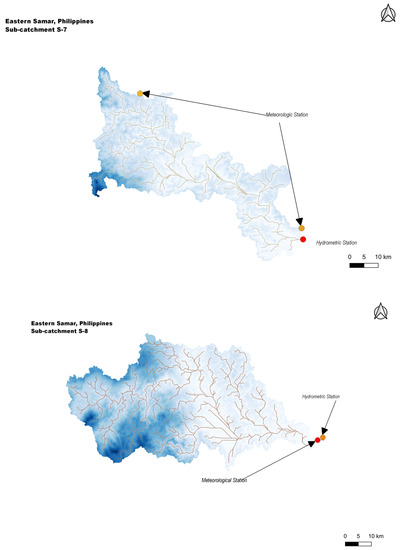
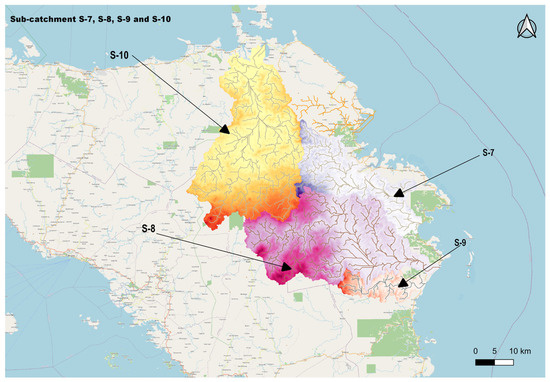
Figure 4.
Study Area (subcatchments S-7, S-8, S-9, and S-10).

Table 2.
Stations and Date Range Used in the Study (daily).
Table 2.
Stations and Date Range Used in the Study (daily).
| Subcatchment Name | Station Number | From | To |
|---|---|---|---|
| S-7 (Oras) | 1155 | 6 November 2013 | 22 December 2018 |
| S-8 (Dolores) | 1767 | 22 March 2016 | 31 December 2018 |
| S-9 (Can-avid) | 93 | 2 January 2013 | 31 December 2018 |
| S-10 (Catubig) | 547 | 9 July 2013 | 2 May 2018 |
Hydrological variable models for rainfall can lead to efficient and accurate modeling of river or subcatchment discharge. Knowledge of this type of information can lead to flood and fatality prevention, but also to dissemination of relief operations, which can lead to optimum water resource management later on. However, there is lack of explorations regarding the methods and appropriate variables that can affect hydrological models, especially in developing countries such as the Philippines.
There have been various records of devastating floods that have submerged the Philippines. Samar, one of the most common victims of typhoons and massive flooding, recorded at least 3000 affected families in the January 2021 incessant rainfall [60], at least 1800 families affected in the December 2017 flooding [61], 2 dead and 40,000 affected in the January 2011 flooding [62], and 6 dead in the December 2008 flooding [63]. Frequently, the floodwaters are caused by incessant rainfall, which causes the ground to exceed its ability to absorb water. Floods also occur when dry streams, creeks, or streams surpass their banks, which causes floodwaters to rise rapidly. These kinds of events are life-threatening, especially to inhabitants near flood-prone areas.
6. Data Collection and Characteristics
Data were obtained from the Advanced Science and Technology Institute (ASTI) of the Department of Science and Technology (DOST) in the Philippines. In this study, the authors used the univariate long short-term memory network (LSTM), alongside discrete wavelet transform (DWT), to simulate rainfall quantities in the following rainfall stations in Samar, Philippines (see Table 2).
This study proposed that the superposition of the base ‘smoothened’ signal and the noise signal modeled by univariate LSTM can be used to model rainfall. There are a total of four subcatchments considered in this study, namely: Oras sub-basin or S-7 (12 April 2016–31 December 2018), Dolores sub-basin or S-8 (22 March 2016–31 December 2018), Can-avid sub-basin or S-9 (2 January 2013–31 December 2018), and Catubig sub-basin or S-10 (9 July 2013–2 May 2018). Due to the varying availability of data per station, the start and end dates in each sub-basin were varying. Table 3 shows the descriptive statistics of the data used in the rainfall model.

Table 3.
Descriptive Statistics of the Data used in the Rainfall Model (in mm).
Figure 5 shows the amount of precipitation in each rainfall station over varying time ranges. As mentioned, the time range varies in each station due to the varying availability of data, because some stations were built earlier or later than the others. Another reason is that some stations were damaged by typhoons, which disrupted the functional ability of the gauges.



Figure 5.
Actual Rainfall Curves for Subcatchments S-7–S-10.
As shown in Figure 5, there are noticeable peaks and high amounts of rainfall in S-8 and S-9 compared to the amount of rainfall in S-7 and S-10. In fact, the maximum amount of rainfall obtained in S-8 is 91.0 mm, while S-9 has 71.5 mm. On the other hand, S-7 and S-10 have 22.4 mm and 14.0 mm, respectively.
7. Overview of the Process
The overview of the process for the rainfall model is shown in the following schematic diagram (see Figure 6). The process will start with data collection from a Philippine government entity, the Department of Science and Technology (DOST). This will be followed by the application of discrete wavelet transform (DWT) and univariate long short-term memory network (LSTM), which will be further discussed in the following sections.
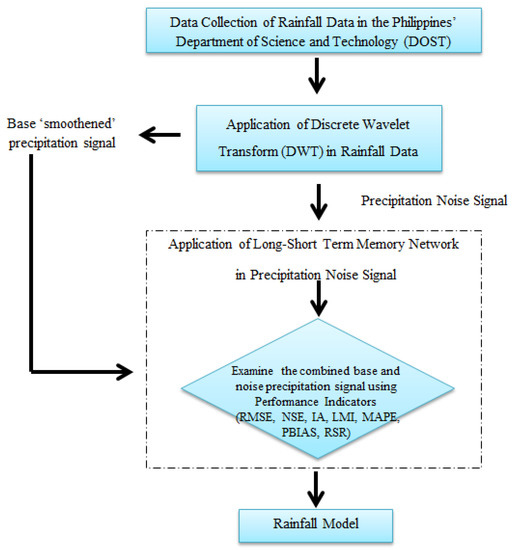
Figure 6.
Schematic Diagram of the Rainfall Model Using Univariate LSTM.
8. Noise Analysis Using DWT and LSTM
This study applied DWT (see Figure 7) to generate a smoothened rainfall ‘base’ curve from varying time ranges (dependent on the available data per rainfall station per subcatchment). The time series or signal are the inputs in the DWT process. The low-pass filter was utilized in the time series to recognize the ‘noise’ from the ‘non-noise’ parts. The level of decomposition used is one, and the thresholding was calculated using the average value of the time series, in this case, rainfall. Each value produced in wavelet transform is thresholded. Soft-thresholding [40], which is defined as replacing the absolute value of coefficient produced in wavelet transform with the threshold value when it is less than or equal to the threshold value, is applied.
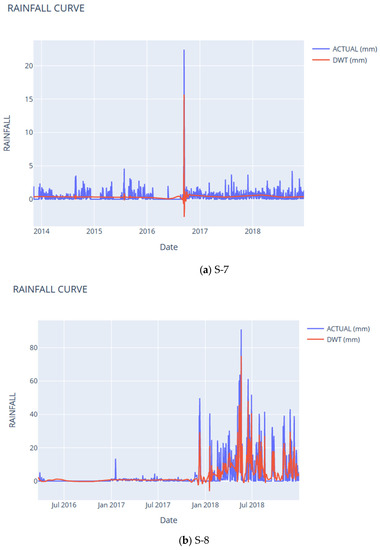
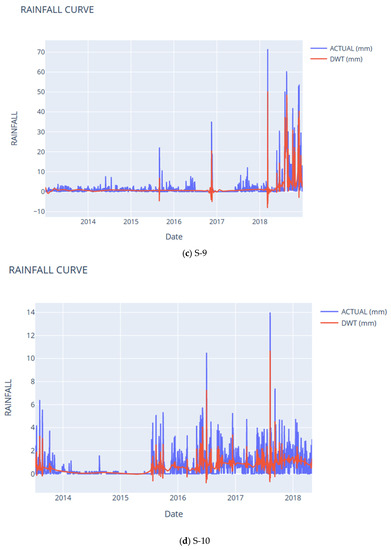
Figure 7.
Actual vs DWT Rainfall Curves for subcatchments S-7–S-10.
The scaling function used is the Daubechies wavelet four, and the soft-thresholding method with the low-pass filter (or the average of the time series as the threshold) was applied. Calculations can be performed manually or by using pywavelets in python.
9. Rainfall Noise Modeling Using LSTM
This study considered one input layer (the rainfall data preprocessed by the inverse distance weighting (IDW) method) and the adaptive moment estimation (Adam) optimizer was used, since, as emphasized by [46], it is suitable for large data and is efficient, as it requires less memory. The maximum number of epochs the model could undergo was set to 400. Therefore, when the validation loss stops improving, the system will stop the training, even if it has not reached epoch 400. An epoch is an iteration, and for each epoch, each data element will undergo training. If the number of epochs is small, the number of iterations the element will undergo will also be small, and can potentially result in underfitting. The activation function used is the rectified linear activation function (ReLU). ReLU has the ability to return the input directly if the value is greater than zero. If the value is less than zero, then it will return zero. ReLU allows the LSTM network to approximate not just a linear function (if it exists), but also accounts for the nonlinearity of the time series. The time series was divided into two datasets: the training and testing datasets; 70% for the former (training), and 30% for the latter (testing). For prediction modeling, data are typically divided into training, testing, and validation data. However, in some cases, training data and testing data [64,65,66] are already sufficient for model prediction. The authors utilized python’s software library, keras v2.11.0, which serves as an interface for the TensorFlow library.
The authors of [4] have subsequently used DWT and LSTM to visualize dengue surges. To the best of the authors’ knowledge, the use of DWT in a rainfall model to smoothen the base or observed rainfall curve, and then utilizing univariate LSTM (See Figure 8) for the noisy signal obtained by DWT, has not yet been used in any rainfall-related studies.
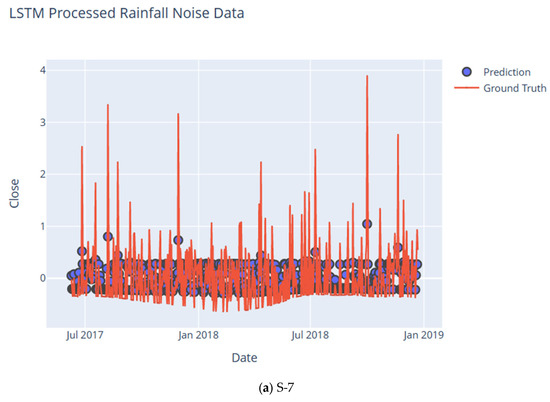
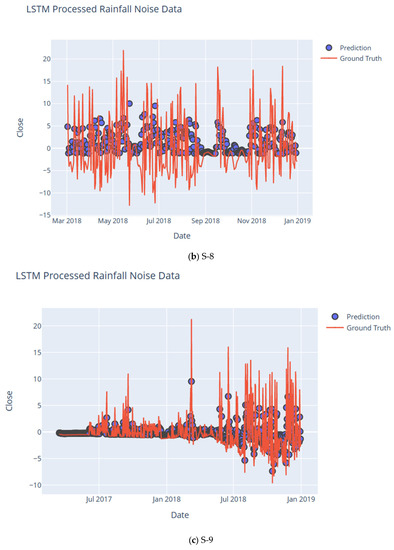
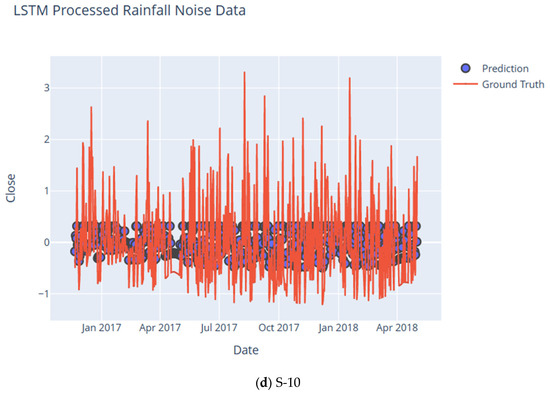
Figure 8.
LSTM Plot for Noise Signal of Rainfall for subcatchments S-7–S-10.
As shown in Figure 9, the approximate or base signal produced by DWT-LSTM was able to capture both time and frequency of the original rainfall time series or signal. This is better illustrated when the significant peak values of the approximate or base signal corresponded to the peak values of the observed rainfall time series or signal.
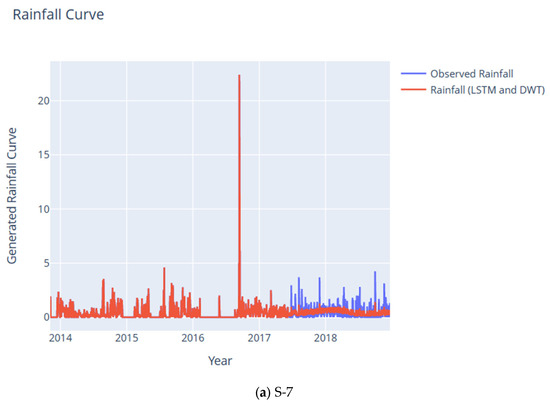
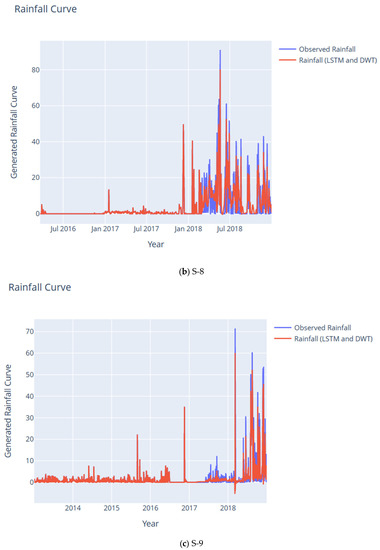
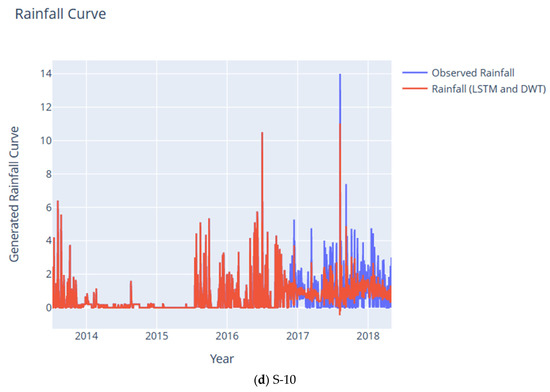
Figure 9.
Reconstructed Rainfall Curves using DWT and LSTM for subcatchments S-7–S-10, continued.
As shown in Table 4, in S-7, the highest peak (in mm), which occurs at 13 September 2016, was also captured by the smoothened ‘denoised’ signal. S-8, on the other hand, has peaks at 8–11 December 2017, 18 January 2018, 6 May 2018, 12–16 May 2018, 19–20 May 2018, 24 May 2018, 15–16 June 2018, 18 June 2018, 21–22 June 2018, 29 June 2018, 29–30 July 2018, 6 August 2018, 19 August 2018, 2–3 November 2018, 26 November 2018, and 12 December 2018. In this study, we used the low-pass filter for the approximate or base signal, and to keep the low-frequency signal where signal oscillations are fewer.

Table 4.
Performance Indicators Results for DWT + LSTM Rainfall.
S-9 has noticeable peaks (in mm) at 17 November 2016, 9 March 2018, 31 July 2018, 2–21 August 2018, 30 August 2018, 8 October 2018, 22 October 2018, 22–23 November 2018, 26–28 November 2018, and 2 December 2018, while S-10 has peaks at 1 July 2016, 9 August 2017, and 9 September 2017.
10. Discussion
There are many studies which made use of noise modeling, especially in hydrology [32,67]. Some studies showed that a model would demonstration high performance indicator values when the noises are modeled separately [32]. In this study, the rainfall time series, which was treated as a signal, was reconstructed into a combination of a base ‘smoothened’ or ‘denoised’ signal and a noise signal.
One of the advantages of using DWT is that it can capture time and frequency information. Thus, filtering noise signals in a stationary, or even nonstationary, time series is still suitable when DWT is used. With DWT, the authors were able to divide the information in the signal into two subsignals: the ‘denoised’ (approximate) signal or time series, and the noise (detailed) signal or time series.
The noise (detailed) signal or time series was then processed by the univariate LSTM (see Figure 8). Figure 9 shows the framework of the DWT and univariate LSTM. The output of LSTM (Figure 8) is then combined to the output of the DWT to be able to obtain the new rainfall curve (Figure 9). As shown, the new rainfall curves (Figure 9) more or less matched the observed rainfall. To measure the DWT and univariate LSTM model performance, we used several indicator metrics, namely: RMSE, CC, NSE, KGE, IA, LMI, MAPE, PBIAS, and RSR (see Table S1).
The reconstructed signals show high performance (see Table S1). As pointed out by [4], LSTM can actually recognize seasonality behaviour in a time series. Precipitation is a time series signal which shows seasonal characteristics. This type of property has been proven in several studies [68,69]. Therefore, despite excluding any type of meteorological variables in modeling rainfall time series and just reconstructing it, the DWT and univariate LSTM model achieved very high performance indicator values. In fact, it was consistently high (CC, NSE, KGE, IA, LMI) with MAPE values at almost zero, and consistently low values for RMSE and RSR.
Some researchers who used minimal metrics of evaluation used an ablation experiment to verify the performance of their proposed rainfall model. In fact, in the paper of [33], the authors emphasized that the use of wavelet-ARIMA-LSTM (W-AL) is superior compared to using a plain LSTM and a plain ARIMA rainfall model. In this study, the authors provided a supplementary table (Table S1) to show the comparison of performance indicators between DWT and LSTM- and LSTM-generated rainfall.
Comparing Table S1 with Table 4, it is clear that the DWT and LSTM model have outperformed the LSTM model in terms of modeling the rainfall of each subcatchment. It can be seen that the only time that the LSTM rainfall outperformed the DWT-LSTM is in the CC value of S-8, where the former (LSTM) obtained a value of 0.98, while the latter (DWT and LSTM) obtained a value of 0.94.
Several studies have discussed the disadvantages of using LSTM alone in the model prediction of rainfall. In fact, Ref. [32], in their proposed rainfall model, emphasized that LSTM, just like the other neural networks, has a tendency to overestimate or underestimate peak rainfalls, therefore affecting the model accuracy. The same goes for [33], who pointed out that a hybrid approach rainfall prediction model has better fitting effects than the other singular ARIMA and LSTM models.
The results of this study, using the proposed method of superposition of the base ‘smoothened’ signal and the noise signal modeled by univariate LSTM, have been proven to be superior to an LSTM-generated rainfall.
Ref. [33] used DWT and ARIMA and LSTM and called it the W-AL model. In the mentioned study, the authors emphasized the effectiveness of using W-AL in the univariate forecasting of rainfall. However, the evaluation metrics used were few. In this study, we used several metrics of evaluation (RMSE, CC, NSE, KGE, IA, LMI, MAPE, PBIAS, and RSR), with the lowest CC value at 0.94. The difference between the research results of this study in comparison to the other studies, such as that of [33], is that this study emphasized the noise signals by using LSTM to model them. Choi et al. (2019) [32] also modeled the noises separately, but this was performed in the concept of heavy rain damage and not in rainfall prediction. Their method involves decision tree, random forest, SVM, DNN, linear regression, and PCA.
To the best of the authors’ knowledge, none of the available rainfall model studies have used the approach performed in this paper. However, it was proven in the works of [33] and [34] that superimposed models (especially with the use of wavelet) can outperform nonhybrid, linear, and nonlinear models. Choi et al. (2019) [32], on the other hand, showed in their work that noise modeling deserves special attention. Combined, this paper emphasized that superimposed models with noise modeling is an effective rainfall modeling method, especially in a country where data is deficient.
11. Conclusions
In this day and age where data science is prominent, and where classical mathematical equations have not established a higher reputation against deep learning (DL), especially with study areas where data are lacking, the use of an effective, time-bound rainfall prediction model is deemed necessary. The authors conclude that the use of DL and DWT to estimate the rainfall parameter of the hydrological model can be effective in modeling some subcatchments in Samar, Philippines. The proposed method of modeling noise signal using LSTM and reconstructing the rainfall time series using DWT has great potential for the advancement of disaster risk reduction measures, especially in countries where data and resources are scarce, such as the Philippines. This study is also beneficial for governments that need strategic and highly targeted risk assessment studies in order to boost proper decision-making, and ultimately result in better disaster risk policies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos14040632/s1, Table S1. Performance Indicators Results for LSTM-Generated Rainfall.
Author Contributions
Conceptualization, I.V.N.; methodology, I.V.N.; software, I.V.N.; validation, I.V.N.; formal analysis, I.V.N.; investigation, I.V.N.; resources, I.V.N.; data curation, I.V.N.; writing—original draft preparation, I.V.N.; review and editing, D.K., Y.H.B., K.K., S.K. and H.S.K.; supervision, H.S.K.; funding, H.S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Foundation of Korea: MSIT No. 2022R1A2C2091773.
Data Availability Statement
Data are publicly available and can be accessed in https://www.kaggle.com/datasets/ahyimi/rainfall-data (accessed on 6 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nalley, D.; Adamowski, J.; Biswas, A.; Gharabaghi, B.; Hu, W. A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrol. 2019, 574, 288–307. [Google Scholar] [CrossRef]
- Gao, L.; Deng, Y.; Yan, X.; Li, Q.; Zhang, Y.; Gou, X. The unusual recent streamflow declines in the Bailong River, north-central China, from a multi-century perspective. Quat. Sci. Rev. 2021, 260, 106927. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Necesito, I.V.; Velasco, J.M.; Kwak, J.W.; Lee, J.H.; Lee, M.J.; Kim, J.S.; Kim, H.S. Combination of Univariate Long-Short Term Memory Network and Wavelet Transform for predicting dengue case density in the National Capital Region, the Philippines. Southeast Asian J. Trop. Med. Public Health 2021, 52, 479–494. [Google Scholar]
- Feng, Q.; Wen, X.; Li, J. Wavelet Analysis-Support Vector Machine Coupled Models for Monthly Rainfall Forecasting in Arid Regions. Water Resour Manag. 2015, 29, 1049–1065. [Google Scholar] [CrossRef]
- Chen, L.; Sun, N.; Zhou, C.; Zhou, J.; Zhou, Y.; Zhang, J.; Zhou, Q. Performance Enhancement Model for Rainfall Forecasting Utilizing Integrated Wavelet-Convolutional Neural Network. Water Resour Manag. 2020, 34, 2371–2387. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Damavandi, H.G.; Shah, R.; Stampoulis, D.; Wei, Y.; Boscovic, D.; Sabo, J. Accurate prediction of streamflow using long short-term memory network: A case study in the Brazos River Basin in Texas. Int. J. Environ. Sci. Dev. 2019, 10, 294–300. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Samui, P.; Jha, R.K. Forecasting monthly precipitation using sequential modelling. Hydrol. Sci. J. 2019, 64, 690–700. [Google Scholar] [CrossRef]
- Qin, J.; Liang, J.; Chen, T.; Lei, X.; Kang, A. Simulating and predicting of hydrological time series based on tensorFlow deep learning. Pol. J. Environ. Stud. 2019, 28, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Wan, X.; Yang, Q.; Jiang, P.; Zhong, P.A. A hybrid model for real-time probabilistic flood forecasting using elman neural network with heterogeneity of error distributions. Water Resour. Manag. 2019, 33, 4027–4050. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Song, T.; Ding, W.; Wu, J.; Liu, H.; Zhou, H.; Chu, J. Flash Flood Forecasting Based on Long Short-Term Memory Networks. Water 2019, 12, 109. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily runoff forecasting using a hybrid model based on variational mode decomposition and deep neural networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
- Goswami, P.; Srividya. A novel neural network design for long range prediction of rainfall pattern. Curr. Sci. 1996, 70, 447–457. [Google Scholar]
- Chattopadhyay, S. Anticipation of summer monsoon rainfall over India by Artificial Neural Network with Conjugate Gradient Descent Learning. arXiv 2006, arXiv:nlin/0611010. [Google Scholar]
- Kannan, M.; Prabhakaran, S.; Ramachandran, P. Rainfall Forecasting Using Data Mining Technique. Int. J. Eng. Technol. 2010, 2, 397–401. [Google Scholar]
- Chattopadhyay, S.; Chattopadhyay, G. Univariate modelling of summer-monsoon rainfall time series: Comparison between ARIMA and ARNN. C. R. Geosci. 2010, 342, 100–107. [Google Scholar] [CrossRef]
- Kannan, S.; Ghosh, S. Prediction of daily rainfall state in a river basin using statistical downscaling from GCM output. Stoch. Environ. Res. Risk Assess. 2011, 25, 457–474. [Google Scholar] [CrossRef]
- Venkata Ramana, R.; Krishna, B.; Kumar, S.R.; Pandey, N.G. Monthly Rainfall Prediction Using Wavelet Neural Network Analysis. Water Resour. Manag. 2013, 27, 3697–3711. [Google Scholar] [CrossRef]
- Joseph, J.; Ratheesh, T.K. Rainfall Prediction using Data Mining Techniques. Int. J. Comput. Appl. 2013, 83, 11–15. [Google Scholar] [CrossRef]
- Nikam, V.B.; Meshram, B.B. Modeling Rainfall Prediction Using Data Mining Method: A Bayesian Approach. In Proceedings of the 2013 Fifth International Conference on Computational Intelligence, Modelling and Simulation, Washington, DC, USA, 24–25 September 2013; pp. 132–136. [Google Scholar] [CrossRef]
- Prasad, N.; Kumar, P.; Mm, N. An Approach to Prediction of Precipitation Using Gini Index in SLIQ Decision Tree. In Proceedings of the 4th International Conference on Intelligent Systems, Modelling and Simulation, Bangkok, Thailand, 29–31 January 2013; pp. 56–60. [Google Scholar] [CrossRef]
- Dutta, P.S.; Tahbilder, H. Prediction of Rainfall using Data-mining Technique over Assam. Indian J. Comput. Sci. Eng. 2014, 5, 85–90. [Google Scholar]
- Gupta, D.; Ghose, U. A comparative study of classification algorithms for forecasting rainfall. In Proceedings of the 4th International Conference on Reliability, Infocom Technologies and Optimization (ICRITO) (Trends and Future Directions), Noida, India, 2–4 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Univariate Time Series Forecasting of Temperature and Precipitation with a Focus on Machine Learning Algorithms: A Multiple-Case Study from Greece. Water Resour. Manag. 2018, 32, 5207–5239. [Google Scholar] [CrossRef]
- Phan, T.-T.-H.; Caillault, E.P.; Bigand, A. Comparative Study on Univariate Forecasting Methods for Meteorological Time Series. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2380–2384. [Google Scholar] [CrossRef]
- Tran Anh, D.; Duc Dang, T.; Pham Van, S. Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks. J 2019, 2, 65–83. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Kim, J.; Kim, H.S. Development of Combined Heavy Rain Damage Prediction Models with Machine Learning. Water 2019, 11, 2516. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, J.; Yu, H.; Liu, D.; Xie, K.; Chen, Y.; Hu, J.; Sun, H.; Xing, F. The Development of a Hybrid Wavelet-ARIMA-LSTM Model for Precipitation Amounts and Drought Analysis. Atmosphere 2021, 12, 74. [Google Scholar] [CrossRef]
- Wei, M.; You, X. Monthly rainfall forecasting by a hybrid neural network of discrete wavelet transformation and deep learning. Water Resour Manag. 2022, 36, 4003–4018. [Google Scholar] [CrossRef]
- Kabbilawsh, P.; Kumar, D.S.; Chithra, N.R. Performance evaluation of univariate time-series techniques for forecasting monthly rainfall data. J. Water Clim. Change 2022, 13, 4151–4176. [Google Scholar] [CrossRef]
- Tsui, F. Time Series Prediction Using a Multi-Resolution Dynamic Predictor. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 1996. ISBN 978-0-591-37804-7. [Google Scholar]
- Hsia, C.H.; Chiang, J.S.; Guo, J.M. Multiple Moving Objects Detection and Tracking Using Discrete Wavelet Transform, Discrete Wavelet Transforms. 2011. Available online: https://www.intechopen.com/books/iscrete-wavelet-transforms-biomedical-applications/multiple-moving-objects-detection-and-tracking-using-discrete-wavelet-transform (accessed on 20 June 2020). [CrossRef]
- Patil, G.M.; Rao, K.S.; Satyanarayana, K. Heart disease classification using discrete wavelet transform coefficients of isolated beats. In Proceedings of the 13th International Conference on Biomedical Engineering, Singapore, 3–6 December 2008; Lim, C.T., Goh, J.C.H., Eds.; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Shmueli, G. Wavelet-based monitoring for biosurveillance. Axioms 2013, 2, 345–370. [Google Scholar] [CrossRef]
- Alimohamadi, Y.; Zahraei, S.M.; Karami, M.; Yaseri, M.; Lotfizad, M.; Holakouie-Naieni, K. Aberration detection of pertussis from the Mazandaran province, Iran, from 2012 to 2018: Application of discrete wavelet transform. J. Acute Dis. 2020, 9, 114–120. [Google Scholar] [CrossRef]
- Yim, S.Y.; Wang, B.; Xing, W. Prediction of early summer rainfall over South China by a physical-empirical model. Clim. Dyn. 2014, 43, 1883–1891. [Google Scholar] [CrossRef]
- Goyal, M.K. Monthly rainfall prediction using wavelet regression and neural network: An analysis of 1901–2002 data, Assam, India. Theor. Appl. Climatol. 2014, 118, 25–34. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Mahmood, A.; Barton, A. Prediction of monthly rainfall in Victoria, Australia: Clusterwise linear regression approach. Atmos. Res. 2017, 188, 20–29. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Application of artificial neural networks to rainfall forecasting in Queensland, Australia. Adv. Atmos. Sci. 2012, 29, 717–730. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Input selection and optimisation for monthly rainfall forecasting in Queensland, Australia, using artificial neural networks. Atmos. Res. 2014, 138, 166–178. [Google Scholar] [CrossRef]
- Hong, K.; Kang, T. A Study on Rainfall Prediction based on Meteorological Time Series. In Proceedings of the 2021 Twelfth International Conference on Ubiquitous and Future Networks (ICUFN), Jeju Island, Republic of Korea, 17–20 August 2021; pp. 302–304. [Google Scholar] [CrossRef]
- Narasimha Murthy, K.V.; Kishore Kumar, G. Distribution and Prediction of Monsoon Rainfall in Homogeneous Regions of India: A Stochastic Approach. Pure Appl. Geophys. 2022, 179, 2577–2590. [Google Scholar] [CrossRef]
- Ray, S.N.; Chattopadhyay, S. Analyzing surface air temperature and rainfall in univariate framework, quantifying uncertainty through Shannon entropy and prediction through artificial neural network. Earth Sci. Inform. 2021, 14, 485–503. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Z.; Wang, G.; Xie, W. Damage Detection on Sudden Stiffness Reduction Based on Discrete Wavelet Transform. Sci. World J. 2014, 2014, 807620. [Google Scholar] [CrossRef]
- Strömbergsson, D.; Marklund, P.; Berglund, K.; Saari, J.; Thomson, A. Mother wavelet selection in the discrete wavelet transform for condition monitoring of wind turbine drivetrain bearings. Wind Energy 2019, 22, 1581–1592. [Google Scholar] [CrossRef]
- Patil, P.B.; Chavan, M.S. A wavelet based method for denoising of biomedical signal. In Proceedings of the International Conference on Pattern Recognition, Informatics and Medical Engineering (PRIME-2012), Salem, India, 21–23 March 2012; pp. 278–283. [Google Scholar] [CrossRef]
- Mathworks. 2012. Available online: https://www.mathworks.com/help/wavelet/gs/choose-a-wavelet.html (accessed on 29 November 2022).
- Jense, A.; la Cour-Harbo, A. Ripples in Mathematics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Gao, R.X.; Yan, R. Wavelets: Theory and Applications for Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-1-4419-1545-0. [Google Scholar]
- Qashqai, P.; Zgheib, R.; Al-Haddad, K. GRU and LSTM Comparison for Black-Box Modeling of Power Electronic Converters. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Dolek, I. LSTM. Deep Learning Turkey. 2018. Available online: https://ishakdolek.medium.com/lstm-d2c281b92aac (accessed on 20 June 2020).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and nse performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Willmott, C.J. On the evaluation of model performance in physicalgeography. In Spatial Statistics and Models; Gaile, G.L., Willmott, C.J., Eds.; D. Reidel: Boston, MA, USA, 1984; pp. 443–460. [Google Scholar] [CrossRef]
- CNN Philippines. Massive Flooding Affects More than 3000 Families in Eastern Samar. 2021. Available online: https://www.cnnphilippines.com/regional/2021/1/12/Eastern-Samar-flooding.html (accessed on 30 August 2022).
- Serafica, R. LOOK: Houses in Eastern Samar town flooded due to Urduja. 2017. Available online: https://www.rappler.com/moveph/191508-houses-taft-eastern-samar-flood-urduja/ (accessed on 30 August 2022).
- PIA (Philippine Information Agency) Eastern Samar. Maslog Mayor Fears Hunger in His Town. 2011. Available online: https://samarnews.com/news_clips16/news317.htm (accessed on 30 August 2022).
- PIA (Philippine Information Agency) Eastern Samar. Philippines: 40,000 Affected, 6 Dead in Floods at Eastern, Northern Samar. 2008. Available online: https://reliefweb.int/report/philippines/philippines-40000-affected-6-dead-floods-eastern-northern-samar (accessed on 30 August 2022).
- Xie, H.; Tang, H.; Liao, Y.-H. Time series prediction based on NARX neural networks: An advanced approach. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Hebei, China, 12–15 July 2009; pp. 1275–1279. [Google Scholar] [CrossRef]
- Koschwitz, D.; Frisch, J.; van Treeck, C. Data-driven heating and cooling load predictions for non-residential buildings based on support vector machine regression and NARX Recurrent Neural Network: A comparative study on district scale. Energy 2018, 165, 134–142. [Google Scholar] [CrossRef]
- Ruslan, F.A.; Samad, A.M.; Zain, Z.M.; Adnan, R. Flood water level modeling and prediction using NARX neural network: Case study at Kelang river. In Proceedings of the 2014 IEEE 10th International Colloquium on Signal Processing and Its Applications, Kuala Lumpur, Malaysia, 7–9 March 2014; pp. 204–207. [Google Scholar] [CrossRef]
- Schoups, G.; Vrugt, J.A. A formal likelihood function for parameter and predictive inference of hydrologic models with correlated, heteroscedastic, and non-Gaussian errors. Water Resour. Res. 2010, 46, 2009WR008933. [Google Scholar] [CrossRef]
- Pryor, S.C.; Schoof, J.T. Changes in the seasonality of precipitation over the contiguous USA. J. Geophys. Res. 2008, 113, D21108. [Google Scholar] [CrossRef]
- Sumner, G.; Homar, V.; Ramis, C. Precipitation seasonality in eastern and southern coastal Spain. Int. J. Climatol. 2001, 21, 219–247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).