Enhancing the Performance of Quantitative Precipitation Estimation Using Ensemble of Machine Learning Models Applied on Weather Radar Data

Abstract

Flash floods are a major weather-related risk, as they cause more than 5000 fatalities annually, according to the World Meteorological Organization. Quantitative Precipitation Estimation is a method used to approximate the rainfall over locations where direct field observations are not available. It represents one of the most valuable information employed by meteorologists and hydrologists for issuing early warnings concerning flash floods. The current study is in line with the efforts to improve radar-based rainfall estimates through the use of machine learning techniques applied on radar data. With this aim, as a proof of concept, six machine learning models are evaluated to make estimations of the radar-based hourly accumulated rainfall using reflectivity data collected on the lowest radar elevation angles, and we employ a new data model for representing these radar data. The data were collected by a WSR-98D weather radar of the Romanian Meteorological Administration, located in the central region of Romania, during 30 non-consecutive days of the convective seasons, between 2016 and 2021. We obtained encouraging results using a stacked machine learning model. In terms of the Root Mean Squared Error evaluation metric, the results of the proposed stacked regressor are better than the radar estimated accumulated rainfall by about 33% and also outperform the baseline computed using the Z-R relationship by about 13%.

1. Introduction

Heavy rainfall may lead to flash floods, overflowing rivers or landslides, representing a frequent and widespread severe weather hazard for population safety and the economy, with flash floods alone causing more than 5000 fatalities annually, according to the World Meteorological Organisation. Quantitative precipitation estimation (QPE) [1] is one of the most important and challenging tasks in meteorology [2], as it represents the primary method for approximating the rainfall over locations where direct field observations are not available, thus providing meteorologists and hydrologists valuable information for early warnings issuing. In spite of the great scientific and technological developments made over the past decades, higher spatial and temporal accuracy of precipitation forecasts [3] is demanded by both meteorologists and the public at large.

QPE is generated using different data sources, including interpolated rain gauges data and weather radar networks. While weather radar data has the advantage of higher spatial and temporal resolution, it is prone to a series of errors due to incorrect radar calibration, signal attenuation, ground clutter, range limitations, anomalous propagation or partial beam filling. Apart from rain gauges [4], weather radars play an increasingly important role in QPE [5], as they are used for urban hydrology [6], hydrological analysis and modeling [7], real-time QPE [8], rainfall climatology [9], rainfall pattern analysis [10,11] and rainfall frequency analysis [12].

One Hour Precipitation (OHP) is a derived WSR-88/98D radar product depicting the estimated one-hour precipitation accumulation, on a 1 degree × 2 km (polar) grid, using the Precipitation Processing System (PPS) algorithm [13]. This product ranges in [0, 203.20 mm] and helps to assess rainfall accumulation for flash flood warnings, urban flood statements and special weather statements. Further, the radar-based hourly accumulated rainfall is denoted as OHP. The Z-R formula is the traditional method for precipitation estimation, using an exponential relation between radar reflectivity factors and precipitation, but it is known to have a low accuracy in precipitation estimation [14]. The Z-R relationship between the radar reflectivity factor Z and the precipitation rate R (mm/h) is $Z=a·R^b$.

Conventional methods currently used in meteorology and climatology for collecting meteorology- and climate-relevant atmospheric data are based on fixed weather stations that are usually located around 50 km apart. This distribution is enough for monitoring parameters with low spatial gradients such as atmospheric pressure but is sparse for precipitation observation. The higher spatial resolution (around 1 × 1 km) of weather radars can enable a more accurate overview of the precipitation field.

In the past decades, efforts have been made to improve the QPE algorithms by applying various merging techniques or by employing multiple data sources, including ground-based sensors, satellite-based sensors and weather radars. The Tropical Rainfall Measuring Mission (TRMM) Multisatellite Precipitation Analysis (TMPA) was combining precipitation estimates from multiple satellites, also integrating rain gauges data where available, at a 0.25° × 0.25° spatial resolution, every 3 h [15]. The program was decommissioned in 2015, being replaced by the Global Precipitation Measurement (GPM) mission. The GPM spacecraft has the capabilities to detect rain and snow through dual-frequency precipitation radar and radiometer measurements [16], and it is not affected by many of the errors common to weather radars, with higher spatial (5–15 km) and temporal (1–3 h) resolution than the TRMM. One of the essential applications of the GPM is the Integrated Multi-Satellite Retrievals for GPM (IMERG) that merges observations from multiple spaceborne sensors, including into an interpolated global gridded precipitation product, with a spatial resolution of 0.1° and a half hour frequency [17]. The proposed National Mosaic and Multi-Sensor Quantitative Precipitation Estimation (NMQ) system [18] integrates doppler radars, rain gauges, satellite and numerical weather prediction (NWP) with the aim of providing QPE over the entire US territory, at high spatial and temporal resolution, for flash flood warnings, data assimilation and NWP verification. The Multi-Radar Multi-Sensor (MRMS) system currently in use by the American National Centers for Environmental Prediction (NCEP) integrates at high spatial resolution (1 km) and high frequency (2 min) 3D radar data with atmospheric environmental data, satellite, lightning and rain gauge data in order to generate a suite of QPE products [19]. The MRMS is based on a dual-polarization radar synthetic QPE that employs the specific attenuation, the specific differential phase or the reflectivity [20]. A more recent approach in QPE is applying machine learning (ML) algorithms that can identify patterns and relationships in the data that may not be apparent to meteorologists or to conventional algorithms.

The current study is in line with the efforts to improve rainfall estimates by employing ML techniques applied on radar data, with concrete benefits for the national meteorological services that are still relying on QPE based on the OHP product generated by single horizontal polarized weather radars, as it is the case with the radar data source used in this study, from the Romanian Meteorological Administration. The main purpose of our study is to evaluate the usefulness of ML models to make estimations of the OHP using the reflectivity data on the first elevation levels. The contribution of the paper is twofold. First, we introduce a data model for representing the data gathered by a given weather radar in a certain location at a given moment. An extensive study is conducted for investigating the performance of deep neural networks (DNNs), Support Vector Regressor (SVRs), k-Nearest Neighbors (kNNs) and Random forests (RFs) for QPE. As a second contribution, two ensembles of ML models [21] combined through stacking are proposed and experimentally evaluated on real data. The experiments performed are aimed at evaluating the suitability of the proposed data model and ML regressors to make estimations of the OHP. With this aim, the proof of concept will use a medium-sized data set. Based on the results obtained, we plan to continue testing the methods on larger data sets. The computational results are compared against ground truth and two baselines: the weather radar’s own estimation for OHP, which is used today by operational meteorologists, and the estimation of the rainfall rate computed using the Z-R relationship [22], a known analytical relationship between the radar reflectivity product and precipitation, which is extensively used throughout the literature and in some existing nowcasting platforms. The study conducted in the paper contributes to the field by exploring the ML models capabilities to improve the radar hourly precipitation estimates, and by providing insights to the implementation of ML in optimizing radar derived rainfall estimation. To the best of our knowledge, our study regarding the OHP estimation using the proposed stacked ML models and reflectivity data on the first two elevation levels is new in the literature.

To conclude, the following research questions are targeted in our study:

RQ1 

To what extent does a stacked ML model increase the performance of estimating the rainfall rate from the reflectivity data compared to individual ML models?

RQ2 

How effective are the ML models designed to make estimations of the OHP using the reflectivity data on the first elevation levels?

RQ3 

Do the stacked ML models bring a statistically significant performance improvement to QPE with respect to the performance of current operational baseline products?

The rest of the paper is organized as follows. Section 2 presents the background concepts needed for our approach and reviews the related work on precipitation estimation and forecasting. Section 3 describes the data set, as well as the data model and representation used in the proposed study, with Section 4 detailing its methodology. Section 5 presents the experimental setup of the study, together with the obtained results and analysis. Our research findings are discussed in Section 6, while the conclusions of our study and directions for future improvement and extension are given in Section 7.

2. Background

We review existing work on precipitation estimation and forecasting in Section 2.1, and follow up with a brief overview of the machine learning models used in our study in Section 2.2.

2.1. Literature Review on Precipitation Estimation and Nowcasting

The literature reveals an increasing interest in precipitation estimation and quantitative precipitation forecasting (QPF) [23]. In the field of QPF, numerical weather prediction models are usually used, while the research in ML-based QPE based on radar reflectivity data is still scarce.

Gabriel Martins Palma Perez [24] proposed a deep learning approach for improving the QPF using a deep neural network for precipitation estimation in the city of Sao Paolo. A deep autoencoder model was also applied as a non-linear dimensionality reduction tool that allowed producing a spatial precipitation forecast with a small number of DNNs. Authors obtained Pearson correlation coefficients varying from 0.5 to 0.64 and Root Mean Squared Error (RMSE) values ranging from 6 to 18 mm/day for daily precipitation estimated using deep learning methods.

Two ML models based on backpropagation neural networks (BPNN) and convolutional neural networks (CNN) were investigated by Tian et al. [14], with the obtained results for precipitation estimation compared with the traditional methods used in meteorological systems. The study addressed the estimation of OHP using a 25 × 25 matrix filled with the values of the radar reflectivity at the first elevation (i.e., R01). The experimental evaluation was conducted on a radar data set collected from the center area of Taizhou in Zhejiang province, China. The comparison revealed that the BPNN model outperformed (in terms of Mean Squared Error) the Z-R baseline method with 75.84%, while the CNN model surpassed the traditional model with 82.30%.

Ridwan et al. [25] applied several ML models to predict the rainfall data in Terengganu, Malaysia. A comparative study was conducted using four regression models: Bayesian Linear Regression, Boosted Decision Tree Regression (BDTR), Decision Forest Regression and Neural Network Regression. Experiments were conducted on data consisting of the average rainfall from 10 weather stations. Thiessen polygons were used to estimate station area and projected rainfall as well as different time horizons. The experiments performed highlighted BDTR as the best regressor, with values of $R^2$ measure ranging between 0.553 and 0.989 for daily rainfall forecasting.

The work of Sun et al. [26] focused on providing high-resolution forecasts of regional rainfall, by introducing a convolutional 3D GRU (Conv3D-GRU) model. The model was proposed with the goal of predicting the future rainfall intensity over a relatively short period of time and consisted of several stages. During the first stage, 3D convolutions were applied for extracting the spatial features of radar echo maps with different heights. Then, Gated Recurrent Units (GRUs) were used for encoding and decoding the radar echo maps on time series. Finally, the trained model was used to predict the radar echo maps in the following 1–2 h [26]. A Critical Success Index (CSI) of 0.5231 was obtained for predicting if the rainfall exceeded 0.5 mm/h within the following one, two or four hours.

For precipitation nowcasting, Zhang et al. [27] proposed MFSP-Net, a multi-input multi-output recurrent neural network model based on multimodal fusion and spatiotemporal prediction. The proposed model used precipitation grid data, radar echo data and reanalysis data. Experiments conducted on the data set of Southeast China highlighted a CSI of 0.5415 for predicting if the rainfall exceeded 0.5 mm/h within one hour.

Yo et al. [28] proposed a deep learning approach for radar data-based QPE. ML algorithms were applied to establish a statistical model for QPE in weather stations. The Mosaic Radar data set [29] consisting of time series of gridded radar reflectivities over the Taiwan area was employed for experimental validation. By automatically extracting spatial and temporal features from the input data, the proposed model was designed to associate these features with location-specific precipitation. A mean RMSE of 1.86 mm/h was obtained by averaging the results over 45 weather stations.

Tromel et al. [30] highlighted the superiority of QPE based on data provided by polarimetric weather radars compared to traditional techniques utilizing only the Z reflectivity factor [31]. The study also discussed recent advancements in the field of precipitation nowcasting by using a DL approach combined with increasingly powerful high-performance computers and increased amounts of data. The lack of a database of extreme cases hampers the application of ML approaches in an operational setting [30].

Shin et al. [32] explored the use of two ML methods, regression tree and random forest, in QPE using polarimetric weather radar variables. Their models were trained using Two-Dimensional Video Disdrometer data (2DVD) over four locations, the tests employed data collected by a single weather radar over nine elevation angles, every 10 min, for six rainfall events that corresponded to either stratiform rain or convective rain, while data from 192 rain gauges were used to test the radar QPE. The relationships between dependent and independent variables have been determined, and the most important independent variables were identified. The proposed ML models outperformed the empirical relationships, with performances that depend on the type of rainfall event, and with an average RMSE of 1.389 mm/h for the rainfall estimation for stratiform and convective events.

Moraxu et al. [33] proposed a convolutional neural network that uses three input sources: automatic rain gauge measurement points, European weather radar composite OPERA (Operational Programme for the Exchange of Weather Radar Information) data and SEVIRI (Spinning Enhanced Visible Infrared Imager) thermal infrared satellite imagery in order to estimate the rainfall probability and rainfall rate and accumulation with a spatial resolution of 2 km. A RMSE of 1.488 mm/h for QPE was obtained using the proposed method. The use of satellite data proved to be most relevant for making QPE over the sea, where radar or rain gauges are usually not available.

Ko et al. [34] recently addressed the precipitation nowcasting and estimation topic. The U-Net deep-learning model was adapted for precipitation nowcasting and precipitation estimation from radar images. The precipitation nowcasting was formulated as a classification problem, while the precipitation estimation was defined as a regression one. The authors propose to pre-train the U-Net model to predict radar images in the near future without requiring ground-truth precipitation, and to use of a new loss function for mitigating the problem of class imbalancement problem. Radar images and precipitation data sets collected from South Korea over seven years were used for the experimental validation and highlighted average CSI values of about 0.456 for precipitation nowcasting and average Mean Squared Error of about 1.362 mm/h. Regarding precipitation estimation, an average relative improvement of about 2.2% was obtained using the DL model when compared with ZR-relationship-based precipitation estimation.

2.2. Supervised Learning Models Used

In this section, we briefly present the supervised learning models that were employed in our study.

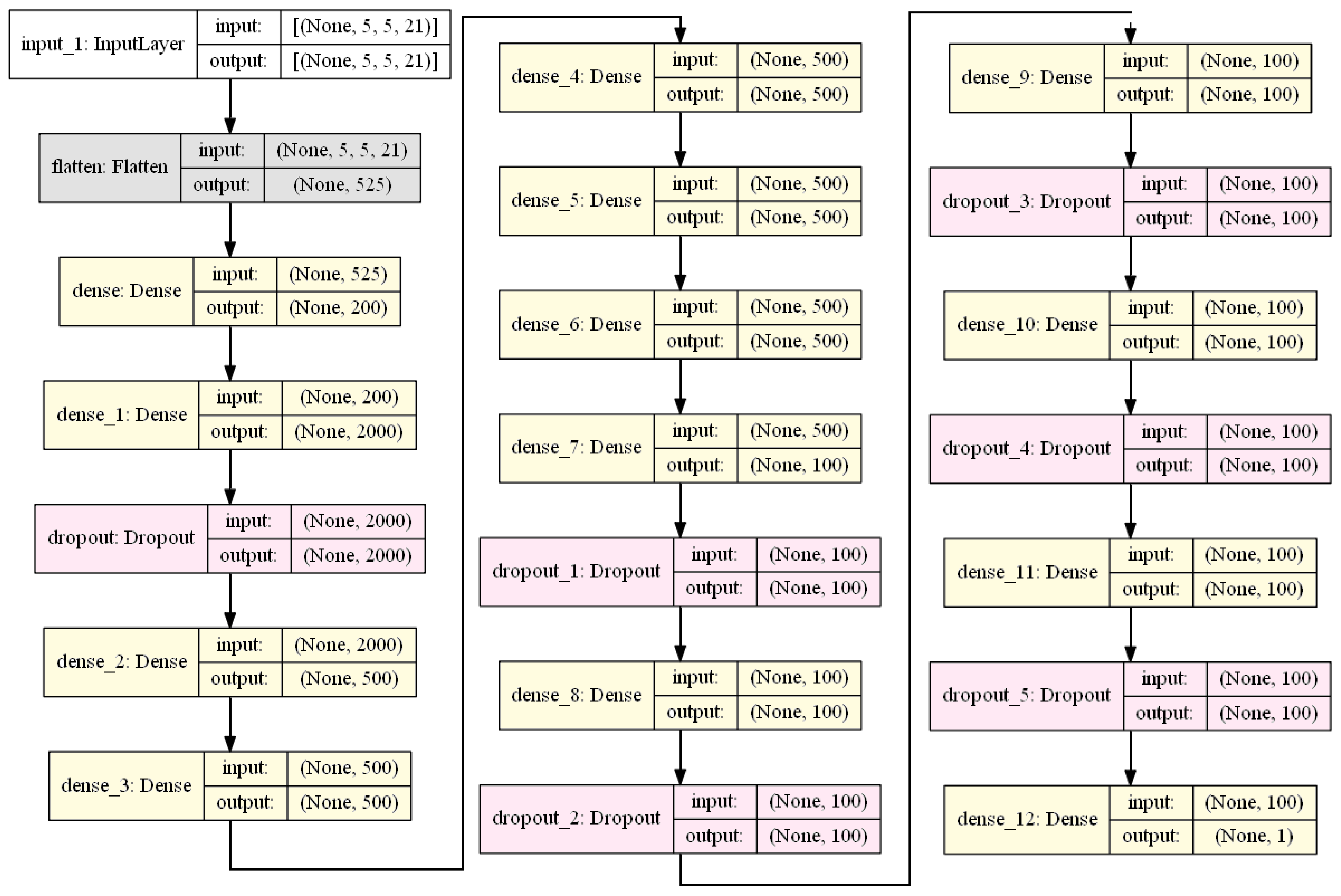
2.2.1. Deep Neural Networks

Neural network (NN) learning methods are especially well suited for approximating target functions which are real-, discrete- or vector-valued [35]. As a biological motivation, neural networks have been modeled to be similar to learning systems that we can find in humans and animals, namely, complex webs of neurons. This morphology has been adopted in computer science by building densely interconnected systems that have as building blocks basic units; these, called artificial neurons, take as input a series of real-valued numbers and produce a single real-valued output [35]. Neural networks are suited for problems that deal with noisy, complex data such as camera, microphone or sensor data. Their success is due to their similarity to effective biological systems, that are able to generalize and associate data that has not been explicitly trained upon during the training phase, and correlate that data to a class where it belongs. Each neuron of the network has an array of parameters, based on which it processes the input data, called weights. The weights are adjusted during the training phase based on the error of the network. The error represents the difference between the correct output and the network output. The learning algorithm used for adjusting the weights based on the error is the backpropagation algorithm.

Unlike classical neural networks, deep neural networks (DNNs) [36] contain multiple hidden layers and have a large number of parameters which makes them able to express complicated target functions, i.e., complex mappings between their input and outputs [37]. Nowadays, DNNs are powerful models in the ML literature applied for complex classification and regression problems in various domains.

Due to their complexity, large DNNs are slow to use and are prone to overfitting, which is a serious problem in supervised learning. Overfitting is a major problem for supervised learning models, in which the model learns “by heart” the training data, but it does not have the capability to generalize well on testing data. An overfit model is discovered through a very good performance on the training data, but a much lower performance on the testing set. A possible cause for overfitting in DNN is the limited training data, as in such cases the relationships learned by the networks may be the result of sampling noise. Thus, these complex relationships will hold in the training data but not in test or real data [37]. There are various methods for addressing and reducing overfitting, such as: (1) stopping the training when the performance on a validation set starts decreasing; (2) introducing weight penalties through regularization techniques soft weight sharing [38]; (3) applying cross-validation; (4) extending the data set to include more training examples; and (5) dropout by randomly dropping neurons and their connections during training [37].

2.2.2. Support Vector Machines

Support vector machines (SVMs) are inductive learning methods originally developed by Cortes and Vapnik for supervised classification [39], but they have been applied in regression tasks as well [40]. The classification using SVMs is formalised as searching for an optimal hyperplane (or set of hyperplanes) having a maximal functional margin hyperplane that separates the training data points. The functional margin of a separating hyperplane is defined as the distance from it to the closest training data points of any class.

The regression method using SVMs is known as $\epsilon$-support vector regression (SVR). $\epsilon$ is an additional hyperparameter used for controlling the algorithm’s error level. Given m training instances (data points) $x_i\in {\mathbf{R}}^d$ with their target value $y_i$, the optimization problem solved by the SVR algorithm is given in Formula (1).

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & \frac{1}{2}{\parallel w\parallel }^2+C\sum _{i=1}^m({\xi }_i^{\prime }+{\xi }_i^{″‘})\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & \left\{\begin{array}{c}{y}_i-(w·x_i+b)\le \epsilon +{{\xi }_i}^{\prime }\hfill \\ (w·x_i+b)-y_i\le \epsilon +{{\xi }_i}^{″}\hfill \\ {\xi }_i^{\prime },{\xi }_i^{″}\ge 0i=1,\cdots ,m\hfill \end{array}\right.\hfill \end{array}$$

(1)

In Formula (1), $b\in \mathbf{R}$ is a bias term, $w\in {\mathbf{R}}^d$ is a vector of weights and C is a regularization hyperparameter used for controlling overfitting (w and b determine the separating hyperplane, whose equation is $w·x+b=0$). ${{\xi }_i}^{\prime }$ and ${\xi }_i^{″}$ are positive values called “slack variables” introduced for allowing regression errors in the learning process, i.e., certain training data points will be allowed to be within the hyperplane margin [41].

For obtaining non-linear regression surfaces, kernel functions [39] (such as Radial Basis Function-RBF, polynomial, sigmoid, etc.) are used for mapping the input data space into a higher dimension [39]. In the linear case, methods such as stochastic gradient descent (SGD) [35] are used to solve the SVR problem faster.

2.2.3. Random Forests

Random forests (RFs) are ensemble learning methods consisting of combinations of several decision tree (DT) predictors using the bagging ensemble learning paradigm. The individual tree predictors are built only on a random subset of features and an arbitrary subset of training examples; thus, overfitting is avoided and better stability is achieved for generalization. As the number of DTs within the forest increases, the generalization error for RF will converge to a limit, due to the law of large numbers.

The RF predictive modeling is used for both classification and regression. The main idea behind RF modeling is to incorporate many DTs built using random samples from the data set. Even if the individual DT models are unstable learners, the combination of them using the bagging perspective lead to a stable and stronger learner. For each individual tree from the forest, the prediction value is computed using some generic random variable $\theta$, which is used to resample the training set and select the directions for each decision tree [42].

Th RF predictive model is used to improve the performance of DT algorithms. The literature presents a two steps method for using random forests as a predictive model. The first step in building a RF model is to construct the smaller decision trees from random bootstrap samples of the original data, each sample containing both positive and negative examples. The number of data samples may depend on the data set dimension. Afterwards, in the second step, the random forest is built by using a majority voting procedure among all decision trees.

2.2.4. k-Nearest Neighbors

k-Nearest Neighbors (kNN) is a simple but widely used machine learning algorithm, with a performance comparable with that of more complex learning models such as NNs or DTs. kNN is considered as one of the top ten algorithms in data mining and machine learning [43] and it has been applied in many practical applications ranging from pattern recognition to feature selection and outlier detection [44]. kNN is a supervised learning paradigm used for both classification and regression, being able to approximate both discrete and continuous target (output) functions [35]. kNN is a type of instance-based learning and belongs to the lazy learning paradigm, where the goal is to provide local approximations of the target function to be learned for the testing instances [35]. Thus, unlike the eager learning methods that are building a global learning hypothesis from the entire training data, kNN simply stores the training data and defers the processing until a new instance must be tested.

The underlying idea behind kNN’s decision rule when estimating the target value of a certain testing object is that of looking to the training data points which are the most similar to the query instance. For a test sample, kNN makes a decision by employing the local information surrounding the query instance: it simply assigns the most frequent classification of the nearest training data points of the testing sample. The value of k indicates how many nearest neighbors will be considered to estimate the target value of the testing data point. kNN is based on the idea of measuring the distance (or similarity) between two instances. The input instances are visualized as data points in a high-dimensional space and thus the distance between them may be measured [45] using a distance function d such as the classical Euclidean distance [35], Chebychey, Minkowski, Mahalanobis [43], etc. A kNN regressor estimates the target value of a query data point q by computing the mean value of the k nearest (in terms of the distance function d) training data points to q.

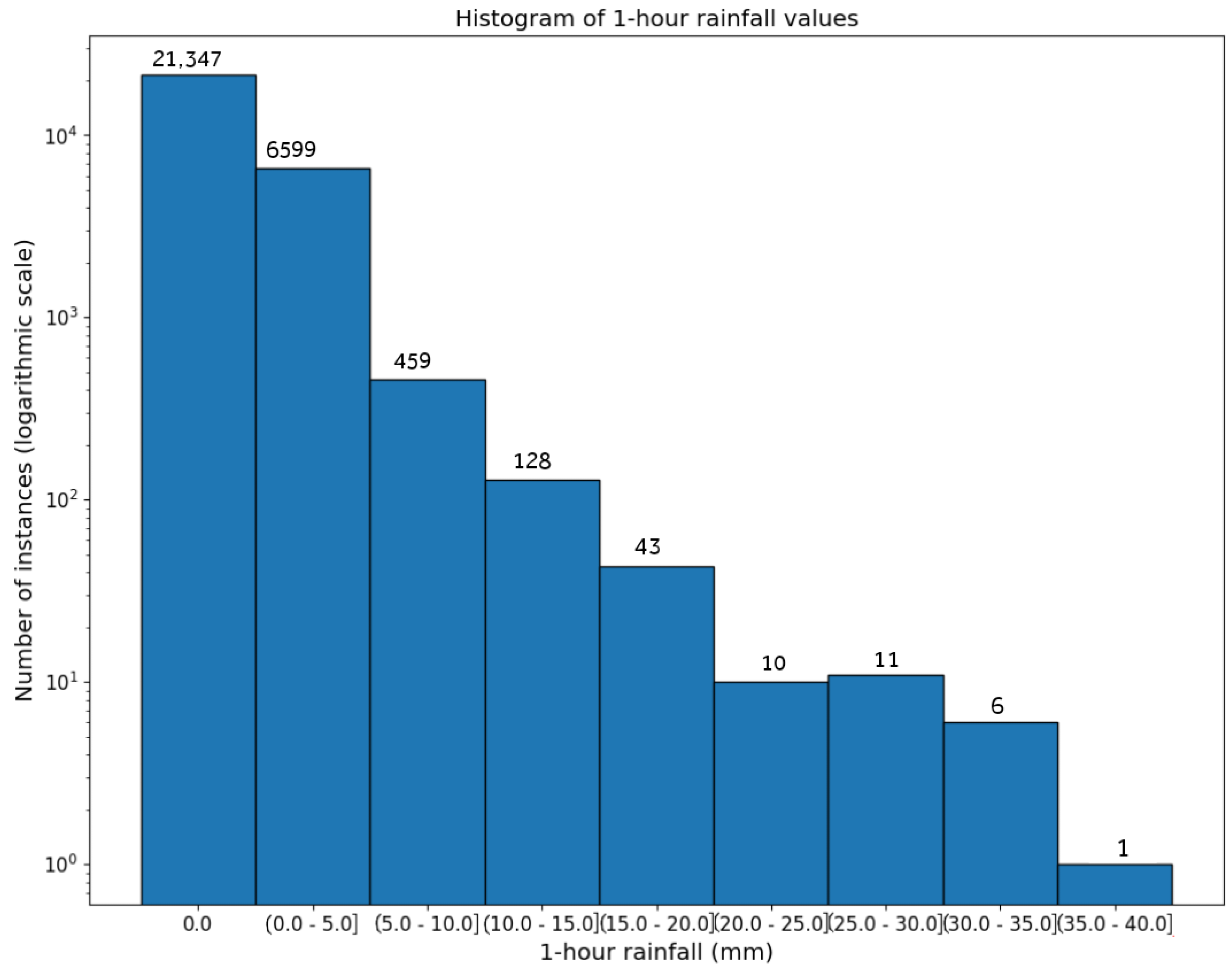
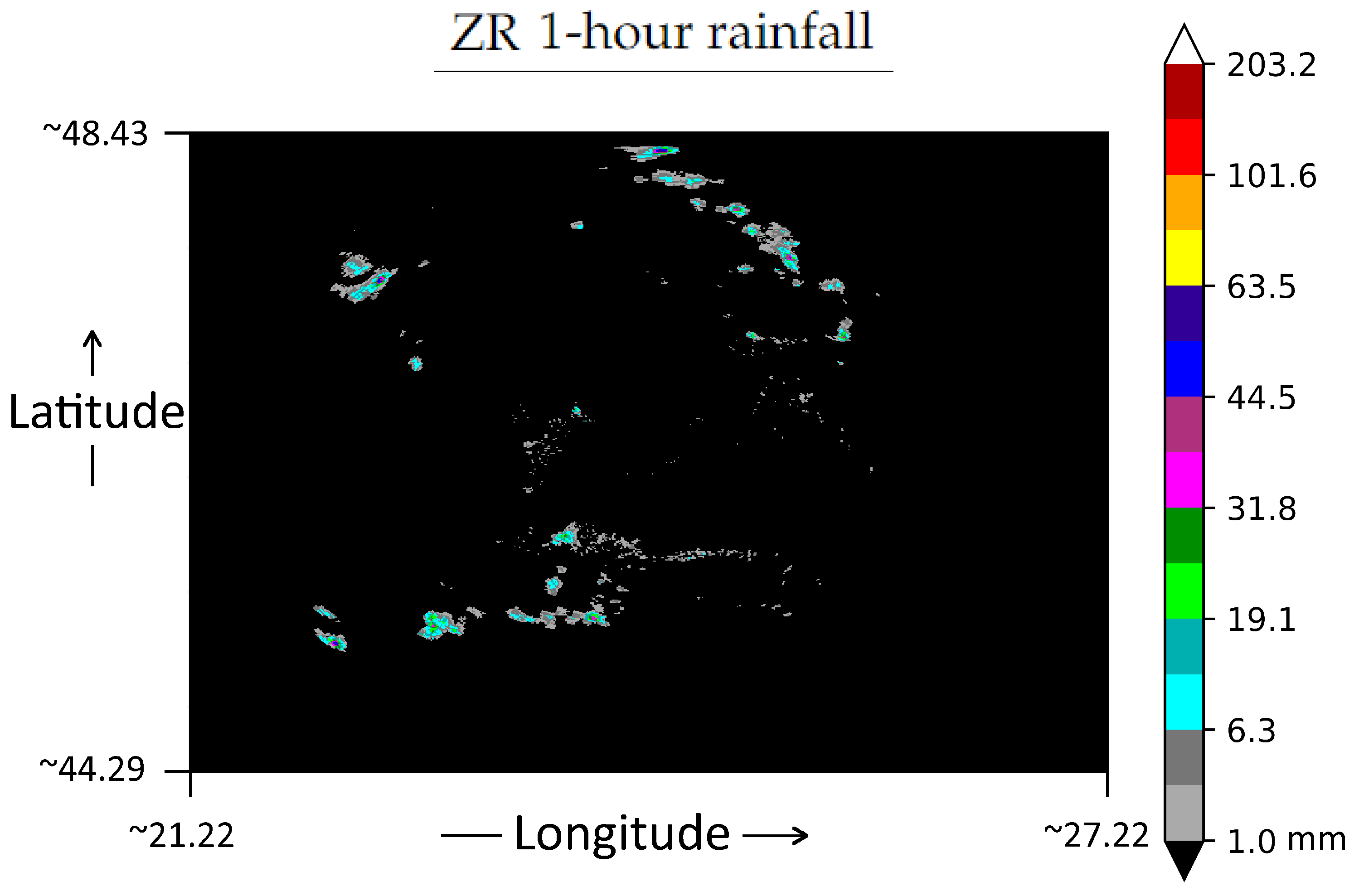
3. Data Set

In our study, we employed two types of meteorological data, namely weather radar data and precipitation data from weather stations. The radar data employed was collected by the WSR-98D single polarized Doppler weather radar of the Romania Meteorological Administration and is located in Bobohalma, Romania. The WSR-98D is capable of providing information regarding cloud systems above an area greater than 250 km in radius, using the VCP-21 scan strategy. This entails a complete scan every 6 minutes, consisting of nine elevation scan levels, starting from 0.5 degrees and increasing with a step of 0.95 over the first four elevation angles. In our experiments, we used reflectivity from the first two elevation angles and OHP that was collected during 30 non-consecutive days of the convective season between May and July, in the years between 2016 and 2021.

The second type of meteorological data is represented by the 1-h rainfall collected by rain gauges from 40 weather stations of the Romanian Meteorological Administration, all located within a 180 km radius from the weather radar in Bobohalma. The observations are transmitted from the rain gauge to the central data base every 10 min, hourly and when reaching certain threshold, and in this study the precipitation data was delivered in a 15-decimal format. Figure 1 depicts the geographical distribution of the weather stations used in the current study.

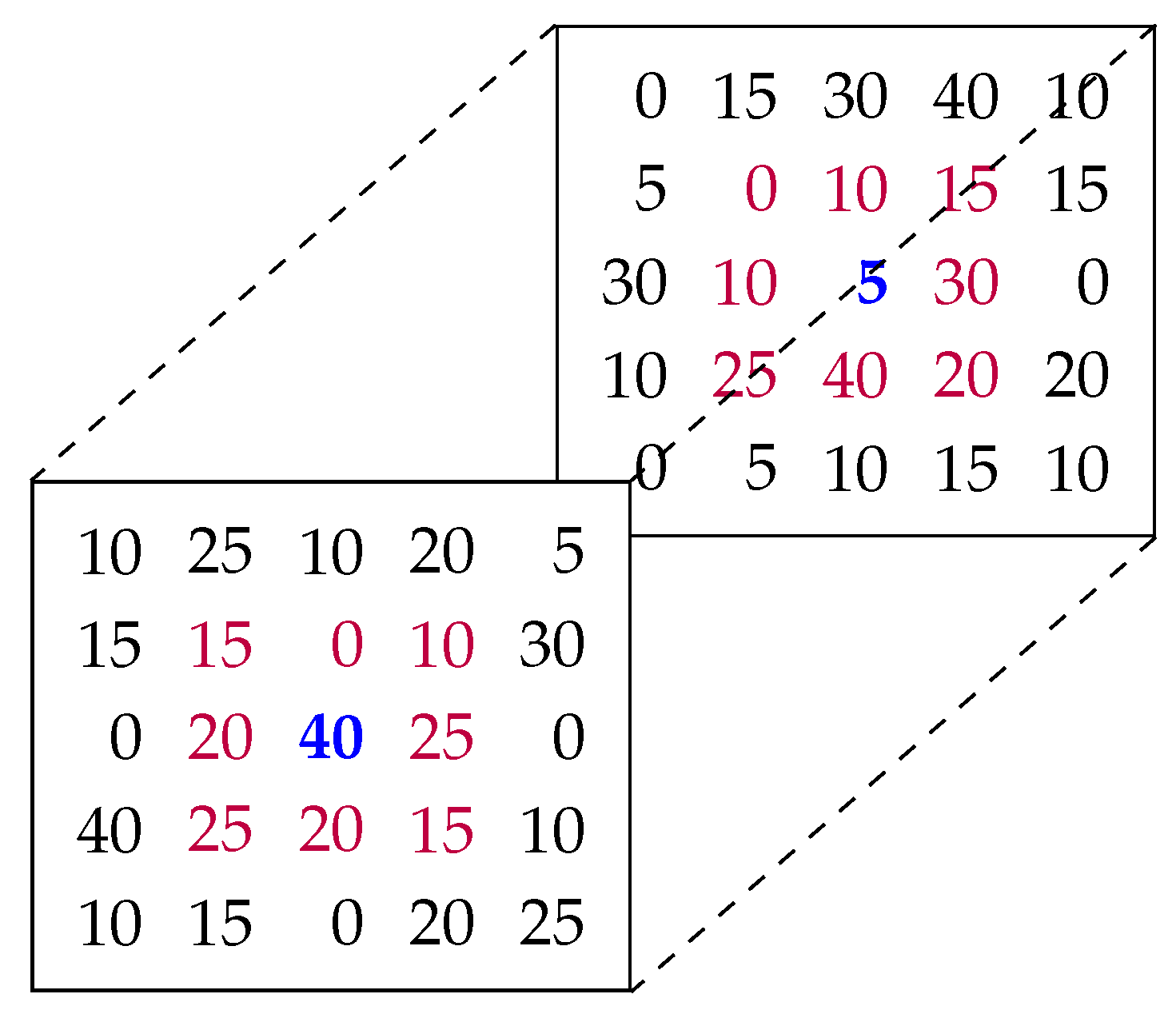
3.1. Data Model

As detailed in Section 3, we employed weather radar data and rainfall data. While the radar data is gathered over a large area around the radar, rainfall data is available only in some specific geographic locations, as it is gathered by weather stations. The ML models that we wanted to create had the goal of estimating the rainfall data from radar data. In other words, the input for an ML model would be radar data while the output would be rainfall data.

We used three radar products in our experiments, as mentioned in Section 3: Reflectivity (R) at the lowest and second lowest elevation angles (i.e., R01 and R02) and OHP. The OHP product is the 1-h rainfall estimation given by the radar and will be used as a baseline comparison. More details about its computation and use are provided in Section 6.2. The two R products were used as input data for our ML models. The 1-h rainfall collected at the weather stations was used as output data.

As explained in Section 1, the goal of the ML models we used was to estimate accumulated precipitation (rainfall) using radar data as input; radar data, in this case, is the reflectivity at the two lowest elevation angles, R01 and R02, as mentioned above (throughout this section we will generally refer to radar reflectivity data as R and to accumulated precipitation data as rainfall). In order to create the data set to be used by the ML models, based on R-rainfall as input–output, it was necessary to create correct R-rainfall pairs. The first step, since we only had rainfall data for specific locations, was to find the correct R data for the locations of each of the weather stations. For R data, for each time step we have a data grid—a matrix, also called a grid map—that gives the data for R in the area around the radar; each point (also called a cell) in the data grid represents the reflectivity value at a certain geographical location. Relative to the data grid, each point has two coordinates, a pair $(i,j)$, where the first coordinate (i) represents the row in the matrix while the second coordinate (j) represents the column in the matrix. The point with coordinates $(0,0)$ is in the top-left corner of the data grid. The radar is in the middle of the data grid (i.e., $i=\left[\frac{nr}{2}\right]$ and $j=\left[\frac{nc}{2}\right]$), where $nr$ is the number of rows and $nc$ is the number of columns from the grid map. For rainfall data, there is one value for each weather station for each time step (ideally, but in reality there are often missing values). Thus, in order to pair the rainfall values with the correct R values, the problem reduces to finding the correct coordinates for each weather station on the radar’s grid map.

For each weather station we have the latitude and longitude coordinates. To find the correct $(i,j)$ matrix coordinates from the latitude/longitude coordinates, we used the latitude/longitude coordinates for the top left point in the data grid (point at $(0,0)$) and the cell size, which represents the real-world size of a cell (a point in the data grid representing a geographical location) in decimal degrees. Formula (2) shows how each coordinate was computed. The idea is that we compute the difference in coordinates finding the distance in decimal degrees between the top-left cell and the weather station (for each coordinate) then we divide this distance by the cell size in order to find the number of cells between the top-left cell and the weather station. This number represents the matrix coordinate for the weather station (either row or column). For finding the i coordinate, we used the latitude and to find the j coordinate we used the longitude. In our specific case, the latitude and longitude for the top-left corner were 44.114 and 21.066, respectively, while the cell size was 0.011 degrees.

$$coordinat{e}_{i/j}=\left[\frac{statio{n}_{lat/long}-corne{r}_{lat/long}}{cell\_size}\right]$$

(2)

where:

-

$coordinat{e}_{i/j}$: the matrix coordinate to be computed (either i or j);

-

$statio{n}_{lat/long}$: the latitude or longitude of the weather station for which the matrix coordinates are computed (latitude is used for computing $coordinat{e}_i$ and longitude for $coordinat{e}_j$);

-

$corne{r}_{lat/long}$: the latitude or longitude of the top-left corner of the data grid (latitude is used for computing $coordinat{e}_i$ and longitude for $coordinat{e}_j$);

-

$cell\_size$: real-world size of a data grid cell, measured in decimal degrees.

3.2. Data Representation

As detailed in Section 3, radar data was gathered every 6 minutes and rainfall data was gathered at the weather stations every hour, in the form of 1-h rainfall. These are two different time scales and two different type of time steps and we needed to differentiate between them in order to clearly express how the experiment was conducted. Therefore, we differentiated them by calling time steps or time moments the steps on the radar scale—the time moments corresponding to each radar scan gathered every 6 min, and we denote it by t; the steps on the weather station scale—the time moments corresponding to each 1-h rainfall data point—are called hour steps or hour moments and are usually denoted by h. It is important to note that time steps and hour steps do not necessarily overlap: hour steps are at every fixed hour (e.g., 00:00, 01:00, 02:00), while time steps do not represent fixed hours or minutes (e.g., we might have steps 00:59 and 01:05 for one day and 00:56 and 01:02 for another day).

In the data set $\mathcal{D}$ used in our study we have, for each hour moment h in a day z, one instance corresponding to each weather station ($g_{ij}$)${}_{h,z}$, where $(i,j)$ are the matrix coordinates for the weather station (determined as presented in Section 3.1) and h represents the hour moment in the day z. The instance ($g_{ij}$)${}_{h,z}$ is represented as an n-dimensional numerical vector ($g_{ij}$)${}_{h,z}={(g_{ij}^1,g_{ij}^2,\cdots ,g_{ij}^n)}_{h,z}$. The ground truth for the instance ($g_{ij}$)${}_{h,z}$ is the 1-hour rainfall provided by the weather station.

The vectorial representation for ($g_{ij}$)${}_{h,z}$ is obtained as follows. From a meteorological viewpoint, the rainfall rate in a certain location $(i,j)$, at a time step t, may be influenced by the values for the reflectivity at previous time steps (e.g., $t-1$, $t-2$, etc.) not only in $(i,j)$, but also in a neighborhood of $(i,j)$. Thus, we are considering a neighborhood of diameter d around $(i,j)$, i.e., a submatrix with $d^2$ cells centered in the location $(i,j)$. From an ML perspective, the intuition behind using data from around a station and not just the value above the station is that multiple data characteristics would give the ML models more informative data from which they will learn to extract only the relevant features which are correlated with the rainfall rate. From a meteorological viewpoint, the data from around the station would help to mitigate the effects of, for instance, storm tilt, under the beam phenomena, etc.

As an example, let us consider the 5 × 5 dimensional data grid from Figure 2. The grid contains the values for $R01$ (front) and $R02$ (behind) for each cell on the data grid, at time step t. The location of the weather station is $(3,3)$ (i.e., $i=3$ and $j=3$) and the diameter d is also 3.

Using a neighborhood of diameter $d=3$ (as shown in Figure 2), the $2·d^2$-length numerical vector $v_{ij}^t$ corresponding to the weather station location ($(3,3)$, in our example) at time t, is obtained by concatenating the linearized sub-matrix containing the values for R01 (the sub-matrix in front) with the linearized sub-matrix containing the values for R02 (the sub-matrix behind): $v_{ij}^t=(15,0,10,20,40,25,25,20,15,0,10,15,10,5,30,25,40,20)$.

In representing the data instance ($g_{ij}$)${}_{h,z}$ corresponding to the weather station located at $(i,j)$ at the hour moment h in a day d, we consider that all the reflectivity values in the neighborhood of $(i,j)$ for a period of 1-h before the current hour moment h, (i.e., $t-1,t-2,\cdots ,t-10$), are relevant for estimating the 1-hour rainfall accumulation at the location $(i,j)$. Since, as mentioned, the time interval between two consecutive radar scans is 6 min, the instance ($g_{ij}$)${}_{h,z}$ corresponding to the weather station located at $(i,j)$ is a $20·d^2$-length numerical vector obtained by concatenating the vectors $v_{ij}^{t-1},v_{ij}^{t-2},\cdots ,v_{ij}^{t-10}$, where time step $t-1$ is the closest time moment before or equal to the hour moment h (for example, if h is equal to 02:00 then $t-1$ must be in the interval [01:55, 02:00]).

A data set $\mathcal{D}$ was formed using the high-dimensional vectors ($g_{ij}$)${}_{h,z}$ corresponding to the weather stations for each hour step h and each day z. The data set includes 30 days worth of meteorological observations. For each instance ($g_{ij}$)${}_{h,z}\in \mathcal{D}$, the 1-h rainfall ($o_{ij}$)${}_{h,z}$ given by the weather station located at ($i,j$) in the day z from an hour moment h is available as the ground truth (true label) of the instance.

Since we gathered data from 40 ground weather stations over 30 days, $\mathcal{D}$ contains 28,800 instances (for every hour we had 40 stations, there are 24 h in a day and 30 days of data). However, there were some missing data, due to the impossibility to gather data from some ground stations at some hours; therefore, $\mathcal{D}$ is a medium-sized data containing 28,605 instances with non-missing values. We used $60\%$ of $\mathcal{D}$ for training the ML models, and $10\%$ of $\mathcal{D}$ for validating them. The remaining $30\%$ from the data set was further used for testing. More details about the training–validation–testing split is given in Section 4.4. The radar and rainfall data sets used for this paper can be found at [46].

To better understand the rainfall data from $\mathcal{D}$, we present the histogram in Figure 3, which illustrates 1-h rainfall recorded at weather stations. The OX axis depicts rainfall in millimeters, while the OY axis shows the number of instances labeled with a certain rainfall rate, using a logarithmic scale. Thus, the histogram shows the number of instances ($g_{ij}$)${}_{h,z}$ for which the ground truth ($o_{ij}$)${}_{h,z}$ was in the interval represented by each bucket. The buckets count values in increments of 5 with the value 0 being counted separately—that is, the first bucket shows the number of instances for which the ground truth was 0, the second bucket shows the number of instances for which the ground truth was between 0 and 5 and so on. Note that the number of instances is on a logarithmic scale due to the large differences between the values in each bin. The instances with ground truth 0 were depicted in a separate bin in order to highlight the high number of such instances—more than three-fourths of the total number.

From Figure 3, we clearly observe a high data imbalance, as more than 75% of the 1-hour rainfall values are 0 while less than 3% are higher than 5. This imbalance is not unexpected as storms are usually localized at certain weather stations and therefore only some of the 40 weather stations will read non-zero values at a time; meanwhile, there are also large periods of time with no storms or meteorological events, when all readings are 0, so it was expected that most values for the 1-h precipitation would be 0 and higher values would be very rare. This, however, raises the difficulty of the regression problem, as ML algorithms tend to have a bias towards the majority class—a tendency to predict lower values or 0 in this case—simply because there are more instances to learn from in those cases. Values that appear very rarely compared to the rest of the data in the set, such as values above 20 in our data, might be considered outliers by a supervised regression model.

4. Methodology

This section introduces our methodology for designing and validating the ML models proposed for the task of estimating the rainfall rate from the reflectivity data. We start by formalizing the regression task in Section 4.1, then Section 4.2 introduces the ML models proposed for answering research question RQ1. The training stage is discussed in Section 4.3 and the testing methodology is further presented in Section 4.4.

4.1. Formalisation

We further present the formalization for the regression task of estimating the one-hour precipitation using the data model and representation previously introduced in Section 3.1.

As previously shown in Section 3.1, we considered the data set ${\displaystyle \mathcal{D}=\bigcup _{i,j,h,z}\{}$($g_{ij}$)${}_{h,z}\}$ consisting of high-dimensional vectors corresponding to each of the weather stations—located at the map coordinates ($i,j$)—at an hour moment h in a specific day z. The high-dimensional real-valued vector corresponding to a weather station in a certain location at a time moment is composed by the reflectivity values at the first two elevations at previous time steps in the neighborhood of the weather station’s location. The 1-h rainfall given by the weather stations was used as ground truth (i.e., the output for the ML models). Let us denote by ${\displaystyle \mathcal{O}=\bigcup _{i,j,h,z}\{}$($o_{ij}$)${}_{h,z}\}$ the set of the 1-hour rainfall given by the weather stations and available as labels for the instances from $\mathcal{D}$.

From a supervised learning perspective, the target function in our learning task is the mapping $rr:\mathcal{D}\to \mathbb{R}$ that assigns the 1-h rainfall rate ($o_{ij}$)${}_{h,z}$ for the weather station instances from $\mathcal{D}$, i.e., ($o_{ij}$)${}_{h,z}=rr($($g_{ij}$)${}_{h,z})$. Consequently, the QPE problem considered in this paper is formalized as a regression problem, more specifically as the problem of learning a hypothesis $\widehat{rr}$ (approximation of the target function $rr$) such that $\widehat{rr}({(g_{ij})}_{h,z})\approx rr({(g_{ij})}_{h,z})$ with a certain degree of confidence.

Thus, the learning problem further approached is formulated as finding a mapping between data instances corresponding to weather stations at a specific hour moment in a day and the rainfall rate at the location of the weather station at the given hour moment.

4.2. ML Models Used

Considering the formalization from Section 4.1, six ML-based regressors were used in our study for investigating the performance of QPE: four individual ML regressors (DNN, SVR, kNN and RF) and two ensemble regressors obtained by combining the individual learners using the stacking learning paradigm. For the DNN regressor we used a custom architecture that will be further detailed, while the other three models (SVR, kNN and RF) were used with their default configurations from scipy [47].

Stacking [48] is a method used in the ensemble learning paradigm [49] which uses multiple individual ML learners for obtaining a better predictive performance. Stacking involves training an ML algorithm (on the top of the stack) to combine the predictions of several individual ML learners (base predictors). The idea behind stacking is the following: the base algorithms are trained on an available training data set, then the algorithm on the top of the stack is trained on the outputs of the base learners (used as inputs) to make the final prediction. Thus, through stacking several heterogeneous learners $L_1,L_2,\cdots ,L_n$ are combined by training a meta-model M which takes as inputs the outputs of the base learners $L_1,L_2,\cdots ,L_n$ and will learn to return the final prediction from these inputs. Figure 4 illustrates a stacking ensemble learner.

The ML literature established that stacking generally provides better predictive performance than any single trained model [50]. Two stacking models were considered in our study, as follows:

• A stacking model denoted by $Stac{k}_{PLS}$ with base the DNN, SVM, kNN and RF regressors (i.e., $n=4$ and $L_1=$ DNN, $L_2=$ SVM, $L_3=k$ NN, $L_4=$ RF) and in the top of the stack the Partial Least Squares (PLS) predictor ($M=$ PLS). The PLS regressor [51] is a variation of the linear least-square regression, where the model reduces the number of variables used for regression; it is especially useful for cases where instances have a high number of variables and there is a high chance that the variables are correlated.
• A stacking model denoted by $Stac{k}_{DNN}$ with base the PLS, kNN and RF regressors (i.e., $n=3$ and $L_1=$ PLS, $L_2=k$NN, $L_3=$ RF) and at the top of the stack our customized DNN predictor ($M=$ DNN).

Regarding the selected ML models, we note that the individual ML regressors (DNN, SVM, kNN and RF) are based on different learning paradigms, as discussed in Section 2.2 and this makes them suitable for stacking. Regarding the stacking models, we decided to employ PLS and DNN on top of the stack, since linear regression and neural network-based models were often used as regression meta-models in stacking [52].

4.3. Training

As presented in Section 3.1, $60\%$ of the data set $\mathcal{D}$ will be used for building the machine learning models. For training our custom DNN model we used a separate validation data set representing $10\%$ of $\mathcal{D}$. The remaining of $30\%$ from the data set will be further used for testing.

For our custom DNN model, we used the architecture presented in Figure 5. In order to increase the readability of the proposed architecture, we color-coded the different layers. The main ones are the Dense layers colored in yellow and the Dropout layers colored in red. There are 2 special layers, the Input layer which specifies the input of the neural network—an image section representing the neighborhood around a location, along with its previous time steps—and a Flatten layer which creates the instance vector described in Section 3.2. For the stacking model that has our neural network model on top, as explained in Section 4.2 ($Stac{k}_{DNN}$), the neural network architecture is the same with the exception of the input layer, which is adjusted to input the previous models’ prediction instead of an image section.

For the other models employed, we used the default parameters as described in the scikit-learn documentation [53]. The SVM model (sklearn.svm.SVR) has a RBF kernel with $\gamma$ being computed as $\frac{1}{n}·var$, where n is the number of instances and $var$ is the variance of the data set, with the stopping tolerance being ${10}^{-3}$. The kNN model (sklearn.neighbors.KNeighborsRegressor) uses 5 neighbors (k = 5) and the Euclidian distance metric, while the algorithm used to compute the nearest neighbors is selected automatically between BallTree, KDTree and Brute-force search, based on the data. The RForest model (sklearn.ensemble.RandomForestRegressor) uses 100 estimators, using bootstrap samples and a modified version of CART for the decision tree algorithm.

4.4. Testing and Performance Evaluation

For assessing the performance of the ML models considered in our study a cross-validation testing methodology using the “2/3-1/3” split rule is applied. Thus, $60\%$ of $\mathcal{D}$ will be used for training the models and $10\%$ for models’ validation, while the remaining of $30\%$ will be further used for testing. Due to the randomness involved in selecting the training-validation-testing data sets, the testing is repeated six times.

Several performance metrics that will be further detailed were computed on each testing data set. Due to the multiple training-testing data splits performed during the cross-validation process, the values for the performance measures were averaged over the 6 runs and a $95\%$ confidence interval (CI) [54] was provided for the average values. The performance of the proposed cross-validation will be detailed in Section 5.2.

4.4.1. Performance Metrics

Given a testing data set consisting of n instances, let us denote by $y_i$ the ground truth for the i-th testing instance and by $\widehat{y_i}$ the prediction (forecast) for the i-th testing instance. The following evaluation measures used in the regression literature are computed:

• Mean absolute error ($MAE$) computes the average of the absolute errors obtained for the testing instances: $MAE=\frac{{\displaystyle \sum _{i=1}^n|y_i-\widehat{y_i}|}}{n}$. Lower values for $MAE$ indicate better regressors.
• $MA{E}_{nz}$ is used for computing the $MAE$ values only for the non zero-labeled testing instances (i.e., precipitations). This measure is particularly relevant, since we are particularly interested in our models being able to accurately estimate the precipitations (i.e., non-zero target outputs). Lower values for $MA{E}_{nz}$ indicate smaller regression errors for the rainfall rate.
• Root mean squared error ($RMSE$) computes the square root of the average of squared errors obtained for the testing instances: $RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{(y_i-\widehat{y_i})}^2}}{n}}$. Lower values for $RMSE$ indicate better regressors.
• $RMS{E}_{nz}$ is used for computing the $RMSE$ values only for the non zero-labeled testing instances. Lower values for $RMS{E}_{non-zero}$ indicate smaller regression errors for the precipitations.
• Multiplicative Bias ($MB$) is used for comparing the average value of the forecast to the average value of the true observations: $MB=\frac{{\displaystyle \sum _{i=1}^n\widehat{y_i}}}{{\displaystyle \sum _{i=1}^n{y}_i}}$. $MB$ expresses the degree of correspondence between the average forecast and the average observation, i.e., how many times the average prediction is bigger or lower than the average ground truth. The closer $MB$ is to 1 the better.
• $M{B}_{nz}$ is used for computing the $MB$ values only for the non zero-labeled testing instances (i.e., precipitations).

5. Results

This section presents the experimental results obtained by evaluating the six regressors described in Section 4.2 following the methodology introduced in Section 4. We start by detailing the experimental setup used in our experiments in Section 5.1, and then illustrate our experimental results and outline the improvements achieved by the ML models with respect to the baseline products used for QPE in Section 5.2.

5.1. Experimental Setup

As detailed in Section 3.1, the rainfall rate in a particular location at a certain time moment might be influenced by the conditions in the neighborhood at the previous time steps. For the hyperpameter d (the diameter of the neighborhood) we are going to experiment with three possible values: 3, 5 and 7. These dimensions of the relevant neighborhood were selected based on minimum, average and maximum convective cell propagation speed which has average values between 15 and 40 km/h, in which case an air parcel represented by an element in the reflectivity matrix would travel 1.5 to 4 km between two radar scans (6 min). As the geographical distance between two neighboring values is about 900 m, for our experiments we chose values for diameter d corresponding to distances between about 0.9 km and 4 km, thus correlated with the above mentioned propagation speeds.

For our experiments, in order to ensure the robustness of the tested machine learning models, we used a cross-validation testing methodology, by repeating six times the training-testing split of the data. For each fold (iteration), we shuffled the instances of the data set in a random order then we split the training, testing and validation data, with an algorithm that ensures that the same indexes are associated to the training, testing and validation data each time (so the only random element is the initial shuffle). In order to make sure that all models were trained and tested over the same data, to have fair comparisons, we associated a fixed seed for each fold and we used that seed for the random shuffling of the data set instances. We note that two points cannot be close enough to be in each others neighborhood because we are only considering the points where we have data from a weather station–and the weather stations are too far apart to have overlapping neighborhoods. This means that, even though we are using random shuffling of the data set, the neighborhoods of all points in the training, testing and validation data sets will be completely separate. From an ML perspective, it is most important to have a separate testing data set, and since the training, validation and testing data sets do not overlap, this is enough to ensure that the training data set cannot influence the measurements taken on the testing data set.

For training our neural networks we used the Adam optimization algorithm [55], with a learning rate of 0.0001, a batch size of 8 and the absolute cubed error loss function—we used a higher degree error than the usual squared error in order to give more weight to higher values which are heavily underrepresented in the data set, as shown in Section 3.2. The other machine learning algorithms were set up with their default parameters, as described in Section 4.3.

The training duration for the neural networks was of 500 epochs. The PLS and SVM models have a tolerance for stopping criterion (which is used to end training when the loss is less than this criterion) of 1 × 10${}^{-6}$ and 1 × 10${}^{-3}$ respectively; the PLS model also has a hard limit on the maximum number of iterations of 500. The RF training time is standard, until the decision trees have been built, whereas the KNN has no training phase, other than storing the training data in a ball tree data structure (for faster lookup during prediction).

5.2. Computational Results and Analysis

For answering research question RQ2, this section presents the computational results obtained by evaluating the proposed ML-based regressors.

Table 1. Experimental results obtained. 95% CIs are used for the results.

Metric	d	DNN	SVM	kNN	RF	${\mathit{Stack}}_{\mathit{PLS}}$	${\mathit{Stack}}_{\mathit{DNN}}$
	3	2.065 ± 0.058	1.774 ± 0.06	1.943 ± 0.107	1.813 ± 0.055	1.734 ± 0.06	2.085 ± 0.1
$RMSE$	5	2.045 ± 0.053	1.774 ± 0.06	1.891 ± 0.055	1.818 ± 0.051	1.734 ± 0.059	2.027 ± 0.079
	7	2.004 ± 0.034	1.774 ± 0.06	1.907 ± 0.047	1.827 ± 0.044	1.764 ± 0.046	2.028 ± 0.083
	3	3.16 ± 0.165	3.507 ± 0.106	3.422 ± 0.112	3.321 ± 0.109	3.328 ± 0.11	3.106 ± 0.118
$RMS{E}_{nz}$	5	3.167 ± 0.164	3.507 ± 0.106	3.424 ± 0.102	3.303 ± 0.113	3.328 ± 0.11	3.107 ± 0.112
	7	3.107 ± 0.105	3.507 ± 0.106	3.428 ± 0.094	3.302 ± 0.1	3.376 ± 0.074	3.123 ± 0.127
	3	1.55 ± 0.057	0.535 ± 0.01	0.833 ± 0.053	0.863 ± 0.014	0.766 ± 0.022	1.500 ± 0.11
$MAE$	5	1.512 ± 0.038	0.535 ± 0.01	0.786 ± 0.022	0.896 ± 0.008	0.766 ± 0.022	1.435 ± 0.079
	7	1.473 ± 0.034	0.535 ± 0.01	0.81 ± 0.032	0.908 ± 0.009	0.768 ± 0.023	1.406 ± 0.087
	3	1.684 ± 0.04	1.804 ± 0.032	1.783 ± 0.052	1.631 ± 0.028	1.595 ± 0.027	1.673 ± 0.053
$MA{E}_{nz}$	5	1.672 ± 0.038	1.804 ± 0.032	1.778 ± 0.025	1.630 ± 0.031	1.596 ± 0.027	1.643 ± 0.037
	7	1.624 ± 0.042	2.218 ± 0.516	2.419 ± 0.791	1.916 ± 0.583	1.601 ± 0.024	1.638 ± 0.042
	3	3.065 ± 0.135	0.206 ± 0.005	1.127 ± 0.047	1.236 ± 0.057	0.945 ± 0.017	2.973 ± 0.280
$MB$	5	2.971 ± 0.125	0.206 ± 0.005	0.898 ± 0.048	1.329 ± 0.056	0.946 ± 0.02	2.81 ± 0.208
	7	2.876 ± 0.121	0.206 ± 0.005	0.909 ± 0.054	1.364 ± 0.055	0.940 ± 0.022	2.736 ± 0.229
	3	0.774±0.037	0.053 ± 0.001	0.266 ± 0.033	0.314 ± 0.014	0.254 ± 0.012	0.759 ± 0.069
$M{B}_{nz}$	5	0.750 ± 0.033	0.053 ± 0.001	0.236 ± 0.019	0.339 ± 0.014	0.253 ± 0.013	0.713 ± 0.049
	7	0.731 ± 0.032	0.053 ± 0.001	0.253 ± 0.025	0.349 ± 0.015	0.256 ± 0.017	0.696 ± 0.055

presents the values for the performance metrics presented in Section 4.4.1 obtained by testing each of the ML models detailed in Section 4.2. As previously discussed, three possible values (3, 5, 7) were considered for the hyperparameter d that denotes the diameter of the neighborhood used for data representation (Section 3.1). For each of the ML models employed, a cross-validation was applied for assessing its performance on the data set described in Section 5.1. 95% CIs were computed for the average values of the performance metrics. For each value of d, the best value obtained for each performance metric is highlighted.

Regarding the impact of the neighborhood hyperparameter d on the results depicted in Table 1, we note that generally there was a slight performance increase for higher values of d.

Considering the results from Table 1, the following reasoning is applied in order to determine the best performing ML model and the best value for the diameter d. Let us denote by M the set of ML models used in our experiments, $M=\{$DNN, SVM, kNN, RF, $Stac{k}_{PLS},Stac{k}_{DNN}\}$ and by $\mathcal{P}M=\{RMSE,RMS{E}_{nz},MAE,MA{E}_{nz},MB,M{B}_{nz}\}$ the set of all performance metrics used for evaluation. For each model $m\in \mathcal{M}$, each value of the hyperparameter $d\in \{3,5,7\}$ and each performance metric $p\in \mathcal{P}M$ we are computing the value $w(m,d,p)$ that expresses how many ML models (other than m) are outperformed by m, using the value d for the neighborhood diameter, in terms of the performance measure p. We mention that only the mean values for the performance metrics will be used in computing the values $w(m,d,p)$, without considering their confidence intervals.

Except $MB$ and $M{B}_{nz}$, for all other performance metrics, lower values are better and express better regression performance. If $m_1$ and $m_2$ are two regression models, then $m_1$ outperforms $m_2$ in terms of the performance measure $p\in \{RMSE,RMS{E}_{nz},MAE,MA{E}_{nz}\}$ iff $p\left(m_1\right)<p\left(m_2\right)$. For $MB$ and $M{B}_{nz}$ values closer to 1 are better: a value of 1 indicates that the average prediction is equal to the average observation; values higher than 1 express how many times the average prediction is bigger than the average ground truth (i.e., the average prediction overestimates the average observation), while values lower than 1 express how many times the average prediction is lower than the average observation (i.e., the average prediction underestimates the average ground truth). Thus, in order to compare the performance of two regressors in terms of the performance metric $p\in \{MB,M{B}_{nz}\}$, we map the values of p in [1, +∞) by reversing the subunitary values. For a given value v of the performance metric $p\in \{MB,M{B}_{nz}\}$, we compute $inv\left(v\right)=\left\{\begin{array}{cc}v& ifv\ge 1\\ \frac{1}{v}& otherwise\end{array}\right.$. After the transformation, values closer to 1 (lower) for both $MB$ and $M{B}_{nz}$ express better regression performance, i.e., the model $m_1$ outperforms $m_2$ in terms of the performance measure $p\in \{MB,M{B}_{nz}\}$ iff $inv\left(p\left(m_1\right)\right)<inv\left(p\left(m_2\right)\right)$.

For each regression model $m\in M$ trained using a diameter $d\in \{1,3,5\}$ for the neighborhood hyperparameter and a performance metric $p\in \mathcal{P}M$ the value $w(m,d,p)$ is computed as ${\displaystyle w(m,d,p)=\sum _{\begin{array}{c}{m}^{\prime }\in \mathcal{M}\\ m^{\prime }\ne m\end{array}}\delta (m,m^{\prime },d,p)}$, where $\delta (m,m^{\prime },d,p)=\left\{\begin{array}{cc}1& ifp(m,d)<p(m^{\prime },d)\\ 0& otherwise\end{array}\right.$, and $p(m,v)$ denotes the value of the performance metric p obtained for the model m using the value d for the diameter. Then, for an ML model m and each value for d, the value $Win(m,d)$ is calculated by summing the values $w(m,d,p)$ for all performance metrics p, i.e., ${\displaystyle Win(m,d)=\sum _{p\in \mathcal{P}M}w(m,d,p)}$. The value $Win(m,d)$ counts how many ML models (other than m) are outperformed by applying m with a diameter d, in terms of the performance metric $p\in \mathcal{P}M$.

Table 2. The values for $Win(m,d)$ computed for each machine learning model $m\in \mathcal{M}$ and each value $d\in \{3,5,7\}$. The last row depicts, for each ML model m, the values for $WIN\left(m\right)$.

d	DNN	SVM	kNN	RF	${\mathit{Stack}}_{\mathit{PLS}}$	${\mathit{Stack}}_{\mathit{DNN}}$
3	13	9	14	18	22	15
5	12	9	13	18	23	16
7	16	10	13	17	23	14
$WIN$	41	28	40	53	68	45

illustrates the values $Win(m,d)$ computed based on the results from Table 1 for each of the ML models m used in our experiments and various values for the diameter d. The “winning” ML model (i.e., the best performing one, denoted by $best$) is declared the one that maximizes ${\displaystyle WIN\left(m\right)=\sum _{d\in \{3,5,7\}}Win(m,d)}$, i.e., ${\displaystyle best=arg\underset{m\in \mathcal{M}}{max}WIN\left(m\right)}$.

From Table 2 we conclude that the best performing ML model in our experiment is the stacked model $Stac{k}_{PLS}$ and for this model there are two values for the diameter hyperparameter d (5 and 7) which provide the highest value (23) for $Win(Stac{k}_{PLS},d)$.

Figure 6 depicts the performance of the $Stac{k}_{PLS}$ model for $d=5$ and $d=7$. The OX axis from the figure depicts the performance metrics employed for evaluation, while the values of these metrics obtained by the $Stac{k}_{PLS}$ regressor are represented on the OY axis. We observed very similar performances for both values of d and also small values for the 95% CIs (see Table 1) expressing the stability of the stacking model. However, slightly better performance metrics values were observed for $d=5$.

From a meteorological point of view, the values 5 and 7 for d represent neighborhoods up to 1.8–4 km, relevant for storm propagation speeds between 18 and 40 km/h, so exactly within the average speed considered for such phenomena. Consequently, $d=3$, which would be relevant for quasi-stationary storms, which have a lower occurrence, displayed a lower performance in our experiments.

6. Discussion

This section discusses our research findings and the threats to validity of our study.

6.1. Time Complexity Analysis

This section discusses the performance of the employed ML models from the computational complexity perspective. An empirical analysis of the time complexity is further conducted, by presenting the exact running time for the training and testing stages of the ML models presented in Section 4.2.

Table 3. Running times (in seconds) for the training and testing stages of the employed ML models. The time was measured for 6 runs, the average time over these 6 runs is presented as well the 95% confidence interval.

Stage	DNN	SVR	kNN	RF	PLS	${\mathit{Stack}}_{\mathit{PLS}}$	${\mathit{Stack}}_{\mathit{DNN}}$
Training	8673 ± 113	66.9 ± 1.15	0.01 ± 0.00	138 ± 10.8	0.23 ± 0.00	13.4 ± 0.67	1330 ± 16.8
Testing	0.52 ± 0.02	34.9 ± 0.99	4.40 ± 0.17	0.25 ± 0.01	0.03 ± 0.00	5.03 ± 0.10	3.28 ± 0.18

shows the training and testing times, measured in seconds. We note that for both the training and testing stages we present the average running time over the six experiments performed during the cross-validation process (as shown in Section 4.4) together with the 95% confidence intervals (CIs) [54]. During one cross-validation step 17,164 instances (60% from the data set) were used for training the models and 8581 (30% from $\mathcal{D}$) for testing. The diameter d of the neighborhood was set to 5 and thus 500 features (i.e., $20·d^2$–as shown in Section 3.2) were used for characterizing the input instances.

The experiments were performed on a workstation desktop with an Intel i9-7960X CPU, an Nvidia RTX 2080Ti graphic card with 11 GB of dedicated graphic memory (VRAM) and 64 GB of memory (RAM).

When analyzing the values in Table 3 it is important to consider the following notes. First the $Stac{k}_{PLS}$ model also uses our $DNN$ model as part of the base models in the stack. The $DNN$ model was trained only once, so the training time of the $DNN$ model was not added to the $Stac{k}_{PLS}$ model—that means that the presented training time is measured only for the other models in the stack. Secondly, one might notice a significant difference between the $Stac{k}_{PLS}$ training time and the RF training time, even though the $Stac{k}_{PLS}$ model contains a RF model as part of its stack, among other models. This difference appears because the RF model was slightly changed from the standalone version to the stack versions (both $Stac{k}_{PLS}$ and $Stac{k}_{DNN}$) to use multiprocessing for training—the stack versions use 16 jobs while the standalone one uses only one.

As previously discussed in Section 5.2, the stacked ensemble model $Stac{k}_{PLS}$ is the best performing ML model, in terms of the quality of the results assessed through the evaluation metrics used. From Table 3, one also observes the efficiency of $Stac{k}_{PLS}$ from the time complexity as well, as both its training and testing stages are fast from the running time perspective.

6.2. Comparison to Baselines

In order to improve our assessment regarding the best performing ML regressor ($Stac{k}_{PLS}$ with $d=5$) identified in Section 5.2, we compared the results with two baseline QPE products: OHP and the estimation of the rainfall rate computed using the Z-R relationship. We note that, for our $Stac{k}_{PLS}$ regressor, the value 5 has been chosen for the hyperparameter d as it provided the best results, as previously discussed in Section 5.2 and illustrated in Figure 6.

As previously discussed, the Z-R formula ($Z=a·R^b$, where $a=300$ and $b=1.4$) is a relationship between the radar reflectivity factor Z and the precipitation rate R (mm/h). Using the Z-R relationship formula, we need to find the rainfall value R (from the Z-R formula) using the radar reflectivity values measured in dBZ. We first compute Z with $Z={10}^{\frac{val}{10}}$, where $val$ is the reflectivity value; then we compute R using $R={\left(\frac{Z}{300}\right)}^{\frac{1}{1.4}}$. In the following, we denote by ZR the value estimated for the rainfall rate R, computed according to the Z-R formula.

Table 4. Comparison between the results of the $Stac{k}_{PLS}$ regressor and the OHP and ZR baselines. 95% CIs are used for the results. The best values for the performance metrics are marked with bold.

ML Model/Baseline	RMSE	${\mathit{RMSE}}_{\mathit{nz}}$	MAE	${\mathit{MAE}}_{\mathit{nz}}$	MB	${\mathit{MB}}_{\mathit{nz}}$
$Stac{k}_{PLS}$ with $d=5$	1.734 ± 0.059	3.328 ± 0.11	0.766 ± 0.022	1.596 ± 0.027	0.946 ± 0.02	0.253 ± 0.013
OHP	2.60 ± 0.334	4.507 ± 0.781	0.657 ± 0.082	2.349 ± 0.310	0.694 ± 0.166	0.280 ± 0.107
ZR	2.012 ± 0.067	3.625 ± 0.138	0.608 ± 0.012	1.882 ± 0.047	0.430 ± 0.01	0.170 ± 0.008

compares the results provided by the $Stac{k}_{PLS}$ regressor with $d=5$ with the values obtained by the OHP and ZR baselines. For a precise comparison, the OHP and ZR values were computed by applying the same experimental methodology as for the ML model (the testing is repeated six times). The performance metrics presented in Section 4.4.1 were averaged during the cross-validation process and 95% CIs were provided for the mean values. The best results are highlighted.

Studying Table 4, we observe that the $Stac{k}_{PLS}$ regressor is outperformed in terms of the average $M{B}_{nz}$ evaluation measure by OHP and in terms of $MAE$ by both OHP and ZR. However, for the OHP product we note high values for the 95% CIs, which denotes a lack of stability. One also observes that ZR outperforms OHP for four performance measures ($RMSE$, $RMS{E}_{nz}$, $MAE$ and $MA{E}_{nz}$), being outperformed in terms of $MB$ and $M{B}_{nz}$. The $Stac{k}_{PLS}$ regressor is more stable, as the 95% CIs are much lower then for OHP and ZR. Overall, out of 12 comparisons, $Stac{k}_{PLS}$ won 9 cases, representing 75%.

For verifying the statistical significance of the improvement achieved by the $Stac{k}_{PLS}$ regressor with respect to OHP and ZR and answering research question RQ3, a one tailed paired Wilcoxon signed-rank test [56,57] was applied. The sample of values for all performance metrics obtained for all evaluations of $Stac{k}_{PLS}$ was tested against the sample of values obtained for OHP and ZR. A p-value of $0.016113$ was obtained, emphasizing that the performance improvement achieved by $Stac{k}_{PLS}$ was statistically significant at a significance level of $0.05$.

6.3. Comparison to Related Work

As the literature review from Section 2.1 revealed, there are numerous approaches in precipitation prediction and forecasting using ML models. However, in the field of QPF, numerical weather prediction models are usually used, while the research in ML-based QPE based on radar reflectivity data is still scarce. From a meteorological point of view, the reviewed models, most of which are using weather radar data and rain gauges as input, seem to outperform the traditional reference QPE methods.

The work that is the most similar to ours is that of Tian et al. [14]. The authors addressed the same problem as in our work, that of estimating the one-hour precipitation based on the values of the reflectivity at the first elevations, but both the data model and the used ML models differed from ours. The authors applied two ML models based on backpropagation neural networks (BPNN) and convolutional neural networks (CNN) and compared their results with the precipitation estimation computed using the Z-R relationship. The input data for the ML models from [14] is a matrix with shape of 25 × 25 which stores the reflectivity data at the first elevation level, while the input data in our approach is represented as a $20·d^2$ real-valued vector, where d is a hyperparameter expressing the diameter of the neighborhood around a location.

The comparison performed by Tian et al. [14] revealed that the BPNN model outperformed (in terms of Mean Squared Error) the Z-R baseline method with 75.84%, while the CNN model surpassed the traditional model with 82.30%. Even if the improvement achieved by our $Stac{k}_{PLS}$ regressor with respect to the baseline Z-R method is only 25.73% (in terms of $MSE$) and 15.71% (in terms of $MS{E}_{nz}$), we note that our $Stac{k}_{PLS}$ model obtained better RMSE values than both the BPNN and CNN models proposed by Tian et al. [14] (with 74.83% and 70.6% lower, respectively).

In addition, the RMSE value obtained by our $Stac{k}_{PLS}$ regressor (an average of 1.734) compares favourably with those provided by the literature approaches for QPE (ranging from 1.167 mm/h [34] to 1.86 mm/h [28]).

6.4. Interpretation from a Meteorological Perspective

To sustain, from a meteorological perspective, the computational results provided in Section 5 and the comparison between the 1-hour estimations provided by our $Stac{k}_{PLS}$ regressor and the OHP and ZR baselines, we depict in Figure 7, Figure 8 and Figure 9 the 1-h rainfall estimations for 27 June 2016 at 18:59 using the $Stac{k}_{PLS}$ regressor, OHP and ZR, respectively. The figures show the rainfall estimation for each geographical location around the radar—one pixel in the image represents one cell in the grid map (the data model used is the one presented in Section 3.1). While the data in study were collected during convective seasons and all selected days contain relevant convective events, this specific interval was selected for better illustrating the effectiveness of the models, as there is a broad range of Reflectivity values and the convective storms have an ample geographical extension.

The maximum between the R01 and R02 values in 27 June 2016 between 18:03 and 18:59 are illustrated in Figure 10. Figure 11 presents the map depicting interpolated weather station data. The interpolation method used is currently in operational service at the Romanian Meteorological Administration, and it is a regression-kriging model that combines ground observations with weather radar precipitation estimates and local topography as ancillary data for generating sub-daily precipitation gridded data sets in high spatial resolution (1000 m × 1000 m) [58]. The weather radar data employed by the interpolation method comes from a national mosaic generated from the first two elevations angles, at 0.01 degree spatial resolution and 1-h temporal resolution.

From a meteorological point of view, when comparing the results with the map depicting interpolated weather station data, the estimations using $Stac{k}_{PLS}$ regressor have outperformed the OHP product currently used in operational activities, as the $Stac{k}_{PLS}$ regressor better identifies both the areas with precipitation and the intensity. Both the $Stac{k}_{PLS}$ regressor and OHP underestimate the precipitation values in the north-eastern part (the upper right side) of the map, which could be because of the distance from the weather radar, which in turn leads to a poor scanning of the lower altitude levels where precipitable clouds usually are to be found. A further observation concerns the overestimations of $Stac{k}_{PLS}$ regressor in the central part of the map, which are due to the ground clutter caused by the hilly and mountainous terrain, but this type of error is usually easily identified by the meteorologist, given its unnatural aspect.

Based on Figure 9 and Figure 11, the Z-R method seems to make the estimation closest to the ground-truth interpolated map, but this is probably due of the interpolation method used by the Romanian Meteorological Administration, which employs besides the weather station data also the radar reflectivity, which would bring the estimation closer to a product that directly employs reflectivity, in this case the Z-R.

6.5. Threats to Validity

The study conducted in this paper, more specifically the experimental evaluation and analyses previously presented may be influenced by some threats to validity and biases that may affect the obtained results and their interpretation. Following the guidelines proposed by Runeson and Martin [59], we further discuss the issues which may have influenced the experimental results and their analysis.

With respect to construct validity, which refers to the validity of the measures used for evaluation, the performance of the ML regressors proposed for estimation of the OHP has been evaluated using metrics employed in regression and forecasting: $MAE$, $RMSE$ and $MB$. $RMSE$ is a measure that is more biased towards bigger errors than the other metrics, thus being able to better express errors for higher values of 1-h precipitation. For reducing the threats to construct validity, we also used metrics to assess if our models are being able to accurately estimate the precipitations (i.e., non-zero target outputs): $MA{E}_{nz}$, $RMS{E}_{nz}$ and $M{B}_{nz}$. As future work we intend to also use classification metrics by applying different thresholds on the precipitation rate, for assessing the performance of estimating high values (i.e., high values of accumulated precipitation), which are important from the operational point of view. In addition, throughout our experiments we followed best practices in building and evaluating ML models such as: model validation during the training, cross-validation for the model evaluation and statistical analysis of the obtained results.

For minimizing threats to internal validity, which it is about internal parameters and experimental settings which could influence the experimental results, various architectures and hyperparameters settings were examined in the experimental part, and the resulting models have been cross-validated. Regarding the threats to external validity, which refers to the generalization capability of the $Stac{k}_{PLS}$ regressor, our proof of concept used a medium-sized real data set provided by the Romanian Meteorological Administration. Given that our hypothesis that the proposed data and ML models provide good performance for QPE estimation stands, we plan to continue testing the proposed methods on larger data sets. The experimental evaluation will be further expanded to other real data sets, to test if the findings of the current study are still valid.

Lastly, regarding reliability, the methodology used for data representation, the architectures employed for the ML regressors and the hyperparameters setting, as well as the testing methodology have been detailed in Section 3 and Section 4 in order to allow the reproducibility of the results. The data used in the experiments is also publicly available at [46]. For increasing the accuracy of the obtained results, we applied a cross-validation experimental methodology by repeating the same experiment six times and we provided a statistical analysis by computing confidence intervals for the obtained performance metrics. To ensure a correct interpretation of the results and the validity of the conclusions, the statistical significance of the improvement achieved by our $Stac{k}_{PLS}$ regressor has been confirmed statistically.

7. Conclusions

The study presented in this paper was conducted with the aim to improve radar-based rainfall estimates by employing machine learning techniques applied on radar data. A data model was introduced by representing a data instance (i.e., a weather station in a certain location) at a time t as a high-dimensional real-valued vector composed of the reflectivity values at time steps preceding t in the neighborhood of the weather station’s location. Thus, the learning problem was formulated as finding a mapping between data instances corresponding to weather stations at a specific time step t in a day d and the rainfall rate at the location of the weather station at the given time. Six ML models (DNNs, SVRs, kNNs, RFs and two ensemble learning models) were then employed to estimate the One Hour Precipitation using the reflectivity data on the first two elevation levels (R01 and R02) using real radar data provided by the Romanian National Meteorological Administration. Besides the radar data, we also employed the corresponding hourly precipitation data collected by rain gauges from Romanian weather stations network.

The computational results highlighted that ensemble learning models are more effective compared to the individual learners and also bring a statistically significant improvement compared against to the OHP and Z-R baselines. Considering the $RMSE$ performance metric, our $Stac{k}_{PLS}$ regressor with $d=5$ outperforms the OHP baseline with 33.3% and the Z-R baseline with 13.82%. The results of our study strengthen the conclusion from previous approaches from the literature [28] that ML-based methods, as opposed to QPE methods based on the Z-R relation, are able to automatically uncover the dynamics and movement of weather systems and to connect the learned patterns to a specific geographic location.

The research questions stated in Section 1 have been answered. As an answer to RQ1 and RQ2, our experimental findings empirically supported the hypothesis that ML models are effective models for making estimations of the OHP using the reflectivity data on the first elevation levels (R01 and R02). In addition, the ensemble learning regressor $Stac{k}_{PLS}$ increased the performance of estimating the rainfall rate compared to individual ML regressor. The statistical significance of the improvement achieved by the $Stac{k}_{PLS}$ model with respect to OHP and ZR has also been highlighted by applying the Wilcoxon signed-rank test, and thus research question RQ3 has been answered as well.

RQ2 and RQ3 have been answered from the viewpoint of operational meteorology as well. The first two radar elevation angles provide enough information to the ML models in order to make sufficiently good estimations of the rainfall accumulation over 1-h intervals, which is among the information of highest importance in meteorology and hydrology, given its impact on human lives and the economy. Although the algorithm was developed for estimating the rainfall rate over 1 h, it can be adapted for sub-hourly intervals, which could provide timely information on dangerous accumulations. Further on, $Stac{k}_{PLS}$ could be integrated in the current 24-h precipitation accumulation methods that employ hourly estimates based on the Z-R relationship. As shown in Section 6, $Stac{k}_{PLS}$ outperforms both statistically and visually the current operational methods employed by nowcasting meteorologists of the Romanian Meteorological Administration. The results presented in this paper, and in similar works, strengthen the trust of nowcasting meteorologists in ML methods and consequently promote the adoption of ML-based solutions in operational meteorology.

Further work will be conducted towards enlarging the data set considered in the experimental part and using other real radar data sets for a better validation of the research findings from this paper. As additional lines of improvement, alternative data models and the integration of heterogeneous data sources will be further investigated. From a computational perspective, we also aim to transform the regression task into a classification one (by using various rainfall rates) and to investigate the classification performance as well. By using classification metrics at different thresholds we will be able to better assess the performance of estimating high values of precipitation, as regions with high values of accumulated precipitation present a higher relevance from the meteorological perspective. Since the current study did not focus on particular types of precipitation, future extensions of the current work may also address the regression task for particular types of precipitation [60], which may help increase the performance of the machine learning regressors.

From a meteorological point of view, immediate improvements could be brought by increasing the number of ground stations that are employed in the experiment, by using data from other public databases and by removing ground clutter from the reflectivity data. For the evaluation of the models, alternative methods could be identified for the interpolation of the ground stations data.