Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.2.1. Observed Ground-Based Data
2.2.2. Reanalysis Data
2.2.3. Digital Elevation Model
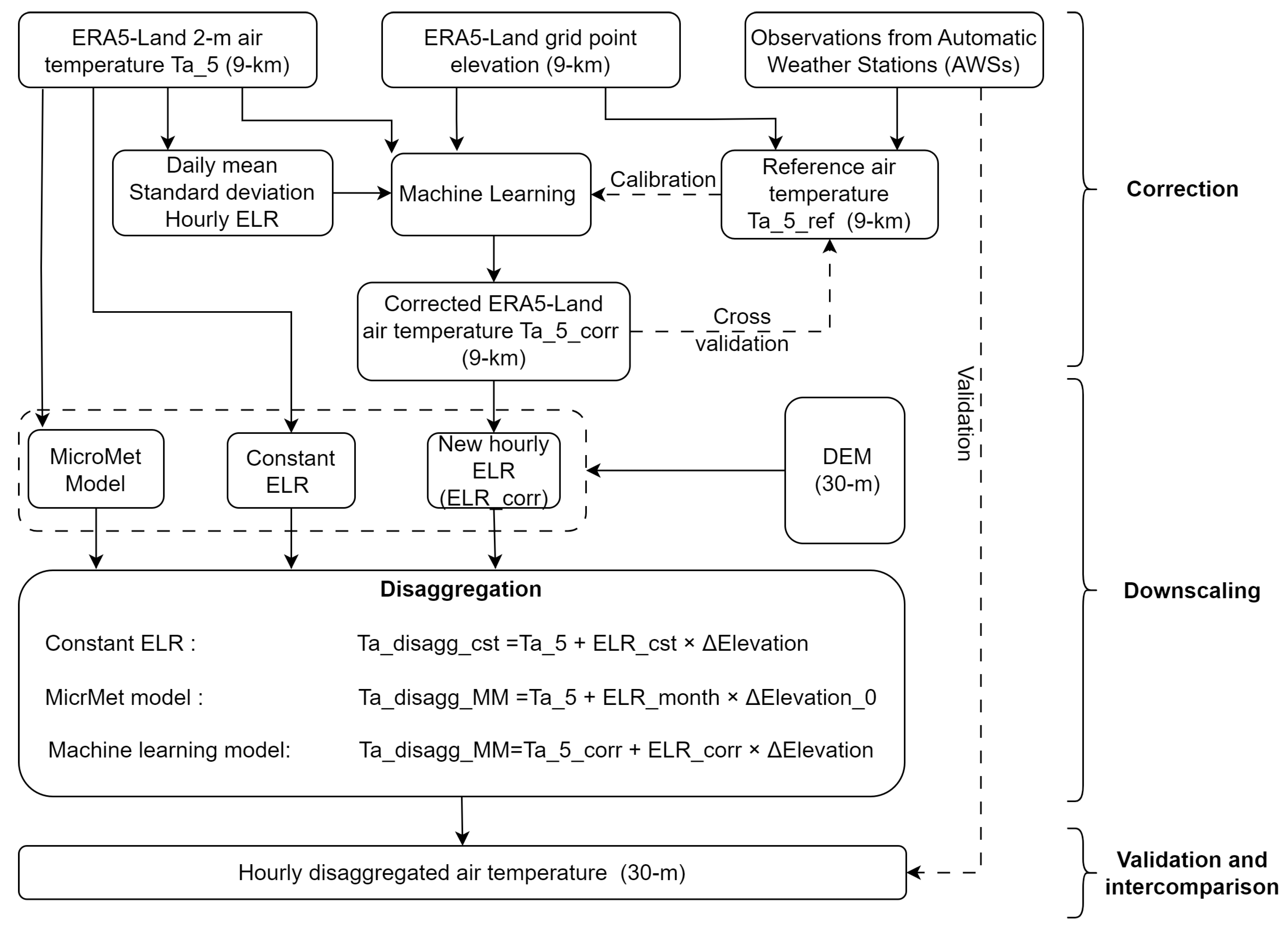
2.3. Methodology
2.3.1. 1st Step: Ta_5 Correction
- MLR
- SVR
- Xgboost
2.3.2. 2nd Step: Disaggregation
2.3.3. 3rd Step: Validation and Results Assessment
3. Results
3.1. Ta_5 Correction
- Reference temperature Ta_5_ref
- Correlation analysis and feature selection
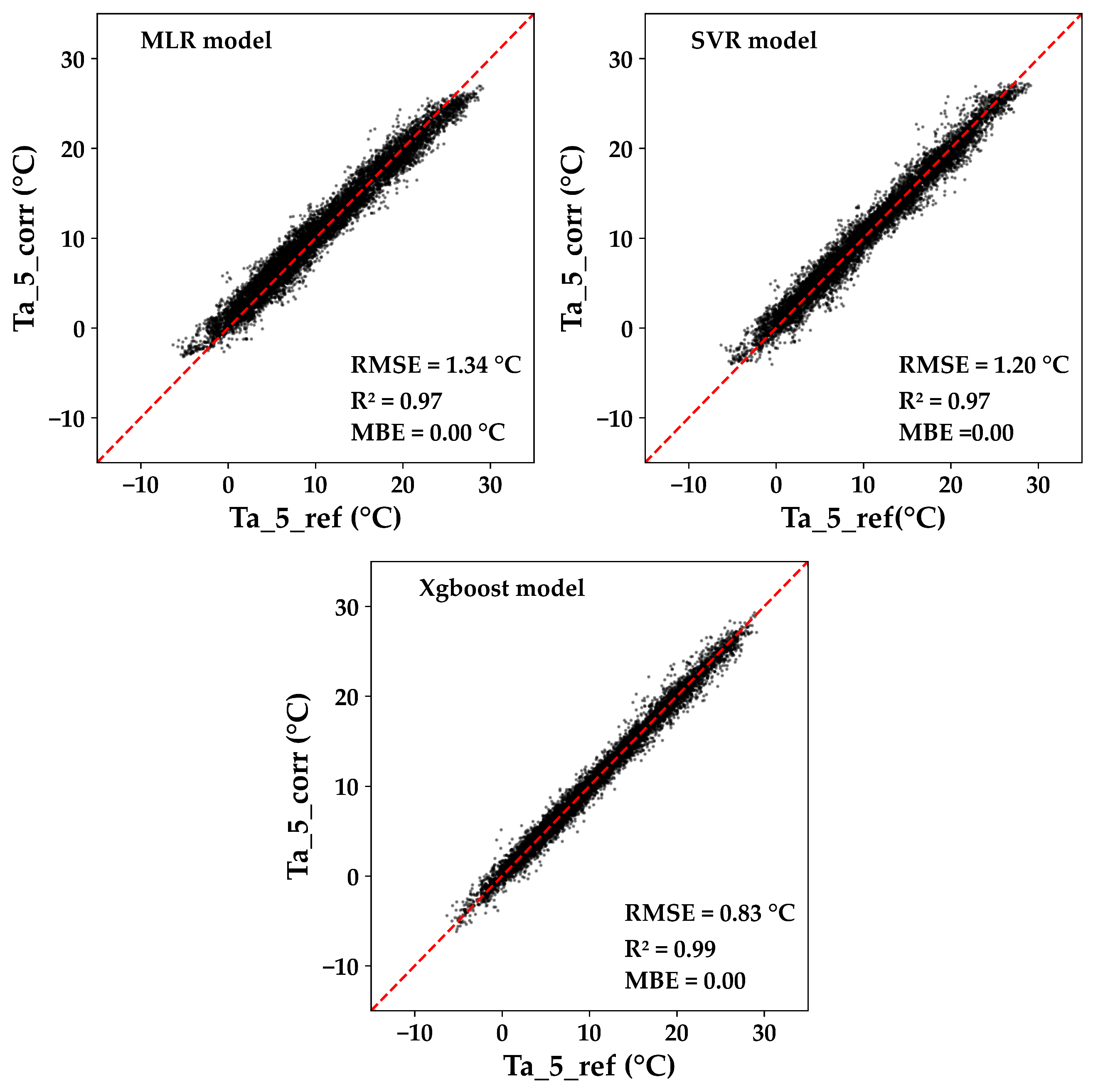
- Machine learning outcome
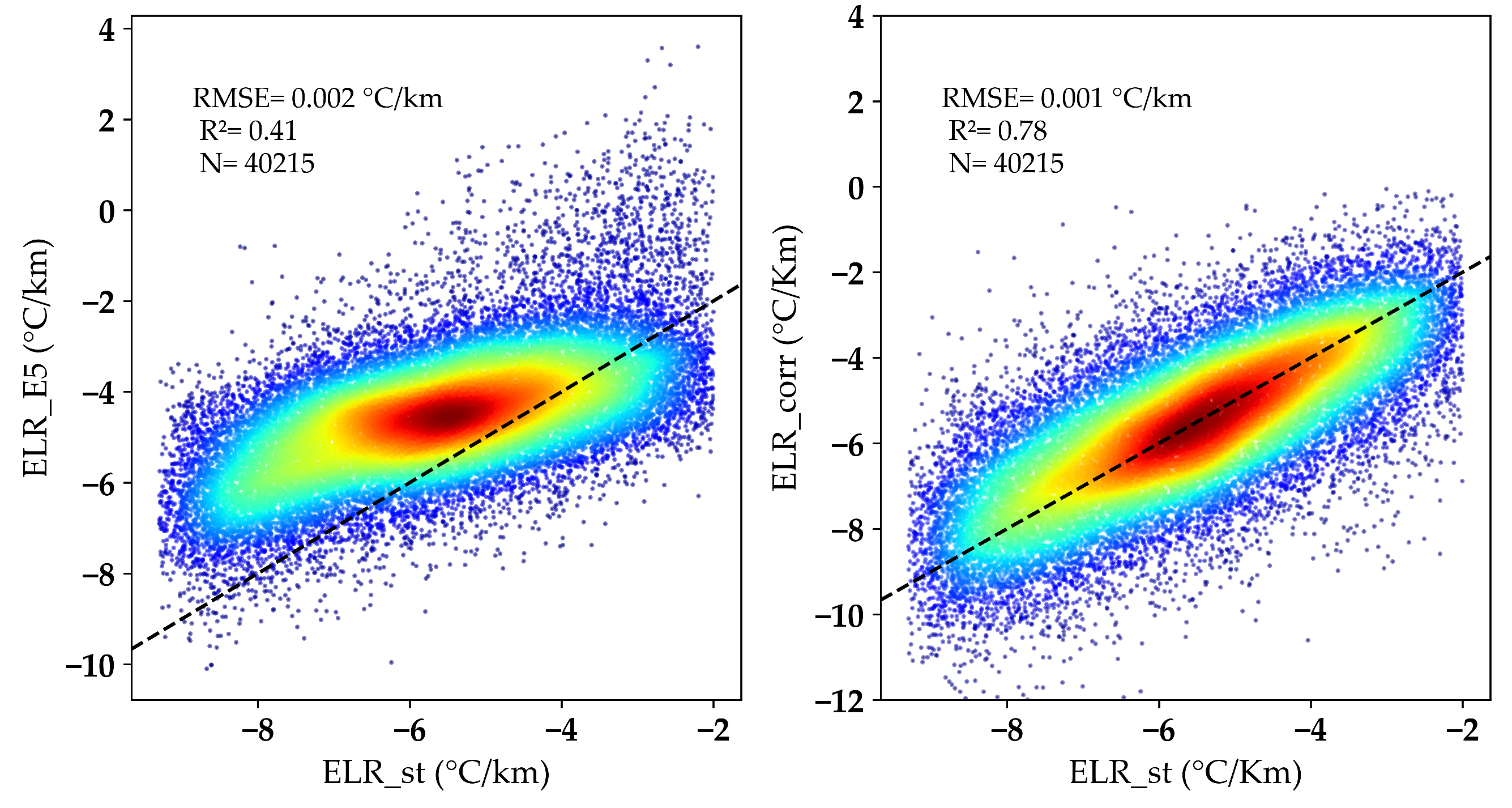
3.2. Ta_5_corr Downscaling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Symbols
| ELR | Environmental Lapse Rate |
| DEM | Digital Elevation Model |
| AWS | Automatic Weather Station |
| MLR | Multiple Linear Regression |
| SVR | Support Vector Regression |
| Xgboost | Extreme Gradient Boosting |
| Ta | Air temperature |
| Ta_5 | ERA5-Land’s air temperature |
| Ta_st | Mesaured air temperature |
| Ta_5_ref | Reference air temperature based on ERA5-Land’s grid points elevation |
| Ta_5_corr | Machine learning based corrected ERA5-Land’s air temperature |
| ELR_cst | Constant ELR of a value of −6.5 C/km |
| ELR_E5 | Corresponding ERA5-Land ELR |
| ELR_st | Measured ELR |
| ELR_corr | Corrected ELR based on ERA5-Land corrected air temperature |
| Ta_disagg_cst | Downscaled ERA5-Land air temperaure based on constant ELR |
| Ta_disagg_MM | Downscaled ERA5-Land air temperaure based on MicorMet model |
| Ta_disagg_ML | Downscaled ERA5-Land air temperaure based on Machine learning models |
| MBE | Mean Bias Error |
| RMSE | Root Mean Squared Error |
| PCC | Pearson Correlation Coefficient |
| E5 | ERA5-Land grid point elevation |
References
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Maselli, F.; Pasqui, M.; Chirici, G.; Chiesi, M.; Fibbi, L.; Salvati, R.; Corona, P. Modeling primary production using a 1 km daily meteorological data set. Clim. Res. 2012, 54, 271–285. [Google Scholar] [CrossRef]
- Tobin, C.; Rinaldo, A.; Schaefli, B. Snowfall limit forecasts and hydrological modeling. J. Hydrometeorol. 2012, 13, 1507–1519. [Google Scholar] [CrossRef]
- Behnke, R.; Vavrus, S.; Allstadt, A.; Albright, T.; Thogmartin, W.E.; Radeloff, V.C. Evaluation of downscaled, gridded climate data for the conterminous United States. Ecol. Appl. 2016, 26, 1338–1351. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, C.D.; Stone, R.C.; Tait, A.B. Improving the use of climate information in decision-making. Nat. Clim. Chang. 2017, 7, 614–616. [Google Scholar] [CrossRef]
- Bjorkman, A.D.; Myers-Smith, I.H.; Elmendorf, S.C.; Normand, S.; Rüger, N.; Beck, P.S.; Blach-Overgaard, A.; Blok, D.; Cornelissen, J.H.C.; Forbes, B.C.; et al. Plant functional trait change across a warming tundra biome. Nature 2018, 562, 57–62. [Google Scholar] [CrossRef]
- Trisos, C.H.; Merow, C.; Pigot, A.L. The projected timing of abrupt ecological disruption from climate change. Nature 2020, 580, 496–501. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 1–20. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958 to 2015. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-resolution and bias-corrected CMIP5 projections for climate change impact assessments. Sci. Data 2020, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kistler, R.; Kalnay, E.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP–NCAR 50-year reanalysis: Monthly means CD-ROM and documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–268. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Holden, Z.A.; Abatzoglou, J.T.; Luce, C.H.; Baggett, L.S. Empirical downscaling of daily minimum air temperature at very fine resolutions in complex terrain. Agric. For. Meteorol. 2011, 151, 1066–1073. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, Z.; Zhang, X. Examination of errors in near-surface temperature and wind from WRF numerical simulations in regions of complex terrain. Weather. Forecast. 2013, 28, 893–914. [Google Scholar] [CrossRef]
- Le Roux, R.; Katurji, M.; Zawar-Reza, P.; Quénol, H.; Sturman, A. Comparison of statistical and dynamical downscaling results from the WRF model. Environ. Model. Softw. 2018, 100, 67–73. [Google Scholar] [CrossRef]
- Alessi, M.J.; DeGaetano, A.T. A comparison of statistical and dynamical downscaling methods for short-term weather forecasts in the US N ortheast. Meteorol. Appl. 2021, 28, e1976. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, S.; Zhang, N.; Zhang, G.; Xu, Y. Downscaling hourly air temperature of WRF simulations over complex topography: A case study of Chongli District in Hebei Province, China. J. Geophys. Res. Atmos. 2022, 127, e2021JD035542. [Google Scholar] [CrossRef]
- Vrac, M.; Drobinski, P.; Merlo, A.; Herrmann, M.; Lavaysse, C.; Li, L.; Somot, S. Dynamical and statistical downscaling of the French Mediterranean climate: Uncertainty assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 2769–2784. [Google Scholar] [CrossRef]
- Vigaud, N.; Vrac, M.; Caballero, Y. Probabilistic downscaling of GCM scenarios over southern India. Int. J. Climatol. 2013, 33, 1248–1263. [Google Scholar] [CrossRef]
- Dulière, V.; Zhang, Y.; Salathé, E.P., Jr. Extreme precipitation and temperature over the US Pacific Northwest: A comparison between observations, reanalysis data, and regional models. J. Clim. 2011, 24, 1950–1964. [Google Scholar] [CrossRef]
- Wang, J.; Fonseca, R.M.; Rutledge, K.; Martín-Torres, J.; Yu, J. A hybrid statistical-dynamical downscaling of air temperature over Scandinavia using the WRF model. Adv. Atmos. Sci. 2020, 37, 57–74. [Google Scholar] [CrossRef]
- Dutra, E.; Muñoz-Sabater, J.; Boussetta, S.; Komori, T.; Hirahara, S.; Balsamo, G. Environmental lapse rate for high-resolution land surface downscaling: An application to ERA5. Earth Space Sci. 2020, 7, e2019EA000984. [Google Scholar] [CrossRef]
- Ekström, M.; Grose, M.R.; Whetton, P.H. An appraisal of downscaling methods used in climate change research. Wiley Interdiscip. Rev. Clim. Chang. 2015, 6, 301–319. [Google Scholar] [CrossRef]
- Soares, P.M.; Cardoso, R.M.; Miranda, P.; de Medeiros, J.; Belo-Pereira, M.; Espirito-Santo, F. WRF high resolution dynamical downscaling of ERA-Interim for Portugal. Clim. Dyn. 2012, 39, 2497–2522. [Google Scholar] [CrossRef]
- Aitken, M.L.; Kosović, B.; Mirocha, J.D.; Lundquist, J.K. Large eddy simulation of wind turbine wake dynamics in the stable boundary layer using the Weather Research and Forecasting Model. J. Renew. Sustain. Energy 2014, 6, 033137. [Google Scholar] [CrossRef]
- Laprise, R.; De Elia, R.; Caya, D.; Biner, S.; Lucas-Picher, P.; Diaconescu, E.; Leduc, M.; Alexandru, A.; Separovic, L. Challenging some tenets of regional climate modelling. Meteorol. Atmos. Phys. 2008, 100, 3–22. [Google Scholar] [CrossRef]
- Warrach-Sagi, K.; Schwitalla, T.; Wulfmeyer, V.; Bauer, H.S. Evaluation of a climate simulation in Europe based on the WRF–NOAH model system: Precipitation in Germany. Clim. Dyn. 2013, 41, 755–774. [Google Scholar] [CrossRef]
- Pan, B. Application of XGBoost algorithm in hourly PM2.5 concentration prediction. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 113, p. 012127. [Google Scholar]
- Cao, B.; Gruber, S.; Zhang, T. REDCAPP (v1. 0): Parameterizing valley inversions in air temperature data downscaled from reanalyses. Geosci. Model Dev. 2017, 10, 2905–2923. [Google Scholar] [CrossRef]
- Winstral, A.; Jonas, T.; Helbig, N. Statistical downscaling of gridded wind speed data using local topography. J. Hydrometeorol. 2017, 18, 335–348. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.; Floyer, J.; Asplin, M.; McKendry, I. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Overland, J.E.; Wang, M. Recent extreme Arctic temperatures are due to a split polar vortex. J. Clim. 2016, 29, 5609–5616. [Google Scholar] [CrossRef]
- Jylhä, K.; Tuomenvirta, H.; Ruosteenoja, K. Climate change projections for Finland during the 21 st century. Boreal Environ. Res. 2004, 9, 127–152. [Google Scholar]
- Hanssen-Bauer, I.; Achberger, C.; Benestad, R.; Chen, D.; Førland, E. Statistical downscaling of climate scenarios over Scandinavia. Clim. Res. 2005, 29, 255–268. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Chica-Olmo, M.; Atkinson, P.M. Downscaling cokriging for image sharpening. Remote Sens. Environ. 2006, 102, 86–98. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Pardo-Igúzquiza, E.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Downscaling Landsat 7 ETM+ thermal imagery using land surface temperature and NDVI images. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 515–527. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
- Waichler, S.R.; Wigmosta, M.S. Development of hourly meteorological values from daily data and significance to hydrological modeling at HJ Andrews Experimental Forest. J. Hydrometeorol. 2003, 4, 251–263. [Google Scholar] [CrossRef]
- Sourp, L.; Gascoin, S.; Wassim Baba, M.; Deschamps-Berger, C. Development of a snow reanalysis pipeline using downscaled ERA5 data: Application to Mediterranean mountains. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22–5117. [Google Scholar]
- Liston, G.E.; Elder, K. A meteorological distribution system for high-resolution terrestrial modeling (MicroMet). J. Hydrometeorol. 2006, 7, 217–234. [Google Scholar] [CrossRef]
- Liston, G.E.; Elder, K. A distributed snow-evolution modeling system (SnowModel). J. Hydrometeorol. 2006, 7, 1259–1276. [Google Scholar] [CrossRef]
- Chaponnière, A.; Boulet, G.; Chehbouni, A.; Aresmouk, M. Understanding hydrological processes with scarce data in a mountain environment. Hydrol. Process. Int. J. 2008, 22, 1908–1921. [Google Scholar] [CrossRef]
- Boudhar, A.; Duchemin, B.; Hanich, H.; Chaponnière, A.; Maisongrande, P.; Boulet, G.; Stitou, J.; Chehbouni, A. Analysis of snow cover dynamics in the Moroccan High Atlas using SPOT-VEGETATION data. Sci. Chang. Planét./Sécher. 2007, 18, 278–288. [Google Scholar]
- Chehbouni, A.; Escadafal, R.; Duchemin, B.; Boulet, G.; Simonneaux, V.; Dedieu, G.; Mougenot, B.; Khabba, S.; Kharrou, H.; Maisongrande, P.; et al. An integrated modelling and remote sensing approach for hydrological study in arid and semi-arid regions: The SUDMED Programme. Int. J. Remote Sens. 2008, 29, 5161–5181. [Google Scholar] [CrossRef]
- Driouech, F.; Déqué, M.; Mokssit, A. Numerical simulation of the probability distribution function of precipitation over Morocco. Clim. Dyn. 2009, 32, 1055–1063. [Google Scholar] [CrossRef]
- Bouras, E.H.; Jarlan, L.; Er-Raki, S.; Balaghi, R.; Amazirh, A.; Richard, B.; Khabba, S. Cereal yield forecasting with satellite drought-based indices, weather data and regional climate indices using machine learning in Morocco. Remote Sens. 2021, 13, 3101. [Google Scholar] [CrossRef]
- Jarlan, L.; Khabba, S.; Er-Raki, S.; Le Page, M.; Hanich, L.; Fakir, Y.; Merlin, O.; Mangiarotti, S.; Gascoin, S.; Ezzahar, J.; et al. Remote sensing of water resources in semi-arid Mediterranean areas: The joint international laboratory TREMA. Int. J. Remote Sens. 2015, 36, 4879–4917. [Google Scholar] [CrossRef]
- Dodson, R.; Marks, D. Daily air temperature interpolated at high spatial resolution over a large mountainous region. Clim. Res. 1997, 8, 1–20. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Lawrence, H.; Albergel, C.; Rosnay, P.; Isaksen, L.; Mecklenburg, S.; Kerr, Y.; Drusch, M. Assimilation of SMOS brightness temperatures in the ECMWF Integrated Forecasting System. Q. J. R. Meteorol. Soc. 2019, 145, 2524–2548. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily activity feature selection in smart homes based on pearson correlation coefficient. Neural Process. Lett. 2020, 51, 1771–1787. [Google Scholar] [CrossRef]
- Sachindra, D.; Huang, F.; Barton, A.; Perera, B. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992; Volume 49. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 1999. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting, R Package Version 0.4-2; 2015, Volume 1, pp. 1–4. Available online: https://cran.r-project.org/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 1 March 2023).
- Pesantez-Narvaez, J.; Guillen, M.; Alcañiz, M. Predicting motor insurance claims using telematics data—XGBoost versus logistic regression. Risks 2019, 7, 70. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Stone, M. Cross-validation: A review. Stat. J. Theor. Appl. Stat. 1978, 9, 127–139. [Google Scholar]
- Mohr, M.; Tveito, O. Daily temperature and precipitation maps with 1 km resolution derived from Norwegian weather observations. In Proceedings of the 13th Conference on Mountain Meteorology/17th Conference on Applied Climatology, Citeseer, Whistler, BC, Canada, 11–15 August 2008; pp. 11–15. [Google Scholar]
- Sluiter, R. Interpolation Methods for the Climate Atlas; KNMI: De Bilt, The Netherlands, 2012. [Google Scholar]
- Hengl, T.; Heuvelink, G.; Perčec Tadić, M.; Pebesma, E.J. Spatio-temporal prediction of daily temperatures using time-series of MODIS LST images. Theor. Appl. Climatol. 2012, 107, 265–277. [Google Scholar] [CrossRef]
- Aalto, J.; Pirinen, P.; Heikkinen, J.; Venäläinen, A. Spatial interpolation of monthly climate data for Finland: Comparing the performance of kriging and generalized additive models. Theor. Appl. Climatol. 2013, 112, 99–111. [Google Scholar] [CrossRef]
- Minder, J.R.; Mote, P.W.; Lundquist, J.D. Surface temperature lapse rates over complex terrain: Lessons from the Cascade Mountains. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Shen, Y.J.; Shen, Y.; Goetz, J.; Brenning, A. Spatial-temporal variation of near-surface temperature lapse rates over the Tianshan Mountains, central Asia. J. Geophys. Res. Atmos. 2016, 121, 14,006–14,017. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Li, X.; Chen, D. Temporal and spatial changes in estimated near-surface air temperature lapse rates on Tibetan Plateau. Int. J. Climatol. 2018, 38, 2907–2921. [Google Scholar] [CrossRef]
- Jobst, A.M.; Kingston, D.G.; Cullen, N.J.; Sirguey, P. Combining thin-plate spline interpolation with a lapse rate model to produce daily air temperature estimates in a data-sparse alpine catchment. Int. J. Climatol. 2017, 37, 214–229. [Google Scholar] [CrossRef]
- Pepin, N.C. The Possible Effects of Climate Change on the Spatial and Temporal Variation of the Altitudinal Temperature Gradient and the Consequences for Growth Potential in the Uplands of Northern England. Ph.D. Thesis, Durham University, Durham, UK, 1994. [Google Scholar]
- Shuttleworth, W.J. Terrestrial Hydrometeorology; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Li, Y.; Zeng, Z.; Zhao, L.; Piao, S. Spatial patterns of climatological temperature lapse rate in mainland China: A multi–time scale investigation. J. Geophys. Res. Atmos. 2015, 120, 2661–2675. [Google Scholar] [CrossRef]
- Kunkel, K.E. Simple procedures for extrapolation of humidity variables in the mountainous western United States. J. Clim. 1989, 2, 656–669. [Google Scholar] [CrossRef]
- Koch, S.E.; DesJardins, M.; Kocin, P.J. An interactive Barnes objective map analysis scheme for use with satellite and conventional data. J. Appl. Meteorol. Climatol. 1983, 22, 1487–1503. [Google Scholar] [CrossRef]
- Kato, T. Prediction of photovoltaic power generation output and network operation. In Integration of Distributed Energy Resources in Power Systems; Elsevier: Amsterdam, The Netherlands, 2016; pp. 77–108. [Google Scholar]


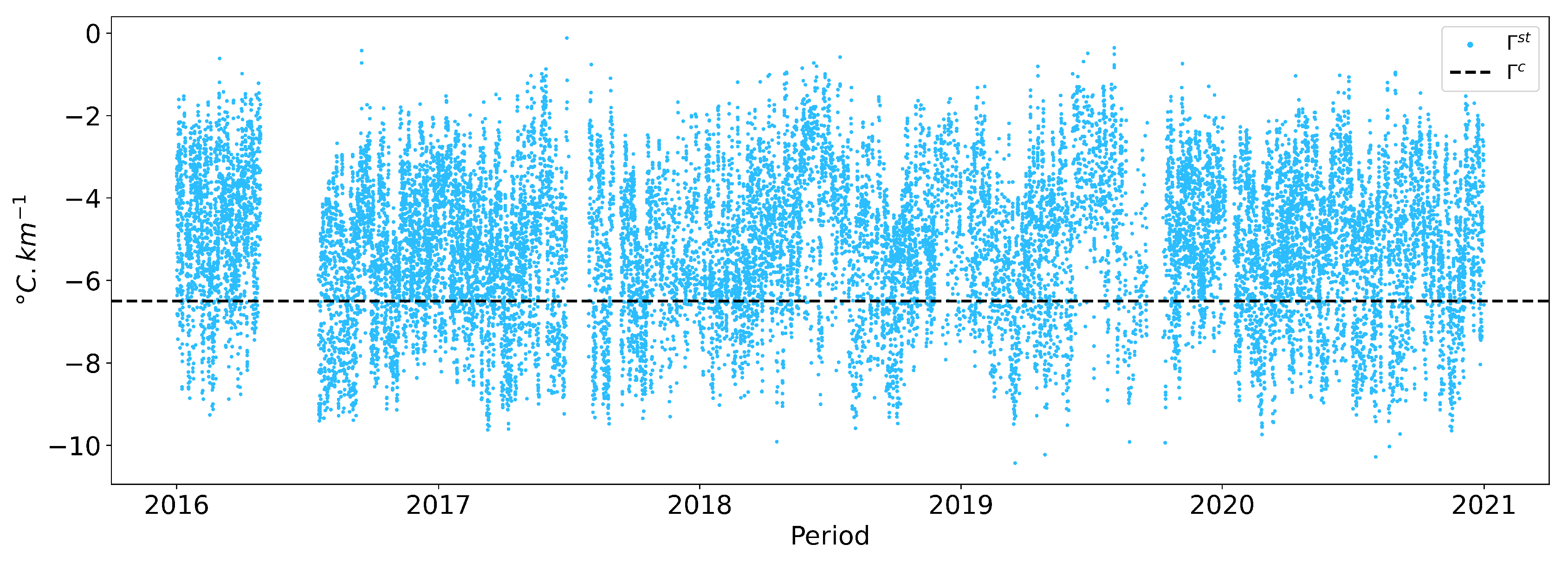
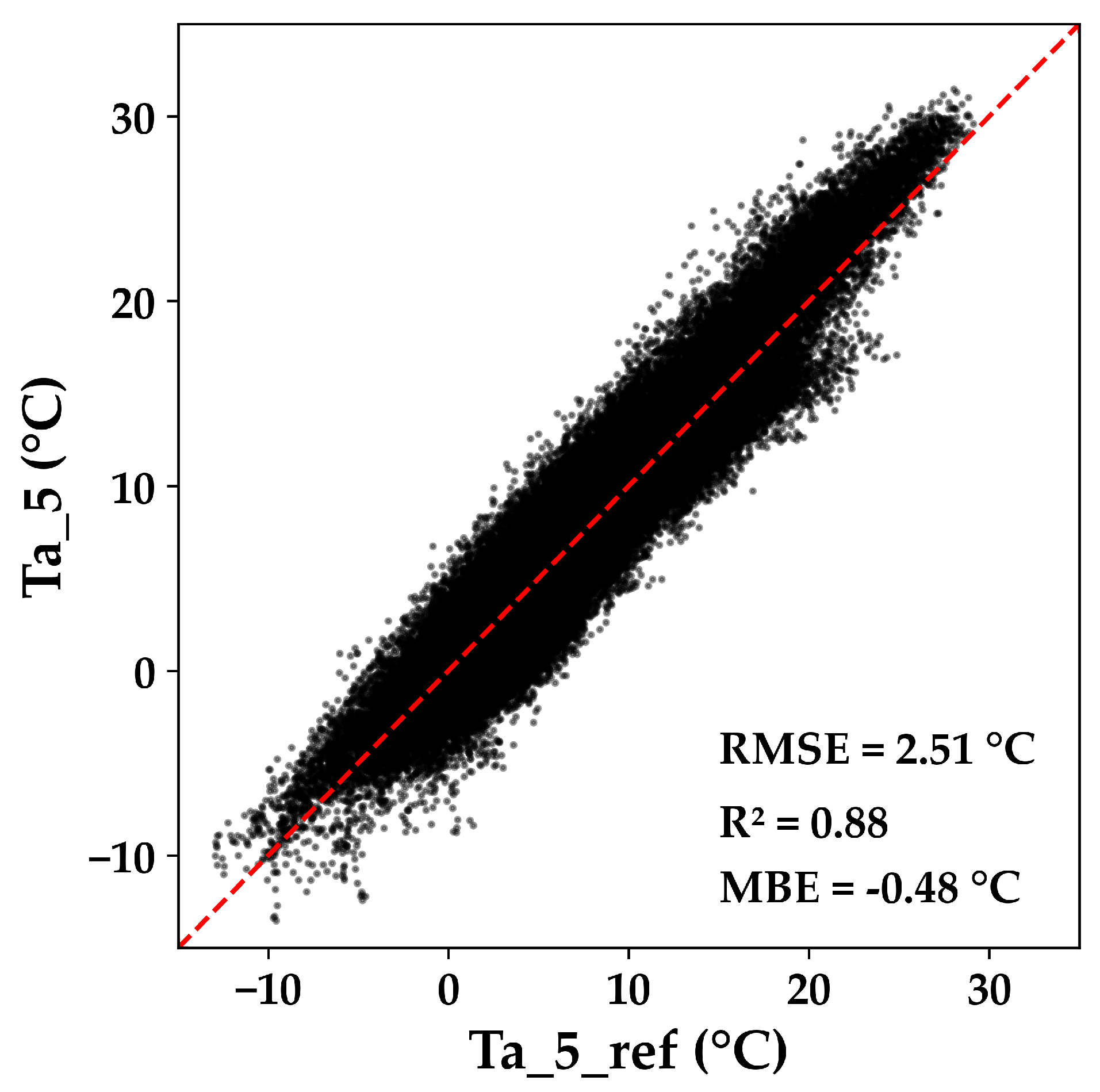

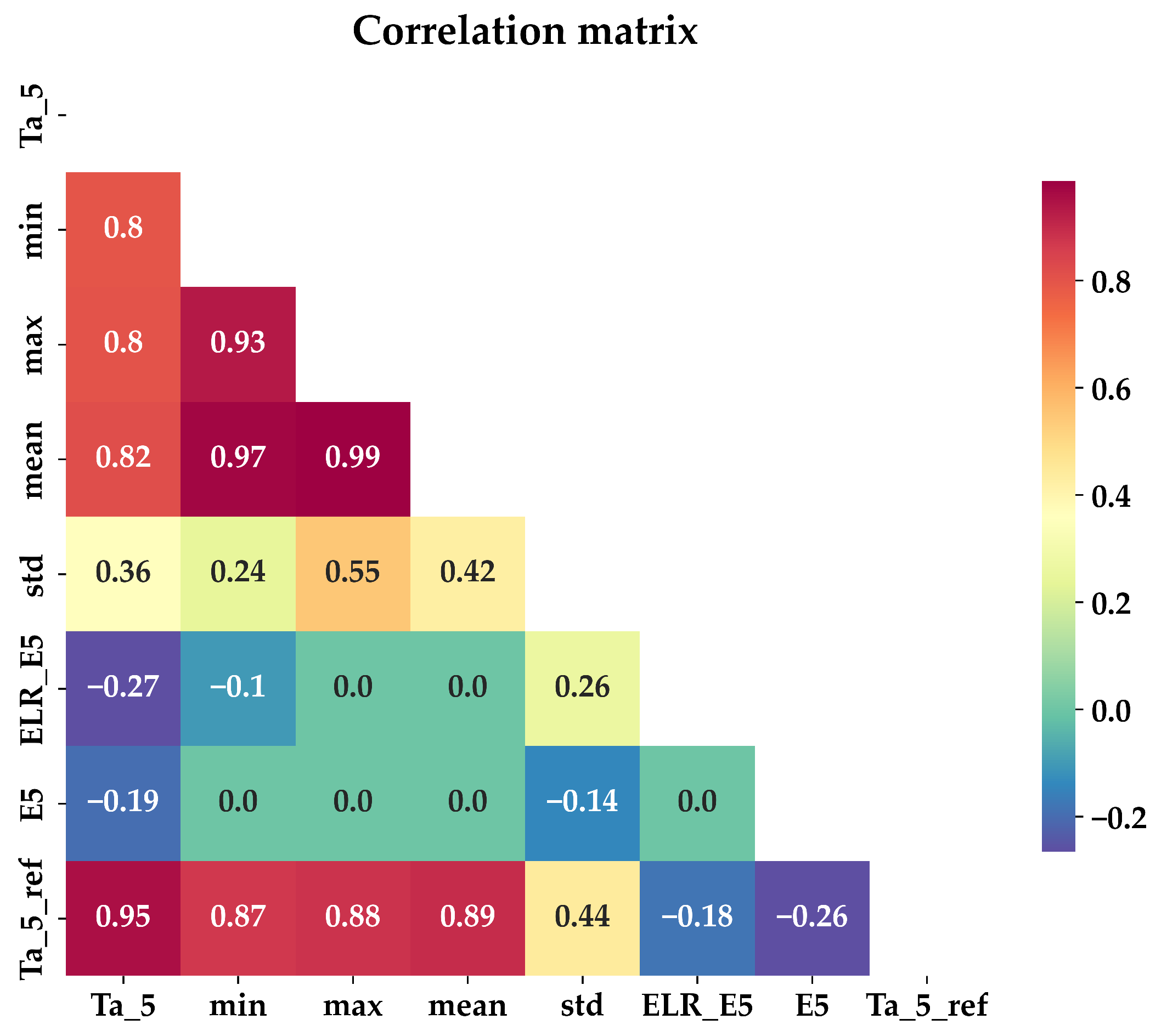


| AWS | Latitude | Longitude | Elevation (m.a.s.l) | Tmean (C) | No. of Observations | Frequency |
|---|---|---|---|---|---|---|
| Imskerbour | 31.21018° | −7.93972° | 1404 | 15.06 | 40,870 | 30 min |
| Aremd | 31.12948° | −7.91967° | 1940 | 12.1 | 43,848 | 30 min |
| Neltner | 31.06579° | −7.91389° | 3207 | 6.04 | 43,829 | 30 min |
| Oukaimden | 31.19328° | −7.86546° | 3230 | 5.85 | 42,644 | 30 min |
| Month | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ELR | 4.4 | 5.9 | 7.1 | 7.8 | 8.1 | 8.2 | 8.1 | 8.1 | 7.7 | 6.8 | 5.5 | 4.7 |
| Cross-Validation (Years) | MLR | SVR | Xgboost | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MBE | RMSE | MBE | RMSE | MBE | |||||
| 2016 | 1.3878 | 0.9500 | 0.3740 | 1.2213 | 0.9690 | 0.2622 | 0.8411 | 0.9877 | 0.0240 | |
| 2017 | 1.3542 | 0.9584 | −0.1944 | 1.2456 | 0.9654 | −0.2187 | 0.8232 | 0.9874 | −0.0123 | |
| 2018 | 1.2935 | 0.9670 | −0.0129 | 1.1828 | 0.9733 | −0.0112 | 0.7891 | 0.9870 | −0.0116 | |
| 2019 | 1.3310 | 0.9654 | 0.1079 | 1.2174 | 0.9696 | 0.1109 | 0.8260 | 0.9872 | −0.0031 | |
| 2020 | 1.3234 | 0.9660 | −0.2734 | 1.1789 | 0.9750 | −0.1608 | 0.8139 | 0.9871 | −0.0104 | |
| Mean | 1.34 | 0.97 | 0.002 | 1.21 | 0.97 | −0.004 | 0.83 | 0.99 | −0.003 | |
| AWS | RMSE | MBE | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cst ELR | MicroMet | ML Models | Cst ELR | MicroMet | ML Models | Cst ELR | MicroMet | ML Models | ||||||||
| MLR | SVR | Xgboost | MLR | SVR | Xgboost | MLR | SVR | Xgboost | ||||||||
| Imskerbour | 2.45 | 2.71 | 1.82 | 1.86 | 1.75 | 0.90 | 0.88 | 0.95 | 0.94 | 0.95 | −0.43 | 0.28 | 0.34 | 0.42 | 0.34 | |
| Aremd | 3.09 | 2.47 | 2.05 | 1.95 | 1.77 | 0.84 | 0.9 | 0.93 | 0.94 | 0.95 | −2.14 | −0.70 | −0.50 | −0.45 | −0.49 | |
| Neltner | 3.29 | 3.00 | 1.61 | 1.55 | 1.41 | 0.76 | 0.81 | 0.94 | 0.95 | 0.95 | −0.49 | −0.67 | 0.10 | 0.02 | 0.08 | |
| Oukaimden | 3.47 | 2.67 | 1.68 | 1.62 | 1.47 | 0.75 | 0.82 | 0.94 | 0.94 | 0.95 | 0.86 | −0.54 | 0.10 | 0.00 | 0.08 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebbar, B.-e.; Khabba, S.; Merlin, O.; Simonneaux, V.; Hachimi, C.E.; Kharrou, M.H.; Chehbouni, A. Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions. Atmosphere 2023, 14, 610. https://doi.org/10.3390/atmos14040610
Sebbar B-e, Khabba S, Merlin O, Simonneaux V, Hachimi CE, Kharrou MH, Chehbouni A. Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions. Atmosphere. 2023; 14(4):610. https://doi.org/10.3390/atmos14040610
Chicago/Turabian StyleSebbar, Badr-eddine, Saïd Khabba, Olivier Merlin, Vincent Simonneaux, Chouaib El Hachimi, Mohamed Hakim Kharrou, and Abdelghani Chehbouni. 2023. "Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions" Atmosphere 14, no. 4: 610. https://doi.org/10.3390/atmos14040610
APA StyleSebbar, B.-e., Khabba, S., Merlin, O., Simonneaux, V., Hachimi, C. E., Kharrou, M. H., & Chehbouni, A. (2023). Machine-Learning-Based Downscaling of Hourly ERA5-Land Air Temperature over Mountainous Regions. Atmosphere, 14(4), 610. https://doi.org/10.3390/atmos14040610







