Author Contributions
Conceptualization, P.S.; methodology, P.S., M.V. and A.B.; software, P.S. and M.V.; validation, P.S. and M.V.; formal analysis, P.S. and M.V.; investigation, P.S., M.V. and A.B.; resources, A.B.; data curation, P.S.; writing—original draft preparation, P.S. and M.V.; writing—review and editing, P.S., M.V., R.H., A.B., A.H., N.C. and F.R.D.; visualization, P.S. and M.V.; supervision, A.B.; project administration, A.B.; funding acquisition, A.B., F.R.D., N.C. and P.S. All authors have read and agreed to the published version of the manuscript.
Figure 1.
The roadside Schancheholen air quality monitoring station (station ID NO0125A), operated by Stanvager municipality, with the ten AirSensEUR units mounted on top. Photo credit: Rolf Haugen.
Figure 1.
The roadside Schancheholen air quality monitoring station (station ID NO0125A), operated by Stanvager municipality, with the ten AirSensEUR units mounted on top. Photo credit: Rolf Haugen.
Figure 2.
Overview map of the study site, showing the locations of the deployed sensor network (black triangles) and the air quality monitoring station used for the co-location. Base map and data from OpenStreetMap and OpenStreetMap Foundation.
Figure 2.
Overview map of the study site, showing the locations of the deployed sensor network (black triangles) and the air quality monitoring station used for the co-location. Base map and data from OpenStreetMap and OpenStreetMap Foundation.
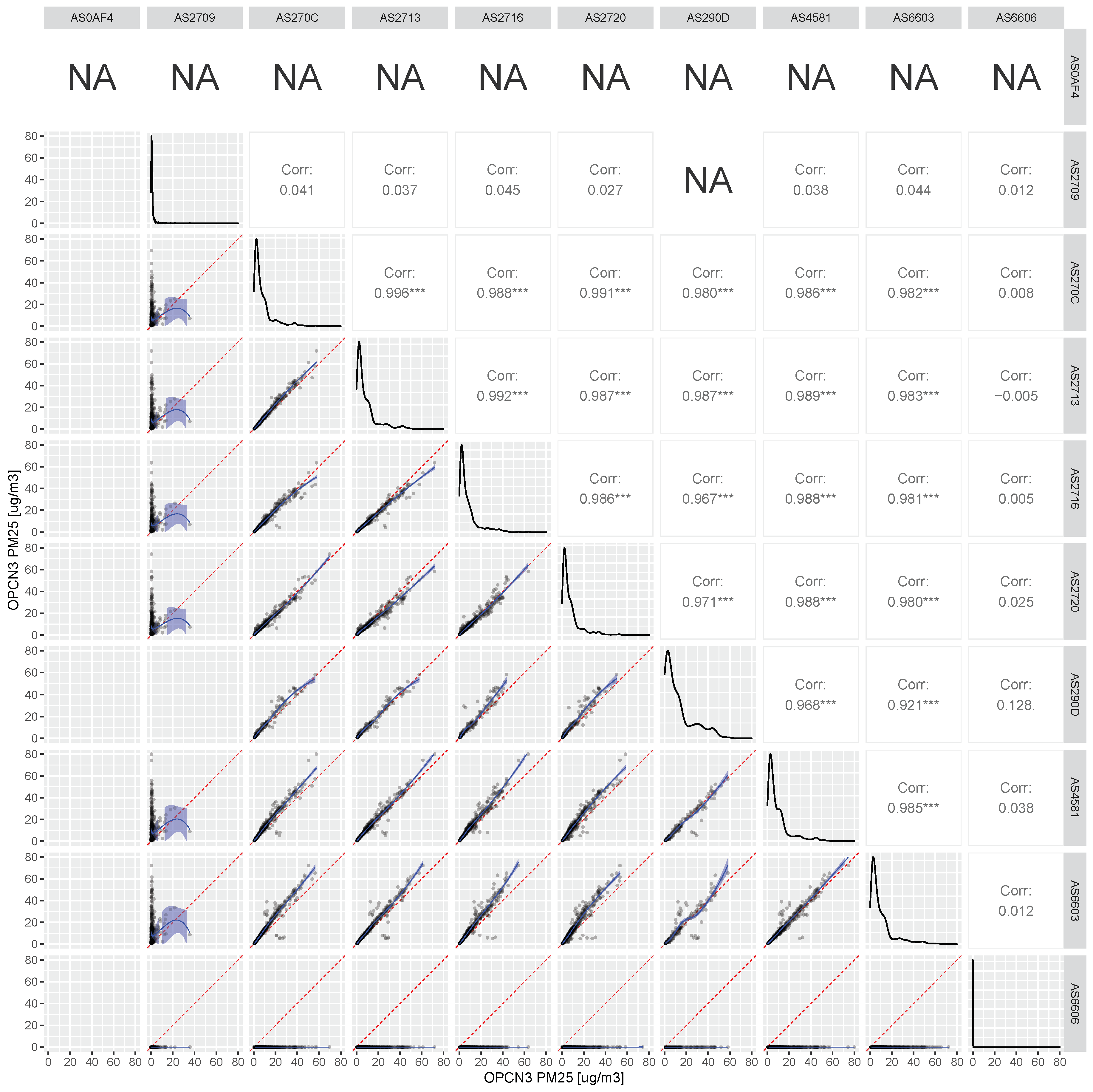
Figure 3.
Sensor-to-sensor intercomparison of the factory-calibrated PM2.5 signal from the OPC-N3 sensors against each other, during the co-location period. Axes labels are shown here in units of g m. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensor. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three star indicate significance levels with p-value of <0.001.
Figure 3.
Sensor-to-sensor intercomparison of the factory-calibrated PM2.5 signal from the OPC-N3 sensors against each other, during the co-location period. Axes labels are shown here in units of g m. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensor. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three star indicate significance levels with p-value of <0.001.
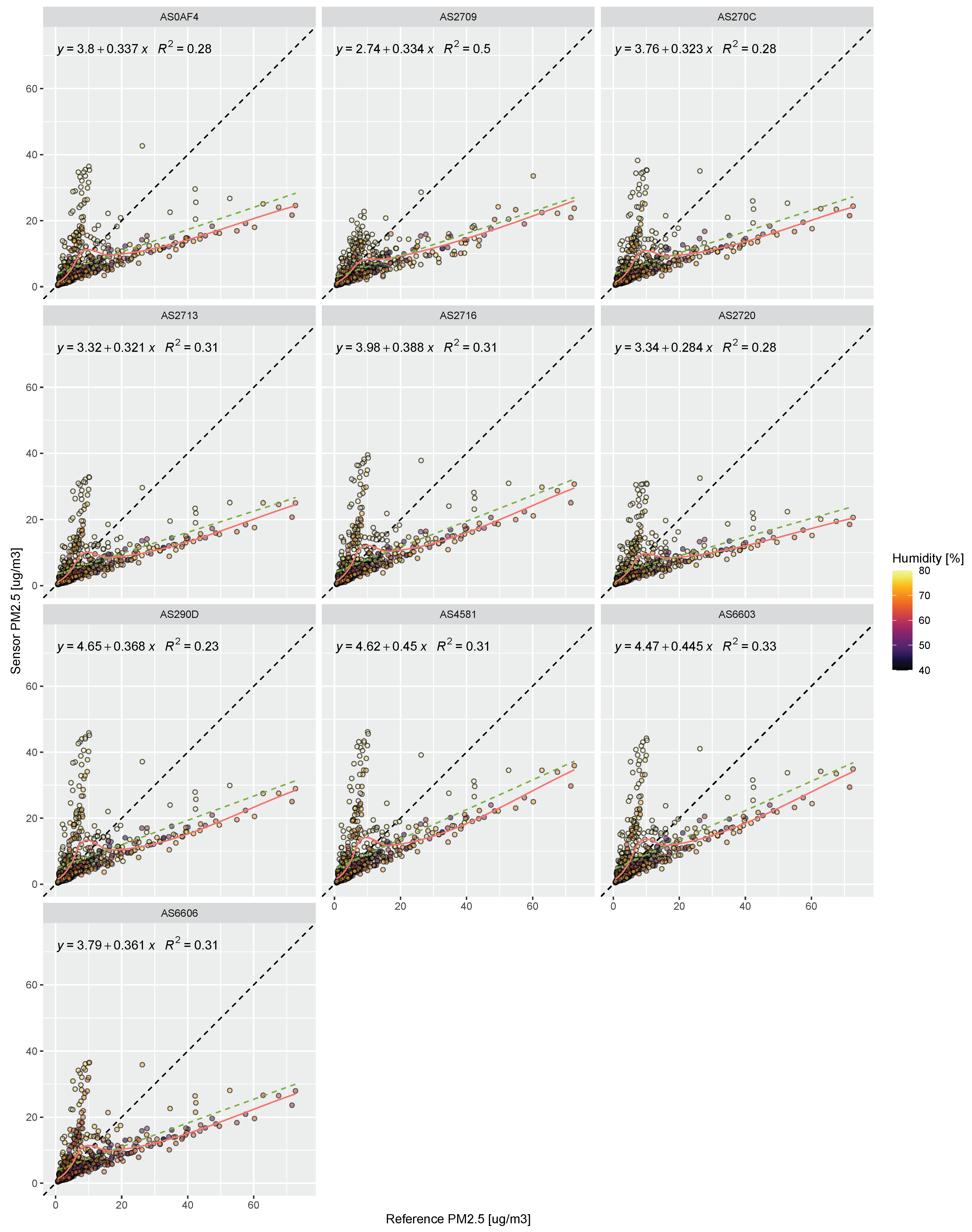
Figure 4.
Relationship between reference PM2.5 and sensor-based factory-calibrated PM2.5. The dashed black line represents the 1:1 reference line. The green dashed line shows a linear regression fit to the data (with the corresponding regression equation and R2 value provided in the top left corner) whereas the red lines indicate a LOESS fit. Relative humidity for each data point is indicated as a color.
Figure 4.
Relationship between reference PM2.5 and sensor-based factory-calibrated PM2.5. The dashed black line represents the 1:1 reference line. The green dashed line shows a linear regression fit to the data (with the corresponding regression equation and R2 value provided in the top left corner) whereas the red lines indicate a LOESS fit. Relative humidity for each data point is indicated as a color.
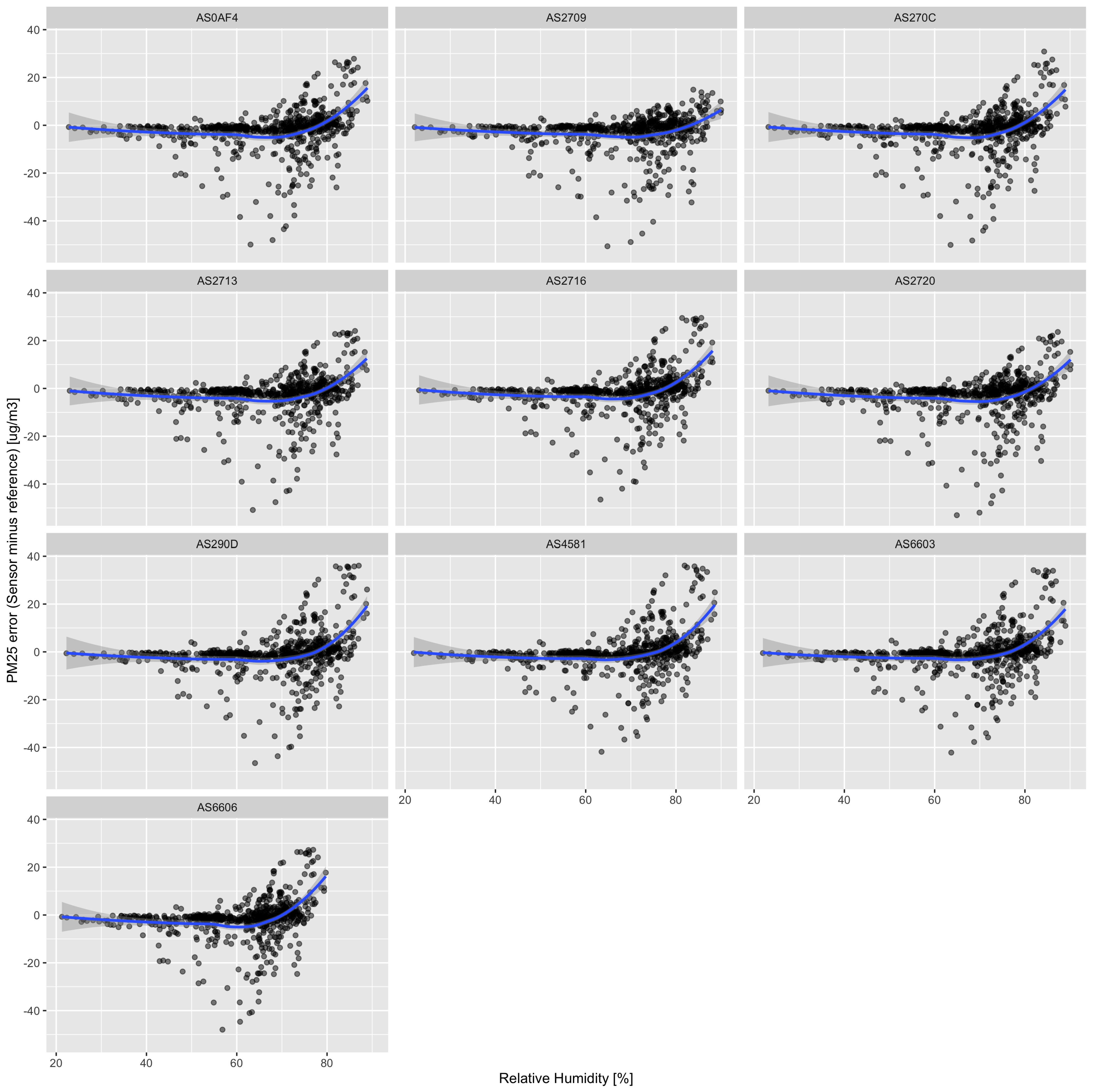
Figure 5.
The PM2.5 error as a function of relative humidity. The blue lines indicate a LOESS fit to the data, with the gray zone around the line showing the 95% confidence interval.
Figure 5.
The PM2.5 error as a function of relative humidity. The blue lines indicate a LOESS fit to the data, with the gray zone around the line showing the 95% confidence interval.
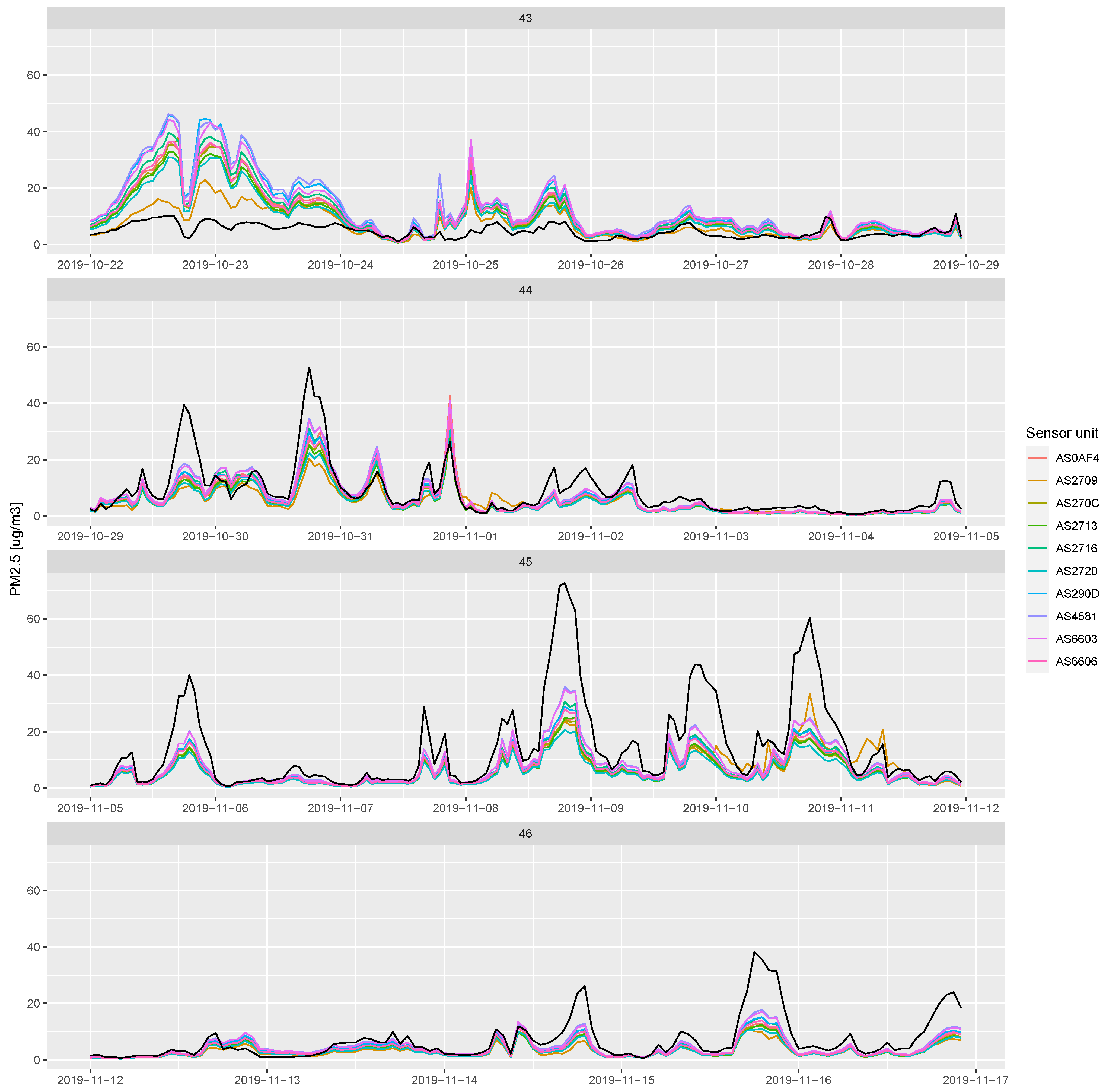
Figure 6.
Time series for PM2.5, faceted by week number for clarity. The black line indicates the values from the Schancheholen reference instrument.
Figure 6.
Time series for PM2.5, faceted by week number for clarity. The black line indicates the values from the Schancheholen reference instrument.
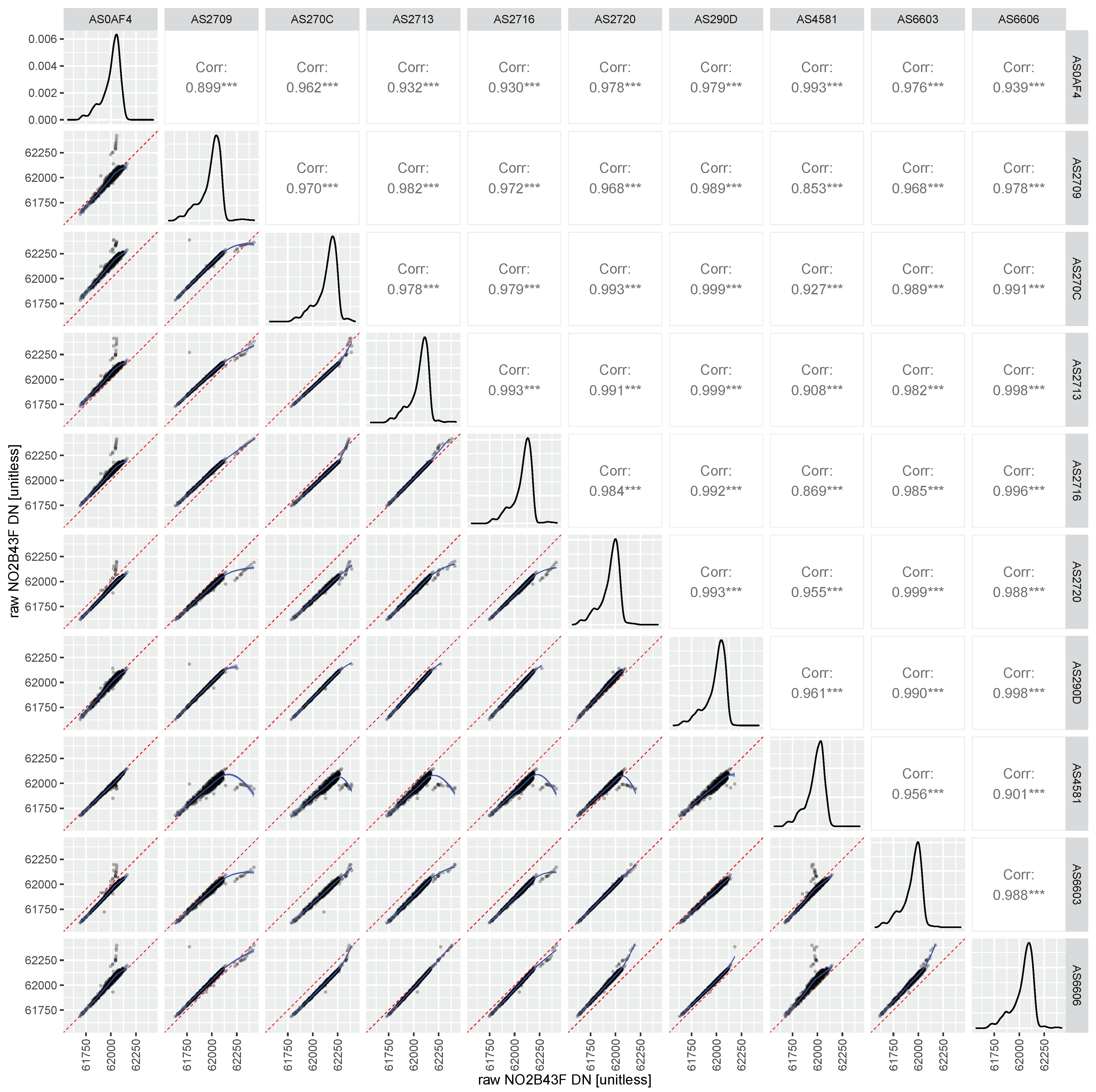
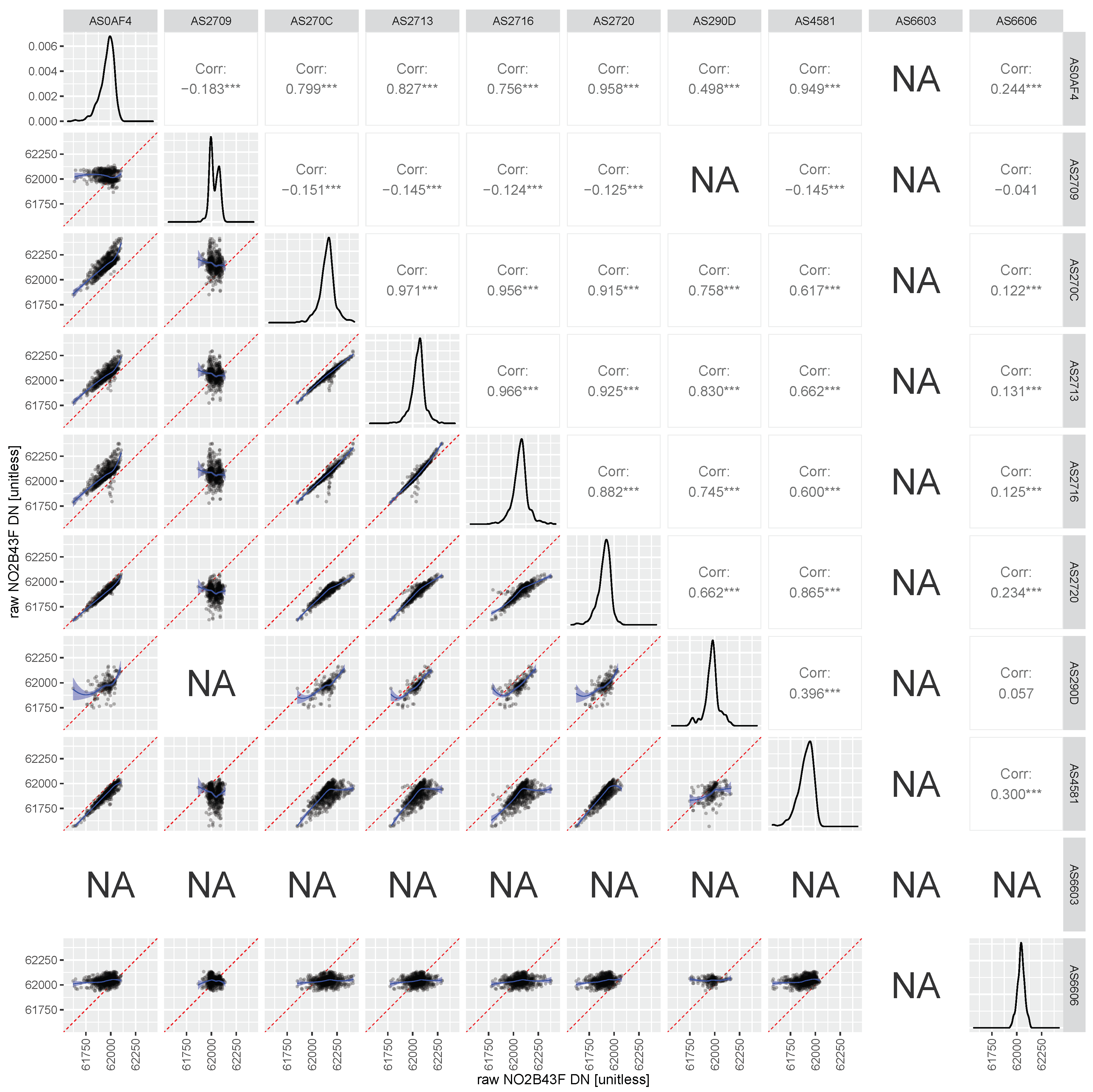
Figure 7.
Sensor-to-sensor intercomparison of raw output of all NO2-B43F sensors against each other, during the co-location period. The axes dimensions are in unitless digital numbers between 0 and 65,535. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three star indicate significance levels with p-value of <0.001.
Figure 7.
Sensor-to-sensor intercomparison of raw output of all NO2-B43F sensors against each other, during the co-location period. The axes dimensions are in unitless digital numbers between 0 and 65,535. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three star indicate significance levels with p-value of <0.001.
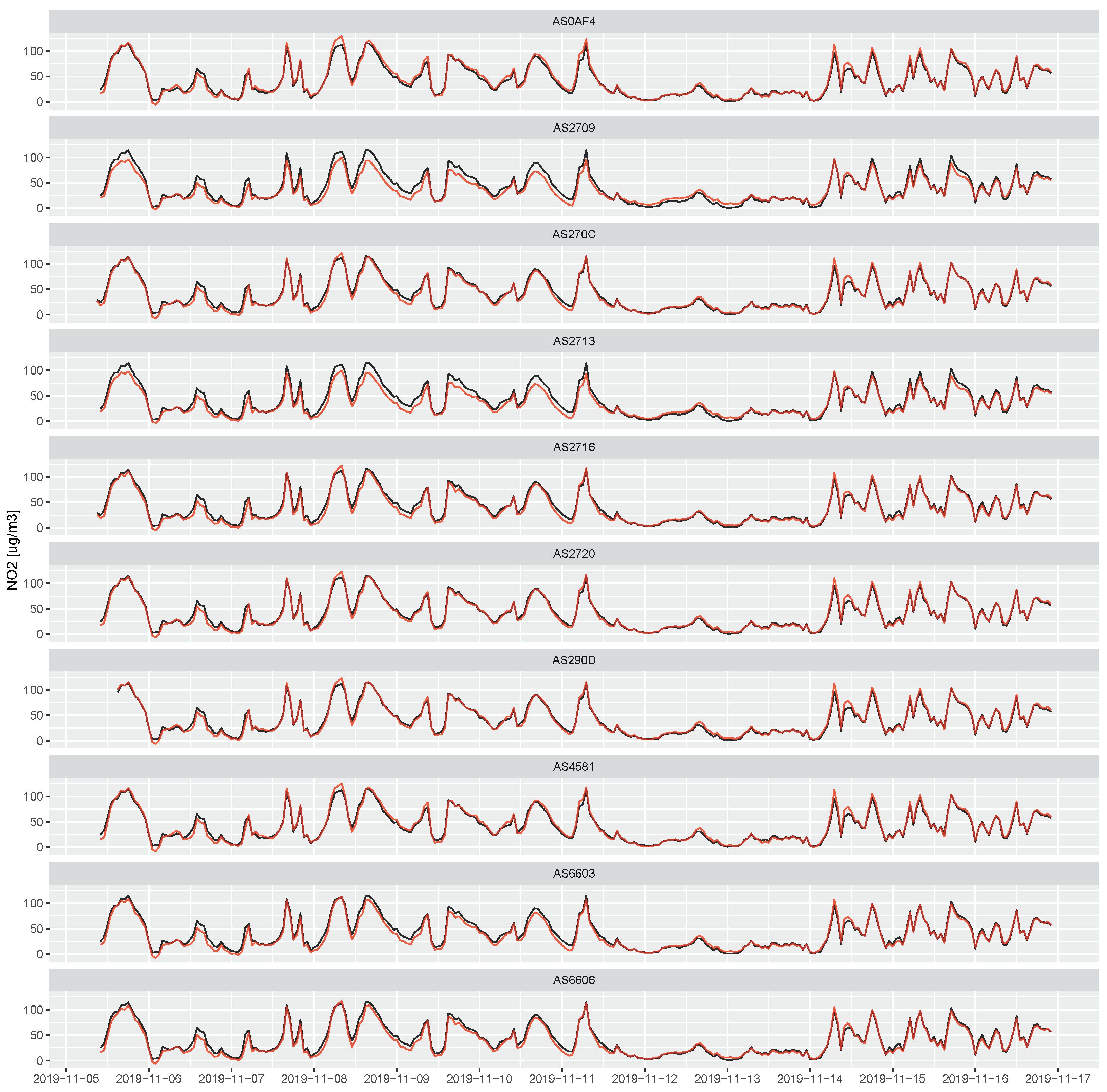
Figure 8.
Time series of calibrated sensor NO2 (red line) against the reference NO2 (black line) during the testing period (5 November 2019 through 16 November 2019).
Figure 8.
Time series of calibrated sensor NO2 (red line) against the reference NO2 (black line) during the testing period (5 November 2019 through 16 November 2019).
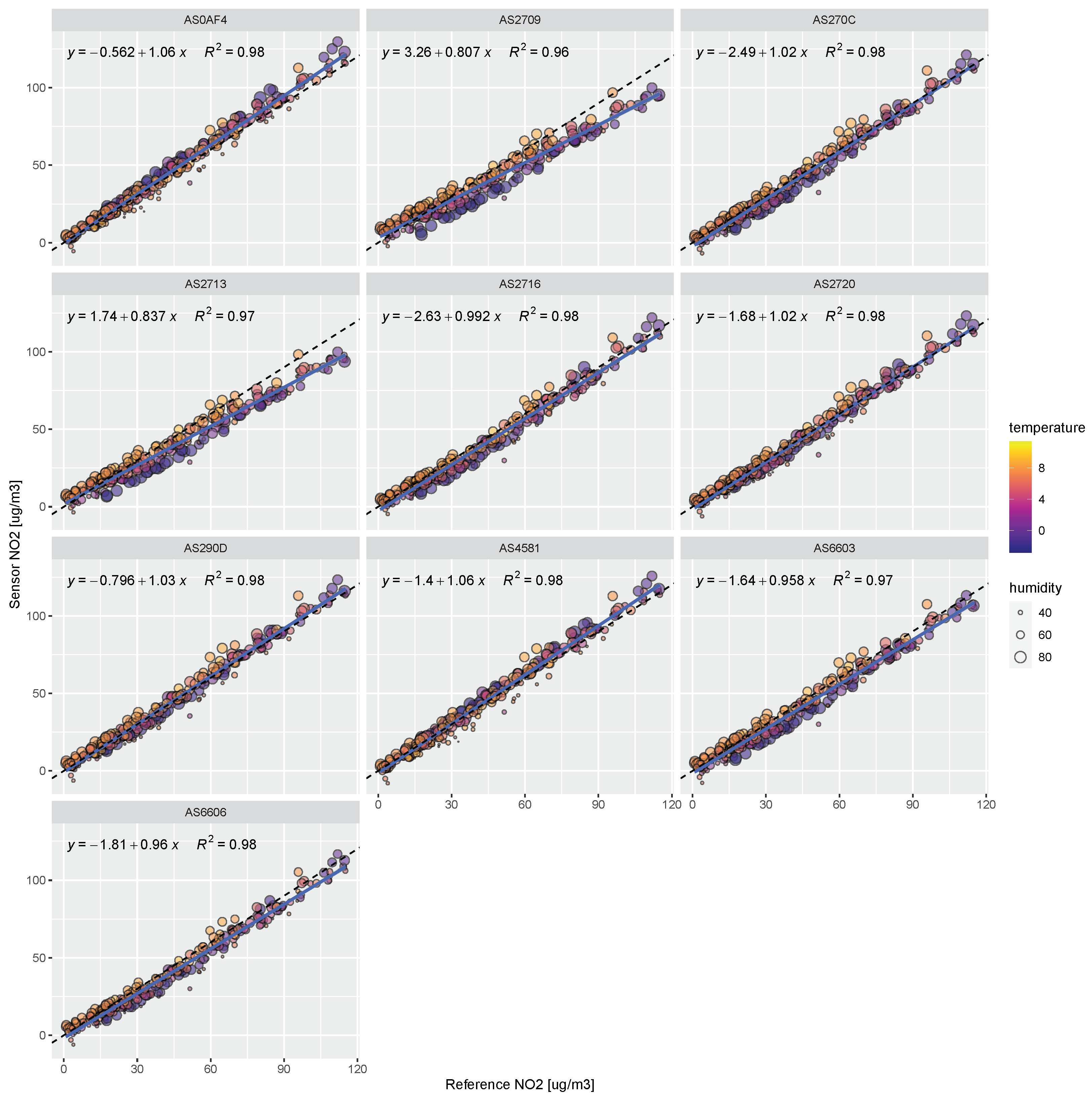
Figure 9.
Scatterplots of calibrated sensor NO2 against the reference NO2. The black dashed line indicates the 1:1 reference line, whereas the blue line shows a linear fit to the data, whose equation is shown in the upper left of each panel. Temperature is given in degrees Celsius, relative humidity in percent.
Figure 9.
Scatterplots of calibrated sensor NO2 against the reference NO2. The black dashed line indicates the 1:1 reference line, whereas the blue line shows a linear fit to the data, whose equation is shown in the upper left of each panel. Temperature is given in degrees Celsius, relative humidity in percent.
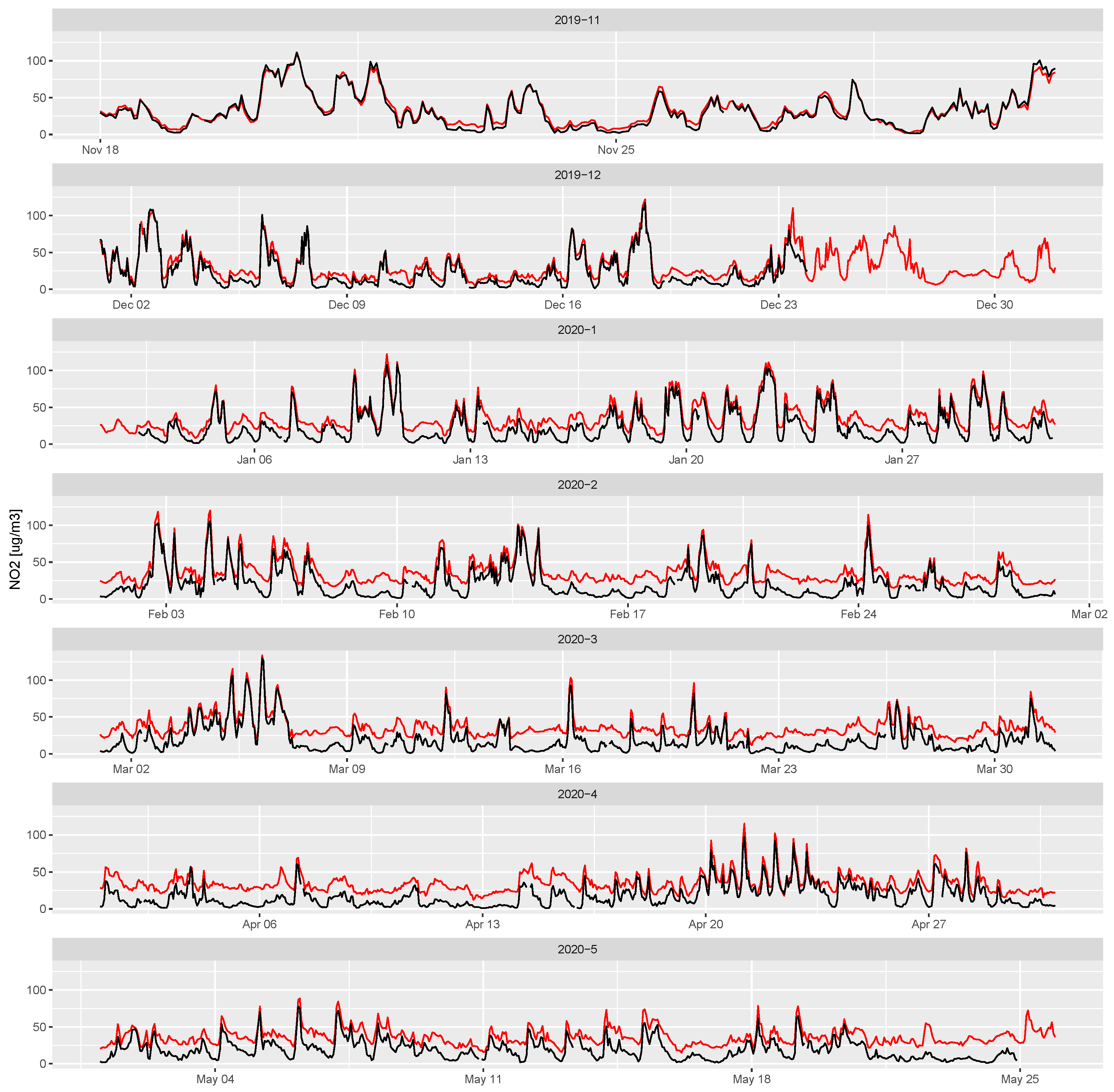
Figure 10.
Time series of calibrated sensor NO2 (red line) against the reference NO2 (black line), for sensor unit AS2713, during the deployment period (18 November 2019 through 25 May 2020), faceted by month for clarity.
Figure 10.
Time series of calibrated sensor NO2 (red line) against the reference NO2 (black line), for sensor unit AS2713, during the deployment period (18 November 2019 through 25 May 2020), faceted by month for clarity.
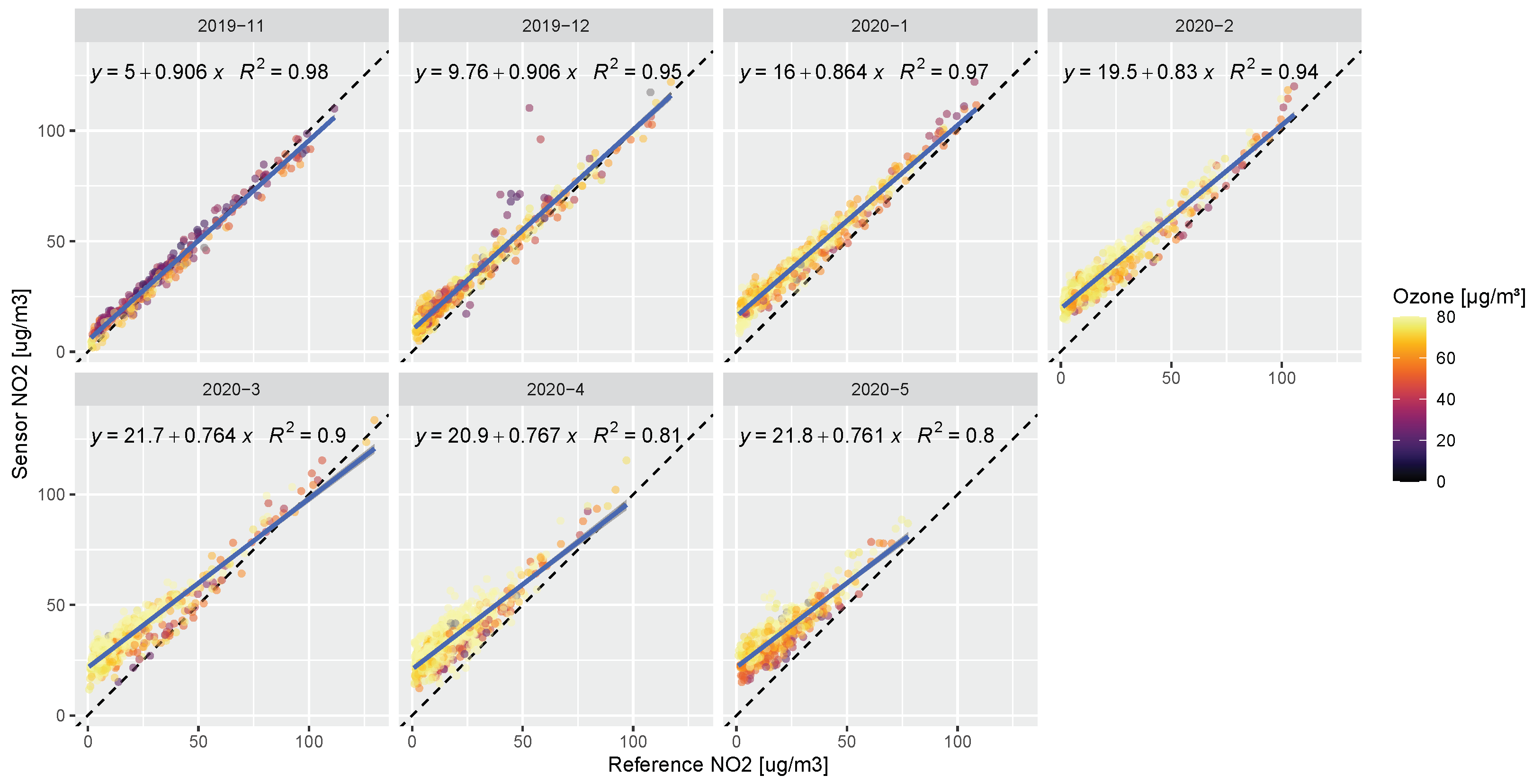
Figure 11.
Scatterplots of calibrated sensor NO2 against the reference NO2, faceted by month from November 2019 to May 2020. The black dashed line indicates the 1:1 reference line, whereas the blue line shows a linear fit to the data, whose equation is shown in the upper left of each panel. The marker colors indicate the ozone concentration, however it should be noted that no ozone observations were available in the area of Stavanger itself, so they had to be taken from a nearby station (Sandve).
Figure 11.
Scatterplots of calibrated sensor NO2 against the reference NO2, faceted by month from November 2019 to May 2020. The black dashed line indicates the 1:1 reference line, whereas the blue line shows a linear fit to the data, whose equation is shown in the upper left of each panel. The marker colors indicate the ozone concentration, however it should be noted that no ozone observations were available in the area of Stavanger itself, so they had to be taken from a nearby station (Sandve).
Figure 12.
Sensor-to-sensor intercomparison of the factory-calibrated PM2.5 signal from the OPC-N3 sensors against each other, during the post-deployment co-location period. Axes labels are shown here in units of g m. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three and no stars indicate significance levels with p-values of <0.001 and >0.10 respectively. Panels labeled NA did not have enough data.
Figure 12.
Sensor-to-sensor intercomparison of the factory-calibrated PM2.5 signal from the OPC-N3 sensors against each other, during the post-deployment co-location period. Axes labels are shown here in units of g m. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three and no stars indicate significance levels with p-values of <0.001 and >0.10 respectively. Panels labeled NA did not have enough data.
Figure 13.
Sensor-to-sensor intercomparison of raw output of all NO2-B43F sensors against each other, during the post-deployment co-location period. The axes dimensions are in unitless digital numbers between 0 and 65,535. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three and no stars indicate significance levels with p-values of <0.001 and >0.10 respectively. Panels labeled NA did not have enough data.
Figure 13.
Sensor-to-sensor intercomparison of raw output of all NO2-B43F sensors against each other, during the post-deployment co-location period. The axes dimensions are in unitless digital numbers between 0 and 65,535. The lower left panels show scatterplots of one sensor’s output against the other (with the red dashed line indicating the 1:1 reference line, and the blue line a smooth LOESS fit to the data). The panels on the diagonal show the histogram of the readings of each individual sensors. The panels on the upper right show the Pearson correlations of the scatterplots on the lower left, where three and no stars indicate significance levels with p-values of <0.001 and >0.10 respectively. Panels labeled NA did not have enough data.
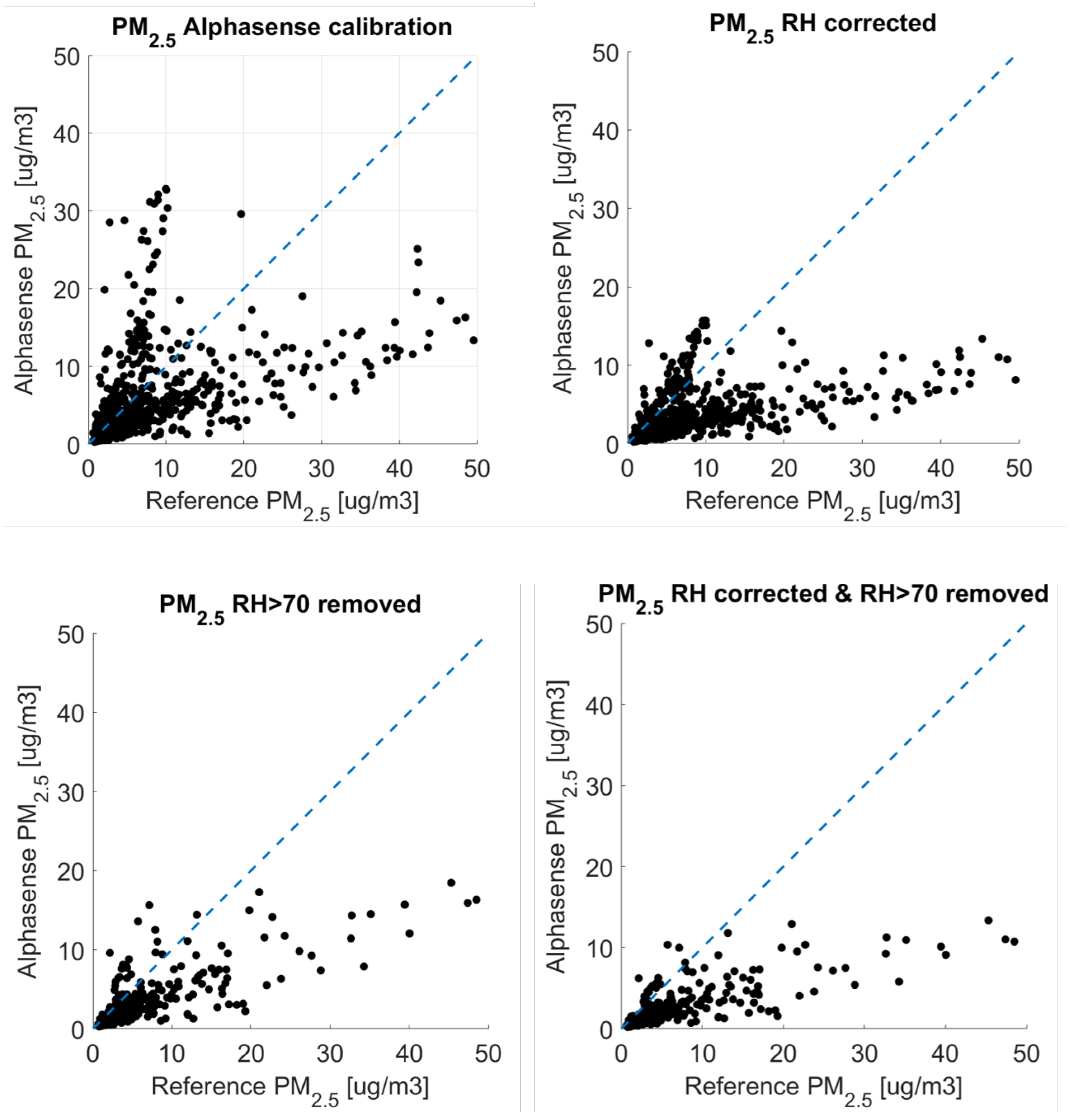
Figure 14.
Sensor-to-reference instrument intercomparison of the PM
2.5 signal from the OPC-N3 sensor AS2713, against the reference equivalent instrument Grimm EDM180. Axes labels are shown here in units of
g m
. The upper left panel show scatterplots of the factory-calibrated sensor’s output against the Grimm 180 (with the blue dashed line indicating the 1:1 reference line). The lower left panel shows a scatterplot of the factory-calibrated sensor’s output with relative humidity values below 70%, against the reference equivalent instrument. The upper right panel shows relative humidity corrected sensor’s output against the reference equivalent instrument, and the lower right panel show scatterplots of the factory-calibrated sensor’s output with relative humidity values below 70%, and corrected for relative humidity effect according to [
33].
Figure 14.
Sensor-to-reference instrument intercomparison of the PM
2.5 signal from the OPC-N3 sensor AS2713, against the reference equivalent instrument Grimm EDM180. Axes labels are shown here in units of
g m
. The upper left panel show scatterplots of the factory-calibrated sensor’s output against the Grimm 180 (with the blue dashed line indicating the 1:1 reference line). The lower left panel shows a scatterplot of the factory-calibrated sensor’s output with relative humidity values below 70%, against the reference equivalent instrument. The upper right panel shows relative humidity corrected sensor’s output against the reference equivalent instrument, and the lower right panel show scatterplots of the factory-calibrated sensor’s output with relative humidity values below 70%, and corrected for relative humidity effect according to [
33].
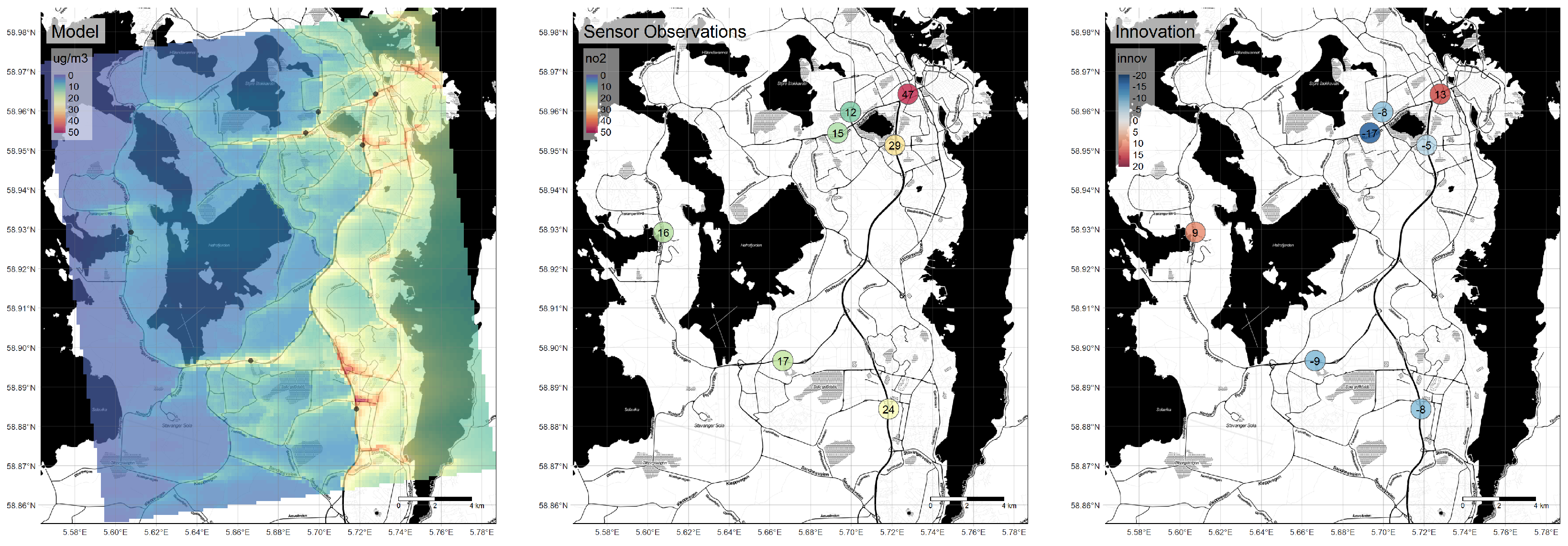
Figure 15.
Input data to the data assimilation process, here shown for 9 January 2020 at 15:00 UTC. The left panel shows the model-predicted NO
2 values, here the uEMEP model developed by MET Norway [
55,
56], the center panel shows the NO
2 observations from the network of AirSensEUR units reported here, and the right panel shows the innovation, i.e., the difference between the model prediction and the actual observation at each location. Base map copyright OpenStreetMap contributors and map tiles by Stamen Design, under CC BY 3.0.
Figure 15.
Input data to the data assimilation process, here shown for 9 January 2020 at 15:00 UTC. The left panel shows the model-predicted NO
2 values, here the uEMEP model developed by MET Norway [
55,
56], the center panel shows the NO
2 observations from the network of AirSensEUR units reported here, and the right panel shows the innovation, i.e., the difference between the model prediction and the actual observation at each location. Base map copyright OpenStreetMap contributors and map tiles by Stamen Design, under CC BY 3.0.
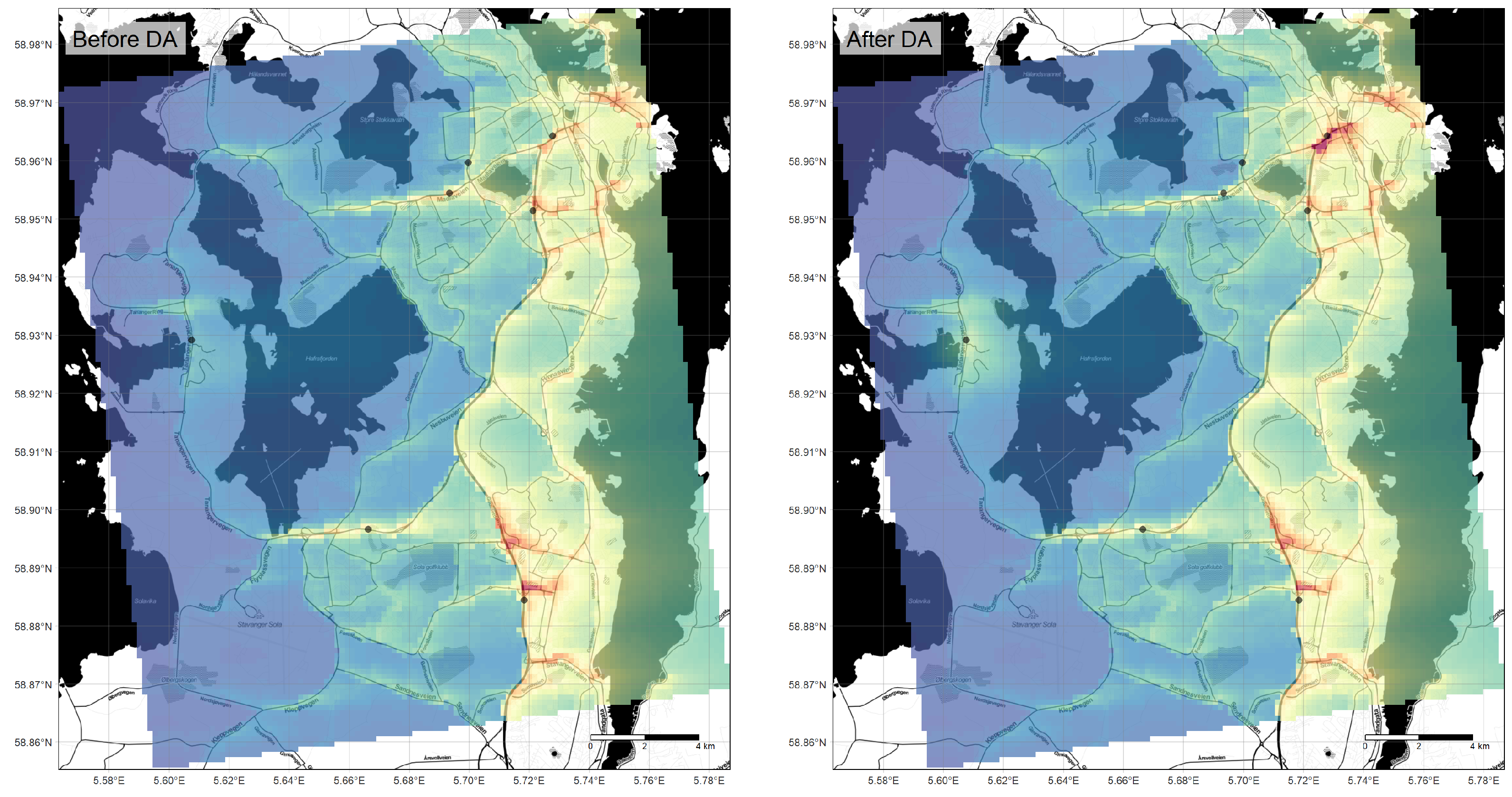
Figure 16.
Example showing simple data assimilation of the Stavanger sensor network in the output from a model. The left panel shows the model-predicted NO2 values for 9 January 2020 at 15:00 UTC, whereas the right panel shows the analysis assimilating the sensor observations for the same time. Black markers indicate the locations of the sensor systems. Base map copyright OpenStreetMap contributors and map tiles by Stamen Design, under CC BY 3.0.
Figure 16.
Example showing simple data assimilation of the Stavanger sensor network in the output from a model. The left panel shows the model-predicted NO2 values for 9 January 2020 at 15:00 UTC, whereas the right panel shows the analysis assimilating the sensor observations for the same time. Black markers indicate the locations of the sensor systems. Base map copyright OpenStreetMap contributors and map tiles by Stamen Design, under CC BY 3.0.
Table 1.
Geographic coordinates of the locations for the seven deployed sensor units, given in decimal degrees (DD) on the WGS84 datum.
Table 1.
Geographic coordinates of the locations for the seven deployed sensor units, given in decimal degrees (DD) on the WGS84 datum.
| Sensor ID | Latitude [DD] | Longitude [DD] |
|---|
| AS0AF4 | 58.95441° N | 5.69336° E |
| AS270C | 58.95972° N | 5.69963° E |
| AS2713 | 58.95138° N | 5.72131° E |
| AS290D | 58.88441° N | 5.71838° E |
| AS2716 | 58.89665° N | 5.66640° E |
| AS2720 | 58.92921° N | 5.60756° E |
| AS4581 | 58.96425° N | 5.72786° E |
Table 2.
Multilinear regression coefficients for all sensor systems.
Table 2.
Multilinear regression coefficients for all sensor systems.
| ID | Term | Estimate | Std. Error | t Value | p Value |
|---|
| AS2716 | (Intercept) | 16,467.95 | 188.04 | 87.58 | 0.000 |
| AS2716 | NO2B43F | −0.26 | 0.00 | −90.76 | 0.000 |
| AS2716 | log(NOB4) | 17.75 | 2.89 | 6.15 | 0.000 |
| AS2716 | log(50 + temperature) | −77.06 | 3.52 | −21.91 | 0.000 |
| AS270C | (Intercept) | 12,239.40 | 343.55 | 35.63 | 0.000 |
| AS270C | NO2B43F | −0.20 | 0.01 | −35.92 | 0.000 |
| AS270C | log(NOB4) | 20.92 | 4.65 | 4.50 | 0.000 |
| AS270C | log(50 + temperature) | 52.45 | 9.53 | 5.50 | 0.000 |
| AS4581 | (Intercept) | 14,850.42 | 215.67 | 68.86 | 0.000 |
| AS4581 | NO2B43F | −0.25 | 0.00 | −70.94 | 0.000 |
| AS4581 | log(NOB4) | 32.17 | 3.35 | 9.61 | 0.000 |
| AS4581 | log(50 + temperature) | 33.33 | 5.09 | 6.55 | 0.000 |
| AS2709 | (Intercept) | 14,796.37 | 378.20 | 39.12 | 0.000 |
| AS2709 | NO2B43F | −0.24 | 0.01 | −39.22 | 0.000 |
| AS2709 | log(NOB4) | −11.38 | 4.59 | −2.48 | 0.013 |
| AS2709 | log(50 + temperature) | 48.15 | 8.63 | 5.58 | 0.000 |
| AS2713 | (Intercept) | 12,907.25 | 196.38 | 65.73 | 0.000 |
| AS2713 | NO2B43F | −0.22 | 0.00 | −65.53 | 0.000 |
| AS2713 | log(NOB4) | 95.16 | 2.41 | 39.48 | 0.000 |
| AS2713 | log(50 + temperature) | 13.91 | 5.52 | 2.52 | 0.012 |
| AS290D | (Intercept) | 15,154.54 | 183.92 | 82.40 | 0.000 |
| AS290D | NO2B43F | −0.25 | 0.00 | −82.31 | 0.000 |
| AS290D | log(NOB4) | 37.18 | 2.11 | 17.61 | 0.000 |
| AS290D | log(50 + temperature) | −21.54 | 4.31 | −5.00 | 0.000 |
| AS6606 | (Intercept) | 15,664.17 | 163.55 | 95.78 | 0.000 |
| AS6606 | NO2B43F | −0.25 | 0.00 | −96.20 | 0.000 |
| AS6606 | log(NOB4) | 7.42 | 2.16 | 3.43 | 0.001 |
| AS6606 | log(50 + temperature) | 16.35 | 4.34 | 3.77 | 0.000 |
| AS0AF4 | (Intercept) | 17,344.91 | 211.91 | 81.85 | 0.000 |
| AS0AF4 | NO2B43F | −0.27 | 0.00 | −84.95 | 0.000 |
| AS0AF4 | log(NOB4) | −8.76 | 3.35 | −2.61 | 0.009 |
| AS0AF4 | log(50 + temperature) | −90.21 | 3.52 | −25.63 | 0.000 |
| AS2720 | (Intercept) | 15,190.69 | 263.70 | 57.61 | 0.000 |
| AS2720 | NO2B43F | −0.25 | 0.00 | −58.60 | 0.000 |
| AS2720 | log(NOB4) | 10.44 | 3.66 | 2.85 | 0.004 |
| AS2720 | log(50 + temperature) | −0.30 | 5.61 | −0.05 | 0.957 |
| AS6603 | (Intercept) | 12,307.27 | 259.40 | 47.44 | 0.000 |
| AS6603 | NO2B43F | −0.21 | 0.00 | −50.27 | 0.000 |
| AS6603 | log(NOB4) | 73.15 | 4.70 | 15.57 | 0.000 |
| AS6603 | log(50 + temperature) | 19.86 | 6.61 | 3.00 | 0.003 |
Table 3.
Summary statistics of applying the sensor-specific multilinear regression models for NO2 to the testing period. MB is the mean bias, MAE is the mean absolute error, and RMSE is the root mean squared error. R2 is the coefficient of determination. All values given in units of g m except R2 (unitless).
Table 3.
Summary statistics of applying the sensor-specific multilinear regression models for NO2 to the testing period. MB is the mean bias, MAE is the mean absolute error, and RMSE is the root mean squared error. R2 is the coefficient of determination. All values given in units of g m except R2 (unitless).
| Sensor ID | MB | MAE | RMSE | |
|---|
| AS0AF4 | 1.96 | 3.78 | 5.01 | 0.98 |
| AS2709 | −4.81 | 7.15 | 8.99 | 0.96 |
| AS270C | −1.70 | 3.55 | 4.70 | 0.98 |
| AS2713 | −5.09 | 6.69 | 8.48 | 0.97 |
| AS2716 | −2.98 | 4.32 | 5.46 | 0.98 |
| AS2720 | −0.83 | 3.04 | 4.12 | 0.98 |
| AS290D | 0.40 | 3.11 | 4.18 | 0.98 |
| AS4581 | 0.94 | 3.53 | 4.68 | 0.98 |
| AS6603 | −3.40 | 4.72 | 5.92 | 0.97 |
| AS6606 | −3.50 | 4.57 | 5.75 | 0.98 |
| Average | −1.90 | 4.45 | 5.73 | 0.98 |
Table 4.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location. RMSE is the root mean squared error and MAD is the mean absolute deviation.
Table 4.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location. RMSE is the root mean squared error and MAD is the mean absolute deviation.
| Sensor Unit | Bias | Std. Dev. | RMSE | MAD | Intercept | Slope | R2 |
|---|
| AS0AF4 | −2.04 | 9.5 | 9.69 | 2.54 | 4.09 | 0.3 | 0.22 |
| AS2709 | −3.12 | 8.31 | 8.86 | 2.19 | 2.99 | 0.3 | 0.41 |
| AS270C | −2.20 | 9.45 | 9.693 | 2.46 | 4.05 | 0.28 | 0.22 |
| AS2713 | −2.66 | 9.24 | 9.61 | 2.61 | 3.6 | 0.28 | 0.25 |
| AS2720 | −2.97 | 9.4 | 9.85 | 2.50 | 3.62 | 0.25 | 0.22 |
| AS290D | −0.92 | 10.31 | 10.34 | 2.61 | 5.01 | 0.32 | 0.18 |
| AS4581 | −0.23 | 9.77 | 9.77 | 2.46 | 5.01 | 0.4 | 0.25 |
| AS6603 | −0.41 | 9.49 | 9.49 | 2.46 | 4.87 | 0.4 | 0.27 |
| AS6606 | −1.85 | 9.30 | 9.48 | 2.452 | 4.12 | 0.32 | 0.25 |
| AS2716 | −1.41 | 9.41 | 9.5 | 2.59 | 4.33 | 0.35 | 0.25 |
| Average | −1.78 | 9.42 | 9.63 | 2.49 | 4.17 | 0.32 | 0.25 |
Table 5.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after correction for relative humidity effects using Köhler theory. RMSE is the root mean squared error and MAD is the mean absolute deviation.
Table 5.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after correction for relative humidity effects using Köhler theory. RMSE is the root mean squared error and MAD is the mean absolute deviation.
| Sensor Unit | Bias | Std. Dev. | RMSE | MAD | Intercept | Slope | R2 |
|---|
| AS0AF4 | −4.82 | 9.08 | 10.28 | 2.42 | 2.34 | 0.19 | 0.32 |
| AS2709 | −5.45 | 8.89 | 10.41 | 2.36 | 1.73 | 0.18 | 0.49 |
| AS270C | −4.91 | 9.138 | 10.36 | 2.37 | 2.31 | 0.18 | 0.32 |
| AS2713 | −5.19 | 9.09 | 10.46 | 2.63 | 2.04 | 0.18 | 0.35 |
| AS2720 | −5.47 | 9.31 | 10.79 | 2.56 | 2.00 | 0.15 | 0.32 |
| AS290D | −4.21 | 9.23 | 10.11 | 2.56 | 2.85 | 0.2 | 0.26 |
| AS4581 | −3.75 | 8.76 | 9.52 | 2.35 | 2.87 | 0.25 | 0.34 |
| AS6603 | −3.86 | 8.719 | 9.52 | 2.35 | 2.78 | 0.25 | 0.36 |
| AS6606 | −4.09 | 8.93 | 9.82 | 2.4 | 2.73 | 0.23 | 0.31 |
| AS2716 | −4.444 | 8.86 | 9.91 | 2.39 | 2.46 | 0.22 | 0.35 |
| Average | −4.62 | 9.00 | 10.12 | 2.44 | 2.41 | 0.20 | 0.34 |
Table 6.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after removing observations with a relative humidity greater than 70 percent. RMSE is the root mean squared error and MAD is the mean absolute deviation.
Table 6.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after removing observations with a relative humidity greater than 70 percent. RMSE is the root mean squared error and MAD is the mean absolute deviation.
| Sensor Unit | Bias | Std. Dev. | RMSE | MAD | Intercept | Slope | R2 |
|---|
| AS0AF4 | −3.2 | 6.44 | 7.19 | 1.85 | 1.57 | 0.35 | 0.63 |
| AS2709 | −3.28 | 6.22 | 7.02 | 1.64 | 1.3 | 0.36 | 0.67 |
| AS270C | −3.15 | 6.47 | 7.18 | 1.8 | 1.63 | 0.35 | 0.63 |
| AS2713 | −3.54 | 6.48 | 7.37 | 2.04 | 1.31 | 0.34 | 0.65 |
| AS2720 | −3.7 | 6.66 | 7.61 | 1.9 | 1.29 | 0.31 | 0.66 |
| AS290D | −2.48 | 6.13 | 6.61 | 1.6 | 1.81 | 0.4 | 0.6 |
| AS4581 | −2.06 | 5.66 | 6.02 | 1.37 | 1.72 | 0.48 | 0.67 |
| AS6603 | −2.02 | 5.75 | 6.08 | 1.37 | 1.8 | 0.48 | 0.66 |
| AS6606 | −3.25 | 8.61 | 9.19 | 2.202 | 2.94 | 0.31 | 0.42 |
| AS2716 | −2.76 | 6.04 | 6.63 | 1.72 | 1.55 | 0.41 | 0.66 |
| Average | −2.94 | 6.45 | 7.09 | 1.75 | 1.69 | 0.38 | 0.63 |
Table 7.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after correction for relative humidity effects using Köhler theory, and after removing observations with a relative humidity greater than 70 percent. RMSE is the root mean squared error and MAD is the mean absolute deviation.
Table 7.
Summary statistics of manufacturer-calibrated PM2.5 mass concentrations against the reference data, during the co-location, after correction for relative humidity effects using Köhler theory, and after removing observations with a relative humidity greater than 70 percent. RMSE is the root mean squared error and MAD is the mean absolute deviation.
| Sensor Unit | Bias | Std. Dev. | RMSE | MAD | Intercept | Slope | R2 |
|---|
| AS0AF4 | −4.23 | 7.11 | 8.26 | 2.08 | 1.26 | 0.25 | 0.61 |
| AS2709 | −4.24 | 6.97 | 8.15 | 2.1 | 1.11 | 0.25 | 0.64 |
| AS270C | −4.2 | 7.15 | 8.27 | 2.02 | 1.31 | 0.25 | 0.61 |
| AS2713 | −4.5 | 7.17 | 8.44 | 2.25 | 1.07 | 0.24 | 0.64 |
| AS2720 | −4.57 | 7.34 | 8.63 | 2.22 | 1.07 | 0.22 | 0.62 |
| AS290D | −3.64 | 6.78 | 7.69 | 1.93 | 1.47 | 0.28 | 0.59 |
| AS4581 | −3.36 | 6.44 | 7.25 | 1.86 | 1.43 | 0.34 | 0.66 |
| AS6603 | −3.35 | 6.52 | 7.32 | 1.83 | 1.5 | 0.34 | 0.65 |
| AS6606 | −4.82 | 9.02 | 10.23 | 2.38 | 2.15 | 0.22 | 0.44 |
| AS2716 | −3.92 | 6.78 | 7.82 | 2 | 1.25 | 0.28 | 0.65 |
| Average | −4.08 | 7.13 | 8.21 | 2.07 | 1.36 | 0.27 | 0.61 |