Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China
Abstract
1. Introduction
2. Materials and Methods
2.1. Satellite Data
2.2. Supplementary Data
2.2.1. Carbon-Tracker
2.2.2. Elevation
2.2.3. Population Density
2.2.4. Land-Use and NDVI
2.2.5. Meteorological Data
2.3. Model Description
2.3.1. Models Based on Bagging Ensemble Methods
- ●
- Random Forest (RF)
- ●
- Extreme Random Forest (ERT)
2.3.2. Models Based on Boosting Ensemble Methods
- ●
- eXtreme Gradient Boosting (XGBoost)
- ●
- Light Gradient Boosting Machine (LightGBM)
- ●
- Categorical + Boosting (CatBoost)
2.4. Model Evaluation
3. Results and Discussion
3.1. Predictive Performance Evaluation and Important Factors
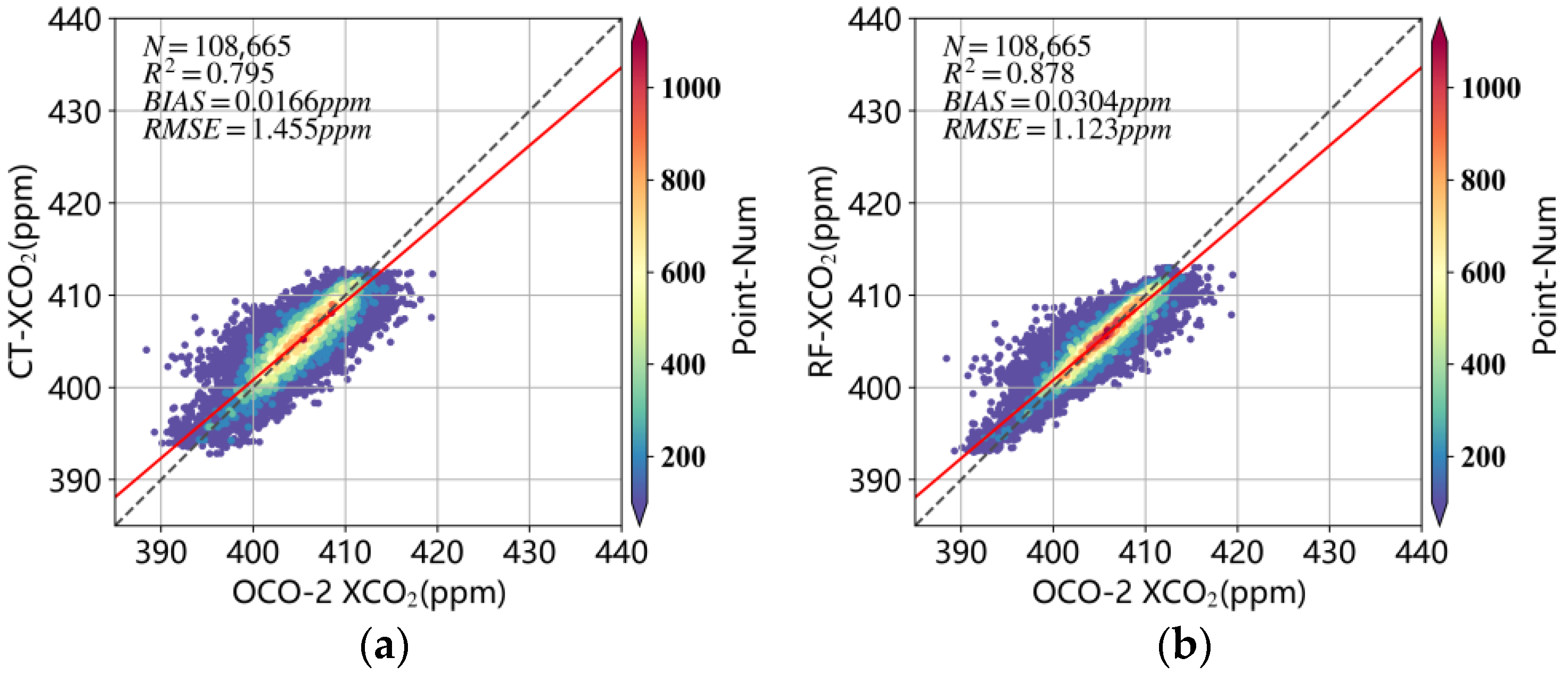
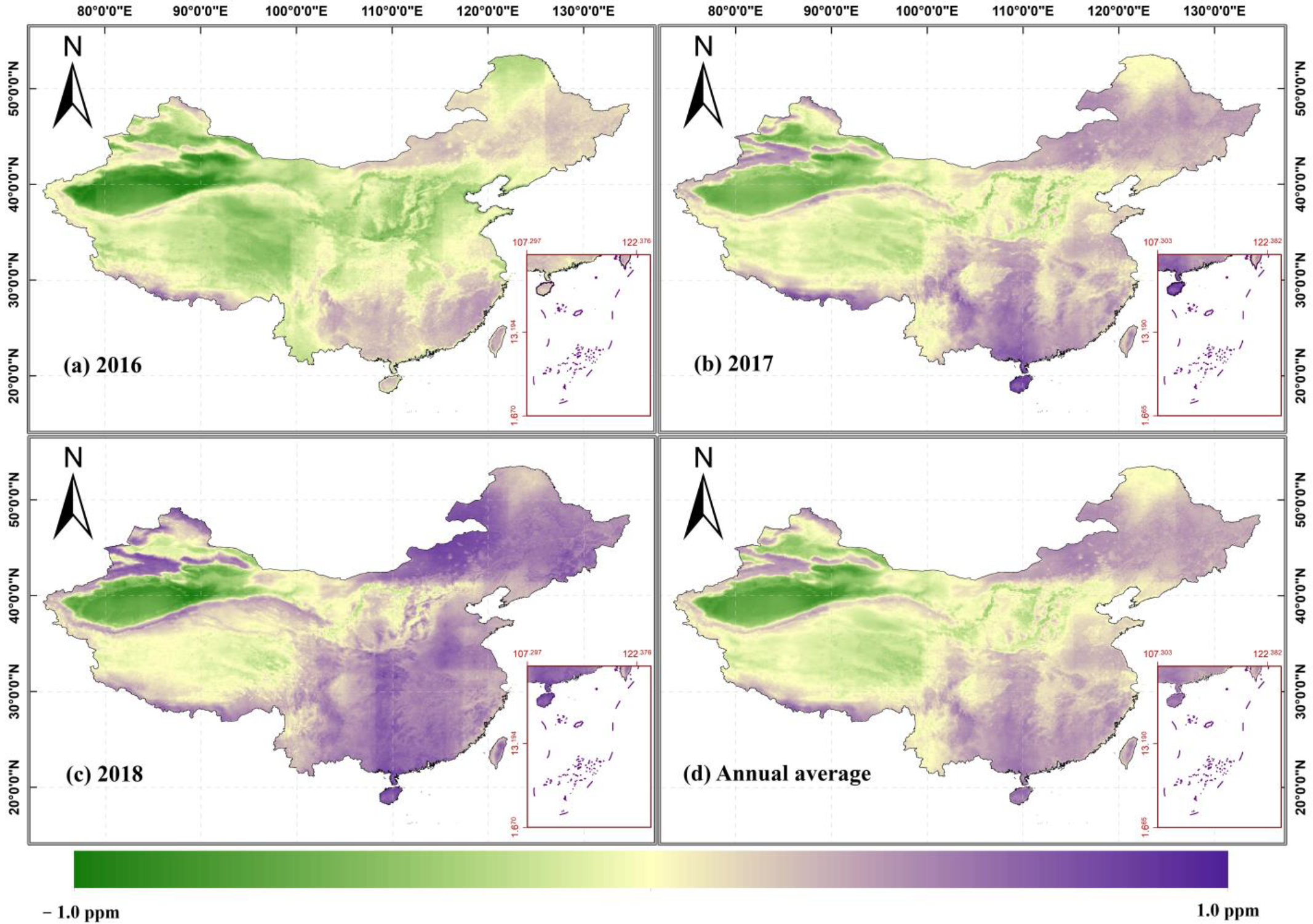
3.2. Comparison of RF XCO2 and CT XCO2
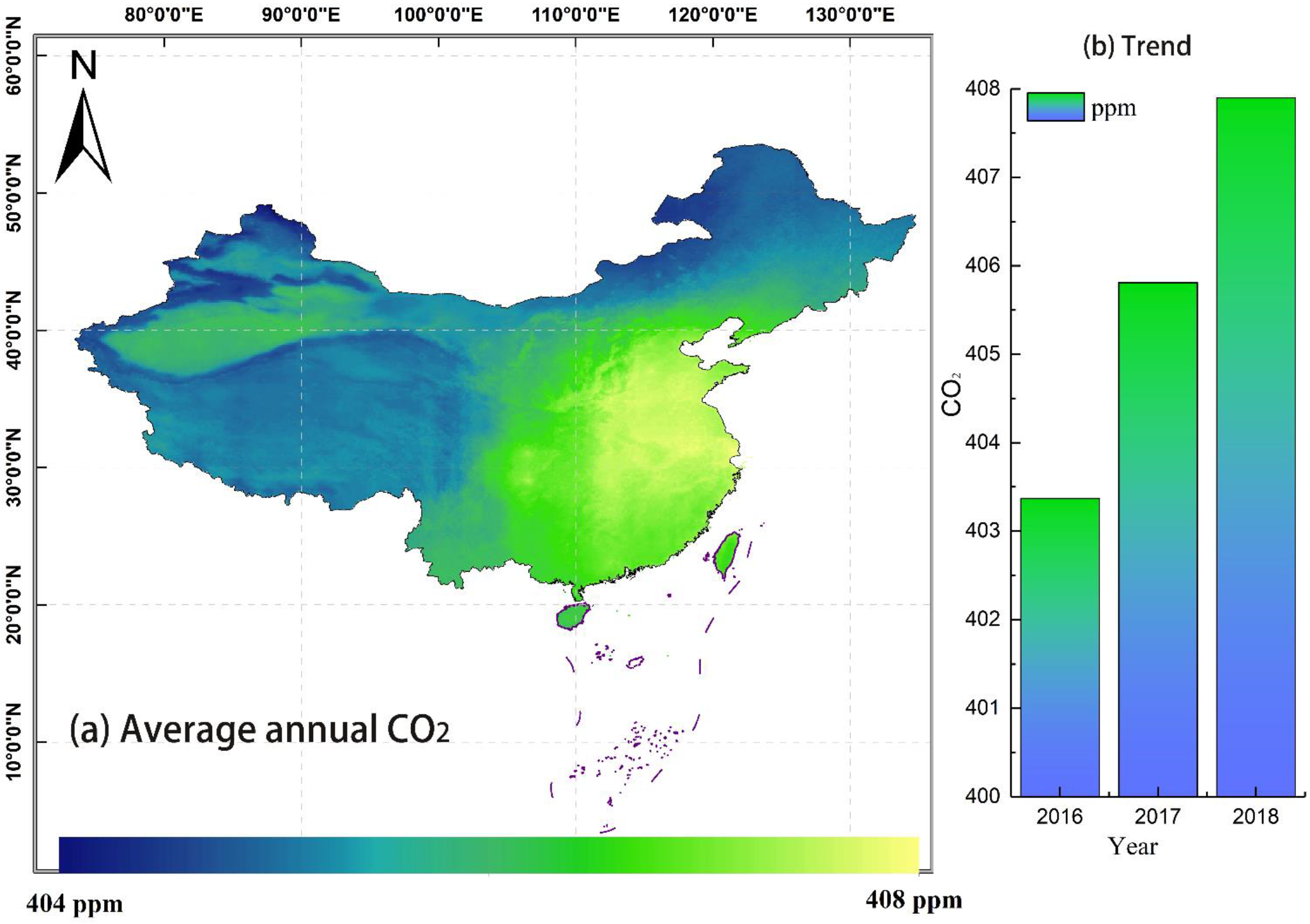
3.3. Spatial Distribution of RF XCO2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge Press: Cambridge, UK, 2021. [Google Scholar]
- Edenhofer, O.; Seyboth, K. Intergovernmental panel on climate change (IPCC). Encycl. Energy Nat. Resour. Environ. Econ. 2013, 26, 48–56. [Google Scholar]
- Hungershoefer, K.; Breon, F.M.; Peylin, P.; Chevallier, F.; Rayner, P.; Klonecki, A.; Houweling, A.; Marshall, J. Evaluation of various observing systems for the global monitoring of CO2 surface fluxes. Atmos. Chem. Phys. 2010, 10, 10503–10520. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Aben, I. Retrievals of atmospheric CO2 from simulated space-borne measurements of backscattered near-infrared sunlight: Accounting for aerosol effects. Appl. Opt. 2009, 48, 3322–3336. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY—Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Zhao, M.; Yue, T.; Zhang, X.; Sun, J.; Jiang, L.; Wang, C. Fusion of multi-source near-surface CO2 concentration data based on high accuracy surface modeling. Atmos. Pollut. Res. 2017, 8, 1170–1178. [Google Scholar]
- Ballav, S.; Naja, M.; Patra, P.K.; Machida, T.; Mukai, H. Assessment of spatio-temporal distribution of CO2 over greater Asia using the WRF–CO2 model. J. Earth Syst. Sci. 2020, 129, 80. [Google Scholar] [CrossRef]
- Andres, R.J.; Boden, T.A.; Bréon, F.M.; Ciais, P.; Davis, S.; Erickson, D.; Gregg, J.S.; Jacobson, A.; Marland, G.; Miller, J.; et al. A synthesis of carbon dioxide emissions from fossil-fuel combustion. Biogeosciences 2012, 9, 1845–1871. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Griffith, D.W.; et al. Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) XCO2measurements with TCCON. Atmos. Meas. Tech. Discuss. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Liang, A.; Gong, W.; Han, G.; Xiang, C. Comparison of Satellite-Observed XCO2 from GOSAT, OCO-2, and Ground-Based TCCON. Remote Sens. 2017, 9, 1033. [Google Scholar] [CrossRef]
- Wu, L.; Meijer, Y.; Sierk, B.; Hasekamp, O.; Butz, A.; Landgraf, J. XCO2 observations using satellite measurements with moderate spectral resolution: Investigation using GOSAT and OCO-2 measurements. Atmos. Meas. Tech. 2020, 13, 713–729. [Google Scholar] [CrossRef]
- Nguyen, H.; Katzfuss, M.; Cressie, N.; Braverman, A. Spatio-temporal data fusion for very large remote sensing datasets. Technometrics 2014, 56, 174–185. [Google Scholar] [CrossRef]
- Tomosada, M.; Kanefuji, K.; Matsumoto, Y.; Tsubaki, H. A Prediction Method of the Global Distribution Map of CO2 Column Abundance Retrieved from GOSAT Observation Derived from Ordinary Kriging. In Proceedings of the ICROS-SICE International Joint Conference 2009, Fukuoka International Congress Center, Fukuoka, Japan, 18–21 August 2009. [Google Scholar]
- Zeng, Z.; Lei, L.; Guo, L.; Zhang, L.; Zhang, B. Incorporating temporal variability to improve geostatistical analysis of satellite-observed CO2 in China. Chin. Sci. Bull. 2013, 58, 1948–1954. [Google Scholar] [CrossRef]
- Hammerling, D.M.; Michalak, A.M.; Kawa, S.R. Mapping of CO2 at high spatiotemporal resolution using satellite observations: Global distributions from OCO-2. J. Geophys. Res. Atmos. 2012, 117, D06306. [Google Scholar] [CrossRef]
- Guo, M.; Wang, X.; Li, J.; Yi, K.; Zhong, G.; Tani, H. Assessment of global carbon dioxide concentration using MODIS and GOSAT data. Sensors 2012, 12, 16368–16389. [Google Scholar] [CrossRef]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial distribution of XCO2 using OCO-2 data in growing seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef]
- Girach, I.A.; Ponmalar, M.; Murugan, S.; Rahman, P.A.; Babu, S.S.; Ramachandran, R. Ramachandran. Applicability of Machine Learning Model to Simulate Atmospheric CO₂ Variability. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4107306. [Google Scholar] [CrossRef]
- He, C.; Ji, M.; Li, T. Deriving Full-Coverage and Fine-Scale XCO2 Across China Based on OCO-2 Satellite Retrievals and CarbonTracker Output. Geophys. Res. Lett. 2022, 49, e2022GL098435. [Google Scholar] [CrossRef]
- Li, J.; Jia, K.; Wei, X.; Xia, M.; Chen, Z.; Yao, Y.; Zhang, X.; Jiang, H.; Yuan, B.; Tao, G.; et al. High-spatiotemporal resolution mapping of spatiotemporally continuous atmospheric CO2 concentrations over the global continent. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102743. [Google Scholar] [CrossRef]
- Wang, W.; He, J.; Feng, H.; Jin, Z. High-Coverage Reconstruction of XCO2 Using Multisource Satellite Remote Sensing Data in Beijing–Tianjin–Hebei Region. Int. J. Environ. Res. Public Health 2022, 19, 10853. [Google Scholar] [CrossRef]
- Zhang, L.; Li, T.; Wu, J. Deriving gapless CO2 concentrations using a geographically weighted neural network: China, 2014–2020. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103063. [Google Scholar] [CrossRef]
- Nassar, R.; Hill, T.G.; McLinden, C.A.; Wunch, D.; Jones, D.B.A.; Crisp, D. Quantifying CO2 emissions from individual power plants from space. Geophys. Res. Lett. 2017, 44, 10045–10053. [Google Scholar] [CrossRef]
- Jacobson, A.R.; Schuldt, K.N.; Miller, J.B.; Oda, T.; Tans, P.; Andrews, A.; Mund, J.; Ott, L.; Collatz, G.J.; Aalto, T.; et al. CarbonTracker CT2019B; NOAA Global Monitoring Laboratory: Boulder, CO, USA, 2020. [Google Scholar]
- Yang, L.; Meng, X.; Zhang, X. SRTM DEM and its application advances. Int. J. Remote Sens. 2011, 32, 3875–3896. [Google Scholar] [CrossRef]
- Tatem, A.J. WorldPop, open data for spatial demography. Sci. Data 2017, 4, 170004. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D. MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2018. [Google Scholar]
- Didan, K. MOD13C1 MODIS/Terra Vegetation Indices 16-Day L3 Global 0.05Deg CMG V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1981 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Brussels, Belgium, 2019. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 569–577. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Lv, Z.; Shi, Y.; Zang, S.; Sun, L. Spatial and Temporal Variations of Atmospheric CO2 Concentration in China and Its Influencing Factors. Atmosphere 2020, 11, 231. [Google Scholar] [CrossRef]
- Falahatkar, S.; Mousavi, S.M.; Farajzadeh, M. Spatial and temporal distribution of carbon dioxide gas using GOSAT data over IRAN. Environ. Monit. Assess. 2017, 189, 627. [Google Scholar] [CrossRef]
- Britter, R.E. Atmospheric Dispersion of Dense Gases. Annu. Rev. Fluid Mech. 1989, 21, 317–344. [Google Scholar] [CrossRef]
- Bie, N.; Lei, L.; He, Z.; Zeng, Z.; Liu, L.; Zhang, B.; Cai, B. Specific patterns of XCO2 observed by GOSAT during 2009–2016 and assessed with model simulations over China. Sci. China Earth Sci. 2020, 63, 384–394. [Google Scholar] [CrossRef]
- Xu, Y.; Ke, C.; Zhan, W.; Li, H.; Yao, L. Variations in satellite-derived carbon dioxide over different regions of China from 2003 to 2011. Atmos. Environ. 2017, 150, 379–388. [Google Scholar] [CrossRef]


| Data Source | Type | Spatial Resolution | Time Resolution |
|---|---|---|---|
| Carbon Tracker | XCO2 | 3° × 2° | 3 h |
| MODIS | NDVI | 0.05° × 0.05° | 8 d |
| Land-Use (LU) | 500 m × 500 m | 1 y | |
| ERA-5 | 2 m temperature (t2m) | 0.25° × 0.25° | 1 h |
| 2 m dewpoint temperature (d2m) | |||
| Surface pressure (sp) | |||
| 10 m v-component of wind (v10) | |||
| 10 m u-component of wind (u10) | |||
| World Pop | Population density (pop) | 1 km × 1 km | 1 y |
| SRTM | DEM | 90 m × 90 m | - |
| Model | Cross-Validation R2 | RMSE (ppm) | MAE (ppm) |
|---|---|---|---|
| RF | 0.878 | 1.123 | 0.867 |
| ERT | 0.845 | 1.261 | 0.931 |
| XGB | 0.841 | 1.279 | 0.952 |
| LGB | 0.832 | 1.312 | 0.981 |
| CatBoost | 0.845 | 1.261 | 0.935 |
| Variable | Importance | Variable | Importance |
|---|---|---|---|
| Longitude | 2.03% | u10 | 0.68% |
| Latitude | 2.23% | v10 | 0.72% |
| CT XCO2 | 83.08% | DEM | 1.51% |
| d2m | 2.72% | pop | 0.81% |
| t2m | 3.12% | LU | 0.2% |
| sp | 1.99% | NDVI | 0.91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Yuan, Y.; Wang, Z.; Luo, L.; Zhang, Z.; Dong, H.; Zhang, C. Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China. Atmosphere 2023, 14, 436. https://doi.org/10.3390/atmos14030436
He S, Yuan Y, Wang Z, Luo L, Zhang Z, Dong H, Zhang C. Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China. Atmosphere. 2023; 14(3):436. https://doi.org/10.3390/atmos14030436
Chicago/Turabian StyleHe, Sicong, Yanbin Yuan, Zihui Wang, Lan Luo, Zili Zhang, Heng Dong, and Chengfang Zhang. 2023. "Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China" Atmosphere 14, no. 3: 436. https://doi.org/10.3390/atmos14030436
APA StyleHe, S., Yuan, Y., Wang, Z., Luo, L., Zhang, Z., Dong, H., & Zhang, C. (2023). Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China. Atmosphere, 14(3), 436. https://doi.org/10.3390/atmos14030436





