Bivariate Hazard Assessment of Combinations of Dry and Wet Conditions between Adjacent Seasons in a Climatic Transition Zone
Abstract
Highlights
- The HRB most frequently suffers from continued dryness followed by transition from dry-ness to wetness.
- Dryness–wetness combinations generally occur more frequent under climate change.
- Frequency of prolonged dryness/wetness escalates more rapidly than abrupt transition events.
- The spatial and temporal preference of inter-seasonal dryness–wetness combinations are elucidated.
- Bivariate hazard assessment of dryness–wetness combinations enriches water-related hazard atlas and facilitates more integrated mitigation planning.
Abstract
1. Introduction
2. Study Area and Data
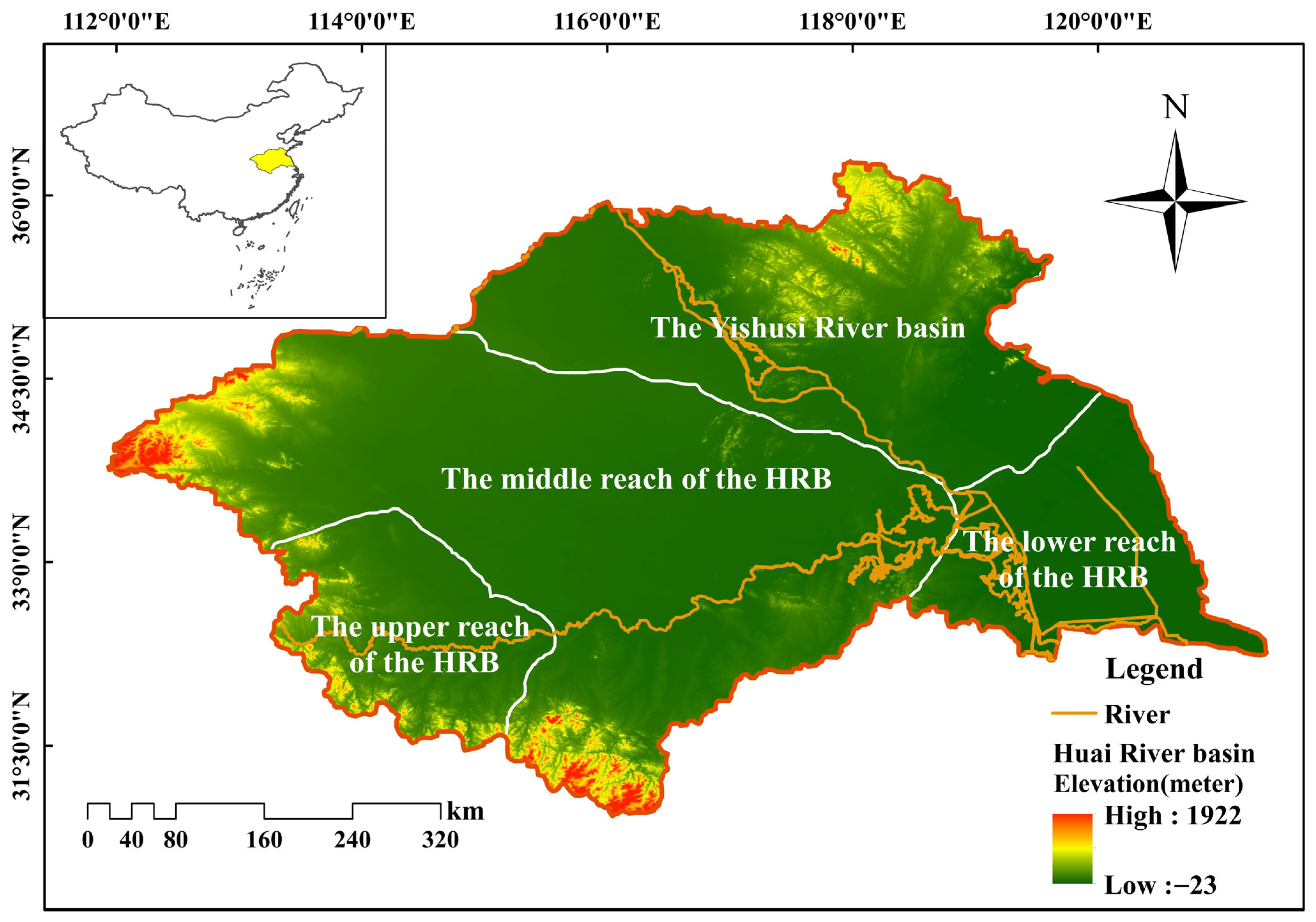
2.1. An Overview of the HRB
2.2. Data Description
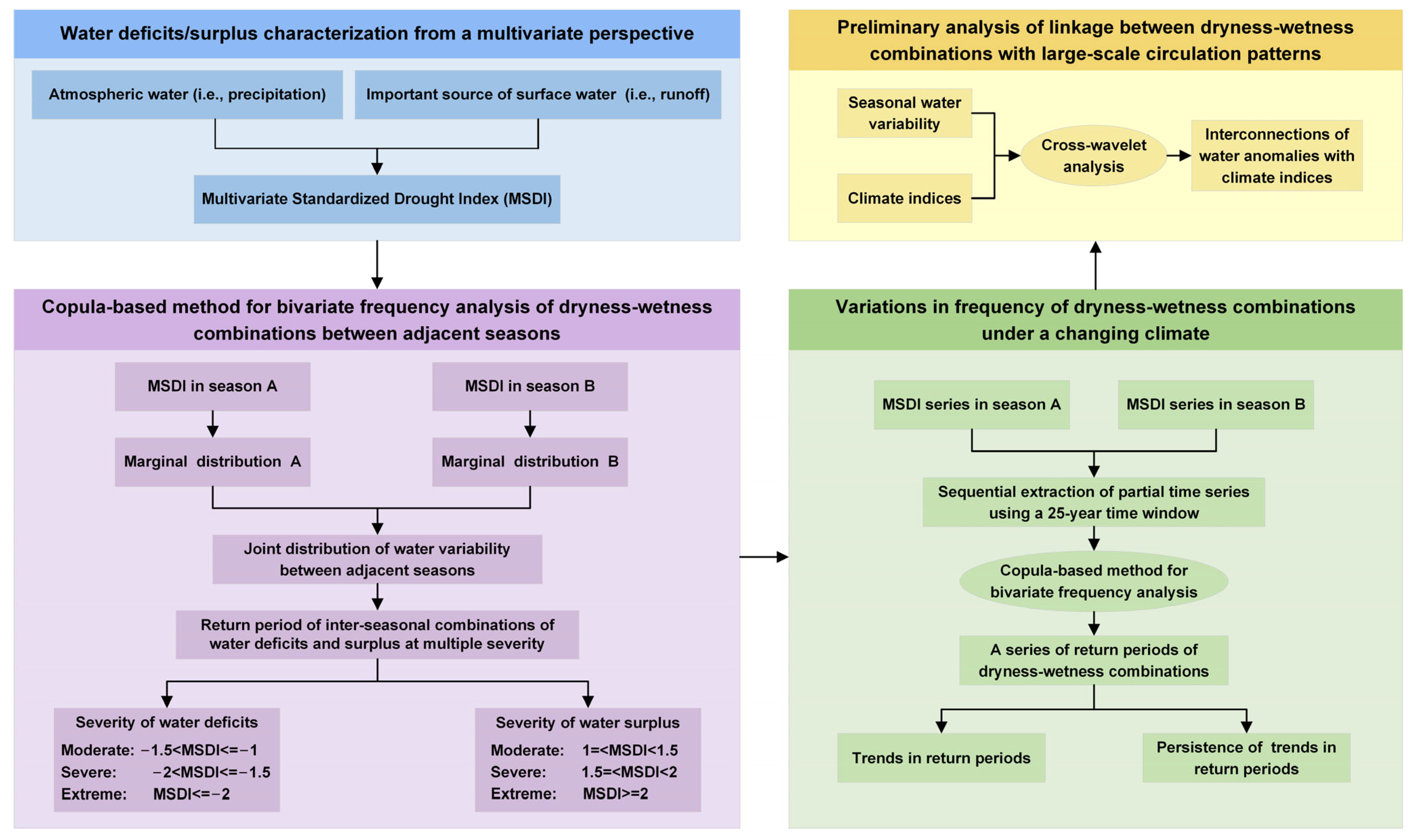
3. Method Description
3.1. Multivariate Standardized Drought Index (MSDI)
3.2. Mann–Kendall (MK) Trend Analysis
3.3. Copula-Based Method for Hazard Assessment of Dryness–Wetness Combinations
3.3.1. Marginal Distribution
3.3.2. Copula Functions for Deriving the Joint Distribution
3.3.3. Joint Return Period
3.4. Rescaled Range (R/S) Analysis
3.5. Wavelet Analysis
4. Results
4.1. An Overview of Water Variability in the HRB
4.2. Frequency Analysis of Inter-Seasonal Combinations of Dry and Wet Conditions in the HRB
4.2.1. The Selection of Suitable Marginal Distributions
4.2.2. The Determination of Appropriate Copulas
4.2.3. Return Periods of Dryness–Wetness Combinations between Adjacent Seasons in the HRB
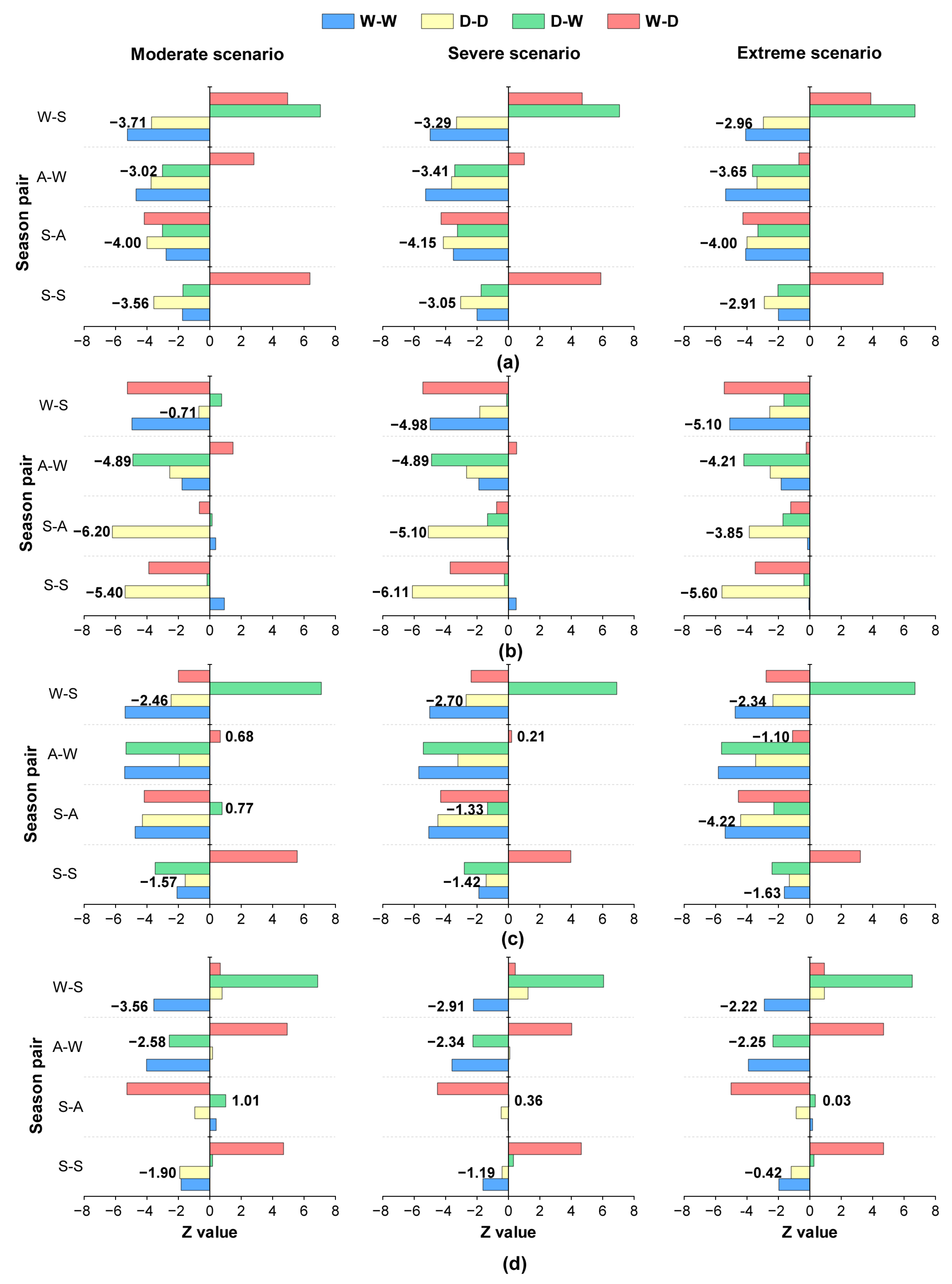
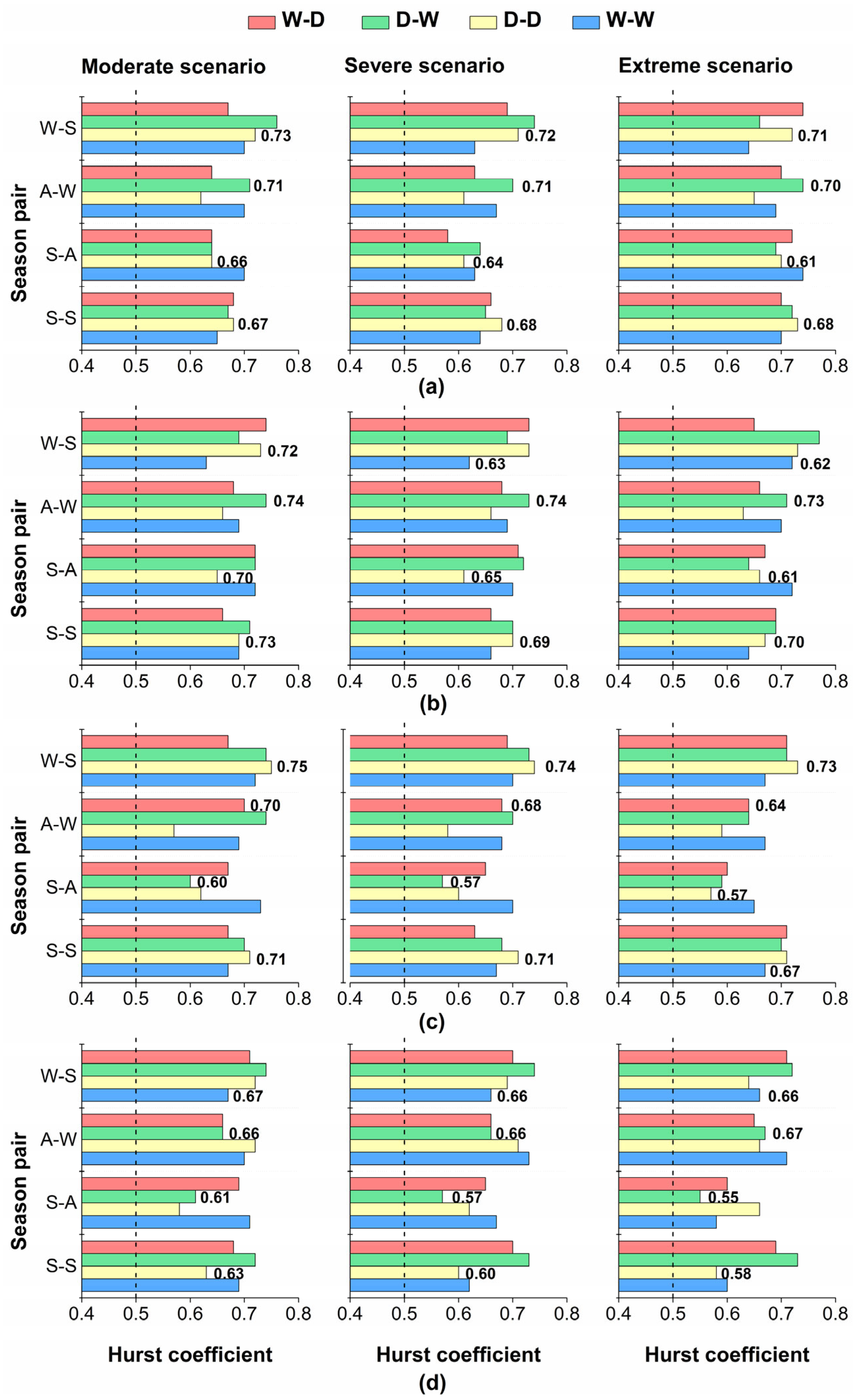
4.3. Temporal Evolution of Frequency of Dryness–Wetness Combinations under Climate Change
4.4. Linkages of Climate Indices with Dry and Wet Conditions in the HRB
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eini, M.; Kaboli, H.S.; Rashidian, M.; Hedayat, H. Hazard and vulnerability in urban flood risk mapping: Machine learning techniques and considering the role of urban districts. Int. J. Disaster Risk Reduct. 2020, 50, 101687. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef]
- Nauditt, A.; Stahl, K.; Rodríguez, E.; Birkel, C.; Formiga-Johnsson, R.M.; Kallio, M.; Ribbe, L.; Baez-Villanueva, O.M.; Thurner, J.; Hann, H. Evaluating tropical drought risk by combining open access gridded vulnerability and hazard data products. Sci. Total Environ. 2022, 822, 153493. [Google Scholar] [CrossRef] [PubMed]
- Niu, J.; Kang, S.; Zhang, X.; Fu, J. Vulnerability analysis based on drought and vegetation dynamics. Ecol. Indic. 2019, 105, 329–336. [Google Scholar] [CrossRef]
- Hu, W.; She, D.; Xia, J.; He, B.; Hu, C. Dominant patterns of dryness/wetness variability in the Huang-Huai-Hai River Basin and its relationship with multiscale climate oscillations. Atmos. Res. 2021, 247, 105148. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Zhang, D.; Ye, X. Investigation of the drought–flood abrupt alternation of streamflow in Poyang Lake catchment during the last 50 years. Hydrol. Res. 2017, 48, 1402–1417. [Google Scholar] [CrossRef]
- Yan, D.-H.; Han, D.-M.; Wang, G.; Yuan, Y.; Hu, Y.; Fang, H.-Y. The evolution analysis of flood and drought in Huai River Basin of China based on monthly precipitation characteristics. Nat. Hazards 2014, 73, 849–858. [Google Scholar] [CrossRef]
- Banner, J.L.; Jackson, C.S.; Yang, Z.L.; Hayhoe, K.; Woodhouse, C.; Gulden, L.; Jacobs, K.; North, G.; Leung, R.; Washington, W.; et al. Climate change impacts on Texas water a white paper assessment of the past, present and future and recommendations for action. Tex. Water J. 2015, 1, 1–19. [Google Scholar]
- Moorhead, J.E.; Gowda, P.H.; Singh, V.P.; Porter, D.O.; Marek, T.H.; Howell, T.A.; Stewart, B. Identifying and Evaluating a Suitable Index for Agricultural Drought Monitoring in the Texas High Plains. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 807–820. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Wang, G.; Wang, J.; Ju, Q.; Yang, C.; Fan, C. Impact of climate change on hydrological extremes in the Yangtze River Basin, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 693–707. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Multi-model ensemble analysis of runoff extremes for climate change impact assessments. J. Hydrol. 2015, 525, 352–361. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.J.; Piao, S.L.; Lü, Y.H.; Ciais, P.; Feng, X.M.; Wang, Y.F. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2015, 9, 38–41. [Google Scholar] [CrossRef]
- Yang, S.; Wu, B.; Zhang, R.; Zhou, S. Relationship between an abrupt drought-flood transition over mid-low reaches of the Yangtze River in 2011 and the intraseasonal oscillation over mid-high latitudes of East Asia. J. Meteorol. Res. 2013, 27, 129–143. [Google Scholar] [CrossRef]
- Ye, J.; He, Y.; Pappenberger, F.; Cloke, H.L.; Manful, D.Y.; Li, Z. Evaluation of ECMWF medium-range ensemble forecasts of precipitation for river basins. Q. J. R. Meteorol. Soc. 2014, 140, 1615–1628. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Garcia, C.; Morán-Tejeda, E. Groundwater level responses to precipitation variability in Mediterranean insular aquifers. J. Hydrol. 2017, 552, 516–531. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Leng, G.; Chang, J. A Hybrid Index for Characterizing Drought Based on a Nonparametric Kernel Estimator. J. Appl. Meteorol. Clim. 2016, 55, 1377–1389. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Fan, J.; Xu, F.; Sun, X.; Dong, W.; Ma, X.; Liu, G.; Cheng, Y.; Wang, H. Construction and Application of Hydrometeorological Comprehensive Drought Index in Weihe River. Atmosphere 2022, 13, 610. [Google Scholar] [CrossRef]
- Farahmand, A.; AghaKouchak, A. A generalized framework for deriving nonparametric standardized drought indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Ren, L.; Yong, B.; Singh, V.P.; Yuan, F.; Jiang, S.; Yang, X. On the mechanisms of two composite methods for construction of multivariate drought indices. Sci. Total. Environ. 2019, 647, 981–991. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. A Nonparametric Multivariate Multi-Index Drought Monitoring Framework. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, G.; Baetz, B.; Li, Y.; Huang, K. Development of a Copula-based Particle Filter (CopPF) Approach for Hydrologic Data Assimilation under Consideration of Parameter Interdependence. Water Resour. Res. 2007, 53, 4850–4875. [Google Scholar] [CrossRef]
- Prairie, J.; Rajagopalan, B.; Lall, U.; Fulp, T. A stochastic nonparametric technique for space-time disaggregation of streamflows. Water Resour. Res. 2007, 43, W03432. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhou, X.; Huang, G.; Wang, X.; Fan, Y.; Cheng, G. A coupled dynamical-copula downscaling approach for temperature projections over the Canadian Prairies. Clim. Dyn. 2017, 51, 2413–2431. [Google Scholar] [CrossRef]
- Lai, C.D.; Balakrishnan, N. Continuous Bivariate Distributions; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G. Copula-based identification of the non-stationarity of the relation between runoff and sediment load. Int. J. Sediment Res. 2017, 32, 221–230. [Google Scholar] [CrossRef]
- Li, J.; Lei, Y.; Tan, S.; Bell, C.D.; Engel, B.A.; Wang, Y. Nonstationary Flood Frequency Analysis for Annual Flood Peak and Volume Series in Both Univariate and Bivariate Domain. Water Resour. Manag. 2018, 32, 4239–4252. [Google Scholar] [CrossRef]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2015, 29, 225–238. [Google Scholar] [CrossRef]
- Zong, H.; Bueh, C.; Chen, L.; Ji, L.; Wei, J. A Typical Mode of Seasonal Circulation Transition: A Climatic View of the Abrupt Transition from Drought to Flood over the Middle and Lower Reaches of the Yangtze River Valley in the Late Spring and Early Summer of 2011. Atmos. Ocean. Sci. Lett. 2012, 5, 349–354. [Google Scholar]
- Wu, Z.; Li, J.; He, J.; Jiang, Z. Large-scale atmospheric singularities and summer long-cycle droughts-floods abrupt alternation in the middle and lower reaches of the Yangtze River. Chin. Sci. Bull. 2006, 51, 2027–2034. [Google Scholar] [CrossRef]
- Nan, S.; Li, J. The relationship between the summer precipitation in the Yangtze River valley and the boreal spring Southern Hemisphere annular mode. Geophys. Res. Lett. 2003, 30, 2262. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Najibi, N.; Devineni, N.; Lu, M. Hydroclimate drivers and atmospheric teleconnections of long duration floods: An application to large reservoirs in the Missouri River Basin. Adv. Water Resour. 2017, 100, 153–167. [Google Scholar] [CrossRef]
- Li, J.Z.; Wang, Y.X.; Li, S.F.; Hu, R. A Nonstationary Standardized Precipitation Index incorporating climate indices as covariates. J. Geophys. Res. Atmos. 2015, 120, 12–082. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, J.; Kang, S.; Zhang, X. Effects of irrigation on water and energy balances in the Heihe River basin using VIC model under different irrigation scenarios. Sci. Total Environ. 2018, 645, 1183–1193. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, L.; Hong, Y.; Zhu, Y.; Yang, X.; Yuan, F.; Jiang, S. Sensitivity analysis of standardization procedures in drought indices to varied input data selections. J. Hydrol. 2016, 538, 817–830. [Google Scholar] [CrossRef]
- Rad, A.M.; Ghahraman, B.; Khalili, D.; Ghahremani, Z.; Ardakani, S.A. Integrated meteorological and hydrological drought model: A management tool for proactive water resources planning of semi-arid regions. Adv. Water Resour. 2017, 107, 336–353. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Kisi, O.; Ay, M. Comparison of Mann–Kendall and innovative trend method for water quality parameters of the Kizilirmak River, Turkey. J. Hydrol. 2014, 513, 362–375. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Evaluating the effect of persistence on long-term trends and analyzing step changes in streamflows of the continental United States. J. Hydrol. 2014, 517, 36–53. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Cherubini, U.; Gobbi, F.; Mulinacci, S.; Romagnoli, S. Dynamic Copula Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Emura, T.; Matsui, S.; Rondeau, V. Survival Analysis with Correlated Endpoints: Joint Frailty-Copula Models; Springer: Singapore, 2019. [Google Scholar]
- Durante, F.; Fernández-Sánchez, J.; Sempi, C. Sklar’s theorem obtained via regularization techniques. Nonlinear Anal. Theory Methods Appl. 2012, 75, 769–774. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Genest, C.; Favre, A.-C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Chamoli, A.; Bansal, A.R.; Dimri, V. Wavelet and rescaled range approach for the Hurst coefficient for short and long time series. Comput. Geosci. 2007, 33, 83–93. [Google Scholar] [CrossRef]
- Robinson, P.M. Gaussian Semiparametric Estimation of Long Range Dependence. Ann. Stat. 1995, 23, 1630–1661. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Matos, J.O.; de Moura, E.P.; Krüger, S.E.; Rebello, J.A. Rescaled range analysis and detrended fluctuation analysis study of cast irons ultrasonic backscattered signals. Chaos Solitons Fractals 2004, 19, 55–60. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- He, Y.; Ye, J.; Yang, X. Analysis of the spatio-temporal patterns of dry and wet conditions in the Huai River Basin using the standardized precipitation index. Atmos. Res. 2015, 166, 120–128. [Google Scholar] [CrossRef]
- Genest, C.; Quessy, J.-F.; Remillard, B. Goodness-of-fit Procedures for Copula Models Based on the Probability Integral Transformation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Day, J.A.; Fung, I.; Liu, W. Changing character of rainfall in eastern China, 1951–2007. Proc. Natl. Acad. Sci. USA 2018, 115, 2016–2021. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, H.; Zhang, R.; Qian, W.; Luo, Z. Comparison of Rainfall Characteristics and Convective Properties of Monsoon Precipitation Systems over South China and the Yangtze and Huai River Basin. J. Clim. 2013, 26, 110–132. [Google Scholar] [CrossRef]


| Categorization | MSDI Thresholds | Occurrence Probability |
|---|---|---|
| Extremely wet | MSDI ≥ 2 | 2.3% |
| Severely wet | 1.5 ≤ MSDI < 2 | 4.4% |
| Moderately wet | 1 ≤ MSDI < 1.5 | 9.2% |
| Nearly normal | −1 < MSDI < 1 | 68.2% |
| Moderately dry | −1.5 < MSDI ≤ −1 | 9.2% |
| Severely dry | −2 < MSDI ≤ −1.5 | 4.4% |
| Extremely dry | MSDI ≤ −2 | 2.3% |
| Name | Expression | Parameter Range | Generator | Kendall’s Tau |
|---|---|---|---|---|
| Gaussian | / | |||
| Frank | ||||
| Gumbel | ||||
| Clayton |
| Type of Dryness–Wetness Combinations | Moderate Scenario | Severe Scenario | Extreme Scenario |
|---|---|---|---|
| The continued dryness | |||
| The continued wetness | |||
| The transition from dryness to wetness | |||
| The transition from wetness to dryness |
| Sub-Basin | Season | Normal | Logistic | GEV | Stable | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | P | RMSE | AIC | H | P | RMSE | AIC | H | P | RMSE | AIC | H | P | RMSE | AIC | ||
| The upper reach of the HRB | Sp | 0 | 0.99 | 0.01 | −484.29 | 0 | 0.96 | 0.02 | −450.48 | 0 | 1.00 | 0.01 | −492.98 | 0 | 0.99 | 0.01 | −480.31 |
| Su | 0 | 0.98 | 0.02 | −462.82 | 0 | 0.99 | 0.02 | −464.64 | 0 | 1.00 | 0.02 | −470.09 | 0 | 0.98 | 0.02 | −458.77 | |
| A | 0 | 0.92 | 0.02 | −464.88 | 0 | 0.99 | 0.02 | −458.25 | 0 | 0.82 | 0.02 | −450.81 | 0 | 0.92 | 0.02 | −460.86 | |
| W | 0 | 1.00 | 0.02 | −475.51 | 0 | 0.98 | 0.02 | −456.84 | 0 | 1.00 | 0.02 | −472.57 | 0 | 1.00 | 0.02 | −471.51 | |
| The Yishusi River basin | Sp | 0 | 0.87 | 0.02 | −437.00 | 0 | 0.81 | 0.03 | −414.88 | 0 | 0.95 | 0.02 | −450.43 | 0 | 0.87 | 0.02 | −433.02 |
| Su | 0 | 1.00 | 0.02 | −466.38 | 0 | 0.99 | 0.02 | −438.35 | 0 | 1.00 | 0.02 | −476.90 | 0 | 1.00 | 0.02 | −462.39 | |
| A | 0 | 1.00 | 0.02 | −465.80 | 0 | 0.99 | 0.02 | −453.86 | 0 | 0.99 | 0.02 | −457.26 | 0 | 1.00 | 0.02 | −461.81 | |
| W | 0 | 1.00 | 0.02 | −457.57 | 0 | 0.99 | 0.02 | −436.69 | 0 | 1.00 | 0.02 | −460.51 | 0 | 1.00 | 0.02 | −453.57 | |
| The middle reach of the HRB | Sp | 0 | 0.94 | 0.02 | −448.92 | 0 | 0.98 | 0.02 | −451.66 | 0 | 0.96 | 0.02 | −448.68 | 0 | 0.94 | 0.02 | −444.92 |
| Su | 0 | 1.00 | 0.02 | −454.72 | 0 | 1.00 | 0.02 | −456.96 | 0 | 1.00 | 0.02 | −448.95 | 0 | 1.00 | 0.02 | −450.73 | |
| A | 0 | 1.00 | 0.01 | −499.75 | 0 | 1.00 | 0.01 | −487.98 | 0 | 1.00 | 0.02 | −475.42 | 0 | 1.00 | 0.01 | −495.76 | |
| W | 0 | 1.00 | 0.01 | −490.26 | 0 | 1.00 | 0.02 | −477.54 | 0 | 1.00 | 0.01 | −499.12 | 0 | 1.00 | 0.01 | −486.28 | |
| The lower reach of the HRB | Sp | 0 | 1.00 | 0.02 | −479.21 | 0 | 0.99 | 0.02 | −452.71 | 0 | 1.00 | 0.02 | −480.53 | 0 | 1.00 | 0.02 | −475.19 |
| Su | 0 | 1.00 | 0.02 | −477.11 | 0 | 0.98 | 0.02 | −448.49 | 0 | 0.99 | 0.02 | −466.89 | 0 | 1.00 | 0.02 | −473.11 | |
| A | 0 | 1.00 | 0.01 | −494.16 | 0 | 0.99 | 0.02 | −457.46 | 0 | 1.00 | 0.01 | −496.56 | 0 | 1.00 | 0.01 | −490.15 | |
| W | 0 | 1.00 | 0.01 | −529.31 | 0 | 1.00 | 0.01 | −488.33 | 0 | 1.00 | 0.01 | −518.05 | 0 | 1.00 | 0.01 | −525.32 | |
| Sub-Basin | S–S | S–A | A–W | W–S |
|---|---|---|---|---|
| The upper reach of HRB | 0.31 | 0.24 | −0.35 | 0.46 |
| The Yishusi River basin | 0.26 | 0.27 | −0.39 | 0.49 |
| The middle reach of HRB | 0.22 | −0.23 | −0.50 | 0.37 |
| The lower reach of HRB | 0.26 | −0.30 | −0.38 | 0.35 |
| Sub-Basin | Adjacent Seasons | Gaussian | Clayton | Gumbel | Frank | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sn | p-Value | AIC | Sn | p-Value | AIC | Sn | p-Value | AIC | Sn | p-Value | AIC | ||
| The upper reach of the HRB | S–S | 0.08 | 0.74 | 1.44 | 0.08 | 0.67 | 1.54 | 0.08 | 0.70 | 1.84 | 0.08 | 0.61 | 1.67 |
| S–A | 0.08 | 0.72 | 1.96 | 0.09 | 0.48 | 1.99 | 0.09 | 0.70 | 2.00 | 0.09 | 0.60 | 2.00 | |
| A–W | 0.10 | 0.55 | 1.42 | / | / | / | / | / | / | 0.09 | 0.65 | 1.12 | |
| W–S | 0.19 | 0.15 | 0.85 | 0.22 | 0.03 | 1.67 | 0.18 | 0.17 | 1.36 | 0.09 | 0.48 | −1.77 | |
| The Yishusi River basin | S–S | 0.12 | 0.36 | 1.90 | / | / | / | / | / | / | 0.09 | 0.63 | 2.00 |
| S–A | 0.09 | 0.64 | 1.83 | 0.09 | 0.72 | 1.90 | 0.11 | 0.57 | 2.00 | 0.10 | 0.49 | 1.96 | |
| A–W | 0.21 | 0.25 | −1.33 | / | / | / | / | / | / | 0.25 | 0.08 | −3.23 | |
| W–S | 0.09 | 0.59 | 1.63 | 0.08 | 0.64 | 1.77 | 0.06 | 0.86 | −0.34 | 0.06 | 0.81 | 0.79 | |
| The middle reach of the HRB | S–S | 0.09 | 0.62 | 1.58 | 0.09 | 0.50 | 1.89 | 0.10 | 0.58 | 1.20 | 0.10 | 0.49 | 1.88 |
| S–A | 0.15 | 0.25 | 1.97 | / | / | / | / | / | / | 0.14 | 0.31 | 1.78 | |
| A–W | 0.15 | 0.43 | 0.44 | / | / | / | / | / | / | 0.15 | 0.29 | 0.06 | |
| W–S | 0.09 | 0.61 | −0.60 | 0.13 | 0.24 | 0.83 | 0.09 | 0.54 | −0.23 | 0.06 | 0.80 | −3.22 | |
| The lower reach of the HRB | S–S | 0.13 | 0.36 | 1.28 | 0.10 | 0.44 | 1.36 | 0.12 | 0.34 | 1.36 | 0.13 | 0.29 | 1.96 |
| S–A | 0.11 | 0.52 | 1.72 | / | / | / | / | / | / | 0.12 | 0.41 | 1.62 | |
| A–W | 0.08 | 0.78 | −0.96 | / | / | / | / | / | / | 0.06 | 0.93 | 0.36 | |
| W–S | 0.08 | 0.72 | 0.97 | 0.06 | 0.88 | 0.15 | 0.08 | 0.64 | −1.42 | 0.09 | 0.56 | 1.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, G.; Liu, T.; Wang, S.; Bao, L.; Fang, W.; Shang, J. Bivariate Hazard Assessment of Combinations of Dry and Wet Conditions between Adjacent Seasons in a Climatic Transition Zone. Atmosphere 2023, 14, 437. https://doi.org/10.3390/atmos14030437
Cheng G, Liu T, Wang S, Bao L, Fang W, Shang J. Bivariate Hazard Assessment of Combinations of Dry and Wet Conditions between Adjacent Seasons in a Climatic Transition Zone. Atmosphere. 2023; 14(3):437. https://doi.org/10.3390/atmos14030437
Chicago/Turabian StyleCheng, Geer, Tiejun Liu, Sinan Wang, Ligao Bao, Wei Fang, and Jianan Shang. 2023. "Bivariate Hazard Assessment of Combinations of Dry and Wet Conditions between Adjacent Seasons in a Climatic Transition Zone" Atmosphere 14, no. 3: 437. https://doi.org/10.3390/atmos14030437
APA StyleCheng, G., Liu, T., Wang, S., Bao, L., Fang, W., & Shang, J. (2023). Bivariate Hazard Assessment of Combinations of Dry and Wet Conditions between Adjacent Seasons in a Climatic Transition Zone. Atmosphere, 14(3), 437. https://doi.org/10.3390/atmos14030437





