Quasi-Synchronous Variations in the OLR of NOAA and Ionospheric Ne of CSES of Three Earthquakes in Xinjiang, January 2020
Abstract
:1. Introduction
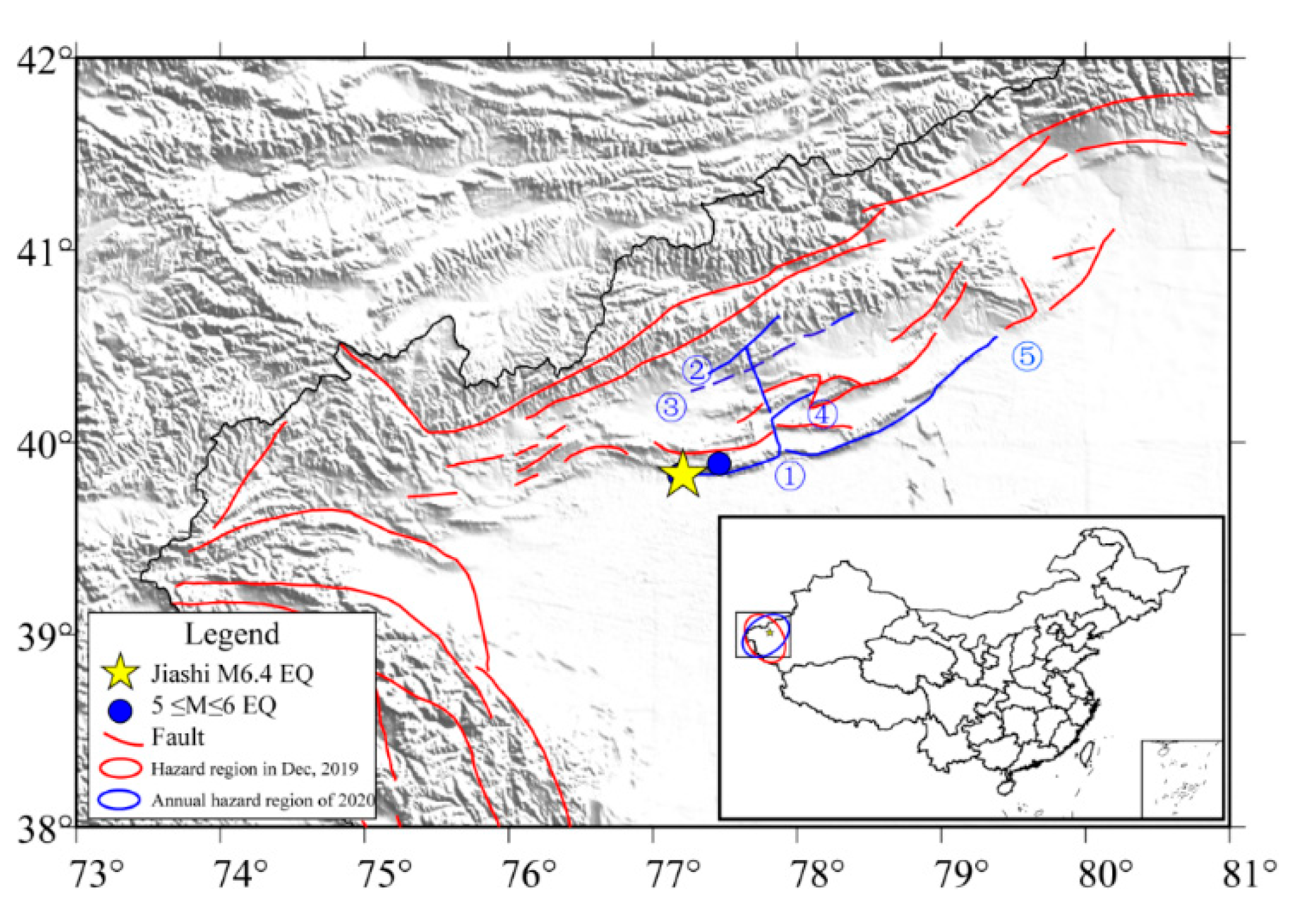
2. Tectonic Environment of Jiashi Earthquake
3. Data and Method
3.1. Data Selection
3.2. Method
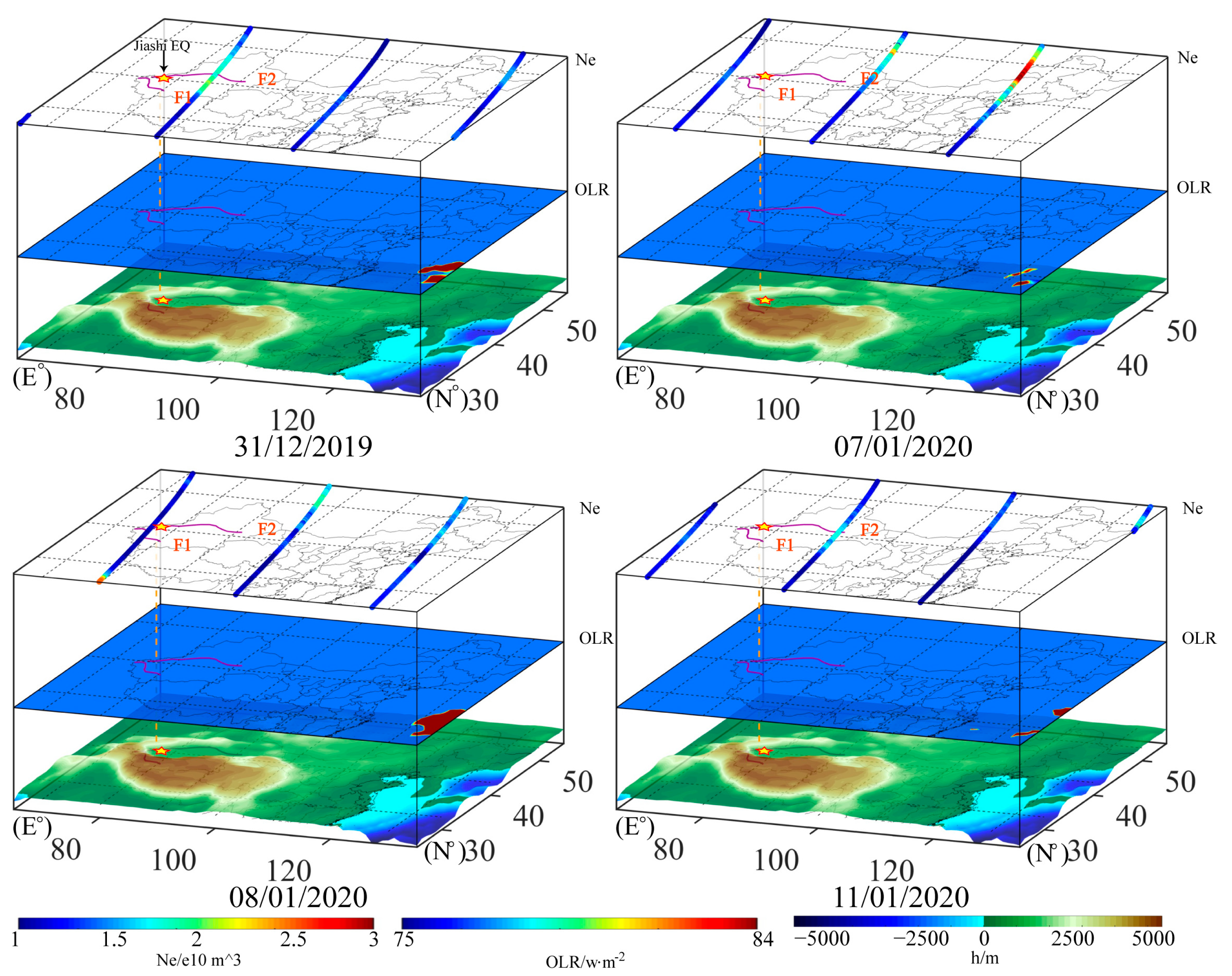
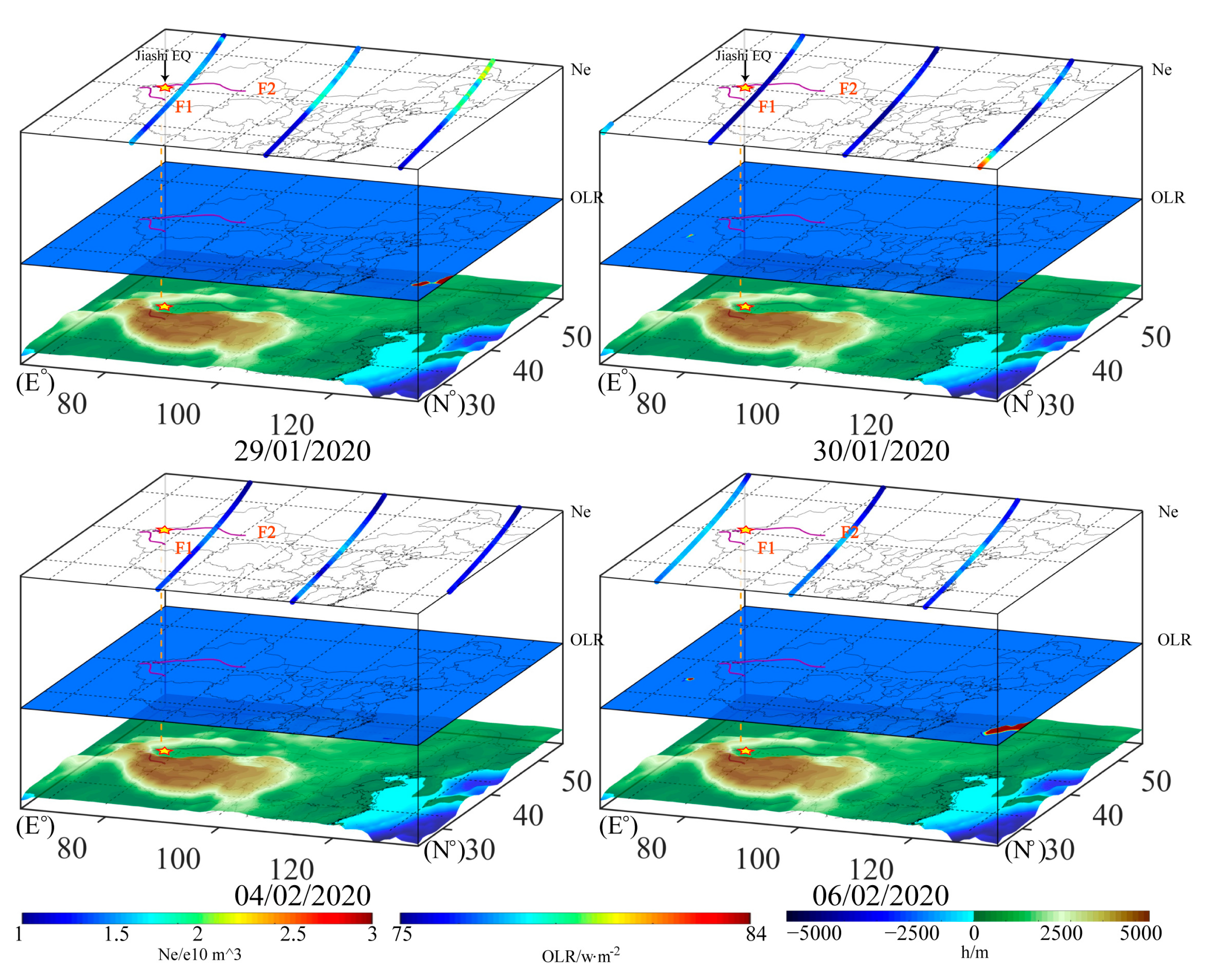
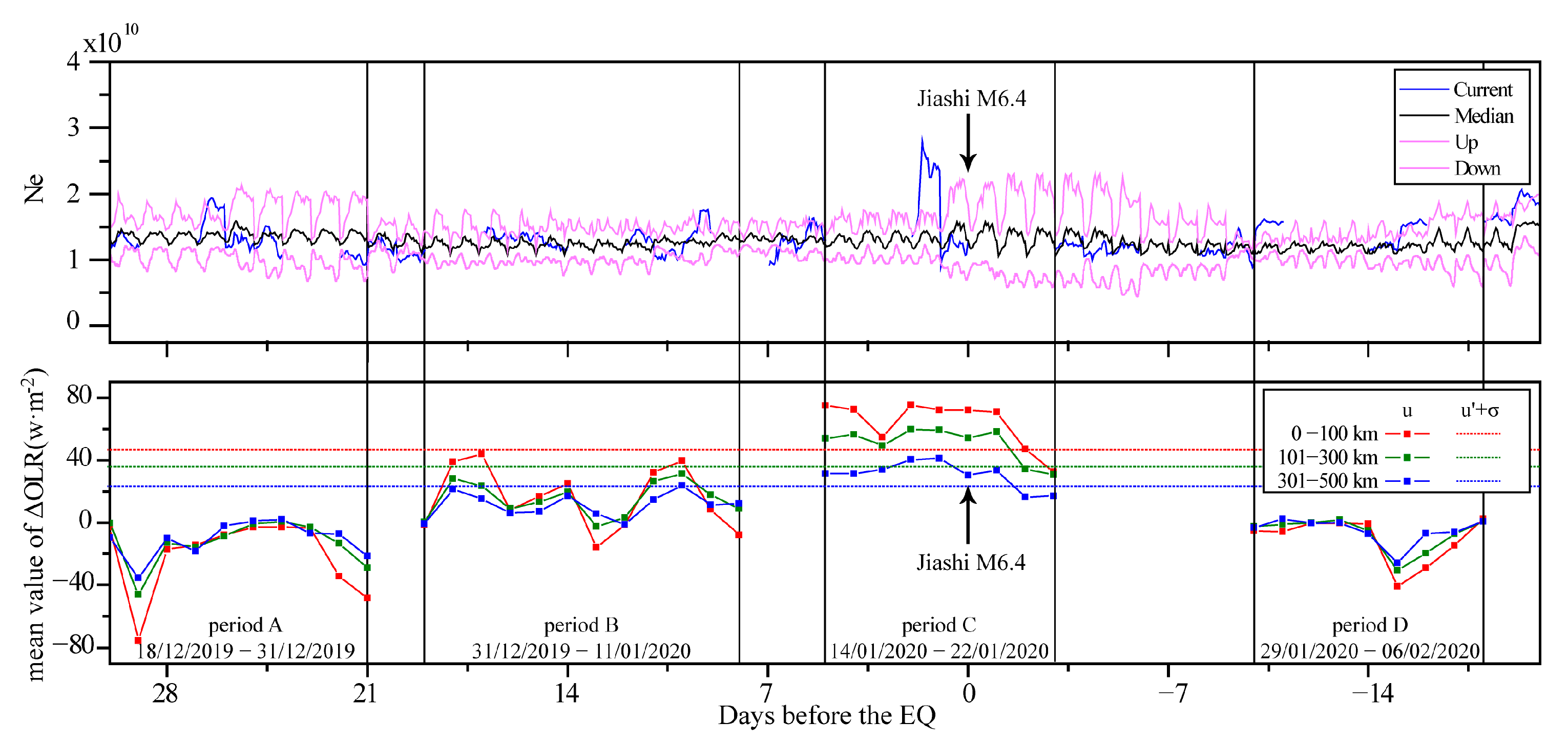
4. Results
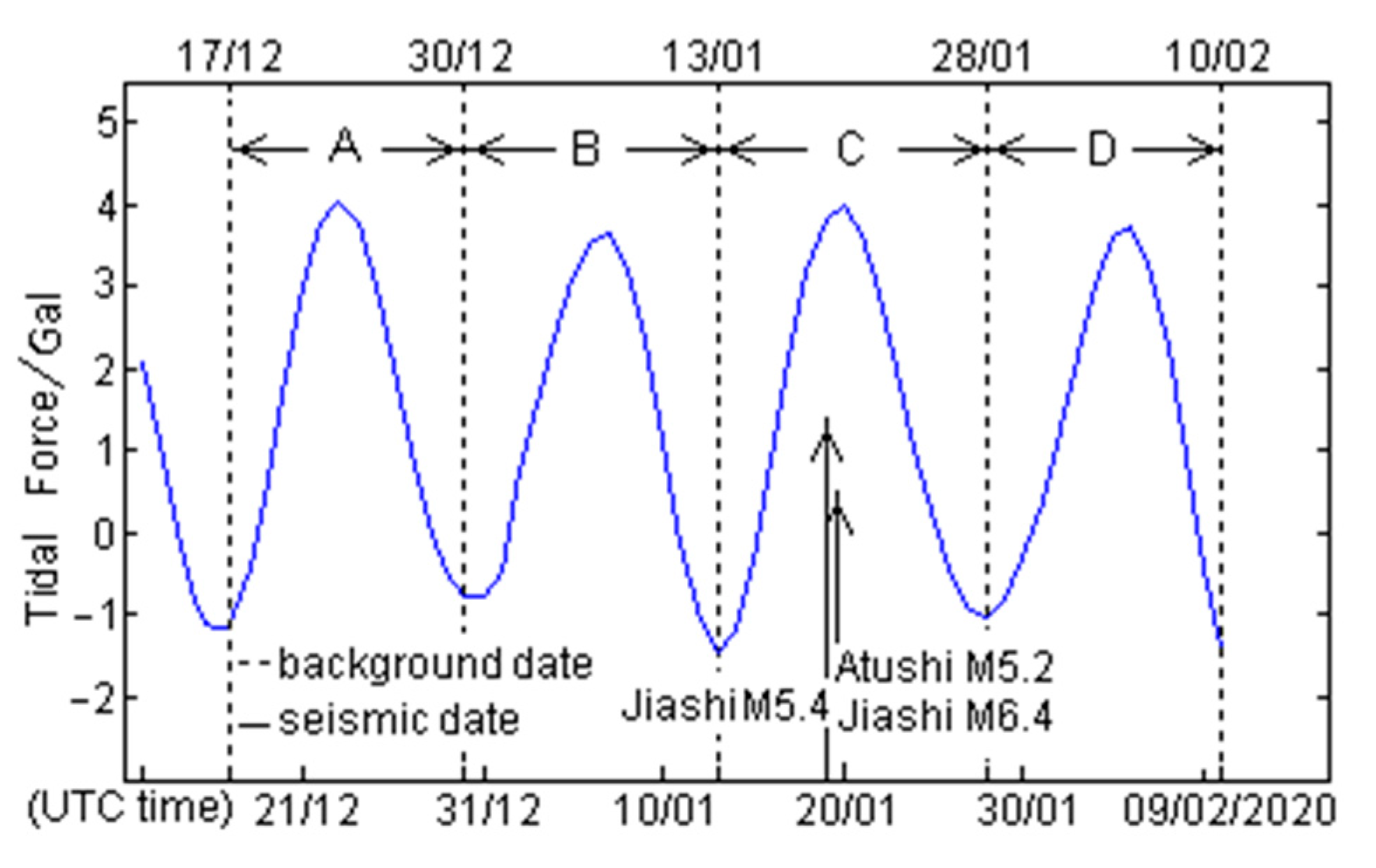
4.1. Tidal Force Change
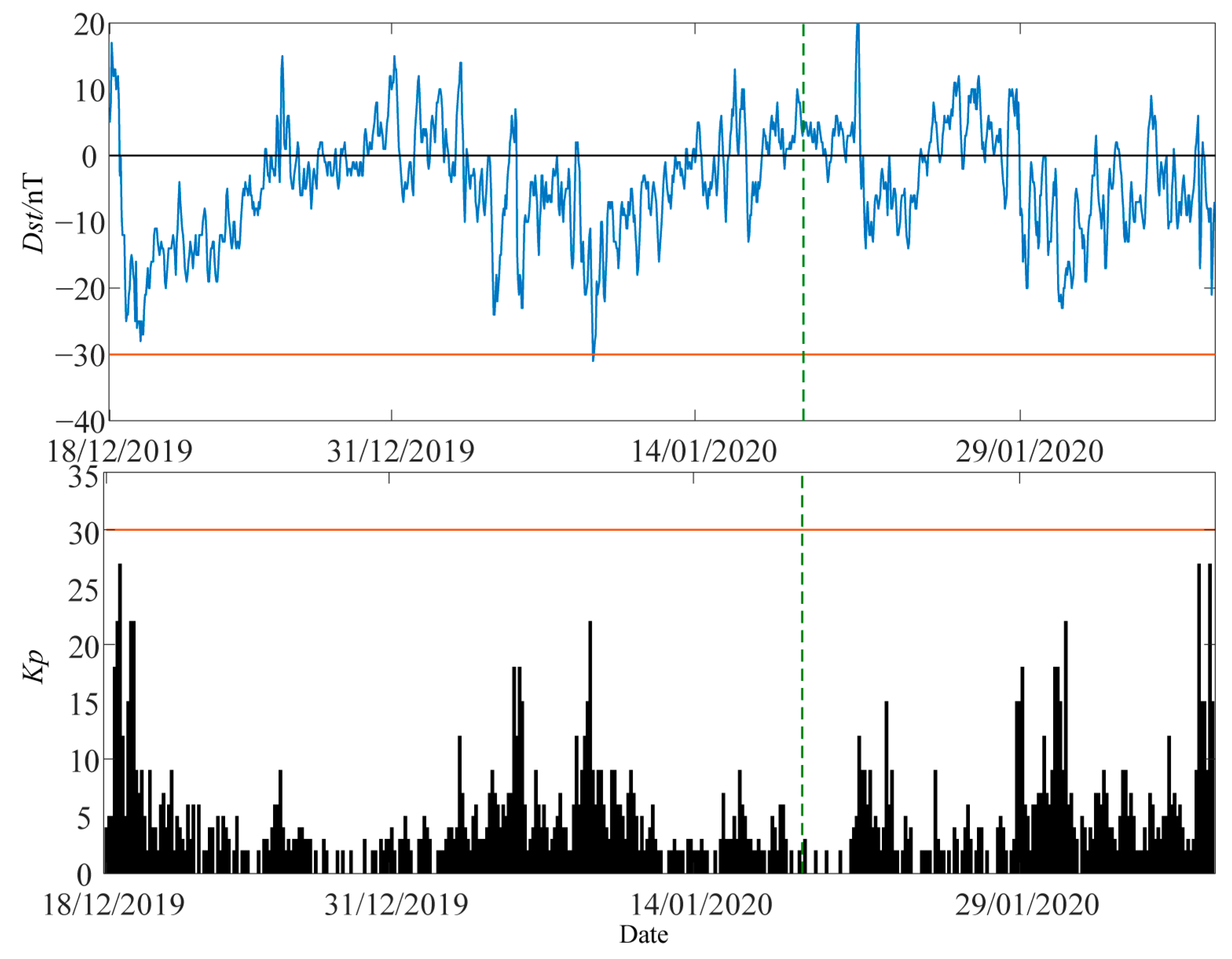
4.2. Space Weather Background
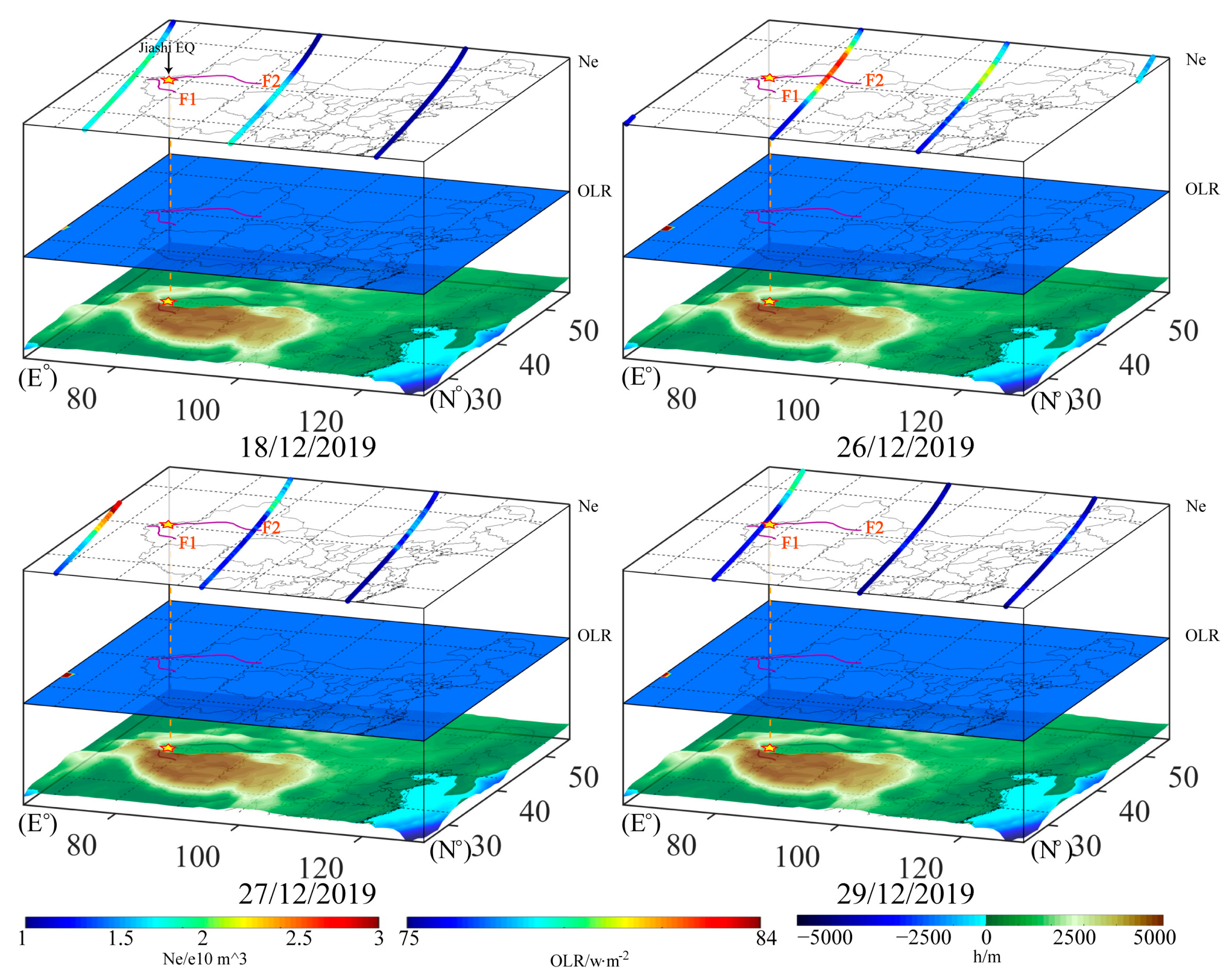
4.3. Temporal and Spatial Change Characteristics of the OLR and Ne
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gorny, V.I.; Salman, A.G.; Tronin, A.A.; Shlin, B.V. The earth outgoing IR radiation as an indicator of seismic activity. Proc. Acad. Sci. USSR 1988, 30, 67–69. [Google Scholar]
- Ouzounov, D.; Liu, D.; Kang, C.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Qin, K.; Wu, L.X.; De, S.A.; Meng, J. Quasi-synchronous multi-parameter anomalies associated with the 2010–2011 New Zealand earthquake sequence. Nat. Hazards Earth Syst. Sci. 2012, 12, 1059–1072. [Google Scholar] [CrossRef]
- Kong, X.; Bi, Y.; Glass, D.H. Detecting Seismic Anomalies in OutgoingLong-wave Radiation Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 649–660. [Google Scholar] [CrossRef]
- Jing, F.; Singh, R.P.; Shen, X. Land–atmosphere–meteorological coupling associated with the 2015 Gorkha (M 7.8) and Dolakha (M7.3) Nepal earthquakes. Geomat. Nat. Hazards Risk 2019, 10, 1267–1284. [Google Scholar] [CrossRef]
- Ghosh, S.; Chowdhury, S.; Kundu, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M.; Chakraborty, S.; Chakrabarti, S.K. Unusual Surface Latent Heat Flux Variations and Their Critical Dynamics Revealed before Strong Earthquakes. Entropy 2022, 24, 23. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Wu, L.; Ding, Y.; Liu, Y.; Chen, S.; Wang, X.; Mao, W. Extraction and discrimination of MBT anomalies possibly associated with the Mw 7.3 Maduo (Qinghai, China) Earthquake on 21 May 2021. Remote Sens. 2021, 13, 4726. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Liu, W.; Zhang, C.; Wu, L. Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance. Remote Sens. 2018, 10, 818. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Paciello, R.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques (RST) for monitoring earthquake prone areas by satellite TIR observations: The case of 1999 Chi-Chi earthquake (Taiwan). J. Asian Earth Sci. 2015, 114, 289–298. [Google Scholar] [CrossRef]
- Pergola, N.; Aliano, C.; Coviello, I.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Mazzeo, G.; Tramutoli, V. Using RST approach and EOS-MODIS radiances for monitoring seismically active regions: A study on the 6 April 2009 Abruzzo earthquake. Nat. Hazards Earth Syst. Sci. 2010, 10, 239–249. [Google Scholar] [CrossRef]
- Kang, C.L.; Zhang, Y.M.; Liu, F.D.; Jing, F. Long-Wave-Radiation Patterns prior to the Wenchuan M8.0 Earthquake. Earthquake 2009, 29, 116–120. [Google Scholar]
- Chakraborty, S.; Sasmal, S.; Chakrabarti, S.K.; Bhattacharya, A. Observational signatures of unusual outgoing longwave radiation (OLR) and atmospheric gravity waves (AGW) as precursory effects of May 2015 Nepal earthquakes. J. Geodyn. 2018, 113, 43–51. [Google Scholar] [CrossRef]
- Piscini, A.; Santis, A.; Dedalo, M.; Gianfranco, C. A Multi-parametric Climatological Approach to Study the 2016 Amatrice-Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Qiang, Z.J.; Kong, L.C.; Guo, M.H.; Zhao, Y. An experimental study on temperature increasing mechanism of satellitic thermo-infrared. Acta Seismol. Sin. 1997, 10, 247–252. [Google Scholar] [CrossRef]
- Dan, S.M.; Liu, F.; Cheng, W.Z. Effect factors on tellite remote sensing heat radiation and application of heat radiation information to earthquake prediction. Inland Earthq. 2002, 16, 372–378. (In Chinese) [Google Scholar]
- Xu, X.D.; Qiang, Z.J.; Dian, C.G. Suddenly increasing temperature on ground surface as one imminent earthquake precursor in case of 1988 Lancang-Gengma earthquakes. Seismol. Geol. 1990, 12, 243–249. (In Chinese) [Google Scholar]
- Blackett, M.; Wooster, M.J.; Malamud, B.D. Exploring land surface temperature earthquake precursors: A focus on the Gujarat (India) Earthquake of 2001. Geophys. Res. Lett. 2011, 38, L15303. [Google Scholar] [CrossRef]
- Qu, C.Y.; Ma, J.; Shan, X.J. Counterevidence for an earthquake precursor of satellite thermal infrared anomalies. Chin. J. Geophys. 2006, 49, 490–495. (In Chinese) [Google Scholar]
- Su, B.; Li, H.; Ma, W.Y.; Zhao, J.; Kang, C. The Outgoing Longwave Radiation Analysis of Medium and Strong Earthquakes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6962–6973. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Liu, W.; Zhang, C.; Li, S.; Yu, M.; Wu, L. Experimental Study on the Thermal Infrared Spectral Variation of Fractured Rock. Remote Sens. 2021, 13, 1191. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Li, Y.Q. Remote sensing-rock mechanics (I)—Laws of thermal infrared radiation from fracturing of discontinuous jointed faults and its meanings for tectonic earthquake omens. Chin. J. Rock Mech. Eng. 2004, 23, 24–30. (In Chinese) [Google Scholar]
- Cui, C.Y.; Deng, M.D.; Geng, N.G. Study on spectral radiation characteristics of rocks under different pressures. Chin. Sci. Bull. 1993, 38, 538–541. (In Chinese) [Google Scholar]
- Wu, L.; Cui, C.; Geng, N.; Wang, J. Remote sensing rock mechanics (RSRM) and associated experimental studies. Int. J. Rock Mech. Min. Sci. 2000, 37, 879–888. [Google Scholar] [CrossRef]
- Heaton, T.H. Tidal triggering of earthquakes. Geophys. J. Int. 1975, 2, 307–326. [Google Scholar] [CrossRef]
- Li, Y.X.; Xu, L.S.; Hu, X.K. Relation between the horizontal tide force which the sun and moon imposes on the seismogenic zone and the focal mechanism. Eathquake 2001, 21, 1–6. (In Chinese) [Google Scholar]
- Wu, A.X.; Zhang, X.D.; Zhang, Y.X.; Li, M.X.; Li, P.A.; Li, G.J. Quantitative extraction of earth tide anomaly information. Recent Dev. World Seismol. 2008, 11, 57. (In Chinese) [Google Scholar]
- Pulinets, S.A.; Legen’ka, A.D.; Alekseev, V.A. Pre-earthquakes effects and their possible mechanisms. In Dusty and Dirty Plasmas, Noise and Chaos in Space and in the Laboratory; Plenum Publishing: New York, NY, USA, 1994; pp. 545–557. [Google Scholar]
- Pulinets, S.A.; Legen’ka, A.D.; Gaivoronskaya, T.V.; Depuev, V.K. Main phenomenological features of ionospheric precursors of strong earthquakes. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1337–1347. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Khegai, V.V.; Boyarchuk, K.A.; Lomonsosov, A.M. Atmospheric electric field as a source of ionospheric variability. Physics-Uspekhi 1998, 41, 515–522. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Pulinets, S.A.; Tsai, Y.B.; Chuo, Y.J. Seismo-ionospheric signatures prior to M ≥ 6.0 Taiwan earthquakes. Geophys. Res. Lett. 2000, 27, 3113–3116. [Google Scholar] [CrossRef]
- Perrone, L.; Korsunava, L.P.; Mikhailov, A.V. Ionospheric precursors for crustal earthquake in Italy. Ann. Geophys. 2010, 28, 941–950. [Google Scholar] [CrossRef]
- Pulinets, S.; Krankowski, A.; Hernandez-Pajares, M.; Marra, S.; Budnikov, P. Ionosphere Sounding for Pre-seismic Anomalies Identification (INSPIRE): Results of the Project and Perspectives for the Short-Term Earthquake Forecast. Front. Earth Sci. 2021, 9, 131. [Google Scholar] [CrossRef]
- Parrot, M.; Benoist, D.; Berthelier, J.J.; Blecki, J.; Chapuis, Y.; Colin, F.; Elie, F.; Fergeau, P.; Lagoutte, D.; Lefeuvre, F. The magnetic field experiment IMSC and its data processing onboard DEMETER: Scientific objectives, description and first results. Planet. Space Sci. 2006, 54, 441–455. [Google Scholar] [CrossRef]
- Sarkar, S.; Gwal, A.K.; Parrot, M. Ionospheric variations observed by the DEMETER satellite in the mid-latitude region during strong earthquake. J. Atmos. Sol.-Terr. Phys. 2007, 54, 502–511. [Google Scholar] [CrossRef]
- Zeng, Z.C.; Zhang, B.; Fang, G.Y.; Wang, D.F.; Yin, H.J. The analysis of ionospheric variations before Wenchuan earthquake with DEMETER data. Chin. J. Geophys. 2009, 52, 11–19. (In Chinese) [Google Scholar]
- Zhang, X.; Shen, X.; Liu, J.; Ouyang, X.; Qian, J.; Zhao, S. Analysis of ionospheric plasma perturbations before Wenchuan earthquake. Nat. Hazards Earth Syst. Sci. 2009, 28, 1259–1266. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Boyarchuk, K.A. Ionospheric Precursors of Earthquakes; Springer: Berlin, Germany, 2004; 315p. [Google Scholar]
- Pulinets, S.; Ouzounov, D. Lithosphere-atmosphere-ionosphere coupling (LAIC) model—A unified concept for earthquake precursor validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Ma, W.Y.; Kang, C.L. Analysis of seismic activity situation in Chinese mainland in 2020 based on seismic remote sensing technology. In Research Report on Earthquake Trend Prediction in China in 2020; De Gruyter Open Access: Berlin, Germany, 2019; pp. 152–155. [Google Scholar]
- Li, C.; Zhang, G.; Shan, X.; Qu, C.Y.; Gong, W.Y.; Jia, R.; Zhao, D.Z. Coseismic deformation and slip distribution of the Ms 6.4 Jiashi, Xinjiang earthquake revealed by Sentinel-1 A SAR imagery. Prog. Geophys. 2021, 36, 481–488. (In Chinese) [Google Scholar]
- Yang, X.P.; Ran, Y.K.; Song, F.M.; Xu, X.W.; Cheng, J.W.; Min, W.; Han, Z.J.; Chen, L.C. The analysis for crust shortening of Kalping thrust tectonic zone, south-western Tianshan, Xinjiang, China. Seismol. Geol. 2006, 28, 194–204. (In Chinese) [Google Scholar]
- Liu, D.F.; Luo, Z.L.; Peng, K.Y. OLR anomalous phenomena before strong earthquakes. Earthquake 1997, 17, 126–132. (In Chinese) [Google Scholar]
- Liu, C.; Guan, Y.; Zheng, X. The technology of space plasma in-situ measurement on the Chinaseismo-electromagnetic satellite. Sci. China Technol. Sci. 2018, 62, 829–838. [Google Scholar] [CrossRef]
- Shen, X.H.; Zhang, X.M.; Yuan, S.G.; Wang, L.W.; Cao, J.B.; Huang, J.P.; Zhu, X.H.; Picozzo, P.; Dai, J.P. The state-of-the-art of the China Seismo-Electromagnetic Satellitemission. Sci. China Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Yan, R.; Guan, Y.B.; Shen, X.H.; Huang, J.P.; Zhang, X.M.; Liu, C.; Liu, D.P. The Langmuir Probe onboard CSES: Data inversion analysismethod and first results. Earth Planet. Phys. 2018, 2, 479–488. [Google Scholar] [CrossRef]
- Tanaka, S.; Ohtake, M.; Sato, H. Spatio-temporal variation of the tidal triggering effect on earthquake occurrence associated with the 1982 South Tonga earthquake of Mw 7.5. Geophys. Res. Lett. 2002, 29, 3-1–3-4. [Google Scholar] [CrossRef]
- Tanaka, S. Tidal triggering of earthquakes prior to the 2011 Tohoku-Oki earthquake (Mw 9.1). Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ma, W.; Kong, X.; Kang, C.; Zhong, X.; Wu, H.; Zhan, X.; Joshi, M. Research on the changes of the tidal force and the air temperature in the atmosphere of Lushan (China) Ms7.0 earthquake. Therm. Sci. 2015, 19 (Suppl. S2), 148. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, C.; Ma, W.; Ren, J.; Wang, Y. Study on thermal anomalies of earthquake process by using tidal-force and outgoing-longwave-radiation. Therm. Sci. 2018, 22, 767–776. [Google Scholar] [CrossRef]
- Chen, W.C.; Ma, W.Y.; Ye, W.; Chen, H.F. The Research of the Seismic Objects of the Tidal Force and the Temperature’s Change with TaiYuan’s YangQu Ms4.6. Adv. Intell. Soft Comput. 2012, 116, 947–953. [Google Scholar]
- Ma, W.Y.; Wang, H.; Li, F.S.; Ma, W.M. Relation between the celestial tide-generating stress and the temperature variations of the Abruzzo M = 6.3 Earthquake in April 2009. Nat. Hazards Earth Syst. Sci. 2012, 12, 819–827. [Google Scholar] [CrossRef]
- Yin, X.C.; Yin, C. Precursors of nonlinear system instability and earthquake prediction. Sci. China Ser. B 1991, 5, 512–518. (In Chinese) [Google Scholar]
- Wu, L.X.; Mao, W.F.; Liu, S.J.; Xu, Z.; Miao, Z. Mechanisms of altering infrared-microwave radiation from stressed rock and key issues on crust stress remote sensing. J. Remote Sens. 2018, 22, 146–161. (In Chinese) [Google Scholar]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Q.; Yan, R.; Lin, J.; Zhao, S.; Chu, W.; Shen, X.; Zeren, Z.; Yang, Y.; Cui, J.; et al. Pre-seismic multi-parameters variations before Yangbi and Madoi earthquakes on May 21, 2021. Nat. Hazard Res. 2023, 3, 27–34. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Romanov, A.; Romanov, A.; Tsybulya, K.; Davidenko, D.; Kafatos, M.; Taylor, P. Atmosphere-ionosphere response to the M9 Tohoku earthquake revealed by multi-instrument space-borne and ground observations: Preliminary results. Eearthquake Sci. 2011, 24, 557–564. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Cui, J.; Zhang, W.; Ma, W.; Ren, J.; Su, B.; Huang, J. Quasi-Synchronous Variations in the OLR of NOAA and Ionospheric Ne of CSES of Three Earthquakes in Xinjiang, January 2020. Atmosphere 2023, 14, 1828. https://doi.org/10.3390/atmos14121828
Yu C, Cui J, Zhang W, Ma W, Ren J, Su B, Huang J. Quasi-Synchronous Variations in the OLR of NOAA and Ionospheric Ne of CSES of Three Earthquakes in Xinjiang, January 2020. Atmosphere. 2023; 14(12):1828. https://doi.org/10.3390/atmos14121828
Chicago/Turabian StyleYu, Chen, Jing Cui, Wanchun Zhang, Weiyu Ma, Jing Ren, Bo Su, and Jianping Huang. 2023. "Quasi-Synchronous Variations in the OLR of NOAA and Ionospheric Ne of CSES of Three Earthquakes in Xinjiang, January 2020" Atmosphere 14, no. 12: 1828. https://doi.org/10.3390/atmos14121828
APA StyleYu, C., Cui, J., Zhang, W., Ma, W., Ren, J., Su, B., & Huang, J. (2023). Quasi-Synchronous Variations in the OLR of NOAA and Ionospheric Ne of CSES of Three Earthquakes in Xinjiang, January 2020. Atmosphere, 14(12), 1828. https://doi.org/10.3390/atmos14121828





