Abstract
For an efficient indoor air purification, it is important to know the detailed airflow distribution in the room. A series of numerical simulations are carried out for five heating regimes using an air–air heat pump, capillary mat on the ceiling, capillary mat on the walls, heated floor, and radiator. The most homogeneous temperature field is obtained for the case with the heated floor. The highest velocity is obtained for the air–air heat pump, while the lowest is obtained for the capillary mat on the ceiling. A portable air cleaner based on the prototype device is introduced into the model and its influence on the velocity and temperature distributions is calculated. Our simulations additionally consider is the transport of an infectious aerosol and its purification inside the air cleaner. The time dependency of the concentration is exponential, and the purification rate depends on the air cleaner’s orientation and heating regime. The efficiency is higher for a purifier with flow in the upwards direction compared to in a horizontal one. In the experimental part, an NaCl solution is dispersed into the air, and the efficiency of purification in the case of the air–air heat pump is evaluated by measuring the time-dependent particle concentrations. These experimental results corroborate the numerical model.
1. Introduction
The transmission of the airborne COVID-19 virus particles and the resulting infection risk are directly related to the indoor airflow pattern and air quality. To reduce the spread of the disease from infected persons, important measures include air filtration using HEPA filters and disinfection using ultraviolet (UV) radiation, in particular short-wavelength (200–280 nm) UV-C radiation [1]. The design of the ventilation system strongly affects the airflow and overall efficiency of the air purification system. Therefore, computational fluid dynamics (CFD) simulations are a valuable tool to assess different scenarios; see, e.g., [2,3] and references therein.
Because reducing the risk of COVID-19 infection is an important and ongoing research topic, a considerable number of investigations have been published since the start of the pandemic. Experimental studies typically measure the particle concentration (e.g., PM 1, PM 10) in the air as a function of time without and with an air purifier [4,5,6,7]. The particles are produced by, e.g., atomizing an NaCl solution, which is used in the experimental part of the present work.
Experimental data are needed for the validation of numerical models. In addition to particle or aerosol concentrations, different quantities can be experimentally measured by the appropriate sensors, e.g., velocity, magnitude, and temperature [8].
For a working air purifier, the average (mean over volume) particle concentration in the room typically follows the exponential law:
where is the initial concentration (at ) and k is the decay rate. A commonly used metric is the clean air delivery rate , which is measured in and where V is the total room (air) volume [7].
The indoor airflow and air purification has been studied numerically using CFD, which provides much more detailed information regarding the temperature and velocity fields compared to experimentation [8] and allows parametric studies to be carried out, e.g., to evaluate the efficiency of different air purifier setups [1,4,9]. Medium and large rooms such as offices, classrooms, auditoriums, and patient rooms are typically considered [1,4,5,8,10,11,12,13,14,15,16,17], although smaller spaces may be of interest as well [18,19].
While a large number of CFD studies have considered the steady-state airflow [4,5,8,11,12,16,17,20,21], the transient flow, which is computationally more demanding, has been modelled as well [1,5,9,10,13,14,15,18,19,21]. For the modelling of turbulence, the k-ε and k-ω models or their variations [4,5,8,9,10,11,12,15,16,17,18,20,21] are typically employed, while more advanced approaches such as Large Eddy Simulation, Detached Eddy Simulation, and the Reynolds Stress Model are suitable for the transient cases [11,14,19,21]. Regarding prediction of the particle concentration, the Eulerian approach [5,8,11,13,14,17,20,21,22] deals with the continuous aerosol concentration field, while the computationally more expensive Lagrangian approach [1,4,9,10,12,13,15,16,18,19,21,22] tracks the trajectories of individual particles. Further considerations on the choice of a CFD model are presented in Section 2.1.
The transport of infectious aerosols is affected by the airflow pattern, which depends on the heating or cooling conditions. The influence of different heating areas located on the wall on the temperature distribution and particle deposition was analysed for a cubic room in [23]; however, radiative heat transfer and air purification were not considered. While the differences between airflow patterns in summer and winter conditions were mentioned in [4] for a more realistic setup including an air purifier, none of the existing studies available in the literature have yet compared the influence of different heating regimes.
In the present work, which is an extended version of our conference paper [24], numerical airflow simulations in a realistic indoor setup are carried out using OpenFOAM finite volume software [25]. The CFD model describes the air velocity and temperature distributions in winter season for the following heating conditions: an air–air heat pump (conditioner), capillary mat on the ceiling, capillary mat on the walls, heated floor, and radiator. Aerosol transport and its purification by a portable air cleaner is modelled as well. A parametric study is carried out in which the influence of the orientation of the air cleaner flow and position of the aerosol source are analysed.
The novelties of the present research are as follows: consideration of five different heating regimes and their effects on the airflow pattern; investigation of the influence of the air cleaner configuration on purification efficiency; and explicit modelling of the airflow and concentration field inside the air cleaner instead of treating it as a black box.
Simulation results are used to enhance the design of an air purification device developed at the University of Latvia. It consists of two hermetically sealed M5 particle filters in a metal frame, several high static pressure fans in parallel to ensure a high airflow rate, and UV-C lamps to disinfect the passing air. Before manufacturing a physical prototype of the air purifier, an experiment was carried out involving the dispersion of an NaCl solution using an air humidifier for the case of the air–air heat pump. PM 1 and 2.5 NaCl particle concentrations were measured at three locations, then the measurements were used to validate the numerical model.
2. Methods
2.1. Computational Fluid Dynamics Model
2.1.1. Heat Transfer
The open-source computational fluid dynamics (CFD) finite volume library OpenFOAM [25] was used to simulate the indoor airflow. The steady-state heat transfer solver buoyantSimpleFoam, which includes buoyancy and turbulence effects, was selected. The temperature field in the solid walls was not solved, as was done in our previous study which included experimental validation [26], instead being modelled using the appropriate boundary conditions.
A room with an internal size of 3 × 3 × 3 m based on the experimental test stands in [27] and equipped with several heating systems, as previously modelled in [26], was considered; see Figure 1. The total air volume in the room was . The finite volume mesh was created using the OpenFOAM mesh generator snappyHexMesh [25] and consisted of about 1.6 million cells, which were mostly hexahedral.
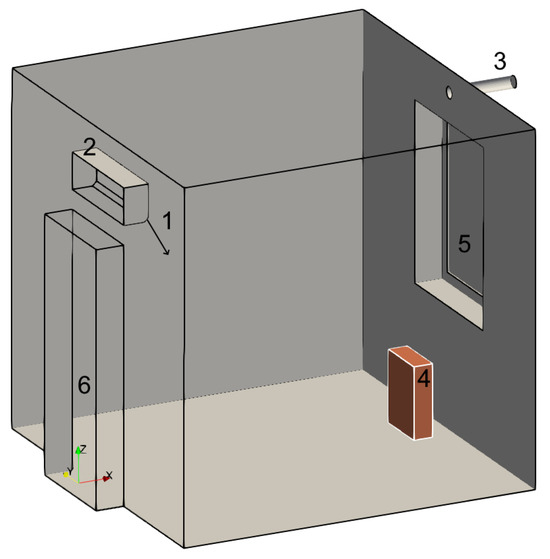
Figure 1.
Configuration of the computational domain without the air cleaner, showing the inlet (1) and air feedback (2) of the air–air heat pump, ventilation outlet (3), radiator (4), window (5) and door (6).
The air density is described by the ideal gas law with a molar mass of 28.96 . The specific heat capacity of the air is , the dynamic viscosity is , and the Prandtl number is 0.7.
For turbulence modelling, the k-ω SST model with default coefficients was selected. At the inlet of the air–air heat pump, a turbulence intensity of 10% and mixing length of 5 cm were applied. Note that there were simulation cases for which the air–air heat pump was turned off and air exchange with the outside environment was disabled.
Because different heating regimes are investigated in the present study, as summarised in Table 1, it is important to consider the radiative heat transfer. This was included using the surface-to-surface (view factor) model. All surfaces were treated as optically grey, opaque, and with an emissivity of 0.9. Test simulations with disabled radiative heat transfer resulted in considerably lower air temperatures (by up to 10 for certain scenarios). The contribution of the solar radiation through the window was neglected, as these additional heat sources are quite low in the winter.

Table 1.
Considered heating scenarios.
The outside wall, floor, and ceiling heat losses according to the Newton’s cooling law were applied with an outside temperature of −6 , heat transfer coefficient of 8 , and a virtual external wall (i.e., not included in the volumetric mesh) for insulation with a U-value of 0.16 . The setup was similar for the window and door except for a higher U-value of 0.8 . At the heated surfaces, the fixed temperature boundary condition was set, with the temperature chosen manually according to the desired mean temperature in the room and the heating power calculated during postprocessing. Finally, a no-flux temperature boundary condition was applied at the outlet, air purifier, and walls which were not exposed to the outside environment.
A first-order upwind scheme was applied for the convective terms [20]. The mesh size (and time step for the aerosol transport simulations; see Section 2.1.2) was chosen based on our previous experience [26,28] to obtain grid-independent results. Field values (temperature, velocity, turbulent quantities) at the probe points and residuals were monitored during the simulation to ensure convergence, and the mean air temperature in the whole domain was monitored. Because the Reynolds-averaged Navier–Stokes (RANS) equations were solved with the airflow not being fully stationary, e.g., due to buoyancy effects when the heat sources are located in the bottom part of the room, under-relaxation was enabled in all simulations using a factor of 0.6 for the temperature, pressure, and turbulent quantities and 0.4 for the velocity. To deal with especially pronounced oscillations, these values were reduced to 0.5 and 0.3, respectively; however, we were unable to eliminate the oscillations completely. Nonetheless, the maximum differences between iterations were much smaller than the differences between the investigated heating regimes and air purifier configurations. The temperature and velocity fields were averaged over the last 2000 iterations of the simulation to obtain representative results.
2.1.2. Aerosol Transport
Modelling the airborne spread of the COVID-19 virus-laden particles remains a key challenge. There are two main CFD particle model categories, namely, the Lagrangian and the Eulerian. The Discrete Phase Model (DPM) falls under the former category; it treats the particles as discrete entities, with each having its own Lagrangian equation of motion. DPM resolves the motion of individual particles with different weights and sizes, including inertial effects and forces such as drag, buoyancy, and gravity.
Eulerian models instead treat the particles collectively as a separate phase while tracking a finite volume element along the fluid flow path. Contrary to Lagrangian models, these methods model the average behaviour of the particles rather than individual particles. Eulerian methods consider the concentration of massless particles as a function of both space and time. When there are no interactions between the particle phase and the fluid phase, such a model is referred to as a Passive Scalar Model (PSM).
While Lagrangian methods are more descriptive, they are much more computationally demanding, as simulating a large number of discrete particles is required for accurate predictions [22]. Equally as important is the choice of airflow model. For steady-state indoor simulations such as the present study, the RANS model with the Eulerian particle transport is commonly used [13,21]. The Lagrangian particle model produces the best results when used in combination with the LES turbulence model [13,21].
The relaxation time, which characterises how long it takes for a particle to adjust its velocity to the flow forces, is an important parameter in understanding the behaviour of particles in a fluid flow. It depends mostly on the size of the particle and the Reynolds number of the fluid Re. The dimensionless particle relaxation time, known as the Stokes number, is defined by the formula
where P is the ratio of the particle density to the fluid density and is the dimensionless particle diameter (, with l being the turbulence length scale) [29]. The coefficient includes the Cunningham correction for the small-particle Stokes resistance.
Because the relaxation time is proportional to the square of the particle diameter, it increases rapidly with increasing particle size. Small particles adjust to a new flow field very quickly (i.e., they closely follow the flow), while larger particles move according to their inertia. In turbulent airflow conditions, particles follow the flow if . In typical room conditions for water particles with a diameter of 2.5 the typical Stokes number is several orders of magnitude less than 1, even when considering Re on the order of .
Considering the small particle size, steady-state airflow, selected RANS turbulence model, and computational costs involved in the parameter study of 75 cases, it was decided to use the Eulerian particle model. For a more thorough explanation and comparison of the different models for indoor particle simulations, see [13,21,22,30].
The transient transport of the infectious aerosol concentration C (dimensionless mass concentration) in the Passive Scalar Model is described by the advection–diffusion equation:
where is the air velocity obtained in the heat transfer simulations, S is the source term (negative-sink), is the effective diffusion coefficient, is the Brownian diffusion coefficient, and is the turbulent diffusion coefficient, with being the turbulent kinematic viscosity calculated by the turbulence model and the turbulent Schmidt number. The so-called frozen flow approach [5,11,12] was applied, meaning that the velocity field does not change over time.
While in general there is no single value for , as it depends on the flow regime [11], constant values are typically used in the literature, for example, 0.7 [20] and 1.0 [8]. As demonstrated in [20], the effect of changing in the range from 0.5 to 0.9 is comparable to the numerical effects of the mesh size and time step. In the present work, an intermediate value of 0.8 was assumed for simplicity, as we believe that other limitations, e.g., the assumption of a frozen velocity field in the simulations and uncertainties in the experiment, have a stronger influence on the results.
Additionally, while it is known that the relative humidity differs in winter and summer and affects the evaporation and sedimentation rate of droplets [15,19], we did not investigate these effects in the present study, as only the heating season was considered and the Eulerian model was used. During the experiment, the relative humidity fluctuated between 26 to 28% and the humidifier’s generation of salt particles had a minimal effect. We believe that the greatest sources of uncertainty are the experimental measurements; therefore, our main results for the purification efficiencies obtained in numerical simulations for different heating regimes and air purifier configurations can be directly compared.
The aerosol purification efficiency of the air cleaner was tested in various spatial orientations (see Figure 2 and Table 2). The simulated device was based upon a prototype with external dimensions of 0.5 × 0.5 × 1 m. Air purifier configurations A–E were selected to demonstrate its influence in several realistic scenarios. Case C is the intended operating mode of the air purifier prototype, while case D has an opposite flow direction and case E has no top lid. Cases A and B demonstrate a possible horizontal setup for two extreme scenarios, namely, flow towards the door and flow towards the radiator. The spatial positions were not changed, as the room was quite small. Application of the purifier in larger rooms would be limited by the maximum airflow rate.
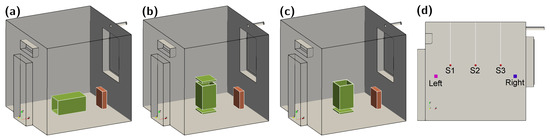
Figure 2.
Configuration of the air cleaner: (a) horizontal, (b) vertical, and (c) vertical with the top lid removed. The pink and blue boxes in (d) are the locations of the left and right concentration sources, respectively, while the red spheres are three sensors hanging from the ceiling during the experiment.

Table 2.
Considered air cleaner configurations (see Figure 2).
The flow rate was set using the meanVelocityForce momentum source in OpenFOAM. With a filter face surface of 0.45 × 0.45 and a face velocity of 0.5 , the resulting volumetric flow rate is . A negative implicit source term (sink) was set for the concentration field (Equation (3)) in a subset of cells within the air purifier, yielding a single-pass efficiency of roughly 99.3%; for comparison, a HEPA filter is required to have an of 99.95% according to ISO standards.
A special boundary condition was applied for the air–air heat pump, as it mixes the outside (fresh) air with the air in the room while recirculating the old air. The magnitude and direction of the velocity at the air inlet was fixed, while air feedback in the upper part of the air–air heat pump was specified as a surface with fixed pressure to ensure the conservation of mass. At the ventilation outlet (above the window, see Figure 1) the air outflow velocity was specified according to the desired air exchange rate. For the concentration field, the value at the inlet of the air–air heat pump was calculated as follows:
where is the single pass filtration efficiency of the air–air heat pump, Q is the volumetric flow rate, and is the average concentration on the surface of the air feedback. When equals zero, the CADR corresponds to the fresh air delivery rate of the air–air heat pump. However, the salt particle filtration efficiency of the built-in filter was not known and had to be determined by experiment.
2.2. Experimental Setup
The NaCl aerosol concentration experiment was conducted in the 3 × 3 × 3 m test stand located at the botanical garden of the University of Latvia [27] under air–air heating conditions (case aa in Table 1 and Figure 3). The relative reduction of the particulate matter suspended in the air due to the air–air heat pump was measured and the decay rate k was found by fitting the curve to Equation (1).
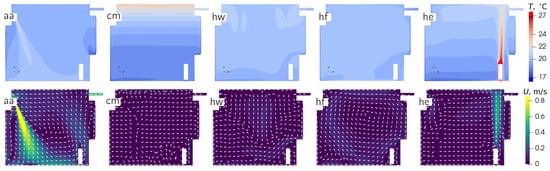
Figure 3.
Temperature and velocity distributions in vertical cross-section for the case without air cleaner and different heating regimes according to Table 1.
The experimental setup consisted of three low-cost PM 1 and 2.5 sensors (SPS30 manufactured by Sensirion) and an air humidifier with a 5% NaCl solution (the air purifier was not present). The sensors were positioned hanging from the ceiling at a head height of 165 cm and along the x axis with equal spacings of 75 cm; see Figure 2d. Two placements of the humidifier were tested, which corresponded to the left and right concentration sources at locations (0.35, 1.5, 1.32) m and (2.65, 1.5, 1.32) m, respectively. The location (0, 0, 0) denotes the bottom left-hand corner of the test stand wall (the corner closest to the reader in Figure 2).
The air humidifier was run for about 90 s while the air–air heat pump was in the on state, which was same as in the numerical model. Water quickly evaporates from the droplets, leaving small NaCl particles [4]. To calculate the CADR values, the mass concentration was measured for 20 min, as recommended by the ANSI/AHAM-AC-1–2006 measurement method [31]. Note that in order to maintain a steady airflow pattern, no mixing fan was used and the louvers of the air–air heat pump were fixed. Additionally, the sensor readings were calibrated to ensure that the mean values of the measurements were the same in equal conditions.
3. Results and Discussion
3.1. Numerical Results—Airflow
3.1.1. Without Air Cleaner
Five different heating scenarios were investigated, as defined in Table 1. For the case with the air–air heat pump (aa), the air exchange rate was set to 0.45 h−1, the air inflow velocity to 2 m s−1, and the inflow direction to 70° from the horizontal. This corresponds to a volumetric flow rate of 294 m3 h−1, the majority of which (about 96%) is reused by the air–air heat pump through the air feedback located in its top part; see Figure 1.
The simulation results for the temperature and velocity distributions in the vertical plane and the line in the centre of the room for the cases without the air cleaner are shown in Figure 3 and Figure A1 of the Appendix A. The required heating powers to maintain a mean air temperature of about 20 for all cases are summarised in Table 3.

Table 3.
Calculated thermal parameters: temperature of the heated surface , heating power , and average (mean) temperature of the air .
A common feature for all considered cases is that the temperature of the window and door is lower than for the walls, as the U-value is higher. Therefore, the typical tendency is for the air to flow downwards along the window and door, forming a cold plume. Due to the heat losses to the outside environment, the temperature of the walls is lower than that of the air close to the wall (except for case hw); hence, the flow near the walls tends to be downwards. Temperature and velocity boundary layers form at these and other surfaces (floor, ceiling), and are more visible in the 1D plots, e.g., Figure A1 in the Appendix A.
The most homogeneous temperature distribution is obtained for the case with the heated floor, which is understandable as the warm air rises and the total area of the floor is large compared to, e.g., a radiator. The heating power is the second lowest among all cases, and the mean air temperature is second highest. The maximum air velocity is rather low, at about 16 cm s−1. A large toroidal vortex is created, with a downward flow near the window and upward flow at the opposite wall; see Figure 3.
The most inhomogeneous temperature field is obtained for the “opposite” heating regime, that is, a capillary mat on the ceiling (heated ceiling), as the warm air stays near the ceiling and the rest of the room (walls, floor) is heated mostly by the thermal radiation. While the heating power is about the same as for the heated floor, the mean air temperature is lower by 0.5 due to the pronounced temperature stratification near the ceiling. The velocity in the whole room is very low, at 8–13 cm s−1, as the cold air flows down at the window and door, and is below 4 cm s−1 further away from the walls.
In contrast, when the capillary mat is installed on the walls, the highest mean air temperature is achieved with the lowest heating power thanks to the large surface area and heat transfer by thermal radiation. The temperature distribution is quite homogeneous (see Figure A1), and the air flows downwards near the windows and door with the maximum velocity of 17 cm s−1 as well as in the centre of the room, where the distance from the heated walls is greatest.
Another case for which heat transfer via thermal radiation is important is radiator heating, as the surface temperature is 49 . As the warm air rises almost vertically, it reaches a maximum velocity of 52 cm s−1. Parts of the floor and wall close to the radiator are heated by up to 35 . The temperature of the ceiling above the radiator is increased as well, though only to about 20 . The flow is slower in the middle of the room, with a velocity of up to 5–10 cm s−1. The heating power is higher by about 10% than in cases cm and hf. This could be improved by enhancing convection in the room, e.g., using a fan.
The heating regime using the air–air heat pump has the highest maximum velocity of 2 m s−1, which means that the thermal comfort condition (drought rate) is not satisfied for such a small test stand. A counterclockwise flow pattern of the largest vortex is created by the inflow from the air–air heat pump. Thanks to effective air mixing, the temperature distribution is quite homogeneous, and it can be observed that the warm high-velocity inlet jet reaches the floor and heats it. The heating power is the highest among all cases, as the cold outside air must be heated to room temperature.
3.1.2. With Air Cleaner
When the air cleaner is introduced into the model, the airflow pattern and temperature distribution are changed, as depicted in Figure 4. Note that all combinations of heating regimes (Table 1) and air cleaner setups (Table 2) are considered in the simulations; however, due to the high total number of cases only certain representative results are shown in the main text; the full results for the other configurations are presented in Figure A2 in the Appendix A.
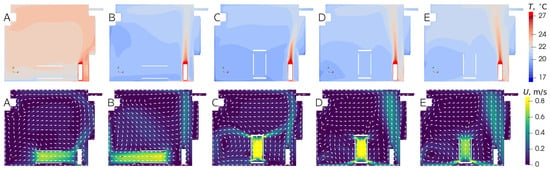
Figure 4.
Temperature (top row) and velocity (bottom row) distributions in vertical cross-section for heating case he and different air cleaner configurations (A–E) according to Table 2.
The change in the global airflow with the air cleaner is especially pronounced for cases with low velocity (cases cm, hw, hf). Depending on the heating regime and air cleaner configuration, the temperature field can be affected by the additional convective heat transfer as well. This effect is especially strong when the flow is directed towards the radiator (configuration A in Figure 4). Another important factor is the outlet of the air cleaner; if it is directed downwards (cases D and E), dust particles can be blown up from the floor, which is undesirable.
Two additional simulations with a heat source consisting of UV lamps inside the air purifier were carried out for heating case aa and purifier configuration C; see Figure A3 in the Appendix A. If the temperature of the air–air heat pump is unchanged (Figure A3b), the mean air temperature increases by 2.8 . This value agrees with a simplified analytical estimation of air heating at a flow rate of : .
By lowering the temperature of the air–air heat pump by 3 (Figure A3c), the mean air temperature drops to approximately the same value as the case without a power source. Note that the heating scenario in case aa was considered here because it has the highest heating power (Table 3); for other heating conditions, the required heating power is below that of the air purifier heat source.
3.2. Numerical Results—Aerosol Transport
Three scenarios were considered for the aerosol transport: uniform, left, and right. The simplest case is uniform, where the initial concentration is homogeneous () and the average concentration typically follows pure exponential decay (see Equation (1)). Conversely, the left and right scenarios (see Figure 2d) depict a more realistic situation in which a concentration source, e.g., a person expelling infectious respiratory aerosols, creates a non-uniform distribution over 400 s. After the source is turned off, the simulation continues for another 400 s and the results are normalised relative to the maximum value.
Due to incomplete air mixing, the concentration curve typically exhibits two phases (short and long time-scales) with respective decay rates and :
The parameters , , and are fitted such that the coefficient . The fast decay rate can be observed due to the source residue quickly clearing promptly after the source has stopped emission. While interpretation of the CADR according to Equation (5) is not straightforward, for both the left and right scenarios the decay rate would be more meaningful.
Together, these three scenarios allow for realistic air purification evaluation. However, the uniform scenario can be misleading, as a homogeneous concentration distribution is unlikely to occur naturally in stagnant airflow conditions. The mean spatial concentration was considered in the simulations, and the final values for all cases are summarised in Figure 5. Representative concentration distributions are shown in Figure 6.
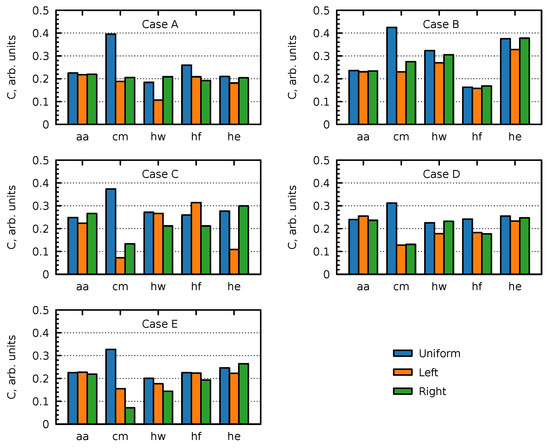
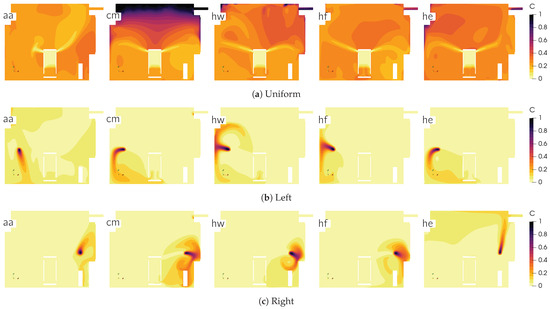
Figure 6.
Concentration distributions in vertical cross-section at for air cleaner configuration C.
As can be seen from the results, the CADR value of an air purifier can vary drastically depending on the heating conditions, device orientation, and pollutant source location. For example, when there is additional air mixing, as recommended in the ANSI/AHAM-AC-1–2006 measurement method [31], the average CADR is 355 m3 h−1 (cases aa), which is 97% of the volumetric flow rate of the purifier.
While good air mixing is beneficial for dispersing infectious aerosols, recirculating the air can actually increase the infection risk [18]. Furthermore, despite good air mixing, case aa ranks the second-worst when considering the left and right sources, with the mean concentration at the end of the simulation being . The additional strong airflow from the air–air heat pump in case aa increases the air mixing, meaning that the mean concentration is roughly the same across all the calculations, with variations below 12%. On the other hand, the case with the heated ceiling (cm) eliminates upward airflow, effectively reducing the ceiling height and room (air) volume, resulting in the highest purification efficiency of . Even though the uniform values are exceptionally high, this is due to the poor air circulation close to the ceiling, as shown in Figure 6, which is caused by buoyancy. The heated floor case (hf) ranks second-best with , followed closely by the case with heated walls (), while the case with the heater (he) ranks second-worst on average, with .
The worst performance for the left and right sources occurs when the purifier flow is directed horizontally towards the door (Case B, he). However, this purifier orientation is the least effective overall across different heating scenarios, with a 25% higher on average. In contrast, configuration A is the second-most efficient (). The vertically oriented purifier cases (E, D, and C) achieve similarly high reductions in aerosols with only small variations in the results ( to ).
3.3. Experimental Results and Validation of Numerical Model
The experiment was carried out as described in Section 2.2. The obtained time dependencies of the concentration at the three sensors are shown in Figure 7. A corresponding numerical simulation was set up to validate the model. The results were normalised relative to the maximum value for both the experiment (solid lines) and simulation (dashed lines).
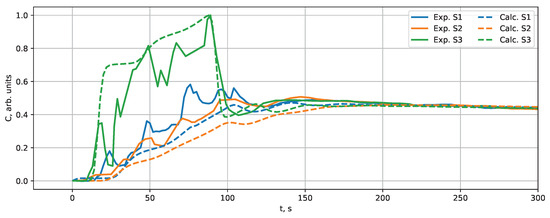
Figure 7.
Comparison of concentration time evolution between the PM 2.5 experiment and calculation for left source. The maximum concentration is normalised to 1 and the simulation end time is .
When the concentration source is turned off, the concentration starts to decrease, mixing with the fresh air, which is due to natural decay as well as NaCl particle filtering inside the air–air heat pump. During the last part of the measurement, the concentration values in all three sensors are practically equal due to the good air mixing provided by the air–air heat pump.
The unknown filtration efficiency of the air–air heat pump in Equation (4) was set to 0.125 to match the mean CADR in the experiment. As demonstrated in Figure 7 (dashed lines), the basic tendencies observed in the experiment are reproduced quite well. The relative concentrations at the end of the simulation are similar. The slopes of experiment and simulation curves may differ because the division operation in the normalisation changes the slope. The decay rate (CADR) is not affected by the normalisation (see Table 4). In the simulation at , the value at S3 relative to S1 and S2 is higher than in experiment. Note that the averaged velocity distribution was used in the simulations, while in reality the velocity fluctuates over time, resulting in non-smooth curves [5,10,20].

Table 4.
Fitted CADR values (m3 h−1) for experiment (PM 2.5) and calculation. The filtration efficiency in the calculation is 0.125. Note that the CADR error at the different sensors varies due to the airflow intensity.
According to the simulation results for case aa (Figure 3), the airflow is created by the air–air heat pump and has a large counterclockwise vortex. The left concentration source is in the downward jet from the air–air heat pump, while the air from the main vortex flows upwards at the positions of the right source and sensor S3. Sensors S1 and S2 are in low-velocity regions. In Figure 7, after turning on the source, the concentration first increases at sensor S3, as the aerosol is directly transported by the air convection. The concentration increase at sensors S1 and S2 is less rapid compared to S3, as expected from the described airflow pattern. In addition, the maximum concentration in S1 and S2 is about 50% lower compared to S3.
Fitting the experimental and calculation data to Equation (1), the CADR values are determined at each sensor position; see Table 4. The natural NaCl concentration decay for PM 2.5 and PM 1 corresponds to a CADR of 5.74 and 2.93 m3 h−1, respectively.
The mass concentration measurement error of the PM 2.5 and PM 1 sensor is 10%. To estimate the CADR uncertainty in the experiment, the measurement time interval of 22.5 min was varied by up to ±2.5 min. With the source on the right, the standard deviations of the CADR are 0.17, 0.64, and 0.67 m3 h−1 for sensors S1–S3, respectively. The largest absolute error of the CADR is found to be 2.73 m3 h−1, which is larger than the variations in CADR between the sensors. Because the air–air heat pump provides intense air mixing, the differences in local CADR were too small to measure with the current apparatus; however, the numerically modelled and experimental CADR values in Table 4 suggest that the local CADR is roughly equal.
4. Summary and Conclusions
Numerical simulations of different heating regimes show that the most homogeneous temperature field is obtained for the case with the heated floor, followed by the cases with the air–air heat pump and capillary mat on the walls; the lowest velocity is found for the case with the capillary mat on the ceiling, followed by cases with the heated floor and capillary mats on the walls.
The air purification efficiency, as evaluated as the mean concentration at the end of the simulation, is strongly influenced (by up to 50% or more) by the location of the aerosol source and the airflow pattern in the room created by the heating device and air cleaner, with the exception of the cases with the air–air heat pump, which show a weak dependence (below 12%) on the air purifier configuration due to good air mixing. High efficiency is observed for the cases with the purifier oriented vertically, regardless of flow direction, as well as for the cases with the purifier oriented horizontally with the flow towards the radiator (variations below 5%). A 25% higher final concentration is obtained for the horizontal orientation with the flow towards the door. Among different heating regimes, the highest purification efficiency for the left and right sources is achieved for the cases with the capillary mat on the ceiling, while for other cases the concentration is higher by 28–55%. The best performing case overall is the vertically oriented purifier with upwards flow combined with the capillary mat on the ceiling.
The concentration of NaCl aerosol was measured in the experiment, and good agreement with the corresponding numerical simulation was obtained. However, a limitation of the present study is that the investigated room was small in size; as the results for larger rooms might differ, additional simulations would be beneficial. The insights obtained from this research into the efficiency of the air purifier will be used to ensure the optimal operation of our developed air purifier prototype.
Author Contributions
Conceptualisation, A.S. and D.D.V.; methodology, A.S., D.D.V., J.T., and J.V.; software, A.S. and D.D.V.; validation, D.D.V.; formal analysis, A.S. and D.D.V.; investigation, A.S., D.D.V., and J.T.; writing—original draft preparation, A.S. and D.D.V.; writing—review and editing, J.T., J.V., and A.J.; visualisation, A.S. and D.D.V.; supervision, J.V. and A.J.; project administration, A.J.; funding acquisition, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
The present research has been supported by the European Regional Development Fund, Project “System for prediction and reduction of COVID-19 infection risk in indoor environment”, No. 1.1.1.1/21/A/046. This project is co-financed by REACT-EU funding for mitigating the consequences of the pandemic crisis.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to technical or time limitations.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CADR | Clean air delivery rate |
| CFD | Computational fluid dynamics |
| HEPA | High-efficiency particulate air |
| PM | Particulate matter |
| PSM | Passive scalar model |
| RANS | Reynolds-averaged Navier–Stokes |
| UV | Ultraviolet |
| C | Normalized dimensionless mass concentration (arbitrary units) |
| Specific heat capacity | |
| D, , | Brownian, turbulent, and effective diffusion coefficient |
| Single-pass filtration efficiency | |
| k | Decay rate |
| Dynamic viscosity | |
| Kinematic viscosity | |
| P | Power |
| Pr, | Laminar and turbulent Prandtl number |
| Q | Volumetric flow rate |
| Re | Reynolds number |
| Density | |
| S | Source term for concentration |
| Sc, | Laminar and turbulent Schmidt number |
| t | Time |
| T | Temperature |
| Velocity | |
| V | Volume |
Appendix A
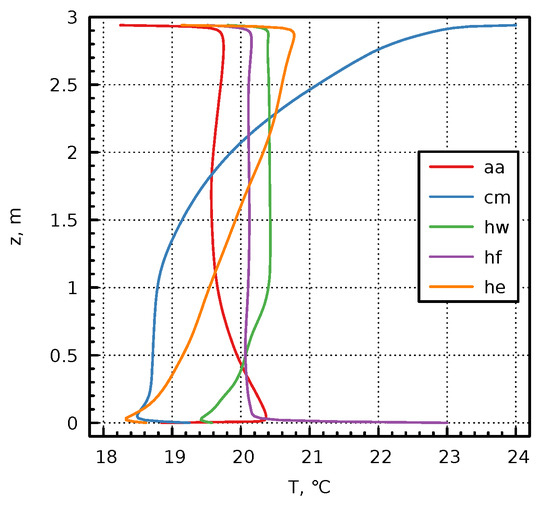
Figure A1.
Vertical temperature distribution in the centre of the room for the case without air cleaner.
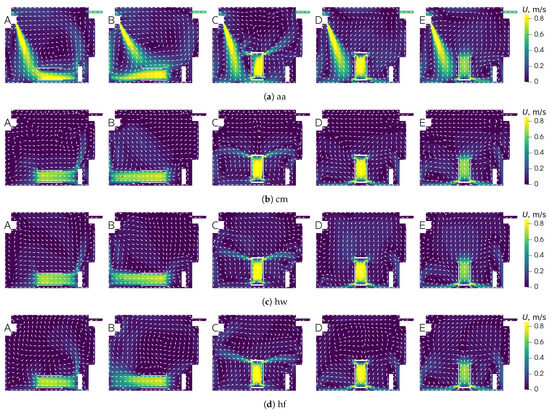
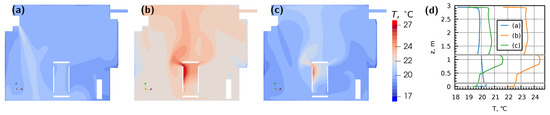
Figure A3.
Temperature distributions in vertical cross-section for heating case aa and air cleaner configuration C: (a) reference case; (b) 318 heat source in the purifier with the inlet temperature of the air–air heat pump not adjusted; (c) 318 heat source in the purifier with reduced inlet temperature of the air–air heat pump. (d) shows the vertical temperature distributions in the centre of the room for cases (a–c); the grey horizontal lines indicate the top and bottom lids of the air cleaner.
References
- Feng, Y.; Zhao, J.; Spinolo, M.; Lane, K.; Leung, D.; Marshall, D.; Mlinaric, P. Assessing the filtration effectiveness of a portable ultraviolet air cleaner on airborne SARS-CoV-2 laden droplets in a patient room: A numerical study. Aerosol Air Qual. Res. 2021, 21, 200608. [Google Scholar] [CrossRef]
- Mohamadi, F.; Fazeli, A. A review on applications of CFD modeling in COVID-19 pandemic. Arch. Comput. Methods Eng. 2022, 29, 3567–3586. [Google Scholar] [CrossRef] [PubMed]
- Rayegan, S.; Shu, C.; Berquist, J.; Jeon, J.; Zhou, L.G.; Wang, L.L.; Mbareche, H.; Tardif, P.; Ge, H. A review on indoor airborne transmission of COVID-19-modelling and mitigation approaches. J. Build. Eng. 2023, 64, 105599. [Google Scholar] [CrossRef]
- Tobisch, A.; Springsklee, L.; Schäfer, L.F.; Sussmann, N.; Lehmann, M.J.; Weis, F.; Zöllner, R.; Niessner, J. Reducing indoor particle exposure using mobile air purifiers—Experimental and numerical analysis. AIP Adv. 2021, 11, 125114. [Google Scholar] [CrossRef]
- Burgmann, S.; Janoske, U. Transmission and reduction of aerosols in classrooms using air purifier systems. Phys. Fluids 2021, 33, 033321. [Google Scholar] [CrossRef]
- Curtius, J.; Granzin, M.; Schrod, J. Testing mobile air purifiers in a school classroom: Reducing the airborne transmission risk for SARS-CoV-2. Aerosol Sci. Technol. 2021, 55, 586–599. [Google Scholar] [CrossRef]
- Küpper, M.; Asbach, C.; Schneiderwind, U.; Finger, H.; Spiegelhoff, D.; Schumacher, S. Testing of an indoor air cleaner for particulate pollutants under realistic conditions in an office room. Aerosol Air Qual. Res. 2019, 19, 1655–1665. [Google Scholar] [CrossRef]
- Srivastava, S.; Zhao, X.; Manay, A.; Chen, Q. Effective ventilation and air disinfection system for reducing coronavirus disease 2019 (COVID-19) infection risk in office buildings. Sustain. Cities Soc. 2021, 75, 103408. [Google Scholar] [CrossRef] [PubMed]
- Dbouk, T.; Roger, F.; Drikakis, D. Reducing indoor virus transmission using air purifiers. Phys. Fluids 2021, 33, 103301. [Google Scholar] [CrossRef]
- Qian, H.; Li, Y.; Sun, H.; Nielsen, P.V.; Huang, X.; Zheng, X. Particle removal efficiency of the portable HEPA air cleaner in a simulated hospital ward. Build. Simul. 2010, 3, 215–224. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Ren, J.; Cao, X. Predicting contaminant dispersion using modified turbulent Schmidt numbers from different vortex structures. Build. Environ. 2018, 130, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Abuhegazy, M.; Talaat, K.; Anderoglu, O.; Poroseva, S.V. Numerical investigation of aerosol transport in a classroom with relevance to COVID-19. Phys. Fluids 2020, 32, 103311. [Google Scholar] [CrossRef] [PubMed]
- Vuorinen, V.; Aarnio, M.; Alava, M.; Alopaeus, V.; Atanasova, N.; Auvinen, M.; Balasubramanian, N.; Bordbar, H.; Erästö, P.; Grande, R.; et al. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf. Sci. 2020, 130, 104866. [Google Scholar] [CrossRef]
- Foster, A.; Kinzel, M. Estimating COVID-19 exposure in a classroom setting: A comparison between mathematical and numerical models. Phys. Fluids 2021, 33, 021904. [Google Scholar] [CrossRef] [PubMed]
- Foat, T.G.; Higgins, B.; Abbs, C.; Maishman, T.; Coldrick, S.; Kelsey, A.; Ivings, M.J.; Parker, S.T.; Noakes, C.J. Modeling the effect of temperature and relative humidity on exposure to SARS-CoV-2 in a mechanically ventilated room. Indoor Air 2022, 32, e13146. [Google Scholar] [CrossRef]
- Liu, S.; Koupriyanov, M.; Paskaruk, D.; Fediuk, G.; Chen, Q. Investigation of airborne particle exposure in an office with mixing and displacement ventilation. Sustain. Cities Soc. 2022, 79, 103718. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Duill, F.F.; Schulz, F.; Beyrau, F.; van Wachem, B. Numerical study on the impact of large air purifiers, physical distancing, and mask wearing in classrooms. Atmosphere 2023, 14, 716. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. On airborne virus transmission in elevators and confined spaces. Phys. Fluids 2021, 33, 011905. [Google Scholar] [CrossRef]
- Sen, N. Transmission and evaporation of cough droplets in an elevator: Numerical simulations of some possible scenarios. Phys. Fluids 2021, 33, 033311. [Google Scholar] [CrossRef]
- Foat, T.; Drodge, J.; Nally, J.; Parker, S. A relationship for the diffusion coefficient in eddy diffusion based indoor dispersion modelling. Build. Environ. 2020, 169, 106591. [Google Scholar] [CrossRef]
- Wang, M.; Lin, C.H.; Chen, Q. Advanced turbulence models for predicting particle transport in enclosed environments. Build. Environ. 2012, 47, 40–49. [Google Scholar] [CrossRef]
- Saidi, M.S.; Rismanian, M.; Monjezi, M.; Zendehbad, M.; Fatehiboroujeni, S. Comparison between Lagrangian and Eulerian approaches in predicting motion of micron-sized particles in laminar flows. Atmos. Environ. 2014, 89, 199–206. [Google Scholar] [CrossRef]
- Sajjadi, H.; Atashafrooz, M.; Delouei, A.A.; Wang, Y. The effect of indoor heating system location on particle deposition and convection heat transfer: DMRT-LBM. Comput. Math. Appl. 2021, 86, 90–105. [Google Scholar] [CrossRef]
- Sabanskis, A.; Vidulejs, D.D.; Teličko, J.; Virbulis, J.; Jakovičs, A. Experimental and numerical evaluation of the efficiency of an indoor air cleaner under different conditions. In Proceedings of the Healthy Buildings 2023 Europe, Aachen, Germany, 11–14 June 2023; pp. 522–530. [Google Scholar]
- OpenFOAM CFD Software. Available online: https://www.openfoam.com/ (accessed on 12 October 2023).
- Sabanskis, A.; Virbulis, J. Experimental and numerical analysis of air flow, heat transfer and thermal comfort in buildings with different heating systems. Latv. J. Phys. Tech. Sci. 2016, 53, 20–30. [Google Scholar] [CrossRef]
- Jakovics, A.; Gendelis, S.; Ratnieks, J.; Sakipova, S. Monitoring and modelling of energy efficiency for low energy testing houses in Latvian climate conditions. Int. J. Energy 2014, 8, 76–83. [Google Scholar]
- Virbulis, J.; Sjomkane, M.; Surovovs, M.; Jakovics, A. Numerical model for prediction of indoor COVID-19 infection risk based on sensor data. J. Phys. Conf. Ser. 2021, 2069, 012189. [Google Scholar] [CrossRef]
- Ounis, H.; Ahmadi, G. A comparison of Brownian and turbulent diffusion. Aerosol Sci. Technol. 1990, 13, 47–53. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, X. On the numerical study of indoor particle dispersion and spatial distribution. Air Soil Water Res. 2012, 5, 23–40. [Google Scholar] [CrossRef]
- ANSI/AHAM AC-1; Method for Measuring Performance of Portable Household Electric Room Air Cleaners. Association of Home Appliance Manufacturers: Washington, DC, USA, 2006.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).