Abstract
Impact and risk assessments in coastal areas are informed by current and future sea level rise and acceleration, which demands a better understanding of drivers for regional sea level acceleration. In our study, we analyze the near-coastal sea level acceleration compared with global values during satellite altimetry (1993–2020) and discuss the potential drivers of regional sea level acceleration. We estimate regional sea level acceleration using high-resolution satellite altimetry sea surface height anomalies. Our study reveals a wide range of regional acceleration estimates, varying from −1.2 to 1.2 mm·yr−2, which can be up to 20 times larger or smaller than the global mean sea level acceleration of 0.07 mm·yr−2. Notably, sea level acceleration near the global coastline is calculated at 0.10 ± 0.03 mm·yr−2, exceeding the global mean sea level acceleration by 40%. Regional patterns of sea level acceleration are in good agreement with acceleration patterns calculated from the steric sea level. However, the magnitude of acceleration is only partially explained by the changes in steric sea level, with increasing contributions from the non-steric component.
1. Introduction
Climate change and sea level rise are happening worldwide—no region on Earth has escaped it [1]. Coastal areas contain large human populations, more significant socio-economic activities and assets, and more fragile ecosystems. Cities, villages, and coastal communities are facing increasing risk of sea level rise and more frequent and severe coastal inundation, which could lead to huge economic losses [1,2,3,4,5]. Decisions about adequate adaptation options and building a suitable coastal defense could take years; therefore, developing an understanding of the drivers of regional sea level acceleration is key for advanced projections of local sea level rise [2].
Sea level rise is not uniform, and despite the fact that scientists have made significant strides in understanding the global rise and acceleration of sea levels [1,6,7], the estimates for the regional and local sea level accelerations remain highly uncertain [8,9]. From tide gauge-based global sea level reconstructions over the past 100 years [10,11,12] and almost global sea level coverage from satellite altimetry over three decades [1,6,7], there is substantial evidence suggesting that the rate of sea level changes has been increasing in recent decades. Annual global mean sea level rise calculated from satellite altimetry (1993–2021) reached a new high in 2021, increasing to 9.7 cm above 1993 [13] compared to 20 cm since 1900 (1900–2018) [1]. According to the Sixth Assessment Report of the IPCC (Intergovernmental Panel on Climate Change) [14], the global sea level continues to rise due to the increased rate of ice mass loss from glaciers and the Greenland and Antarctic ice sheets and the warming of the ocean. Global sea level rise has accelerated since the late 1960s, with a rate of 2.3 mm·yr−1 for 1971–2018, and it has increased to 3.7 mm·yr−1 for 2006–2018 [14]. In addition, observations from space missions since 1993 and in situ observations of sea level components demonstrate that ice mass loss from the Greenland and Antarctic ice sheets is increasing, and observations in the ocean suggest heat uptake by the ocean is increasing, leading to the sea level rise [13,15].
Regional and local sea level acceleration from tide gauge records in individual locations has been studied since the 1990s [10,16,17]. Nevertheless, the interpretation of the results and discussion of an acceleration in coastal sea level [16] is often unclear, indicating the necessity for a better understanding of drivers of regional sea level rise and acceleration. Recent regional sea level acceleration studies based on satellite altimetry data have discussed the role of sea level variability in detecting a robust trend and acceleration in time series, with PDO and ENSO variability from the Pacific Ocean regions removed [8,18]. The removal of variability is contributing to an improved understanding of the physical mechanisms driving sea level changes. However, for practical applications (e.g., adaptation), removed variability could be observed in the future and might even exceed projected sea level rise in short-term projections [8,19,20,21].
In this study, we provide new insights into regional and near-coastal level acceleration by analyzing satellite altimetry data from 1993–2020. We identify the areas with positive/negative sea level acceleration along the coast, calculated from satellite altimetry, and discuss potential drivers for regional sea level acceleration. We highlight the difficulties in providing a robust estimate of the acceleration in near-coastal sea levels due to limitations of satellite altimetry data in coastal areas and challenges in communicating the calculated regional acceleration to end users, motivated by the importance of understanding the regional sea level changes for adaptation purposes.
2. Materials and Methods
2.1. Data
We calculate regional sea level acceleration using 28 years of satellite altimetry observations (1993–2020) and complement these with steric sea level data. In this study, we denote regional as the ocean basin with spatial scales larger than 100 km. Full-gridded sea surface height anomalies were obtained from NASA JPL (Jet Propulsion Laboratory) (https://podaac.jpl.nasa.gov/dataset/SEA_SURFACE_HEIGHT_ALT_GRIDS_L4_2SATS_5DAY_6THDEG_V_JPL2205 (accessed on 3 April 2023)) [22] with a spatial resolution of 0.17° × 0.17° between 1993 and 2020 and the latitude ranging from 80° N to 80° S. This is a combined altimetry product derived from several altimeters.
Using satellite altimetry data, we calculated the global mean sea level acceleration from the global mean time series of sea level, while near-coastal sea level acceleration is estimated from the time series within the area of 0.2° around the global coastline. By doing so, we utilize available altimetry data within 20 km from the coast [9,23] and denote them as the ‘near coastal’ sea level.
To examine the drivers of regional sea level acceleration, we examine the acceleration of the steric sea level. The Institute of Atmospheric Physics (IAP) steric sea level (1993–2020) with a 1° × 1° horizontal resolution for the upper 2000 m layers is used here, which shows advantages in reducing the sampling errors by infilling data gaps with available observations following an improved ensemble optimal interpolation method [24]. We re-grid IAP data to the resolution of the satellite altimetry data (0.17° × 0.17°). The IAP steric sea level is obtained from the Institute of Atmospheric Physics, Chinese Academy of Sciences (http://www.ocean.iap.ac.cn/pages/dataService/dataService.html (accessed on 3 April 2023)) [24]. The monthly IAP steric data, referring to thermosteric changes, are corrected for biases in XBT and MBT temperature data [24]. We have not made any corrections for Pinatubo in gridded datasets of altimetry and steric sea level time series due to the lack of information on regional patterns associated with volcanic eruption.
In this study, we consider two dominant climate indexes impacting the sea level acceleration: El Niño-Southern Oscillation (ENSO) from https://psl.noaa.gov/enso/mei-/data/meiv2.data (accessed on 3 April 2023) and Pacific Decadal Oscillation (PDO) from https://www.ncdc.noaa.gov/teleconnections/pdo/ (accessed on 3 April 2023) [7]; both indexes are monthly data for 1993–2020. MEI index represents the ENSO signal and is the Multivariate ENSO index, which combines several climate variables including sea surface temperature and pressure, surface wind, and outgoing long-wavelength radiation over the tropical Pacific [7,25].
2.2. Methods
We apply a regression model to estimate the regional and global mean sea level acceleration, and annual and semi-annual cycles are removed from the time series, as we apply a 6- and 12-month least-square fit prior to analysis:
where is time, to coefficients are estimated following the least-squares fit, and is the reprocessed sea level time series. We estimate acceleration using the conventional method as twice the quadratic coefficient (Equation (1)). The calculations of acceleration are implemented using the function polyfit in MATLAB, which also provides key statistics for estimating the confidence interval at a 95% level with the function polyparci. The standard deviation is calculated from what the polyfit model could not fit in the observational data, and in this analysis, we assume the residuals are pure noise following Veng and Andersen (2021) [25]. The p value is calculated to test if the regional acceleration is statistically significant.
To determine the contribution of internal variability to regional and global mean sea level acceleration, we apply a linear regression model to the climate indexes following Moreira et al. (2021) [7], and annual and semi-annual cycles are removed from the time series prior to analysis [7]:
where is time, to coefficients are estimated following the least-squares fit, and is the reprocessed sea level time series.
3. Results
Using satellite altimetry, we have calculated a global mean sea level acceleration of 0.07 ± 0.01 mm·yr−2. Our estimate of the global mean sea level acceleration is in good agreement with the previously estimated acceleration of 0.08 ± 0.01 mm·yr−2 by Veng and Andersen (2021) [26], within the margin of errors in both estimates.
To explore the changes in patterns of regional sea level acceleration, we calculate the patterns of regional acceleration from satellite altimetry, IAP steric, and their difference from 1993 to 2020 (Figure 1a–c). Regional acceleration in most locations is 10–20 times larger/smaller than the global mean number (Figure 1a), with extreme estimates from −5.1 mm·yr−2 to 4.15 mm·yr−2 in individual locations, mainly in dynamically active parts of the ocean, e.g., Kuroshio, the Southern Ocean, and the North Atlantic. Almost 48% of the ocean area covered by the satellite altimetry demonstrates a positive value of acceleration, while 28% is negative and 24% is inconclusive or statistically not significant. Regional acceleration patterns (Figure 1a) mimic the PDO/ENSO patterns in the Pacific [8,26].
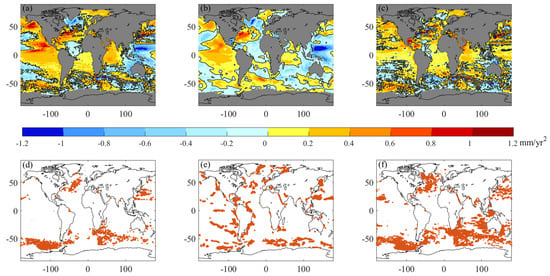
Figure 1.
Acceleration (mm·yr−2) from satellite altimetry (a); IAP (b) and their difference (c) for 1993–2020. Statistical significance test of the estimates of acceleration for (d) satellite altimetry, (e) IAP steric; and (f) the difference between estimates from satellite altimetry and IAP steric.
There is agreement between the patterns for steric sea level acceleration calculated using IAP steric sea level datasets from Cheng et al., 2017 [26] and for sea level acceleration from satellite altimetry (Figure 1a–c). However, the map of the differences between the acceleration from satellite altimetry and steric sea levels shows there is a large contribution from other sources not associated with steric sea level changes. Statistical significance tests of the estimates of acceleration for satellite altimetry, IAP steric, and the difference between estimates from satellite altimetry and IAP steric are presented in Figure 1d–f, illustrating that the acceleration in areas with large internal variability is not statistically significant. Correlation maps shown in Figure S1 provide evidence of a strong correlation between the patterns (Figure 1a–c).
To determine the contribution of internal variability, represented by PDO and ENSO, we calculate the patterns of regional acceleration from satellite altimetry, IAP steric, and their difference from 1993 to 2020 after removing internal variability (Figure 2a–c). Figure 2 shows that the acceleration from both satellite altimetry and the IAP steric sea level decreases in the Pacific Ocean after the removal of variability associated with ENSO and PDO. The significance test proves that many areas in the Northwestern Pacific have no significant acceleration of the steric sea level after removing the internal variability.
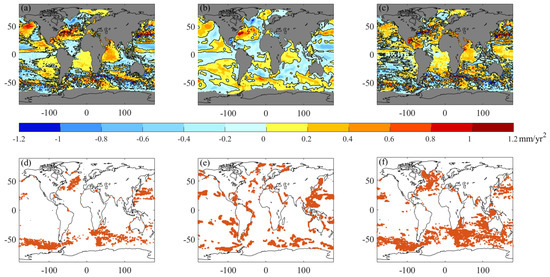
Figure 2.
Acceleration (mm·yr−2) from satellite altimetry (a); IAP (b) and their difference (c) after removing the internal variability for 1993–2020. Statistical significance test of the estimates of acceleration for (d) satellite altimetry, (e) IAP steric, and (f) the difference between estimates from satellite altimetry and IAP steric after removing the internal variability.
Global near-coastal sea level acceleration, calculated from the satellite altimetry grid points close to the coastline, is 0.10 ± 0.03 mm·yr−2 (Figure 3a,b), exceeding the global mean sea level acceleration of 0.07 ± 0.01 mm·yr−2 by 40%. We have calculated the difference between the time series of sea level close to the coast and global mean sea level (Figure S2b), obtaining a significant residual acceleration of 0.03 ± 0.03 mm·yr−2 in the difference. Around 24% of near-coastal locations display a negative value of acceleration, and 61% of near-coastal locations exceed the estimate of global mean acceleration (Figure 4a).
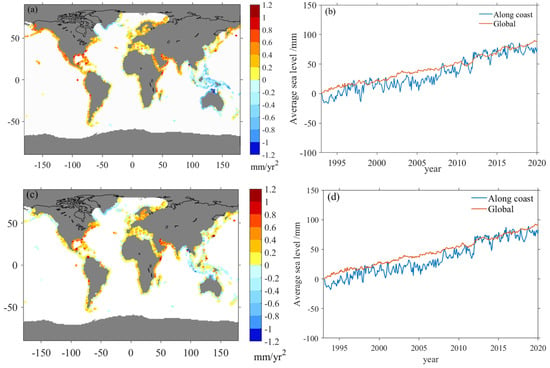
Figure 3.
Acceleration calculated using satellite altimetry data close to coastline (a). Global mean sea level time series from 1993–2020 are represented by the red line, and global near-coastal mean sea level is represented by blue, calculated from satellite altimetry values close to the coastline (b). Acceleration close to the coastline after removing the internal variability (c). Global mean sea level time series after removing the internal variability are represented by the red line, and global near-coastal mean sea level after removing the internal variability is represented by blue (d).
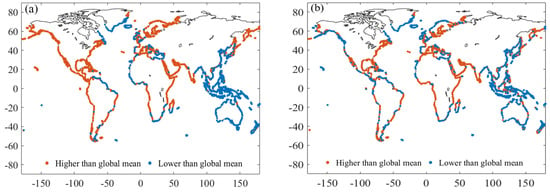
Figure 4.
Near-coastal locations with acceleration exceeding the global estimate (brown) and below the global estimate (blue) (a). Near-coastal locations with acceleration exceeding the global estimate (brown) and below the global estimate (blue) after removing the internal variability (b).
The global mean for near-coastal sea level, calculated from satellite altimetry along the coastline, is 3.5 ± 0.3 mm·yr−1 compared to our global mean trend of 3.1 ± 0.3 mm·yr−1 (Figure 3b). The near-global coastline sea level trend is statistically different from the global mean sea level trend, with a rate of difference in the time series of 0.4 ± 0.3 mm·yr−1 (Figure S2).
After removing ENSO and PDO signals (Figure 3c,d), global near-coastal sea level acceleration decreases from 0.10 ± 0.03 mm·yr−2 to 0.09 ± 0.03 mm·yr−2, while the global mean sea level acceleration decreases from 0.07 ± 0.01 mm·yr−2 to 0.04 ± 0.01 mm·yr−1. The removal of internal variability, associated with ENSO and PDO, leads to a decrease in the global mean sea level acceleration by approximately 0.03 mm·yr−2 as previously reported by Nerem et al. (2018) [6]. After the removal of ENSO and PDO signals, the calculated near-coastal sea level acceleration exceeds the global mean sea level acceleration by 125%. Compared with the global mean sea level acceleration, the global near-coastal sea level acceleration is less influenced by the removal of internal variability. The global near-coastal sea level trend changes from 3.5 ± 0.3 mm·yr−1 to 3.6 ± 0.3 mm·yr−1 with the removal of internal variability, and the global mean sea level trend changes from 3.1 ± 0.3 mm·yr−1 to 3.2 ± 0.1 mm·yr−1 after removing the internal variability (Table S1). After removing the internal variability (Figure 4b), there is a slight decrease (4%) in near-coastal locations exceeding the estimate of the global mean acceleration, which is mainly located on the Atlantic coast of America.
To interpret the evolution of the regional acceleration pattern, we calculate the sea level acceleration for a twenty-year moving window from satellite altimetry (Figure 5), IAP steric (Figure 6), and the difference between them (Figure 7). Patterns of acceleration for satellite altimetry and the steric sea level are changing with time (Figure 5 and Figure 6). The time-varying spatial pattern of acceleration from satellite altimetry and IAP steric sea levels shows high homogeneity, which is prominently observed in the Pacific Ocean and other regions [8]. The regional acceleration map of the moving window from altimetry and IAP steric shows a homogenous time-varying spatial pattern in the North Atlantic and the Indian oceans (Figure 5 and Figure 6).
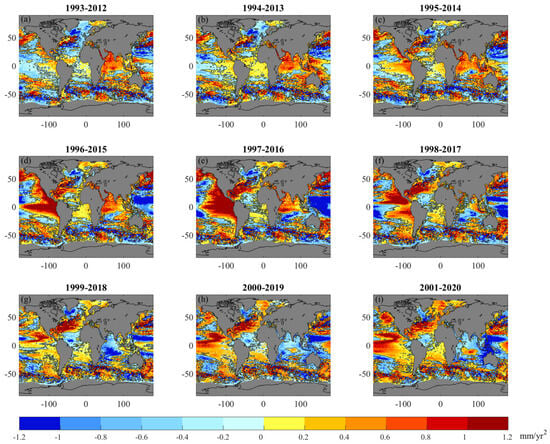
Figure 5.
Evolution of the satellite altimetry patterns of acceleration for moving 20-year time window by one year since 1993.
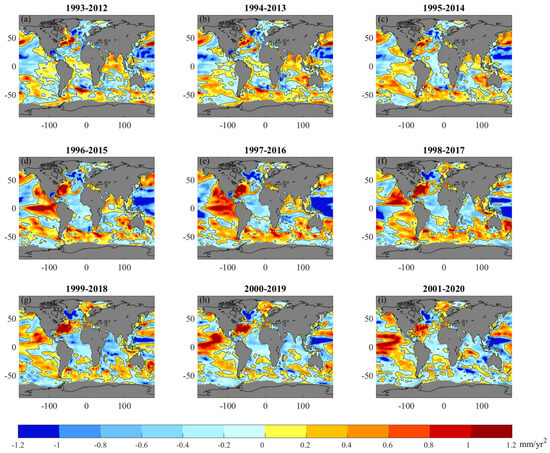
Figure 6.
Evolution of the steric sea level patterns of acceleration for moving 20-year time window by one year since 1993.
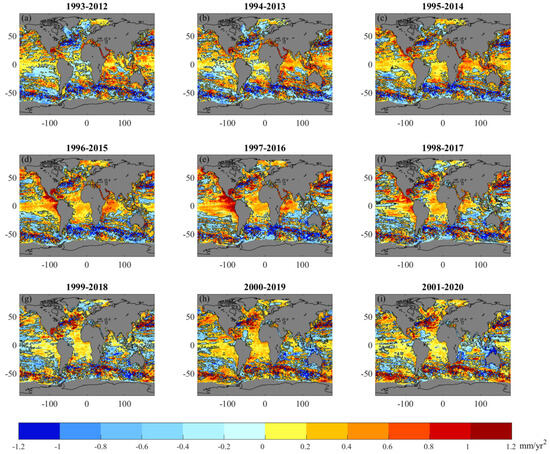
Figure 7.
Evolution of the differences between acceleration calculated from satellite altimetry and steric sea level for 20-year time period shifted by one year since 1993.
With the starting year of the moving window changing from 1993 to 1997, the acceleration becomes stronger in the eastern tropical Pacific and extends northwestward until it reaches the North American coast for both altimetry and IAP steric; then the pattern weakens largely followed by strengthening again. At the same time, in the central and western North Pacific, the acceleration patterns of the moving window display the opposite signs (Figure 5 and Figure 6). With the starting year of the moving window changing since 1998, the weakening of regional acceleration patterns from both altimetry and IAP steric is observed in the Indian Ocean. Since 1993, there has been a strengthening of spatial acceleration patterns from both altimetry and IAP steric sea levels in the North Atlantic Subtropical Gyre region, accompanied by a weakening of spatial acceleration patterns in the Subpolar Gyre region.
4. Discussion
Using high-resolution gridded satellite altimetry data, we have estimated that sea level acceleration close to the coast is 0.10 ± 0.03 mm·yr−2, exceeding the global mean sea level acceleration of 0.07 ± 0.01 mm·yr−2 by 40%. Considering the dense population and concentrative infrastructures in coastal zones, the higher increase rate of sea level rise will place low-lying coastal regions under great threat due to global warming. Elevated water levels caused by accelerated sea level rise will exacerbate coastal flooding and erosion. The implications for adaptation are that decision makers and planners require a skillful understanding of such coastal processes along coastlines, and more attention should be paid to densely populated areas.
Faster acceleration at near-coastal locations compared to the global mean sea level acceleration could be explained by numerous near-coastal processes and ocean adjustment mechanisms in shelf seas [27,28,29], including local atmospheric effects or coastal trapped waves, baroclinic instabilities, shelf currents, and freshwater transport in estuaries [27,28,29,30]. In addition, there are some well-known limitations of satellite altimetry data close to the coastline, resulting from land contamination and the lack of optimized geophysical corrections applied to the coastal zones [9]. However, despite the large uncertainties, satellite altimetry data have been used for many applications along the coastline, e.g., estimating local vertical land movement [31,32,33], assessing interannual sea level variability along the coastal areas of the USA [34], and assessing coastal vulnerability facing sea level rise in Indian Sundarban delta [35]. Also, the uncertainty ranges of sea level acceleration estimated from gridded satellite altimetry for four different regions along the coastal United States are consistent with tide gauge acceleration envelopes [36].
We calculated the near-coastal sea level acceleration from the gridded satellite altimetry to make it comparable with global mean sea level acceleration. The error estimation in our acceleration is relatively conservative and does not reflect the uncertainties in the original datasets, as discussed in several publications [9,33]. Our estimations of sea level acceleration are dependent on the time slices, and the relatively short period of satellite altimetry limits our present understanding of coastal, regional, and global sea level acceleration. Longer records of high-resolution satellite altimetry along with improved corrections are in demand for robust sea level acceleration evaluation in the future. Sea level acceleration for coastal locations (not considered in this study) could be enhanced by subsidence from groundwater extraction, urbanization, and tectonic activities [5,9,31]. However, incorporating changes in sea level acceleration due to tectonic activities and land movement is beyond the scope of this analysis, particularly given the limitations of satellite altimetry data close to the coastline.
The removal of natural variability, represented by ENSO and PDO, reveals that there are decreases in sea level acceleration from both satellite altimetry and the IAP steric sea level in the Pacific Ocean from 1993–2020. Our study supports the role of ENSO and PDO for satellite altimetry sea level acceleration, which has been previously discussed in several studies [6,7,26]. Our regional acceleration estimates reflect the challenges of separating the wide range of variability resulting from complex interactions of various climate signals [7], and we demonstrate the sea level acceleration results with and without the removal of ENSO and PDO. We have performed this for the purpose of communicating the observed sea level changes to policy makers and the general public, considering their interest in the interpretation of observed changes and the use of observations for adaptation purposes.
In the Pacific Ocean, changes in the acceleration patterns from 1997–2016, in which the eastern tropical Pacific has the largest area of acceleration while the central and western North Pacific has the largest area of deceleration, are consistent with the significant climate shift in the PDO [25,37,38].
In the Indian Ocean, the weakening of spatial acceleration patterns from both altimetry and IAP steric has been observed in the coastal regions of South Asia since 1998. Changes in the patterns of acceleration in the Indian Ocean might be explained by the decadal variability in sea surface height associated with decadal Indian Ocean basin mode (DIOB), supported by previous studies [19,20,39]. However, the mechanisms for decadal variability in the Indian Ocean are not fully explained [19,40]. Since 1993, there has been a strengthening of regional acceleration patterns from both altimetry and IAP steric sea levels in the North Atlantic Subtropical Gyre region, accompanied by a weakening of spatial acceleration patterns in the Subpolar Gyre region (Figure 5 and Figure 6). We attribute these patterns to the decadal sea level fluctuations partly driven by surface wind and heat flux associated with climate modes, e.g., the North Atlantic Oscillation (NAO) in combination with changes in the Atlantic Multidecadal Oscillation (AMO), as suggested by Han et al., 2019 [20]. This is supported by modelling studies [41,42] with evidence that on a decadal timescale, variability in the North Atlantic is a combination of internal variability [43,44]. The dipole of the spatial acceleration pattern in the Subtropical Gyre and Subpolar Gyre regions is thought to be a distinctive fingerprint of the AMOC (Atlantic Meridional Overturning Circulation) [19,45,46,47], suggesting that changes in the AMOC can be gyre-specific rather than an isolated basin-scale cell [19]. However, there are open questions about the variability in the AMOC due to limited direct measurements of the AMOC, which are only available over a decade [48].
Large uncertainties in observations [15,24,26] and the large variability in relatively short time series contribute to the lack of robust estimates for acceleration, which has been discussed previously [26,39,49]. As the need for more detailed sea level information near the coast with a focus on impacts and adaptations is emerging, there is a growing demand for sustainable sea level monitoring and related observations (e.g., steric sea level) to improve our understanding of the sea level rise and its acceleration in coastal areas.
5. Conclusions
Sea level acceleration close to the global coastline is 0.10 ± 0.03 mm·yr−2, calculated from satellite altimetry, and exceeds the global mean sea level acceleration of 0.07 ± 0.01 mm·yr−2 by 40%. The regional patterns of sea level acceleration are mainly explained by the changes in steric sea level, compared to the increased contribution from ice mass loss from the sheets and glaciers suggested as the main driver for acceleration in the global mean sea level in a previous study [8]. However, there is a caveat whereby for regional sea level patterns, the magnitude of acceleration from the steric sea level is relatively smaller compared to the estimates from the satellite altimetry data. The calculated difference in the patterns is increasing, suggesting there is an additional non-steric contribution to the regional accelerations.
The regional acceleration calculated from the gridded satellite altimetry data displays almost 20 times larger/smaller estimates for acceleration compared to the global mean value of 0.07 mm·yr−2. Compared to previous studies, in which part of the internal variability was removed, our estimates provide evidence of a large redistribution of heat and ocean mass by the previously detected climate modes (e.g., PDO and ENSO) in the Pacific regions [8]. The similarity in the patterns of acceleration in satellite altimetry and the steric sea level suggests common mechanisms for redistribution by ocean dynamics [20]. It seems that dynamical changes in the ocean are driving the patterns of acceleration on a regional scale and along the global coastline, in contrast to the ice mass loss contribution to the global mean sea level acceleration.
Sea level rise along the global coastline will increase the frequency of flooding and intensify the risks for millions of people living in low-lying coastal areas [1,2]. Policy makers and planners require a robust estimate of the rate of sea level rise and its acceleration for adequate adaptation options. However, there is an open question as to whether the near-coastal acceleration calculated from satellite altimetry data is a robust feature, considering the changes in ocean dynamics are amplifying the global mean sea level acceleration in large ocean basins and along the coast. In addition, there is the crucial task of improving the communication/delivery of the required scientific information about future sea level changes between scientists and policy makers, coastal engineers, and the public. For stakeholders in charge of coastal planning and risk assessment, the availability of robust scientific information is crucial for decision-making about adaptation options.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos14101573/s1, Figure S1: Map of correlation coefficients between altimetry and IAP steric for 1993–2020 (a) and correlation coefficients between altimetry and the difference for 1993–2020 (b); Figure S2: Panel (a) Global mean sea level time series 1993–2020 are represented by the red line, and global near-coastal mean sea level (1993–2020) is represented by blue color. Global near-coastal mean sea level is calculated from satellite altimetry values close to the coastline. Panel (b) The difference between global near-coastal sea level and global mean sea level is represented by blue dots.; Table S1: Estimates of trend (mm·yr−1) and acceleration (mm·yr−2) for global near-coastal and global mean sea levels.
Author Contributions
S.J., Y.Q. and H.P. designed the study. Y.Q., S.J. and H.P. performed the analyses. Y.Q. and S.J. prepared the manuscript. Y.Q., S.J. and H.P. provided suggestions, ideas, and discussion and improved the writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are supported by the State Key Laboratory of Earth Surface Processes and Resource Ecology (2022-ZD-05), Beijing Normal University. SJ is supported by NERC NC International programme: Future states of the global Coastal ocean: Understanding for Solutions (FOCUS: NE/X006271/1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors declare that all data supporting the findings of our study are available within the paper.
Acknowledgments
The authors gratefully acknowledge Yonggang Liu for the helpful suggestions. Authors are grateful to the comments from three reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allan, R.P.; Hawkins, E.; Bellouin, N.; Collins, B. IPCC, 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 3–32. [Google Scholar] [CrossRef]
- Pörtner, H.O.; Roberts, D.C.; Poloczanska, E.S.; Mintenbeck, K.; Tignor, M.; Alegría, A.; Craig, M.; Langsdorf, S.; Löschke, S.; Möller, V.; et al. (Eds.) IPCC, 2022: Summary for Policymakers. In Climate Change 2022: Impacts, Adaptation and Vulnerability; Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; pp. 3–33. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Jackson, L.P.; Grinsted, A.; Lincke, D.; Marzeion, B. Flood damage costs under the sea level rise with warming of 1.5 °C and 2 °C. Environ. Res. Lett. 2018, 13, 074014. [Google Scholar] [CrossRef]
- Brown, S.; Jenkins, K.; Goodwin, P.; Lincke, D.; Vafeidis, A.T.; Tol, R.S.; Warren, R.; Nicholls, R.J.; Jevrejeva, S.; Sanchez Arcilla, A.; et al. Global costs of protecting against sea-level rise at 1.5 to 4.0 °C. Clim. Change 2021, 167, 4. [Google Scholar] [CrossRef]
- Abadie, L.M.; Jackson, L.P.; Murieta, E.S.; Jevrejeva, S.; Galarraga, I. Comparing urban coastal flood risk in 136 cities under two alternative sea-level projections: RCP 8.5 and an expert opinion-based high-end scenario. Ocean Coast. Manag. 2020, 193, 105249. [Google Scholar] [CrossRef]
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-changedriven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Moreira, L.; Cazenave, A.; Palanisamy, P. Influence of interannual variability in estimating the rate and acceleration of present-day global mean sea level. Glob. Planet. Change 2021, 199, 103450. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Frederikse, T.; Nerem, R.S.; Fasullo, J.T.; Adhikari, S. Investigating the acceleration of regional sea level rise during the satellite altimeter era. Geophys. Res. Lett. 2020, 47, e2019GL086528. [Google Scholar] [CrossRef]
- Prandi, P.; Meyssignac, B.; Ablain, M.; Spada, G.; Ribes, A.; Benveniste, J. Local sea level trends, accelerations and uncertainties over 1993–2019. Sci. Data 2021, 8, 1. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Matthews, A.P.; Spada, G. Trends and acceleration in global and regional sea levels since 1807. Glob. Planet. Change 2014, 113, 11–12. [Google Scholar] [CrossRef]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481–484. [Google Scholar] [CrossRef]
- Frederikse, T.; Jevrejeva, S.; Riva, R.E.M.; Dangendorf, S. A Consistent Sea-Level Reconstruction and Its Budget on Basin and Global Scales over 1958–2014. J. Clim. 2018, 31, 1267–1280. [Google Scholar] [CrossRef]
- Johnson, G.C.; Lumpkin, R.L. (Eds.) State of the Climate in 2020. Global Oceans; American Meteorological Society: Boston, MA, USA, 2021. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Hewitt, H.T.; Xiao, C. Ocean, Cryosphere and Sea Level Change. In Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1211–1362. [Google Scholar] [CrossRef]
- Wouters, B.; van de Wal RS, W. Global sea level budget 1993-present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar]
- Douglas, B.C. Global sea level acceleration. J. Geophys. Res. 1992, 97, 12699–12706. [Google Scholar] [CrossRef]
- Woodworth, P.L.; White, N.; Jevrejeva, S.; Holgate, S.; Church, J.A.; Gehrels, W.R. Evidence for the accelerations of sea level on multi-decade and century timescales. Int. J. Climatol. 2009, 29, 777–789. [Google Scholar] [CrossRef]
- Royston, S.; Watson, C.S.; Legrésy, B.; King, M.A.; Church, J.A.; Bos, M.S. Sea-level trend uncertainty with pacific climatic variability and temporally-correlated noise. J. Geophys. Res. Ocean. 2018, 123, 1978–1993. [Google Scholar] [CrossRef]
- Han, W.; Meehl, G.A.; Stammer, D.; Hu, A.; Hamlington, B.; Kenigson, J.; Palanisamy, H.; Thompson, P. Spatial patterns of sea level variability associated with natural internal climate modes. Surv. Geophys. 2017, 38, 217–250. [Google Scholar] [CrossRef]
- Han, W.; Stammer, D.; Thompson, P.; Ezer, T.; Palanisamy, H.; Zhang, X.; Domingues, C.; Zhang, L.; Yuan, D. Impacts of basin-scale climate modes on coastal sea level: A review. Surv. Geophys. 2019, 40, 1493–1541. [Google Scholar] [CrossRef]
- Wang, J.; Church, J.A.; Zhang, X.; Chen, X. Reconciling global mean and regional sea level change in projections and observations. Nat. Commun. 2021, 12, 990. [Google Scholar] [CrossRef]
- Fournier, S.; Willis, J.; Killett, E.; Qu, Z.; Zlotnicki, V. JPL MEaSUREs Gridded Sea Surface Height Anomalies Version 2205. 2022. Available online: https://deotb6e7tfubr.cloudfront.net/s3-edaf5da92e0ce48fb61175c28b67e95d/podaac-ops-cumulus-docs.s3.us-west-2.amazonaws.com/merged_alt/open/L4/docs/Documentation_SSH_Measures_V2205_Final.pdf?A-userid=None&Expires=1695387427&Signature=TiAoUOLUmRGqY9LeZwB5qk24b7140~gRe1S-LaQFLJtpoY-mOakPQzMmjnO0~GjaSdyd-micQyYpCJbM~8vbK6wR~ryeg1MnK-ldteUm2UXIAbWL3zDDbs-H8NauZSKTpsZkd~mB1mSNya1FmaWpFslrvKPESa~j4emQNB8WmDQiSLs38lk3GJH7OAgDdYu8g3ds2ATk28wBQ~tONwSe1P7QbHfNu0eEjFjGAHzCtAUNdkRPfwabq0LtnXtsFP~YvyrI1o-AyOH01I0QnWd2jPN0Idw5reHwWjB-vNjHWs~pzlCeyVZXaz9SZTOBvOb6ebUhJs9lm0jt1CDDrr2Mvw__&Key-Pair-Id=K2FIJB4PE30EQE (accessed on 21 September 2022).
- Cazenave, A.; Gouzenes, Y.; Birol, F.; Leger, F.; Passaro, M.; Calafat, F.M.; Shaw, A.; Nino, F.; Legeais, J.F.; Oelsmann, J.; et al. Sea level along the world’s coastlines can be measured by a network of virtual altimetry stations. Commun. Earth Environ. 2022, 3, 117. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J.; Zhu, J. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef]
- Zhang, L.; Delworth, T.L. Analysis of the characteristics and mechanisms of the Pacific decadal oscillation in a suite of coupled models from the Geophysical Fluid Dynamics Laboratory. J. Clim. 2015, 28, 7678–7701. [Google Scholar]
- Veng, T.; Andersen, O.B. Consolidating sea level acceleration estimates from satellite altimetry. Adv. Space Res. 2021, 68, 496–503. [Google Scholar] [CrossRef]
- Cipollini, P.; Benveniste, J.; Birol, F.; Fernandes, M.J.; Obligis, E.; Passaro, M.; Strub, P.T.; Valladeau, G.; Vignudelli, S.; Wilkin, J. Satellite altimetry in coastal regions. In Satellite Altimetry Over the Oceans and Land Surfaces; Stammer, D., Cazenave, A., Eds.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2018; pp. 343–373. [Google Scholar] [CrossRef]
- Durand, F.; Piecuch, C.G.; Becker, M.; Papa, F.; Raju, S.V.; Khan, J.U.; Ponte, R.M. Impact of continental freshwater runoff on coastal sea level. Surv. Geophys. 2019, 40, 1437–1466. [Google Scholar]
- Woodworth, P.L.; Melet, A.; Marcos, M.; Ray, R.D.; Wöppelmann, G.; Sasaki, Y.N.; Cirano, M.; Hibbert, A.; Huthnance, J.M.; Monserrat, S.; et al. Forcing Factors Causing Sea Level Changes at the Coast. Surv. Geophys. 2019, 40, 1351–1397. [Google Scholar] [CrossRef]
- The Climate Change Initiative Coastal Sea Level Team. Coastal sea level anomalies and associated trends from Jason satellite altimetry over 2002–2018. Sci. Data 2020, 7, 357. [Google Scholar] [CrossRef]
- Ostanciaux, É.; Husson, L.; Choblet, G.; Robin, C.; Pedoja, K. Present-day trends of vertical ground motion along the coast lines. Earth Sci. Rev. 2012, 110, 74–92. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Kleinherenbrink, M.; Riva, R.; Frederikse, T. A comparison of methods to estimate vertical land motion trends from GNSS and altimetry at tide gauge stations. Ocean Sci. 2018, 14, 187–204. [Google Scholar] [CrossRef]
- Volkov, D.L.; Lee, S.L.; Domingues, R.; Zhang, H.; Goes, M. Interannual Sea Level Variability Along the Southeastern Seaboard of the United States in Relation to the Gyre-Scale Heat Divergence in the North Atlantic. Geophys. Res. Lett. 2019, 46, 7481–7490. [Google Scholar] [CrossRef]
- Ghosh, S.; Mistri, B. Assessing coastal vulnerability to environmental hazards of Indian Sundarban delta using multi-criteria decision-making approaches. Ocean Coast. Manag. 2021, 209, 105641. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Chambers, D.P.; Frederikse, T.; Dangendorf, S.; Fournier, S.; Buzzanga, B.; Nerem, R.S. Observation-based trajectory of future sea level for the coastal United States tracks near high-end model projections. Commun. Earth Environ. 2022, 3, 230. [Google Scholar] [CrossRef]
- Cayan, D.R.; Kammerdiener, S.A.; Dettinger, M.D.; Caprio, J.M.; Peterson, D.H. Changes in the onset of spring in the western United States. Bull. Amer. Meteor. Soc. 2001, 82, 399–415. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.S.; Hurrell, J.W. Pacific interdecadal cli- mate variability: Linkages between the tropics and the North Pacific during boreal winter since 1900. J. Clim. 2004, 17, 3109–3124. [Google Scholar] [CrossRef]
- Cazenave, A.; Moreira, L. Contemporary sea-level changes from global to local scales: A review. Proc. R. Soc. A 2022, 478, 20220049. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, S.; Gnanaseelan, C.; Deepa, J.S. Multidecadal to decadal variability in the equatorial Indian Ocean subsurface temperature and the forcing mechanisms. Clim. Dyn. 2020, 54, 3475–3487. [Google Scholar] [CrossRef]
- Delworth, T.L.; Zeng, F. The impact of the North Atlantic Oscillation on climate through its influence on the Atlantic meridional overturning circulation. J. Clim. 2016, 29, 941–962. [Google Scholar] [CrossRef]
- Kim, W.M.; Yeager, S.; Danabasoglu, G. Atlantic multidecadal variability and associated climate impacts initiated by ocean thermohaline dynamics. J. Clim. 2020, 33, 1317–1334. [Google Scholar] [CrossRef]
- Borchert, L.F.; Müller, W.A.; Baehr, J. Atlantic ocean heat transport influences interannual-to-decadal surface temperature predictability in the North Atlantic region. J. Clim. 2018, 31, 6763–6782. [Google Scholar] [CrossRef]
- Menary, M.B.; Robson, J.; Allan, R.P.; Booth BB, B.; Cassou, C.; Gastineau, G.; Gregory, J.; Hodson, D.; Jones, C.; Mignot, J.; et al. Aerosol-forced AMOC changes in CMIP6 historical simulations. Geophys. Res. Lett. 2020, 47, e2020GL088166. [Google Scholar] [CrossRef]
- Zhang, R. Coherent surface-subsurface fingerprint of the Atlantic meridional overturning circulation. Geophys. Res. Lett. 2008, 35, L20705. [Google Scholar] [CrossRef]
- Caesar, L.; Rahmstorf, S.; Robinson, A.; Feulner, G.; Saba, V. Observed fngerprint of a weakening Atlantic Ocean overturning circulation. Nature 2018, 556, 191–196. [Google Scholar] [CrossRef]
- Sallenger, A.H.; Doran, K.S.; Howd, P.A. Hotspot of accelerated sea-level rise on the Atlantic coast of North America. Nat. Clim. Change 2012, 2, 884–888. [Google Scholar] [CrossRef]
- McCarthy, G.D.; Brown, P.J.; Flagg, C.N.; Goni, G.; Houpert, L.; Hughes, C.W.; Hummels, M.; Inall, M.; Jochumsen, K.; Larsen, K.M.H.; et al. Sustainable observations of the AMOC: Methodology and technology. Rev. Geophys. 2020, 58, e2019RG000654. [Google Scholar] [CrossRef]
- Kleinherenbrink, M.; Riva, R.; Scharroo, R. A revised acceleration rate from the altimetry-derived global mean sea level record. Sci. Rep. 2019, 9, 10908. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).