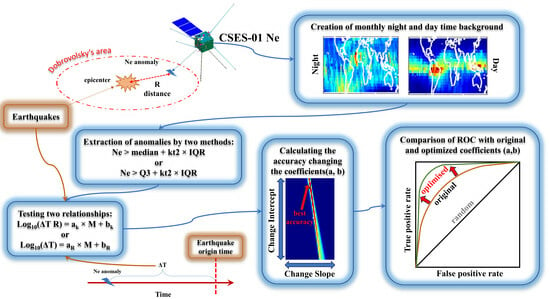
CSES-01 Electron Density Background Characterisation and Preliminary Investigation of Possible Ne Increase before Global Seismicity
Abstract
:1. Introduction
1.1. Ionosphere and Its Characterisation
1.2. Previous Studies on Seismo-Ionospheric Disturbances
1.3. CSES Satellite Mission
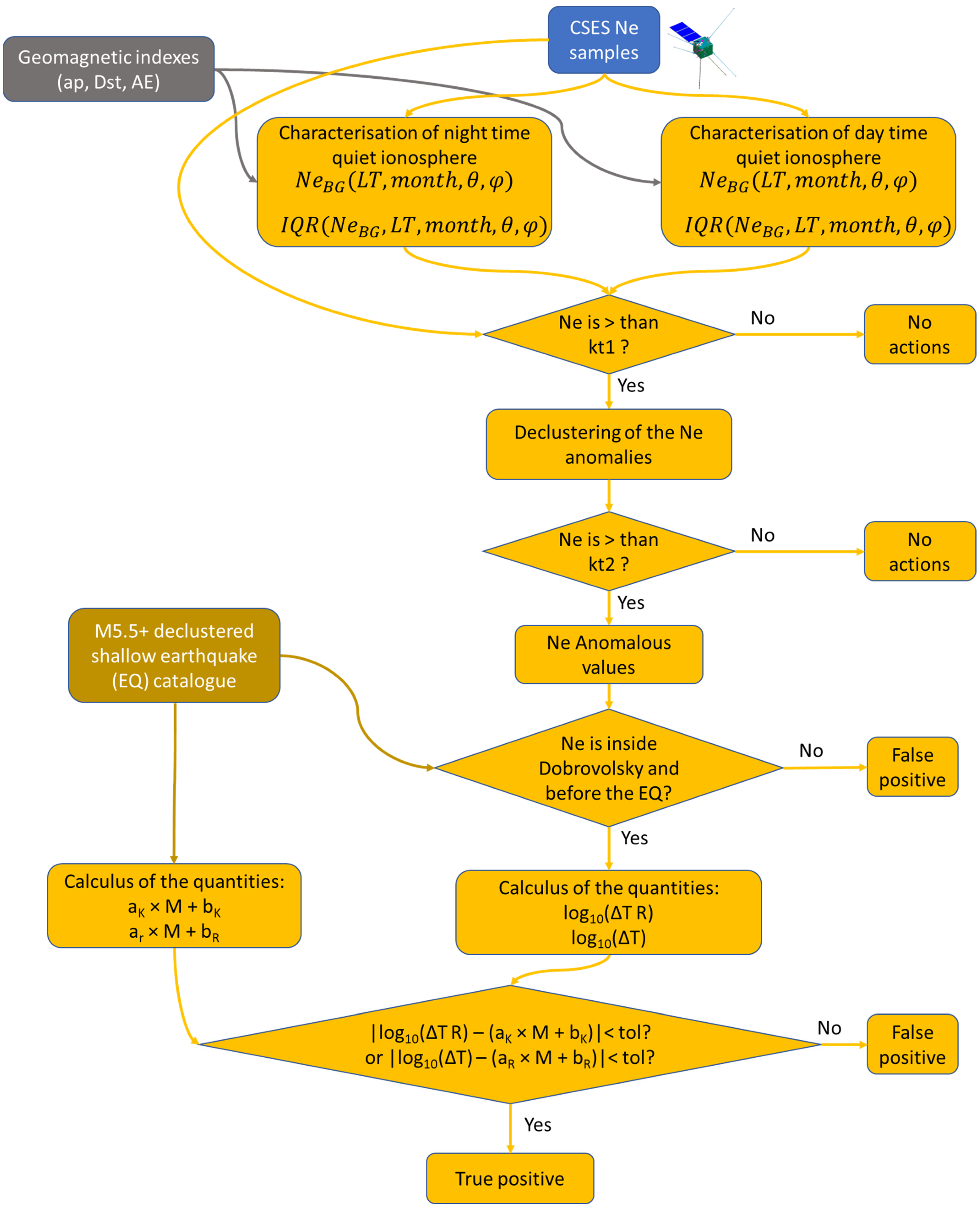
2. Materials and Methods
- Data organisation by cells, regions, and local time;
- Data selection in geomagnetic quiet time;
- Background estimation end extraction of samples with higher Ne;
- Preparation of the earthquake catalogue;
- Declustering of the high Ne samples;
- Extraction of the anomalies;
- Testing the possible relationship between the distance and anticipation time of anomalies and earthquake magnitude;
- Assessment of prediction capability with confusion matrix and ROC curves.
2.1. Background Characterisation
2.1.1. Data Organisation by Cells, Regions, and Local Time
2.1.2. Data Selection in Geomagnetic Quiet Time
- The equatorial region with ap ≤ 32 nT in the previous 24 h, |Dst| ≤ 20 nT during acquisition, and |Dst| ≤ 30 nT in the previous 24 h.
- The mid-latitude region with ap ≤ 32 nT, |Dst| ≤ 20 nT during acquisition, |Dst| ≤ 30 nT in the previous 24 h, AE ≤ 300 nT in the previous 6 h, and AE ≤ 200 nT during the acquisition.
2.1.3. Background Estimation End Extraction of Samples with Higher Ne
2.2. Correlation of Electron Density Anomalies with Earthquakes
2.2.1. Preparation of the Earthquake Catalogue
2.2.2. Declustering of the High Ne Samples
2.2.3. Extraction of the Anomalies
- Anomaly = Ne > Median + kt2 × IQR;
- Anomaly = Ne > Q3 + kt2 × IQR (if kt2 = 1.5, this is the definition of a mild positive outlier).
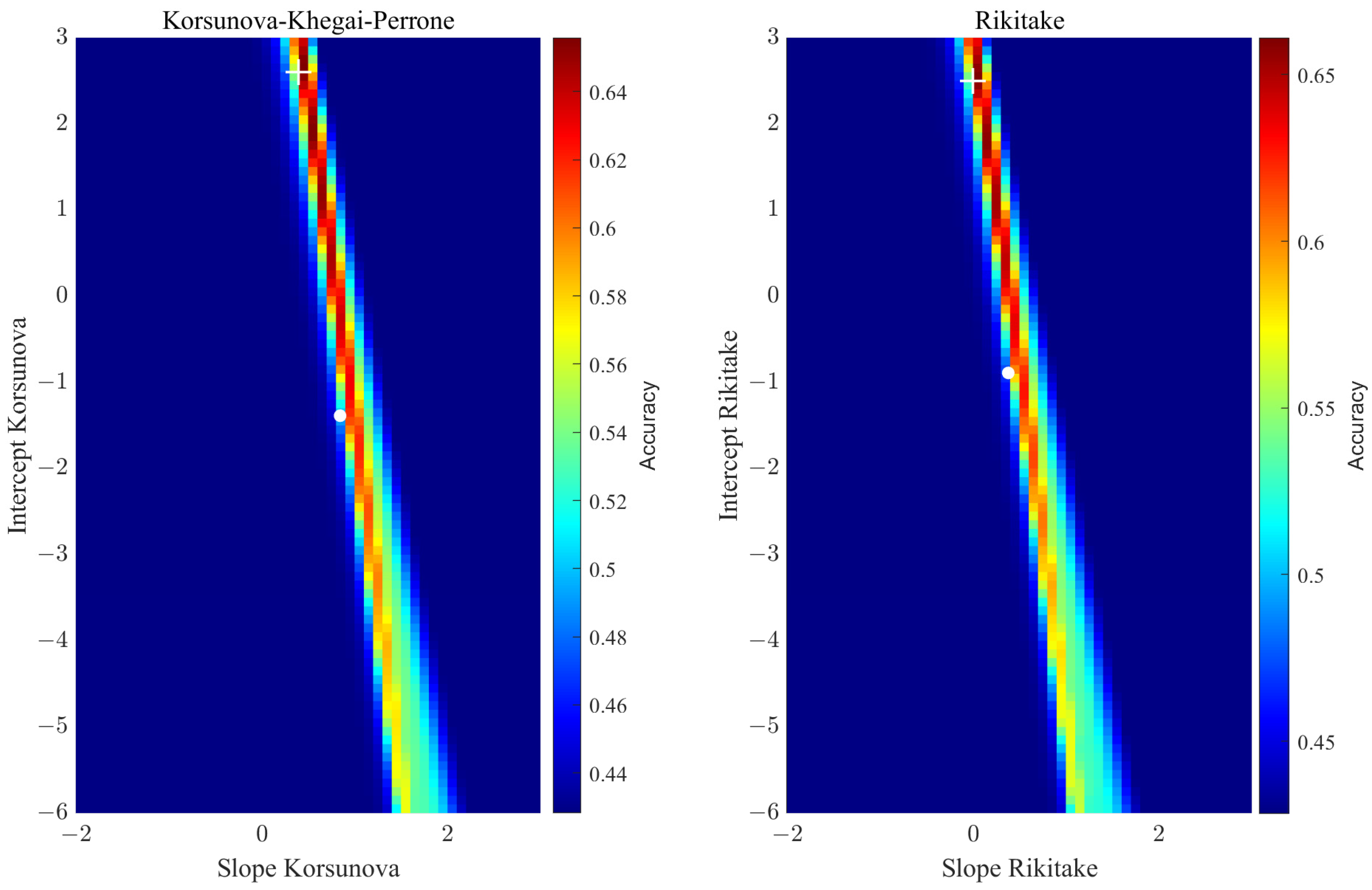
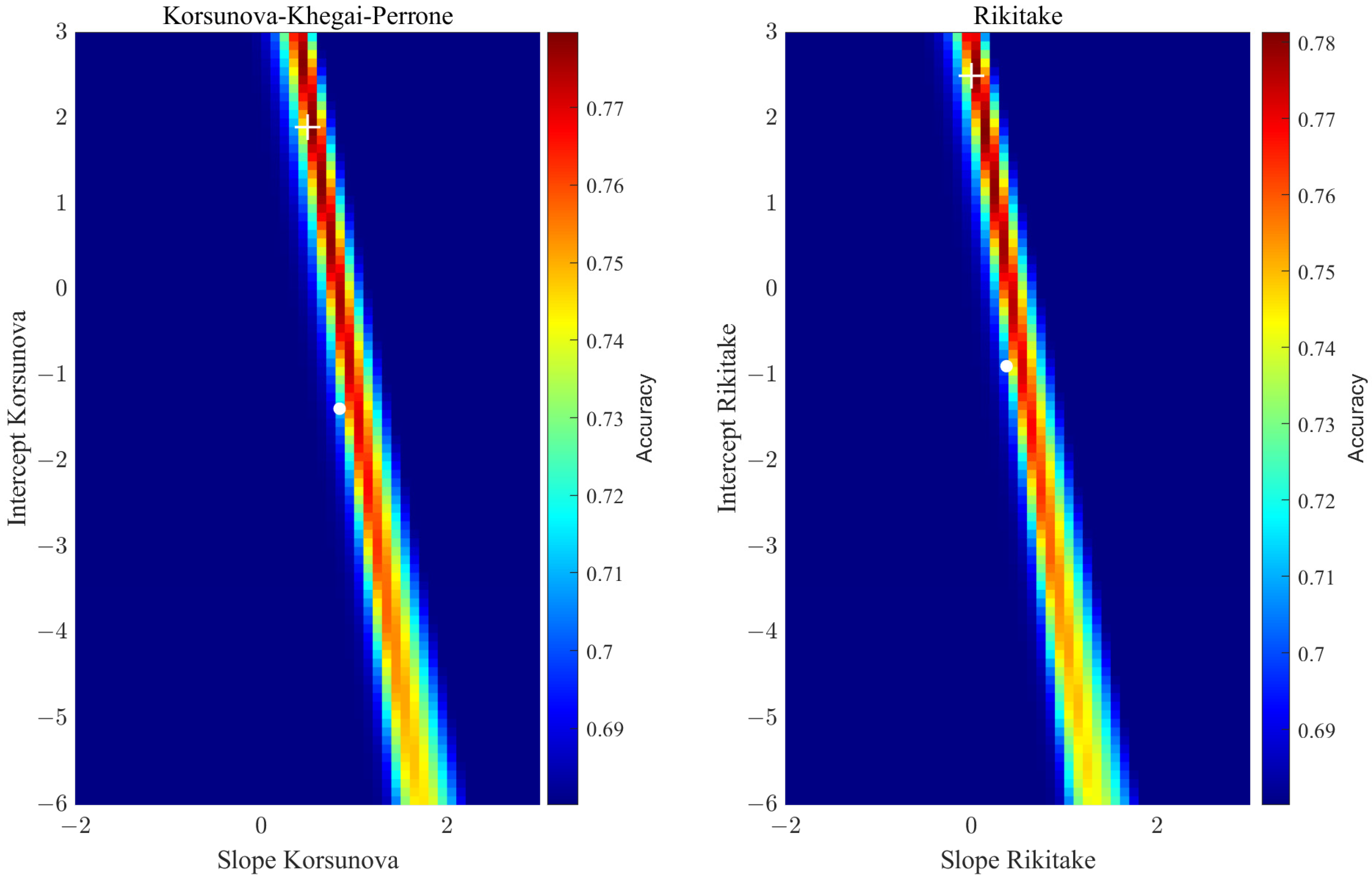
2.2.4. Testing the Possible Relationship between the Distance and Anticipation Time of Anomalies and Earthquake Magnitude
- Log10(ΔT × R); decimal logarithm of the product of anticipation time “ΔT” in days of the anomaly with respect to the earthquake and distance “R” in kilometres of the anomaly and the earthquake.
- Log10(ΔT);
- The above quantities are compared with:
- ak × M + bk; coefficients of the Korsunova–Khegai–Perrone relationship.
- aR × M + bR; coefficients for Rikitake’s law.
- |Log10(ΔT × R) – (ak × M + bk)| < tol for the Korsunova–Khegai–Perrone relationship.
- |Log10(ΔT) – (aR × M + bR)| < tol for Rikitake’s law.
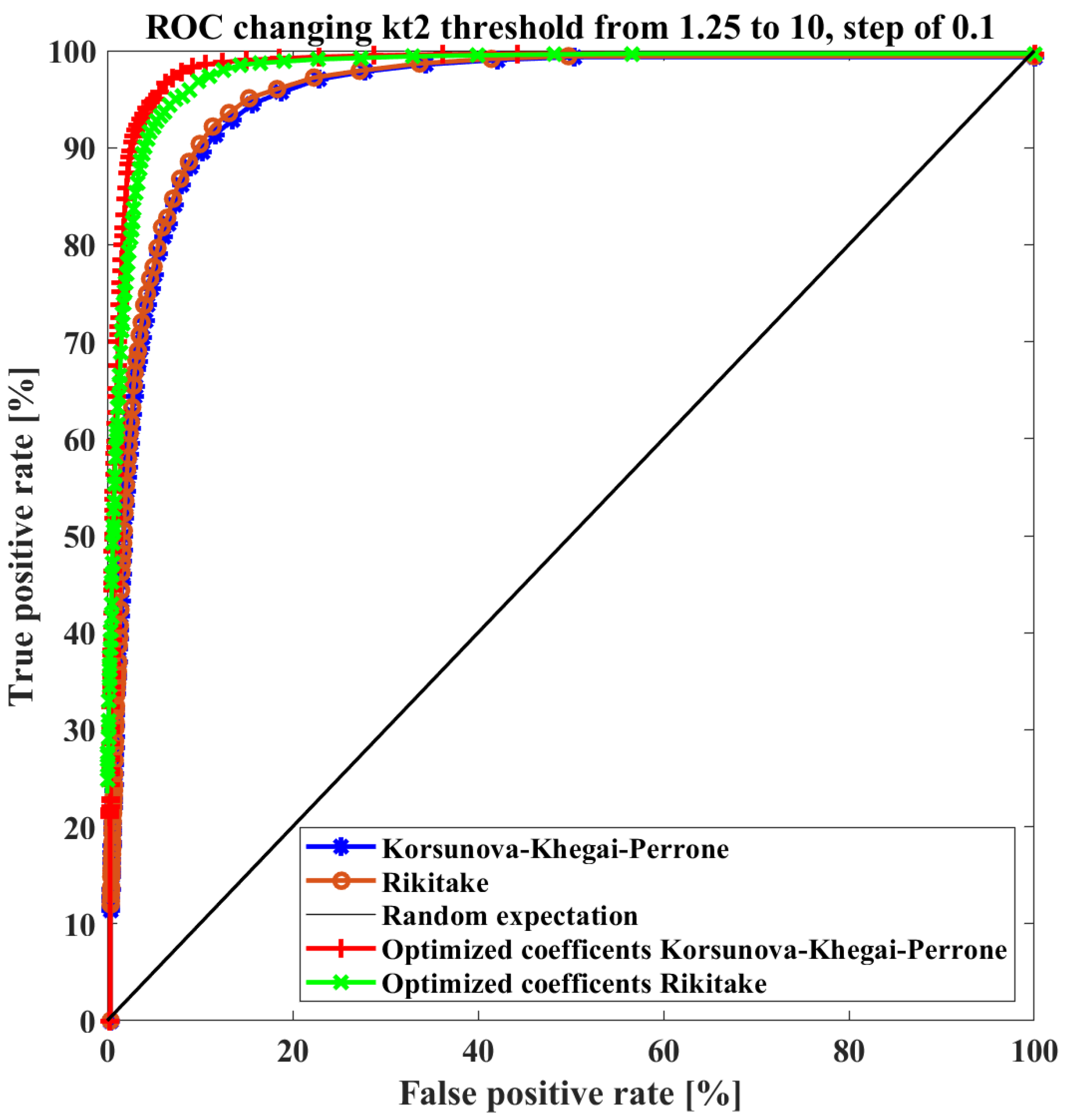
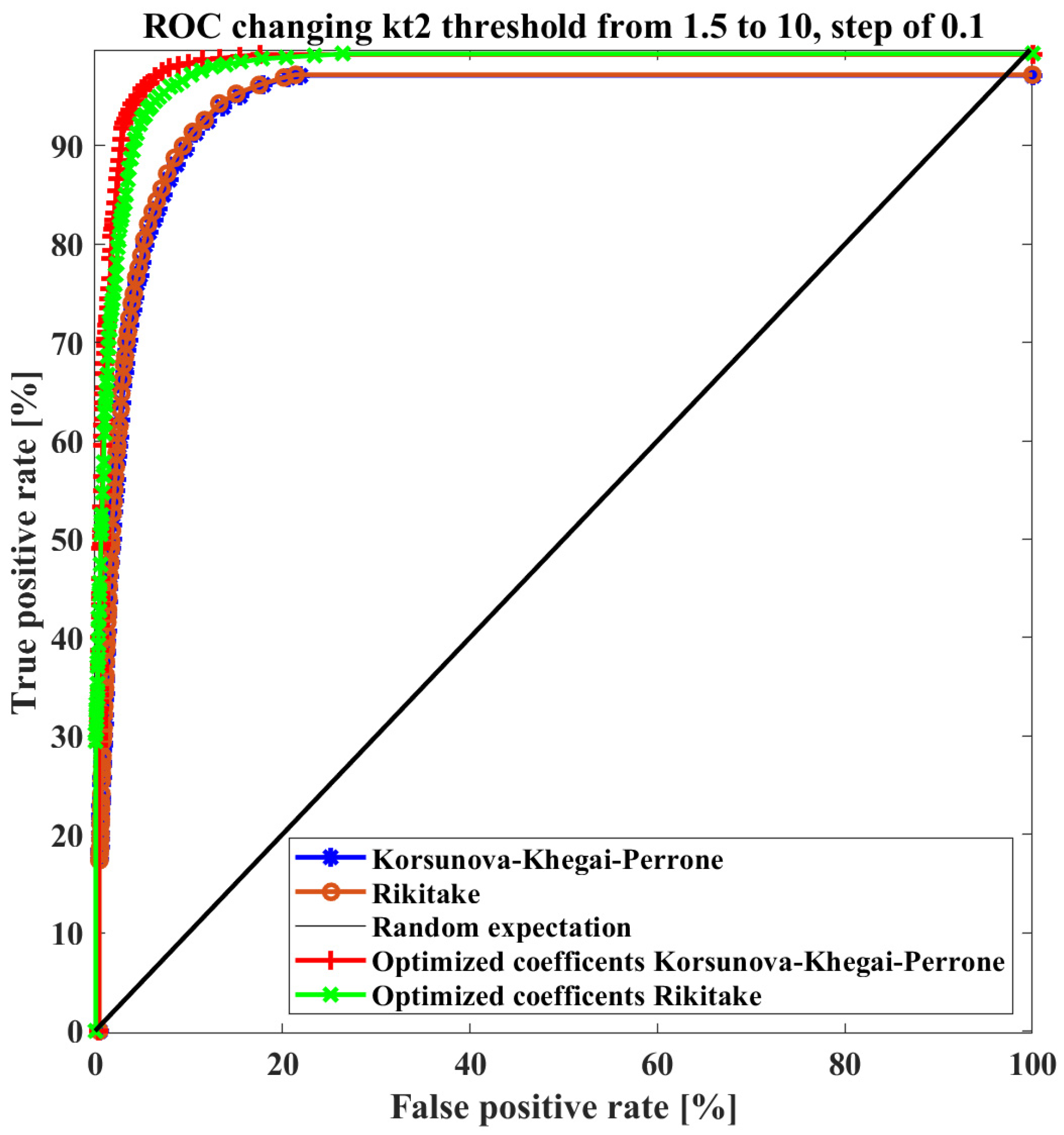
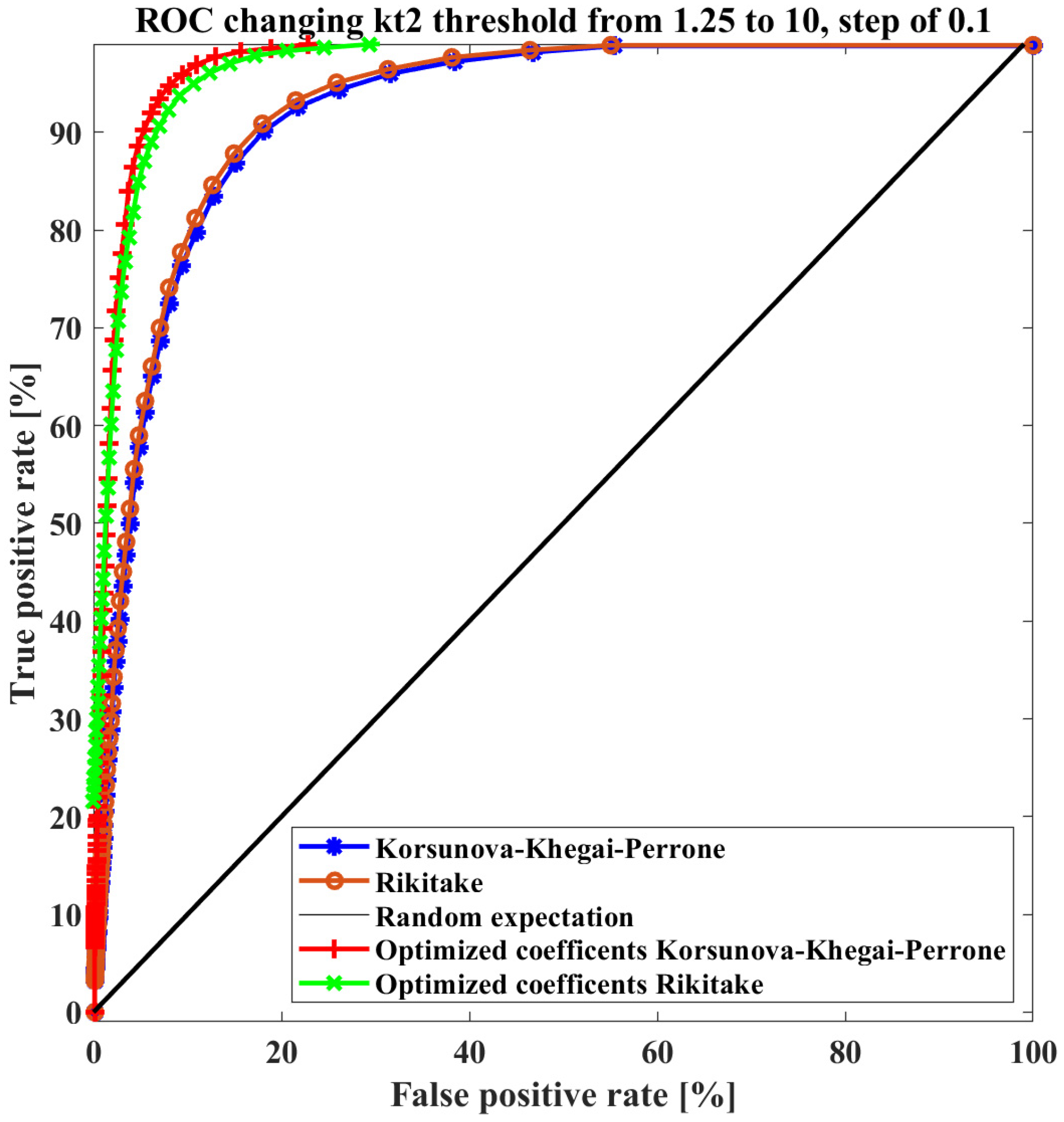
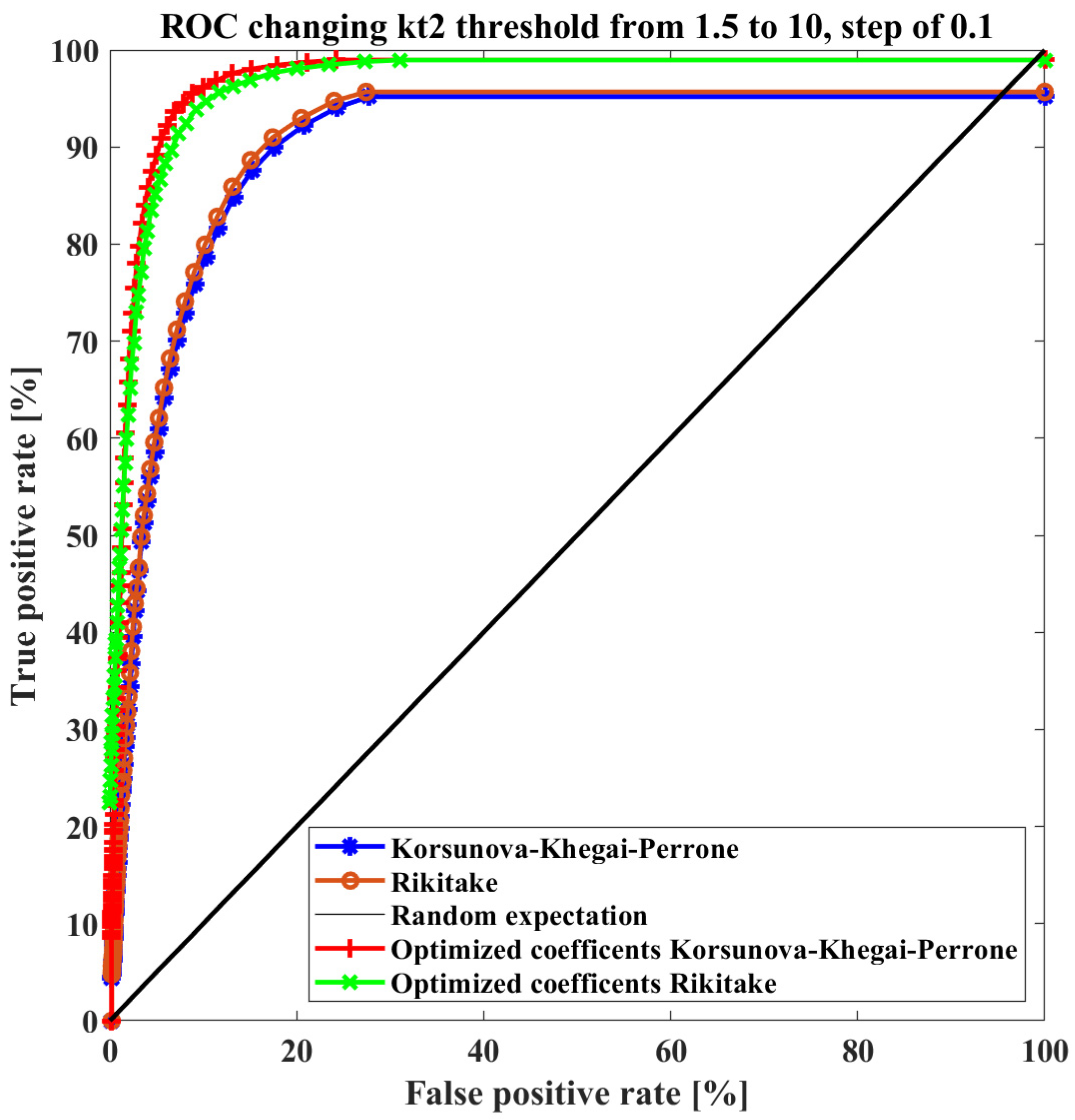
2.2.5. Assessment of Prediction Capability with Confusion Matrix and ROC Curves
- A “true positive” (TP) is a cell with Ne anomalies associated with an incoming earthquake.
- A “false positive” (FP) is a cell with Ne anomalies not associated with incoming earthquakes.
- A “true negative” (TN) is a cell without Ne anomalies and without earthquakes.
- A “false negative” (FN) is a cell without Ne anomalies but with one or more earthquakes.
3. Results
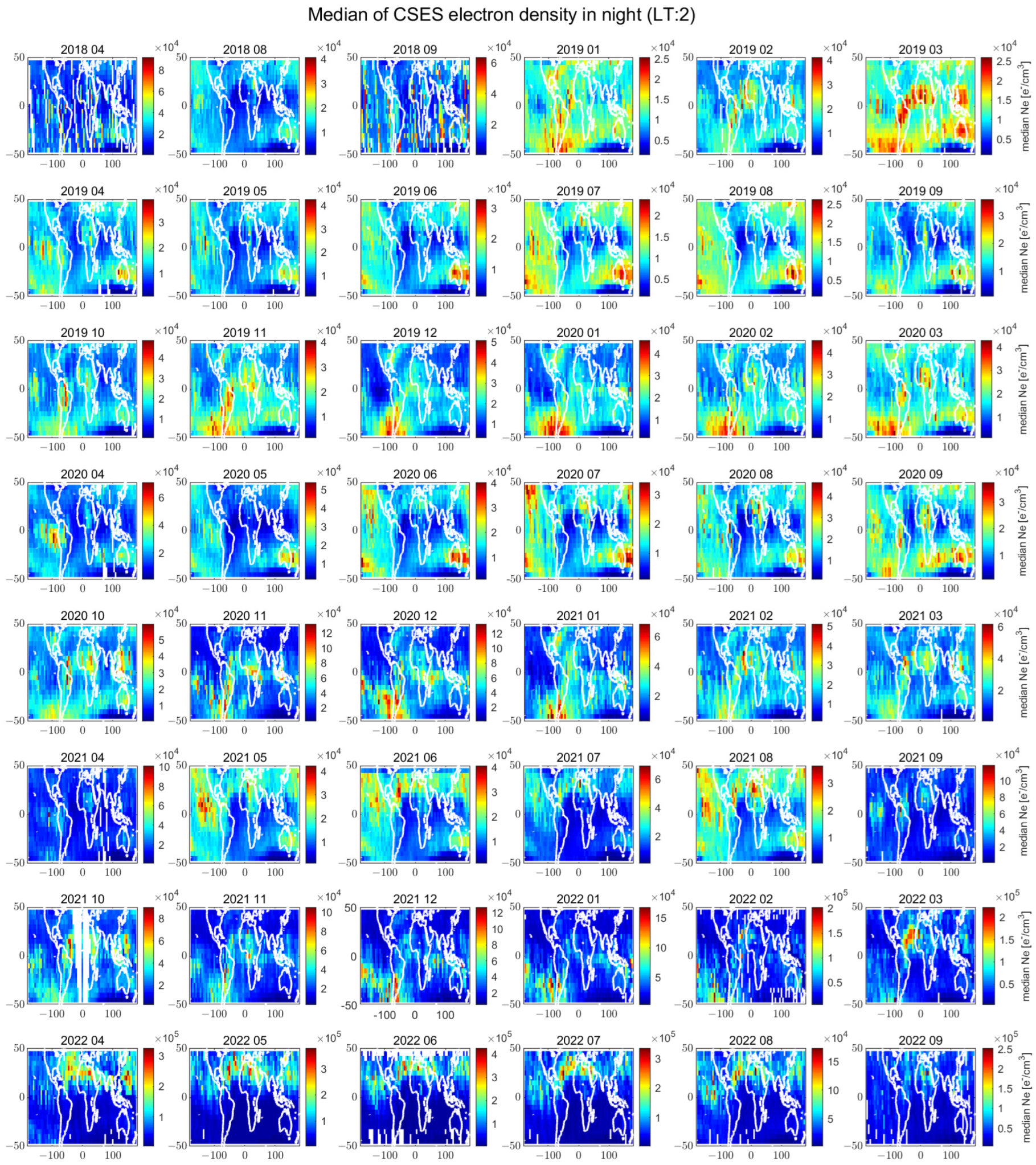
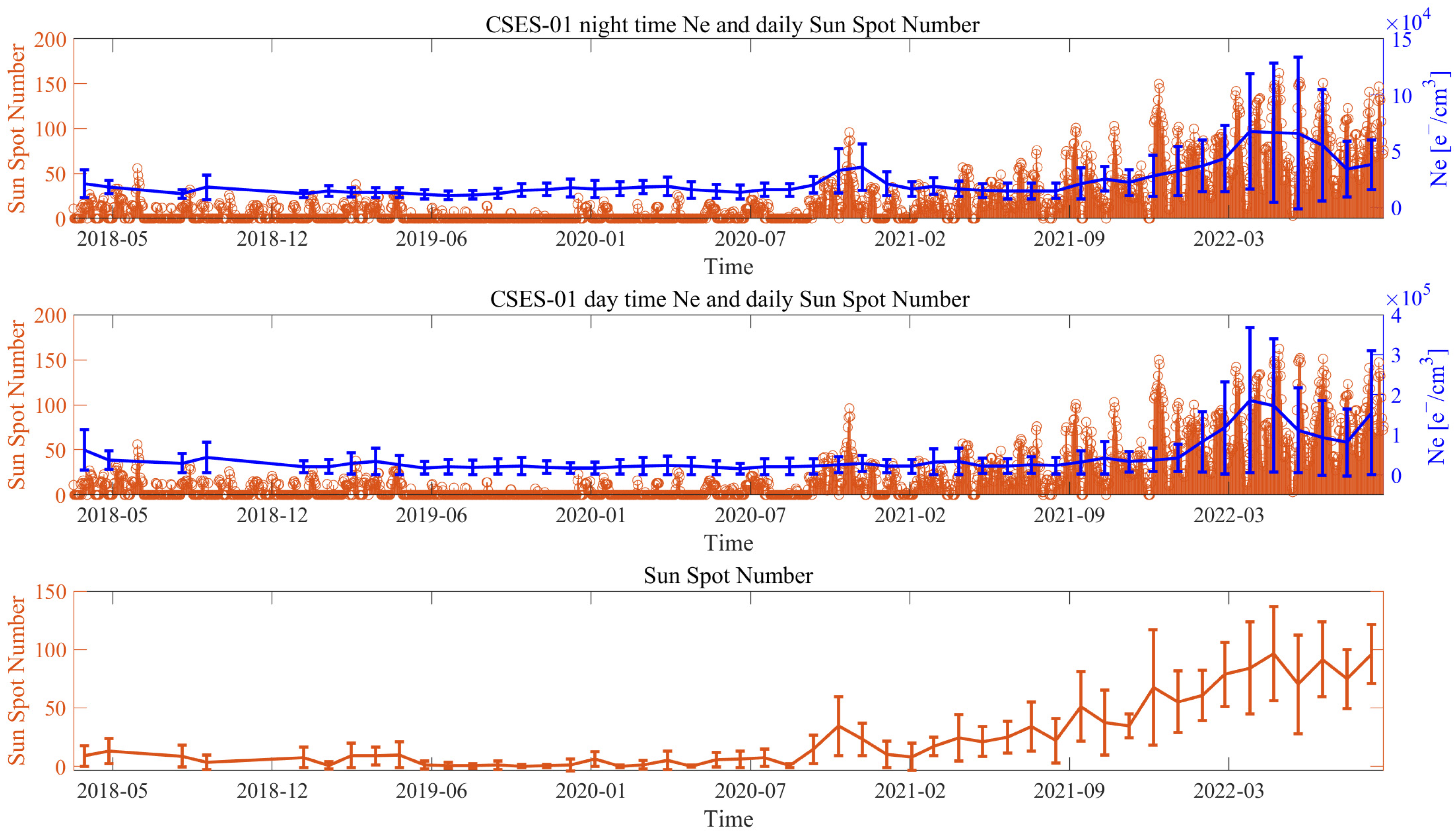
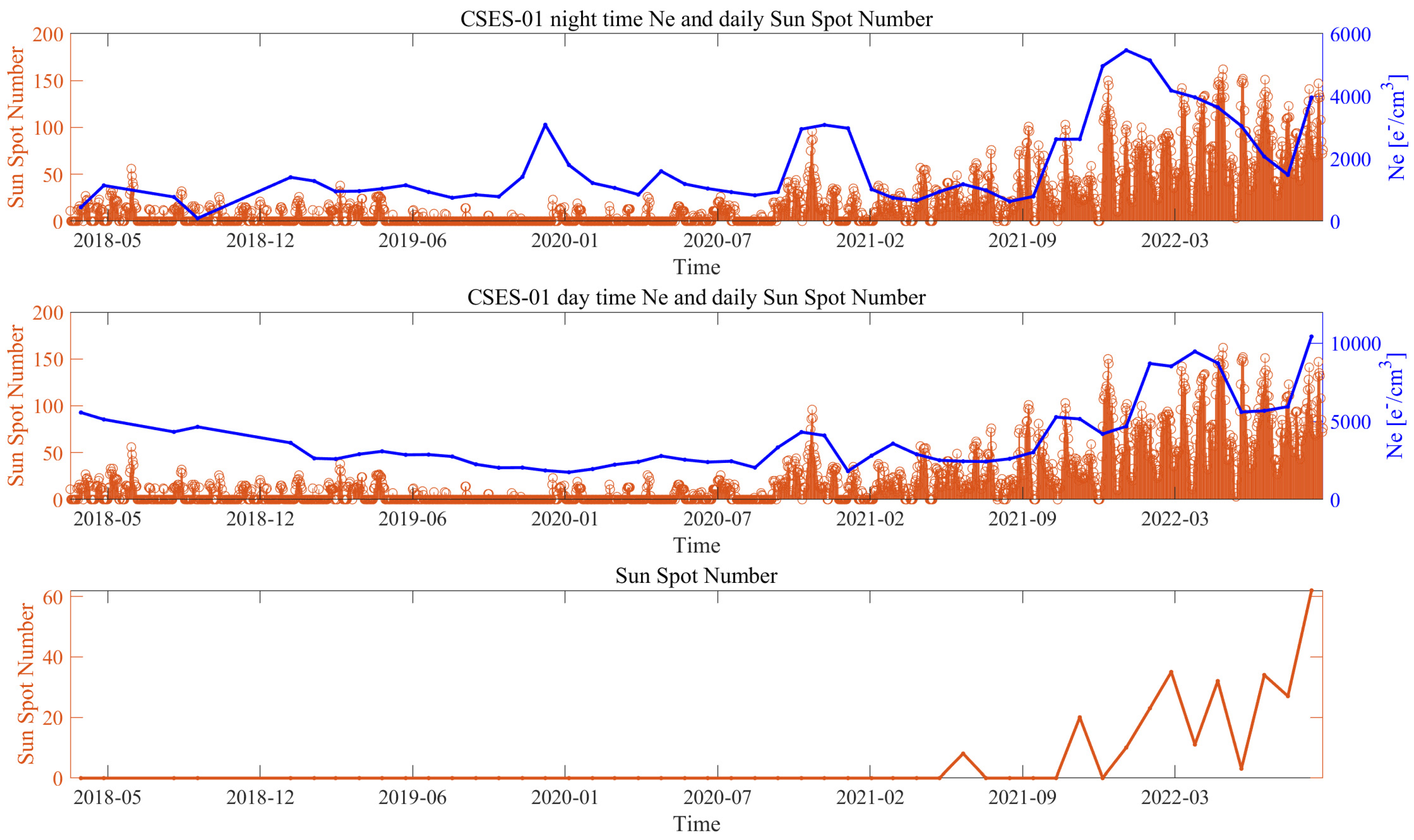
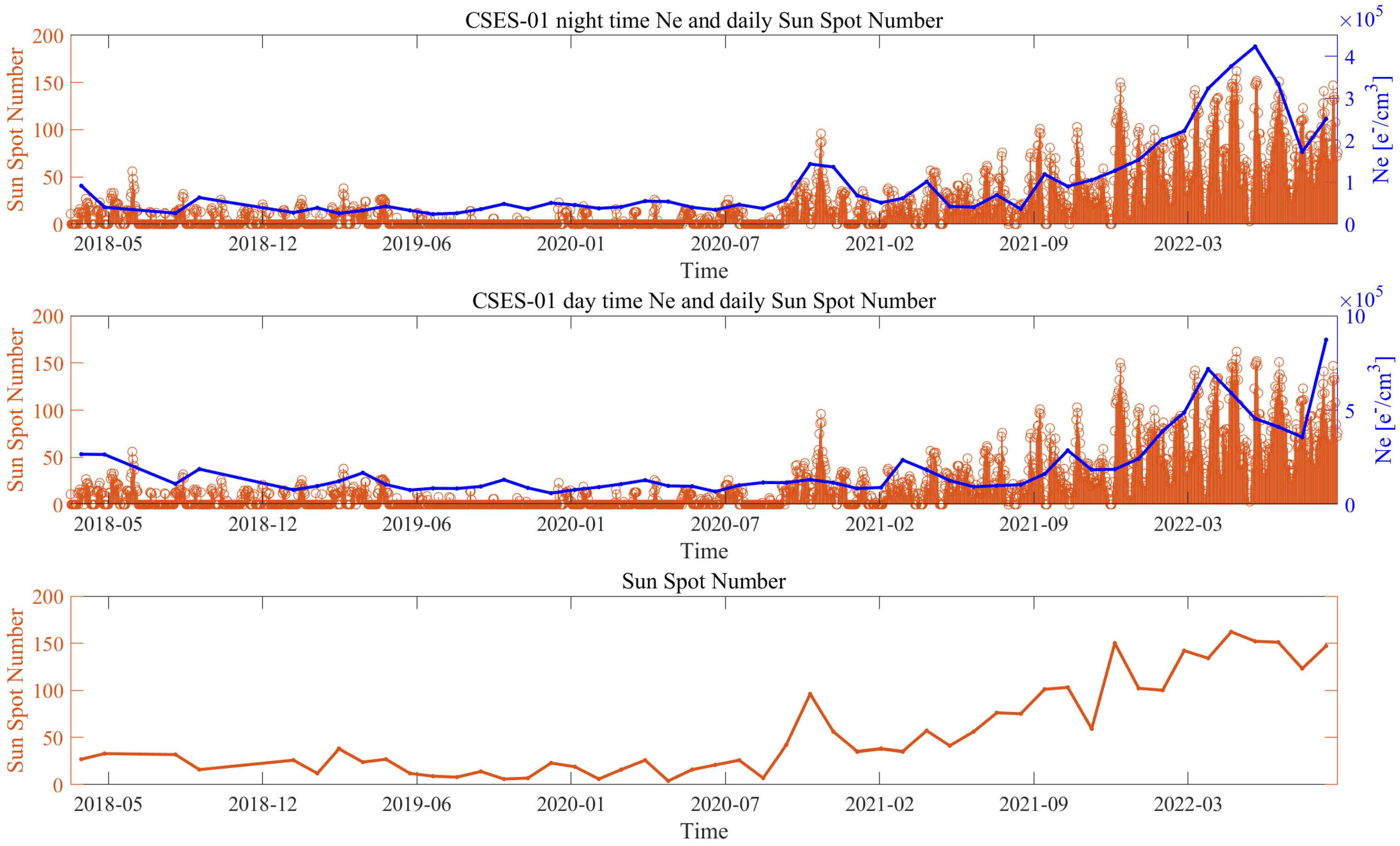
3.1. Ionospheric Background Satellite Ne Characterisation
3.1.1. Background for Night- and Daytime
3.1.2. Comparison of the Ionospheric Background with Solar Activity
3.2. Correlation of CSES Ne Anomalies with Earthquakes
3.2.1. Results Testing the Mid-Latitude Anomalies Defined over Median and IQR
3.2.2. Results Testing the Mid-Latitude Anomalies Defined as “Outlier”
3.2.3. Results Testing the Equatorial Anomalies Defined over Median and IQR
3.2.4. Results Testing the Equatorial Anomalies Defined as “outlier”
4. Discussion
5. Conclusions
- CSES-01 Ne data are reliable measurements of the status of the ionosphere. In fact, the observations permitted constructing an ionospheric background highly in agreement with solar activity (R = 0.85 for daytime and R = 0.89 for nighttime).
- Increases in CSES-01 Ne with respect to the background seem statistically related to the seismic activity of shallow M5.5+ worldwide earthquakes as supported by the accuracy higher of 50% (≥78% for the mild outlier anomaly definition) for all the explored cases in this paper. This further supports statistically the existence of ionospheric disturbances before the earthquakes.
- The anticipation time of the identified CSES-01 Ne ionospheric anomalies seems to not depend on earthquake magnitude due to the null best coefficient obtained for the “Rikitake” law. Despite this, the distance of the ionospheric anomaly from the earthquake seems to increase with earthquake magnitude both in equatorial and mid-latitude regions, as suggested by positive slopes (0.4 and 0.5) estimated for the “Korsunova-Khegai-Perrone” law.
- This study is limited to one parameter (Ne), one type of anomaly (increase in electron density) and one satellite. Future studies can try to integrate multiple parameters and include other types of anomalies.
- The investigation time before the earthquakes depends on the same earthquake time. For example, an earthquake in 2022 has more than three years of CSES data, while an earthquake in 2019 is only several months. Extension of CSES-01 and integration with at least a second CSES satellite would permit a larger dataset with more time coverage.
- We preferred to investigate the anomalies inside Dobrovolsky’s area as the earthquake preparation zone, as it is physically related to the seismic event, but other areas (physically related or not and even fixed) may be used.
- We limited our study to the anticipation time and distance of the anomalies with respect to the incoming earthquake. Still, it is also worth investigating the intensity of the anomaly, its duration/extension in space (on the satellite, they are intrinsically related), direction with respect to the epicentre as well as the eventual influence of the earthquake focal mechanism, location of the earthquake (sea/land or Northern/Southern Hemispheres), etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Comparison of CSES-01 Ne Background in Mid-Latitude and Equatorial Regions with Solar Activity
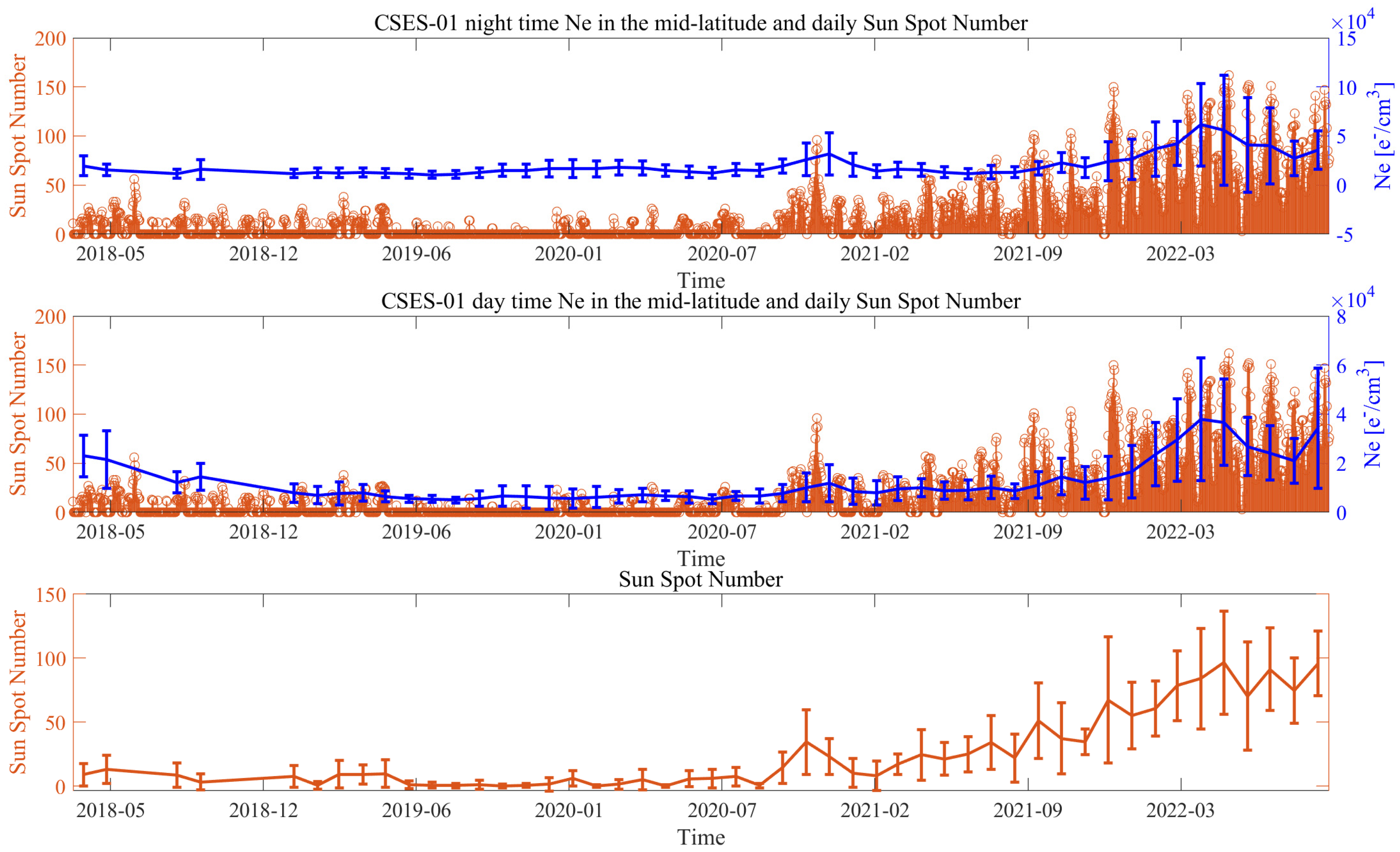

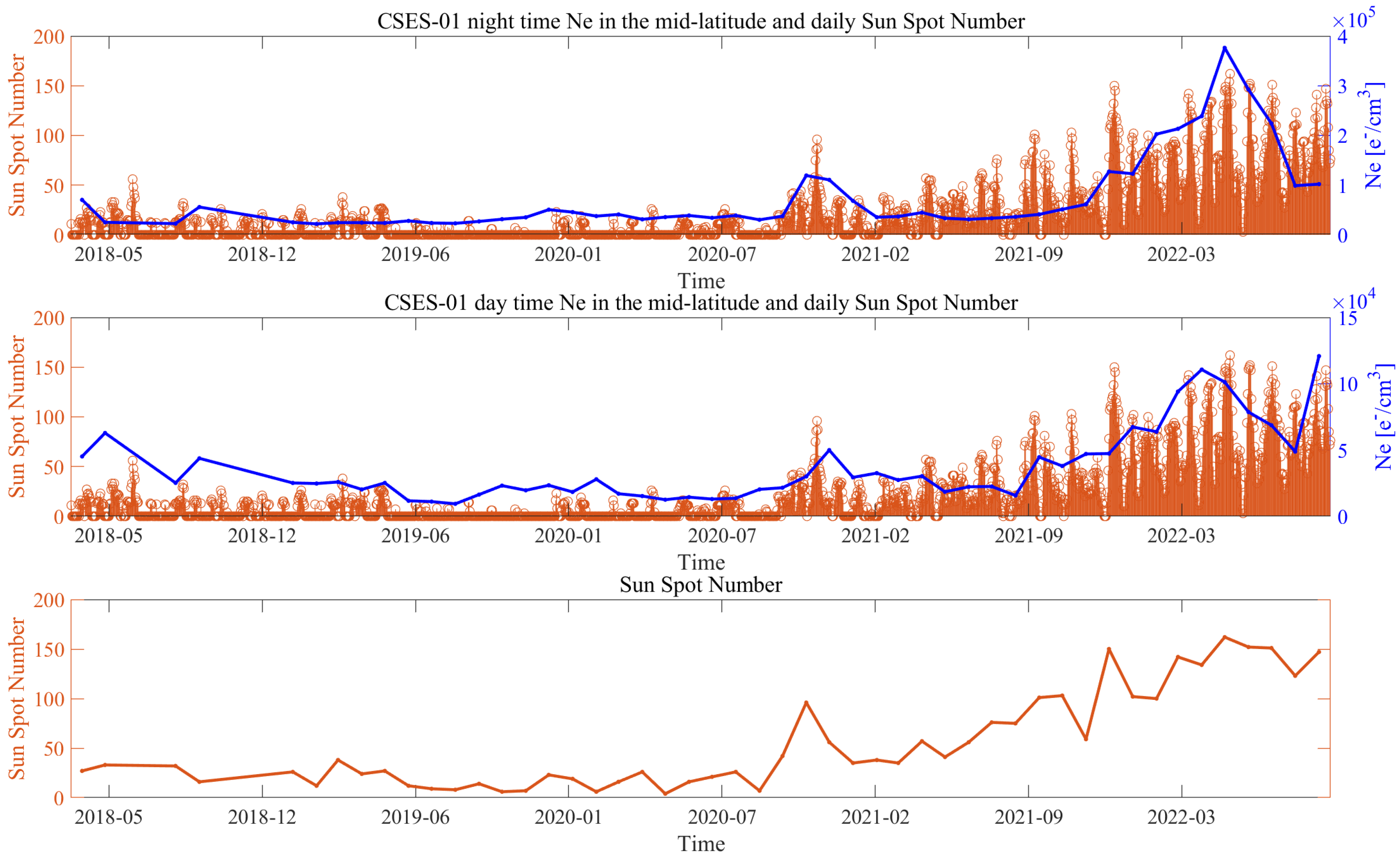
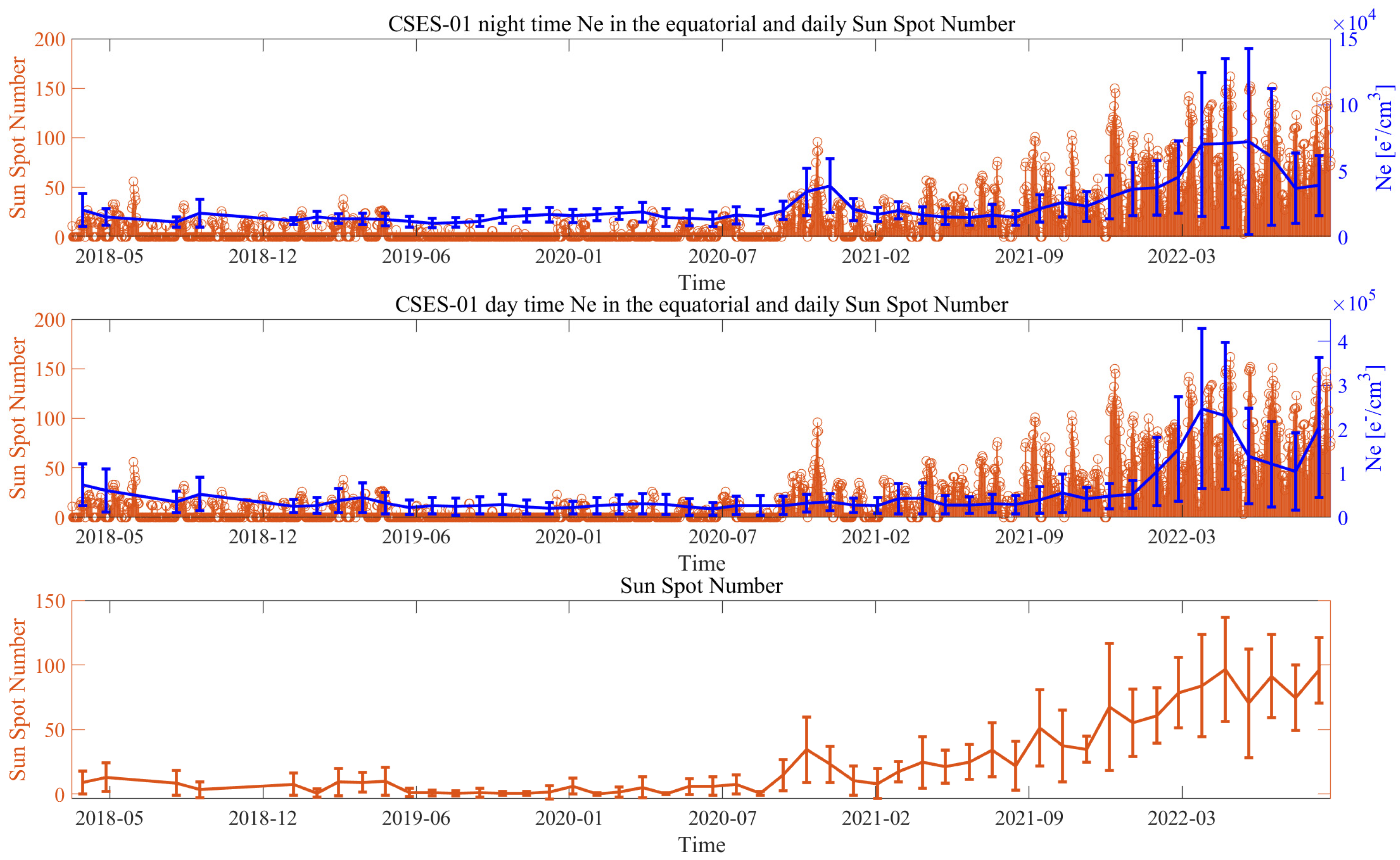
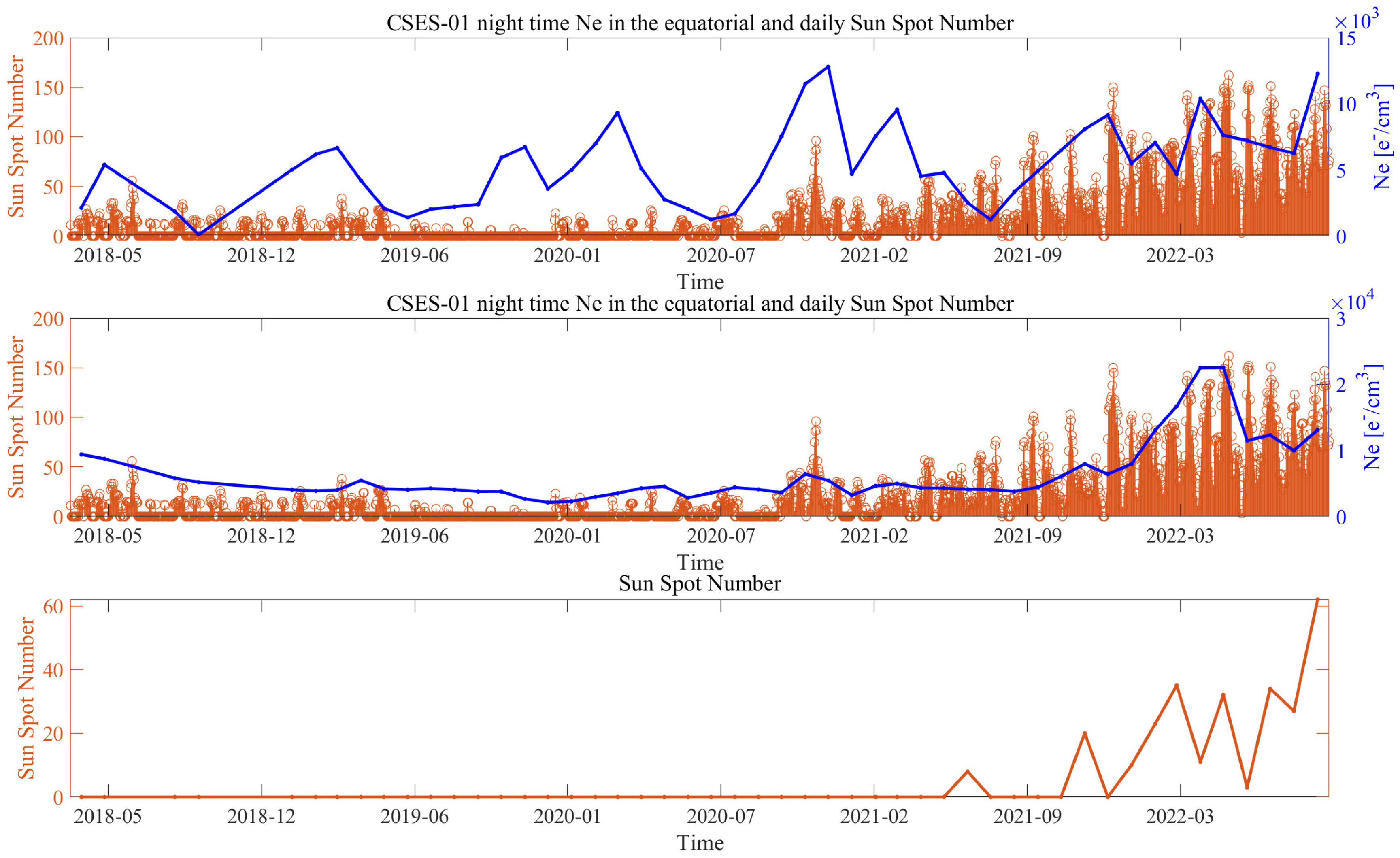
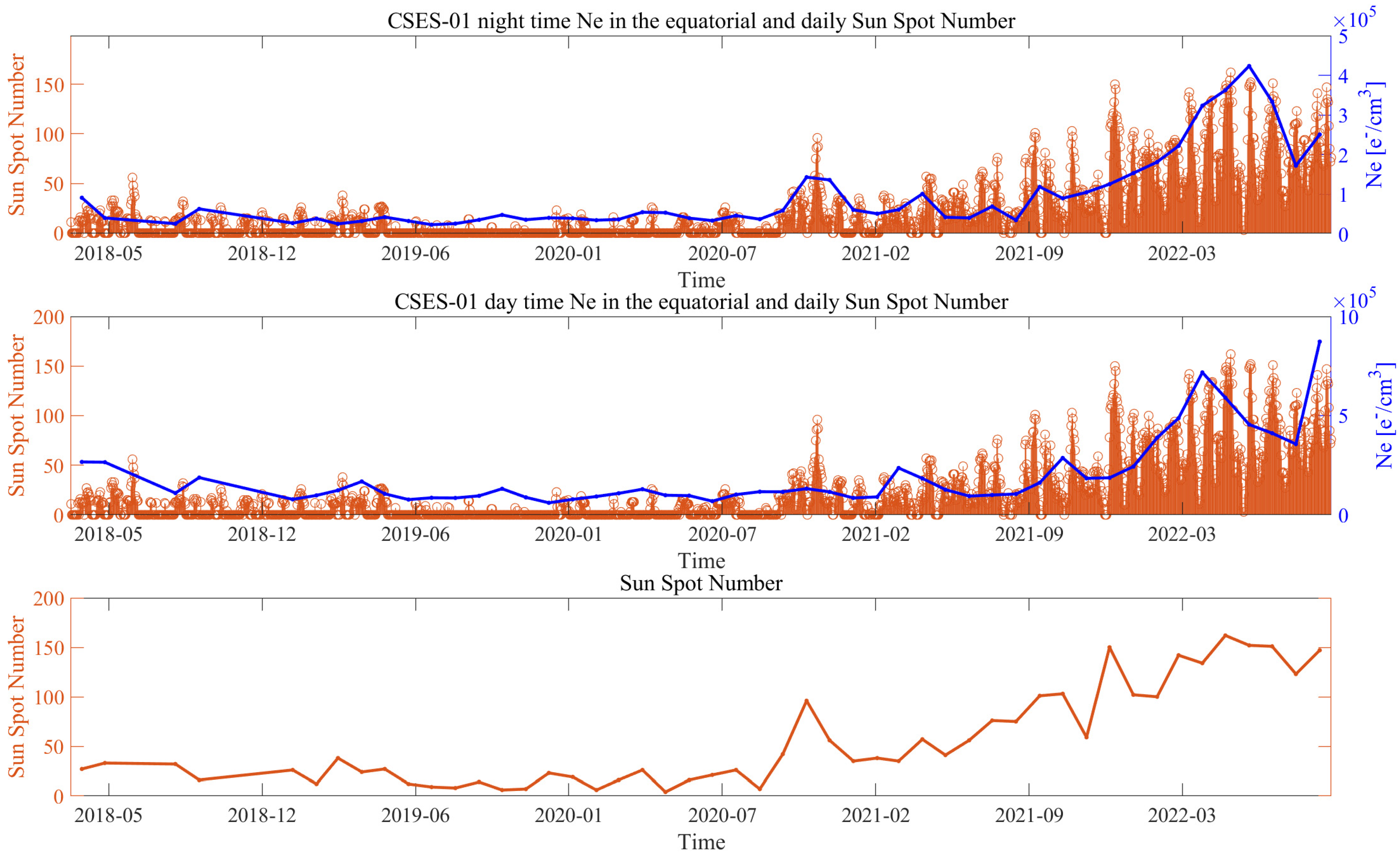
Appendix B
List of Parameters
| Parameter | Long Name | Notes on the Parameter and Its Result Implications |
|---|---|---|
| kt1 | Threshold to pre-select a dataset for anomaly extraction | This parameter does not have direct implications for the final results, but it permits us to reduce the original dataset when we search for anomalies in order to improve the computational efficiency |
| kt2 | Threshold to define the anomaly | This parameter is the threshold to define an anomaly. Higher kt2 implies the selection of fewer anomalies and in statistical distribution, it means selecting values on the positive tail of the distribution. |
| ak | Slope of the “Korsunova-Khegai-Perrone” law | This parameter is set to ak = 0.844 or optimised on the real data, selecting maximum accuracy. |
| bk | Intercept of the “Korsunova-Khegai-Perrone” law | This parameter is set to bk = −1.386 or optimised on the real data, selecting maximum accuracy. |
| aR | Slope of the “Rikitake” law | This parameter is set to aR = 0.38 or optimised on the real data, selecting maximum accuracy. |
| bR | Intercept of the “Rikitake” law | This parameter is set to bR = −0.89 or optimised on the real data, selecting maximum accuracy. |
| ΔT | Anticipation time | Anticipation time in days of a CSES-01 Ne anomaly with respect to a future earthquake |
| R | Distance | Distance of an anomaly from the epicentre in km |
References
- Hulburt, E.O. Ionization in the Upper Atmosphere of the Earth. Phys. Rev. 1928, 31, 1018–1037. [Google Scholar] [CrossRef]
- Briand, C.; Clilverd, M.; Inturi, S.; Cecconi, B. Role of Hard X-ray Emission in Ionospheric D-Layer Disturbances during Solar Flares. Earth Planets Space 2022, 74, 41. [Google Scholar] [CrossRef]
- Marconi, G. Radio Telegraphy. J. Am. Inst. Electr. Eng. 1922, 41, 561–570. [Google Scholar] [CrossRef]
- Piggott, W.R.; Rawer, K. 1913—U.R.S.I. Handbook of Ionogram Interpretation and Reduction. 1978. Available online: https://repository.library.noaa.gov/view/noaa/10404 (accessed on 1 October 2023).
- Huang, X.; Reinisch, B.W. Vertical Electron Content from Ionograms in Real Time. Radio Sci. 2001, 36, 335–342. [Google Scholar] [CrossRef]
- Scotto, C.; Sabbagh, D. The Accuracy of Real-Time hmF2 Estimation from Ionosondes. Remote Sens. 2020, 12, 2671. [Google Scholar] [CrossRef]
- McNamara, L.F.; Cooke, D.L.; Valladares, C.E.; Reinisch, B.W. Comparison of CHAMP and Digisonde Plasma Frequencies at Jicamarca, Peru. Radio Sci. 2007, 42, 1–14. [Google Scholar] [CrossRef]
- Merlino, R.L. Understanding Langmuir Probe Current-Voltage Characteristics. Am. J. Phys. 2007, 75, 1078–1085. [Google Scholar] [CrossRef]
- Sabbagh, D.; Ippolito, A.; Marchetti, D.; Perrone, L.; De Santis, A.; Campuzano, S.A.; Cianchini, G.; Piscini, A. Satellite-Based Electron Density Background Definition at Mid-Latitudes and Comparison with IRI-2016 Model under Different Solar Conditions. Adv. Space Res. 2023, 72, 1183–1195. [Google Scholar] [CrossRef]
- Chen, H.; Han, P.; Hattori, K. Recent Advances and Challenges in the Seismo-Electromagnetic Study: A Brief Review. Remote Sens. 2022, 14, 5893. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Nickolaenko, A.P.; Hobara, Y. Seismogenic ULF/ELF Wave Phenomena: Recent Advances and Future Perspectives. OJER 2023, 12, 45–113. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.A.; Solovieva, M.; Molchanov, O.A. A Statistical Study on the Correlation between Lower Ionospheric Perturbations as Seen by Subionospheric VLF/LF Propagation and Earthquakes. J. Geophys. Res. 2010, 115, A09305. [Google Scholar] [CrossRef]
- Song, R.; Hattori, K.; Zhang, X.; Liu, J.; Yoshino, C. Detecting the Ionospheric Disturbances in Japan Using the Three-Dimensional Computerized Tomography. JGR Space Phys. 2021, 126, e2020JA028561. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Legen’ka, A.D. Spatial–Temporal Characteristics of Large Scale Disturbances of Electron Density Observed in the Ionospheric F-Region before Strong Earthquakes. Cosm. Res. 2003, 41, 9. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Parrot, M.; Saradjian, M.R. Electron and Ion Density Variations before Strong Earthquakes (M>6.0) Using DEMETER and GPS Data. Nat. Hazards Earth Syst. Sci. 2010, 10, 7–18. [Google Scholar] [CrossRef]
- Li, M.; Parrot, M. Statistical Analysis of the Ionospheric Ion Density Recorded by DEMETER in the Epicenter Areas of Earthquakes as Well as in Their Magnetically Conjugate Point Areas. Adv. Space Res. 2018, 61, 974–984. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Parrot, M.; Bortnik, J. ULF Wave Activity Observed in the Nighttime Ionosphere Above and Some Hours Before Strong Earthquakes. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028396. [Google Scholar] [CrossRef]
- Parrot, M.; Pinçon, J.-L. Is There an Earthquake Weather? OJER 2020, 09, 69–82. [Google Scholar] [CrossRef]
- He, L.; Heki, K. Three-Dimensional Distribution of Ionospheric Anomalies Prior to Three Large Earthquakes in Chile: Three-Dimensional Spatial Structure of VTEC Anomalies. Geophys. Res. Lett. 2016, 43, 7287–7293. [Google Scholar] [CrossRef]
- He, L.; Heki, K. Three-Dimensional Tomography of Ionospheric Anomalies Immediately Before the 2015 Illapel Earthquake, Central Chile. J. Geophys. Res. Space Phys. 2018, 123, 4015–4025. [Google Scholar] [CrossRef]
- Eisenbeis, J.; Occhipinti, G. The TEC Enhancement Before Seismic Events Is an Artifact. JGR Space Phys. 2021, 126, e2020JA028733. [Google Scholar] [CrossRef]
- Bertello, I.; Piersanti, M.; Candidi, M.; Diego, P.; Ubertini, P. Electromagnetic Field Observations by the DEMETER Satellite in Connection with the 2009 L’Aquila Earthquake. Ann. Geophys. 2018, 36, 1483–1493. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Chen, W.; Zhu, K.; Marchetti, D.; Cheng, Y.; Fan, M.; Wang, S.; Wen, J.; Zhang, D.; et al. Are There One or More Geophysical Coupling Mechanisms before Earthquakes? The Case Study of Lushan (China) 2013. Remote Sens. 2023, 15, 1521. [Google Scholar] [CrossRef]
- De Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential Earthquake Precursory Pattern from Space: The 2015 Nepal Event as Seen by Magnetic Swarm Satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
- Ghamry, E.; Mohamed, E.K.; Sekertekin, A.; Fathy, A. Integration of Multiple Earthquakes Precursors before Large Earthquakes: A Case Study of 25 April 2015 in Nepal. J. Atmos. Sol.-Terr. Phys. 2023, 242, 105982. [Google Scholar] [CrossRef]
- Fan, M.; Zhu, K.; De Santis, A.; Marchetti, D.; Cianchini, G.; Piscini, A.; He, X.; Wen, J.; Wang, T.; Zhang, Y.; et al. Analysis of Swarm Satellite Magnetic Field Data for the 2015 Mw 7.8 Nepal Earthquake Based on Nonnegative Tensor Decomposition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient Effects in Atmosphere and Ionosphere Preceding the 2015 M7.8 and M7.3 Gorkha–Nepal Earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Wu, L.; Qi, Y.; Mao, W.; Lu, J.; Ding, Y.; Peng, B.; Xie, B. Scrutinizing and Rooting the Multiple Anomalies of Nepal Earthquake Sequence in 2015 with the Deviation–Time–Space Criterion and Homologous Lithosphere–Coversphere–Atmosphere–Ionosphere Coupling Physics. Nat. Hazards Earth Syst. Sci. 2023, 23, 231–249. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Piscini, A.; Campuzano, S.A.; De Carvalho, W.V.J.O. Pre-Earthquake Chain Processes Detected from Ground to Satellite Altitude in Preparation of the 2016–2017 Seismic Sequence in Central Italy. Remote Sens. Environ. 2019, 229, 93–99. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Jin, S.; Piscini, A.; Campuzano, S.A. Magnetic Field and Electron Density Anomalies from Swarm Satellites Preceding the Major Earthquakes of the 2016–2017 Amatrice-Norcia (Central Italy) Seismic Sequence. Pure Appl. Geophys. 2020, 177, 305–319. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Di Giovambattista, R.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling Effects Prior to the 2018 Mw = 7.5 Indonesia Earthquake from Seismic, Atmospheric and Ionospheric Data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Shen, X. Swarm-TEC Satellite Measurements as a Potential Earthquake Precursor Together with Other Swarm and CSES Data: The Case of Mw7.6 2019 Papua New Guinea Seismic Event. Front. Earth Sci. 2022, 10, 820189. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A Multiparametric Approach to Study the Preparation Phase of the 2019 M7.1 Ridgecrest (California, United States) Earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, K.; Yan, R.; Zhima, Z.; Shen, X.; Chen, W.; Cheng, Y.; Fan, M.; Wang, T.; Wen, J.; et al. Ionospheric Effects of Natural Hazards in Geophysics: From Single Examples to Statistical Studies Applied to M5.5+ Earthquakes. Proceedings 2023, 87, 34. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Soldani, M.; Piscini, A.; Sabbagh, D.; Cianchini, G.; Perrone, L.; Orlando, M. Swarm Satellite Magnetic Field Data Analysis Prior to 2019 Mw = 7.1 Ridgecrest (California, USA) Earthquake. Geosciences 2020, 10, 502. [Google Scholar] [CrossRef]
- De Santis, A.; Perrone, L.; Calcara, M.; Campuzano, S.; Cianchini, G.; D’arcangelo, S.; Di Mauro, D.; Marchetti, D.; Nardi, A.; Orlando, M.; et al. A Comprehensive Multiparametric and Multilayer Approach to Study the Preparation Phase of Large Earthquakes from Ground to Space: The Case Study of the June 15 2019, M7.2 Kermadec Islands (New Zealand) Earthquake. Remote Sens. Environ. 2022, 283, 113325. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Marchetti, D. Study of the Preparation Phase of Turkey’s Powerful Earthquake (6 February 2023) by a Geophysical Multi-Parametric Fuzzy Inference System. Remote Sens. 2023, 15, 2224. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, K.; Marchetti, L.; Zhang, Y.; Chen, W.; Cheng, Y.; Fan, M.; Wang, S.; Wang, T.; Wen, J.; et al. Quick Report on the ML = 3.3 on 1 January 2023 Guidonia (Rome, Italy) Earthquake: Evidence of a Seismic Acceleration. Remote Sens. 2023, 15, 942. [Google Scholar] [CrossRef]
- Korsunova, L.P.; Khegai, V.V. Medium-Term Ionospheric Precursors to Strong Earthquakes. Int. J. Geomagn. Aeron. 2006, 6, GI3005. [Google Scholar] [CrossRef]
- Perrone, L.; Korsunova, L.P.; Mikhailov, A.V. Ionospheric Precursors for Crustal Earthquakes in Italy. Ann. Geophys. 2010, 28, 941–950. [Google Scholar] [CrossRef]
- Perrone, L.; De Santis, A.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Carbone, M.; Cesaroni, C.; Cianchini, G.; De Franceschi, G.; De Santis, A.; et al. Ionospheric Anomalies Detected by Ionosonde and Possibly Related to Crustal Earthquakes in Greece. Ann. Geophys. 2018, 36, 361–371. [Google Scholar] [CrossRef]
- Ippolito, A.; Perrone, L.; De Santis, A.; Sabbagh, D. Ionosonde Data Analysis in Relation to the 2016 Central Italian Earthquakes. Geosciences 2020, 10, 354. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory Worldwide Signatures of Earthquake Occurrences on Swarm Satellite Data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Zhu, K.; Soldani, M.; D’Arcangelo, S.; Orlando, M.; Wang, T.; Cianchini, G.; Di Mauro, D.; et al. Worldwide Statistical Correlation of Eight Years of Swarm Satellite Data with M5.5+ Earthquakes: New Hints about the Preseismic Phenomena from Space. Remote Sens. 2022, 14, 2649. [Google Scholar] [CrossRef]
- Rikitake, T. Earthquake Precursors in Japan: Precursor Time and Detectability. Tectonophysics 1987, 136, 265–282. [Google Scholar] [CrossRef]
- Yan, R.; Parrot, M.; Pinçon, J.-L. Statistical Study on Variations of the Ionospheric Ion Density Observed by DEMETER and Related to Seismic Activities: Ionospheric Density and Seismic Activity. J. Geophys. Res. Space Phys. 2017, 122, 12421–12429. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Perrone, L.; Campuzano, S.A.; Cianchini, G.; Cesaroni, C.; Di Mauro, D.; Orlando, M.; Piscini, A.; Sabbagh, D.; et al. Statistical Correlation Analysis of Strong Earthquakes and Ionospheric Electron Density Anomalies as Observed by CSES-01. Il Nuovo C. C 2021, 44, 1–4. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Davidenko, D. Lithosphere-Atmosphere-Ionosphere-Magnetosphere Coupling-A Concept for Pre-Earthquake Signals Generation. In Geophysical Monograph Series; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 77–98. ISBN 978-1-119-15694-9. [Google Scholar]
- Han, C.; Yan, R.; Marchetti, D.; Pu, W.; Zhima, Z.; Liu, D.; Xu, S.; Lu, H.; Zhou, N. Study on Electron Density Anomalies Possibly Related to Earthquakes Based on CSES Observations. Remote Sens. 2023, 15, 3354. [Google Scholar] [CrossRef]
- Freund, F. Pre-Earthquake Signals: Underlying Physical Processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.; Ouillon, G.; Scoville, J.; Sornette, D. Earthquake Precursors in the Light of Peroxy Defects Theory: Critical Review of Systematic Observations. Eur. Phys. J. Spec. Top. 2021, 230, 7–46. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An Improved Coupling Model for the Lithosphere-Atmosphere-Ionosphere System. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Etiope, G.; Martinelli, G. Migration of Carrier and Trace Gases in the Geosphere: An Overview. Phys. Earth Planet. Inter. 2002, 129, 185–204. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) Model—An Unified Concept for Earthquake Precursors Validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Xu, J.-G.; Feng, D.-C.; Mangalathu, S.; Jeon, J.-S. Data-Driven Rapid Damage Evaluation for Life-Cycle Seismic Assessment of Regional Reinforced Concrete Bridges. Earthq. Eng. Struct. Dyn. 2022, 51, 2730–2751. [Google Scholar] [CrossRef]
- Shen, X.; Zong, Q.-G.; Zhang, X. Introduction to Special Section on the China Seismo-Electromagnetic Satellite and Initial Results. Earth Planet. Phys. 2018, 2, 439–443. [Google Scholar] [CrossRef]
- Alfonsi, L.; Ambroglini, F.; Ambrosi, G.; Ammendola, R.; Assante, D.; Badoni, D.; Belyaev, V.A.; Burger, W.J.; Cafagna, A.; Cipollone, P.; et al. The HEPD Particle Detector and the EFD Electric Field Detector for the CSES Satellite. Radiat. Phys. Chem. 2017, 137, 187–192. [Google Scholar] [CrossRef]
- Lagoutte, D.; Brochot, J.Y.; de Carvalho, D.; Elie, F.; Harivelo, F.; Hobara, Y.; Madrias, L.; Parrot, M.; Pinçon, J.L.; Berthelier, J.J.; et al. The DEMETER Science Mission Centre. Planet. Space Sci. 2006, 54, 428–440. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A Constellation to Study the Earth’s Magnetic Field. Earth Planet Sp. 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Yan, R.; Guan, Y.; Shen, X.; Huang, J.; Zhang, X.; Liu, C.; Liu, D. The Langmuir Probe Onboard CSES: Data Inversion Analysis Method and First Results. Earth Planet. Phys. 2018, 2, 479–488. [Google Scholar] [CrossRef]
- Yan, R.; Zhima, Z.; Xiong, C.; Shen, X.; Huang, J.; Guan, Y.; Zhu, X.; Liu, C. Comparison of Electron Density and Temperature from the CSES Satellite with Other Space-Borne and Ground-Based Observations. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027747. [Google Scholar] [CrossRef]
- Diego, P.; Coco, I.; Bertello, I.; Candidi, M.; Ubertini, P. Ionospheric Plasma Density Measurements by Swarm Langmuir Probes: Limitations and Possible Corrections. Ann. Geophys. Discuss. 2019. preprint. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From Ionospheric Climate to Real-time Weather Predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Spogli, L.; Sabbagh, D.; Regi, M.; Cesaroni, C.; Perrone, L.; Alfonsi, L.; Di Mauro, D.; Lepidi, S.; Campuzano, S.A.; Marchetti, D.; et al. Ionospheric Response Over Brazil to the August 2018 Geomagnetic Storm as Probed by CSES-01 and Swarm Satellites and by Local Ground-Based Observations. JGR Space Phys. 2021, 126, e2020JA028368. [Google Scholar] [CrossRef]
- Yang, Y.-Y.; Zhima, Z.-R.; Shen, X.-H.; Chu, W.; Huang, J.-P.; Wang, Q.; Yan, R.; Xu, S.; Lu, H.-X.; Liu, D.-P. The First Intense Geomagnetic Storm Event Recorded by the China Seismo-Electromagnetic Satellite. Space Weather 2020, 18, e2019SW002243. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, K.; Zhang, H.; Zhima, Z.; Yan, R.; Shen, X.; Chen, W.; Cheng, Y.; He, X.; Wang, T.; et al. Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption. Remote Sens. 2022, 14, 5001. [Google Scholar] [CrossRef]
- D’Arcangelo, S.; Bonforte, A.; De Santis, A.; Maugeri, S.R.; Perrone, L.; Soldani, M.; Arena, G.; Brogi, F.; Calcara, M.; Campuzano, S.A.; et al. A Multi-Parametric and Multi-Layer Study to Investigate the Largest 2022 Hunga Tonga–Hunga Ha’apai Eruptions. Remote Sens. 2022, 14, 3649. [Google Scholar] [CrossRef]
- Ghamry, E.; Marchetti, D.; Yoshikawa, A.; Uozumi, T.; De Santis, A.; Perrone, L.; Shen, X.; Fathy, A. The First Pi2 Pulsation Observed by China Seismo-Electromagnetic Satellite. Remote Sens. 2020, 12, 2300. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The Thirteenth Generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Yang, Y.; Hulot, G.; Vigneron, P.; Shen, X.; Zhima, Z.; Zhou, B.; Magnes, W.; Olsen, N.; Tøffner-Clausen, L.; Huang, J.; et al. The CSES Global Geomagnetic Field Model (CGGM): An IGRF-Type Global Geomagnetic Field Model Based on Data from the China Seismo-Electromagnetic Satellite. Earth Planets Space 2021, 73, 45. [Google Scholar] [CrossRef]
- Gou, X.; Li, L.; Zhou, B.; Zhang, Y.; Xie, L.; Cheng, B.; Feng, Y.; Wang, J.; Miao, Y.; Zhima, Z.; et al. Electrostatic Ion Cyclotron Waves Observed by CSES in the Equatorial Plasma Bubble. Geophys. Res. Lett. 2023, 50, e2022GL101791. [Google Scholar] [CrossRef]
- Nose, M.; Iyemori, T.; Sugiura, M.; Kamei, T. Dst Index; World Data Center for Geomagnetism, Kyoto: Kyoto, Japan, 2015. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Reasenberg, P. Second-Order Moment of Central California Seismicity, 1969–1982. J. Geophys. Res. 1985, 90, 5479–5495. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyse Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Molchan, G.M. Earthquake Prediction as a Decision-Making Problem. PAGEOPH 1997, 149, 233–247. [Google Scholar] [CrossRef]
- Yu, Z.; Hattori, K.; Zhu, K.; Fan, M.; Marchetti, D.; He, X.; Chi, C. Evaluation of Pre-Earthquake Anomalies of Borehole Strain Network by Using Receiver Operating Characteristic Curve. Remote Sens. 2021, 13, 515. [Google Scholar] [CrossRef]
- Piscini, A.; De Santis, A.; Marchetti, D.; Cianchini, G. A Multi-Parametric Climatological Approach to Study the 2016 Amatrice–Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Tornatore, V.; Cesaroni, C.; Pezzopane, M.; Alizadeh, M.M.; Schuh, H. Performance Evaluation of VTEC GIMs for Regional Applications during Different Solar Activity Periods, Using RING TEC Values. Remote Sens. 2021, 13, 1470. [Google Scholar] [CrossRef]
- Liu, H.; Stolle, C.; Förster, M.; Watanabe, S. Solar Activity Dependence of the Electron Density in the Equatorial Anomaly Regions Observed by CHAMP. J. Geophys. Res. Atmos. 2007, 112, A11311. [Google Scholar] [CrossRef]
- Bilitza, D.; Truhlik, V.; Richards, P.; Abe, T.; Triskova, L. Solar Cycle Variations of Mid-Latitude Electron Density and Temperature: Satellite Measurements and Model Calculations. Adv. Space Res. 2007, 39, 779–789. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, T.J.Y.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and Ionospheric Coupling Phenomena Associated with Large Earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Generation of ULF Electromagnetic Emissions by Microfracturing. Geophys. Res. Lett. 1995, 22, 3091–3094. [Google Scholar] [CrossRef]





| R | CSES-01 Ne Background Whole Regions | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nighttime | Daytime | ||||||||
| Minimum | Mean | Maximum | St. Dev | Minimum | Mean | Maximum | St. Dev | ||
| Sunspot number | Minimum | 0.524 | 0.603 | 0.659 | 0.561 | 0.790 | 0.754 | 0.813 | 0.769 |
| Mean | 0.691 | 0.862 | 0.892 | 0.821 | 0.827 | 0.847 | 0.851 | 0.843 | |
| Maximum | 0.693 | 0.841 | 0.867 | 0.800 | 0.761 | 0.773 | 0.774 | 0.764 | |
| St. dev | 0.435 | 0.801 | 0.812 | 0.771 | 0.688 | 0.682 | 0.666 | 0.672 | |
| R | CSES-01 Ne Background Mid-Latitude Regions | ||||||||
| Nighttime | Daytime | ||||||||
| Minimum | Mean | Maximum | St. Dev | Minimum | Mean | Maximum | St. Dev | ||
| Sunspot number | Minimum | 0.525 | 0.643 | 0.580 | 0.561 | 0.790 | 0.738 | 0.766 | 0.756 |
| Mean | 0.690 | 0.848 | 0.823 | 0.821 | 0.827 | 0.863 | 0.868 | 0.843 | |
| Maximum | 0.692 | 0.808 | 0.806 | 0.800 | 0.761 | 0.806 | 0.811 | 0.780 | |
| St. dev | 0.651 | 0.750 | 0.767 | 0.771 | 0.651 | 0.728 | 0.726 | 0.693 | |
| R | CSES-01 Ne Background Equatorial Region | ||||||||
| Nighttime | Daytime | ||||||||
| Minimum | Mean | Maximum | St. Dev | Minimum | Mean | Maximum | St. Dev | ||
| Sunspot number | Minimum | 0.366 | 0.595 | 0.656 | 0.545 | 0.701 | 0.756 | 0.813 | 0.769 |
| Mean | 0.477 | 0.863 | 0.893 | 0.819 | 0.830 | 0.843 | 0.851 | 0.843 | |
| Maximum | 0.481 | 0.845 | 0.868 | 0.801 | 0.762 | 0.766 | 0.774 | 0.764 | |
| St. dev | 0.435 | 0.801 | 0.812 | 0.771 | 0.688 | 0.682 | 0.666 | 0.672 | |
| Law Being Tested | “Korsunova-Khegai-Perrone” | “Rikitake” | |||
|---|---|---|---|---|---|
| Earthquake | Earthquake | ||||
| Yes | No | Yes | No | ||
| CSES-01 Ne anomaly | Yes | TP = 5113 | FP = 17,803 | TP = 5555 | FP = 17,361 |
| No | FN = 34 | TN = 17,531 | FN = 32 | TN = 17,533 | |
| Law Being Tested | “Korsunova-Khegai-Perrone” | “Rikitake” | |||
|---|---|---|---|---|---|
| Earthquake | Earthquake | ||||
| Yes | No | Yes | No | ||
| CSES-01 Ne anomaly | Yes | TP = 2429 | FP = 8302 | TP = 2656 | FP = 8075 |
| No | FN = 71 | TN = 29,679 | FN = 76 | TN = 29,674 | |
| Law Being Tested | “Korsunova-Khegai-Perrone” | “Rikitake” | |||
|---|---|---|---|---|---|
| Earthquake | Earthquake | ||||
| Yes | No | Yes | No | ||
| CSES-01 Ne anomaly | Yes | TP = 9047 | FP = 48,366 | TP = 9718 | FP = 47,695 |
| No | FN = 108 | TN = 38,923 | FN = 108 | TN = 38,923 | |
| Law Being Tested | “Korsunova-Khegai-Perrone” | “Rikitake” | |||
|---|---|---|---|---|---|
| Earthquake | Earthquake | ||||
| Yes | No | Yes | No | ||
| CSES-01 Ne anomaly | Yes | TP = 4639 | FP = 25,375 | TP = 4994 | FP = 25,020 |
| No | FN = 235 | TN = 66195 | FN = 226 | TN = 66,204 | |
| Region | Anomaly Definition | Law under Test | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Korsunova–Khegai–Perrone | Rikitake | ||||||||
| Slope ak | Intercept bk | Accuracy | EQs with Anomalies | Slope ar | Intercept br | Accuracy | EQs with Anomalies | ||
| Mid-Latitude regions | Median, Interquartile | 0.4 | 2.6 | 65.6% | 262 (79.9%) | 0.0 | 2.5 | 66.1% | 267 (81.4%) |
| Mild-Outlier | 0.4 | 2.6 | 84.2% | 212 (64.6%) | 0.0 | 2.5 | 84.5% | 210 (64.0%) | |
| Equatorial region | Median, Interquartile | 0.5 | 1.9 | 58.0% | 877 (86.1%) | 0.0 | 2.5 | 58.2% | 881 (86.5%) |
| Mild-Outlier | 0.5 | 1.9 | 78.0% | 715 (70.2%) | 0.0 | 2.5 | 78.1% | 727 (71.3%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Marchetti, D.; Zhu, K.; Sabbagh, D.; Yan, R.; Zhima, Z.; Shen, X.; Cheng, Y.; Fan, M.; Wang, S.; et al. CSES-01 Electron Density Background Characterisation and Preliminary Investigation of Possible Ne Increase before Global Seismicity. Atmosphere 2023, 14, 1527. https://doi.org/10.3390/atmos14101527
Chen W, Marchetti D, Zhu K, Sabbagh D, Yan R, Zhima Z, Shen X, Cheng Y, Fan M, Wang S, et al. CSES-01 Electron Density Background Characterisation and Preliminary Investigation of Possible Ne Increase before Global Seismicity. Atmosphere. 2023; 14(10):1527. https://doi.org/10.3390/atmos14101527
Chicago/Turabian StyleChen, Wenqi, Dedalo Marchetti, Kaiguang Zhu, Dario Sabbagh, Rui Yan, Zeren Zhima, Xuhui Shen, Yuqi Cheng, Mengxuan Fan, Siyu Wang, and et al. 2023. "CSES-01 Electron Density Background Characterisation and Preliminary Investigation of Possible Ne Increase before Global Seismicity" Atmosphere 14, no. 10: 1527. https://doi.org/10.3390/atmos14101527
APA StyleChen, W., Marchetti, D., Zhu, K., Sabbagh, D., Yan, R., Zhima, Z., Shen, X., Cheng, Y., Fan, M., Wang, S., Wang, T., Zhang, D., Zhang, H., & Zhang, Y. (2023). CSES-01 Electron Density Background Characterisation and Preliminary Investigation of Possible Ne Increase before Global Seismicity. Atmosphere, 14(10), 1527. https://doi.org/10.3390/atmos14101527