MaxEnt SeismoSense Model: Ionospheric Earthquake Anomaly Detection Based on the Maximum Entropy Principle
Abstract
1. Introduction
2. Data
2.1. TEC Grid Product
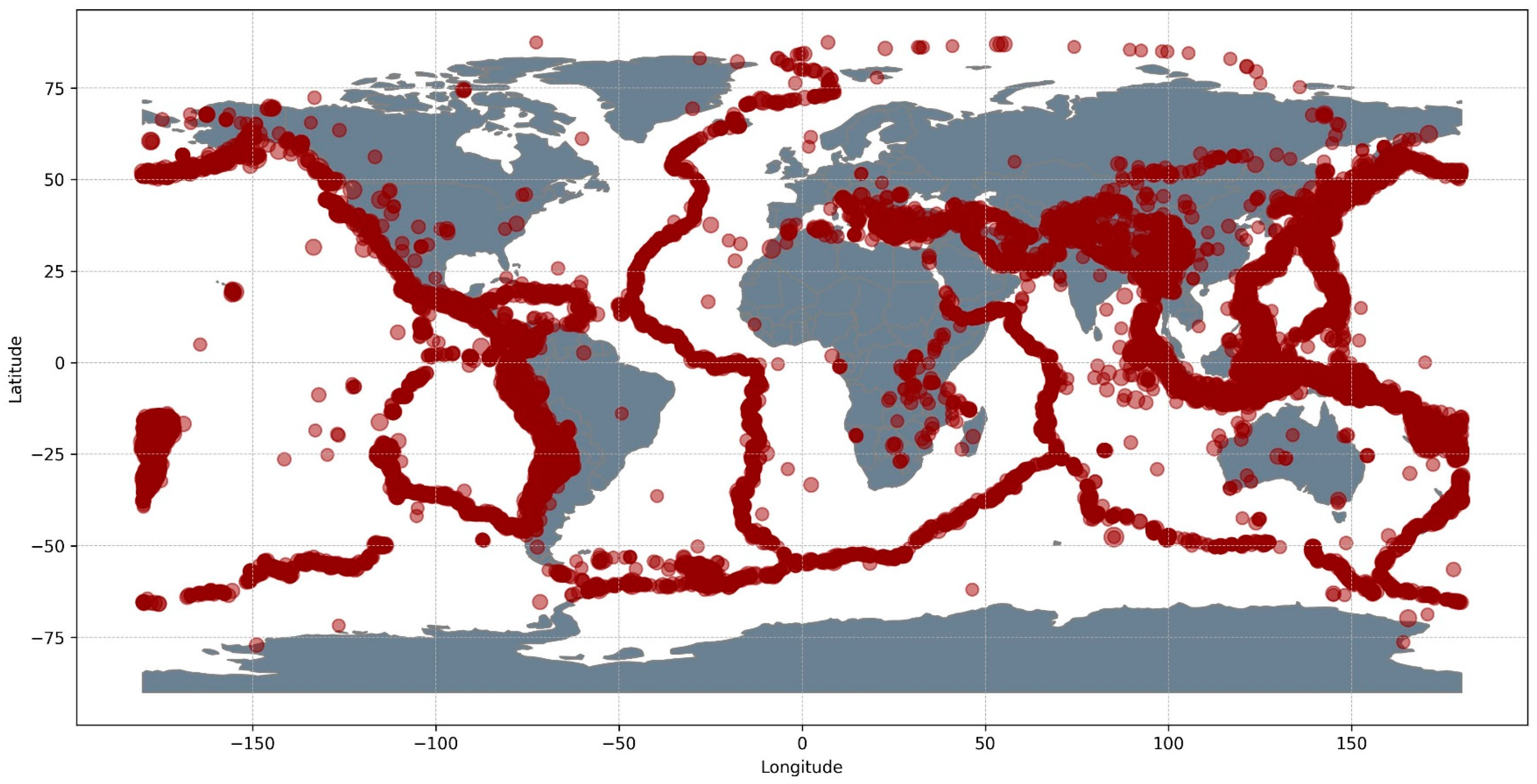
2.2. Earthquake Catalogue
2.3. Other Disturbance Indicators
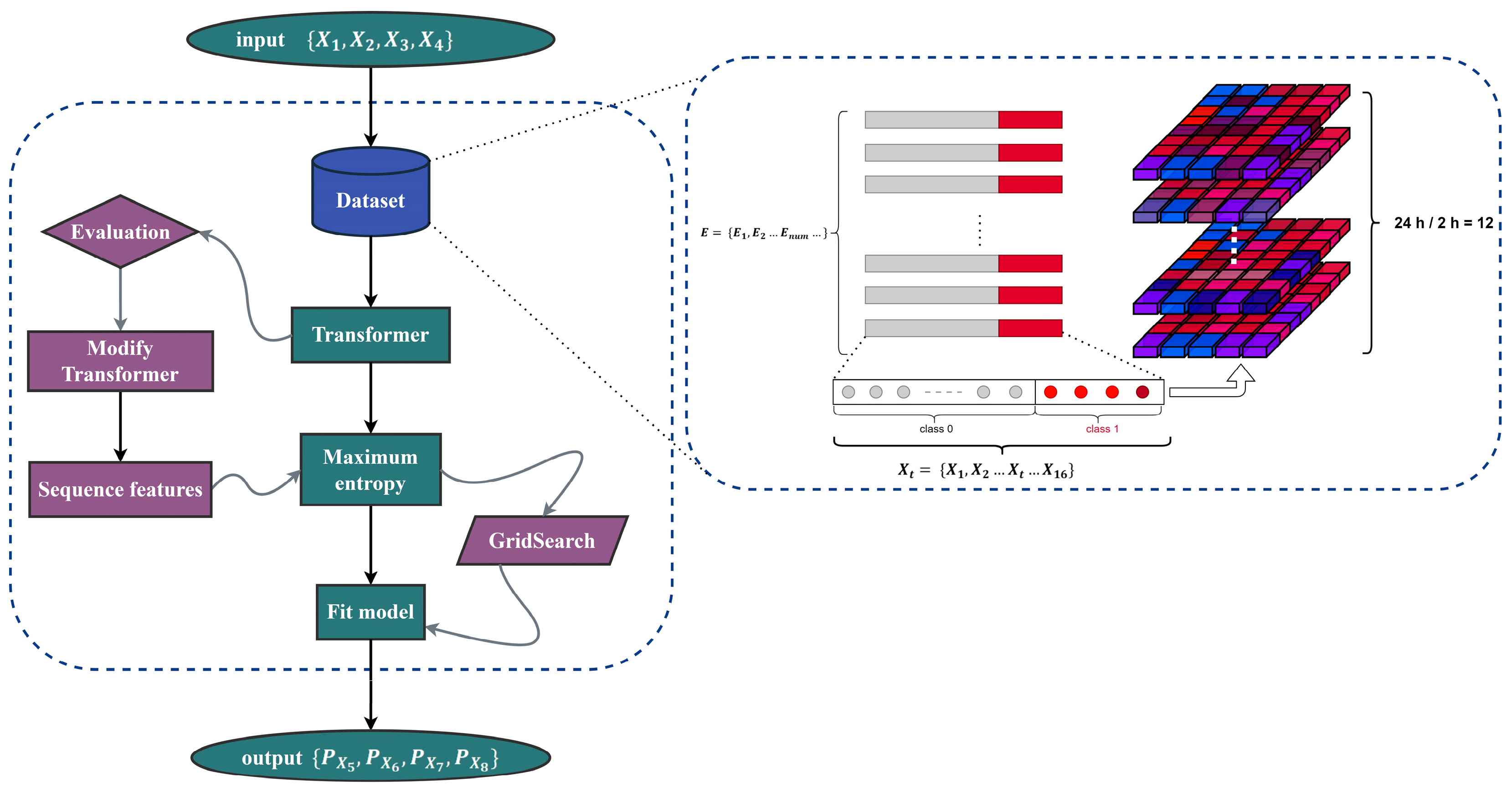
3. Methods
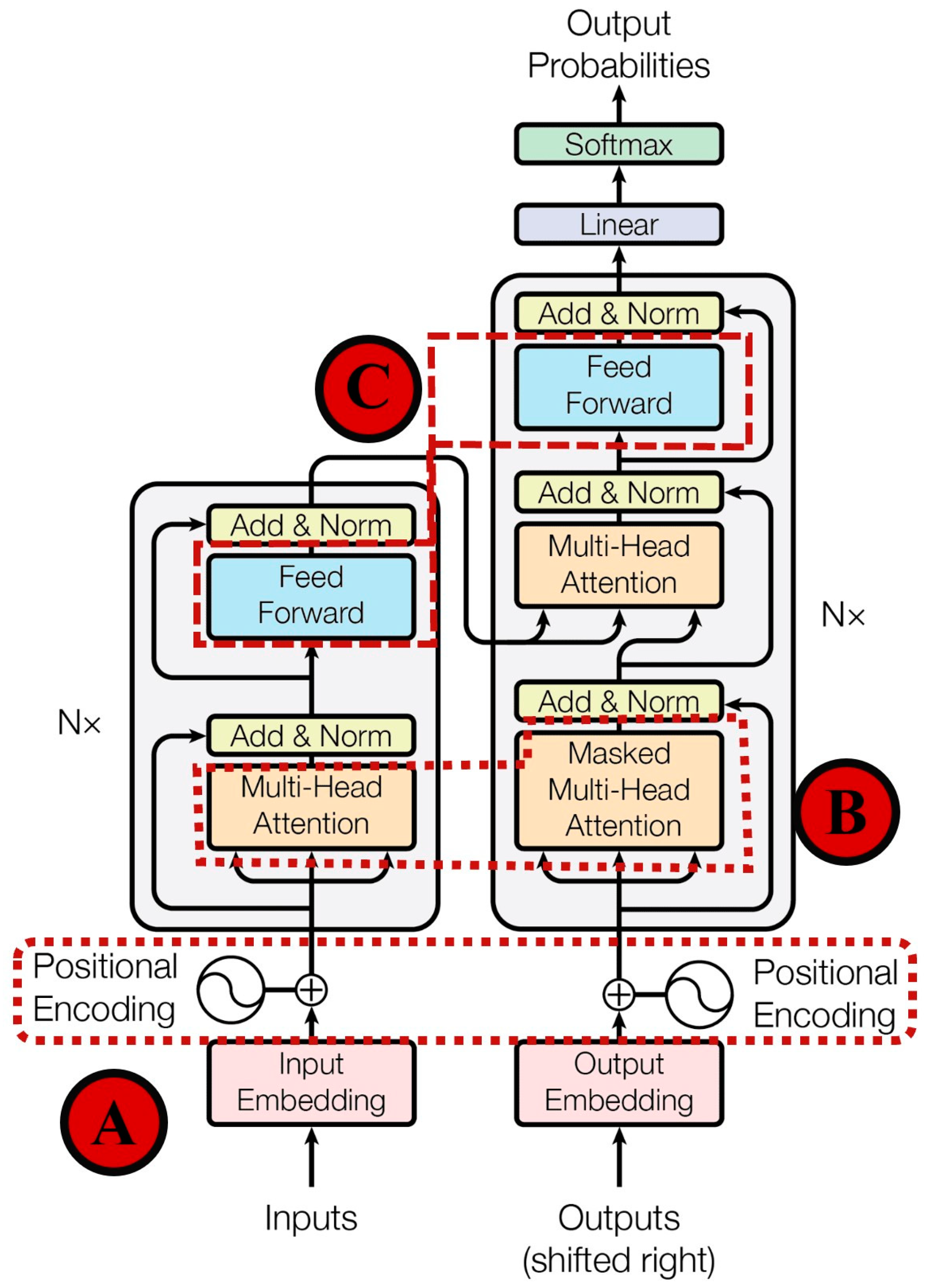
3.1. Transformer
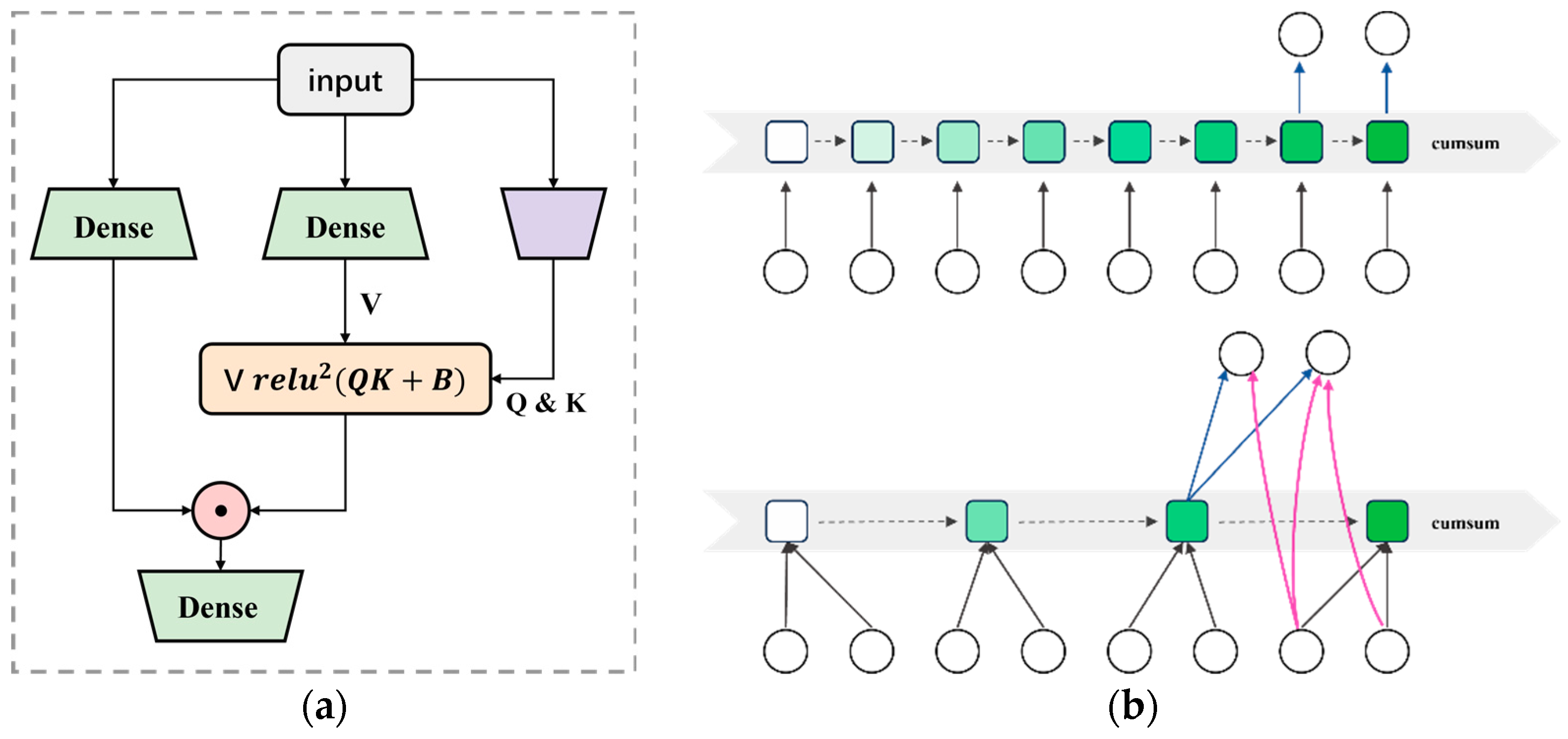
- ITransformer
- 2.
- Flashformer
- 3.
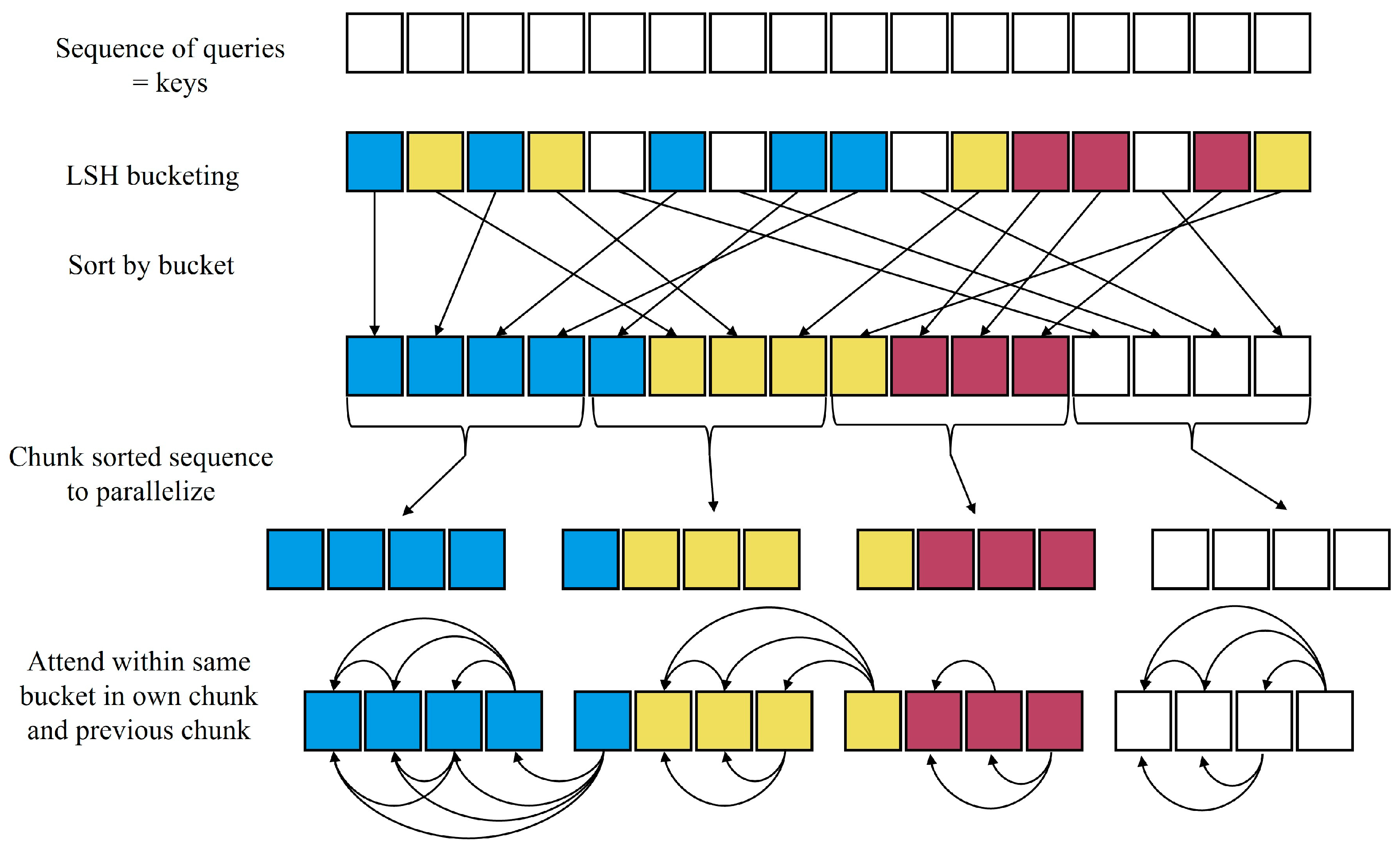
- Reformer
- 4.
- Informer
- 5.
- Flowformer
3.2. Maximum Entropy
3.3. Grid Search and Cross-Validation
4. Results
4.1. Evaluation of Improvement Model
Accuracy Evaluation
4.2. Ablation Experiments
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leonard, R.S.; Barnes, R., Jr. Observation of ionospheric disturbances following the Alaska earthquake. J. Geophys. Res. 1965, 70, 1250–1253. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, M.; Yu, T.; Wan, W.; Lei, J.; Liu, L.; Ning, B. Is an unusual large enhancement of ionospheric electron density linked with the 2008 great Wenchuan earthquake? J. Geophys. Res. Space Phys. 2008, 113, 1–6. [Google Scholar] [CrossRef]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for earthquake precursors from space: A critical review. Front. Earth Sci. 2021, 9, 676775. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Liu, X. GNSS Atmospheric Seismology; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Sharma, G.; Champati Ray, P.K.; Kannaujiya, S. Ionospheric Total Electron Content for Earthquake Precursor Detection. In Remote Sensing of Northwest Himalayan Ecosystems; Navalgund, R.R., Kumar, A.S., Nandy, S., Eds.; Springer: Singapore, 2019; pp. 57–66. [Google Scholar]
- Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) Anomalies as Earthquake Precursors: Unveiling the Geophysical Connection Leading to the 2023 Moroccan 6.8 Mw Earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L.; Trejo Soto, M.E.; Aggarwal, S.P. A combined approach using b-value and ionospheric GPS-TEC for large earthquake precursor detection: A case study for the Colima earthquake of 7.7 Mw, Mexico. Acta Geod. Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Tsolis, G.; Xenos, T. Seismo-ionospheric coupling correlation analysis of earthquakes in Greece, using empirical mode decomposition. Nonlinear Process. Geophys. 2009, 16, 123–130. [Google Scholar] [CrossRef]
- Oikonomou, C.; Haralambous, H.; Muslim, B. Investigation of ionospheric precursors related to deep and intermediate earthquakes based on spectral and statistical analysis. Adv. Space Res. 2017, 59, 587–602. [Google Scholar] [CrossRef]
- Afraimovich, E.; Kiryushkin, V.; Perevalova, N. Determination of the characteristics of ionospheric perturbations in the near-field region of an earthquake epicenter. J. Commun. Technol. Electron. C/C Radiotekhnika I Elektron. 2002, 47, 739–747. [Google Scholar]
- Maekawa, S.; Horie, T.; Yamauchi, T.; Sawaya, T.; Ishikawa, M.; Hayakawa, M.; Sasaki, H. A statistical study on the effect of earthquakes on the ionosphere, based on the subionospheric LF propagation data in Japan. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2006; pp. 2219–2225. [Google Scholar]
- Liu, J.; Chen, Y.; Pulinets, S.; Tsai, Y.; Chuo, Y. Seismo-ionospheric signatures prior to M ≥ 6.0 Taiwan earthquakes. Geophys. Res. Lett. 2000, 27, 3113–3116. [Google Scholar] [CrossRef]
- Wang, X.; Jia, J.; Yue, D.; Ke, F. Analysis of ionospheric VTEC disturbances before and after the Yutian Ms7. 3 earthquake in the Xinjiang Uygur Autonomous Region. Geod. Geodyn. 2014, 5, 8–15. [Google Scholar]
- Liu, C.-Y.; Liu, J.-Y.; Chen, Y.-I.; Qin, F.; Chen, W.-S.; Xia, Y.-Q.; Bai, Z.-Q. Statistical analyses on the ionospheric total electron content related to M≥ 6.0 earthquakes in China during 1998–2015. Terr. Atmos. Ocean. Sci. 2018, 29, 485–498. [Google Scholar] [CrossRef]
- Thomas, J.; Huard, J.; Masci, F. A statistical study of global ionospheric map total electron content changes prior to occurrences of M ≥ 6.0 earthquakes during 2000–2014. J. Geophys. Res. Space Phys. 2017, 122, 2151–2161. [Google Scholar] [CrossRef]
- Chen, H.; Han, P.; Hattori, K. Recent Advances and Challenges in the Seismo-Electromagnetic Study: A Brief Review. Remote Sens. 2022, 14, 5893. [Google Scholar] [CrossRef]
- Xiong, P.; Long, C.; Zhou, H.; Battiston, R.; De Santis, A.; Ouzounov, D.; Zhang, X.; Shen, X. Pre-Earthquake Ionospheric Perturbation Identification Using CSES Data via Transfer Learning. Front. Environ. Sci. 2021, 9, 779255. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the international standard for the ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Nava, B.; Coisson, P.; Radicella, S. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Li, M.; Huo, X. Performance analysis of different NeQuick ionospheric model parameters. Acta Geod. Cartogr. Sin. 2017, 46, 421. [Google Scholar]
- Raymund, T.D.; Austen, J.R.; Franke, S.; Liu, C.; Klobuchar, J.; Stalker, J. Application of computerized tomography to the investigation of ionospheric structures. Radio Sci. 1990, 25, 771–789. [Google Scholar] [CrossRef]
- Llewellyn, S.K. Documentation and Description of the Bent Ionospheric Model; US Department of Commerce, National Technical Information Service: Alexandria, VA, USA, 1973.
- Pignalberi, A.; Pezzopane, M.; Rizzi, R.; Galkin, I. Effective solar indices for ionospheric modeling: A review and a proposal for a real-time regional IRI. Surv. Geophys. 2018, 39, 125–167. [Google Scholar] [CrossRef]
- Natras, R.; Goss, A.; Halilovic, D.; Magnet, N.; Mulic, M.; Schmidt, M.; Weber, R. Regional ionosphere delay models based on CORS data and machine learning. NAVIGATION J. Inst. Navig. 2023, 70, navi.577. [Google Scholar] [CrossRef]
- Ghaffari Razin, M.R.; Voosoghi, B. Ionosphere time series modeling using adaptive neuro-fuzzy inference system and principal component analysis. GPS Solut. 2020, 24, 51. [Google Scholar] [CrossRef]
- Sivavaraprasad, G.; Ratnam, D.V. Performance evaluation of ionospheric time delay forecasting models using GPS observations at a low-latitude station. Adv. Space Res. 2017, 60, 475–490. [Google Scholar] [CrossRef]
- Ogunsua, B.; Laoye, J.; Fuwape, I.; Rabiu, A. The comparative study of chaoticity and dynamical complexity of the low-latitude ionosphere, over Nigeria, during quiet and disturbed days. Nonlinear Process. Geophys. 2014, 21, 127–142. [Google Scholar] [CrossRef]
- Lin, J.-W. Ionospheric total electron content anomalies due to Typhoon Nakri on 29 May 2008: A nonlinear principal component analysis. Comput. Geosci. 2012, 46, 189–195. [Google Scholar] [CrossRef]
- Lin, X.; Wang, H.; Zhang, Q.; Yao, C.; Chen, C.; Cheng, L.; Li, Z. A spatiotemporal network model for global ionospheric TEC forecasting. Remote Sens. 2022, 14, 1717. [Google Scholar] [CrossRef]
- Xiao, Z.; Xiao, S.G.; Hao, Y.Q.; Zhang, D.H. Morphological features of ionospheric response to typhoon. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J. Neural network modeling of the ionospheric electron content at global scale using GPS data. Radio Sci. 1997, 32, 1081–1089. [Google Scholar] [CrossRef]
- Ji, E.Y.; Moon, Y.J.; Park, E. Improvement of IRI global TEC maps by deep learning based on conditional Generative Adversarial Networks. Space Weather 2020, 18, e2019SW002411. [Google Scholar] [CrossRef]
- Cesaroni, C.; Spogli, L.; Aragon-Angel, A.; Fiocca, M.; Dear, V.; De Franceschi, G.; Romano, V. Neural network based model for global Total Electron Content forecasting. J. Space Weather Space Clim. 2020, 10, 11. [Google Scholar] [CrossRef]
- Li, X.; Zhou, C.; Tang, Q.; Zhao, J.; Zhang, F.; Xia, G.; Liu, Y. Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote Sens. 2021, 13, 3849. [Google Scholar] [CrossRef]
- Srivani, I.; Prasad, G.S.V.; Ratnam, D.V. A deep learning-based approach to forecast ionospheric delays for GPS signals. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1180–1184. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, C.; Wang, C.; Zhao, J.; Liu, Y.; Xia, G.; Zhao, Y. Global ionospheric TEC prediction based on deep learning. Chin. J. Radio Sci. 2021, 36, 553–561. [Google Scholar]
- Chen, Z.; Liao, W.; Li, H.; Wang, J.; Deng, X.; Hong, S. Prediction of global ionospheric TEC based on deep learning. Space Weather 2022, 20, e2021SW002854. [Google Scholar] [CrossRef]
- Tang, J.; Li, Y.; Ding, M.; Liu, H.; Yang, D.; Wu, X. An ionospheric TEC forecasting model based on a CNN-LSTM-attention mechanism neural network. Remote Sens. 2022, 14, 2433. [Google Scholar] [CrossRef]
- Zewdie, G.K.; Valladares, C.; Cohen, M.B.; Lary, D.J.; Ramani, D.; Tsidu, G.M. Data-driven forecasting of low-latitude ionospheric total electron content using the random forest and LSTM machine learning methods. Space Weather 2021, 19, e2020SW002639. [Google Scholar] [CrossRef]
- Wen, Z.; Li, S.; Li, L.; Wu, B.; Fu, J. Ionospheric TEC prediction using Long Short-Term Memory deep learning network. Astrophys. Space Sci. 2021, 366, 3. [Google Scholar] [CrossRef]
- Reddybattula, K.D.; Nelapudi, L.S.; Moses, M.; Devanaboyina, V.R.; Ali, M.A.; Jamjareegulgarn, P.; Panda, S.K. Ionospheric TEC forecasting over an Indian low latitude location using long short-term memory (LSTM) deep learning network. Universe 2022, 8, 562. [Google Scholar] [CrossRef]
- Tang, R.; Zeng, F.; Chen, Z.; Wang, J.-S.; Huang, C.-M.; Wu, Z. The comparison of predicting storm-time ionospheric TEC by three methods: ARIMA, LSTM, and Seq2Seq. Atmosphere 2020, 11, 316. [Google Scholar] [CrossRef]
- Iluore, K.; Lu, J. Long short-term memory and gated recurrent neural networks to predict the ionospheric vertical total electron content. Adv. Space Res. 2022, 70, 652–665. [Google Scholar] [CrossRef]
- Bi, C.; Ren, P.; Yin, T.; Zhang, Y.; Li, B.; Xiang, Z. An Informer Architecture-Based Ionospheric foF2 Model in the Middle Latitude Region. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Shih, C.Y.; Lin, C.Y.T.; Lin, S.Y.; Yeh, C.H.; Huang, Y.M.; Hwang, F.N.; Chang, C.H. Forecasting of Global Ionosphere Maps with Multi-Day Lead Time Using Transformer-Based Neural Networks. Space Weather 2024, 22, e2023SW003579. [Google Scholar] [CrossRef]
- Wu, X.; Fan, C.; Tang, J.; Cheng, Y. Forecast of global ionospheric TEC using an improved Transformer model. Adv. Space Res. 2024; in press. [Google Scholar]
- Xia, G.; Liu, M.; Zhang, F.; Zhou, C. CAiTST: Conv-attentional image time sequence transformer for ionospheric TEC maps forecast. Remote Sens. 2022, 14, 4223. [Google Scholar] [CrossRef]
- Lin, M.; Zhu, X.; Tu, G.; Chen, X. Optimal Transformer Modeling by Space Embedding for Ionospheric Total Electron Content Prediction. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Feltens, J.; Schaer, S. IGS Products for the Ionosphere. In Proceedings of the 1998 IGS Analysis Center Workshop, Darmstadt, Germany, 9–11 February 1998; pp. 3–5. [Google Scholar]
- Kagan, Y.Y. Accuracy of modern global earthquake catalogs. Phys. Earth Planet. Inter. 2003, 135, 173–209. [Google Scholar] [CrossRef]
- Yu, T.; Mao, T.; Wang, Y.; Wang, J. Study of the ionospheric anomaly before the Wenchuan earthquake. Chin. Sci. Bull. 2009, 54, 1080–1086. [Google Scholar] [CrossRef]
- Astafyeva, E.; Shalimov, S.; Olshanskaya, E.; Lognonné, P. Ionospheric response to earthquakes of different magnitudes: Larger quakes perturb the ionosphere stronger and longer. Geophys. Res. Lett. 2013, 40, 1675–1681. [Google Scholar] [CrossRef]
- Pulinets, S.; Legen’Ka, A.; Gaivoronskaya, T.; Depuev, V.K. Main phenomenological features of ionospheric precursors of strong earthquakes. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1337–1347. [Google Scholar] [CrossRef]
- Shah, M.; Jin, S. Statistical characteristics of seismo-ionospheric GPS TEC disturbances prior to global Mw ≥ 5.0 earthquakes (1998–2014). J. Geodyn. 2015, 92, 42–49. [Google Scholar] [CrossRef]
- Ulukavak, M.; Yalçınkaya, M.; Kayıkçı, E.T.; Öztürk, S.; Kandemir, R.; Karslı, H. Analysis of ionospheric TEC anomalies for global earthquakes during 2000-2019 with respect to earthquake magnitude (Mw ≥ 6.0). J. Geodyn. 2020, 135, 101721. [Google Scholar] [CrossRef]
- Colonna, R.; Filizzola, C.; Genzano, N.; Lisi, M.; Tramutoli, V. Optimal Setting of Earthquake-Related Ionospheric TEC (Total Electron Content) Anomalies Detection Methods: Long-Term Validation over the Italian Region. Geosciences 2023, 13, 150. [Google Scholar] [CrossRef]
- López-Urias, C.; Vazquez-Becerra, G.E.; Nayak, K.; López-Montes, R. Analysis of Ionospheric Disturbances during X-Class Solar Flares (2021–2022) Using GNSS Data and Wavelet Analysis. Remote Sens. 2023, 15, 4626. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The geomagnetic Kp index and derived indices of geomagnetic activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Lei, J.; Thayer, J.P.; Forbes, J.M. Ionosphere response to recurrent geomagnetic activity: Local time dependency. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Loewe, C.A.; Prölss, G.W. Classification and mean behavior of magnetic storms. J. Geophys. Res. Space Phys. 1997, 102, 14209–14213. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Baumjohann, W.; Kennel, C.; Coroniti, F.V.; Kivelson, M.; Pellat, R.; Walker, R.; Lühr, H.; Paschmann, G. Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. Space Phys. 1992, 97, 4027–4039. [Google Scholar] [CrossRef]
- Pujol, S.; Bedirhanoglu, I.; Donmez, C.; Dowgala, J.D.; Eryilmaz-Yildirim, M.; Klaboe, K.; Koroglu, F.B.; Lequesne, R.D.; Ozturk, B.; Pledger, L. Quantitative evaluation of the damage to RC buildings caused by the 2023 southeast Turkey earthquake sequence. Earthq. Spectra 2024, 40, 505–530. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Chuo, Y.; Tsai, H.F. Variations of ionospheric total electron content during the Chi-Chi earthquake. Geophys. Res. Lett. 2001, 28, 1383–1386. [Google Scholar] [CrossRef]
- Silina, A.; Liperovskaya, E.; Liperovsky, V.; Meister, C.-V. Ionospheric phenomena before strong earthquakes. Nat. Hazards Earth Syst. Sci. 2001, 1, 113–118. [Google Scholar] [CrossRef]
- Pulinets, S.; Contreras, A.L.; Bisiacchi-Giraldi, G.; Ciraolo, L. Total electron content variations in the ionosphere before the Colima, Mexico, earthquake of 21 January 2003. Geofísica Int. 2005, 44, 369–377. [Google Scholar] [CrossRef]
- Mehdi, S.; Shah, M.; Naqvi, N.A. Lithosphere atmosphere ionosphere coupling associated with the 2019 M w 7.1 California earthquake using GNSS and multiple satellites. Environ. Monit. Assess. 2021, 193, 501. [Google Scholar] [CrossRef]
- Krankowski, A.; Zakharenkova, I.E.; Shagimuratov, I.I. Response of the ionosphere to the Baltic Sea earthquake of 21 September 2004. Acta Geophys. 2006, 54, 90–101. [Google Scholar] [CrossRef]
- Potirakis, S.; Minadakis, G.; Eftaxias, K. Relation between seismicity and pre-earthquake electromagnetic emissions in terms of energy, information and entropy content. Nat. Hazards Earth Syst. Sci. 2012, 12, 1179–1183. [Google Scholar] [CrossRef]
- Potirakis, S.; Minadakis, G.; Nomicos, C.; Eftaxias, K. A multidisciplinary analysis for traces of the last state of earthquake generation in preseismic electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2011, 11, 2859–2879. [Google Scholar] [CrossRef]
- Donner, R.V.; Potirakis, S.M.; Balasis, G.; Eftaxias, K.; Kurths, J. Temporal correlation patterns in pre-seismic electromagnetic emissions reveal distinct complexity profiles prior to major earthquakes. Phys. Chem. Earth Parts A/B/C 2015, 85, 44–55. [Google Scholar] [CrossRef]
- Pulinets, S. The synergy of earthquake precursors. Earthq. Sci. 2011, 24, 535–548. [Google Scholar] [CrossRef]
- Hua, W.; Dai, Z.; Liu, H.; Le, Q. Transformer quality in linear time. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 9099–9117. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Huang, Z.; Shi, X.; Zhang, C.; Wang, Q.; Cheung, K.C.; Qin, H.; Dai, J.; Li, H. Flowformer: A transformer architecture for optical flow. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 668–685. [Google Scholar]





| Data | Timespan | Source |
|---|---|---|
| TEC grid product | 2000–2023 | Ionosphere Associate Analysis Centers (IAACs) of the International GNSS Service |
| Earthquake catalogue | 2000–2023 | US Geological Survey |
| Kp & F10.7 | 2000–2023 | GFZ |
| AE & Dst | 2000–2023 | Geomagnetism at the University of Kyoto |
| ITransformer | Flashformer | Reformer | Informer | Flowformer | |
|---|---|---|---|---|---|
| 0.106 1 | 0.587 | 3.537 | 8.122 | 0.756 | |
| ) | 0.221 1 | 0.601 | 1.192 | 1.891 | 0.684 |
| RMSE (/TECU) | 0.325 1 | 0.766 | 1.881 | 2.849 | 0.869 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, Z.; Chen, Y.; Wang, J.; Fu, J. MaxEnt SeismoSense Model: Ionospheric Earthquake Anomaly Detection Based on the Maximum Entropy Principle. Atmosphere 2024, 15, 419. https://doi.org/10.3390/atmos15040419
Wang L, Li Z, Chen Y, Wang J, Fu J. MaxEnt SeismoSense Model: Ionospheric Earthquake Anomaly Detection Based on the Maximum Entropy Principle. Atmosphere. 2024; 15(4):419. https://doi.org/10.3390/atmos15040419
Chicago/Turabian StyleWang, Linyue, Zhitao Li, Yifang Chen, Jianjun Wang, and Jihua Fu. 2024. "MaxEnt SeismoSense Model: Ionospheric Earthquake Anomaly Detection Based on the Maximum Entropy Principle" Atmosphere 15, no. 4: 419. https://doi.org/10.3390/atmos15040419
APA StyleWang, L., Li, Z., Chen, Y., Wang, J., & Fu, J. (2024). MaxEnt SeismoSense Model: Ionospheric Earthquake Anomaly Detection Based on the Maximum Entropy Principle. Atmosphere, 15(4), 419. https://doi.org/10.3390/atmos15040419






