The Impact of Surface Waves and Spray Injection Velocities on Air–Sea Momentum and Heat Fluxes
Abstract
:1. Introduction
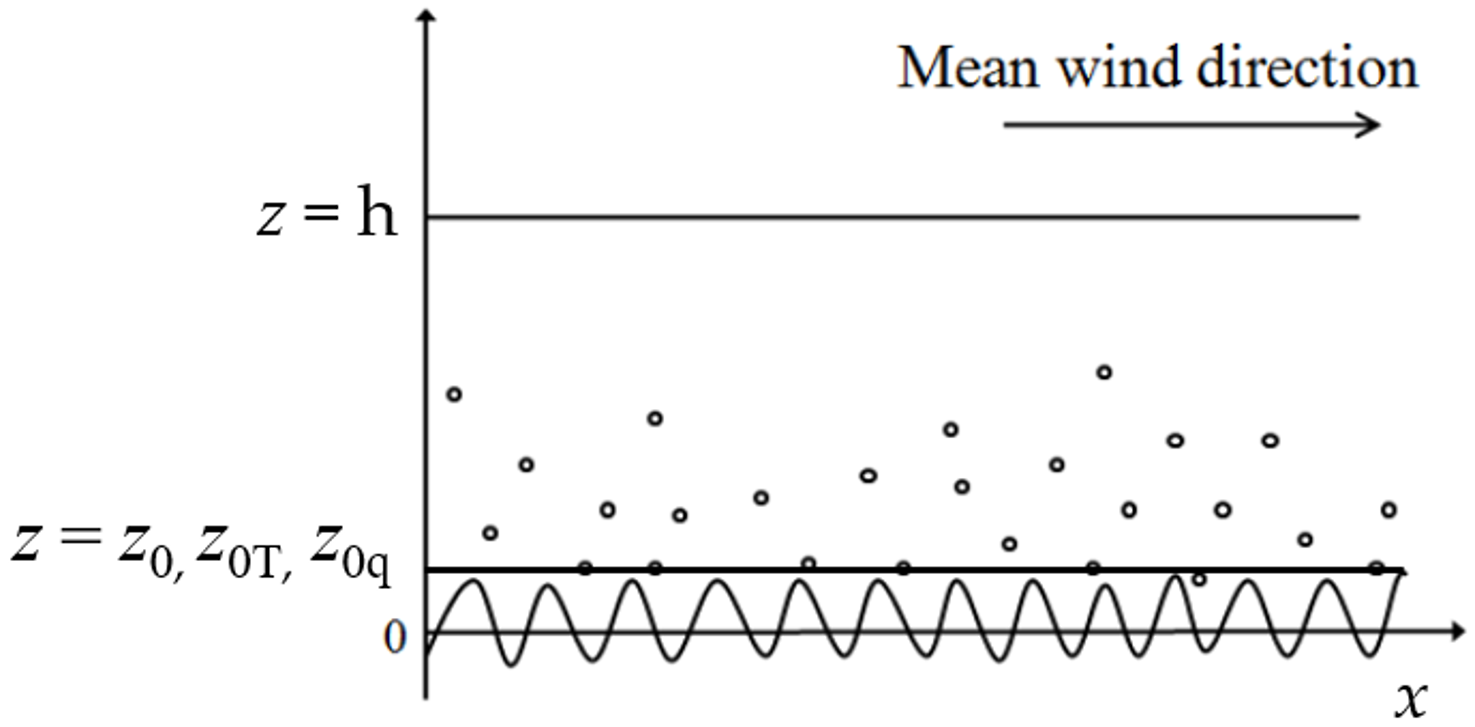
2. Mathematical Description of the MASL Model
2.1. MOST for the Spray-Laden MASL
2.2. Momentum and Enthalpy Conservation Equations of the Spray-Laden MASL
2.2.1. Momentum Conservation Equation
2.2.2. Enthalpy Conservation Equation
2.3. Introduction of New Fluxes to the MOST for Spray-Laden MASL
2.4. Parameterizations
2.4.1. Sea Surface Roughness Length
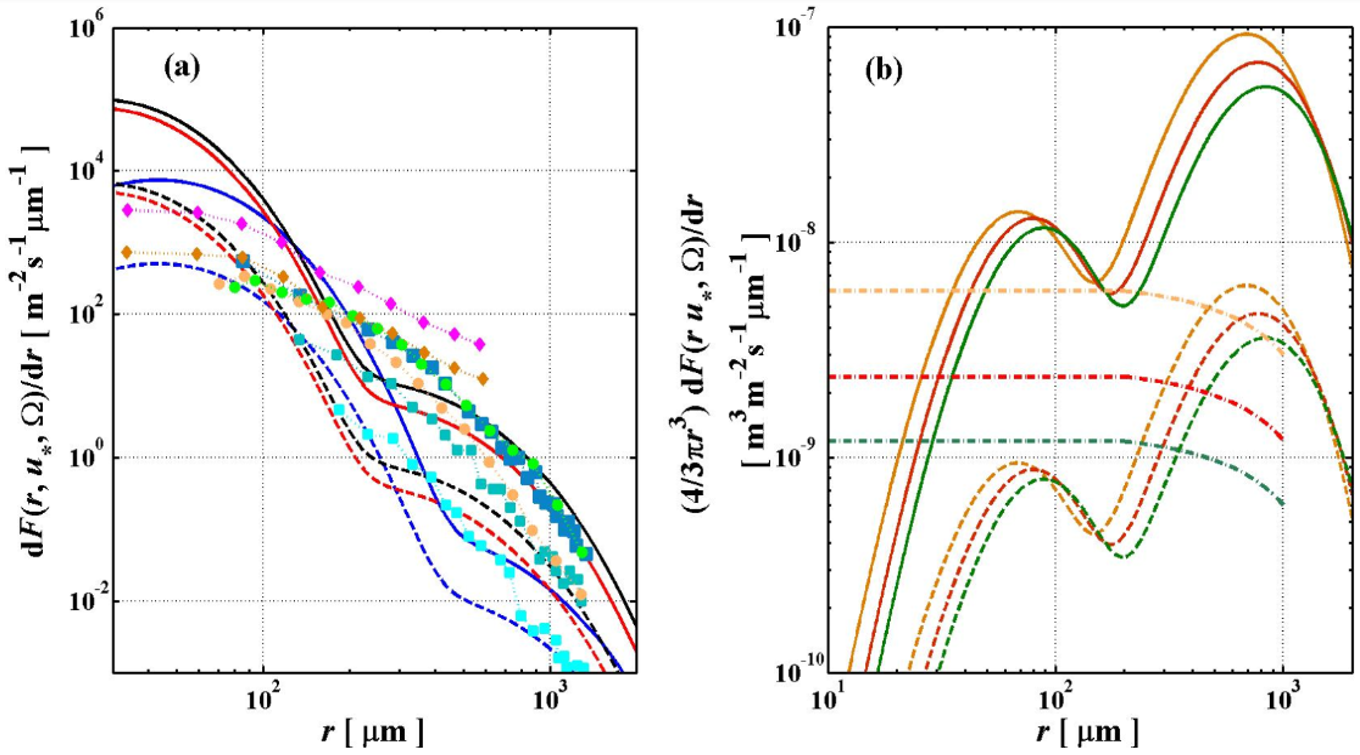
2.4.2. Spray-Induced Momentum Flux
3. Numerical Experiments and Results
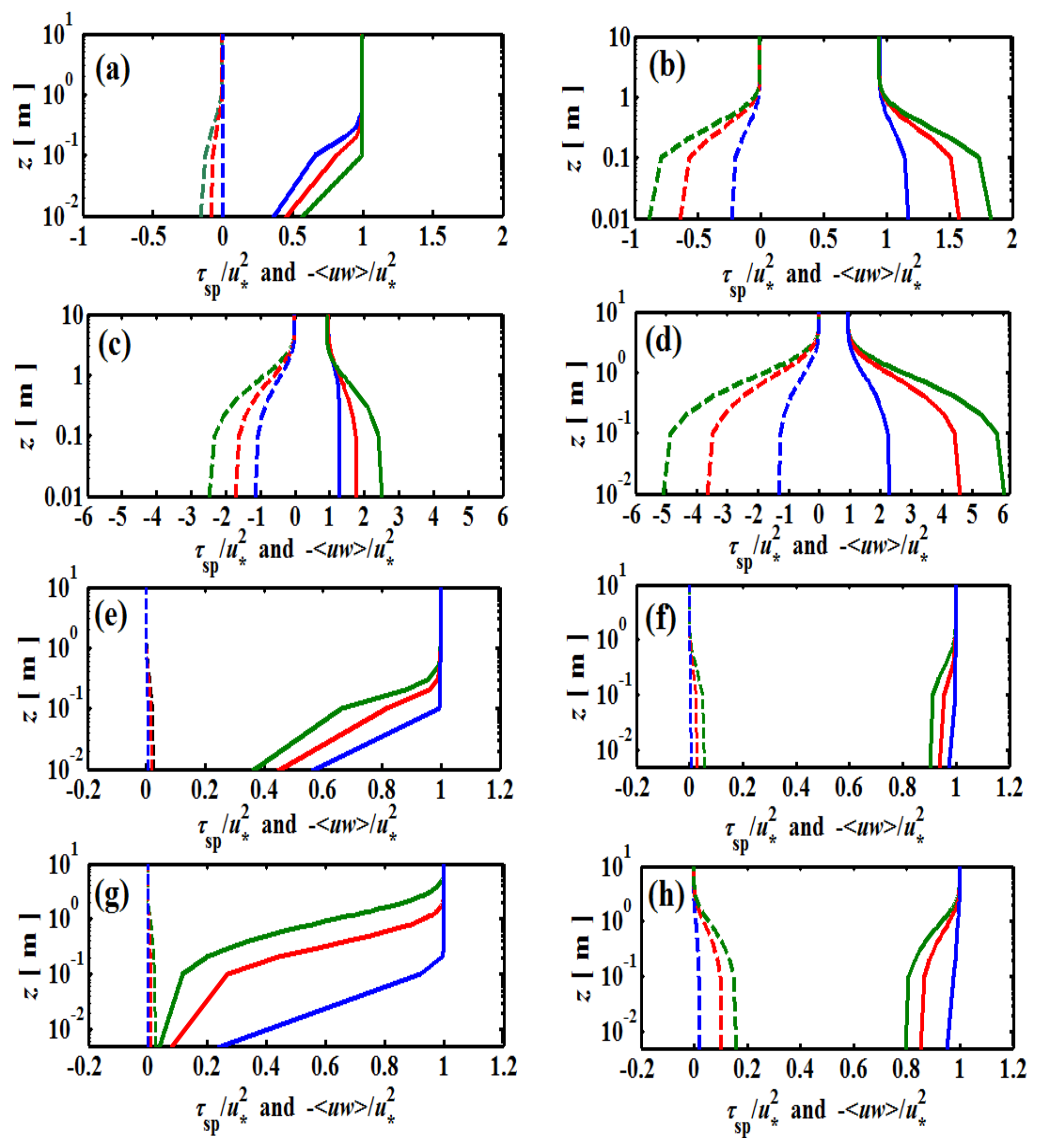
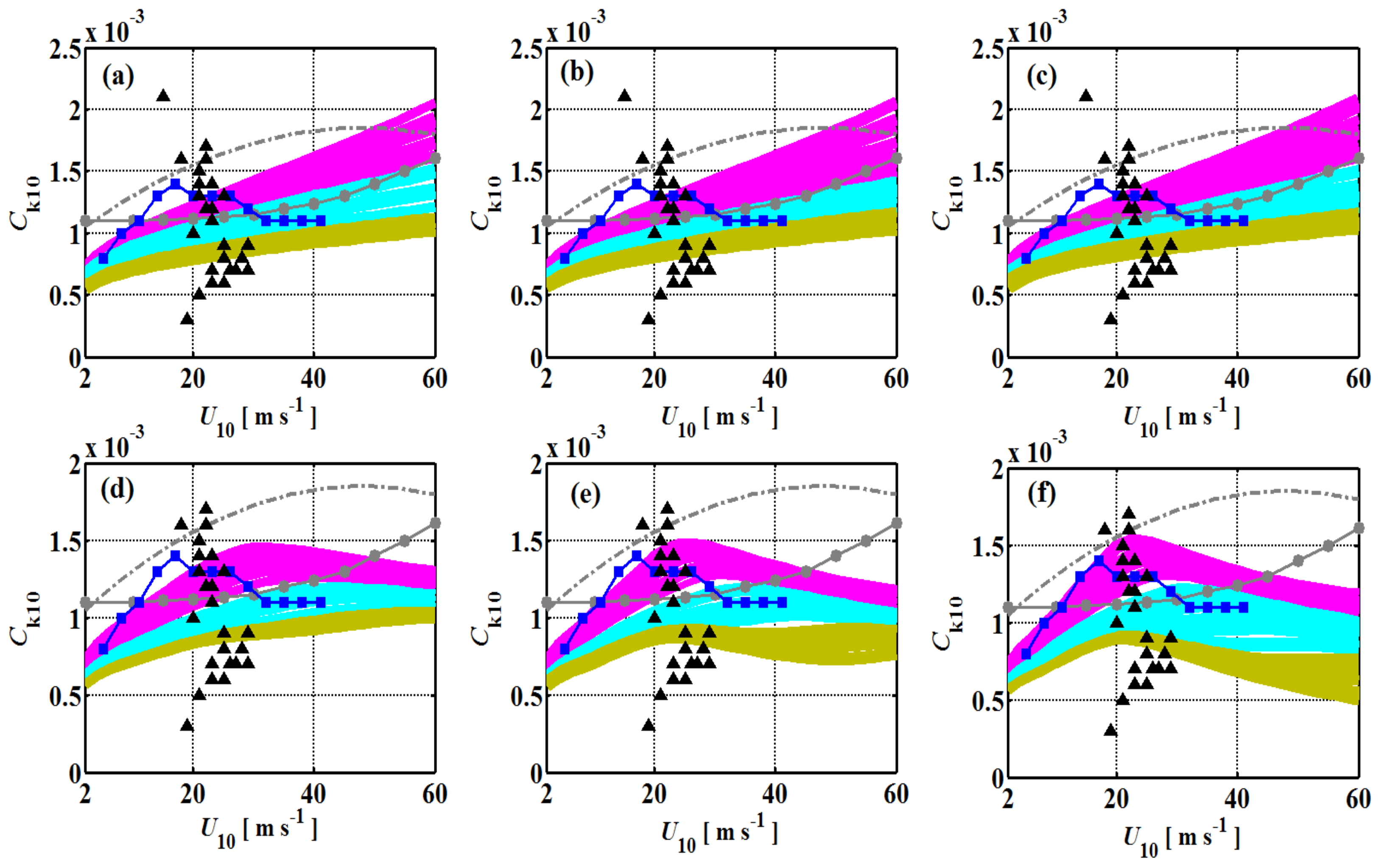
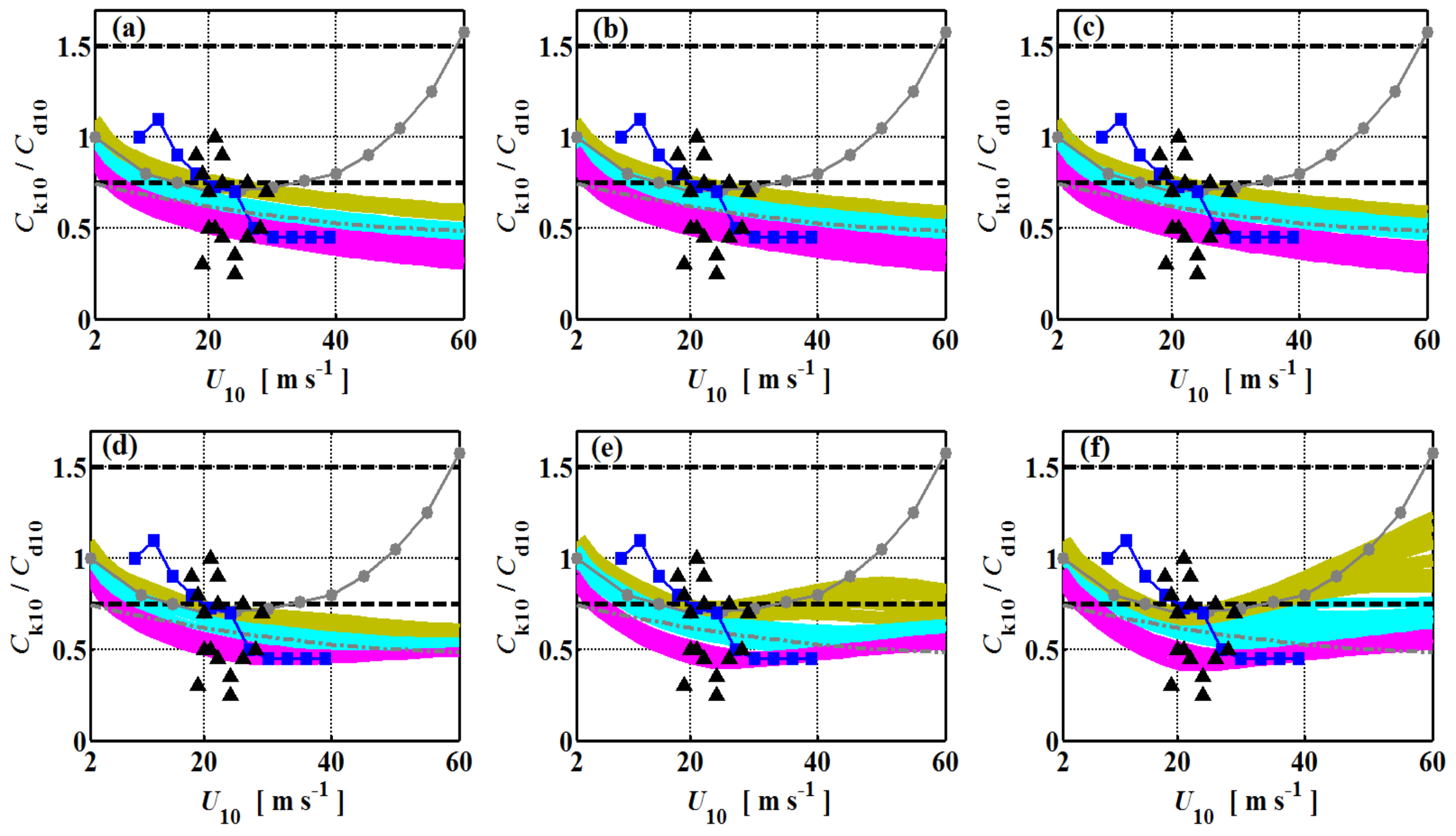
3.1. Momentum Fluxes in the MASL
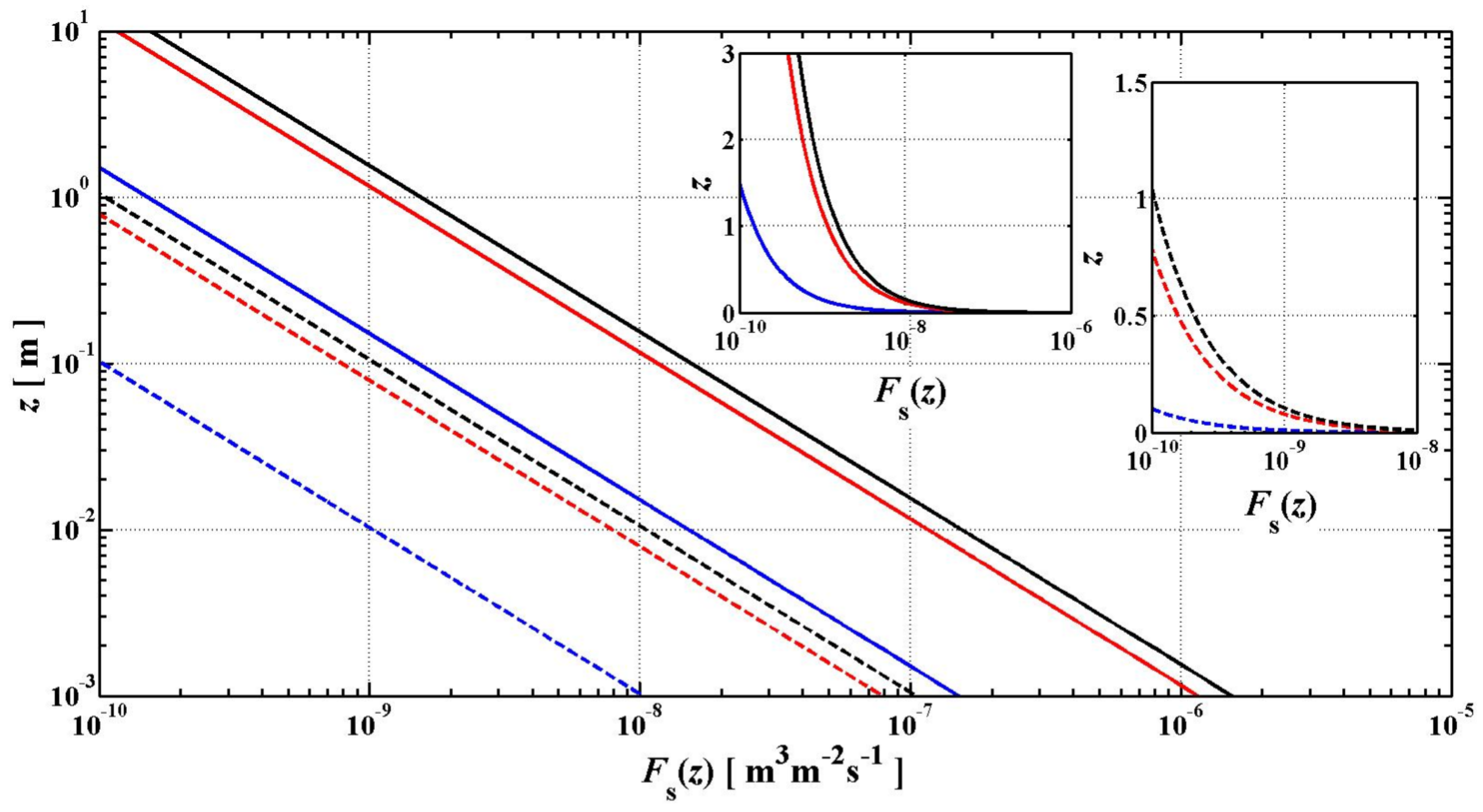
3.2. Enthalpy Fluxes in the MASL
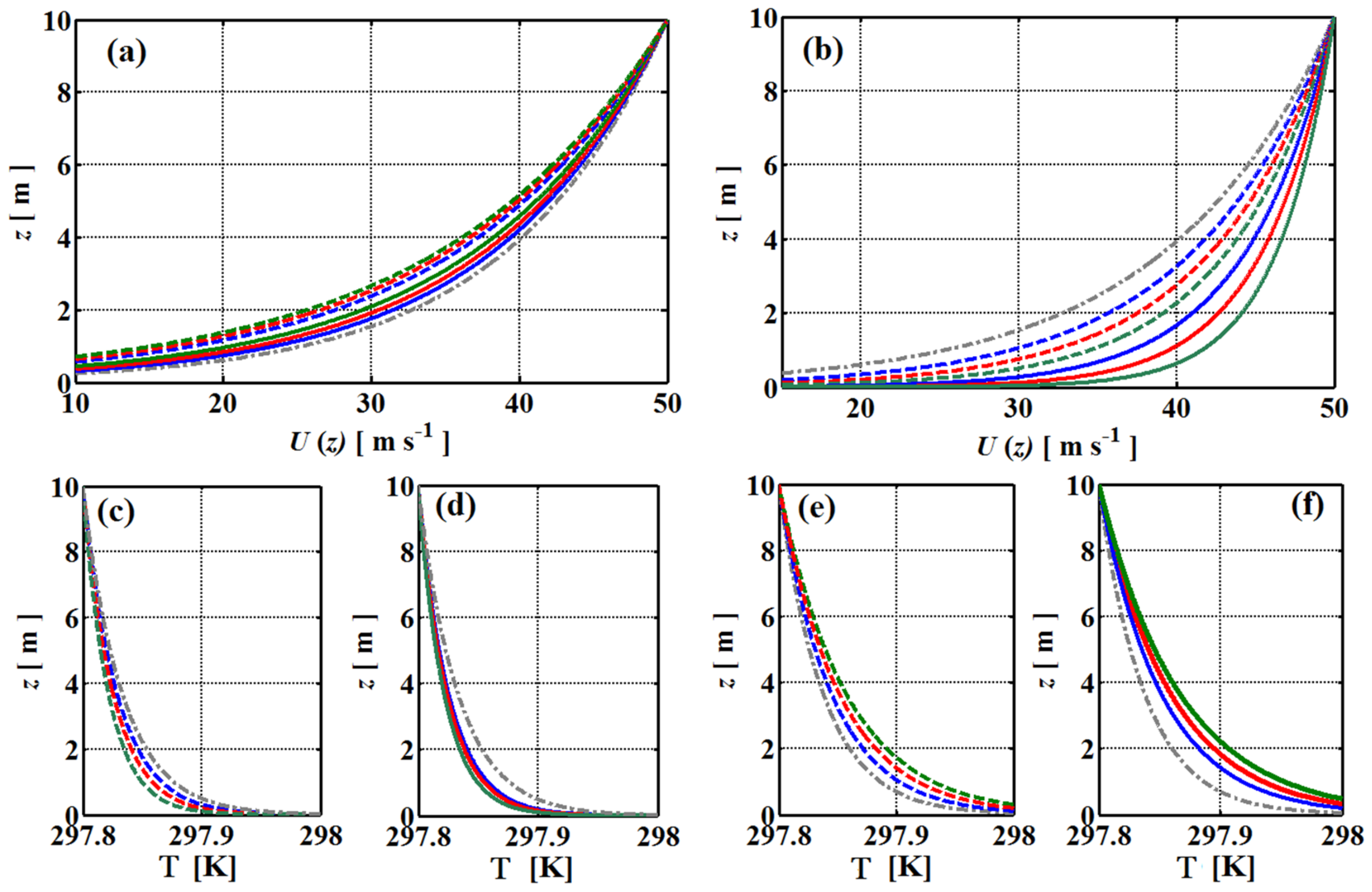
3.3. Vertical Profiles of Mean Wind Speeds and Temperature
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, J.B.; Huang, Y.S. An approximate solution of wave-modified Ekman current for gradually varying eddy viscosity. Deep Sea Res. Part I Oceanogr. Res. Pap. 2011, 58, 668–676. [Google Scholar] [CrossRef]
- Hell, M.C.; Ayet, A.; Chapron, B. Swell generation under extra-tropical storms. J. Geophy. Res. Oceans 2021, 126, e2021JC017637. [Google Scholar] [CrossRef]
- Voermans, J.J.; Rapizo, H.; Ma, H.Y.; Qiao, F.L.; Babanin, A.V. Air-sea momentum fluxes during cyclone olwyn. J. Phys. Oceanogr. 2019, 49, 1369–1379. [Google Scholar] [CrossRef]
- Wu, L.C.; Rutgersson, A.; Sahle, E.; Larsen, X.G. The impact of waves and sea spray on modelling storm track and development. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 27967. [Google Scholar] [CrossRef]
- Chen, Y.J.; Yu, X. Enhancement of wind stress evaluation method under storm conditions. Clim. Dyn. 2016, 47, 3833–3843. [Google Scholar] [CrossRef]
- Zhang, T.; Song, J.B.; Li, S.; Yang, L.G. The effects of wind-driven waves and ocean spray on the drag coefficient and near-surface wind profiles over the ocean. Acta Ocean. Sin. 2016, 35, 79–85. [Google Scholar] [CrossRef]
- Zhang, T.; Song, J.B. Effects of sea-surface waves and ocean spray on air-sea momentum fluxes. Adv. Atmos. Sci. 2018, 35, 469–478. [Google Scholar] [CrossRef]
- Veron, F. Ocean spray. Ann. Rev. Flu. Mech. 2015, 47, 507–538. [Google Scholar] [CrossRef]
- Alamaro, M.; Emanuel, K.; Colton, J.; McGillis, W.; Edson, J. Experimental investigation of air-sea transfer of momentum and enthalpy at high wind speed. In Preprints, Proceedings of the 25th Conference on Hurricanes and Tropical Meteorology, San Diego, CA, USA, 29 April 2002; American Meteorological Society: Boston, MA, USA, 2002; pp. 667–668. [Google Scholar]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279. [Google Scholar] [CrossRef]
- Jarosz, E.; Mitchell, D.A.; Wang, D.W.; Teague, W.J. Bottom-up determination of air-sea momentum exchange under a major tropical cyclone. Science 2007, 315, 1707–1709. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Donelan, M.; Haus, B.; Reul, N.; Plant, W.; Stiassnie, M.; Graber, H.; Brown, O.; Saltzman, E. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Black, P.G.; D’Asaro, E.A.; Drennan, W.M.; French, J.R.; Niiler, P.P.; Sanford, T.B.; Terrill, E.J.; Walsh, E.J.; Zhang, J.A. Air–Sea Exchange in Hurricanes: Synthesis of Observations from the Coupled Boundary Layer Air–Sea Transfer Experiment. Bull. Am. Meteorol. Soc. 2007, 88, 357–374. [Google Scholar] [CrossRef]
- Curcic, M.; Haus, B.K. Revised estimates of ocean surface drag in strong winds. Geophys. Res. Lett. 2020, 47, e2020GL087647. [Google Scholar] [CrossRef]
- Liu, B.; Guan, C.; Xie, L. The wave state and sea spray related parameterization of wind stress applicable from low to extreme winds. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Shi, J.; Zhong, Z.; Li, X.; Jiang, G.; Zeng, W.; Li, Y. The influence of wave state and sea spray on drag coefficient from low to high wind speeds. J. Ocean Univ. China 2016, 15, 41–49. [Google Scholar] [CrossRef]
- Sroka, S.; Emanuel, K. A review of parameterizations for enthalpy and momentum fluxes from sea spray in tropical cyclones. J. Phys. Oceanogr. 2021, 51, 3053–3069. [Google Scholar] [CrossRef]
- Shpund, J.; Pinksy, M.; Khain, A. Microphysical structure of the marine boundary layer under strong wind and spray formation as seen from simulations using a 2D explicit microphysical model. Part I: The impact of large eddies. J. Atmos. Sci. 2011, 68, 2366–2384. [Google Scholar] [CrossRef]
- Shpund, J.; Zhang, J.; Pinsky, M.; Khain, A. Microphysical structure of the marine boundary layer under strong wind and spray formation as seen from simulations using a 2D explicit microphysical model. Part II: The role of sea spray. J. Atmos. Sci. 2012, 69, 3501–3514. [Google Scholar] [CrossRef]
- Shpund, J.; Zhang, J.; Pinsky, M.; Khain, A. Microphysical structure of the marine boundary layer under strong wind and sea spray formation as seen from a 2D explicit microphysical mode. Part III: Parameterization of height-dependent droplet size distribution. J. Atmos. Sci. 2014, 71, 1914–1934. [Google Scholar] [CrossRef]
- Bianco, L.; Bao, J.W.; Fairall, C.; Michelson, S. Impact of sea-spray on the atmospheric surface layer. Bound. Layer Meteorol. 2011, 140, 361. [Google Scholar] [CrossRef]
- Rastigejev, Y.; Suslov, S.A. Effect of evaporating sea spray on heat fluxes in a marine atmospheric boundary layer. J. Phys. Oceanogr. 2019, 49, 1927–1948. [Google Scholar] [CrossRef]
- Chen, X. How do planetary boundary layer schemes perform in hurricane conditions: A comparison with large-eddy simulations. J. Adv. Model. Earth Sys. 2022, 14, e2022MS003088. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.A.; Matak, L.; Momen, M. The impact of adjusting momentum roughness length on strong and weak Hurricane Forecasts: A comprehensive analysis of weather simulations and observations. Mon. Wea. Rev. 2023, 151, 1287–1302. [Google Scholar] [CrossRef]
- Troitskaya, Y.; Ezhova, E.; Soustova, I.; Zilitinkevich, S.S. On the effect of sea spray on the aerodynamic surface drag under sever winds. Ocean Dyn. 2016, 66, 659–669. [Google Scholar] [CrossRef]
- Druzhinin, O.A.; Troitskaya, Y.I.; Zilitinkevich, S.S. The study of droplet-laden turbulent airflow over waved water surface by direct numerical simulation. J. Geophys. Res. Oceans 2017, 122, 1789–1807. [Google Scholar] [CrossRef]
- Druzhini, O.A.; Troitskaya, Y.I.; Zilitinkevich, S.S. The study of momentum, mass and heat transfer in a droplet-laden turbulent airflow over a waved-water surface by direct numerical simulation. J. Geophys. Res. Oceans 2018, 123, 8346–8365. [Google Scholar] [CrossRef]
- Bao, J.W.; Fairall, C.W.; Michelson, S.; Bianco, L. Parameterizations of sea-spray impact on the air-sea momentum and heat fluxes. Mon. Wea. Rev. 2011, 139, 3781–3797. [Google Scholar] [CrossRef]
- Troitskaya, Y.; Kandaurov, A.; Ermakova, O.; Kozlov, D.; Sergee, D.; Zilitinkevich, S. The “bag breakup” spume droplet generation mechanism at high winds. Part I: Spray generation function. J. Phys. Oceanogr. 2018, 48, 2167–2188. [Google Scholar] [CrossRef]
- Högström, U.L.F. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation. Top. Micrometeorol. A Festschr. Arch Dye. 1988, 42, 55–78. [Google Scholar]
- Foken, T. 50 years of the Monin–Obukhov similarity theory. Bound. Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V.K. Impact of ocean spray on the dynamics of the marine atmospheric boundary layer. Bound. Layer Meteorol. 2011, 140, 383–410. [Google Scholar] [CrossRef]
- Troitskaya, T.; Druzhinin, O.; Kozlov, D.; Zilitinkevich, S. The “bag breakup” spume droplet generation mechanism at high winds. Part II: Contribution to momentum and enthalpy transfper. J. Phys. Oceanogr. 2018, 48, 2189–2207. [Google Scholar] [CrossRef]
- Janssen, P.A. Quasi-linear theory of wind-wave generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Ortiz-Suslow, D.G.; Haus, B.K.; Mehta, S.; Laxague, N.J. Sea spray generation in very high winds. J. Atmos. Sci. 2016, 73, 3975–3995. [Google Scholar] [CrossRef]
- Veron, F.; Hopkins, C.; Harrison, E.; Mueller, J. Sea spray spume droplet production in high wind speeds. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Fairall, C.; Banner, M.; Peirson, W.; Asher, W.; Morison, R. Investigation of the physical scaling of sea spray spume droplet production. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the exchange of momentum over the open ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Hara, T.; Sullivan, P.P. Wave boundary layer turbulence over surface waves in a strongly forced condition. J. Phys. Oceanogr. 2015, 45, 868–883. [Google Scholar] [CrossRef]
- Emanuel, K.A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics. J. Atmos. Sci. 1995, 52, 3969–3976. [Google Scholar] [CrossRef]
- Zweers, N.; Makin, V.; Vries, J.; Kudryavtsev, V. The impact of spray-mediated enhanced enthalpy and reduced drag coefficients in the modelling of tropical cyclones. Bound. Layer Meteorol. 2015, 155, 501–514. [Google Scholar] [CrossRef]
- Haus, B.K.; Jeong, D.; Donelan, M.A.; Zhang, J.A.; Savelyev, I. Relative rates of sea-air heat transfer and frictional drag in very high winds. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Troitskaya, Y.; Sergeev, D.; Kandaurov, A.; Vdovin, M.; Zilitinkevich, S. The effect of foam on waves and the aerodynamic roughness of the water surface at high winds. J. Phys. Oceanogr. 2019, 49, 959–981. [Google Scholar] [CrossRef]
- Reul, N.; Chapron, B. A model of sea-foam thickness distribution for passive microwave remote sensing applications. J. Geophy. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Golbraikh, E.; Shtemler, Y.M. Foam input into the drag coefficient in hurricane conditions. Dyn. Atmos. Oceans 2016, 73, 1–9. [Google Scholar] [CrossRef]
- Hwang, P.A.; Reul, N.; Meissner, T.; Yueh, S. Whitecap and wind stress observations by microwave radiometers: Global coverage and extreme conditions. J. Phys. Oceanogr. 2019, 49, 2291–2307. [Google Scholar] [CrossRef]
- Callaghan, A.H. On the relationship between the energy dissipation rate of surface-breaking waves and oceanic whitecap coverage. J. Phys. Oceanogr. 2018, 48, 2609–2626. [Google Scholar] [CrossRef]
- Xie, Z. Numerical modelling of wind effects on breaking waves in the surf zone. Ocean Dyn. 2017, 67, 1251–1261. [Google Scholar] [CrossRef]

| (m s−1) | ||
|---|---|---|
| 30 | 0.95 | 0.2 |
| 30 | 0.95 | 0.6 |
| 30 | 0.95 | 1.0 |
| 30 | 0.05 | 0.2 |
| 30 | 0.05 | 0.6 |
| 30 | 0.05 | 1.0 |
| 50 | 0.95 | 0.2 |
| 50 | 0.95 | 0.6 |
| 50 | 0.95 | 1.0 |
| 50 | 0.05 | 0.2 |
| 50 | 0.05 | 0.6 |
| 50 | 0.05 | 1.0 |
| (m s−1) | ||
|---|---|---|
| 0.2 | ||
| 0.2 | ||
| 0.2 | ||
| 0.6 | ||
| 0.6 | ||
| 0.6 | ||
| 1.0 | ||
| 1.0 | ||
| 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T. The Impact of Surface Waves and Spray Injection Velocities on Air–Sea Momentum and Heat Fluxes. Atmosphere 2023, 14, 1500. https://doi.org/10.3390/atmos14101500
Zhang T. The Impact of Surface Waves and Spray Injection Velocities on Air–Sea Momentum and Heat Fluxes. Atmosphere. 2023; 14(10):1500. https://doi.org/10.3390/atmos14101500
Chicago/Turabian StyleZhang, Ting. 2023. "The Impact of Surface Waves and Spray Injection Velocities on Air–Sea Momentum and Heat Fluxes" Atmosphere 14, no. 10: 1500. https://doi.org/10.3390/atmos14101500
APA StyleZhang, T. (2023). The Impact of Surface Waves and Spray Injection Velocities on Air–Sea Momentum and Heat Fluxes. Atmosphere, 14(10), 1500. https://doi.org/10.3390/atmos14101500





