Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Severe Nuclear Accident Model and Dataset Generation
2.1.1. Definition of the Multi-Nuclide Source Term
2.1.2. Locations of Monitoring Sites
2.1.3. Other Input Data
2.1.4. Dataset Generation
2.2. Inversion Model Based on TCN
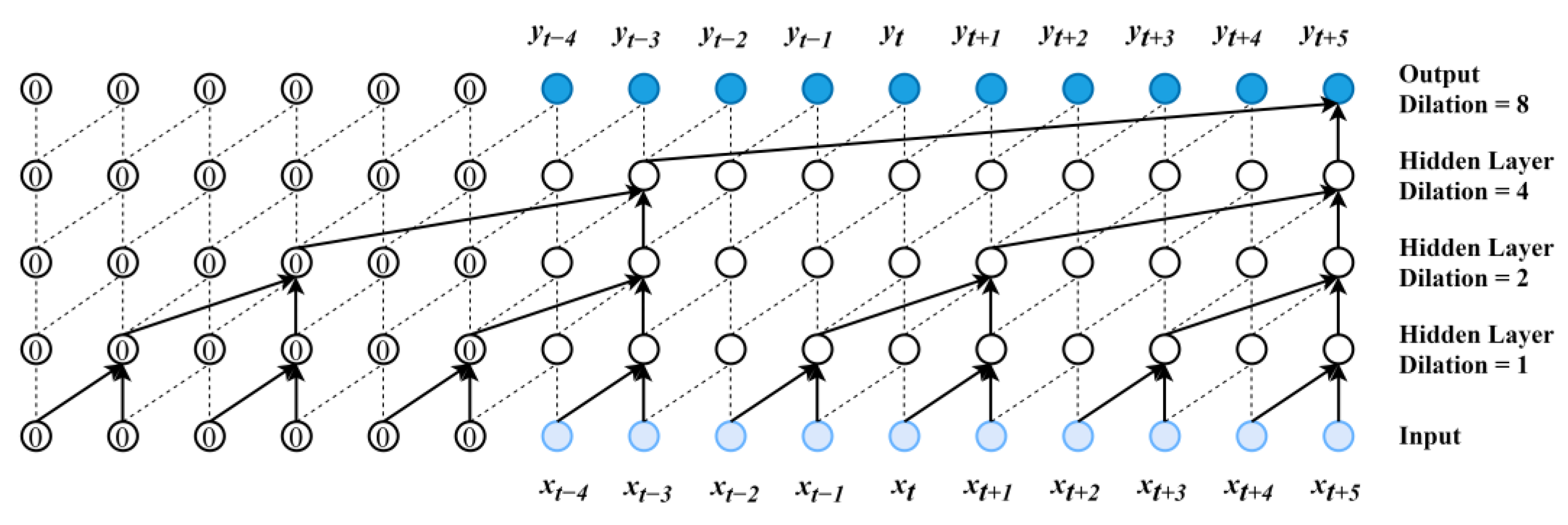
2.2.1. TCN Algorithm
2.2.2. Multi-Nuclide Source Term Inversion Model Based on TCN
- (a)
- First, the gamma dose rate data from the two monitoring points are pre-processed by converting the gamma dose rate for 10 h into a 10 × 10 matrix, i.e., the first row is the gamma dose rate at time step 1, the tenth row is the gamma dose rate at time steps 1 to 10, and all missing data are filled with the default value “0”.
- (b)
- To avoid the distortion effects of using default values, a masking unit [30] was used to mask the fixed values in the input sequence signal, locating the time steps to be skipped. If the input data are equal to the given value, the time step is omitted in all the subsequent layers of the model. As shown in Figure 3c, only one valid data point remains in the first row after processing through the mask unit.
- (c)
- The gamma dose rate at the tenth time step was used as an example. Sequence information of the gamma dose rate was extracted using the TCN. Feature extraction of gamma dose rate data from two monitoring points was done using n convolution kernels. The nonlinear activation function of the data features was computed by the ReLU activation function, which introduced nonlinear elements to the neurons and allowed the neural network to approximate any other nonlinear function. The deep network was dispersed to avoid overfitting by the weight regularization layer [31] and the dropout layer [32].
- (d)
- Gamma dose rate data, release height, atmospheric stability, wind speed, mixed layer height, and precipitation type were combined as input data.
- (e)
- Input data were fed to the full connection layer, and the release rates of the seven nuclides were output.
2.3. Inversion Model Based on 2D-CNN
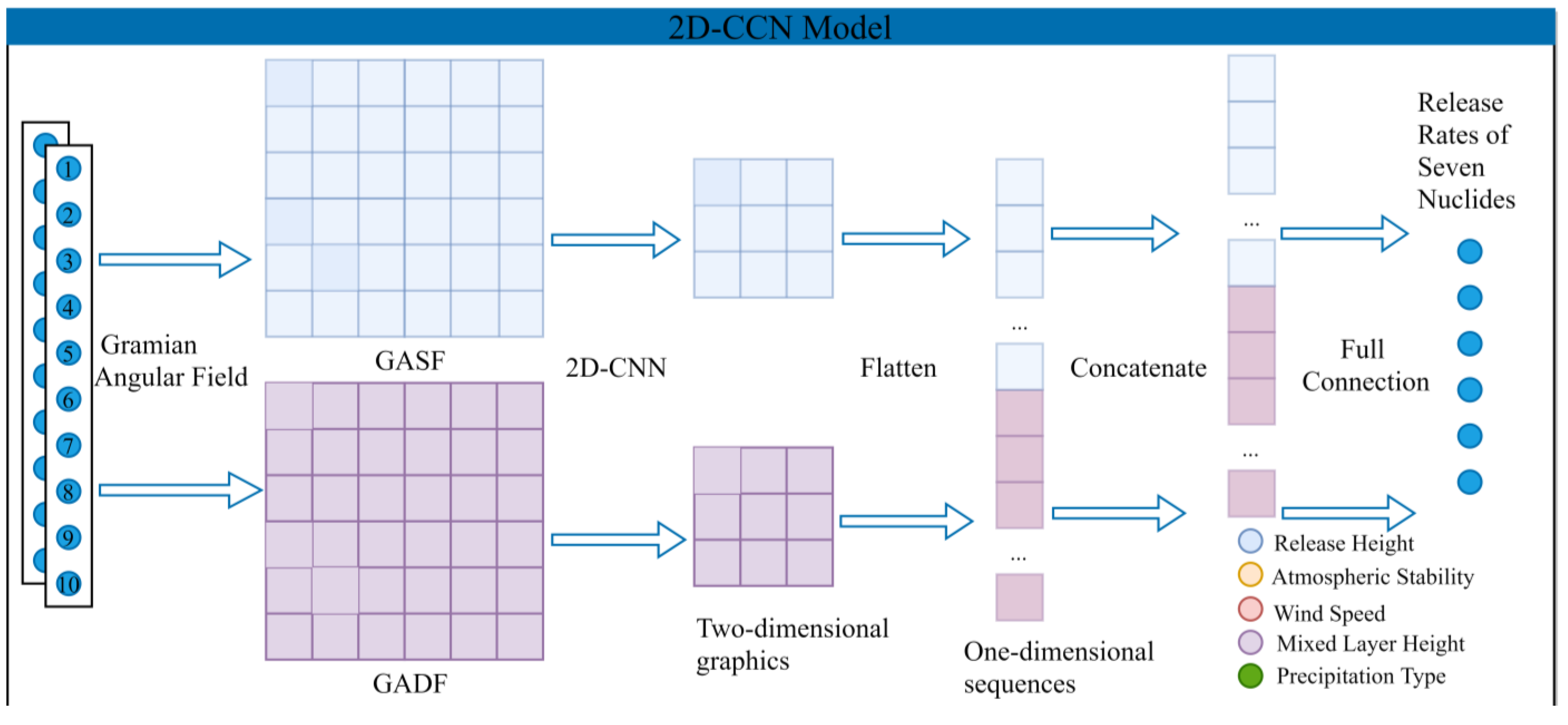
2.3.1. Gramian Angular Field
- (1)
- First, the one-dimensional time series was normalized, and the normalized time series was denoted by .
- (2)
- The timestamp of was then used as the radius. The value corresponding to the time stamp was used as the cosine angle. The was re-projected to polar coordinates based on the radius and cosine angle.
- (3)
- Finally, was converted into a Gramian angular summation field (GASF) in image format based on the sum of the trigonometric functions between each point. The was converted into a Gramian angular difference field (GADF) based on the difference in trigonometric functions. GASF and GADF are defined in Equations (2) and (3).
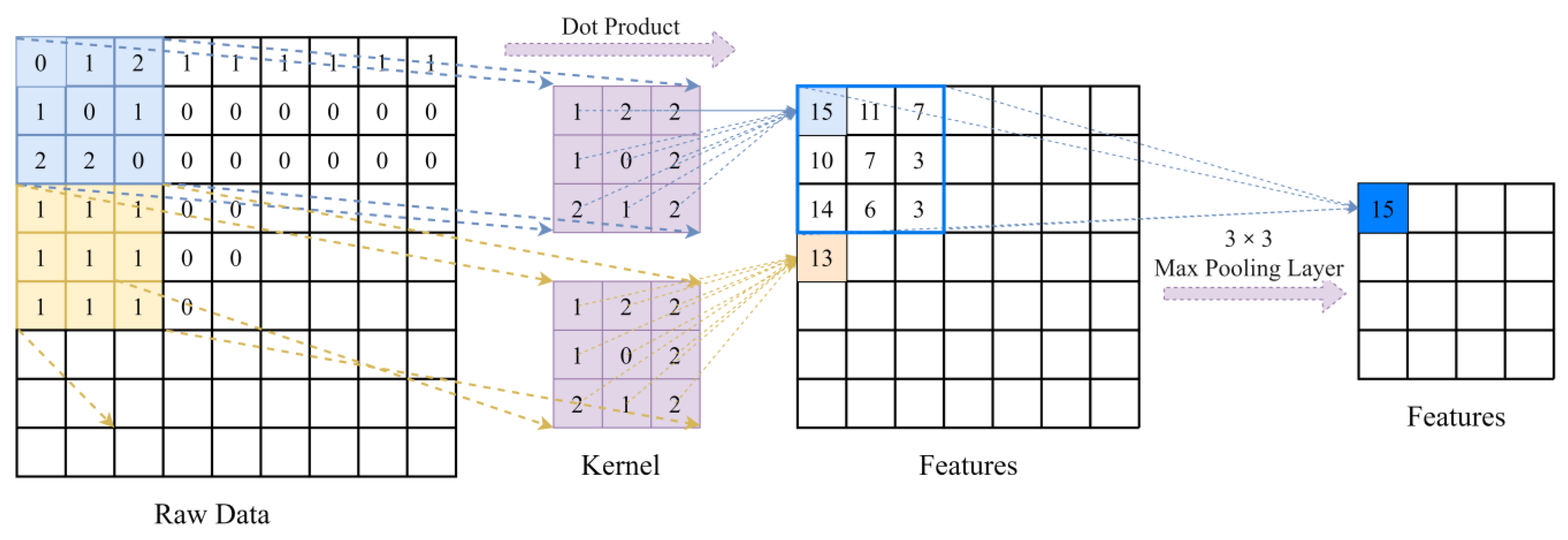
2.3.2. 2D-CNN Algorithm
2.3.3. Multi-Nuclide Source Term Inversion Model Based on 2D-CNN
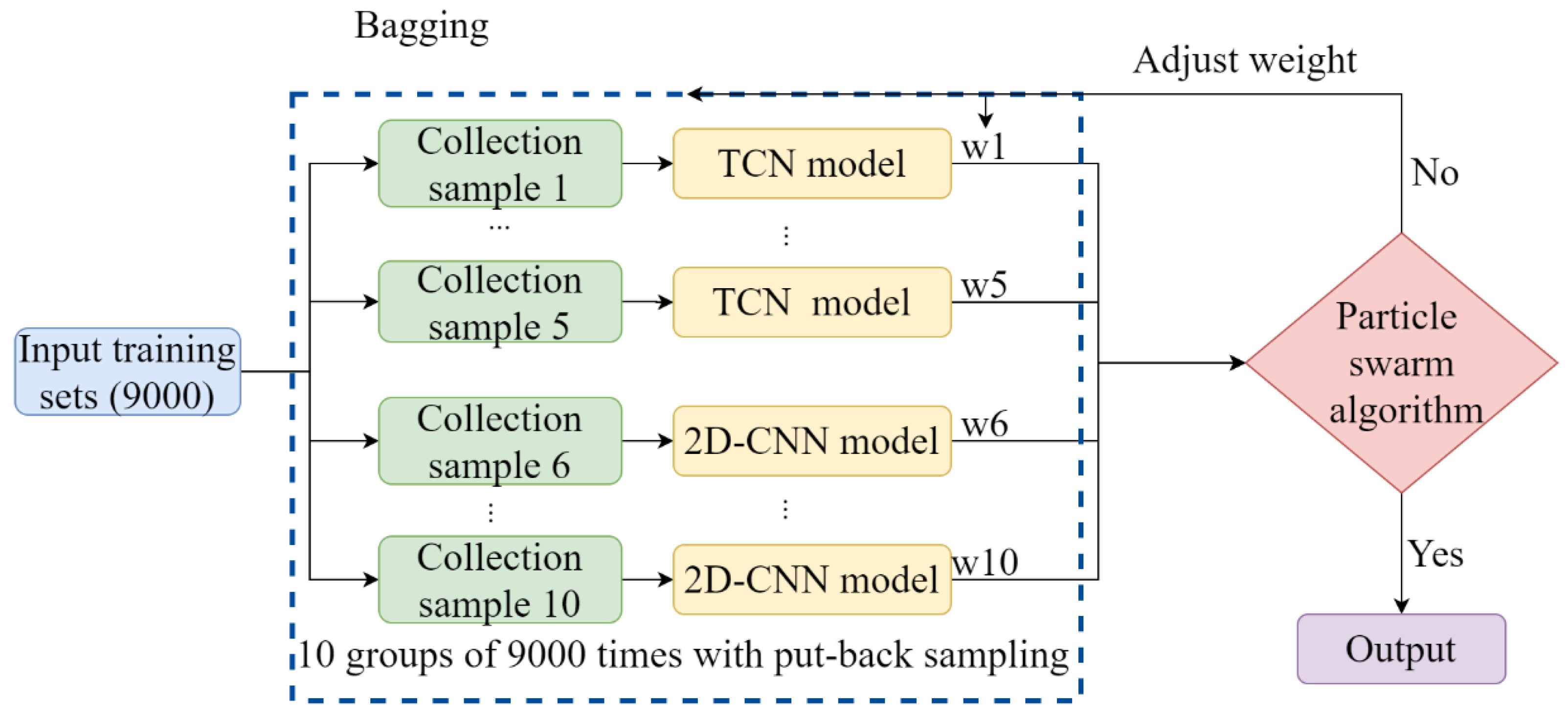
2.4. Model Fusion Method Based on Improved Bagging Method
2.4.1. Bagging
- (1)
- First, times with put-back sampling is performed from the training dataset of size to obtain dataset , which is repeated times to obtain datasets of size .
- (2)
- Then, base algorithm models are selected, and base learners are constructed with the input data set .
- (3)
- Finally, the output of the fusion model is obtained by linearly averaging the output of each base learner.
2.4.2. Multi-Nuclide Source Term Inversion Model Based on Fusion Model
2.5. BOHB Algorithm
2.6. PSO Algorithm
2.7. Estimation Metrics
3. Results
3.1. Hyperparameter Optimization of TCN and 2D-CNN Models
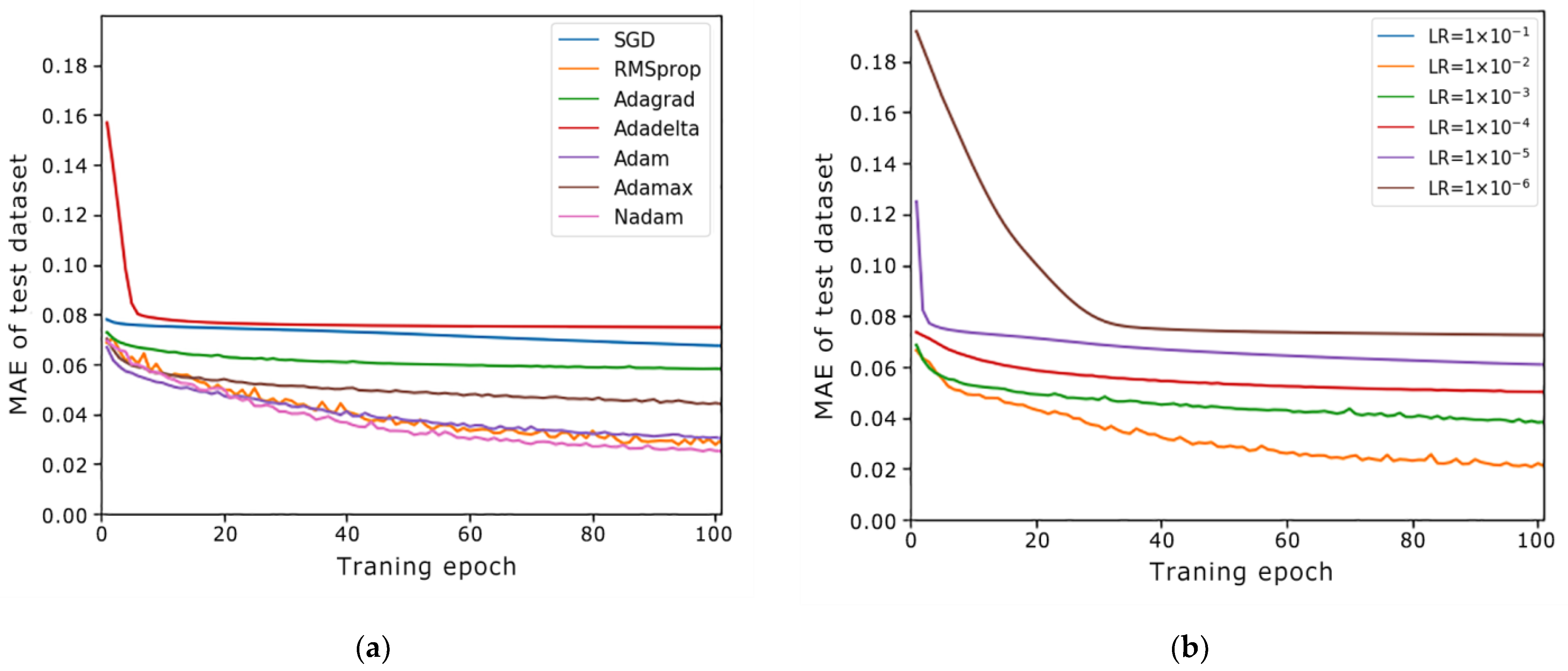
3.1.1. Learning Rate
3.1.2. Other Hyperparameters
3.1.3. Multi-Nuclide Emission Rate Estimation Performance of TCN and 2D-CNN Models
3.2. Fusion of TCN and 2D-CNN Models Based on Bagging Method
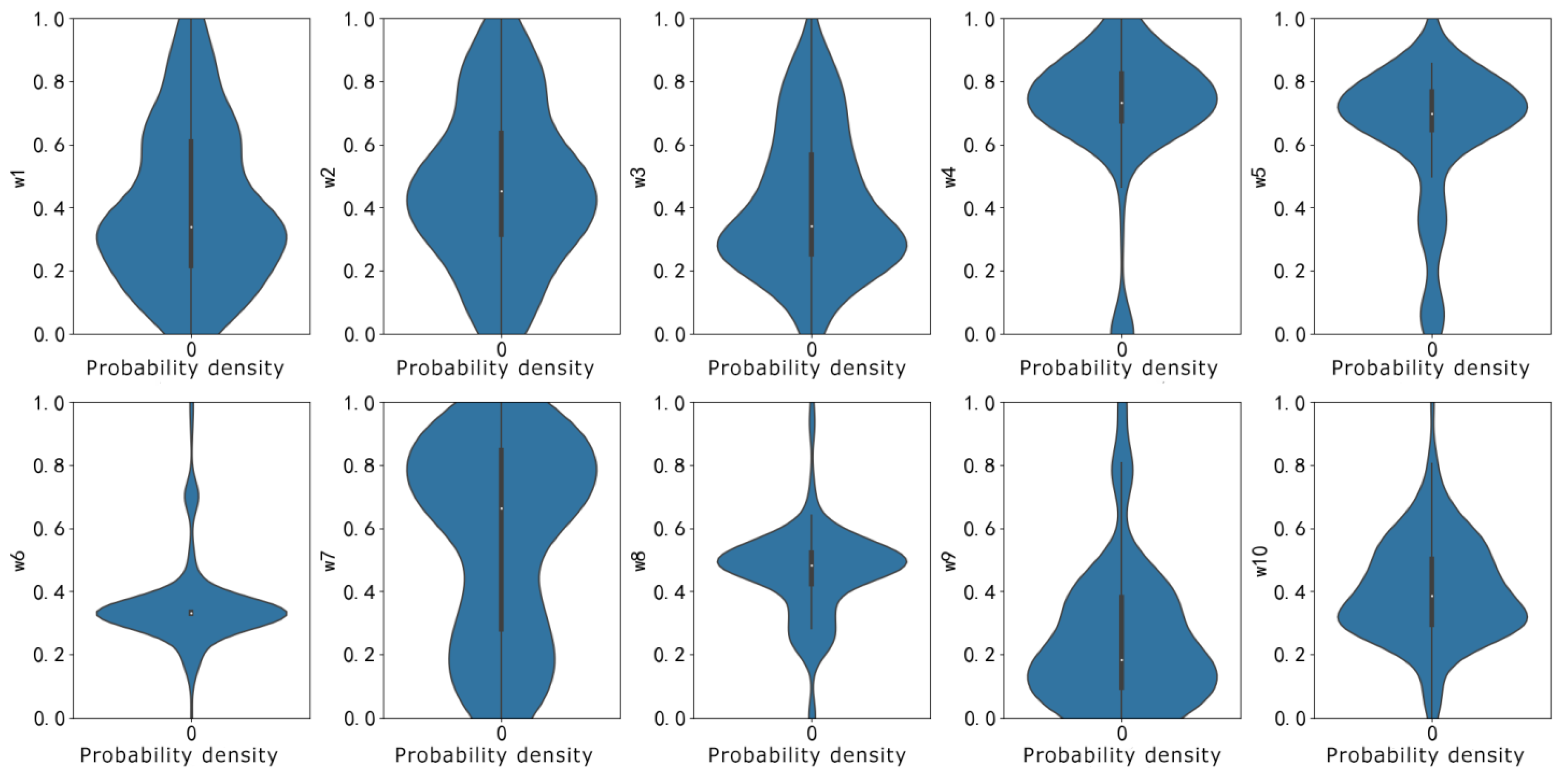
3.2.1. Weight Optimization through PSO Algorithm
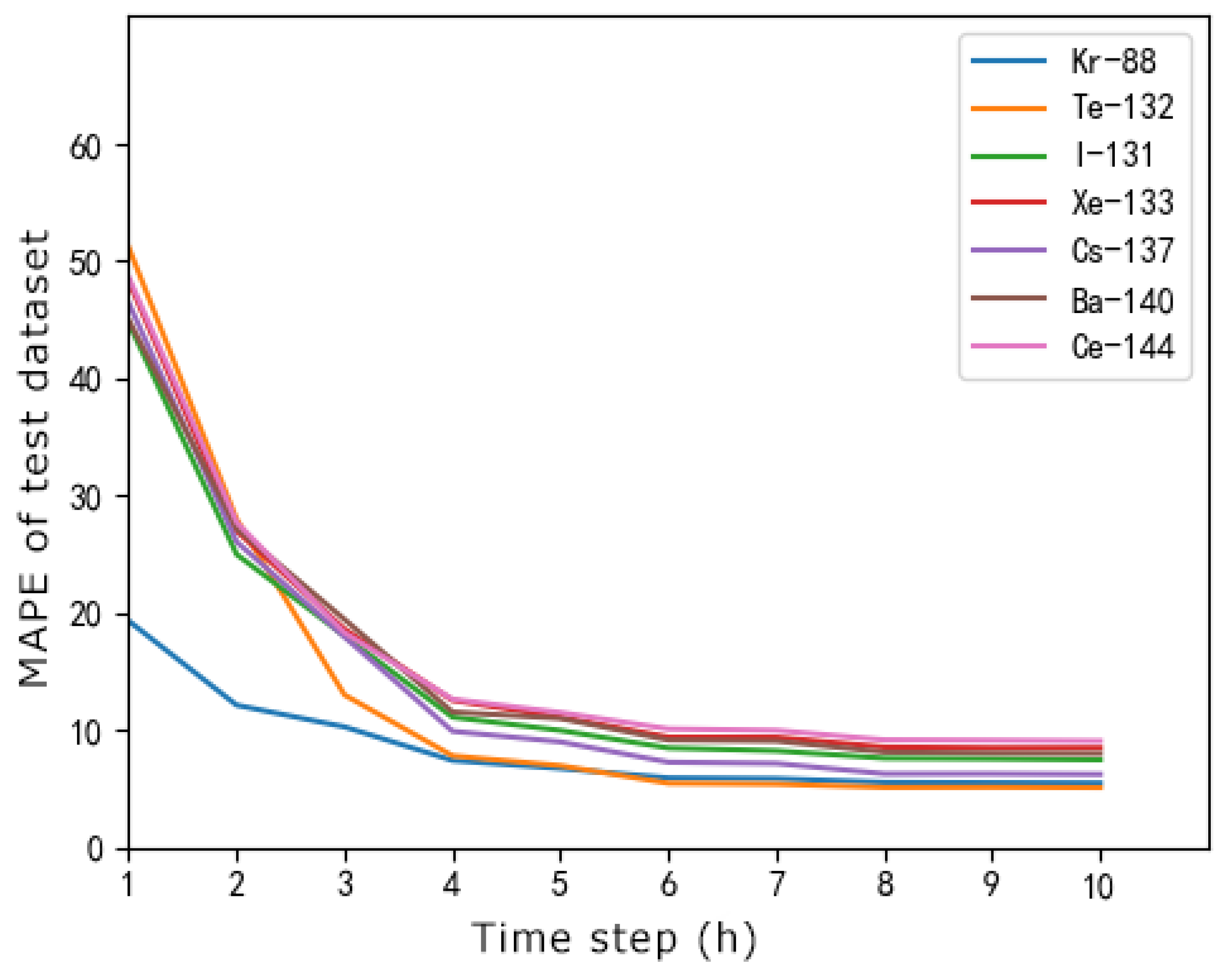
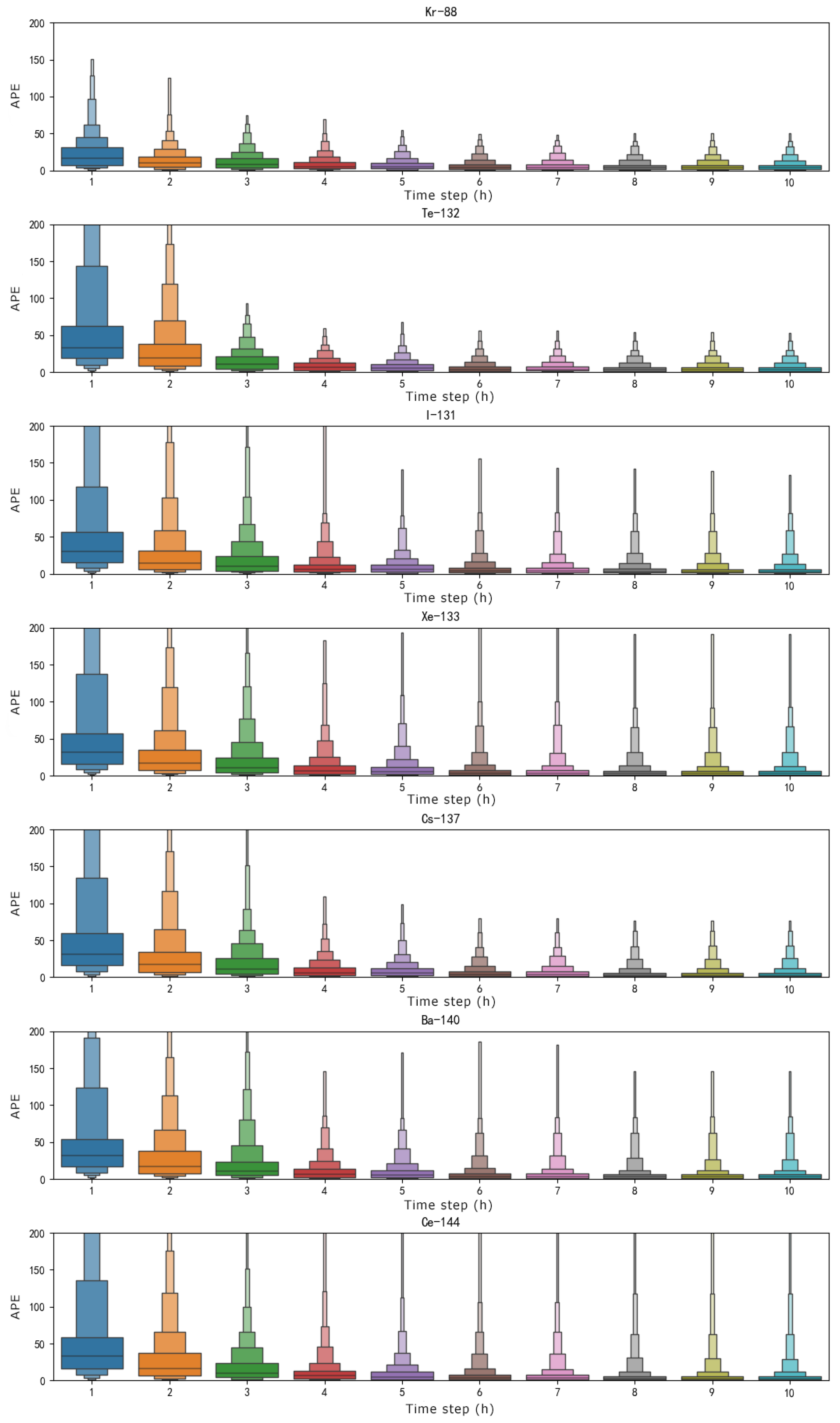
3.2.2. Multi-Nuclide Emission Rate Estimation Performance
3.3. Noise Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, D. Nuclear energy and nuclear safety: Analysis and reflection on the Fukushima nuclear accident in Japan. J. Nanjing Univ. Aeronaut. Astronaut. 2012, 44, 597–602. [Google Scholar]
- Kathirgamanathan, P.; McKibbin, R.; McLachlan, R.I. Source Release-Rate Estimation of Atmospheric Pollution from a NonSteady Point Source at a Known Location. Environ. Model. Assess. 2004, 9, 33–42. [Google Scholar] [CrossRef]
- Liu, Y. Research on Inversion Model of Nuclear Accident Source Terms Based on Variational Data Assimilation. Ph.D. Thesis, Tsinghua University, Beijing, China, 2017. [Google Scholar]
- Katata, G.; Ota, M.; Terada, H.; Chino, M.; Nagai, H. Atmospheric discharge and dispersion of radionuclides during the Fukushima Dai-ichi Nuclear Power Plant accident. Part I: Source term estimation and local-scale atmospheric dispersion in early phase of the accident. J. Environ. Radioact. 2012, 109, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Du Bois, P.B.; Laguionie, P.; Boust, D.; Korsakissok, I.; Didier, D.; Fiévet, B. Estimation of marine source-term following Fukushima Daiichi accident. J. Environ. Radioact. 2021, 114, 2–9. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Li, H.; Fang, S.; Mao, Y.; Qu, J. Research on Source Inversion for Nuclear Accidents Based on Variational Data Assimilation with the Dispersion Model Error. In Proceedings of the 2018 26th International Conference on Nuclear Engineering, London, UK, 22–26 July 2018. [Google Scholar] [CrossRef]
- Tsiouri, V.; Andronopoulos, S.; Kovalets, I.; Dyer, L.L.; Bartzis, J.G. Radiation source rate estimation through data assimilation of gamma dose rate measurements for operational nuclear emergency response systems. Int. J. Environ. Pollut. 2012, 50, 386–395. [Google Scholar] [CrossRef]
- Tsiouri, V.; Kovalets, I.; Andronopoulos, S.; Bartzis, J. Emission rate estimation through data assimilation of gamma dose measurements in a Lagrangian atmospheric dispersion model. Radiat. Prot. Dosim. 2011, 148, 34–44. [Google Scholar] [CrossRef]
- Drews, M.; Lauritzen, B.; Madsen, H.; Smith, J.Q. Kalman filtration of radiation monitoring data from atmospheric dispersion of radioactive materials. Radiat. Prot. Dosim. 2004, 111, 257–269. [Google Scholar] [CrossRef]
- Zhang, X.; Su, G.; Yuan, H.; Chen, J.; Huang, Q. Modified ensemble Kalman filter for nuclear accident atmospheric dispersion: Prediction improved and source estimated. J. Hazard. Mater. 2014, 280, 143–155. [Google Scholar] [CrossRef]
- Zavisca, M.; Kahlert, H.; Khatib-Rahbar, M.; Grindon, E.; Ang, M. A Bayesian Network Approach to Accident Management and Estimation of Source Terms for Emergency Planning. In Probabilistic Safety Assessment and Management; Springer: London, UK, 2004. [Google Scholar] [CrossRef]
- Zheng, X.; Itoh, H.; Kawaguchi, K.; Tamaki, H.; Maruyama, Y. Application of Bayesian nonparametric models to the uncertainty and sensitivity analysis of source term in a BWR severe accident. Reliab. Eng. Syst. Saf. 2015, 138, 253–262. [Google Scholar] [CrossRef]
- Davoine, X.; Bocquet, M. Inverse modelling-based reconstruction of the Chernobyl source term available for long-range transport. Atmos. Chem. Phys. 2007, 7, 1549–1564. [Google Scholar] [CrossRef]
- Jeong, H.-J.; Kim, E.-H.; Suh, K.-S.; Hwang, W.-T.; Han, M.-H.; Lee, H.-K. Determination of the source rate released into the environment from a nuclear power plant. Radiat. Prot. Dosim. 2005, 113, 308–313. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Zhang, S. Simultaneous inversion of time-dependent source term and fractional order for a time-fractional diffusion equation. J. Comput. Appl. Math. 2020, 368, 112566. [Google Scholar] [CrossRef]
- Tichý, O.; Šmídl, V.; Hofman, R.; Evangeliou, N. Source term estimation of multi-specie atmospheric release of radiation from gamma dose rates. Q. J. R. Meteorol. Soc. 2018, 144, 2781–2797. [Google Scholar] [CrossRef]
- Zhang, X.; Raskob, W.; Landman, C.; Trybushnyi, D.; Li, Y. Sequential multi-nuclide emission rate estimation method based on gamma dose rate measurement for nuclear emergency management. J. Hazard. Mater. 2017, 325, 288–300. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Raskob, W.; Landman, C.; Trybushnyi, D.; Haller, C.; Yuan, H. Automatic plume episode identification and cloud shine reconstruction method for ambient gamma dose rates during nuclear accidents. J. Environ. Radioact. 2017, 178, 36–47. [Google Scholar] [CrossRef]
- Fang, S.; Dong, X.; Zhuang, S.; Tian, Z.; Chai, T.; Xu, Y.; Zhao, Y.; Sheng, L.; Ye, X.; Xiong, W. Oscillation-free source term inversion of atmospheric radionuclide releases with joint model bias corrections and non-smooth competing priors. J. Hazard. Mater. 2022, 440, 129806. [Google Scholar] [CrossRef]
- Li, X.; Sun, S.; Hu, X.; Huang, H.; Li, H.; Morino, Y.; Wang, S.; Yang, X.; Shi, J.; Fang, S. Source inversion of both long- and short-lived radionuclide releases from the Fukushima Daiichi nuclear accident using on-site gamma dose rates. J. Hazard. Mater. 2019, 379, 120770. [Google Scholar] [CrossRef]
- Sun, S.; Li, X.; Li, H.; Shi, J.; Fang, S. Site-specific (Multi-scenario) validation of ensemble Kalman filter-based source inversion through multi-direction wind tunnel experiments. J. Environ. Radioact. 2019, 197, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Ling, Y.; Yue, Q.; Chai, C.; Shan, Q.; Hei, D.; Jia, W. Nuclear accident source term estimation using Kernel Principal Component Analysis, Particle Swarm Optimization, and Backpropagation Neural Networks. Ann. Nucl. Energy 2020, 136, 107031. [Google Scholar] [CrossRef]
- Yue, Q.; Jia, W.; Huang, T.; Shan, Q.; Hei, D.; Zhang, X.; Ling, Y. Method to determine nuclear accident release category via environmental monitoring data based on a neural network. Nucl. Eng. Des. 2020, 367, 110789. [Google Scholar] [CrossRef]
- Ling, Y.; Yue, Q.; Huang, T.; Shan, Q.; Hei, D.; Zhang, X.; Jia, W. Multi-nuclide source term estimation method for severe nuclear accidents optimized by Bayesian optimization and hyperband. J. Hazard. Mater. 2021, 414, 125546. [Google Scholar] [CrossRef] [PubMed]
- Ling, Y.; Huang, T.; Yue, Q.; Shan, Q.; Hei, D.; Zhang, X.; Shi, C.; Jia, W. Improving the estimation accuracy of multi-nuclide source term estimation method for severe nuclear accidents using temporal convolutional network optimized by Bayesian optimization and hyperband. J. Environ. Radioact. 2022, 242, 106787. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.Y.; Martinez, J.J.F.; Fajardo, A.C. Day-ahead solar irradiation forecasting utilizing gramian angular field and convolutional long short-term memory. IEEE Access 2020, 8, 18741–18753. [Google Scholar] [CrossRef]
- Till, J.E.; Meyer, H.R. Radiological Assessment. A Textbook on Environmental Dose Analysis; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1983. [Google Scholar] [CrossRef]
- Malamud, H. Reactor Safety Study—An Assessment of Accident Risks. U.S.; Nuclear Regulatory Commission: Rockville, MD, USA, 1975. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018. [Google Scholar] [CrossRef]
- Yang, H.; Yin, L. CNN based 3D facial expression recognition using masking and landmark features. In Proceedings of the 2017 Seventh International Conference on Affective Computing and Intelligent Interaction (ACII), San Antonio, TX, USA, 23–26 October 2017. [Google Scholar]
- Yin, R.; Shu, S.; Li, S. An image moment regularization strategy for convolutional neural networks. CAAI Trans. Intell. Syst. 2016, 11, 43–48. [Google Scholar]
- Baldi, P.; Sadowski, P.J. Understanding dropout. Adv. Neural Inf. Proc. Syst. 2013, 26, 2814–2822. [Google Scholar]
- Chao, L.; Chen, W.; Yu, L.; Changfeng, X.; Xiufeng, Z. A review of structural optimization of convolutional neural networks. Acta Autom. Sin. 2020, 46, 24–37. [Google Scholar]
- Peng, X.; Zhang, B.; Gao, D. Research on fault diagnosis method of rolling bearing based on 2DCNN. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; Volume 8, pp. 2–24. [Google Scholar] [CrossRef]
- Jie, H.J.; Wanda, P. RunPool: A dynamic pooling layer for convolution neural network. Int. J. Comput. Intell. Syst. 2020, 13, 66–76. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Cui, J.; Yang, B. A review of Bayesian optimization methods and applications. J. Softw. 2018, 29, 3068–3090. [Google Scholar]
- Jiang, M.; Chen, Y. A review of the development of Bayesian optimization algorithms. Comput. Eng. Des. 2010, 14, 3254–3259. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and efficient hyperparameter optimization at scale. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar] [CrossRef]
- Liu, J. Basic Theory of Particle Swarm Algorithm and its Improvement Research. Ph.D. Thesis, Central South University, Changsha, China, 2009. [Google Scholar]
- Sko. Available online: https://pypi.org/project/sko/ (accessed on 7 June 2020).
- Keras. Available online: https://keras.io/zh/optimizers/ (accessed on 17 September 2019).





| Nuclide | Half-Life | Activity per MW (1012 Bq/MW) | Atmospheric Immersion Dose Conversion Factor (Sv s−1 per Bq m−3) | Ground Deposition Dose Conversion Factor (Sv s−1 per Bq m−2) | Approximate Order of Magnitude of Release Rate (Bq/h) |
|---|---|---|---|---|---|
| Kr-88 | 2.8 h | 830 | 1.02 × 10−13 | 1018 | |
| Te-132 | 3.3 d | 1400 | 1.03 × 10−14 | 2.28 × 10−16 | 1018 |
| I-131 | 8.1 d | 940 | 1.82 × 10−14 | 3.76 × 10−16 | 1018 |
| Xe-133 | 5.3 d | 1940 | 1.56 × 10−15 | 1019 | |
| Cs-137 | 30.1 y | 70 | 7.74 × 10−18 | 2.85 × 10−19 | 1017 |
| Ba-140 | 12.8 d | 1800 | 8.58 × 10−15 | 1.80 × 10−16 | 1018 |
| Ce-144 | 284 d | 990 | 8.53 × 10−16 | 2.03 × 10−17 | 1018 |
| Auxiliary Data | Value Range | Description |
|---|---|---|
| Release Height | 0–60 m | Release height affects the maximum extent of nuclide dispersion, and wind speed will vary at different heights. |
| Atmospheric Stability | A–G | Pasquill’s atmospheric stability category, indicating the tendency and degree of the air mass to return to or move away from the original equilibrium position after the air is disturbed in a vertical direction. A–G indicate conditions from an extremely unstable to an extremely stable state. |
| Wind Speed | 0–12 m/s | Wind speed directly affects the diffusion rate of radionuclides. |
| Mixed Layer Height | 100–800 m | Mixed layer height affects the diffusion of nuclides in the vertical direction. |
| Precipitation Type | None Light Rain (rainfall rate < 25 mm/h) Medium Rain (rainfall rate between 25 and 75 mm/h) Heavy Rain (rainfall rate > 75 mm/h) Light Snow (visibility > 1 km) Middle Snow (visibility between 0.5 and 1 km) Heavy Snow (visibility < 0.5 km) | Precipitation will accelerate deposition of the nuclide. |
| Source Term | Auxiliary Data | Time (h) | Gamma Dose Rate (mSv/h) | |||
|---|---|---|---|---|---|---|
| Radionuclide | Release Rate (Bq/h) | 1 Km Downwind | 5 Km Downwind | |||
| 88Kr | 2.67 × 1018 | Release Height (m) | 37 | 1 | 3240 | 538 |
| 132Te | 4.7 × 1018 | Wind Speed (m/s) | 8 | 2 | 3700 | 620 |
| 131I | 9.8 × 1018 | Mixed Layer Height (m) | 457 | 3 | 4500 | 800 |
| 133Xe | 2.7 × 1019 | Atmospheric Stability | C | 4 | 4000 | 800 |
| 137Cs | 6.98 × 1017 | Precipitation Type | Heavy Snow | 5 | 5000 | 800 |
| 140Ba | 7.45 × 1018 | 6 | 6000 | 900 | ||
| 144Ce | 3.63 × 1018 | 7 | 5000 | 900 | ||
| 8 | 5000 | 1000 | ||||
| 9 | 6000 | 900 | ||||
| 10 | 6000 | 1000 | ||||
| Parameter | Value Range |
|---|---|
| Number of convolutional kernels | 0–64 |
| Width of convolutional kernels | 2, 4, 8 |
| Number of fully connected layer neurons | 8–256 |
| Model | Optimizer | Learning Rate | Number of Convolution Kernels | Convolution Kernel Width | Fully Connected Layers Number of Neurons | Batch Size | Loss |
|---|---|---|---|---|---|---|---|
| 2D-CNN | Nadam | 10−2 | 48 | 2 | 96 | 128 | 0.0138 |
| TCN | Nadam | 10−2 | 40 | 8 | 48 | 2048 | 0.0196 |
| Base Learner | Weight | Value | Base Learner | Weight | Value |
|---|---|---|---|---|---|
| TCN | w1 | 0.39 | 2D-CNN | w6 | 0.37 |
| TCN | w2 | 0.48 | 2D-CNN | w7 | 0.21 |
| TCN | w3 | 0.32 | 2D-CNN | w8 | 0.52 |
| TCN | w4 | 0.76 | 2D-CNN | w9 | 0.14 |
| TCN | w5 | 0.71 | 2D-CNN | w10 | 0.42 |
| Fusion Model | Loss: 0.0082 | ||||
| Model | MAPE (%) |
|---|---|
| TCN | 17.31 |
| 2D-CNN | 14.53 |
| Fusion Model | 8.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, Y.; Liu, C.; Shan, Q.; Hei, D.; Zhang, X.; Shi, C.; Jia, W.; Wang, J. Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model. Atmosphere 2023, 14, 148. https://doi.org/10.3390/atmos14010148
Ling Y, Liu C, Shan Q, Hei D, Zhang X, Shi C, Jia W, Wang J. Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model. Atmosphere. 2023; 14(1):148. https://doi.org/10.3390/atmos14010148
Chicago/Turabian StyleLing, Yongsheng, Chengfeng Liu, Qing Shan, Daqian Hei, Xiaojun Zhang, Chao Shi, Wenbao Jia, and Jing Wang. 2023. "Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model" Atmosphere 14, no. 1: 148. https://doi.org/10.3390/atmos14010148
APA StyleLing, Y., Liu, C., Shan, Q., Hei, D., Zhang, X., Shi, C., Jia, W., & Wang, J. (2023). Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model. Atmosphere, 14(1), 148. https://doi.org/10.3390/atmos14010148






