Estimating PM_2.5 Concentrations Using an Improved Land Use Regression Model in Zhejiang, China

Abstract

Fine particulate matter (PM_2.5) pollution affects the environment and poses threat to human health. The study of the influence of land use and other factors on PM_2.5 is crucial for the rational development and utilization of territorial space. To explore the intrinsic mechanism between PM_2.5 pollution and related factors, this study used the land use regression (LUR) model, and introduced geographically weighted regression (GWR), and random forest (RF) to optimize the basic LUR model. The basic LUR model was constructed to predict the annual average PM_2.5 concentrations using three elements: artificial surfaces, forest land, and wind speed as explanatory variables, with adjusted R² of 0.645. The improved LUR models based on GWR and RF, with an adjusted R² of 0.767 and 0.821, respectively, show better fitting effects. The LUR simulation results show that the PM_2.5 pollution in the northern Zhejiang is more serious and concentrated. The concentrations are also higher in regions such as the river valley plains in central Zhejiang and the coastal plains in southeastern Zhejiang. These findings show that pollution emissions should be further reduced and environmental protection should be strengthened.

1. Introduction

Fine particulate matter (PM_2.5) refers to particles in ambient air with an aerodynamic equivalent diameter of 2.5 μm or less. PM_2.5 affects the environment and climate [1] and is also extremely hazardous to human health [2,3]. Based on micro-level studies on PM_2.5 formation mechanisms, an increasing number of studies have confirmed that, as an atmospheric pollutant, PM_2.5 has obvious regional transport characteristics [4,5]. The distribution of PM_2.5 is more influenced by macro-level factors, and scholars have explored the effects of land use, transportation, and meteorological conditions on PM_2.5 [6,7,8,9]. Land is closely related to PM_2.5. On the one hand, different land use types are sources or sinks of PM_2.5 [10,11]. The artificial surfaces not only carry many pollution emission sites such as factory emissions and traffic emissions, but also have difficulty in blocking and adsorbing dust, making regional PM_2.5 concentrations prone to increase. Vegetation cover such as forestland has a strong adsorption effect on air pollutants, which helps to reduce regional PM_2.5 concentrations. On the other hand, regional land use patterns also influence local climate and thus have an indirect effect on PM_2.5 [12,13]. Studying the influence of land use on PM_2.5 means understanding the formation mechanism of this pollutant from a systemic perspective, to guide the rational development, use, and protection of territorial space. In addition, it can also predict and simulate the spatial distribution based on the quantitative study of the relationship between land use and PM_2.5 [14,15,16].

Based on the relationship between PM_2.5 and related factors, the regression relationship between station monitoring data and elements such as land use can be analyzed, and a regression model of PM_2.5 and these factors can be developed to simulate concentrations within the region. This method has been applied in the Small Area Variations in Air Quality and Health (SAVIAH) project in Europe, where scholars have mapped air pollution distribution based on regression methods, using land use, traffic, and other relevant factors as explanatory variables [17]. The method came to be known as the land use regression (LUR) model. Instead of pursuing complex physicochemical processes, LUR models are based on the analysis of the relationship between air pollutant concentrations and relevant factors, and can make predictions according to measured data [18,19,20]. Currently, the LUR model begins to be applied to the study of environmental issues besides atmospheric pollutants [21]. In addition, the development of the LUR model presents an in-depth trend from different angles. Scholars have conducted extended research from different perspectives. Firstly, the data used for modeling have been further enriched. Landscape pattern indicators, aerosol optical depth, point of interest (POI), and three-dimensional (3D) data are introduced into the model to help improve the accuracy and the spatio-temporal resolution of the simulation [22,23,24]. Secondly, the spatio-temporal scale of the study has been expanded. LUR was first used to simulate mean concentrations at urban spatial scales and over long periods. However, now there are studies on the distribution of pollutants at different points over 24 h, spanning across provinces, urban clusters, and countries [25,26,27]. Lastly, and most importantly, LUR modeling methods have developed significantly. Nonlinear regression, geographically weighted regression (GWR), generalized summation models, and machine learning have effectively improved the models [28,29,30]. Therefore, here we take Zhejiang Province as the study area and estimate PM_2.5 concentrations using LUR, GWR, and random forest (RF). In previous studies, applying LUR at province-level administrative units in China [22,23,31,32], Liu et al. used land use, population density, road networks, and distance to the ocean data to simulate the spatial distribution of PM_2.5 concentrations in Shanghai [31], but ignored POI, meteorological, and socio-economic factors. Wu et al. used land use, population density, road length, and POI data to estimate spatial variations in PM_2.5 in Beijing [22], but did not consider meteorological and socio-economic factors. We used more comprehensive predictor variables, including land use data, road data, POI data, meteorological data, and socio-economic data. Moreover, in studies predicting PM_2.5 concentrations in China, few studies compared the spatial distribution results and model accuracy of LUR, GWR, and RF, while we provide a comparative analysis of the models.

Zhejiang Province’s strong internal linkages in economic and social activities, rapid economic growth, rising population, and increasing urban scale have put enormous pressure on the regional atmospheric environment. As one of the major provinces in the Yangtze River Delta region, the duration and influence of hazy days in Zhejiang Province has been increasing since the 1970s, especially since 2000 [33]. A previous study shows that from January 2015 to April 2018, the change in air quality in northern Zhejiang was worse than that in southern Zhejiang. For example, the air quality in Hangzhou, the capital of Zhejiang Province, decreased by 6.69%. In contrast, the air quality in Lishui and Zhoushan in southern Zhejiang improved by 8.04% and 4.67%, respectively [34]. As the industrial structure continues to be optimized, and as the Air Pollution Prevention and Control Action Plan is implemented in full, PM_2.5 pollution in Zhejiang Province has improved significantly in recent years. The Department of Ecology and Environment of Zhejiang Province has issued a range of PM_2.5 concentrations of 15–28 µg/m³ for the 11 cities in 2021. Further studies are needed to track its changing characteristics. Based on the mechanism and characteristics between PM_2.5 and land use, the LUR model can be better applied to PM_2.5 spatial distribution simulation, which helps us study the PM_2.5 distribution characteristics in Zhejiang Province. It also helps us understand the causes of pollution to a certain extent, and to explore the inner formation mechanism of the influence of land use structure and other factors on PM_2.5. The main objectives of the study are: (1) exploring the correlation between PM_2.5 and the explanatory variables in the study area; (2) establishing a basic LUR model and improved LUR models based on GWR and RF methods for more accurate regional PM_2.5 simulation; and (3) providing a comparative analysis of the LUR, GWR, and RF.

2. Materials and Methods

2.1. Data Sources

Figure 1 shows the location of the study area and spatial distribution of monitoring sites and land use types. Data collection includes PM_2.5 concentration monitoring data, land use data, road data, POI data, meteorological data, and socio-economic data.

The PM_2.5 concentration data used hourly monitoring data of pollutants in μg/m³ from 1 January 2020 to 31 December 2020 at state-controlled air quality monitoring stations. Data were obtained from the China National Environmental Monitoring Centre (http://www.cnemc.cn/, accessed on 20 June 2022). This study was mainly based on the annual average PM_2.5 concentration. For the validity of the data, PM_2.5 concentration data were pre-processed. Firstly, anomalous values with concentration values less than zero or meaningless were excluded. Secondly, according to the China Ambient Air Quality Standards (GB 3095-2012) on data validity, there should be at least 20 h of average concentration or sampling time per day. When calculating the annual average concentrations, there should be at least 324 daily average concentration values per year and at least 27 daily average concentration values per month (at least 25 daily average concentration values in February). According to the above principles, invalid data were eliminated and 49 valid annual average data sites were retained in total.

Land use data were obtained from the global land cover data “GlobeLand30 (V2020)” (http://www.globallandcover.com/home.html?type=data, accessed on 20 June 2022) [35,36]. Road network lengths were used to represent traffic flow, which was obtained from OpenStreetMap (OSM). Meteorological data, including wind speed, precipitation, air temperature, and sea level pressure, were obtained from ground-based weather stations and sourced from the National Climatic Data Center (NCDC) (https://www.ncdc.noaa.gov/, accessed on 20 June 2022). Population data were obtained from the WorldPop open population dataset (https://www.worldpop.org/, accessed on 20 June 2022) [37].

2.2. Methods

The LUR model (involving GWR, RF, and other spatial analysis methods) as well as related model testing methods were used in this study.

The core idea of the LUR model is to construct regression relationships between air pollutant concentrations at monitoring stations and factors such as land use and geographical elements of emission sources within a certain spatial scale. To build the fitted model, the basic LUR was subjected to a multiple linear regression using the ordinary least squares (OLS) method. The regression model was then used to simulate the atmospheric pollutant concentrations and finally generate the spatial distribution of pollutants [31,38]. The multiple linear regression equation is as follows:

$$Y=a_0+a_1{X}_1+a_2{X}_2+a_3{X}_3+\dots +a_n{X}_n+\mu$$

(1)

where $Y$ is the atmospheric pollutant concentration value; $X_i$ is the explanatory variable that is ultimately included in the model; $a_i$ is the unknown parameter; and $\mu$ is the random error term.

From a geographical perspective, the regression model should take spatial non-stationarity into account, i.e., changes in the relationship between variables caused by changes in geographical location. GWR reflects the spatial heterogeneity of the parameters, allowing the relationship between variables to vary with spatial location [39]. By introducing the geographic location factor into the regression equation, the expression of the GWR model is as follows:

$$Y={\beta }_0\left(u_i,v_i\right)+{{\displaystyle \sum }}^{ }{\beta }_k\left(u_i,v_i\right)x_{ik}+{\epsilon }_i (i=1,2,\dots ,n; k=1,2,\dots ,p)$$

(2)

where $k$ is the number of independent variables in the model; $x_{ik}$ is the $k$th independent variable of sample $i$; ($u_i,v_i$) is the geographical coordinates (longitude, latitude) of the $i$th sample; ${{\displaystyle \sum }}^{ }{\beta }_k\left(u_i,v_i\right)$ is the regression coefficient of the $k$th independent variable in the $i$th sample, as a function of geographical location; and ${\epsilon }_i$ is the random error, which should obey a normal distribution.

Using classification techniques (predicting data classification results from a classifier based on a training set) as an important source, and incorporating the idea of integrated learning algorithms, a machine learning algorithm that builds multiple classification trees (decision trees) and combines them in a bootstrap aggregating (Bagging) manner has been proposed and widely used. Because of the integration of multiple decision trees (weak learners), this learning method is known as RF. A diagram of the modeling process is shown in Figure 2. First, multiple training samples were randomly selected from the data sets to construct the classification and regression tree (CART). In the process of training, $m$ features were randomly selected from all features for the best split. The final prediction result is the mean of all decision trees’ predictions [40]. Similar to the classical regression model, random forest regression can construct the relationship between the explanatory variables ($x_1$, $x_2$, …, $x_n$) and the atmospheric pollutant concentration $Y$.

Randomness is reflected in two aspects. On the one hand, randomness is reflected in the selection of the samples, i.e., the training set is a bootstrap sample from the data sets. On the other hand, randomness is reflected in the selection of the features. When constructing the decision trees, instead of including all $M$ features of the sample in the node split, $m$ ($m\ll M$) features were randomly selected as feature variables, making each decision tree distinct from the others.

2.3. Selected Factors

Before exploring the influence of factors on PM_2.5, this study analyzed the correlation between PM_2.5 and the explanatory variables.

Table 1. Correlation analysis results.

Types	Factors	Explanatory Variables	Pearson’s Correlation Coefficients
Land use	Area of cropland within a 10 km buffer zone radius of the monitoring station	CL	0.308 *
	Area of forestland within a 10 km buffer zone radius of the monitoring station	FL	−0.485 **
	Area of grassland within a 10 km buffer zone radius of the monitoring station	GL	−0.533 **
	Area of artificial surfaces within a 10 km buffer zone radius of the monitoring station	AS	0.545 **
Geographical elements of emission sources	Length of all roads within a 10 km buffer zone radius of the monitoring station	AR	0.525 **
	Length of trunk roads within a 10 km buffer zone radius of the monitoring station	TR	0.449 **
	Length of primary roads within a 10 km buffer zone radius of the monitoring station	PR	0.543 **
	Length of secondary roads within a 10 km buffer zone radius of the monitoring station	SR	0.414 **
	Number of catering services within a 10 km buffer zone radius of the monitoring station	CS	0.456 **
	Number of car parks within a 10 km buffer zone radius of the monitoring station	CP	0.470 **
	Number of petrol stations within a 10 km buffer zone radius of the monitoring station	PS	0.575 **
Meteorology	Annual average wind speed	WS	−0.247 **
	Annual precipitation	Prec	0.492 **
Population	Population within a 10 km buffer zone radius of the monitoring station	Pop	0.422 **

** Correlation is significant at the 0.01 level (two-tailed); * correlation is significant at the 0.05 level (two-tailed).

shows the correlation analysis results of 14 factors which finally used explanatory variables in the multiple regression model. Here, we used more comprehensive predictor variables compared to previous studies [22,23,31,32], including land use, road length, POI, as well as meteorological and socio-economic variables.

Among the land use factors, according to the classification system of GlobeLand30 data, there are eight first-class land cover types in Zhejiang Province. However, the analysis of the correlation between different land use types and PM_2.5 pollution must be based on a certain scale. Since the proportion of shrubland, wetland, and bare land in Zhejiang Province is all well below 1%, only five types of land—cropland, forest land, grassland, water, and artificial surfaces (construction land)—were selected. Pearson coefficients of these variables and annual average PM_2.5 concentrations were calculated for correlation analysis. The results show that among the five types of land within a buffer zone of 2 km, 3 km, 5 km, and 10 km radius, the water variable was excluded as it failed to pass the significance test. The correlation coefficients of area of other four types of land within the buffer zone of 10 km radius was the highest and passed the significance test. The complete results of the correlation coefficients between land use variables and PM_2.5 concentrations are shown in

Table A1. Correlation coefficients between the area of each land type and PM_2.5 concentration at different buffer radii. The missing value is attributed to insufficient data on the area of forestland within a buffer zone of 2 km.

Types	2 km	3 km	5 km	10 km
Area of cropland	0.053	0.060	0.041	0.308 *
Area of forestland	-	−0.389 **	−0.483 **	−0.485 **
Area of grassland	−0.244 *	−0.323 *	−0.399 **	−0.533 **
Area of water	−0.180	−0.177	−0.122	0.064
Area of artificial surfaces	0.331 *	0.375 **	0.523 **	0.545 **

** Correlation is significant at the 0.01 level (two-tailed); * correlation is significant at the 0.05 level (two-tailed).

in Appendix A.

Among the geographical elements of emission sources, this study used road length to represent the emission intensity of traffic sources. Because of the unavailability of traffic density data here, we used road length data. Previous researches have demonstrated that road length can be a feasible substitute for traffic density factor [41,42]. The lengths of four types of road networks—motorway, trunk road, primary road, and secondary road, within a buffer zone of 2 km, 3 km, 5 km, and 10 km radii centered on the 49 monitoring stations in Zhejiang Province—were extracted. The Pearson correlation analysis shows that among the length of all roads within a buffer zone of 2 km, 3 km, 5 km, and 10 km radii, the correlation coefficients of that within the buffer zone of the 10 km radius were the highest, as well as the length of trunk roads, primary roads, and secondary roads. The length of motorway within the buffer zone of 10 km radius was excluded as it failed to pass the significance test. Four types of POI data were obtained from factories, catering services, car parks, and petrol stations, through the Gaode Map open platform. The number of POIs within a 2 km, 3 km, 5 km, and 10 km buffer zone centered on the 49 monitoring stations was calculated, and then analyzed by Pearson correlation with the annual average PM_2.5 concentration of the stations. The results show that the factories variable was excluded as it failed to pass the significance test. The correlation coefficients of other three types of POIs within the buffer zone of 10 km radius was the highest. The complete results of the correlation coefficients between geographical elements of emission sources and PM_2.5 concentration are shown in

Table A2. Correlation coefficients between geographical elements of emission sources and PM_2.5 concentration at different buffer radii.

Types	2 km	3 km	5 km	10 km
Length of all roads	0.345 **	0.382 **	0.477 **	0.525 **
Number of factories	−0.027	−0.141	−0.070	0.140
Number of catering services	0.146	0.270 *	0.400 **	0.456 **
Number of car parks	0.276 *	0.336 **	0.443 **	0.470 **
Number of petrol stations	0.268 *	0.291 *	0.472 **	0.575 **

** Correlation is significant at the 0.01 level (two-tailed); * correlation is significant at the 0.05 level (two-tailed).

in Appendix A.

For the meteorological factors, wind speed, precipitation, air temperature, and sea level pressure were considered. The Pearson correlation analysis shows that air temperature and sea level pressure were excluded as the two variables failed to pass the significance test. The complete results of the correlation coefficients between meteorological factors and PM_2.5 concentration are shown in

Table A3. Correlation coefficients between meteorology and PM_2.5 concentration.

Types	Correlation coefficients
Annual average wind speed	−0.247 **
Annual precipitation	0.492 **
Annual air temperature	−0.121
Annual sea level pressure	0.113

** Correlation is significant at the 0.01 level (two-tailed).

in Appendix A. Among the socioeconomic factors, this study investigates their influence on PM_2.5 pollution from both demographic and economic perspectives. For the population, the correlation between population and PM_2.5 concentration within different buffer zones centered on national ambient air quality monitoring stations was studied. The results show that the correlation coefficients of population within the buffer zone of 10 km radius was the highest meteorological factors. The complete results of the correlation coefficients between population and PM_2.5 concentration are shown in

Table A4. Correlation coefficients between population and PM_2.5 concentration at different buffer radii.

Types	2 km	3 km	5 km	10 km
Population	0.243	0.256 *	0.376 **	0.422 **

** Correlation is significant at the 0.01 level (two-tailed); * correlation is significant at the 0.05 level (two-tailed).

in Appendix A. For the economy, based on the environmental Kuznets curve theory, the panel data of GDP, per capita GDP, and an annual average PM_2.5 concentration of 11 cities in Zhejiang Province in 2020 were used for the analysis. The coefficients for GDP and per capita GDP in the liner regression were −1.42 and −1.3, respectively, and were both significant at the 0.01 level.

To avoid multicollinearity, only the factors with the strongest correlation within the buffer zones of different radii were retained. Fourteen factors were finally used as explanatory variables in the multiple regression model. The area of water, the length of motorway, the number of factories, air temperature, and sea level pressure were excluded as they failed to pass the significance test.

3. Results

3.1. The Basic Land Use Regression Model

In the multiple stepwise linear regression, the variable Y in the regression model is the average PM_2.5 concentration in 2020 at each station. The most significant explanatory variable was gradually added to the regression equation. Based on the regression coefficients and statistics, the variables that were not significant or could not improve the fitting effect were removed until there were no variables that needed to be removed or no variables that could be introduced. Moreover, as samples with absolute values of standardized residuals greater than 2.5 affect the normal distribution of residuals, these samples need to be excluded. Therefore, the final model was constructed based on 48 samples.

The multiple stepwise linear regression model contains three explanatory variables, namely the area of artificial surfaces within a 10 km buffer zone radius, the area of forestland within a 10 km buffer zone radius, and the wind speed.

Table 2. Multiple stepwise linear regression model parameters.

Variables	Coefficient	T	Beta	VIF	Ad-R2	RMSE	p-Value
Intercept	34.234868	12.933 **	-	-	0.645	2.46	0.000 **
AS	0.000056	3.759 **	0.416	1.619
FL	−0.000072	−3.851 **	−0.446	1.777
WS	−0.424674	−5.690 **	−0.525	1.126

** Correlation is significant at the 0.01 level (2-tailed); T: t-test statistic value; Beta: standardized coefficient; VIF: variance inflation factor; RMSE: root mean square error.

shows the multiple stepwise linear regression model parameters. The model was better fitted with an adjusted R² of 0.645. The root mean squared error (RMSE) was 2.46, with good accuracy. The standardized coefficients of artificial surfaces, forest land, and wind speed were 0.416, −0.446, and −0.525, respectively. In addition to reflecting the direction of each factor’s contribution to PM_2.5, it also indicates that wind speed plays a relatively more important role in reducing PM_2.5 pollution when the land use type is similar. In summary, the equation for the multiple stepwise linear regression is shown below:

$$\mathrm{Y}=0.000056\times \mathrm{AS}-0.000072\times \mathrm{FL}-0.424674\times \mathrm{WS}+34.234868$$

(3)

The constructed regression equation was subjected to residual analysis to verify the reasonableness of the hypothesis and the reliability of the data. The significance of the Kolmogorov–Smirnov (K-S) test was 0.200 and the significance of the Shapiro–Wilk (S-W) test was 0.505, and the residuals were consistent with a normal distribution.

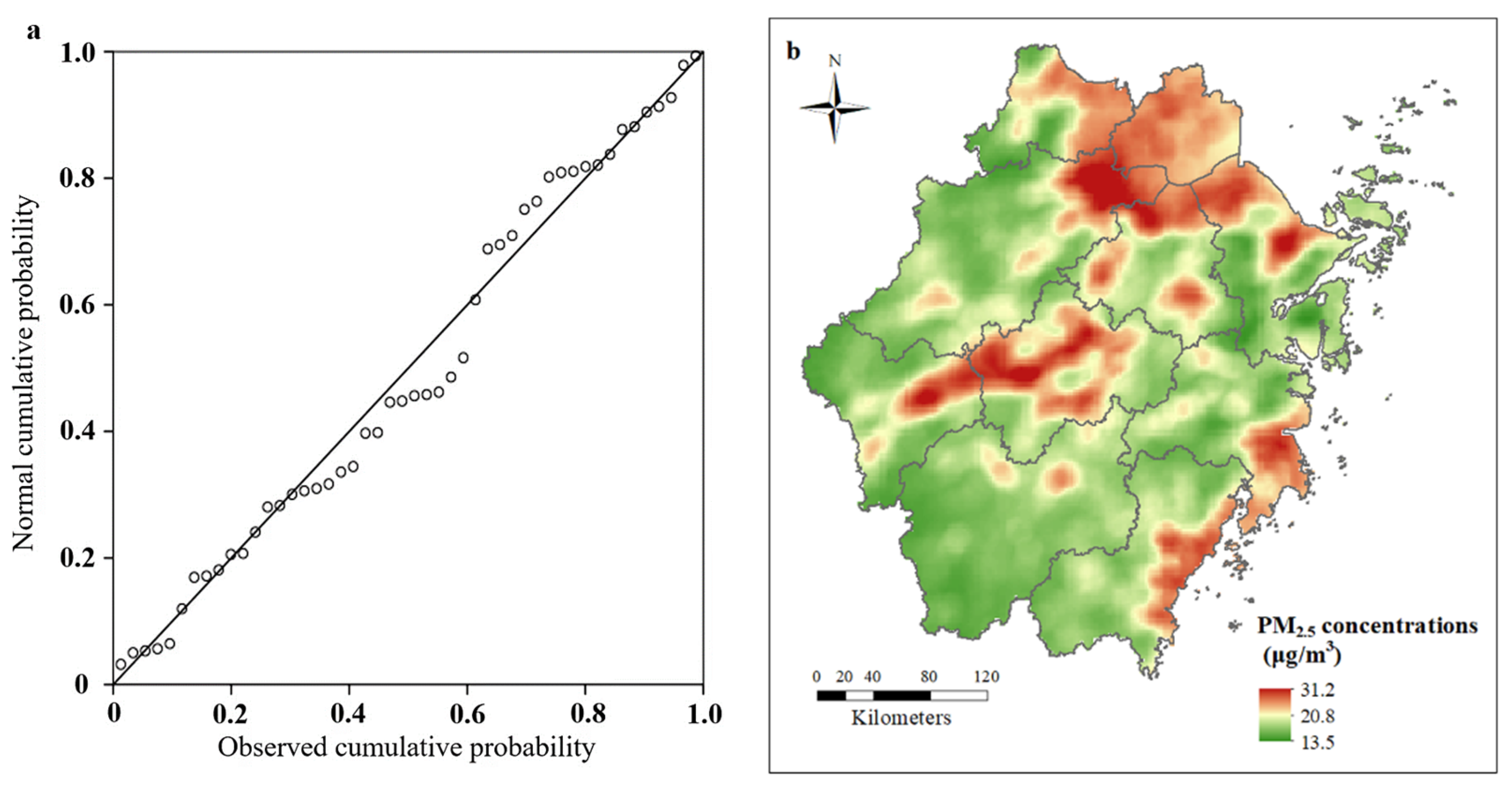
Figure 3a shows the probability–probability (P-P) plot of the standardized residuals. The scatter was distributed around the straight line y = x, indicating that the standardized residuals conform to a standard normal distribution, verifying that the regression hypothesis holds and that the data are reliable. The accuracy of the constructed model was then tested using the leave-one-out cross-validation method, and the RMSE was 2.56. Based on a 2 km × 2 km fishnet, Zhejiang Province was divided into a total of 26,329 grids, and each grid’s area of artificial surfaces within a buffer zone of 10 km radius, the area of forestland within a buffer zone of 10 km radius, and the annual average wind speed were extracted. The values of the explanatory variables were substituted into the obtained model and the gridded PM_2.5 concentration values were calculated to simulate the spatial distribution of PM_2.5 concentrations, as shown in Figure 3b.

3.2. Improved LUR Model Based on Geographically Weighted Regression

Since only a few variables were ultimately included in the regression equation, some variables that affect PM_2.5 concentrations were ignored. In particular, there were differences between regions in socio-economic and natural environment, which may cause the relationship or structure between the explanatory variables and PM_2.5 to change spatially. Therefore, this study considered the spatial heterogeneity and further analyzed the effect of the relevant factors in different regions based on the GWR method.

To avoid global multicollinearity between variables in the GWR, three factors, the area of artificial surfaces within a 10 km buffer zone radius, the area of forestland within a 10 km buffer zone radius, and the wind speed, were used as explanatory variables for the analysis. Figure 4 shows the coefficient of the three variables in the GWR. The results show that the area of artificial surfaces has a positive effect on the increase in PM_2.5 concentration. This is attributed to the rapid expansion of artificial surfaces as urbanization progresses, gathering a large number of industrial activities, energy emissions, etc., which directly contributes to the increase in PM_2.5 concentrations [11]. The coefficient of artificial surfaces gradually increases from northeast to southwest. This indicates that the area of artificial surfaces in southwest Zhejiang has a stronger positive effect on the increase in the PM_2.5 concentration than that in northeast Zhejiang. The area of forestland has a negative effect on the increase in PM_2.5 concentration. This is due to the dust-blocking effect of the vegetation leaves and absorption effect of the stem surfaces to weaken the PM_2.5 concentrations [43]. The absolute value of the coefficient of forestland gradually increases from southwest to northeast. This indicates that forestland in northeast Zhejiang has a stronger negative effect on PM_2.5 than in the southwest region. The coefficient of wind speed shows a trend that is higher in the east and lower in the west. As in the case of the annual mean wind speed, the effect on decreasing PM_2.5 concentration may be enhanced as the wind speed increases.

The global adjusted R² of the GWR model was 0.767. The local R² of the samples ranged from a minimum of 0.53 to a maximum of 0.88, with an average of 0.65. The normality of the standardized residuals of the model was tested and the significance of the Shapiro–Wilk (S-W) test was 0.944, which is much greater than 0.05, indicating that it conforms to a normal distribution. The P-P plot of the standardized residuals is shown in Figure 5a. In addition, the standardized residuals should also show a random rather than a clustering distribution in terms of geographical distribution. The global Moran index (Moran I) was used for diagnosis and the results showed a global Moran index of −0.15 with a p-value of 0.23, with no significant clustering trend. The above analysis indicates that the model is reliable. Compared with the basic LUR model, the GWR-based improved LUR model has a higher simulation accuracy with a residual sum of squares of 148.18, an RMSE of 1.757, and an Akaike information criterion (AICc) of 214.73.

The simulation results of the spatial distribution of the GWR-based improved LUR model are shown in Figure 5b, which are generally consistent with the results of the multiple linear regression simulation. The PM_2.5 pollution concentration areas are roughly the same, mainly in the urbanized areas of northern Zhejiang, central Zhejiang, and southeastern Zhejiang.

3.3. Improved LUR Model Based on Random Forest Regression

The improved LUR model based on random forest regression aims to use the screened factors as explanatory variables based on the results from the correlation analysis. Then, the random forest regression was applied for model construction. The training and validation sets were divided in a ratio of 8:2. The optimal parameters were determined using a random search cross-validation method. The number of decision trees in the final model was 600, and the maximum eigenvalue was 3.

The variables, in descending order of contribution to the model, are precipitation, cropland, grassland, forestland, wind speed, population, and artificial surfaces. Unlike the stepwise regression screening results, precipitation and cropland played a greater role in the random forest model.

Figure 6a shows the linear fit of the model predictions to the actual values. The predicted values of the model largely matched the actual values, with the scatter concentrated around the diagonal line, indicating a good fit. The adjusted R² for the training set of the model was 0.82, with an RMSE of 2.64 and a mean absolute error (MAE) of 1.34. The adjusted R² for the validation set was 0.65, with an RMSE of 6.04 and a MAE of 1.90.

The simulation results of spatial distribution based on random forest regression are shown in Figure 6b, which are significantly different from those of multiple linear regression and GWR simulation, but the judgment of high pollution areas is roughly the same.

3.4. Model Comparisons

The evaluation of the different models on each indicator is shown in

Table 3. Regression model evaluation.

	MAE	RMSE	Adjust R2	AICc
Multiple linear regression	1.95	2.46	0.645	229.94
Geographically weighted regression	1.39	1.76	0.767	214.73
Random forest training set	1.34	2.64	0.821	-
Random forest validation set	1.90	6.04	0.645	-

MAE: mean absolute error; RMSE: root mean square error; AICc: Akaike information criterion.

. To deepen the understanding of the different models, a comparative analysis of the regression models is provided, based on indicators such as MAE, RMSE, adjusted R², and modified AICc.

It can be seen that the GWR-based improved LUR model performs better on all four indicators compared to multiple linear regression. The GWR-based improved LUR model shows less deviation between predicted and measured values, better accuracy of model fit, and higher precision. However, it is also noteworthy that the results of multiple stepwise linear regression identify the relevant factors which provide the best fit for GWR. The RF-based LUR model has a much higher adjusted coefficient of determination for the training set and a much smaller MAE, while also performing well in the validation set. However, the RMSE is relatively large, which could be attributed to the limited samples, making the fit results more accidental. It indicates that the accuracy of the model needs to be improved by introducing more samples or selecting more suitable explanatory variables to take advantage of the random forest’s ability to handle a large number of explanatory variables. Similar to previous studies with a small number of monitoring sites [44,45], here we achieved the spatial distribution of PM_2.5 concentrations based on 49 monitoring sites, but the issue of distribution and the number of monitoring sites still needs to be addressed in the future. More monitoring sites could increase the precision of PM_2.5 concentration estimation [46]. Furthermore, although an improved LUR model with acceptable accuracy was developed using GWR and RF, the accuracy of this model could be further improved by introducing more predictors under a spatially uniform distribution of monitoring stations.

The average PM_2.5 concentrations obtained by different methods for each city in 2020 were compared and analyzed, and the results are shown in

Table 4. Each city’s average PM_2.5 concentrations based on monitoring stations and regression model simulations.

	Monitoring Sites (μg/m³)	Multiple Linear Regression (μg/m³)	Geographically Weighted Regression (μg/m³)	Random Forest Regression (μg/m³)
Hangzhou	28.86	19.32	17.67	22.91
Ningbo	22.90	19.85	19.48	22.74
Wenzhou	25.23	19.22	16.66	21.90
Jiaxing	27.88	23.87	26.35	25.52
Huzhou	25.98	20.33	19.00	23.27
Shaoxing	28.60	20.91	21.11	22.43
Jinhua	27.46	21.45	19.94	21.83
Quzhou	25.96	18.73	17.29	23.07
Zhoushan	16.75	18.64	18.45	22.01
Taizhou	24.53	19.51	18.49	21.49
Lishui	21.23	17.29	15.72	21.17
Zhejiang Province	25.03	19.60	18.45	22.36

. The values in the three models were derived from the zonal statistics of the raster simulation results. The overall trend of PM_2.5 spatial distribution in Zhejiang Province obtained by different methods is similar, but the average PM_2.5 concentrations in prefecture-level cities obtained from different models are quite different. First, the average PM_2.5 concentrations obtained based on the national control air quality monitoring sites are generally larger. This is because apart from the control points, the vast majority of stations are arranged within the urban area of the city. As analyzed in the previous section, urban areas are where PM_2.5 pollution sources are concentrated, and land use patterns are not conducive to PM_2.5 dispersion. Therefore, the average value based on monitoring stations mainly reflects the pollution situation in the urban area. However, the zonal statistics results obtained through the models reflect the city-wide pollution concentration.

Due to the different underlying logic and methodology, the results based on the regression model simulations differ significantly from those based on the monitoring sites; (the simulated average PM_2.5 concentrations are relatively low), while the differences between the different regression models are relatively small. Geographically weighted regression simulations yielded the lowest mean PM_2.5 concentrations for each city in the zonal statistics. It is also worth noting the relatively high estimate of pollution for Jiaxing at 26.35 μg/m³. Due to the inclusion of more explanatory variables and a different model structure, the random forest regression simulation results give different PM_2.5 pollution emissions for each city compared to the other two regression models. The simulation results of the RF-based improved LUR show a small difference between the upper and lower limits.

4. Conclusions

We established a basic LUR model and improved LUR models based on geographically weighted regression and random forest methods to simulate the distribution of PM_2.5 concentration. The basic LUR model was established based on the multiple stepwise linear regression method. The three elements of artificial surfaces, forest land, and wind speed were finally included as explanatory variables. The model was well fitted with an adjusted R² of 0.645. The average RMSE of the leave-one-out cross-validation was 2.56. The results of the basic LUR model show that PM_2.5 pollution was concentrated in the northern part of Zhejiang Province. The concentrations were also higher in regions such as the river valley plains in central Zhejiang and the coastal plains in southeastern Zhejiang. The explanatory variables of the GWR-based improved LUR model exhibited spatial heterogeneity. The adjusted R² of the GWR-based improved LUR model reached 0.767, showing a better fit. In the RF-based improved LUR model, precipitation and cropland showed greater contribution than the factors of artificial surfaces, forest land, and wind speed. The adjusted R² of the training model reaches 0.821, which is a significant improvement compared with the basic LUR model. The PM_2.5 concentration simulation results of different models differ in some regions, but the distribution of high-pollution areas in three models are roughly the same, concentrated in northern Zhejiang, the river valley plains in central Zhejiang, and the coastal plains in southeastern Zhejiang. These findings indicate that more effective measures to reduce air pollutants need to be implemented.