Next Article in Journal
Inversion Method for Multiple Nuclide Source Terms in Nuclear Accidents Based on Deep Learning Fusion Model
Previous Article in Journal
A Comparative Study of Air Pollutant Concentrations before the COVID-19 Pandemic and in the New Normal in the Región de Murcia (Spain)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 14
Issue 1
10.3390/atmos14010146
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Climate Variability and Climate Change in Sub-Daily Maximum Intensities: A Case Study in Cartagena, Colombia

by
Alfonso Arrieta-Pastrana
,
Manuel Saba
* and
Adriana Puello Alcázar
Civil Engineering Program, Faculty of Engineering, Universidad de Cartagena, Avenida del Consulado #Calle 30 No. 48-152, Cartagena de Indias 130001, Colombia
*
Author to whom correspondence should be addressed.
Atmosphere 2023, 14(1), 146; https://doi.org/10.3390/atmos14010146
Submission received: 11 November 2022 / Revised: 21 December 2022 / Accepted: 4 January 2023 / Published: 9 January 2023
(This article belongs to the Section Climatology)
Browse Figures
Versions Notes

Abstract

:
The present work analyses a time series of maximum intensities for sub-daily durations of 10 min, 20 min, up to 100 min, and their relationship with the maximum rainfall observations in twenty-four hours (P24), the total annual rainfall (PT), and the maximum, average, and minimum temperatures, using the records of the Rafael Núñez Airport station in the city of Cartagena de Indias, recorded from 1970 to 2015. The series of maximum intensities were obtained from the pluviographic records existing in the station. The analysis seeks to find evidence of climate change and climate variability. The series were tested for homogeneity, stationarity, trend, and periodicity. The degree of cross-correlation and temporal correlation between the different series were determined. Temperature series show homogeneity problems, while no correlation was found between the temperatures and the maximum sub-daily intensities, with the maximum rainfall observations in twenty-four hours and the total annual rainfall. The presence of marked periodicities was found in all the series, with a greater signal in the maximum. No significant trends were found in any of the series. Intensities and maximum rainfall observations in 24 h were found. In general, the series are stationary and do not show trends. Non-homogeneities in the series and the presence of periodicities can lead to an interpretation of non-stationarity and trend.

1. Introduction

In the scientific world, there is consensus that climate change is mainly associated with the gradual variation in the long-term average temperature, producing an impact on average and extreme rainfall observations [1]. This has created the growing conviction that the calculation of the intensity–duration–frequency (IDF) curves used in many engineering applications [2,3], such as in agriculture [4] and in soil erosivity [5], must be rethought. Nevertheless, often there is a limitation regarding poor sub-daily records of intensities with great uncertainties, due to different causes, among which are poor quality data, limitations in the length of the record, types of models used, parameter estimation methods, among others [6,7].
Some authors propose that the projections of extreme rainfall and sea level rises should be updated every five years [8]. Generally, estimates are made from daily rains [9] and multiple procedures and theories have been proposed for the calculation of extreme intensities. The latter can be calculated with conventional empirical methods [10,11,12], based on regional climate change models and the inclusion of uncertainty in the IDF curves [3,13,14,15,16], and with general circulation models [17,18].
Improvements in the capture of global information for IDF estimates are made using climate information from meteorological radars [19,20,21,22] and with remote sensors [23].
Regarding the theories for the calculation, the multifractal theory is found in the literature [24,25,26], along with Archimedes’ copula concept [27,28], and Frank’s copula function, among others [29,30]. Additionally, there are approaches to consider the uncertainty (Bayesian models) [31], the use of Markov chains to represent extreme rains [32], processes and disaggregation based on daily precipitation [33], the presence of multi-scale behaviour, and the use of weighted moments [34], among others.
The uncertainty of the IDF is evaluated, starting from the hypothesis that climate change will alter the patterns of precipitation in space and time, design storms (a hypothetical discrete rainstorm characterized by a specific duration, temporal distribution, rainfall intensity, return frequency, used as parameter for hydraulic engineering design) [35,36], the effect of urbanization, and topography on extreme rainfall patterns [37]. Agilan and Umamahesh (2017) [38] propose methodologies for the calculation of the IDF in non-stationary systems, showing the use of several covariates such as time, local temperature, and urbanization, among others. Other authors question the representativeness of the non-stationarity of the IDF curves, due to the covariance and arguing that the non-stationary models are superior to the stationary ones [39]. This issue is pertinent, for example, in Canada, a web-based tool is being built for the development of IDF curves to support decision-making [40]. In Colombia, on 31 December 2019, a new decree of the Ministry of Housing, City and Territory entered into force, which raises the need to consider the effects of variability in the calculation of the intensity for the design of engineering works and climate change in the country.
Morbidelli et al. (2020) [41] present a historical analysis of the temporal evolution of a large database of rain gauges worldwide, where they collect data from 25,423 rain gauge stations, mainly from Australia, the United States, Italy, and Spain. They state that the old registrations were made manually, with daily and occasional monthly resolutions. Mechanical records appear in the middle of the twentieth century, with resolutions of 1 h or 30 min, while digital records are from the last thirty years of the twentieth century. This limits the investigations which require long series of sub-daily records, such as the effects of weather and short-term heavy rains. Morbidelli et al. (2020) [41] evaluated that on average, only 50% of the stations provide useful data at any time resolution.
The hypotheses of stationarity and non-stationarity of hydrological series are under discussion; some suggest that climate change and climate variability have collapsed the stationarity hypothesis, producing implications in the hydrological design [42,43], and creating a different definition of the frequency of extreme events [44]. Divergent theses are found in the literature on the matter, as some authors consider the theory that stationarity “is dead” [45,46], others claim that it is “immortal” [47,48], as well as that it is a premature “death” [49].
This article presents the case study of Cartagena, Colombia. The objective of this work is to evaluate the behaviour of the maximum sub-daily intensities obtained from the pluviograph of the meteorological station of the Rafael Núñez Airport in the city of Cartagena, from 1970 to 2015, to evaluate the effects of variability and climate change evident in the series, which could affect the design parameters in engineering.

Location of Study Area

The area selected for the study was the city of Cartagena, in Colombia, South America. located in the Caribbean coast, approximately on 10°25′20″ N and 75°32′25″ W. Cartagena is a touristic place; in 1984; UNESCO declared the city as a historical and cultural heritage of humanity. Figure 1 shows the location of the study area.
The city of Cartagena presents low volumes of precipitation that do not exceed 1000 mm per year. The intra-annual regime is approximately bimodal, with a main rainy season in September, October, and November and two dry seasons from December to April and in June–July. The quantity of rainy days during the year is 50 to 100. Because of its topography, without major mountainous elements, the distribution of the temperature is very homogeneous, around 28 °C. The climate has been classified as warm, semi-arid, and semi-humid [50].

2. Methodology

For this study, the time series of the station of the Institute of Hydrology, Meteorology and Environmental Studies of Colombia (IDEAM, for its initials in Spanish), located at the Rafael Núñez Airport in the city of Cartagena, Colombia, were selected. All the rainfall observations recorded graphically by means of pluviograph in the station from the year 1970 to the year 2015 were taken. Around 4500 rainfall observations were manually analysed. Each of the rainfall observations were analysed with maximum intensity for each given duration, with an interval duration of 10 min. The rainfall with the highest intensity for each year was selected and the series of maximum intensities were built for durations of 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 min. For the same recording period (1970–2015), the series of maximum, minimum, mean temperatures, maximum annual rainfall in twenty-four hours, and total annual rainfall recorded in the same season were taken.
The selected data series were graphed as a function of the recording time. A linear function was fitted to show macro-trend effects. Descriptive statistics for all series, mean, standard deviation, coefficient of variation, autocorrelation coefficients, and cross-correlation coefficients between all series were calculated.
Subsequently, the homogeneity test was performed on all series, using the Pettitt tests [51,52], SNHT [53,54], Buishand [55], Von Neumann [56], and the stationarity tests applying the Augmented Dickey–Fuller test (ADF) [57], the Phillips–Perron test [58], and the KPSS test [59,60].
For the trend criterion, the Mann–Kendall test was applied [52,61,62]. Additionally, spectral analysis was performed for all series. The spectral analysis of a time series is a tool used in hydrology [63,64] to obtain the periodic components of a time series. It expresses the process as a sum of trigonometric periodic sequences.
For all the calculations of statistical tests of homogeneity, stationarity, trend, and spectral analysis, the XLSTAT 2020® software was used.
The series presenting homogeneity problems were corrected according to Equation (1), making them coincide with the final section of each series. Subsequently, the tests of stationarity, trend and spectral analysis were applied again.
From the results of the spectral analysis, the four harmonics that showed the greatest periodic signal for each of the series were selected and four residual synthetic series were generated for each one, called R1, R2, R3, and R4. Periodicity with the highest signal were removed. The R1 series corresponds to the original series minus the periodic function corresponding to the harmonic that showed the highest signal. The R2 series corresponds to the residual of the difference between the original series and the two periodic series, the product of the two harmonics that showed the highest value in the spectral analysis, and as well as for the series R3 and R4. The Ris have no mathematical relationship between them, and what is sought is to eliminate the periodicities with the greatest weight and analyze if the series, after removing the periodicities, continues to show some behaviour and/or trend. Finally, the tests of stationarity and trend were applied to the generated series.

3. Results

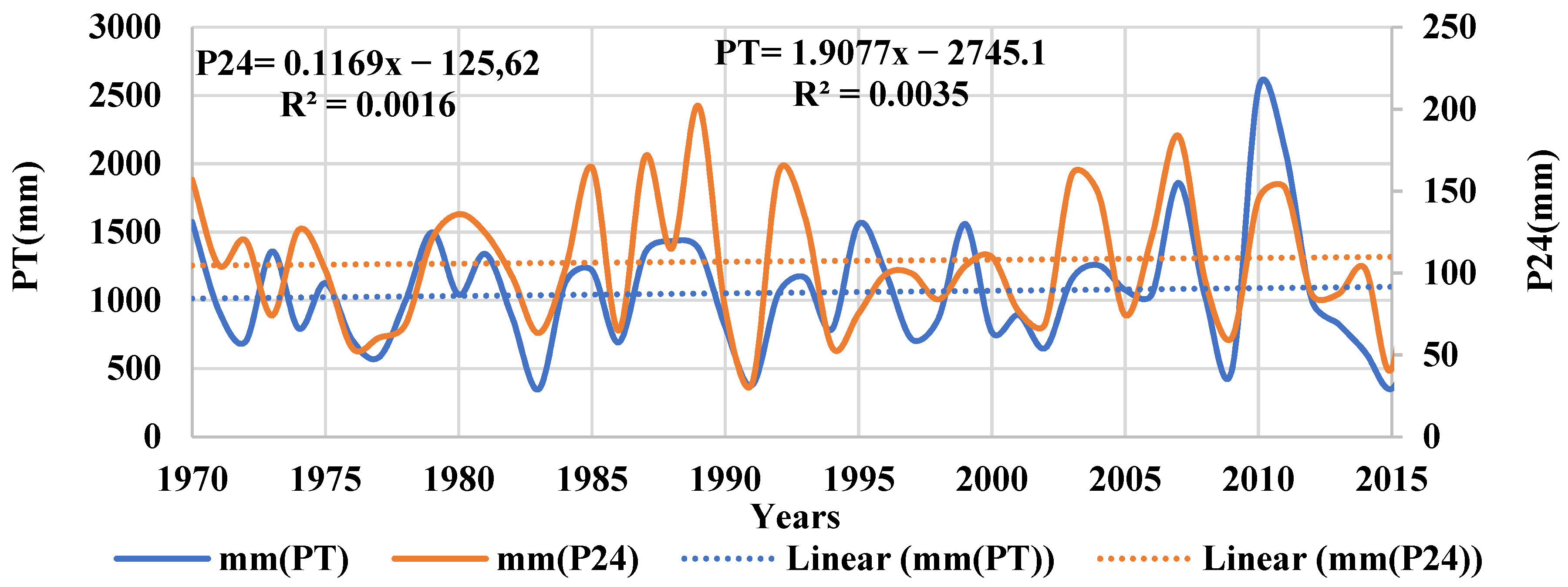
Figure 2 shows the original series smoothed by the graphical software taken from IDEAM of total annual precipitation (PT) and maximum annual precipitation in twenty-four hours (P24). A linear function was fitted to infer the presence of trends. Both series show a positive slope (0.1169 mm/year, for P24, and 1.9077 mm/year, for PT).
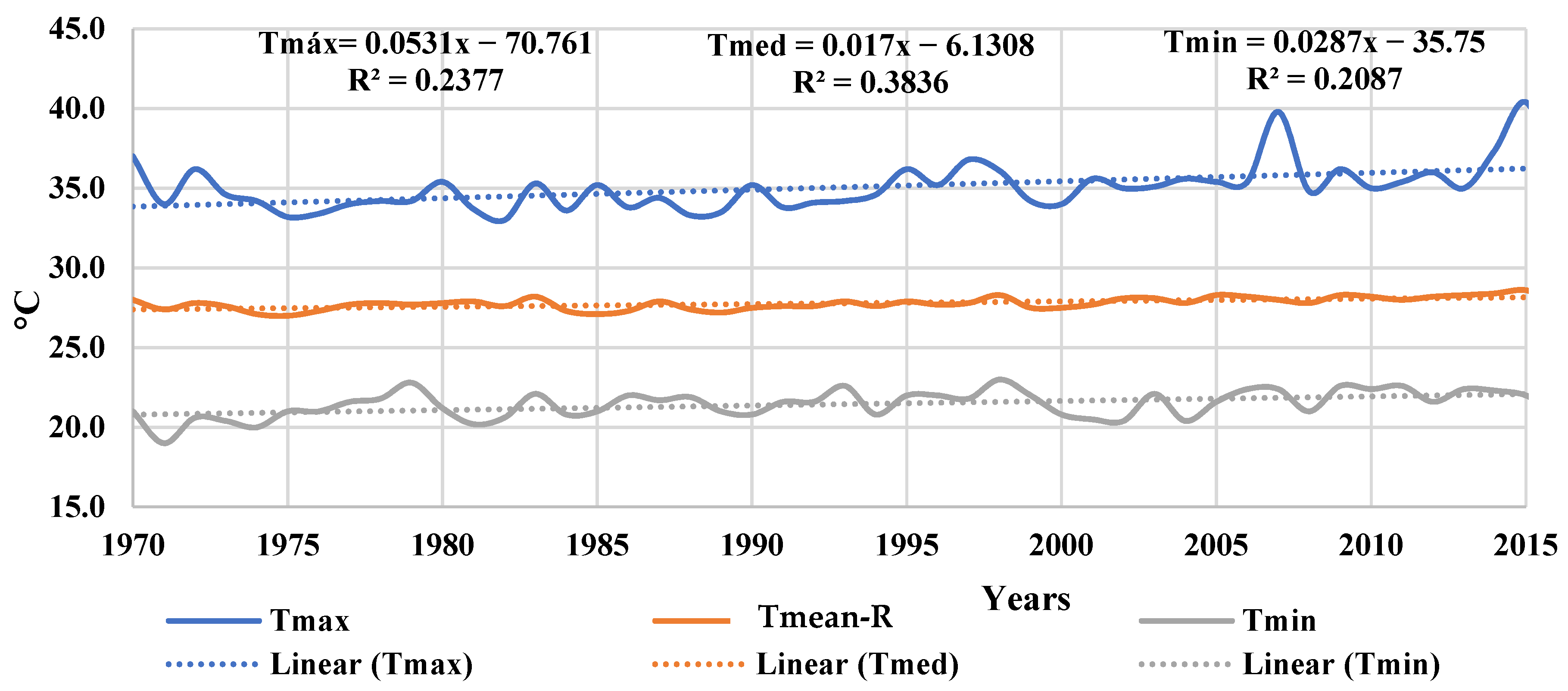
Figure 3 shows the original series of maximum, average, and minimum temperatures taken from IDEAM, smoothed by the graphical software used. A linear function was fitted to the data to analyse the presence of trends (R2 means determination coefficient). The three series show a positive slope, 0.0531 °C/year for the maximum temperature, 0.017 °C/year for the average temperature, and 0.0287 °C/year for the minimum temperature.
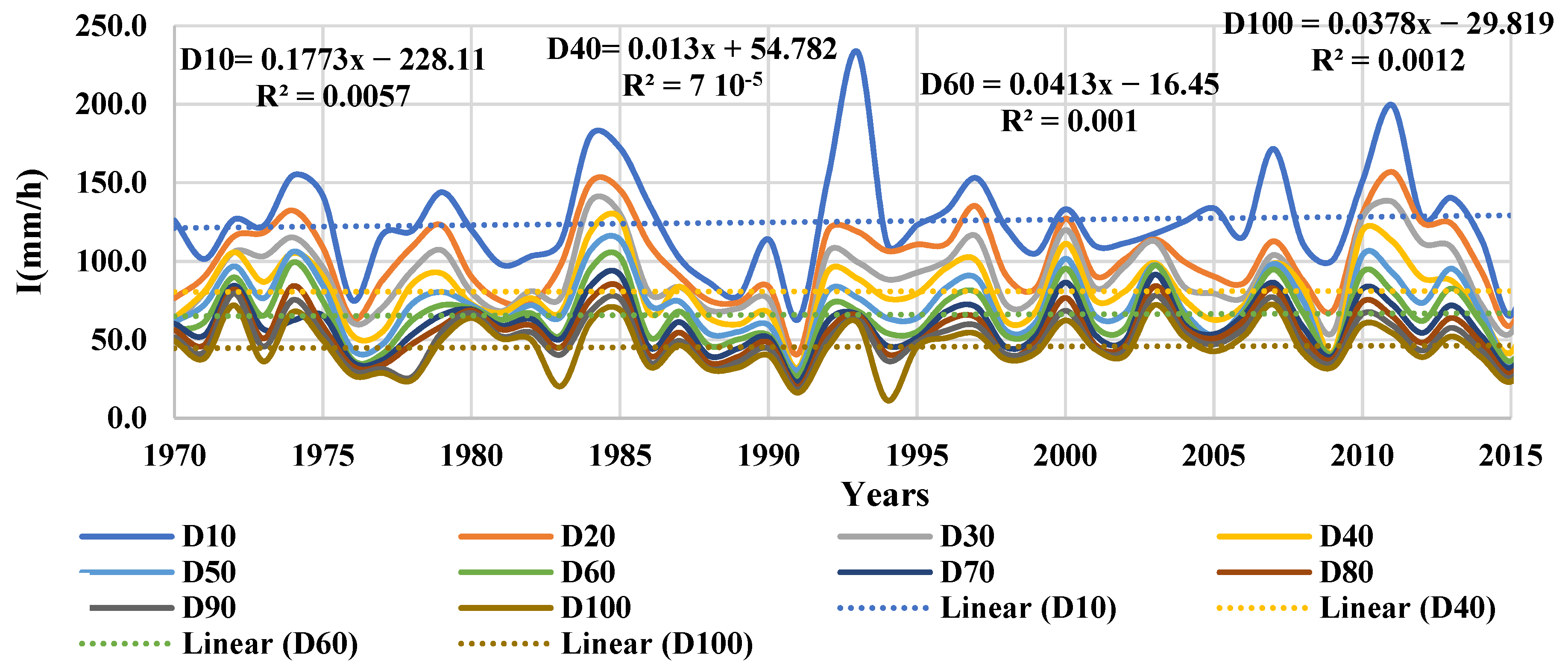
Figure 4 shows the time series of maximum intensities for a given duration of rain of ten minutes (D10), twenty minutes (D20), thirty minutes (D30), forty minutes (D40), fifty minutes (D50), sixty minutes (D60), seventy minutes (D70), eighty minutes (D80), ninety minutes (D90), and one hundred minutes (D100), (Table A3).
The intensity series were taken from Herrera and Llamas (2018) [65], and are based on the IDF concept of Chow et al. (1993; pag. 78) and Jain Sharad and Singh Vijay (2019, pag, 552) [66,67]. Subsequently, for each duration, the maximum intensity value was taken for each year.
Four durations of rains D10, D40, D60, and D100 were taken, to which a linear function was fitted. The results show a positive growth trend in the selected series, from 0.013 mm/h per year to 0.1773 mm/hour per year.
According to the results shown in Figure 2, Figure 3 and Figure 4, all series show an ascending line that could be associated with climate change and/or climate variability 8 × 10−5.
Fadhel et al. (2017) [68] found an increase in the intensity of the rains for all the return periods and a great uncertainty in the future IDF curves. On the other hand, Madsen et al. (2009) [69], in Denmark, found an increase in intensities of the order of 10%. Additionally, they consider that the changes are not statistically significant.

3.1. Descriptive Statistics

According to the results shown in the Table 1, for intensities D10 to D100, the coefficient of variation (CV) varied between 0.24 and 0.33. The total precipitation (PT) showed a value of 0.34, the P24 a value of 0.38, and the temperatures present values between 0.01 and 0.04. Therefore, temperatures present 8 to 25 times less variation than rainfall and intensities. When analysing the Pearson correlation coefficient according to the scale of Cohen (1988) [70] (Table 2), between the different series, it can be observed that the cross-correlation coefficient between the maximum precipitation in twenty-four hours (P24), and the other series CORR(P24) with the intensities, (D10 to D100), vary between 0.34 and 0.66. This is considered a moderate to strong correlation, while the correlation with PT (0.6) is considered strong. The correlation with temperatures varies between −0.13 and 0.03, being in the null range. The correlations found between PT and the intensities (D10 to D100) are between 0.34 and 0.42, considered as moderate. The correlations between PT, with temperatures varying between −0.04 and 0.189, are in the range between weak and null. The temporal correlations or autocorrelations (CORR(T)) of the intensities (D10-D100, PT and P24), show values between −0.01 and 0.11. This is considered as null correlation. The maximum and mean temperatures show a moderate correlation. The correlation between maximum temperature, intensities, and rainfall (D10 to D100, PT and P24) is zero. On the other hand, the maximum temperature shows a strong correlation with the mean temperature and a moderate correlation with the minimum temperature. The correlation between mean temperature, intensities, and rainfall is considered weak-to-zero, while it has a strong correlation with the maximum and minimum temperature. The minimum temperature has a weak-to-zero correlation, compared with intensities and rainfall, and a moderate correlation with maximum and average temperatures.
There is a moderate to strong correlation between the maximum intensities for a given duration and the total annual and maximum rainfall in twenty-four hours. Finally, a strong correlation between maximum 24 h rainfall and total annual rainfall is found. In another case study, Kenabatho et al. (2012) [71], in Botswana (South Africa), found comparable results, that as the temperature increases, the rainfall decreases.

3.2. Homogeneity of the Series

To evaluate the homogeneity of the series, the XLSTAT 2020 software was used, using the Pettitt, SNHT, Buishand, and Von Neumann tests. Table 3 shows that the series of maximum, average, and minimum temperatures present non-homogeneity problems for the four tests used for the evaluation. The other series are homogeneous for all the evaluation criteria applied.
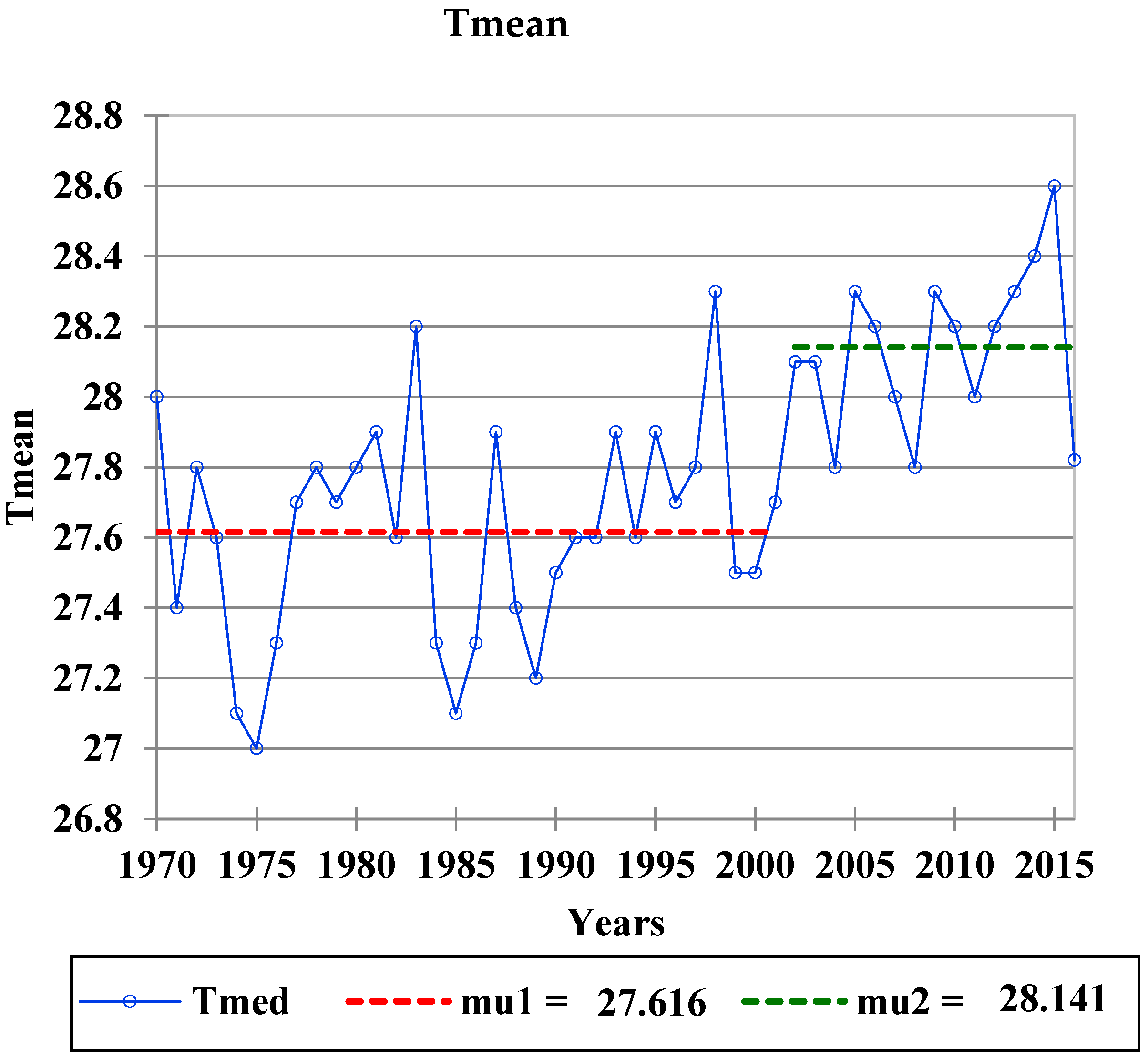
Figure 5 shows the non-homogeneity of the mean temperature series, analysed with the Buishand test, where in the period between 1970–2001, the mean value was 27.616 °C, and between 2002 and 2015, the mean was 28.141 °C, giving a difference of 0.525 °C.
Results of non-homogeneity show the maximum temperature series, analysed with the Buishand test, where in the period 1970–1994, the mean value was 34.324 °C, and between 1995 and 2015, the mean was 35.915 °C, giving a difference of 1.591 °C.
Similarly, there is non-homogeneity of the minimum temperature series, analysed with the Buishand test, where in the period 1970–1985, the mean value was 20.944 °C, and between 1986 and 2015, the mean was 21.715 °C, giving a difference of 0.771 °C.

3.3. Stationarity and Tendency of the Series

For the analysis of stationarity and trend of the series, the XLSTAT 2020 software was used, applying the Dickey–Fuller test, the Phillips–Perron test, and the KPSS test for the stationarity criterion and the Mann–Kendall test for the trend criterion.
Table 4 presents the results of the stationarity test. According to the Phillips–Perron criterion, all the series are non-stationary. While according to the Dickey–Fuller criterion, 53% of the series are stationary and 47% are non-stationary. According to the KPSS criterion, 80% of the series are stationary and 20% are non-stationary. The Phillips–Perron criterion is discarded, due to the low sensitivity shown by the series in this test. Taking as reference the Dickey–Fuller and KPSS criteria, all series of maximum intensities for durations between D10 and D60 are stationary. The series of mean and minimum temperatures are all non-stationary. The series of total annual precipitation (PT) are stationary. Of the other series (D70 to D100, P24, Tmax), 50% are stationary and the other 50% are non-stationary. Therefore, in general, the stationarity criterion prevails (66%).
In the evaluation of the trend considering the Mann–Kendall criterion, the maximum, average, and minimum temperatures show trends, and the other series (D10 to D100, PT, P24) did not show trends.
Mailhot et al. (2007) [72], in southern Quebec, Canada, calculate IDF curves using a regional climate change model. They conclude that there is no clear indication of non-stationarity, the uncertainty increases with the return period, and the results are dependent on the model.
The IDF curves were built with the stationary assumption, and it is possible that the intensification of the hydrological cycle due to climate change makes the extreme series non-stationary. Additionally, higher values are found for non-stationary than stationary analysis [73].
The variation in precipitation in the state of Rio de Janeiro, Brazil, was characterized, in the period 1983–2017. After performing tests of normality, homogeneity, and trend, (Buishand test) breaking points in 29.34% of the studied sites were found, as well as downward trends in average annual rainfall observations in 58.69% of the analysed sites [74].

3.4. Periodicities in the Series

To analyse the periodicities or cycles in each of the series, a spectral analysis was performed on each series using the XLSTAT 2020 software.
In Table 5, the magnitude of the periodic signal for each period expressed in years is shown in percentage of the periodogram. The color red represents the signal with the highest magnitude for each series, yellow the second highest value, and in descending order blue the third and green the fourth highest value. The right column shows the average value for the maximum intensities for durations between 10 min and 100 min. The highest signal for the maximum intensities corresponds to the period of 2.61 years, in descending order the periodicity of 3.62 years, in the third magnitude, 11.75 years and in the fourth magnitude 9.4 years. For the series of maximum rainfall observations in 24 h (P24), the highest signal is for 3.62 years, followed by 4.7 years, 2.61 years, and 2.47 years. For total annual precipitation (PT), the highest signal occurs in a period of 3.62 years, followed in order of highest value by 7.83 years, 2.94 years, and 3.13 years. In summary, the signal with the greatest presence is the period of 3.62 years, followed in order of importance by 2.61, 4.7, 11.75, and 9.4 years.
In Table 6, the results of the spectral analysis expressed as a percentage of the p periodogram for the temperature series (original series) are shown consolidated. The presence of a strong signal is appreciated in the period of 47 years, followed by 15.67 years, 9.4 years, and 11.75 years. The maximum temperature shows an important frequency at 2.47 years.

Correction for Non-Homogeneity

Considering that not all the series analyzed present homogeneity problems, the series with homogeneity problems were corrected, making them coincide with the final section of the series. The series corrected are those of the maximum, average, and minimum temperatures.
To correct the series for non-homogeneity, the following expression was used (1):
x ′ t = x t − X 1 − S 1 X S 2 X + X 2 −
where X t ′ is the value corrected for non-homogeneity, x t the initial value of the sub-series to correct for non-homogeneity, X 1 − the average value of sub-series 1, S 1 X the standard deviation of sub-series 1, S 2 X Standard deviation of sub-series 2, and X 2 − the average value of sub-series 2.
The series corrected for homogeneity are called corrected maximum temperature (Tmax-R), corrected mean temperature (Tmean-R), and corrected minimum temperature (Tmin-R), (Table A4).
Table 7 shows the non-stationarity and trend results for the maximum, average, and minimum temperature series, corrected for homogeneity, where the stationarity and trend tests were applied again. According to the Dickey–Fuller criterion, the results are identical to the series without correction. Whereas, with the KPSS test, the series are stationary. The Mann–Kendall trend test showed that the corrected series have no trend. For the temperatures, it can be concluded that the apparent trend of the original series is the product of non-homogeneity.
In Table 8, the results of the spectral analysis expressed in percentage are presented for the maximum, average, and minimum temperatures, corrected for homogeneity, where it can be seen that the frequency of the highest signal is 15.67 years, followed by 2.47 years and 11.75 years, while the frequency of 47 years shown in the original series disappears.
Table 9 shows the signal from P24, PT, the average of the intensities for all durations from 10 min to 100 min (Average D), and the average of the spectral signal for the maximum, mean, and minimum temperatures of the corrected series. Rainfall has a strong signal in the period of 3.62 years, while for temperatures, the strongest signal is in 15.67 years. Around 2.47 to 2.61 years, an important signal is presented for all series. The average of the four columns on the left is consolidated. According to the consolidated result, the greatest signal is given by the periodicity of 3.62 years, followed in order by 4.7, 15.67, and 2.61 years.
Other authors, such as B. Li et al. (2020) [75], studied the effect of change in land use and cover, and the influence of regional climate change on runoff. They use the Mann–Kendall test to assess linear and nonlinear trends in potential evapotranspiration, precipitation, and runoff in the Yihe River basin in eastern China, in the period 1951–2013. They found that evapotranspiration, precipitation, and runoff showed periodicities between 3–6 years and between 13–16 years, for which they found that climate variability is the main cause of the decrease in runoff. It is concluded that human activity is the main cause of the change in runoff.
On the other hand, J. H. Lee et al. (2020) [76] analysed the climatic relationships between large-scale climatic indices and the variability of precipitation in Taiwan, using correlation and regression between monthly precipitation and indices based on atmospheric–ocean circulation. They find a consistent association between the tropical ENSO and the March–October and November rainfall patterns.
Moreover, in another study, Singh and Qin (2020) [77] analyse rainfall observations in Southeast Asia, at the level of global climatic indices, in a long-term series (1951–2014). They studied the short- and long-term variability of rainfall, using extreme rainfall rates, and analysed the effect of the oceanic–atmospheric behaviour on a large scale. Associations were found with global climatic indices such as El Niño, (3.4–4.0), Southern Oscillation, Madden–Julian Oscillation, and global mean temperature indices for land and ocean.

3.5. Effect of Periodicity

To evaluate the effect of periodicity on stationarity and trend in each of the series, synthetic series were built by extracting the main signals of periodicities to the series of temperatures, total annual precipitation, maximum rainfall in 24 h and maximum intensities for each given duration, 10 to 100 min. For example, the R1 series corresponds to the original series minus the periodic function corresponding to the harmonic with the highest signal for the original series. The R2 series corresponds to the difference of the original series minus the two series corresponding to the two harmonics with the highest signal, as well as for the R3 and R4 series.
Table A1 shows the results of the stationarity and trend test using the XLSTAT 2020 software, for the PT, P24 series, and corrected temperatures. The Phillips–Perron test is discarded (it does not show sensitivity), the Dickey–Fuller and KPSS tests are used for the stationarity criterion, and the Mann–Kendall test for trend. The results show that according to the Dickey–Fuller criterion, 60% of the series are stationary, and according to the KPSS test, 100% of the series are stationary. The trend tests show that no series has a trend.
Table A2 summarizes the tests of stationarity and trends for the maximum intensities for given durations of 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 min, with their respective residual series, R1, R2, R3, and R4. According to the Dickey–Fuller test, for the durations between 10 min and 60 min (D10 to D60), 97% of the series are stationary, and according to the KPSS test, 100%. From the duration of 70 to 100 min (D70–D100), according to the Dickey–Fuller test, only 20% of the series are stationary, while for the KPSS test criterion, 100% are stationary. According to the Mann–Kendall trend criterion, 100% of the series show no trends.
In the literature, works are found highlighting similar results. Hailegeorgis et al. (2013) [78] analyse the IDF curves and perform trend and stationarity tests. They conclude that stationarity and trend depend on the data series used, finding the stationarity criterion valid. On the other hand, Fatichi et al. (2014) [79] state that stochastic climate variability is the fundamental source of uncertainty, which makes it difficult to transfer results on spatial and temporal scales, and its uncertainty is similar to or greater than the signal produced by climate change. Umar et al. (2019) [80] evaluated the behaviour of rainfall and annual temperatures in the Hadejia River basin in Nigeria, using the Mann–Kendall trend test, in a period of 36 years (1980–2015). They found an increasing trend in precipitation and temperature, which was statistically insignificant.
In the present study, in general, according to the results of the maximum intensities for a given duration, for the maximum annual precipitation in 24 h and for the total annual precipitation, no conclusive results of non-stationarity were found. Additionally, it was found that the series have no trends. Therefore, periodic components can show a false indicator of non-stationarity.

4. Conclusions

The objective of this study was to evaluate whether there is evidence of the effects of climate change and climate variability in the series of maximum sub-daily intensities in the city of Cartagena that merit new approaches to calculate and restructure the currently existing design parameters for the engineering works.
It was found that all the original precipitation series (maximum intensities, PT, P24) analysed were homogeneous and with no significant trend. The original temperature series showed trends and the presence of non-homogeneity. The trend in the temperature series disappears with the correction for non-homogeneity. The stationarity tests do not have a similar degree of sensitivity, which can influence the interpretation of the non-stationarity results. No correlation was found between temperatures and maximum intensities, maximum rainfall in 24 h, or with total annual rainfall, which allows establishing functional relationships between temperature and maximum intensities used in engineering designs. The non-stationarity in the original series of temperatures in a large percentage is due to problems of homogeneity and periodicity, and the temperature series show a moderate to strong temporal correlation.
The series of maximum sub-daily intensities, with durations between 10 and 60 min, are stationary and without trend, while the series of maximum sub-daily intensities with durations between 70 and 100 min showed non-stationarity results in 40% of the cases. This is possibly attributable to the origin of the data. This could be due to the fact that the samples for selection of the maximum intensities decrease with the duration of the rain. In general, the maximum intensities for sub-daily durations are stationary and without trend, with the presence of periodic components.
A strong periodic signal for the 3.62 year period was found in the series of maximum intensities and total and maximum rainfall in 24 h, while for temperatures, the strongest signal is at 15.67 years. All series showed a significant periodic component between 2.47 and 2.61 years. Another one of the significant frequencies, marked mainly in the series of maximum intensities and maximum precipitation in 24 h, corresponds to 4.7 years.
No evidence of climate change was found in the records of maximum sub-daily intensities to infer that in the future, the maximum design intensities in engineering works will be higher or lower. For future studies it is recommended to unify the selection methods of the maximum sub-daily intensities.

Author Contributions

Data curation, A.P.A.; investigation, A.A.-P.; supervision, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data will be available upon reasonable request.

Acknowledgments

The authors would like to acknowledge the IDEAM for providing the data on which this study is based.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Results of the stationarity and trend tests for the original series (PT, P24, Tmax-R, Tmean-R, and Tmin-R) and residuals (R1, R2, R3, and R4).
Table A1. Results of the stationarity and trend tests for the original series (PT, P24, Tmax-R, Tmean-R, and Tmin-R) and residuals (R1, R2, R3, and R4).
VariableStationarityTrend
Dickey–Fuller (Stationarity ADF)Phillips–PerronKPSS Mann–Kendall
PTPTSNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
P24P24NSNSSNT
R1SNSSNT
R2SNSSNT
R3NSNSSNT
R4NSNSSNT
Tmáx-RTmax-RSNSSNT
R1SNSSNT
R2NSNSSNT
R3NSNSSNT
R4NSNSSNT
Tmean-RTmean-RNSNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4NSNSSNT
Tmin-RTmean-RNSNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4NSNSSNT
Table
Table A2. Results of the stationarity and trend tests for the original series (D10 to D100) and residuals (R1, R2, R3, and R4), respectively.
Table A2. Results of the stationarity and trend tests for the original series (D10 to D100) and residuals (R1, R2, R3, and R4), respectively.
VariableStationarityTrend
Dickey–Fuller (Stationarity ADF)Phillips–PerronKPSS Mann–Kendall
D10D10SNSSNT
R1SNSSNT
R2SNSSNT
R3NSNSSNT
R4SNSSNT
D20D20SNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
D30D30SNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
D40D40SNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
D50D50SNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
D60D60SNSSNT
R1SNSSNT
R2SNSSNT
R3SNSSNT
R4SNSSNT
D70D70NSNSSNT
R1SNSSNT
R2NSNSSNT
R3NSNSSNT
R4NSNSSNT
D80D80NSNSSNT
R1SNSSNT
R2NSNSSNT
R3NSNSSNT
R4SNSSNT
D90D90NSNSSNT
R1NSNSSNT
R2NSNSSNT
R3NSNSSNT
R4SNSSNT
D100D100NSNSSNT
R1NSNSSNT
R2NSNSSNT
R3NSNSSNT
R4NSNSSNT
Table
Table A3. Time series of maximum intensities for a given duration of rain of ten minutes (D10), twenty minutes (D20), thirty minutes (D30), forty minutes (D40), fifty minutes (D50), sixty minutes (D60), seventy minutes (D70), eighty minutes (D80), ninety minutes (D90), and one hundred minutes (D100).
Table A3. Time series of maximum intensities for a given duration of rain of ten minutes (D10), twenty minutes (D20), thirty minutes (D30), forty minutes (D40), fifty minutes (D50), sixty minutes (D60), seventy minutes (D70), eighty minutes (D80), ninety minutes (D90), and one hundred minutes (D100).
Maximum Intensities of Precipitation (mm/h)PTP24Temperature (°C)
DURATION MINUTESTotal
Annual		Max
(24 h)		°C°C°C
YearsD10D20D30D40D50D60D70D80D90D100mm (PT)mm (P24)TmaxTmeanTmin
1970126.0076.5060.0063.8061.2056.0060.2056.3051.6049.201574.40157.0037.0028.0021.00
1971101.4090.0080.0080.6072.2061.2052.7046.6042.0038.10926.40104.7034.0027.4019.00
1972126.60115.80106.00105.8096.8089.8084.4082.1079.5072.00697.10120.0036.2027.8020.60
1973122.40118.20103.2086.9076.4065.3056.6050.8045.6036.101358.3074.1034.6027.6020.40
1974154.80132.30115.20105.30106.2099.4062.4084.2075.4067.90793.80126.4034.2027.1020.00
1975141.60108.6096.0090.3084.5074.6065.4058.4053.5049.601126.80101.6033.2027.0021.00
197675.0063.3060.8052.7043.4037.1035.7033.0030.2027.30711.7054.4033.4027.3021.00
1977117.0087.9070.6055.1047.0041.0037.1034.1031.4028.80582.2060.5034.0027.7021.60
1978119.40109.2094.0085.4072.8062.3053.2047.3026.3024.20994.6068.6034.2027.8021.80
1979144.00123.00107.0092.3080.4072.0065.7058.7054.8050.201497.50120.7034.2027.7022.80
1980120.0090.0080.0072.8072.0070.0069.3068.6067.0063.801041.40135.9035.4027.8021.20
198197.8074.7068.2067.2063.0062.7059.0056.5052.1050.701340.10124.4033.7027.9020.20
1982103.2073.2081.0076.5072.0066.9063.3059.3054.8050.10878.3098.0033.0027.6020.60
1983112.2097.5076.6067.5064.4052.6050.5045.2040.4020.30349.1063.4035.3028.2022.10
1984180.00150.00138.00118.50106.8094.8084.1075.4068.0061.301130.90102.7033.6027.3020.80
1985172.20145.50130.20127.40113.80102.8091.5083.4076.3069.101219.20164.5035.2027.1021.00
1986135.60110.4079.4066.9072.0051.5044.9039.8035.6032.60692.5064.9033.8027.3022.00
1987102.0090.6083.6083.9074.4068.0061.3054.6049.3046.401350.80171.3034.4027.9021.70
198886.4075.0068.8063.8053.8046.2039.6035.3031.6031.001433.70115.0033.3027.4021.90
198978.0073.8070.0059.9055.1050.3044.5039.3036.0032.401378.00201.8033.5027.2021.00
1990114.0084.0076.0067.5059.4052.9051.4048.3044.4040.10805.6077.8035.2027.5020.80
199163.0041.1031.0032.3030.8027.1023.1020.0018.1016.30378.3032.5033.8027.6021.60
1992153.00119.40105.6093.6081.0071.5061.9055.3049.9045.601053.00161.5034.1027.6021.60
1993233.40118.8099.4089.0076.7068.3066.2065.6062.9061.101165.20133.4034.2027.9022.60
1994111.00106.5088.4076.2063.7054.2046.1040.8036.5011.30788.5054.8034.6027.6020.80
1995123.00110.7092.8079.4063.8055.1051.3048.3048.4045.301557.8075.3036.2027.9022.00
1996132.60111.30100.2095.9083.4074.9068.2062.1055.9051.201208.8099.1035.2027.7022.00
1997153.00135.00116.00100.5089.3080.3070.8064.2059.1053.80714.1099.7036.8027.8021.80
1998121.2090.9072.4061.7055.8052.6045.2039.8040.7037.40869.6083.9036.1028.3023.00
1999105.0082.8077.6068.0061.1057.1052.5048.2044.9041.601559.20104.2034.2027.5022.00
2000133.20127.20120.00111.20101.6095.3086.5076.7068.5062.30767.10109.8034.0027.5020.80
2001109.8090.6083.0075.0065.2058.5053.0046.7044.7043.90892.5076.7035.6027.7020.50
2002111.60101.4096.8080.9066.8057.2049.6046.1043.0039.80650.9069.1035.0028.1020.40
2003117.60114.00112.8098.9097.6097.3091.5084.1078.1072.101156.10159.9035.1028.1022.10
2004125.4099.6083.6075.6067.8065.1059.7057.6054.5051.701256.80148.2035.6027.8020.40
2005133.8090.3079.4062.6052.8047.7053.5050.8047.1042.601076.6074.4035.4028.3021.60
2006115.8086.1076.8072.0069.0067.1065.7062.0057.1052.301045.20122.3035.4028.2022.40
2007171.60112.80104.0098.6098.4094.8086.4082.7077.1072.401859.80183.7039.8028.0022.40
2008111.0087.6081.8083.1074.8067.1057.9051.1045.8041.401025.4095.3034.8027.8021.00
2009100.8068.7054.6042.2037.4041.2039.6037.7035.2032.50487.8060.5036.2028.3022.60
2010151.20130.50127.80119.40103.9093.2082.5074.3066.5059.902550.80145.1035.0028.2022.40
2011199.50156.90138.00112.8092.8080.8072.5065.0059.2054.202100.10151.9035.4028.0022.60
2012127.80124.80111.8089.4073.4061.9054.3048.1043.1038.901002.2087.1036.0028.2021.60
2013140.40123.90108.8087.6095.3082.7071.9063.9057.6052.10826.9087.2035.0028.3022.40
2014114.0093.6072.4064.8067.1060.9052.4047.9042.9038.70621.10102.7037.4028.4022.30
201565.4059.1054.4042.0035.6036.4032.1028.6025.7023.30352.5041.7040.4028.6022.00
2016136.20121.50108.2094.5082.7073.4066.3062.6057.3052.20826.40173.9035.5027.8020.90
Table
Table A4. The series corrected for homogeneity are called corrected maximum temperature (Tmax-R), corrected4mean temperature (Tmean-R), and corrected minimum temperature (Tmin-R).
Table A4. The series corrected for homogeneity are called corrected maximum temperature (Tmax-R), corrected4mean temperature (Tmean-R), and corrected minimum temperature (Tmin-R).
Hydrological Series Reconstruction
Tmax-RTmean-RTmin-R
40.3028.4021.80
35.4028.0020.10
39.0028.3021.40
36.4028.1021.30
35.7027.8020.90
34.1027.7021.80
34.4027.9021.80
35.4028.2022.30
35.7028.3022.40
35.7028.2023.20
37.7028.3021.90
34.9028.4021.10
33.8028.1021.40
37.5028.6022.70
34.7027.9021.60
37.3027.8021.80
35.1027.9022.00
36.0028.4021.70
34.2028.0021.90
34.6027.8021.00
37.3028.1020.80
35.1028.1021.60
35.5028.1021.60
35.7028.4022.60
36.4028.1020.80
36.2028.4022.00
35.2028.2022.00
36.8028.3021.80
36.1028.7023.00
34.2028.1022.00
34.0028.1020.80
35.6028.2020.50
35.0028.1020.40
35.1028.1022.10
35.6027.8020.40
35.4028.3021.60
35.4028.2022.40
39.8028.0022.40
34.8027.8021.00
36.2028.3022.60
35.0028.2022.40
35.4028.0022.60
36.0028.2021.60
35.0028.3022.40
37.4028.4022.30
40.4028.6022.00
35.5027.8020.90

References

  1. IPCC. Climate Change 2022: Impacts, Adaptation and Vulnerability Climate Change 2022: Impacts, Adaptation and Vulnerability. Available online: https://www.ipcc.ch/report/ar6/wg2/ (accessed on 11 April 2022).
  2. Ganguli, P.; Coulibaly, P. Assessment of future changes in intensity-duration-frequency curves for Southern Ontario using North American (NA)-CORDEX models with nonstationary methods. J. Hydrol. Reg. Stud. 2019, 22, 100587. [Google Scholar] [CrossRef]
  3. Hosseinzadehtalaei, P.; Tabari, H.; Willems, P. Precipitation intensity–duration–frequency curves for central Belgium with an ensemble of EURO-CORDEX simulations, and associated uncertainties. Atmos. Res. 2018, 200, 1–12. [Google Scholar] [CrossRef]
  4. Cochrane, L.; Lewis, S.C.; Engdaw, M.M.; Thornton, A.; Welbourne, D.J. Using farmer-based metrics to analyze the amount, seasonality, variability and spatial patterns of rainfall amidst climate change in southern Ethiopia. J. Arid Environ. 2020, 175, 104084. [Google Scholar] [CrossRef]
  5. Grillakis, M.G.; Polykretis, C.; Alexakis, D.D. Past and projected climate change impacts on rainfall erosivity: Advancing our knowledge for the eastern Mediterranean island of Crete. Catena 2020, 193, 104625. [Google Scholar] [CrossRef]
  6. Chandra, R.; Saha, U.; Mujumdar, P.P. Model and parameter uncertainty in IDF relationships under climate change. Adv. Water Resour. 2015, 79, 127–139. [Google Scholar] [CrossRef]
  7. Huang, Y.F.; Mirzaei, M.; Amin, M.Z.M. Uncertainty quantification in rainfall intensity duration frequency curves based on historical extreme precipitation quantiles. Procedia Eng. 2016, 154, 426–432. [Google Scholar] [CrossRef] [Green Version]
  8. DeGaetano, A.T.; Castellano, C.M. Future projections of extreme precipitation intensity-duration-frequency curves for climate adaptation planning in New York State. Clim. Serv. 2017, 5, 23–35. [Google Scholar] [CrossRef]
  9. Lima, C.H.R.; Kwon, H.H.; Kim, Y.T. A local-regional scaling-invariant Bayesian GEV model for estimating rainfall IDF curves in a future climate. J. Hydrol. 2018, 566, 73–88. [Google Scholar] [CrossRef]
  10. Elsebaie, I.H. Developing rainfall intensity–duration–frequency relationship for two regions in Saudi Arabia. J. King Saud Univ. Eng. Sci. 2012, 24, 131–140. [Google Scholar] [CrossRef] [Green Version]
  11. AlHassoun, S.A. Developing an empirical formulae to estimate rainfall intensity in Riyadh region. J. King Saud Univ. Eng. Sci. 2011, 23, 81–88. [Google Scholar] [CrossRef]
  12. Al Mamoon, A.; Joergensen, N.E.; Rahman, A.; Qasem, H. Derivation of new design rainfall in Qatar using L-moment based index frequency approach. Int. J. Sustain. Built Environ. 2014, 3, 111–118. [Google Scholar] [CrossRef] [Green Version]
  13. Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
  14. Wang, D.; Hagen, S.C.; Alizad, K. Climate change impact and uncertainty analysis of extreme rainfall events in the Apalachicola River basin, Florida. J. Hydrol. 2013, 480, 125–135. [Google Scholar] [CrossRef]
  15. Kuo, C.C.; Gan, T.Y.; Hanrahan, J.L. Precipitation frequency analysis based on regional climate simulations in Central Alberta. J. Hydrol. 2014, 510, 436–446. [Google Scholar] [CrossRef]
  16. So, B.J.; Kim, J.Y.; Kwon, H.H.; Lima, C.H. R Stochastic extreme downscaling model for an assessment of changes in rainfall intensity-duration-frequency curves over South Korea using multiple regional climate models. J. Hydrol. 2017, 553, 321–337. [Google Scholar] [CrossRef]
  17. Lima, C.H.R.; Kwon, H.H.; Kim, J.Y. A Bayesian beta distribution model for estimating rainfall IDF curves in a changing climate. J. Hydrol. 2016, 540, 744–756. [Google Scholar] [CrossRef]
  18. Shahabul Alam, M.; Elshorbagy, A. Quantification of the climate change-induced variations in intensity-duration-frequency curves in the Canadian Prairies. J. Hydrol. 2015, 527, 990–1005. [Google Scholar] [CrossRef]
  19. Endreny, T.A.; Imbeah, N. Generating robust rainfall intensity-duration-frequency estimates with short-record satellite data. J. Hydrol. 2009, 371, 182–191. [Google Scholar] [CrossRef]
  20. Wright, D.B.; Smith, J.A.; Villarini, G.; Baeck, M.L. Estimating the frequency of extreme rainfall using weather radar and stochastic storm transposition. J. Hydrol. 2013, 488, 150–165. [Google Scholar] [CrossRef]
  21. Paixao, E.; Mirza, M.M.Q.; Shephard, M.W.; Auld, H.; Klaassen, J.; Smith, G. An integrated approach for identifying homogeneous regions of extreme rainfall events and estimating IDF curves in Southern Ontario, Canada: Incorporating radar observations. J. Hydrol. 2015, 528, 734–750. [Google Scholar] [CrossRef]
  22. Marra, F.; Morin, E. Use of radar QPE for the derivation of intensity-duration-frequency curves in a range of climatic regimes. J. Hydrol. 2015, 531, 427–440. [Google Scholar] [CrossRef]
  23. Wright, D.B.; Mantilla, R.; Peters-Lidard, C.D. A remote sensing-based tool for assessing rainfall-driven hazards. Environ. Model. Softw. 2017, 90, 34–54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Langousis, A.; Veneziano, D.; Furcolo, P.; Lepore, C. Multifractal rainfall extremes: Theoretical analysis and practical estimation. Chaos Solitons Fractals 2009, 39, 1182–1194. [Google Scholar] [CrossRef]
  25. García-Marín, A.P.; Morbidelli, R.; Saltalippi, C.; Cifrodelli, M.; Estévez, J.; Flammini, A. On the choice of the optimal frequency analysis of annual extreme rainfall by multifractal approach. J. Hydrol. 2019, 575, 1267–1279. [Google Scholar] [CrossRef]
  26. Emmanouil, S.; Langousis, A.; Nikolopoulos, E.I.; Anagnostou, E.N. Quantitative assessment of annual maxima, peaks-over-threshold and multifractal parametric approaches in estimating intensity-duration-frequency curves from short rainfall records. J. Hydrol. 2020, 589, 125151. [Google Scholar] [CrossRef]
  27. Palynchuk, B.A.; Guo, Y. A probabilistic description of rain storms incorporating peak intensities. J. Hydrol. 2011, 409, 71–80. [Google Scholar] [CrossRef]
  28. Li, H.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Zhang, J. Non-stationary frequency analysis of annual extreme rainfall volume and intensity using Archimedean copulas: A case study in eastern China. J. Hydrol. 2019, 571, 114–131. [Google Scholar] [CrossRef]
  29. Ariff, N.M.; Jemain, A.A.; Ibrahim, K.; Zin, W.W. IDF relationships using bivariate copula for storm events in Peninsular Malaysia. J. Hydrol. 2012, 470, 158–171. [Google Scholar] [CrossRef]
  30. Bezak, N.; Šraj, M.; Mikoš, M. Copula-based IDF curves and empirical rainfall thresholds for flash floods and rainfall-induced landslides. J. Hydrol. 2016, 541, 272–284. [Google Scholar] [CrossRef]
  31. Liuzzo, L.; Notaro, V.; Freni, G. Uncertainty related to climate change in the assessment of the DDF curve parameters. Environ. Model. Softw. 2017, 96, 1–13. [Google Scholar] [CrossRef]
  32. Burgess, C.P.; Taylor, M.A.; Stephenson, T.; Mandal, A. Frequency analysis, infilling and trends for extreme precipitation for Jamaica (1895–2100). J. Hydrol. Reg. Stud. 2015, 3, 424–443. [Google Scholar] [CrossRef] [Green Version]
  33. De Paola, F.; Galdiero, E.; Giugni, M.; Pugliese, F. Sustainable development of storm-water systems in African cities considering climate change. Procedia Eng. 2015, 119, 1181–1191. [Google Scholar] [CrossRef] [Green Version]
  34. Bairwa, A.K.; Khosa, R.; Maheswaran, R. Developing intensity duration frequency curves based on scaling theory using linear probability weighted moments: A case study from India. J. Hydrol. 2016, 542, 850–859. [Google Scholar] [CrossRef]
  35. Tfwala, C.M.; van Rensburg, L.D.; Schall, R.; Mosia, S.M.; Dlamini, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Clim. Risk Manag. 2017, 16, 1–9. [Google Scholar] [CrossRef]
  36. Hassanzadeh, E.; Nazemi, A.; Adamowski, J.; Nguyen, T.H.; Van-Nguyen, V.T. Quantile-based downscaling of rainfall extremes: Notes on methodological functionality, associated uncertainty and application in practice. Adv. Water Resour. 2019, 131, 103371. [Google Scholar] [CrossRef]
  37. Yang, Z.; Burn, D.H. Automatic feature selection and weighting for the formation of homogeneous groups for regional IDF estimation. J. Hydrol. 2019, 575, 292–307. [Google Scholar] [CrossRef]
  38. Agilan, V.; Umamahesh, N.V. What are the best covariates for developing non-stationary rainfall Intensity-Duration-Frequency relationship? Adv. Water Resour. 2017, 101, 11–22. [Google Scholar] [CrossRef]
  39. Agilan, V.; Umamahesh, N.V. Is the covariate based non-stationary rainfall IDF curve capable of encompassing future rainfall changes? J. Hydrol. 2016, 541, 1441–1455. [Google Scholar] [CrossRef]
  40. Simonovic, S.P.; Schardong, A.; Sandink, D.; Srivastav, R. A web-based tool for the development of Intensity Duration Frequency curves under changing climate. Environ. Model. Softw. 2016, 81, 136–153. [Google Scholar] [CrossRef]
  41. Morbidelli, R.; García-Marín, A.P.; Al Mamun, A.; Atiqur, R.M.; Ayuso-Muñoz, J.L.; Taouti, M.B.; Saltalippi, C. The history of rainfall data time-resolution in a wide variety of geographical areas. J. Hydrol. 2020, 590, 125258. [Google Scholar] [CrossRef]
  42. Poveda, G.; Álvarez, D.M. El colapso de la hipótesis de estacionariedad por cambio y variabilidad climática: Implicaciones para el diseño hidrológico en ingeniería. Rev. Ing. 2012, 1, 65–76. [Google Scholar] [CrossRef]
  43. Obeysekera, J.; Salas, J.D. Quantifying the uncertainty of design floods under nonstationary conditions. J. Hydrol. Eng. 2014, 19, 1438–1446. [Google Scholar] [CrossRef]
  44. Obeysekera, J.; Salas, J.D. Frequency of recurrent extremes under nonstationarity. J. Hydrol. Eng. 2016, 21, 1–9. [Google Scholar] [CrossRef]
  45. Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
  46. Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Krysanova, V. On critiques of Stationarity is dead: Whither water management? Water Resour. Res. 2015, 51, 7785–7789. [Google Scholar] [CrossRef] [Green Version]
  47. Montanari, A.; Koutsoyiannis, D. Modeling and mitigating natural hazards: Stationarity is immortal! Water Resour. Res. 2014, 50, 9748–9756. [Google Scholar] [CrossRef]
  48. Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. (Meurtre par imprudence de concepts scientifiques: Le cas de la stationnarité). Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
  49. Matalas, N.C. Comment on the announced death of stationarity. J. Water Resour. Plan. Manag. 2012, 138, 311–312. [Google Scholar] [CrossRef]
  50. Arrieta-Pastrana, A.; Saba, M.; Alcázar, A.P. Analysis of climate variability in a time series of precipitation and temperature data: A case study in Cartagena de Indias, Colombia. Water 2022, 14, 1378. [Google Scholar] [CrossRef]
  51. Rougé, C.; Ge, Y.; Cai, X. Detecting gradual and abrupt changes in hydrological records. Adv. Water Resour. 2013, 53, 33–44. [Google Scholar] [CrossRef]
  52. Tekleab, S.; Mohamed, Y.; Uhlenbrook, S. Hydro-climatic trends in the Abay/Upper Blue Nile basin, Ethiopia. Phys. Chem. Earth 2013, 61, 32–42. [Google Scholar] [CrossRef]
  53. Mahmoud, S.H.; Gan, T.Y. Urbanization and climate change implications in flood risk management: Developing an efficient decision support system for flood susceptibility mapping. Sci. Total Environ. 2018, 636, 152–167. [Google Scholar] [CrossRef] [PubMed]
  54. Taxak, A.K.; Murumkar, A.R.; Arya, D.S. Long term spatial and temporal rainfall trends and homogeneity analysis in Wainganga basin, Central India. Weather. Clim. Extrem. 2014, 4, 50–61. [Google Scholar] [CrossRef] [Green Version]
  55. Adri Buishand, T.; Brandsma, T. Comparison of circulation classification schemes for predicting temperature and precipitation in The Netherlands. Int. J. Climatol. A J. R. Meteorol. Soc. 1997, 17, 875–889. [Google Scholar] [CrossRef]
  56. Färe, R.; Primont, D.; Weber, W.L. Technical change and the von Neumann coefficient of uniform expansion. Eur. J. Oper. Res. 2020, 280, 754–763. [Google Scholar] [CrossRef]
  57. Steland, A. Weighted Dickey-Fuller processes for detecting stationarity. J. Stat. Plan. Inference 2007, 137, 4011–4030. [Google Scholar] [CrossRef] [Green Version]
  58. Escobari, D.; Garcia, S.; Mellado, C. Identifying bubbles in Latin American equity markets: Phillips-Perron-based tests and linkages. Emerg. Mark. Rev. 2017, 33, 90–101. [Google Scholar] [CrossRef] [Green Version]
  59. De Jong, R.M.; Amsler, C.; Schmidt, P. A robust version of the KPSS test based on indicators. J. Econom. 2007, 137, 311–333. [Google Scholar] [CrossRef]
  60. Lee, D.; Schmidt, P. On the power of the KPSS test of stationarity against fractionally-integrated alternatives. J. Econom. 1996, 73, 285–302. [Google Scholar] [CrossRef]
  61. Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
  62. Sun, S.; Fang, C. Water use trend analysis: A non-parametric method for the environmental Kuznets curve detection. J. Clean. Prod. 2018, 172, 497–507. [Google Scholar] [CrossRef]
  63. Rosenquist, S.E.; Moak, J.W.; Green, A.D.; Flite III, O.P. Understanding hydrologic variation through time-series analysis. In Proceedings of the 2010 South Carolina Water Resources Conference, Columbia, SC, USA, 13–14 October 2010; pp. 1–5. Available online: https://tigerprints.clemson.edu/cgi/viewcontent.cgi?article=1144&context=scwrc (accessed on 3 January 2023).
  64. Fleming, S.W.; Marsh, L.A.; Aly, A.H.; Adams, A. Practical applications of spectral analysis to hydrologic time series. Hydrol. Process. 2002, 16, 565–574. [Google Scholar] [CrossRef]
  65. Herrera, H.J.; Llamas, C.A. Actualización de Las Curvas de Intensidad, Duración y Frecuencia (IDF) Para la Estación Aeropuerto Rafael Nuñez de la Ciudad de Cartagena de Indias DT y C. Master’s Thesis, University of Cartagena, Bolívar, Columbia, 2018. [Google Scholar]
  66. Chow, V.T.; Maidment, D.R.; Mays, L.W. Hidrología Aplicada; McGraw-Hill Education: New York, NY, USA, 1993. [Google Scholar]
  67. Jain, S.K.; Singh, V.P. Engineering Hydrology, an Introduction to Processes, Analysis, and Modeling; McGraw Hill Education: New York, NY, USA, 2019. [Google Scholar]
  68. Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Uncertainty of intensity–duration–frequency (IDF) curves due to varied climate baseline periods. J. Hydrol. 2017, 547, 600–612. [Google Scholar] [CrossRef] [Green Version]
  69. Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity-duration-frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
  70. Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates Publishers: New York, NY, USA, 1988. [Google Scholar]
  71. Kenabatho, P.K.; Parida, B.P.; Moalafhi, D.B. The value of large-scale climate variables in climate change assessment: The case of Botswana’s rainfall. Phys. Chem. Earth 2012, 50, 64–71. [Google Scholar] [CrossRef]
  72. Mailhot, A.; Duchesne, S.; Caya, D.; Talbot, G. Assessment of future change in intensity-duration-frequency (IDF) curves for Southern Quebec using the Canadian Regional Climate Model (CRCM). J. Hydrol. 2007, 347, 197–210. [Google Scholar] [CrossRef]
  73. Vu, T.M.; Mishra, A.K. Nonstationary frequency analysis of the recent extreme precipitation events in the United States. J. Hydrol. 2019, 575, 999–1010. [Google Scholar] [CrossRef]
  74. Sobral, B.S.; de Oliveira-Júnior, J.F.; Alecrim, F.; Gois, G.; Muniz-Júnior, J.G.; de Bodas Terassi, P.M.; Zeri, M. PERSIANN-CDR based characterization and trend analysis of annual rainfall in Rio De Janeiro State, Brazil. Atmos. Res. 2020, 238, 104873. [Google Scholar] [CrossRef]
  75. Li, B.; Shi, X.; Lian, L.; Chen, Y.; Chen, Z.; Sun, X. Quantifying the effects of climate variability, direct and indirect land use change, and human activities on runoff. J. Hydrol. 2020, 584, 124684. [Google Scholar] [CrossRef]
  76. Lee, J.H.; Yang, C.Y.; Julien, P.Y. Taiwanese rainfall variability associated with large-scale climate phenomena. Adv. Water Resour. 2020, 135, 103462. [Google Scholar] [CrossRef]
  77. Singh, V.; Qin, X. Study of rainfall variabilities in Southeast Asia using long-term gridded rainfall and its substantiation through global climate indices. J. Hydrol. 2020, 585, 124320. [Google Scholar] [CrossRef]
  78. Hailegeorgis, T.T.; Thorolfsson, S.T.; Alfredsen, K. Regional frequency analysis of extreme precipitation with consideration of uncertainties to update IDF curves for the city of Trondheim. J. Hydrol. 2013, 498, 305–318. [Google Scholar] [CrossRef] [Green Version]
  79. Fatichi, S.; Rimkus, S.; Burlando, P.; Bordoy, R. Does internal climate variability overwhelm climate change signals in streamflow? The upper Po and Rhone basin case studies. Sci. Total Environ. 2014, 493, 1171–1182. [Google Scholar] [CrossRef] [PubMed]
  80. Ramli, M.F.; Aris, A.Z.; Jamil, N.R.; Aderemi, A.A. Evidence of climate variability from rainfall and temperature fluctuations in semi-arid region of the tropics. Atmos. Res. 2019, 224, 52–64. [Google Scholar] [CrossRef]
Atmosphere 14 00146 g001 550
Figure 1. Location of study area: (a) Colombia; (b) Bolivar department (in yellow); (c) City of Cartagena and location of Rafael Núñez Airport Station.
Figure 1. Location of study area: (a) Colombia; (b) Bolivar department (in yellow); (c) City of Cartagena and location of Rafael Núñez Airport Station.
Atmosphere 14 00146 g001
Atmosphere 14 00146 g002 550
Figure 2. Time series of total annual precipitation and maximum precipitation in 24 h.
Figure 2. Time series of total annual precipitation and maximum precipitation in 24 h.
Atmosphere 14 00146 g002
Atmosphere 14 00146 g003 550
Figure 3. Time series of maximum, mean, and minimum temperatures.
Figure 3. Time series of maximum, mean, and minimum temperatures.
Atmosphere 14 00146 g003
Atmosphere 14 00146 g004 550
Figure 4. Time series of maximum annual intensities for a given rainfall duration in minutes.
Figure 4. Time series of maximum annual intensities for a given rainfall duration in minutes.
Atmosphere 14 00146 g004
Atmosphere 14 00146 g005 550
Figure 5. Results of the Buishand test, for the mean temperature (Tmean), expressed in degrees Celsius.
Figure 5. Results of the Buishand test, for the mean temperature (Tmean), expressed in degrees Celsius.
Atmosphere 14 00146 g005
Table
Table 1. Descriptive statistics of each of the series under study.
Table 1. Descriptive statistics of each of the series under study.
D10D20D30D40D50D60D70D80D90D100PT P24TmaxTmeanTmin
Mean125.30102.0090.3080.8073.1065.9059.4055.0050.3045.401056.90107.3035.1027.8021.50
STDDEV32.1624.8023.0720.9919.5118.1315.8015.5714.8514.96440.5640.641.490.380.86
CV0.260.240.260.260.270.270.270.280.290.330.420.380.040.010.04
CORR (P24)0.400.350.410.510.530.590.620.620.630.660.601.000.03−0.13−0.01
CORR (PT)0.400.350.420.460.390.400.440.390.390.421.000.60−0.02−0.040.19
CORR (T)0.080.090.110.01−0.010.030.060.000.020.040.060.040.490.620.46
CORR (Tmax)0.04−0.01−0.04−0.07−0.040.030.080.080.120.12−0.020.031.000.640.31
CORR (Tmean)−0.05−0.12−0.14−0.23−0.22−0.16−0.05−0.10−0.07−0.07−0.04−0.130.641.000.52
CORR (Tmin)0.230.080.01−0.09−0.08−0.070.00−0.07−0.06−0.040.19−0.010.310.521.00
D10 to D100 in (mm/h); T in °C; PT and P24 in mm. STDDEV = Standard deviation; CV = (Coefficient of Variation), Cross-correlation coefficient between the maximum precipitation in twenty-four hours (P24), and the other series (CORR (P24)); Cross-correlation coefficient between total annual precipitation (PT) and the other series (CORR (PT)); temporal autocorrelation coefficient (CORR (T)); Cross-correlation coefficient between the maximum temperature (Tmax) and the other series (CORR (Tmax)); Cross-correlation coefficient between the mean temperature (Tmean), and other series (CORR (Tmean)); Cross-correlation coefficient between the minimum temperature (Tmin) and the other series (CORR (Tmin)).
Table
Table 2. Cohen scale [70].
Table 2. Cohen scale [70].
Correlation Coefficient RangeInterpretation
0–0.1Null correlation
0.1–0.3Weak correlation
0.3–0.5Moderate correlation
0.5–1Strong correlation
Table
Table 3. Results of homogeneity tests.
Table 3. Results of homogeneity tests.
Homogeneity Test
VariablePettitt SNHT Buishand Von Neumann
PTHHHH
P24HHHH
TmaxNHNHNHNH
TmeanNHNHNHNH
TminNHNHNHNH
D10HHHH
D20HHHH
D30HHHH
D40HHHH
D50HHHH
D60HHHH
D70HHHH
D80HHHH
D90HHHH
D100HHHH
H = Homogeneous, NH = No Homogeneous.
Table
Table 4. Test of stationarity and trend of the original series.
Table 4. Test of stationarity and trend of the original series.
StationarityTrend
VariableDickey–Fuller (Stationarity ADF)Phillips–Perron KPSS Mann–Kendall
PTSNSSNT
P24NSNSSNT
TmaxSNSNST
TmeanNSNSNST
TminNSNSNST
D10SNSSNT
D20SNSSNT
D30SNSSNT
D40SNSSNT
D50SNSSNT
D60SNSSNT
D70NSNSSNT
D80NSNSSNT
D90NSNSSNT
D100NSNSSNT
S = stationarity, T = Trend, NS = No stationarity, NT = No Trend.
Table
Table 5. Summary of the frequencies of greater significance in each series (% of periodogram), for the maximum intensities, total precipitation, and maximum precipitation in twenty-four hours (D10 to D100, PT and P24).
Table 5. Summary of the frequencies of greater significance in each series (% of periodogram), for the maximum intensities, total precipitation, and maximum precipitation in twenty-four hours (D10 to D100, PT and P24).
PeriodicityP24 (%)PTD100D90D80D70D60D50D40D30D20D10Average D
47.000.142.263.862.932.922.732.381.290.661.691.020.952.04
23.505.453.994.564.014.815.372.611.110.550.490.020.282.38
15.674.243.251.921.841.343.372.393.042.183.834.784.342.90
11.750.944.135.6812.1610.088.039.0210.9411.348.019.627.989.29
9.403.391.992.075.084.483.326.108.699.6315.0216.5911.018.20
7.833.9814.492.752.682.102.261.502.225.805.365.802.713.32
6.710.320.543.383.604.014.594.586.104.775.7010.5713.376.07
5.886.297.503.141.641.580.973.362.961.531.692.401.302.06
5.221.427.216.234.394.263.233.103.805.326.366.683.354.67
4.7012.863.623.225.005.074.106.797.348.3411.2911.4013.127.57
4.270.750.471.661.240.370.910.210.190.270.360.081.560.68
3.925.723.424.883.152.283.632.171.253.303.572.182.942.94
3.6220.6416.9112.889.4314.5213.6617.9816.1812.777.295.598.5011.88
3.364.621.205.689.198.529.365.345.191.772.012.574.895.45
3.132.637.813.935.117.4910.8510.117.487.024.171.780.005.79
2.945.3612.075.513.253.995.193.474.505.343.713.268.754.70
2.760.392.220.780.640.560.640.751.950.870.801.910.290.92
2.616.571.1619.1817.3314.4712.5214.1812.7913.4414.769.027.1313.48
2.476.550.943.363.682.953.411.620.891.851.631.111.192.17
2.350.351.492.050.960.300.490.060.020.190.351.673.320.94
2.243.810.850.111.262.171.241.921.251.450.270.031.461.12
2.141.180.721.000.310.500.000.130.150.210.921.211.090.55
2.042.371.762.191.121.230.120.220.671.390.720.710.480.89
Table
Table 6. Summary of the frequencies of greater significance in each series (% of the periodogram), for the maximum, average, and minimum temperatures of the original series.
Table 6. Summary of the frequencies of greater significance in each series (% of the periodogram), for the maximum, average, and minimum temperatures of the original series.
PeriodicityTmaxTmeanTminAverage T
47.0029.5034.648.3224.15
23.503.654.817.675.37
15.674.3612.7821.8513.00
11.755.449.883.676.33
9.408.891.7110.827.14
7.830.990.930.560.83
6.710.600.012.961.19
5.886.760.252.063.02
5.220.306.583.253.38
4.701.425.885.194.16
4.273.920.400.171.50
3.921.802.586.663.68
3.621.686.290.562.84
3.362.230.327.803.45
3.130.321.170.690.73
2.942.630.360.021.00
2.762.331.530.761.54
2.612.830.735.152.90
2.479.943.931.415.09
2.350.690.993.401.70
2.241.040.200.460.57
2.142.202.951.582.24
2.046.491.064.984.18
Table
Table 7. Test for stationarity and trend for corrected temperature series.
Table 7. Test for stationarity and trend for corrected temperature series.
StaconarityTrend
VariableDickey–Fuller (Stationarity ADF)Phillips–PerronKPSSMann–Kendall
Tmax-RSNSSNT
Tmean-RNSNSSNT
Tmin-RNSNSSNT
S = Stacionarity T = Trend
NS = No Stacionarity NT = No Trend
Table
Table 8. Significant periods for the temperature series corrected for homogeneity.
Table 8. Significant periods for the temperature series corrected for homogeneity.
PeriodicityTmax-RTmean-RTmin-RAverage T-R
47.007.120.830.652.87
23.506.691.513.573.93
15.671.5421.7325.6716.31
11.7512.426.602.697.24
9.405.302.557.755.20
7.830.570.940.640.72
6.710.751.015.672.48
5.886.320.151.672.71
5.220.338.693.554.19
4.700.689.454.714.95
4.273.851.390.772.00
3.921.035.698.084.93
3.622.068.161.964.06
3.365.660.787.394.61
3.130.722.130.751.20
2.941.510.540.110.72
2.761.435.231.202.62
2.615.962.086.894.98
2.4716.468.052.248.92
2.350.222.483.982.23
2.244.240.930.451.87
2.146.365.032.074.49
2.048.794.037.536.78
Table
Table 9. Results of the relative importance of the periodicity by groups of variables (maximum precipitation in 24 h, total precipitation, maximum sub-daily intensities, and maximum, mean, and minimum temperatures) and the general consolidated.
Table 9. Results of the relative importance of the periodicity by groups of variables (maximum precipitation in 24 h, total precipitation, maximum sub-daily intensities, and maximum, mean, and minimum temperatures) and the general consolidated.
PeriodicityP24 (%)PTAverage DAverage T-RConsolidated
47.000.142.262.042.871.83
23.505.453.992.383.933.94
15.674.243.252.9016.316.68
11.750.944.139.297.245.40
9.403.391.998.205.204.70
7.833.9814.493.320.725.63
6.710.320.546.072.482.35
5.886.297.502.062.714.64
5.221.427.214.674.194.37
4.7012.863.627.574.957.25
4.270.750.470.682.000.97
3.925.723.422.944.934.25
3.6220.6416.9111.884.0613.37
3.364.621.205.454.613.97
3.132.637.815.791.204.36
2.945.3612.074.700.725.71
2.760.392.220.922.621.54
2.616.571.1613.484.986.55
2.476.550.942.178.924.65
2.350.351.490.942.231.25
2.243.810.851.121.871.91
2.141.180.720.554.491.74
2.042.371.760.896.782.95
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Arrieta-Pastrana, A.; Saba, M.; Puello Alcázar, A. Analysis of Climate Variability and Climate Change in Sub-Daily Maximum Intensities: A Case Study in Cartagena, Colombia. Atmosphere 2023, 14, 146. https://doi.org/10.3390/atmos14010146

AMA Style

Arrieta-Pastrana A, Saba M, Puello Alcázar A. Analysis of Climate Variability and Climate Change in Sub-Daily Maximum Intensities: A Case Study in Cartagena, Colombia. Atmosphere. 2023; 14(1):146. https://doi.org/10.3390/atmos14010146

Chicago/Turabian Style

Arrieta-Pastrana, Alfonso, Manuel Saba, and Adriana Puello Alcázar. 2023. "Analysis of Climate Variability and Climate Change in Sub-Daily Maximum Intensities: A Case Study in Cartagena, Colombia" Atmosphere 14, no. 1: 146. https://doi.org/10.3390/atmos14010146

APA Style

Arrieta-Pastrana, A., Saba, M., & Puello Alcázar, A. (2023). Analysis of Climate Variability and Climate Change in Sub-Daily Maximum Intensities: A Case Study in Cartagena, Colombia. Atmosphere, 14(1), 146. https://doi.org/10.3390/atmos14010146

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop