A Rainfall Forecast Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm
Abstract
:1. Introduction
2. Data and Methods
2.1. Area of Experiment
2.2. Introduction to Data
2.3. Inversion Process of GNSS PWV
3. Construction of Short-Term Rainfall Early Warning Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm
- Construction of the linear rainfall early warning model based on GNSS tropospheric parameters. The construction of the traditional rainfall early warning model mainly includes the following three aspects:
- Determination of rainfall predictors, which are different from existing studies that only use the variation and rate of change of PWV or ZTD. This experiment selected five parameters as rainfall predictors, namely the PWV value, variation and rate of change of PWV, and variation and rate of change of ZTD.
- Determination of forecasting parameters thresholds: currently forecasting parameter thresholds are commonly determined using the empirical methods [7,21], but this method has shortcomings such as long determination time, poor universality, and low practicability. The percentile method, on the other hand, can determine the corresponding optimal parameter thresholds of the original dataset quickly by setting percentile points in the long time sequence [22]. Therefore, the percentile method was introduced to determine the optimal thresholds of PWV- and ZTD-related parameters.
- Construction of the rainfall early warning model on a shorter time scale: existing studies usually take a year, given the scale of the study, without giving any consideration to seasonal variations of tropospheric parameters and rainfall. However, these variations are among the important factors affecting the precision of the rainfall early warning model. Therefore, this study considered the seasonal characteristics of each parameter and constructed a rainfall early warning model on a seasonal scale. After preparing the above three steps, the least square fitting algorithm can be used to fit the primary irregular PWV and ZTD time series in the different seasons, and further calculate the PWV and ZTD variation, variation rate, and PWV value in each fitting window. The threshold corresponding to the five predicted parameters will be calculated according to the percentile method and follows the principle of the highest TDR and the lowest FFR. The construction of the linear rainfall early warning model, based on the GNSS tropospheric parameters, was completed using the aforementioned three steps.
- Construction of rainfall early warning model based on the BP-NN algorithm. The construction of the BP-NN based model mainly includes two parts:
- Construction of the BP-NN model. Firstly, the lead one hour PWV, T, P and rainfall data as the input information are input the BP-NN model; the corresponding output information is the next hour rainfall. When constructing the non-linear rainfall model using the BP-NN algorithm, the two key parameters are the learning rate and the number of nodes in the hidden layer. The determination of the optimal thresholds for each parameter is crucial to the precision of the model [33,34,35]. Based on the Kolmogrov theory and the theory from Reference [36], the optimal values for the learning rate and the number of nodes in the hidden layer can be calculated using the following formula:where and are the number of nodes in the hidden layer and input layer, respectively, and is the learning rate. After setting the BP-NN key parameters using the above formula, the BP-NN rainfall early warning model can be obtained by inputting data to the model. The Levenberg-Marquardt (L-M) algorithm, an improved weight correction method of BP-NN method, is selected to overcome the disadvantages of slow convergence speed, local minimum, and training paralysis of the traditional BP-NN [4].
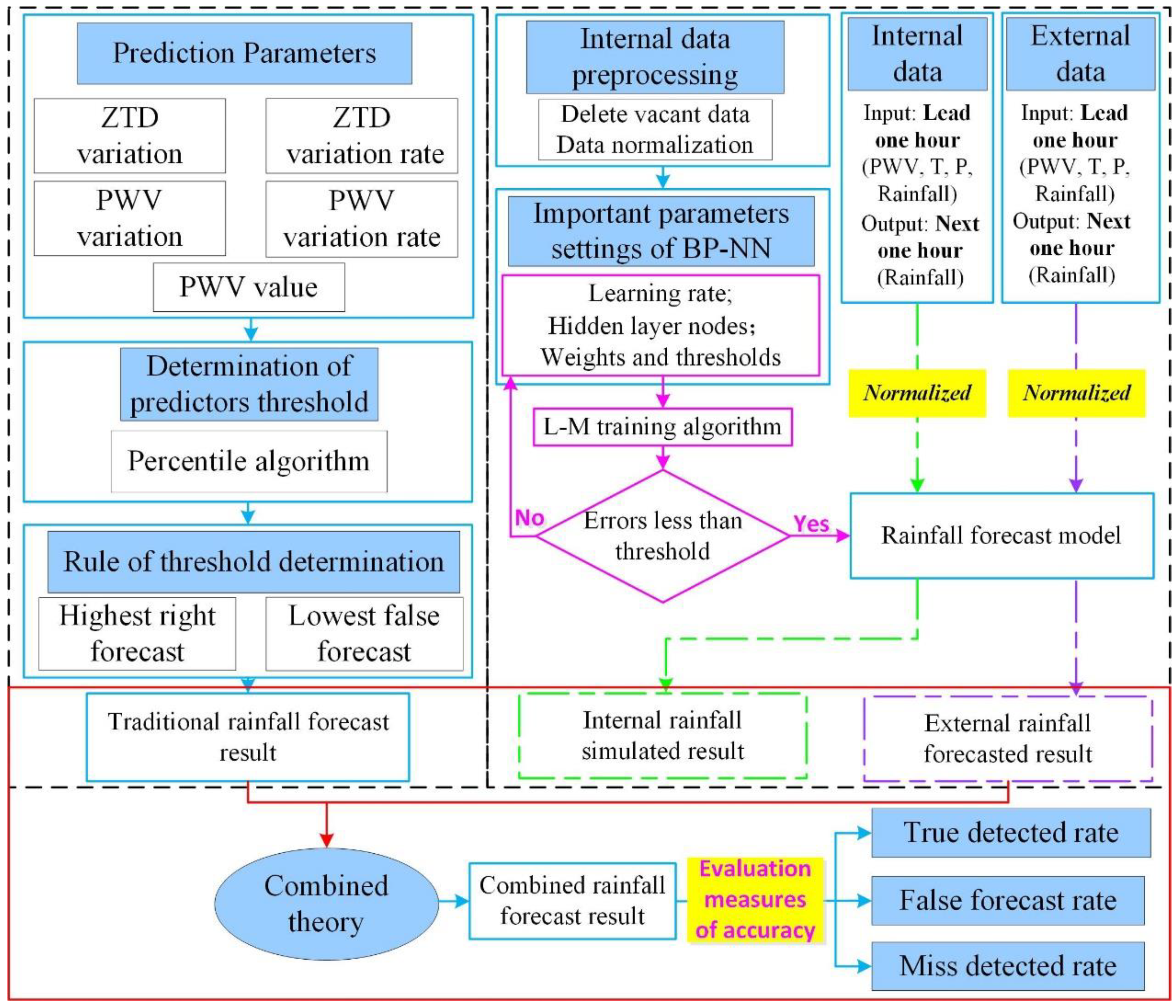
- Validation of the BP-NN model. The internal and external consistency validation experiment consists of comparing the original modeling rainfall data and the rainfall data outputted by the model to verify the results of the rainfall simulation. In addition, rainfall forecasts can be obtained by inputting the unused data into the constructed rainfall early warning model. Therefore, the PWV, T, P and rainfall data of ERA-5 in 2018 were used to train the BP-NN model and test the model accuracy, and the unknown data in 2019 for the trained model were used to validate the model ac-curacy. The internal and external experiments followed the flowchart in Figure 2.
- Construction of rainfall early warning model based on GNSS and the BP-NN algorithm:
4. Experimental Verification
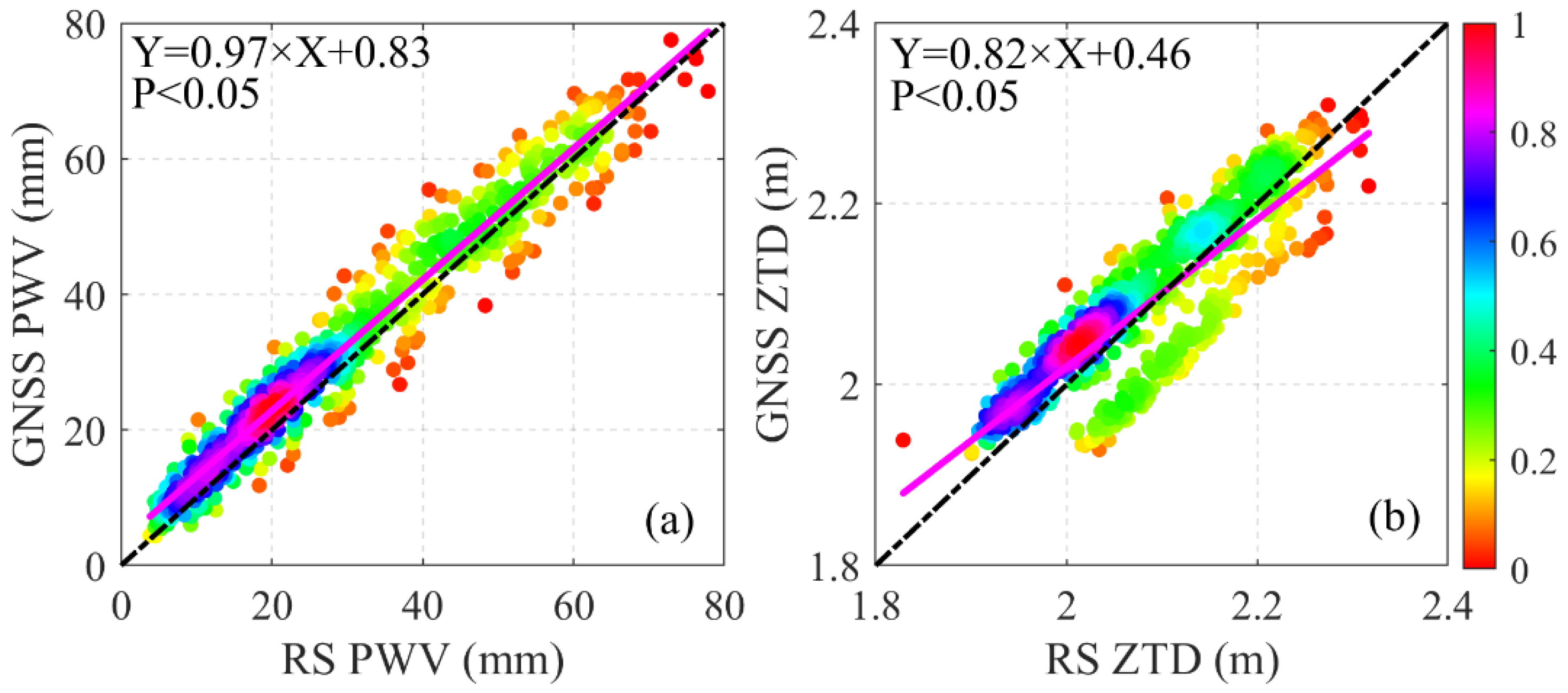
4.1. Precision Verification of GNSS ZTD and PWV
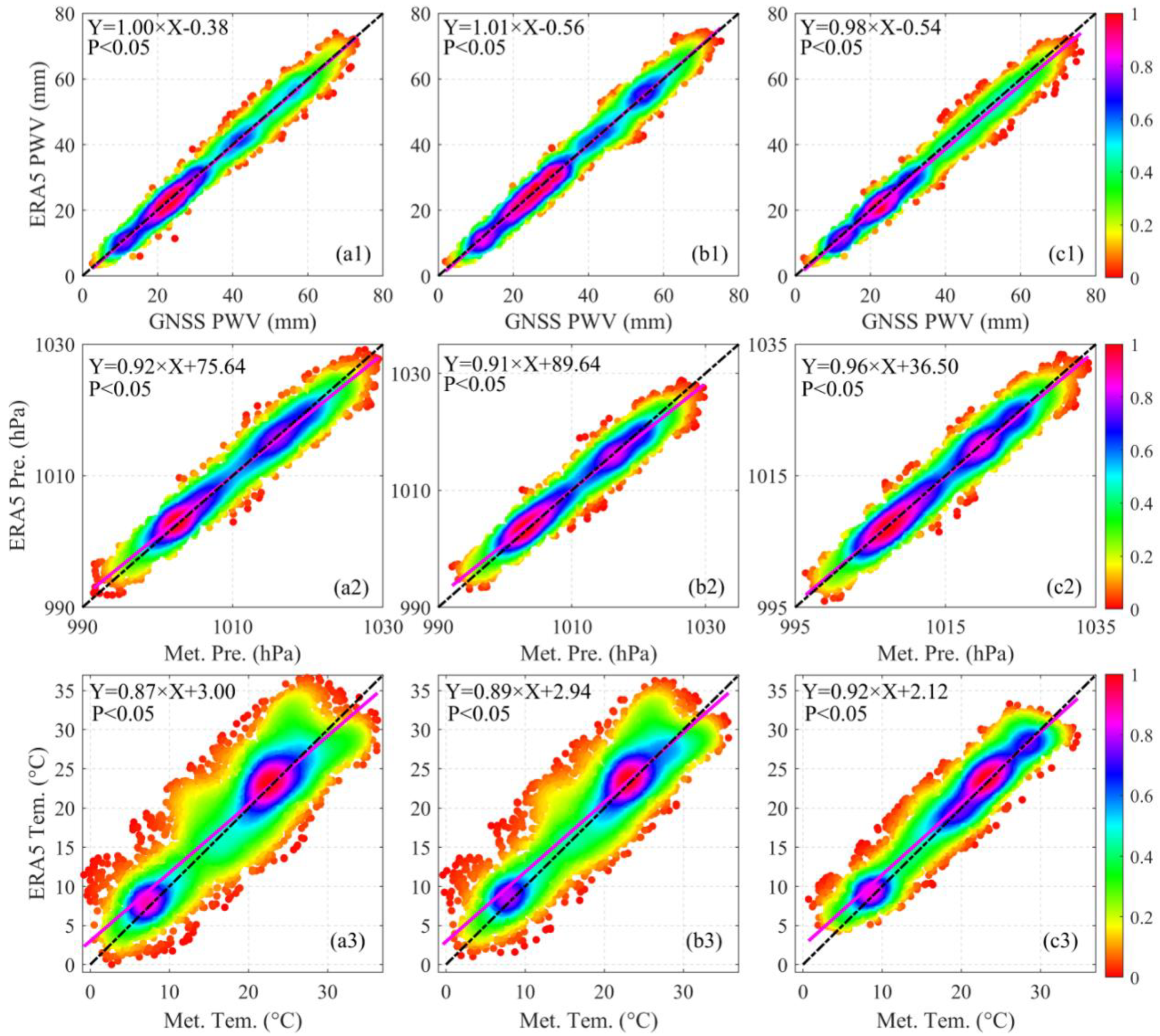
4.2. Precision Verification of ERA-5 Meteorological Data
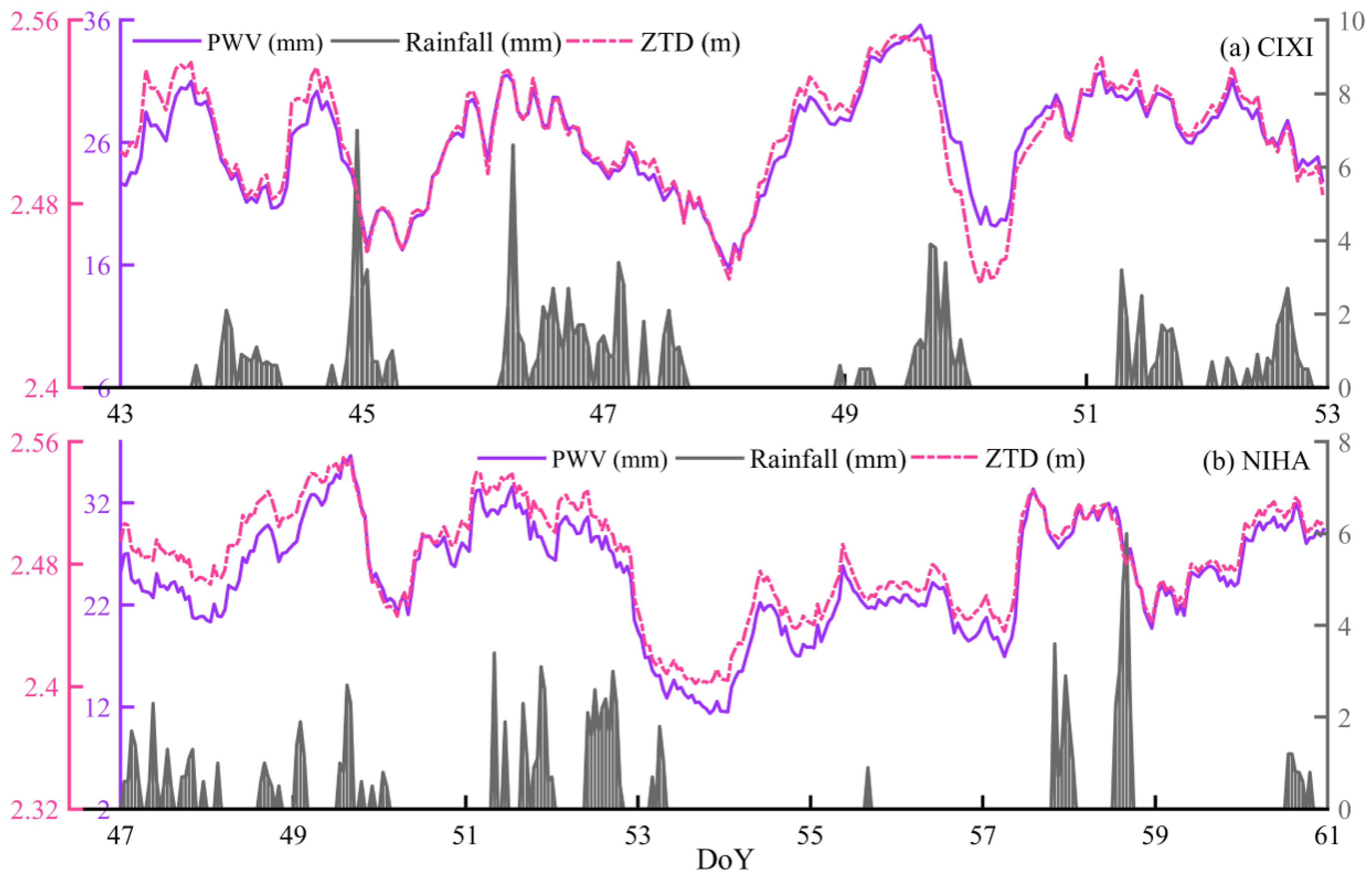
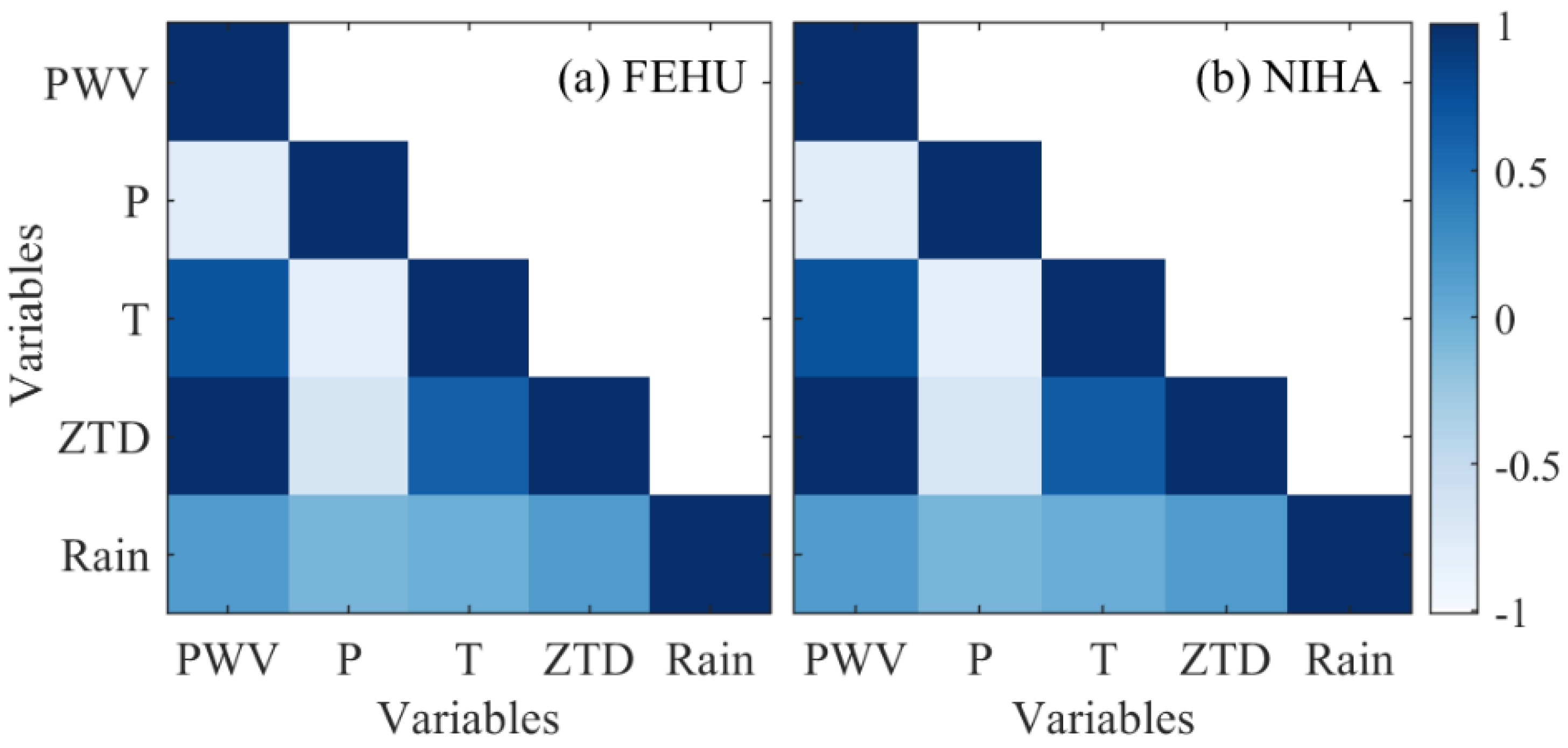
4.3. Correlation Analysis of Rainfall, PWV, and Meteorological Factors
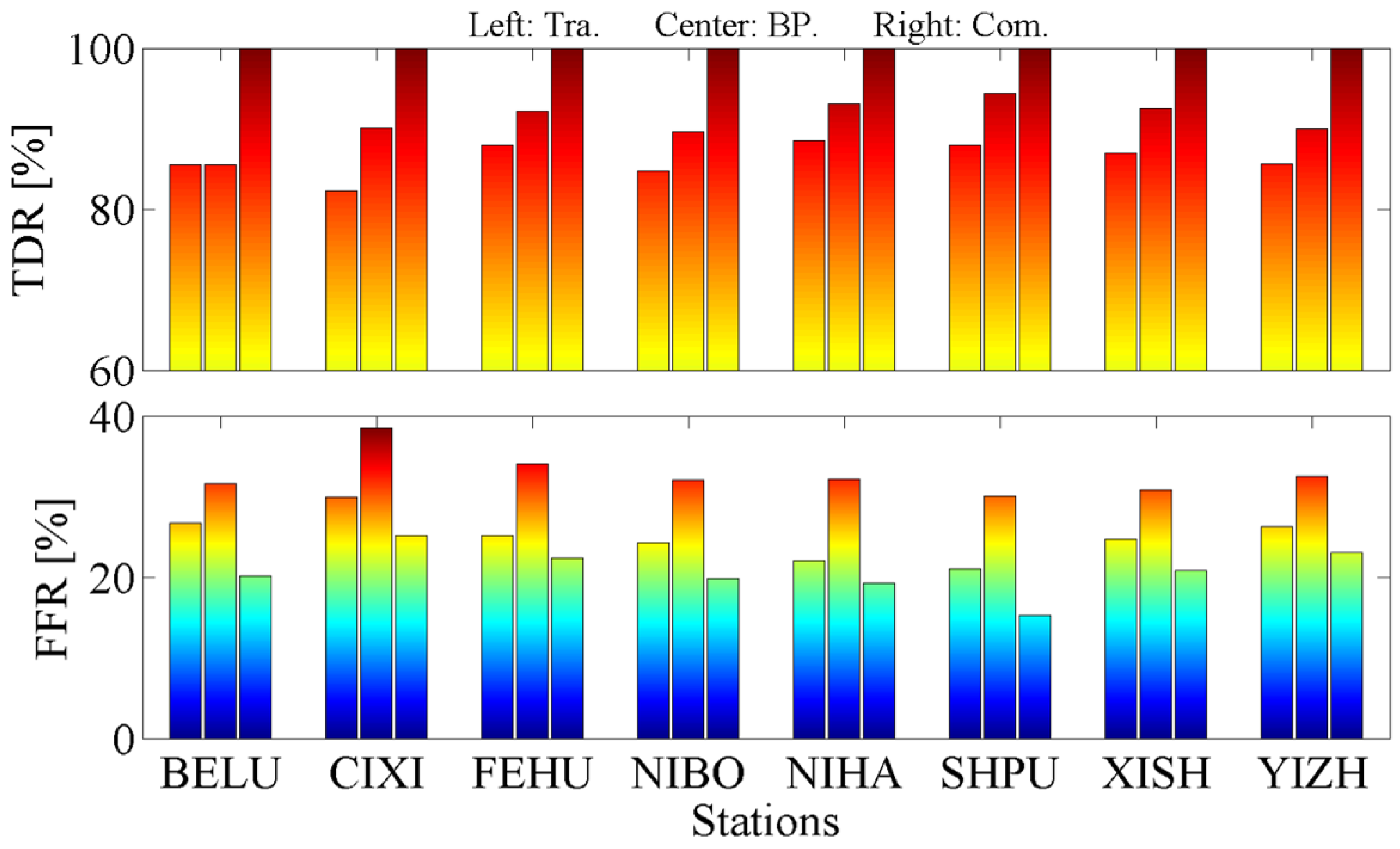
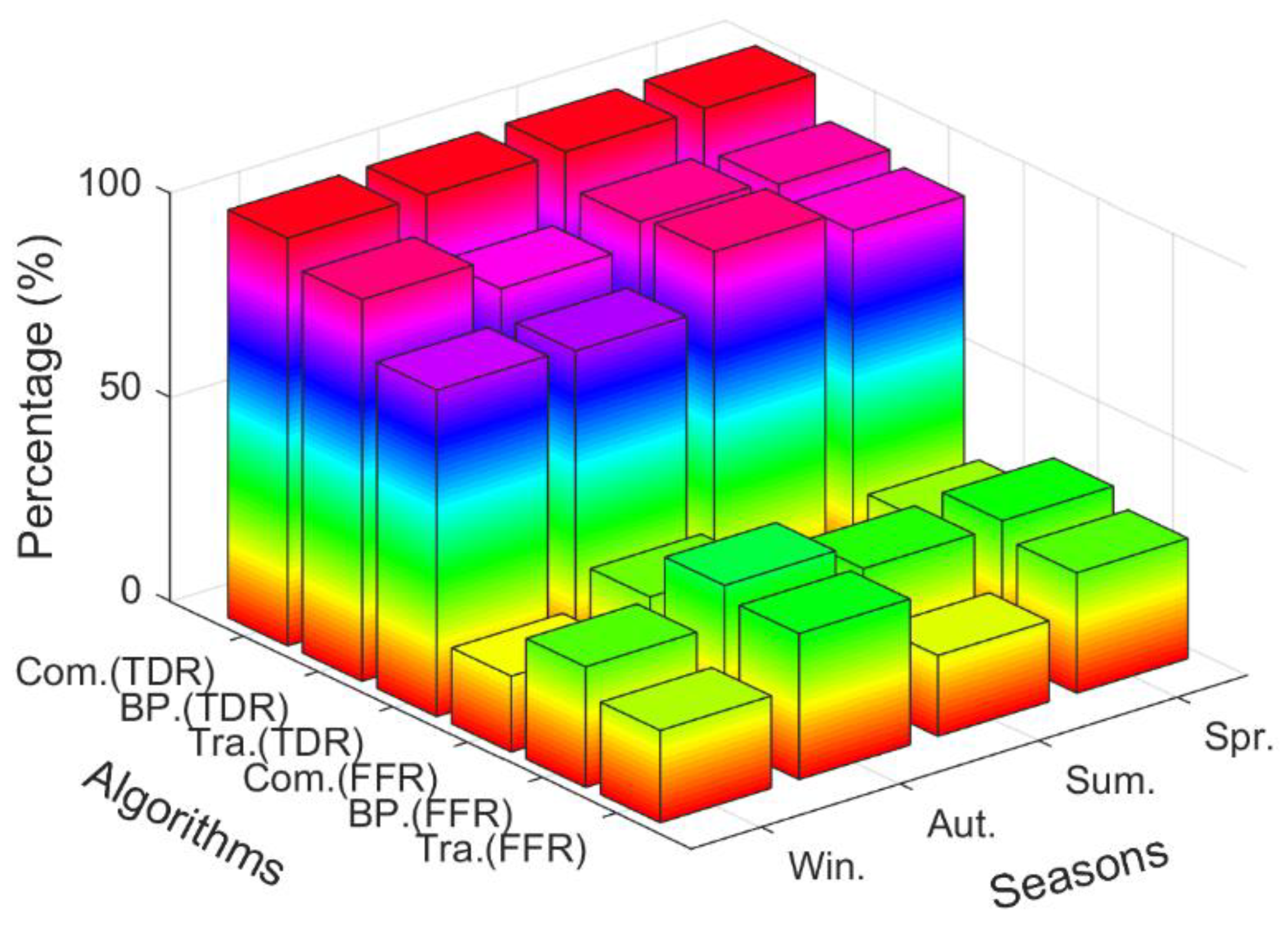
4.4. Verification of the Rainfall Early Warning Model Based on GNSS and the BP-NN Algorithm
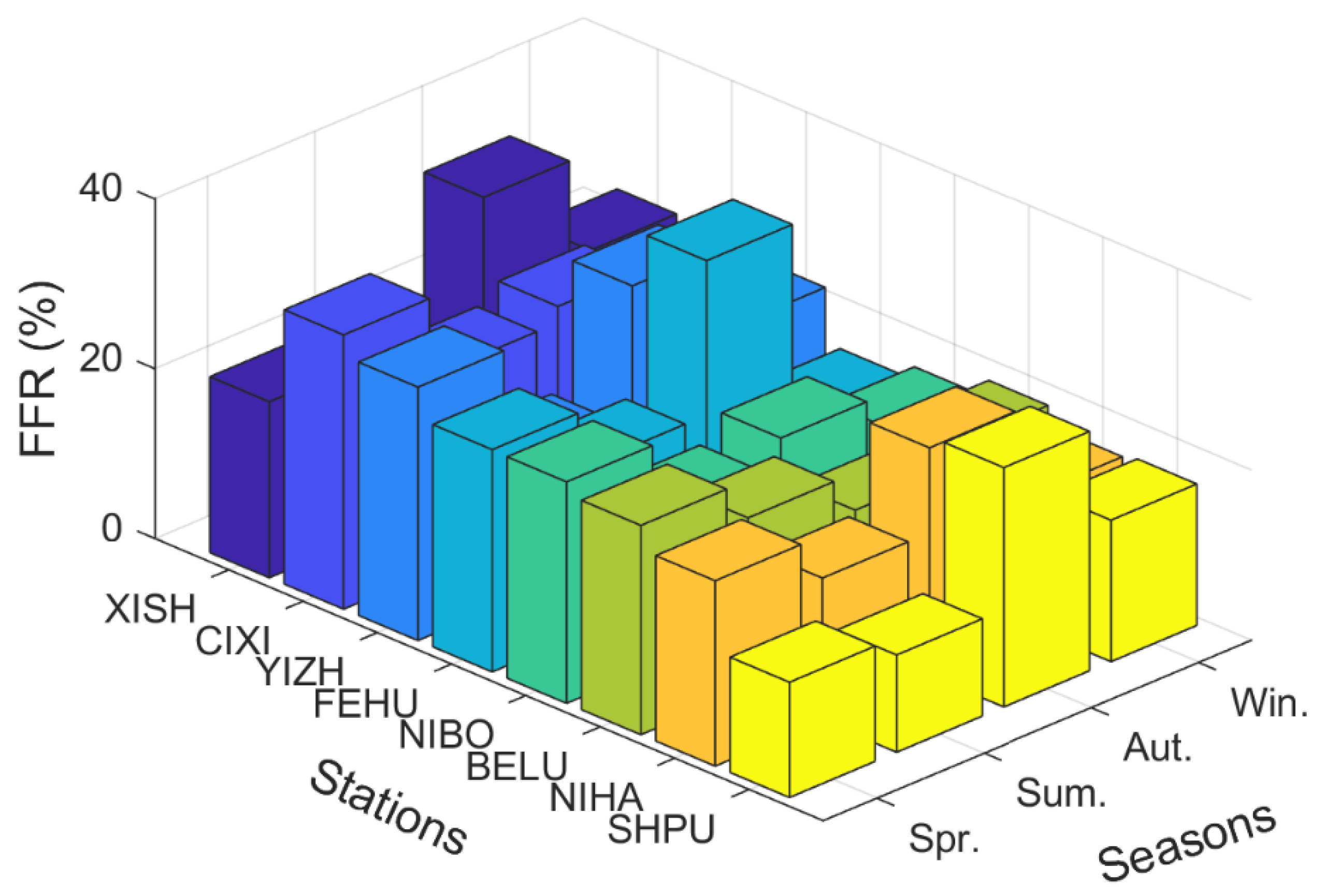
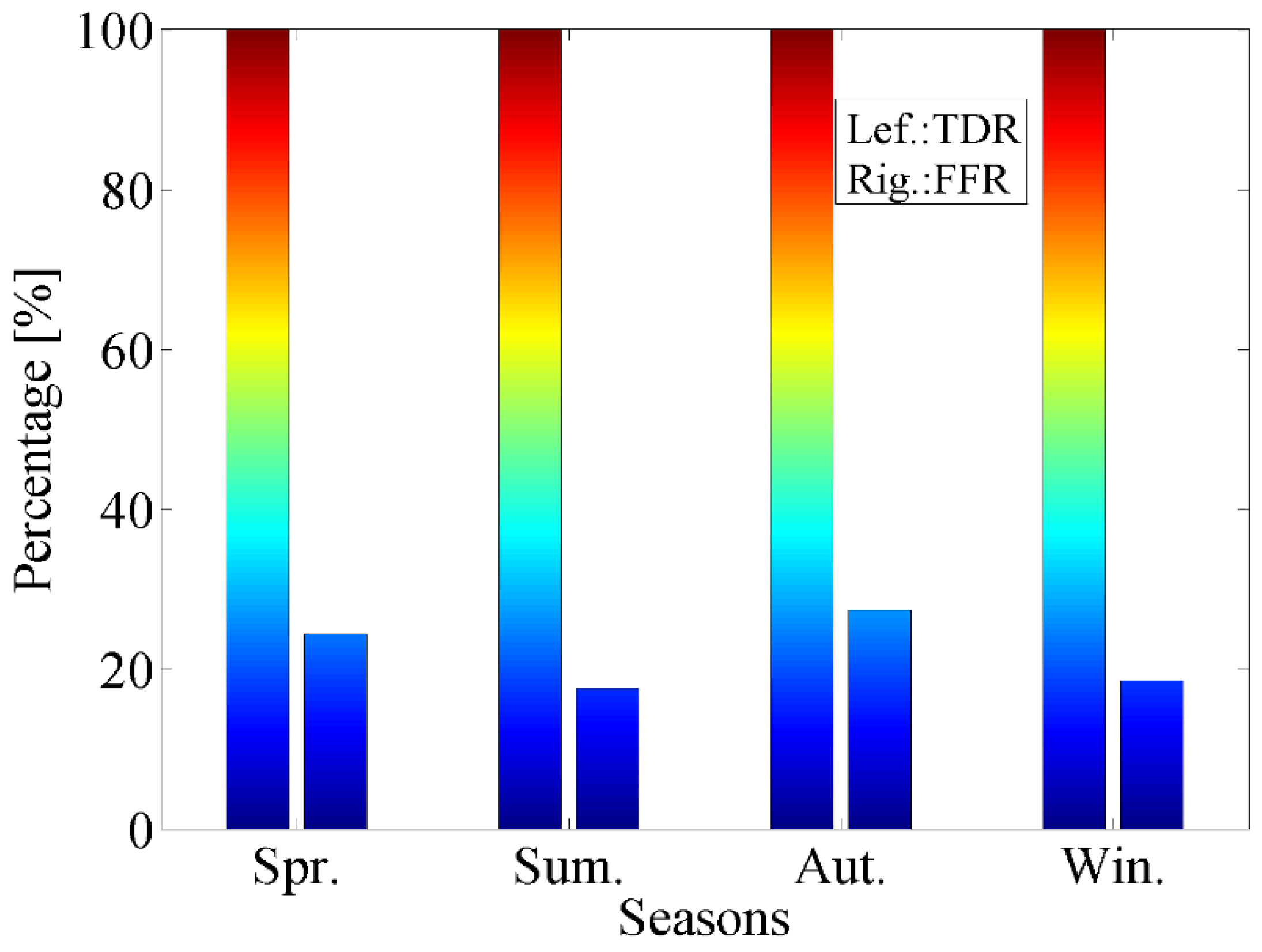
4.5. Precision Comparison of Rainfall Early Warning Models
4.6. Precision Comparison with Existing Rainfall Early Warning Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, S.G.; Park, J.-U.; Cho, J.-H.; Park, P. Seasonal variability of GPS-derived Zenith Tropospheric Delay (1994–2006) and climate implications. J. Geophys. Res. 2007, 112, D09110. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS-PWV based improved long-term rainfall prediction algorithm for tropical regions. Remote Sens. 2019, 11, 2643. [Google Scholar] [CrossRef] [Green Version]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J.T. GPS-derived PWV for rainfall nowcasting in tropical region. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Yao, W.; Ma, X.; Yao, Y.; Liu, L. Short-term rainfall forecast model based on the improved Bp–nn algorithm. Sci. Rep. 2019, 9, 19751. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, Z.; Shafri, H.Z.M.; Norman, M. A GNSS-based weather forecasting approach using Nonlinear Auto Regressive Approach with Exogenous Input (NARX). J. Atmos. Sol.-Terr. Phys. 2018, 178, 74–84. [Google Scholar] [CrossRef]
- Zhao, Q.; Du, Z.; Li, Z.; Yao, W.; Yao, Y. Two-step precipitable water vapor fusion method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5801510. [Google Scholar] [CrossRef]
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 12465. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, K.; Yang, L.; Wu, S.; Li, L. Evaluation and Calibration of MODIS Near-Infrared Precipitable Water Vapor over China Using GNSS Observations and ERA-5 Reanalysis Dataset. Remote Sens. 2021, 13, 2761. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Nilsson, T.; Heinkelmann, R.; Ge, M.; Glaser, S.; Schuh, H. Real-time retrieval of precipitable water vapor from GPS and BeiDou observations. J. Geod. 2015, 89, 843–856. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Ge, M.; Heinkelmann, R.; Nilsson, T.; Soja, B.; Dick, G.; Schuh, H. Estimation and evaluation of real-time precipitable water vapor from GLONASS and GPS. GPS Solut. 2016, 20, 703–713. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Ye, J.; Zhang, S.; Han, F. Precipitable Water Vapor Retrieval and Analysis by Multiple Data Sources: Ground-Based GNSS, Radio Occultation, Radiosonde, Microwave Satellite, and NWP Reanalysis Data. J. Sens. 2018, 2018, 3428303. [Google Scholar] [CrossRef]
- He, Q.; Shen, Z.; Wan, M.; Li, L. Precipitable Water Vapor Converted from GNSS-ZTD and ERA5 Datasets for the Monitoring of Tropical Cyclones. IEEE Access 2020, 8, 87275–87290. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A Drought Monitoring Method Based on Precipitable Water Vapor and Precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Yuan, H. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Wen, H.; Dang, Y.; Li, L. Short-Term PM2.5 concentration prediction by combining GNSS and meteorological factors. IEEE Access 2020, 8, 115202–115216. [Google Scholar] [CrossRef]
- Zhao, Q.; Su, J.; Li, Z.; Yao, P.; Yao, Y. Adaptive Aerosol Optical Depth Forecasting Model Using GNSS Observation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4105009. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, P.; Yao, W.; Yao, Y. Adaptive AOD forecast model based on GNSS—Derived PWV and meteorological parameters. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5800610. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yao, W.; Yao, Y. Hourly Rainfall Forecast Model Using Supervised Learning Algorithm. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4100509. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, X. An improved rainfall forecasting model based on GNSS observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol.-Terr. Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A data-driven approach for accurate rainfall prediction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9323–9331. [Google Scholar] [CrossRef] [Green Version]
- De Pondeca, M.S.; Zou, X. A case study of the variational assimilation of GPS zenith delay observations into a mesoscale model. J. Appl. Meteorol. 2001, 40, 1559–1576. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Li, Z. Real-time precise point positioning-based zenith tropospheric delay for precipitation forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef]
- Guan, Z.; Tian, Z.; Xu, Y.; Dai, H. Rainfall predict and comparing research based on Arcgis and BP neural network. In Proceedings of the 2016 3rd International Conference on Materials Engineering, Taiyuan, China, 27–28 February 2016. [Google Scholar] [CrossRef] [Green Version]
- Hashim, F.R.; Daud, N.N.; Ahmad, K.A.; Adnan, J.; Rizman, Z.I. Prediction of rainfall based on weather parameter using artificial neural network. J. Fundam. Appl. Sci. 2017, 9, 493–502. [Google Scholar] [CrossRef] [Green Version]
- Benevides, P.; Catalao, J.; Nico, G. Neural network approach to forecast hourly intense rainfall using GNSS precipitable water vapor and meteorological sensors. Remote Sens. 2019, 11, 966. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. J. Atmos. Sol.-Terr. Phys. 2019, 182, 85–92. [Google Scholar] [CrossRef]
- Li, P.W.; Wang, X.Y.; Chen, Y.Q. Use of GPS signal delay for real-time atmospheric water vapor estimation and rainfall nowcast in Hong Kong. In Proceedings of the First International Symposium on Cloud-Prone & Rainy Areas Remote Sensing, Hong Kong, China, 6–8 October 2005. [Google Scholar]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Dharia, A.; Adeli, H. Neural network model for rapid forecasting of freeway link travel time. Eng. Appl. Artif. Intell. 2003, 16, 607–613. [Google Scholar] [CrossRef]
- Li, F.; Liu, C. Application study of BP neural network on stock market prediction. In Proceedings of the 2009 Ninth International Conference on Hybrid Intelligent Systems IEEE, Shenyang, China, 12–14 August 2009; Volume 3, pp. 174–178. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Kung, S.Y.; Hwang, J.N. An Algebraic Projection Analysis for Optimal Hidden Units Size and Learning Rates in Back-Propagation Learning. In Proceedings of the IEEE 1988 International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; Volume 1, pp. 363–370. [Google Scholar]
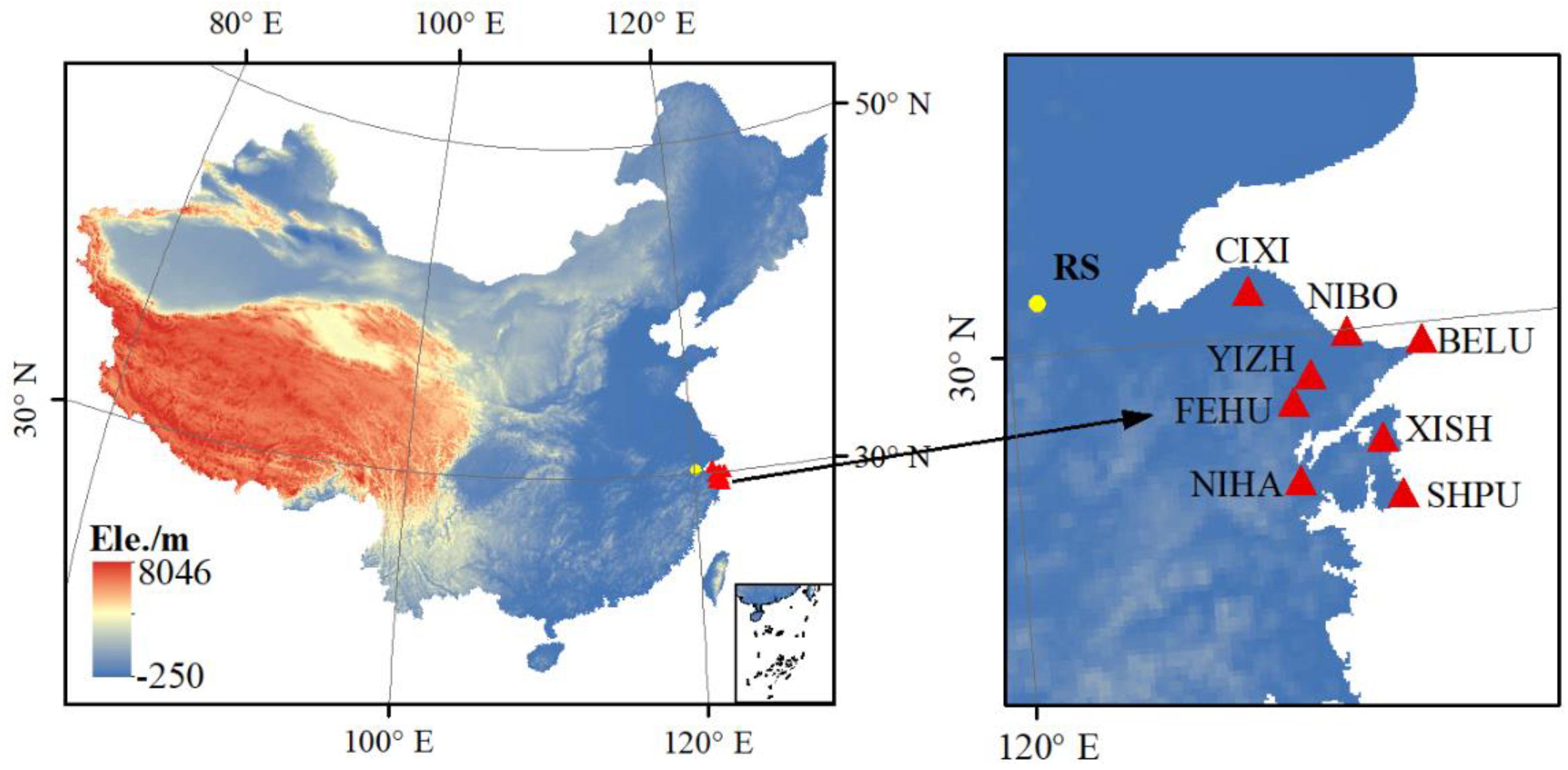
| GNSS Stations | Latitude (°) | Longitude (°) | Elevation (m) |
|---|---|---|---|
| SHPU | 29.22 | 121.96 | 23.60 |
| NIHA | 29.32 | 121.44 | 54.92 |
| XISH | 29.48 | 121.88 | 32.40 |
| FEHU | 29.67 | 121.44 | 66.95 |
| YIZH | 29.79 | 121.54 | 20.52 |
| NIBO | 29.97 | 121.75 | 38.63 |
| BELU | 29.90 | 122.13 | 67.11 |
| CIXI | 30.19 | 121.26 | 18.86 |
| RS | 30.23 | 120.17 | 43.00 |
| Data | Spatiotemporal Resolution | Period | Data Resource |
|---|---|---|---|
| ERA-5 PWV, P, T and Rainfall | hourly | 2018–2019 | https://www.ecmwf.int/en/forcasts/datasets/reanalysis-datasets/era5 (accessed on 3 August 2021) |
| GNSS PWV/ZTD | Station, hourly | 2019 | Ningbo City Survey and Mapping Bureau |
| RS PWV/ZTD | Station, 12 h | 2019 | ftp://ftp.ncdc.noaa.gov/pub/data/igra/ (accessed on 15 May 2021) |
| Comparison Types | RMS | MBE | R2 |
|---|---|---|---|
| GNSS PWV vs. ERA5 PWV | 2.66 mm | 0.94 mm | 0.99 |
| GNSS P vs. ERA5 P | 3.33 hPa | 2.69 hPa | 0.97 |
| GNSS T vs. ERA5 T | 3.36 °C | 0.54 °C | 0.92 |
| GNSS PWV vs. RS PWV | 3.27 mm | 2.71 mm | 0.98 |
| GNSS ZTD vs. RS ZTD | 49 mm | 6 mm | 0.98 |
| TDR | FFR | MDR | |
|---|---|---|---|
| Tra. | 86.18 | 25.04 | 13.82 |
| BP. | 90.91 | 32.72 | 9.09 |
| Com. | 100 | 20.75 | 0 |
| Indexes Studies | Period | Input Parameter | TDR | FFR | Algorithm |
|---|---|---|---|---|---|
| Benevides et al. [21] | 2015 | PWV variation and rate | 75% | 60–70% | least square (LS) |
| Yao et al. [7] | 2017 | PWV value, variation and rate | 80% | 66% | LS |
| Zhao et al. [23] | 2018 | PWV variation and rate | >80% | 60–70% | LS |
| Manandhar et al. [3] | 2018 | PWV variation rate and second derivative | 87% | 38% | LS |
| Manandhar et al. [29] | 2019 | PWV, solar radiation, DOY | 70% | 20% | SVM |
| Benevides et al. [28] | 2019 | PWV, P, T, and H | 64% | 22% | Artificial Neural Network (ANN) |
| Liu et al. [4] | 2019 | PWV, P, T, and H | >96% | 40% | BP-NN |
| Zhao et al. [22] | 2020b | PWV/ZTD value, variation and rate | 96% | 29% | LS |
| This study | — | PWV variation rate and second derivative, P and T | 100% | 20.75% | LS + BP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Zhang, W.; Li, C.; Hu, Z. A Rainfall Forecast Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm. Atmosphere 2022, 13, 1045. https://doi.org/10.3390/atmos13071045
Fu H, Zhang W, Li C, Hu Z. A Rainfall Forecast Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm. Atmosphere. 2022; 13(7):1045. https://doi.org/10.3390/atmos13071045
Chicago/Turabian StyleFu, Huanian, Wenfeng Zhang, Chunjin Li, and Zaihuang Hu. 2022. "A Rainfall Forecast Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm" Atmosphere 13, no. 7: 1045. https://doi.org/10.3390/atmos13071045
APA StyleFu, H., Zhang, W., Li, C., & Hu, Z. (2022). A Rainfall Forecast Model Based on GNSS Tropospheric Parameters and BP-NN Algorithm. Atmosphere, 13(7), 1045. https://doi.org/10.3390/atmos13071045





