Abstract
Global Navigation Satellite Systems (GNSS) tomography is a well-recognized modeling technique for reconstruction, which can be used to investigate the spatial structure of water vapor with a high spatiotemporal resolution. In this study, a refined near real-time tomographic model is developed based on multi-source data including GNSS observations, Global Forecast System (GFS) products and surface meteorological data. The refined tomographic model is studied using data from Hong Kong from 2 to 11 October 2021. The result is compared with the traditional model with physical constraints and is validated by the radiosonde data. It is shown that the root mean square error (RMSE) values of the proposed model and traditional model are 0.950 and 1.763 g/m3, respectively. The refined model can decrease the RMSE by about 46%, indicating a better performance than the traditional one. In addition, the accuracy of the refined tomographic model is assessed under both rainy and non-rainy conditions. The assessment shows that the RMSE in the rainy period is 0.817 g/m3, which outperforms the non-rainy period with the RMSE of 1.007 g/m3.
1. Introduction
Water vapor (WV) is considered as an essential climate variable [1], which not only closely links to climate change, but also greatly affects the formation and evolution of convective systems [2,3,4,5]. Although traditional techniques, e.g., radiosonde [6], water vapor radiometer [7] and meteorological satellites [8], can be used to obtain WV information at a high accuracy, they have apparent disadvantages, e.g., low spatiotemporal resolution, high cost and low all-weather availability [9,10,11]. Over the last three decades, the emerging Global Navigation Satellite Systems (GNSS) have been used to retrieve precipitable water vapor (PWV), which is the total atmospheric WV contained in a vertical column of a unit area with a high spatiotemporal resolution and high accuracy [12,13,14,15,16]. This is mainly due to the advantageous properties of GNSS atmospheric remote sensing, i.e., global coverage, long-term stability, cost effectiveness and all-weather capability [17,18,19,20]. It should be noted that although GNSS-derived PWV has been widely used in atmospheric research and the detection of various types of severe weather events [21,22,23,24,25,26,27], it cannot reflect the multi-dimensional distribution of PWV. To address this limitation, the GNSS tomographic technique was introduced during the past two decades [28] and has become an effective way for the determination of high-accuracy regional multi-dimensional atmospheric water vapor fields [29,30,31]. With the ongoing development of this technique, GNSS-derived atmospheric products have also extended their applications, especially in the meteorological community [32,33,34,35].
Flores et al. [28] first proposed the GNSS tomography technique and applied it to the estimation of four-dimensional (4D) tropospheric wet refractivity (WR) field. According to [28], the region of interest was discretized into several voxels, i.e., the so-called voxel-based model, and by using the slant wet delays (SWD) estimated from the GNSS signals as well as the intercepts in each voxel, the multi-dimensional WR field was obtained. However, during the tomographic periods, subject to the spatial distributions of the GNSS satellites and ground-based GNSS receivers in the local network, some designated voxels were crossed by inadequate satellite signals, which often result in poor geometry of observed signals and unsolvable problems [34], i.e., ill-posed tomographic equations. To resolve the ill-posed problem, a common way adopted in traditional methods is to use physical constraints, e.g., the horizontal constraints [36], vertical constraints [37] and adjacent constraints [38]. Another method is to retrieve SWDs over a rather long period of time to obtain more observations [2,39,40]. However, the use of a long period may miss a large number of short-term features contained in the time series of WV due to its rapidly changing characteristics in the spatiotemporal domains. The other method is to add a scale factor [41,42], a height factor [43], a WV unit index [44] and other metrics to those GNSS signals passing through the sides of the tomographic regions. It is noted that although the inclusion of empirical values of WV or radiosonde data over a long period is necessary for this method, these values may also depress the inversion accuracy due to the fact that the empirical values are unable to accurately reflect the actual situations of those epochs. With regard to the methodologies for a tomographic solution, various types of methods have been proposed and applied, e.g., the least-squares method [45,46], the singular value decomposition method [28], the Kalman filter [47,48] and the algebraic reconstruction technique (ART) [44,49,50]. These methods are practicable for the ill-posed tomographic equations but are unable to thoroughly eliminate the unsolvable problems due to the insufficient number of GNSS observations in the tomographic model.
Previous studies have demonstrated that extending the tomographic cycle or adding reconstructed observations can effectively increase the number of GNSS observations [39,40,41,42,43,44]. Nowadays, with the increasing number of multi-constellation GNSS satellites, including the Global Positioning System (GPS), Galileo, Global Navigation Satellite System (GLONASS) and BeiDou Navigation Satellite System (BDS), it is possible to observe more GNSS signals in each epoch. For example, Bender et al. [51] simulated the GNSS data, including the GPS, GLONASS, and Galileo for tomographic modeling, and results showed that using a combination of the above three systems, the number of SWDs greatly increased in comparison to the case that only a single system was used. Benevides et al. [52] also performed a similar study, in which a combination of GPS and Galileo data was adopted, and its results demonstrated that the anomalies in the distribution of PWV were recovered by using the combined data. It should be noted that the aforementioned studies were all conducted using the simulated dataset. Although the simulated data can be used to demonstrate the superiority of the data from multi-GNSS constellations to some extent, the adverse impacts caused by the observation errors obtained in the GNSS observations are not easy to analyze. To test the above-mentioned advantages of using a combination of multiple GNSS constellations, several researchers have also conducted similar experiments using GNSS observations [53,54,55]. For example, Zhao et al. [53] adopted observations from a combination of GPS, BDS and GLONASS, and results showed that the number of the satellite rays increased, but the accuracy of the constructed three-dimensional (3D) WV fields was not greatly improved. Dong et al. [54] also performed a similar experiment using data from GPS, BDS and GLONASS to construct a 3D WV field, and results demonstrated that the performance resulting from multi-GNSS data was similar to or slightly better than that obtained from a GPS-only system.
Using the above-mentioned approaches, the observing geometry can be optimized, but the inverse problem of the ill-posed matrix still cannot be effectively resolved, since some voxels are not crossed by a sufficient number of GNSS signals, especially at lower layers. To avoid the inversion problem with an ill-posed matrix, apart from the voxel-based tomography [56], other methods can be used to obtain the water-vapor density (WVD) in a tomographic region, e.g., the parameterization approach [57,58], function-based method [59,60] and high flexibility GNSS tomographic (HFGT) technique [61].
The physical constraints adopted in tomographic models assume that the distribution of WV follows specific rules, which may not necessarily agree well with real situations. To deal with this issue, multi-source data, e.g., data from different observing techniques and from different institutions, can be used as prior information in the tomographic system to improve the accuracy of the constructed WV field. Pany [62] introduced the inclusion of GNSS-derived slant total delays (STDs) and slant hydrostatic delays (SHDs) estimated from the European Centre for Medium-Range Weather Forecast (ECMWF) model to the tomographic observations to effectively compensate the loss brought by the signals observed at lower elevation angles. Zhang et al. [63] developed a GNSS-remote sensing (GNSS-RS) tomographic model, which fully exploited the observations from GNSS and RS measurements, and results showed that the use of the RS data led to a 28% decrease in the mean of the root mean square error (RMSE) of the WV profiles in comparison to the use of GNSS-only results. Heublein et al. [45] adopted the SWDs estimated from the combination of GNSS and the Interferometric Synthetic Aperture Radar (InSAR) technique due to the fact that the horizontal resolution of the InSAR-derived products is much higher than that of GNSS. Furthermore, apart from the InSAR-derived SWDs, surface meteorological data obtained from three meteorological stations were also included as the prior information of the tomographic model, which could improve the accuracy of the WVDs in the bottom layer [64]. However, the above studies were generally conducted using reanalysis data with latency; thus, these data cannot be applied to a real-time or near real-time (NRT) tomographic modeling process. For near real-time tomographic modeling, a number of experiments have been conducted using data from various sources. Zhang et al. [65] also developed an NRT tropospheric system using additional data obtained from the Global Forecast System (GFS) model provided by the National Centers for Environmental Prediction (NCEP), and a WR field with a horizontal resolution of 0.5° was reconstructed over a large area.
According to all the aforementioned analyses, the main problem in GNSS tomography is the ill-posed tomographic matrix. As a result, multi-source post-processing data from the RS, InSAR, radiosonde and reanalysis products can effectively improve the accuracy of the WV field, but it may not perform well in the NRT tomographic modeling. A tomographic model using GFS data was proposed for the NRT tropospheric tomography, which shows a better performance compared to the regular post-processing data [65]. In this study, a new NRT tomographic model with high spatial resolution was developed using multi-source data, including GNSS observations, GFS data and surface meteorological data, and the performance of the new model was also assessed.
The rest of this paper is organized as follows. Section 2 describes the multi-source data used in the tomographic system, including surface meteorological observations and those data obtained from the GFS. Section 3 presents data-processing strategies and principles for constructing a tomographic model. The development of the NRT tomographic model proposed in this study is described in Section 4. Conclusions are given in Section 5.
2. Data
In this study, GNSS observations, surface meteorological observations and the GFS model provided by the NCEP were used for the tomographic model and radiosonde data were used for validation of the tomographic result. In addition, precipitation data obtained from the operational rainfall stations in the Hong Kong region were also used for the model assessment.
GNSS observations obtained at 15 stations from the Hong Kong Continuously Operating Reference Stations (CORS) network (https://www.geodetic.gov.hk/sc/satref/rawstream.htm, accessed on 11 October 2021) over the 10-day period 2–11 October, i.e., day-of-year (DOY) 274–283, were processed to obtain tropospheric products for tomographic modeling. The CORS network receives signals from multi-GNSS, including the GPS, GLONASS, Galileo and BDS systems over the period studied. The real-time orbit and clock corrections (SSRA00WHU0) and other essential products from the IGS analysis data center at Wuhan University were used for real-time ZTD estimation. According to a comparison of ZTD estimations over the HKSC station with those derived from the radiosonde observations over its in situ radiosonde station, the RMSEs of the GPS-only and multi-GNSS ZTD estimations are 21.62 and 20.68 mm, respectively.
Since the meteorological observations are required for data processing and the constraints of a tomographic model, in this study, meteorological data including temperature, pressure and relative humidity with a 1 min sampling rate were collected from 11 surface weather stations in the Hong Kong, which can be downloaded from the Geodetic Survey Section of Survey and Mapping Office (https://www.geodetic.gov.hk/en/satref/satref.htm, accessed on 11 October 2021). Figure 1 shows the designated tomographic region and the geographical distribution of GNSS, weather and radiosonde stations used in this study.
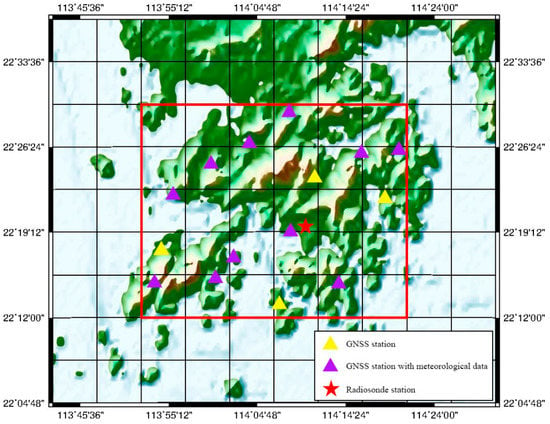
Figure 1.
Tomographic region (square with red outline) and geographical distribution of GNSS, meteorological and radiosonde stations. The yellow triangles denote the GNSS stations without meteorological sensors; the purple triangles denote the GNSS stations with meteorological observations; the red star denotes the radiosonde station.
GFS provides 384 h forecast grids with 0.25° × 0.25° spatial resolution and 6 h temporal resolution at 00, 06, 12 and 18 UTC per day. In this paper, the 6 h forecasts at 00 and 12 UTC (i.e., updated at 18 and 06 UTC) from DOY 273 to 282 in 2021 were used (https://nomads.ncep.noaa.gov/pub/data/nccf/com/gfs, accessed on 11 October 2021). The GFS-derived products including temperature, specific humidity and geopotential height on various pressure levels were used in the newly constructed tomographic system after the vertical and horizontal interpolations to the tomographic voxels.
To validate tomographic profiles, radiosonde observations from the only radiosonde station in the Hong Kong region (HKM00045004, as shown in Figure 1), which can be downloaded from the Integrated Global Radiosonde Archive (IGRA, https://www1.ncdc.noaa.gov/pub/data/igra, accessed on 11 October 2021), over the whole period studied were taken as the reference. The sounding balloons are launched only twice per day at 00 and 12 UTC. The WVD was calculated with the WV pressure and temperature observations at different pressure levels from the radiosonde station, which were used as the reference for the performance assessment of the tomographic results. For the further assessment of the tomographic model developed on rainy and non-rainy phases, the hourly precipitation records at King’s Park station in the time period from DOY 274 to 283 were used as the reference.
3. Methodology
3.1. Determination of Slant Water Vapor
Prior to the determination of slant water vapor (SWV), the zenith tropospheric delay (ZTD) needs to be obtained first. In this study, the ZTDs during the 10-day period studied were estimated from GNSS observations using the RTKLIB V2.4.3 with the precise point positioning (PPP) approach, as suggested by the previous study [66]. Apart from the ZTDs, the horizontal tropospheric gradients were also obtained from the data-processing software. More details regarding the data-processing strategy for the GNSS-derived ZTDs can be found in Table 1.

Table 1.
Strategy for data processing using the PPP approach.
The ZTD is divided into the zenith wet delay (ZWD) and zenith hydrostatic delay (ZHD), the ZWD can be obtained by subtracting the ZHD from ZTD. Generally, the ZHD can be determined using the Saastamoinen model, which is a function of the surface pressure over the GNSS station [67]. It is noted that four of the GNSS stations were not equipped with meteorological sensors. Thus, these stations lack meteorological data. In this case, the inverse distance weighting (IDW) interpolation method was used to calculate the temperature and pressure values for the stations using observations from other close stations [17]. To test the rationality of using this method, the accuracy of the obtained results was assessed during the same period, and results showed that the RMSEs of the temperature and pressure were 0.595 °C and 2.655 hPa, respectively. Hence, the IDW method was used in the following experiments to obtain interpolated meteorological values for those GNSS stations that are not equipped with meteorological sensors. Then, the SWD can be obtained by:
where and are the wet mapping function and gradient model, respectively, both of which can be obtained from the Global Mapping Function (GMF) [68]; and are the elevation and azimuth angle of the satellite, respectively; and are the horizontal gradients in the North–South and East–West directions, respectively; is the residual component. Then, the SWD is converted to SWV using the following formula:
where is the conversion factor, which can be obtained using the following weighted mean temperature (denoted by ) and physical constants:
where is the density of liquid water; is the specific gas constants for WV; and are two physical constants and their values were suggested by the authors of [69].
To calculate , in this study, the linear model developed by Chen [70] was used (see the formula below), which is more appropriate than the empirical model developed by Bevis et al. [69] in the Hong Kong region [22,23].
where is the surface temperature of the station.
3.2. Construction of a Tomographic Model
Although the number of observations is much larger than the parameters to be estimated in a tomographic model, the ill-posed problem still exists in the observation equations. To solve this problem, in this study, two schemes were adopted in the construction of a tomographic model: the first one applied background fields to the tomographic model; the other one used physical constraints in addition to the observation equations in conventional methods. To further improve the performance of the constructed model, the two schemes were also expanded into two cases: with and without the usage of surface meteorological data. As a result, four schemes were adopted for the construction of the tomographic models, as shown in Table 2.

Table 2.
Four schemes adopted for the construction of the tomographic models.
The SWV obtained in Section 3.1 can be expressed as the sum of the WVD (see the following formula) along the signal path, which is denoted by :
where , and are the indices of the voxel in the latitudinal, longitudinal and vertical directions, respectively; and are the crossing distance of the signal and the WVD, respectively, in the voxel . Then, the observation equation is:
where is the coefficient matrix formed by the ; and are the numbers of the SWVs and voxels in the tomographic area, respectively; is the WVD of each voxel.
It is widely accepted that, in the construction of tomographic models, physical constraints are required to solve the aforementioned ill-posed problem. In this study, physical constraints—including horizontal and vertical constraints—were adopted. For the horizontal constraint, the WVDs in a certain layer are assumed to be continuous and the WVD in the -th voxel is a weighted average of its neighbors [28]:
where is the number of voxels in the layer; is the weighted horizontal coefficient and is determined based on the Gaussian weighting function [71]. The horizontal constraint function can be expressed as:
where is the coefficient matrix of the horizontal constraint; and are the same as those described in Equation (6).
For the vertical constraint, generally, WV is assumed to decrease exponentially in accordance with its vertical distribution [72]. Hence, the WVDs of tomographic voxels in adjacent vertical layers are also assumed to follow this variation trend
where the and are the WVD of the adjacent voxels in the -th and -th layer, respectively; and are the height of the -th and -th layer, respectively; is the scale height of the atmospheric water vapor. The following formula presents the function of the vertical constraint:
where is the coefficient matrix of the vertical constraint.
The observation equations (Equation (6)) and the two constraint functions (Equations (8) and (9)) together form the tomographic model of Scheme 1 (See Table 2). The WVDs at the bottom layer in the area of interest are estimated using the constraint of the surface meteorological values:
where is the coefficient matrix. is the WVDs of voxels at the bottom layer and can be computed using:
where represents the temperature (in kelvins), and is the WV pressure:
where represents the relative humidity.
The model constructed from Scheme 2 is to add Equation (11) to that of Scheme 1:
As mentioned above, the latitude, longitude, temperature, relative humidity and geopotential height at all pressure levels were obtained from GFS data. The temperature, specific humidity and pressure values at the midpoints of each voxel were interpolated using data at the nearest eight surrounding grid points of the GFS model in the horizontal and vertical domains. The WVDs of the background field were computed using Equation (12) and the WV pressure was calculated using
where and represent the specific humidity and pressure, respectively.
Scheme 3 is to apply the initial values of the WVDs in each voxel, which are computed using products from the GFS. Additionally, the tomographic model constructed from Scheme 4 is to add Equation (11) to that of Scheme 3:
Compared to Scheme 1 and Scheme 2, the main difference between Scheme 3 and Scheme 4 is the use of the WVDs calculated from GFS as the a priori values for the tomographic model.
3.3. Algebraic Reconstruction Technique
In this study, the algebraic reconstruction technique (ART) method was selected to solve the above tomographic model. To avoid the ill-posed problem in the inversion of a large sparse matrix, the simultaneous iterative reconstruction technique (SIRT) was used in the ART method. The SIRT method (see the formula below) can simultaneously calculate the biases of all reconstructed and observed SWVs and correct the WVDs in line with the crossing distances.
where represents the WVD in the -th voxel during the -th iteration step; is the crossing distance of signal in the -th voxel; is the relaxation parameter, which affects the extent of correction and regulates the convergence in each iteration step. The relaxation parameter is determined by the spectral radius of the iteration matrix in Equation (6) [73]. The normalized cumulative periodogram (NCP) rule was selected as the stopping condition in each iteration, according to [74]. The principle underlying the NCP rule is to terminate the iteration when the residuals resemble white noise. The residual is the difference value of the SWV observation and reconstructed SWV:
where is the vector of the residuals from all SWVs during the -th iteration. The rest of the notations in Equation (14) are the same as those in Equation (6).
4. Experiments and Results
4.1. Model Configuration
Based on the distribution of the GNSS stations in the Hong Kong region, the area of interest for the construction of the tomographic models for this study was determined as follows. The latitudes were from 22.20° N to 22.50° N with a 0.06° resolution (about 7 km) and the longitudes were from 113.87° E to 114.35° E with a 0.08° resolution (about 9 km). The height of the top layer of the tomography was 10,656 m and the vertical resolution varied from 400 m at the bottom layer to 1298 m at the top layer, which yielded 420 voxels for the tomographic models. In addition, the model’s update cycle was determined as 30 min.
4.2. Assessment of Results
Radiosonde data, which are from sounding balloons only launched at 00 and 12 UTC per day, were used as the reference for the validation of the tomographic models. Due to the limited number of the reference data over the 10-day period studied, only 20 sets of tomographic results could be assessed. The RMSEs resulting from each of the four schemes (as shown in Table 2) for each layer, i.e., the standard pressure levels determined by the World Meteorology Organization [75] and the whole profile, i.e., from the surface to the designated top boundary of the model, were calculated using the following formula:
where and represent the WVD values resulting from the constructed tomographic model and the reference values obtained from the radiosonde profile at the -th level, respectively; is the number of all vertical levels.
In this study, several types of tomographic results obtained from different combinations of inputs including SWDs/SWVs from multi-GNSS (i.e., GPS, GLONASS, Galileo and BDS2) or GPS-only observation, surface meteorological observations and GFS background information were obtained and their performances were evaluated using the radiosonde data. In addition, the accuracy of the tomographic models during rainy and non-rainy periods was also analyzed.
4.2.1. Comparison of Model Performances Obtained Using Multi-GNSS and GPS Observations
The first experiment mainly focused on the comparison of the performances of the models constructed from the four schemes mentioned in Section 3 and using multi-GNSS and GPS-only data. The differences made by the use of background and surface meteorological data were also assessed. Table 3 lists the mean of the 20 sets of RMSEs for the whole profiles at 20 epochs during the period of DOY 274–283.

Table 3.
Comparison of the mean values of 20 sets of RMSEs (g/m3) for the whole profile resulting from multi-GNSS and GPS-only data, and four schemes over the period studied.
It can be seen from Table 3 that the results obtained from GPS-only data were slightly better than those obtained from multi-GNSS data, regardless of other information, e.g., surface meteorological data or background information being used. This phenomenon was also revealed in the previous study [53], which shows that the maximal and minimal of the RMS from multi-GNSS were both larger than that of GPS only. Compared to Scheme 1 and Scheme 2, the tomographic results from Scheme 3 and Scheme 4 show a notable improvement in terms of the RMS, which means the inclusion of background fields in the model has a large positive impact on the tomographic performance.
To further investigate the impact of the surface meteorological data on the tomographic results at each height level, a comprehensive experiment was conducted, and the results will be shown in the next section. It should be noted that, because the accuracy of the tomographic results from GPS-only is better than multi-GNSS data, the SWDs derived from GPS only were used in the following studies.
4.2.2. Performances of Model Resulting from Using Surface Meteorological Data
The RMSEs listed in the above section were obtained for the whole profile; thus, it cannot reflect the tomographic accuracy at different heights. To investigate the performance of the four schemes at different height levels, Table 4 lists the RMSE of WVD at each standard pressure level starting from 925 hPa to 250 hPa.

Table 4.
RMSE (g/m3) of WVD recovered from each scheme at each standard pressure level.
As indicated in Table 4, the use of the surface meteorological data has little effect on the accuracy of the tomographic results from Schemes 3 and 4 which use the GFS model as prior information. The reason is likely that the background information was estimated by the well-developed GFS meteorological parameters, hence the surface meteorological data showed insignificant influence. However, for Schemes 1 and 2 (without the use of the GFS model as prior information), the accuracy of WVDs at the layers greater than 500 hPa (i.e., below about 5500 m in the study area) was significantly improved in the case that the surface meteorological data were used, especially for the bottom layer, i.e., 925 hPa. This improvement is probably due to the large density of the WV at the bottom layer, where there are large variations in WVD. In general, the use of the surface meteorological data leads to improved tomographic accuracy, to a certain extent, especially from the schemes that use physical constraints.
Figure 2 shows the mean RMSEs and relative errors (RE) of the WVDs at different layers of the constructed tomographic model at 00 and 12 UTC resulting from the four schemes. The RMSE of Scheme 1 under 3 km is above 2 g/m3, while the RMSE of Scheme 2 at the bottom layer significantly decreases after the surface meteorological data are used. The RMSE of Schemes 3 and 4 at all layers are less than 2 g/m3, which demonstrates the superiority of the use of background information or surface meteorological data in the tomographic process. Compared with Scheme 3, the RMSE of Scheme 4 is about 10.7% smaller, which demonstrates the effectiveness of the inclusion of as much meteorological data as possible. Unlike the RMSE, the RE increases with height because the WV amount decreases rapidly with the height.
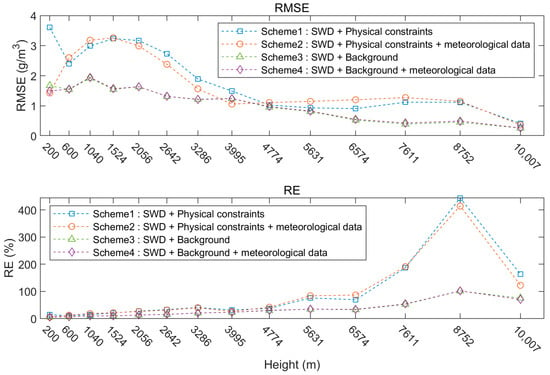
Figure 2.
Statistical results of RMSE and RE during the experiment period at each tomographic layer and four tomographic schemes.
4.2.3. Comparison of Model Performances over Rainy and Non-Rainy Periods
To investigate whether the tomographic results are affected by weather conditions, the accuracy of tomographic results for days with and without rainfall was investigated. Hourly precipitation data from the King’s Park station in Hong Kong were collected and used to classify rainy and non-rainy periods. As indicated by relevant precipitation records, Hong Kong experienced rainfall over the period 8–10 October 2021. Detailed hourly cumulative rainfall data collected in the 3-day period are presented in Figure 3.
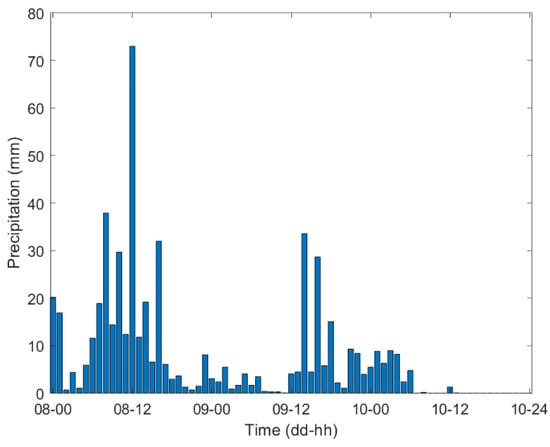
Figure 3.
Hourly cumulative rainfall data in the 3-day period 8–10 October 2021 from the King’s Park station.
To investigate the performance of the refined tomographic method, i.e., Scheme 4, under different weather conditions, the RMSE during rainy and non-rainy days was compared. As mentioned above, during the whole 10-day period studied, rainfall events occurred during the 3 days of 8–10 October, while the other 7-day time-period was regarded as a non-rainy phase. Figure 4 depicts the RMSEs of the tomographic profiles at each day over the whole period studied, and Table 5 lists the mean RMSEs in the rainy and non-rainy periods, respectively.
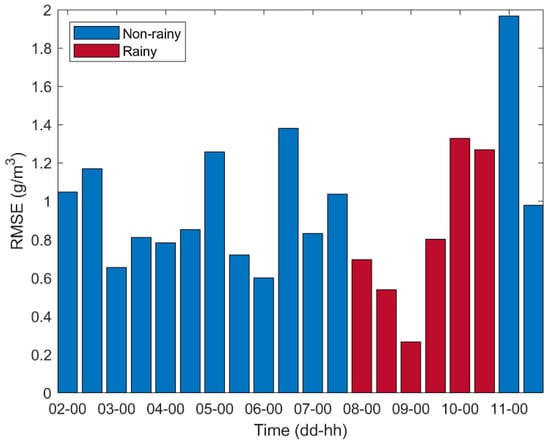
Figure 4.
RMSEs of Scheme 4 during rainy and non-rainy phases in the period studied.

Table 5.
RMSEs (g/m3) of Scheme 4 during rainy and non-rainy periods.
It can be seen from Table 5 that the accuracy of the tomographic results from Scheme 4 during rainy days is better than that during the non-rainy days. Figure 5 depicts the WVD and their RMSEs obtained from our refined tomographic model during the rainy and non-rainy days, respectively. It is notable that the WVD shows a smooth decreasing trend from a high layer to a low layer during both phases. At each layer, the WVD during the rainy phase is higher than that during the non-rainy phase. In addition, the RMSEs at different layers show large fluctuations, the value during the non-rainy phase is higher than that during the rainy phase at most of the layers, and the maximum RMSE is found at the layer of 1040 m.
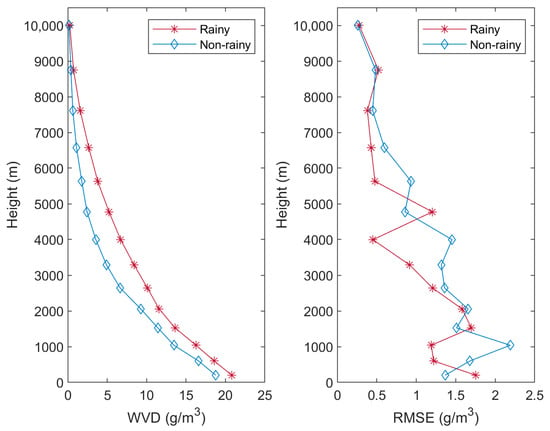
Figure 5.
WVD (left) and RMSE (right) of the refined tomographic model during rainy (red) and non-rainy (blue) phases.
Figure 6 shows the variation of WVD and RE with height at four epochs during the above two phases. Compared to the rainy days, the REs of the tomographic results show large fluctuations at different height levels during the non-rainy days. This is mainly due to the fact that the WVD has a more complicated vertical structure during the non-rainy days than the rainy days. This also demonstrates that the vertical distribution of water vapor has an obvious influence on the accuracy of the tomographic technique. This phenomenon has also been proven in the previous study [76]. According to [76], large RMSEs of the tomographic model are found below 4 km and sharp growth in the RE values is also demonstrated in the height range. However, the accuracy of the refined tomographic model, i.e., Scheme 4, presents little fluctuations at all height levels, as shown in Figure 2.
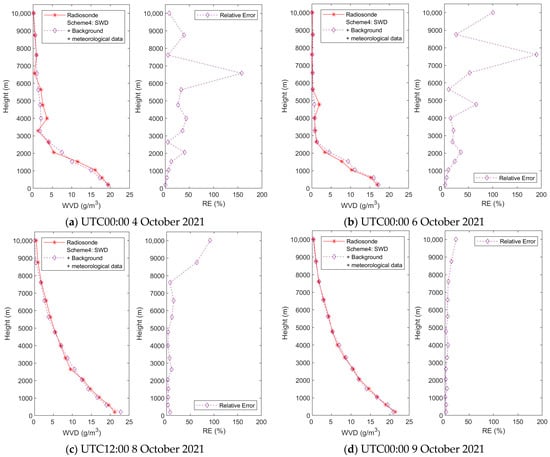
Figure 6.
Vertical profiles of WVD and RE with respect to radiosonde results during non-rainy phases at two epochs (a,b) and rainy phases at other two epochs (c,d).
5. Conclusions
GNSS tomography is a prospective method for the reconstruction of 4D water vapor at high spatiotemporal resolutions, but the use of GNSS-only data is often insufficient for the observing geometry of the tomography. For this issue, we proposed using multi-source data for a high spatiotemporal resolution of NRT tomographic modeling, and an NRT processing system that is applicable for the use of multi-source data was selected and tested. Ten-day data from the CORS network in Hong Kong, China, were selected as the test data and the radiosonde data from IGRA were used as the reference for the accuracy assessment of the tomographic model constructed.
Statistical results demonstrate that the refined model developed using multi-source data improved the accuracy of the tomographic model compared to the traditional constraint model. In NRT tomography, the RMSE resulting from the use of the constraint model was about 1.797 g/m3, which improved by 9% after surface meteorological data were included in the tomographic system. However, the RMSE of the tomographic model that uses GFS and surface meteorological data was insignificantly different compared to the case using GFS only. Compared to the traditional constraint model, the RMSE resulting from the adoption of GFS data reduced by about 46%. Moreover, statistical results during both rainy and non-rainy periods indicated that the refined tomographic model lead to good accuracy in both cases, and the accuracy of the refined model during rainy periods was better than non-rainy periods. This suggests that a tomographic model constructed based on multi-source data can be applied to the monitoring of precipitation.
The poor observing geometry of GNSS signals is the main problem in GNSS tomography, which can be effectively handled by the inclusion of the physical constraints or multi-source data. In contrast with the physical constraints, the inclusion of the multi-source data can provide accurate initial values and optimize the estimates for WVD at the tomographic voxels; therefore, it is more suitable for the tomography, especially for the real-time and near real-time applications. The future work aims at the investigation of the influence of the meteorological forecasts from different models on the tomography and the performance evaluation using the data covering a longer period.
Author Contributions
Conceptualization, L.T. and K.Z.; methodology, L.T., K.Z., S.W. and X.W.; validation, L.T., K.Z. and X.W.; formal analysis, L.T. and H.L.; resources, X.W., H.L., N.D., J.S. and D.Z.; writing—original draft preparation, L.T.; writing—review and editing, K.Z., S.W., X.W., H.L. and D.Z.; supervision, K.Z. and X.W.; funding acquisition, K.Z., X.W., L.T. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant Nos. 41874040, 41730109 and 41904033), the Programme of Introducing Talents of Discipline to Universities (grant No. B20046), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (grant No. SJCX21_1016), and the Open Research Fund of Jiangsu Key Laboratory of Resources and Environmental Information Engineering, CUMT (grant No. JS202110).
Data Availability Statement
IGRA radiosonde dataset can be obtained from ftp://ftp.ncdc.noaa.gov/pub/data/igra (accessed on 11 October 2021). GNSS observations in Hong Kong are obtained from https://www.geodetic.gov.hk/sc/satref/rawstream.htm (accessed on 11 October 2021). GFS forecasts are obtained from https://nomads.ncep.noaa.gov/pub/data/nccf/com/gfs (accessed on 11 October 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Global Climate Observing System (GCOS). Surface Vapour. 2021. Available online: https://gcos.wmo.int/en/essential-climate-variables/surface-vapour (accessed on 1 March 2022).
- Seko, H.; Shimada, S.; Nakamura, H.; Kato, T. Three-dimensional distribution of water vapor estimated from tropospheric delay of GPS data in a mesoscale precipitation system of the Baiu front. Earth Planets Space 2000, 52, 927–933. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Amer. Meteor. Soc. 2010, 84, 1205–1217. [Google Scholar] [CrossRef]
- De Haan, S.; van der Marel, H.; Barlag, S. Comparison of GPS slant delay measurements to a numerical model: Case study of a cold front passage. Phys. Chem. Earth 2002, 27, 317–322. [Google Scholar] [CrossRef]
- Ha, S.; Kuo, Y.; Guo, Y.; Rocken, C.; Van Hove, T. Comparison of GPS slant wet delay measurements with model simulations during the passage of a squall line. Geophys. Res. Lett. 2002, 29, 21–28. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, B.; Chan, S.; Cao, Y.; Gao, Y.; Zhang, K. Analysis and modeling of water vapor and temperature changes in Hong Kong using 40-year radiosonde data: 1973–2012. Int. J. Clim. 2014, 35, 462–474. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Wickert, J.; Schmidt, T.; Song, S.; Gendt, G.; Ge, M.; Rothacher, M. Validation of GPS slant delays using water vapour radiometers and weather models. Meteorol. Z. 2008, 17, 807–812. [Google Scholar] [CrossRef]
- Wei, J.; Li, Y.; Zhang, K.; Liao, M.; Bai, W.; Liu, C.; Liu, Y.; Wang, X. An evaluation of Fengyun-3C radio occultation atmospheric profiles over 2015–2018. Remote Sens. 2020, 12, 2116. [Google Scholar] [CrossRef]
- Elliott, W.P. On detecting long-term changes in atmospheric moisture. Clim. Change 1995, 31, 349–367. [Google Scholar] [CrossRef]
- Babatunde, A.; Schulz, J. Analysis of water vapor over Nigeria using radiosonde and satellite data. J. Appl. Meteorol. Clim. 2012, 51, 1855–1866. [Google Scholar]
- Ho, S.; Zhou, X.; Kuo, Y.; Hunt, D.; Wang, J. Global evaluation of radiosonde water vapor systematic biases using GPS radio occultation from COSMIC and ECMWF analysis. Remote Sens. 2010, 2, 1320. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Yoshihara, T.; Tsuda, T.; Hirahara, K. High time resolution measurements of precipitable water vapor from propagation delay of GPS satellite signals. Earth Planets Space 2000, 52, 479–493. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Qiu, C.; Wang, X.; Li, Z.; Zhang, S.; Li, H.; Zhang, J.; Yuan, H. The Performance of different mapping functions and gradient models in the determination of slant tropospheric delay. Remote Sens. 2020, 12, 130. [Google Scholar] [CrossRef]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers. GPS Solut. 2020, 24, 12. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; He, C.; Cheng, Y.; Li, X. Determination of zenith hydrostatic delay and its impact on GNSS-derived integrated water vapor. Atmos. Meas. Technol. 2017, 10, 2807–2820. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, K.; Shen, Z.; Wu, S.; Liu, Z.; Tong, L. A new adaptive absolute method for homogenizing GNSS-derived precipitable water vapor time series. Earth Space Sci. 2021, 8, e2021EA001716. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, K.; Wu, S.; Wan, M.; Lin, Y. Retrieving precipitable water vapor from real-time precise point positioning using VMF1/VMF3 forecasting products. Remote Sens. 2021, 13, 3245. [Google Scholar] [CrossRef]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Marshall, J.L. Ground-based GNSS ZTD/IWV estimation system for numerical weather prediction in challenging weather conditions. Atmos. Res. 2014, 138, 414–426. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Hong, Y. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Qiu, C.; Zhang, S.; Zhang, J.; Xie, M.; Li, L. Development of an improved model for prediction of short-term heavy precipitation based on GNSS-derived PWV. Remote Sens. 2020, 12, 4101. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Choy, S.; Wu, S.; Jiang, C.; Zhang, J.; Qiu, C.; Li, L.; Zhang, K. A new cumulative anomaly-based model for the detection of heavy precipitation using GNSS-derived tropospheric products. IEEE Trans. Geosci. Remote Sens. 2021, 60. [Google Scholar] [CrossRef]
- Foster, J.; Bevis, M.; Schroeder, T.; Merrifield, M.; Yoaz, B.-S. El Niño, water vapor, and the Global Positioning System. Geophys. Res. Lett. 2000, 27, 2697–2700. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Liu, Y.; Yao, W.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Yu, W.; Chen, B.; Dai, W.; Luo, X. Real-time precise point positioning using tomographic wet refractivity fields. Remote Sens. 2018, 10, 928. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the Signature of Severe Weather Events in Australia Using GPS Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1839–1847. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys.-Germany 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Bouin, M.N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS water vapour tomography: Preliminary results from the ESCOMPTE field experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef]
- Gradinarsky, L.P. Ground-Based GPS Tomography of water vapor: Analysis of simulated and real data. J. Meteorol. Soc. Jpn. 2004, 82, 551–560. [Google Scholar] [CrossRef][Green Version]
- Troller, M.; Geiger, A.; Brockmann, E.; Kahle, H.G. Determination of the spatial and temporal variation of tropospheric water vapour using CGPS networks. Geophys. J. Int. 2006, 167, 509–520. [Google Scholar] [CrossRef]
- Manning, T.; Zhang, K.; Rohm, W.; Choy, S.; Hurter, F. Detecting severe weather using GPS tomography: An Australian case study. J. Glob. Position. Syst. 2012, 11, 58–70. [Google Scholar] [CrossRef]
- Natalia, H.; Estera, T.; Gregor, M.; Witold, R.; Robert, W. Assimilation of GNSS tomography products into the weather research and forecasting model using radio occultation data assimilation operator. Atmos. Meas. Technol. 2019, 12, 4829–4848. [Google Scholar]
- Nan, D.; Zhang, S.; Wu, S.; Wang, X.; Zhang, K. A new approach for GNSS tomography from a few GNSS stations. Atmos. Meas. Technol. 2018, 11, 3511–3522. [Google Scholar]
- Zhu, M.; Liu, Z.; Hu, W. Observing water vapor variability during three super typhoon events in Hong Kong based on GPS water vapor tomographic modeling technique. J. Geophys. Res.-Atmos. 2020, 125, e2019JD032318. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. Local tomography troposphere model over mountains area. Atmos. Res. 2009, 93, 777–783. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys.-Germany 2014, 32, 911–923. [Google Scholar] [CrossRef]
- Flores, A.; Gradinarsky, L.P.; Elósegui, P.; Elgered, G.; Davis, J.L.; Rius, A. Sensing atmospheric structure: Tropospheric tomographic results of the small-scale GPS campaign at the Onsala Space Observatory. Earth Planets Space 2000, 52, 941–945. [Google Scholar] [CrossRef]
- Rohm, W. The ground GNSS tomography–unconstrained approach. Adv. Space Res. 2013, 51, 501–513. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Wickert, J.; Ramatschi, M.; Ge, M.; Gendt, G.; Rothacher, M.; Raabe, A.; Tetzlaff, G. Estimates of the information provided by GPS slant data observed in Germany regarding tomographic applications. J. Geophys. Res. 2009, 114, D06303. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Q. Maximally using GPS observation for water vapor tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7185–7196. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y. An improved troposphere tomographic approach considering the signals coming from the side face of the tomographic area. Ann. Geophys.-Germany 2017, 35, 87–95. [Google Scholar] [CrossRef]
- Zhang, W.; Ding, N.; Zhang, S. Inclusion of Side Signals on GNSS Water Vapor Tomography with a New Height Factor Model; Springer: Singapore, 2020; pp. 76–88. [Google Scholar]
- Yao, Y.B.; Zhao, Q.Z.; Zhang, B. A method to improve the utilization of GNSS observation for water vapor tomography. Ann. Geophys.-Germany 2016, 34, 143–152. [Google Scholar] [CrossRef]
- Heublein, M.; Bradley, P.E.; Hinz, S. Observing geometry effects on a global navigation satellite system (GNSS)-based water vapor tomography solved by least squares and by compressive sensing. Ann. Geophys.-Germany 2020, 38, 179–189. [Google Scholar] [CrossRef]
- Hirahara, K. Local GPS tropospheric tomography. Earth Planets Space 2000, 52, 935–939. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Li, P. Wet refractivity tomography with an improved kalman-filter method. Adv. Atmos. Sci. 2006, 23, 693–699. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust kalman filtering for GNSS troposphere tomography. Atmos. Meas. Technol. 2014, 7, 1475–1486. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.; Raabe, A.; Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef]
- Xiaoying, W.; Ziqiang, D.; Enhong, Z.; Fuyang, K.E.; Yunchang, C.; Lianchun, S. Tropospheric wet refractivity tomography using multiplicative algebraic reconstruction technique. Adv. Space Res. 2014, 53, 156–162. [Google Scholar] [CrossRef]
- Bender, M.; Stosius, R.; Zus, F.; Dick, G.; Wickert, J.; Raabe, A. GNSS water vapour tomography–Expected improvements by combining GPS, GLONASS and Galileo observations. Adv. Space Res. 2011, 47, 886–897. [Google Scholar] [CrossRef]
- Benevides, P.; Nico, G.; Catalao, J.; Miranda, P.M.A. Analysis of Galileo and GPS integration for GNSS tomography. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1936. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Cao, X.; Yao, W. Accuracy and reliability of tropospheric wet refractivity tomography with GPS, BDS, and GLONASS observations. Adv. Space Res. 2019, 63, 2836–2847. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S. 3-D water vapor tomography in Wuhan from GPS, BDS and GLONASS observations. Remote Sens. 2018, 10, 62. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Cao, X.; Zhou, F.; Xia, P. An optimal tropospheric tomography method based on the multi-GNSS observations. Remote Sens. 2018, 10, 234. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Ma, H. An optimal troposphere tomography technique using the WRF model outputs and topography of the area. Remote Sens. 2020, 12, 1442. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.; Wu, S.; Wang, X.; Zhang, K. Adaptive node parameterization for dynamic determination of boundaries and nodes of GNSS tomographic models. J. Geophys. Res.-Atmos. 2018, 123, 1990–2003. [Google Scholar] [CrossRef]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS water vapor tomography: New parameterized approaches. J. Geodesy. 2011, 85, 539–550. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S. B-spline function-based approach for GPS tropospheric tomography. GPS Solut. 2020, 24, 193–205. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Schuh, H. The effect of function-based and voxel-based tropospheric tomography techniques on the GNSS positioning accuracy. J. Geodesy. 2021, 95, 78–94. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, N.; Zhang, Y.; Li, L.; Yang, X.; Zhao, Q. A new approach of the global navigation satellite system tomography for any size of GNSS network. Remote Sens. 2020, 12, 617. [Google Scholar] [CrossRef]
- Pany, T. Measuring and modeling the slant wet delay with GPS and the ECMWF NWP model. Phys. Chem. Earth. 2002, 27, 347–354. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Holden, L.; Wang, X.; Zheng, N. GNSS-RS tomography: Retrieval of tropospheric water vapor fields using GNSS and RS observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Marion, H.; Fadwa, A.; Bastian, E.; Xiao, X.Z.; Stefan, H. Compressive sensing reconstruction of 3D wet refractivity based on GNSS and InSAR observations. J. Geodesy. 2019, 93, 197–217. [Google Scholar]
- Zhang, W.; Lou, Y.; Liu, W.; Huang, J.; Wang, Z.; Zhou, Y.; Zhang, H. Rapid troposphere tomography using adaptive simultaneous iterative reconstruction technique. J. Geodesy. 2020, 94, 76. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Li, Z.; Li, S.; Cong, Q.; Li, H.; Shaotian, Z.; Li, L. The impact of different ocean tide loading models on GNSS estimated zenith tropospheric delay using precise point positioning technique. Remote Sens. 2020, 12, 3080. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Chen, Y. Inversing the content of vapor in atmosphere by GPS observations. Mod. Surv. Mapp. 2005, 28, 3–6. [Google Scholar]
- Song, S.; Zhu, W.; Ding, J.; Peng, J. 3D water-vapor tomography with Shanghai GPS network to improve forecasted moisture field. Chin. Sci. Bull. 2006, 51, 607–614. [Google Scholar] [CrossRef]
- Elósegui, P.; Ruis, A.; Davis, J.L.; Ruffini, G.; Keihm, S.J.; Bürki, B.; Kruse, L.P. An experiment for estimation of the spatial and temporal variations of water vapor using GPS data. Phys. Chem. Earth 1998, 23, 125–130. [Google Scholar] [CrossRef]
- He, L.; Liu, L.; Su, X.; Xu, C.; Duan, P. Algebraic reconstruction algorithm of vapor tomography. Acta Geod. Geophys. 2015, 1, 32–38. [Google Scholar]
- Hansen, P.C.; Jørgensen, J.S. AIR Tools II: Algebraic iterative reconstruction methods, improved implementation. Numer. Algorithms 2017, 79, 107–137. [Google Scholar] [CrossRef]
- Wright, J.M., Jr. Federal Meteorological Handbook No. 3: Rawinsonde and Pibal Obervations; Office of the Federal Coordinator for Meteorology; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1997. [Google Scholar]
- Yao, Y.; Liu, C.; Xu, C.; Tan, Y.; Fang, M. A refined tomographic window for GNSS-derived water vapor tomography. Remote Sens. 2020, 12, 2999. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).