Exploring Non-Linear Dependencies in Atmospheric Data with Mutual Information
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mutual Information
2.2. Removing Known Effects
2.3. Estimation Methods
- Ordinary and conditional MI,
- Simple programming interface for common analysis tasks,
- Analysis of time dependency with lags,
- Support for both discrete and continuous variables,
- Optional integration with pandas data frames,
- Efficient, parallel, and tested algorithms.
3. Examples
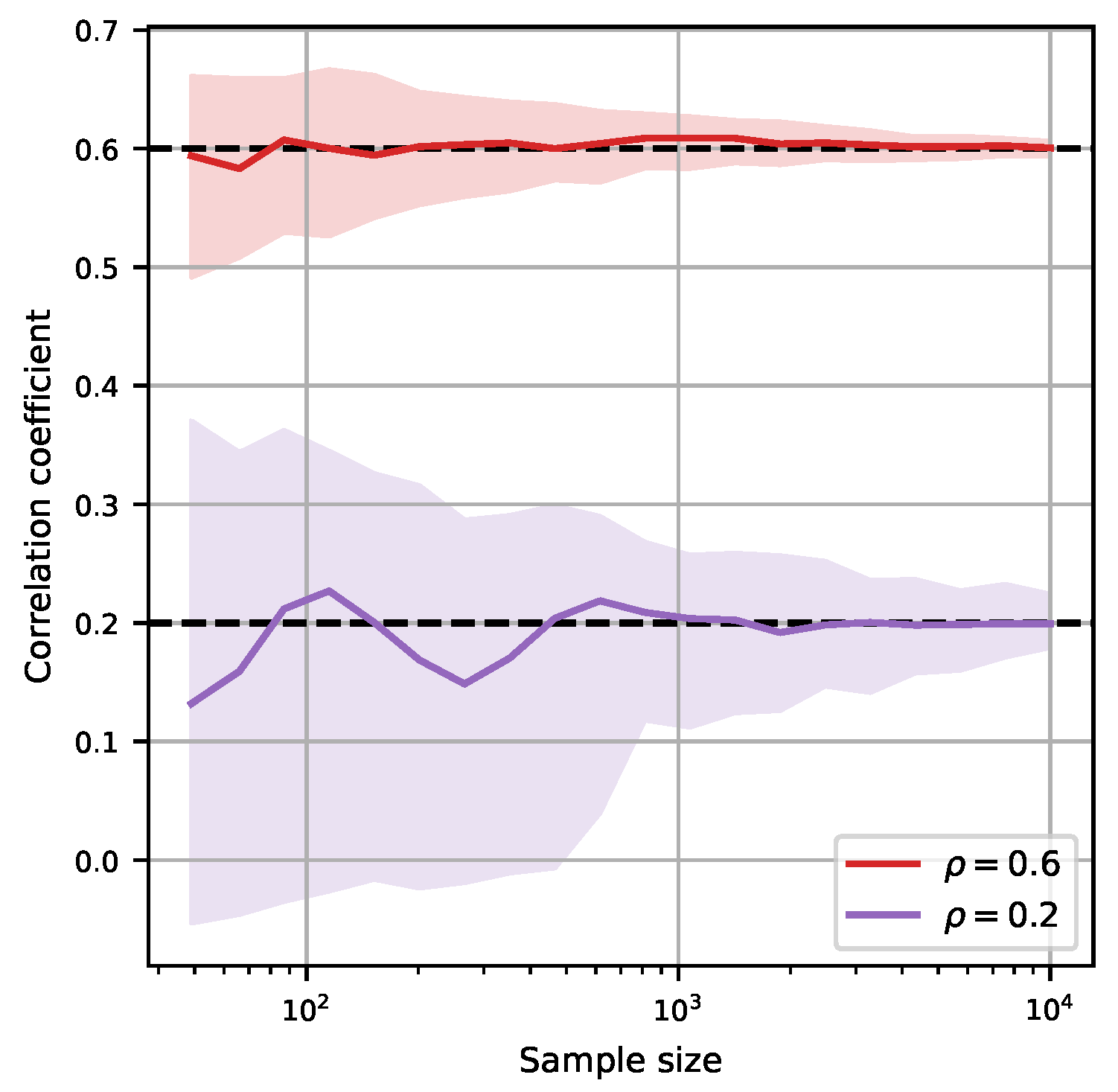
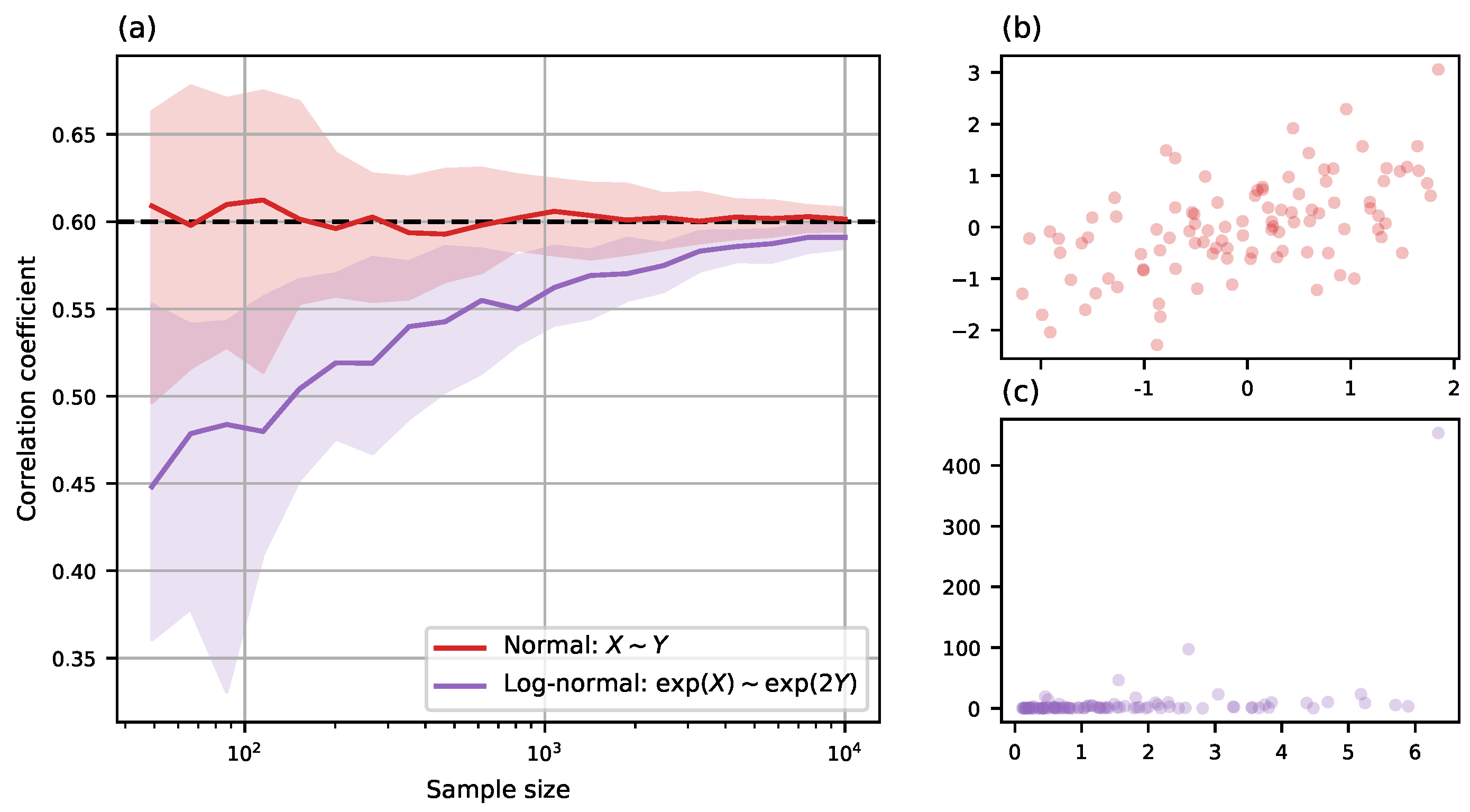
3.1. Sample Size and Accuracy
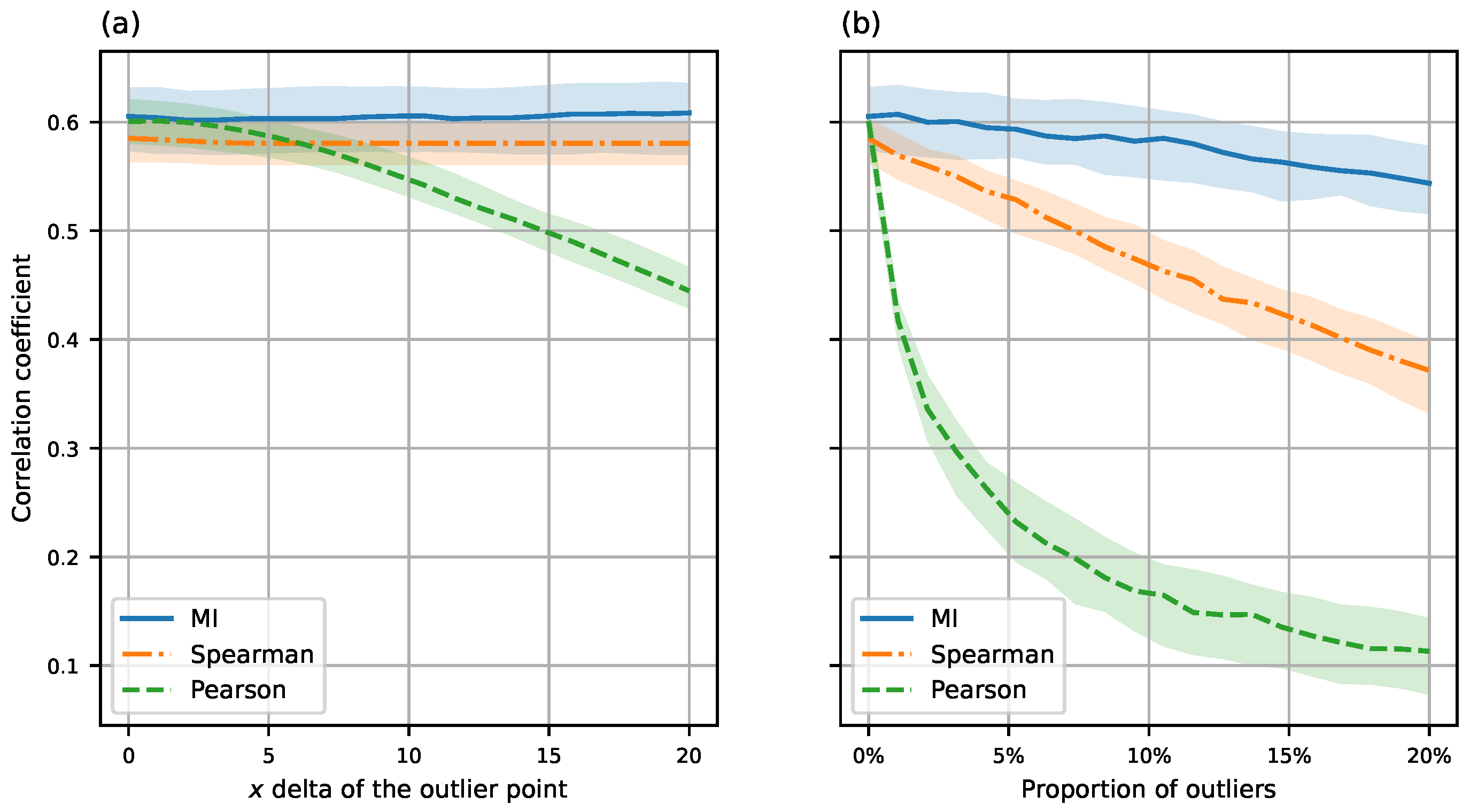
3.2. Robustness
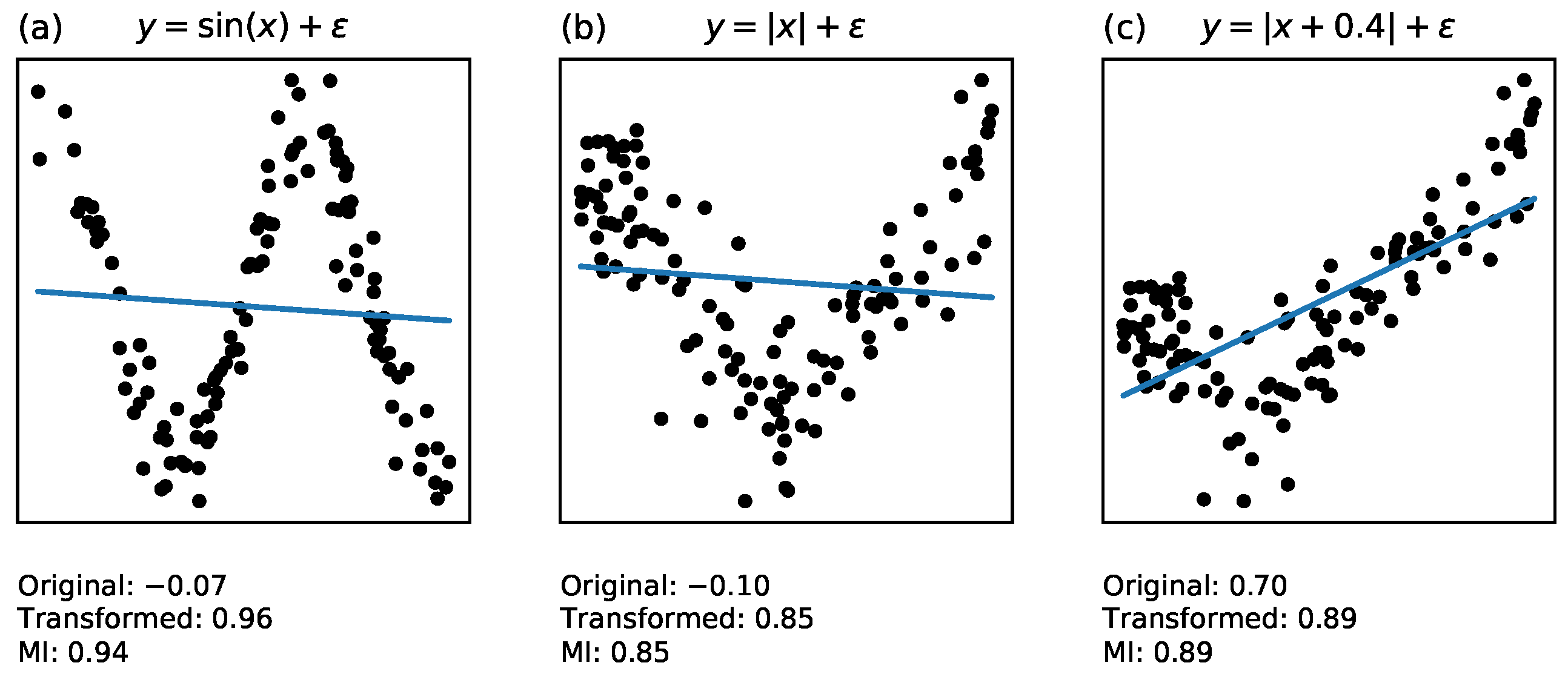
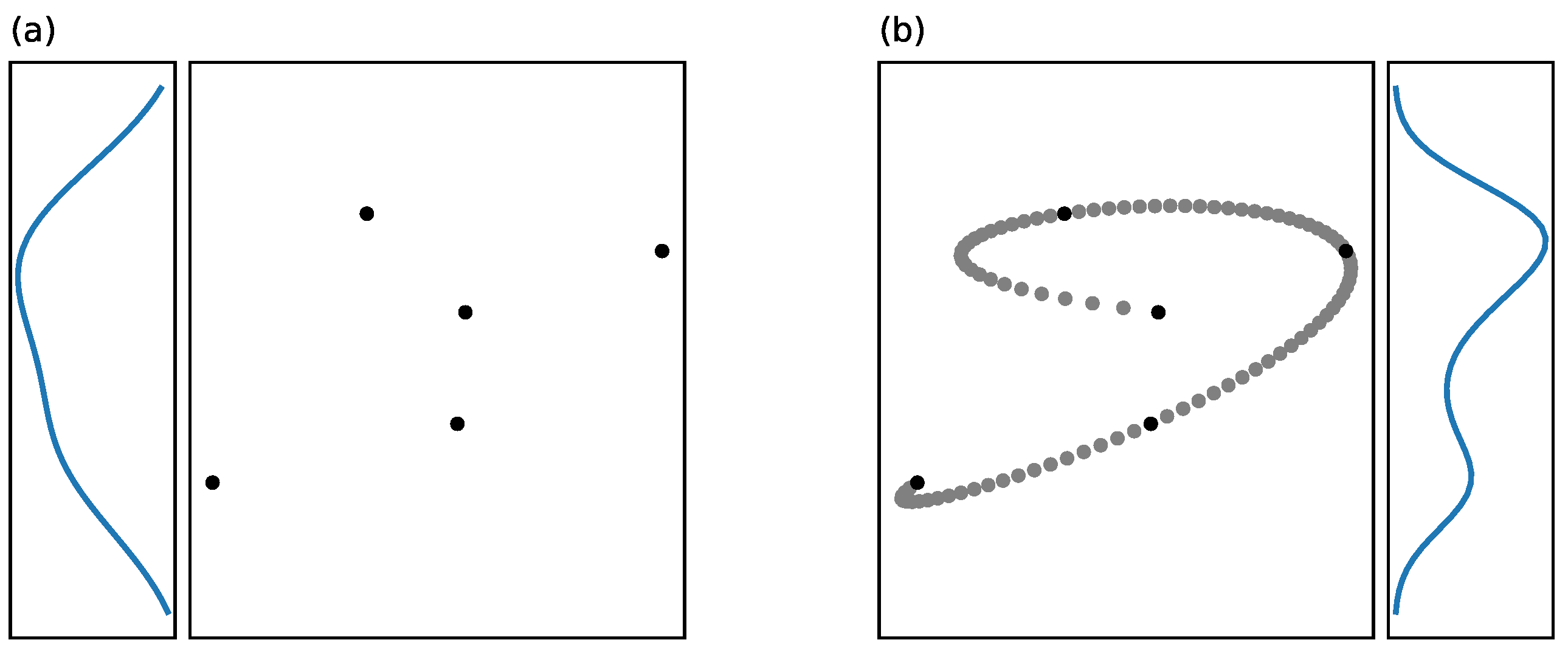
3.3. Transformation Invariance
3.4. Autocorrelated Data
4. Case Studies
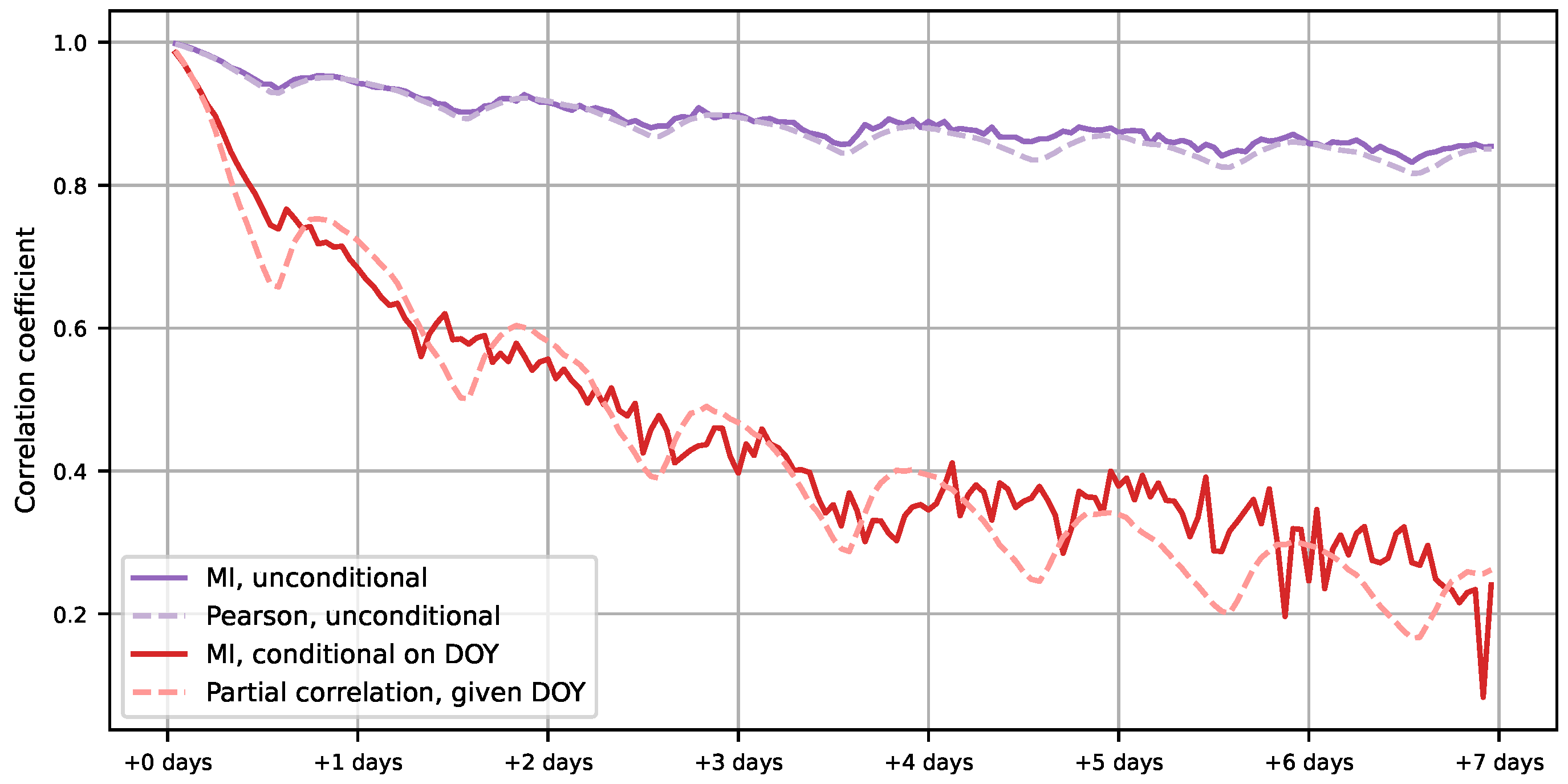
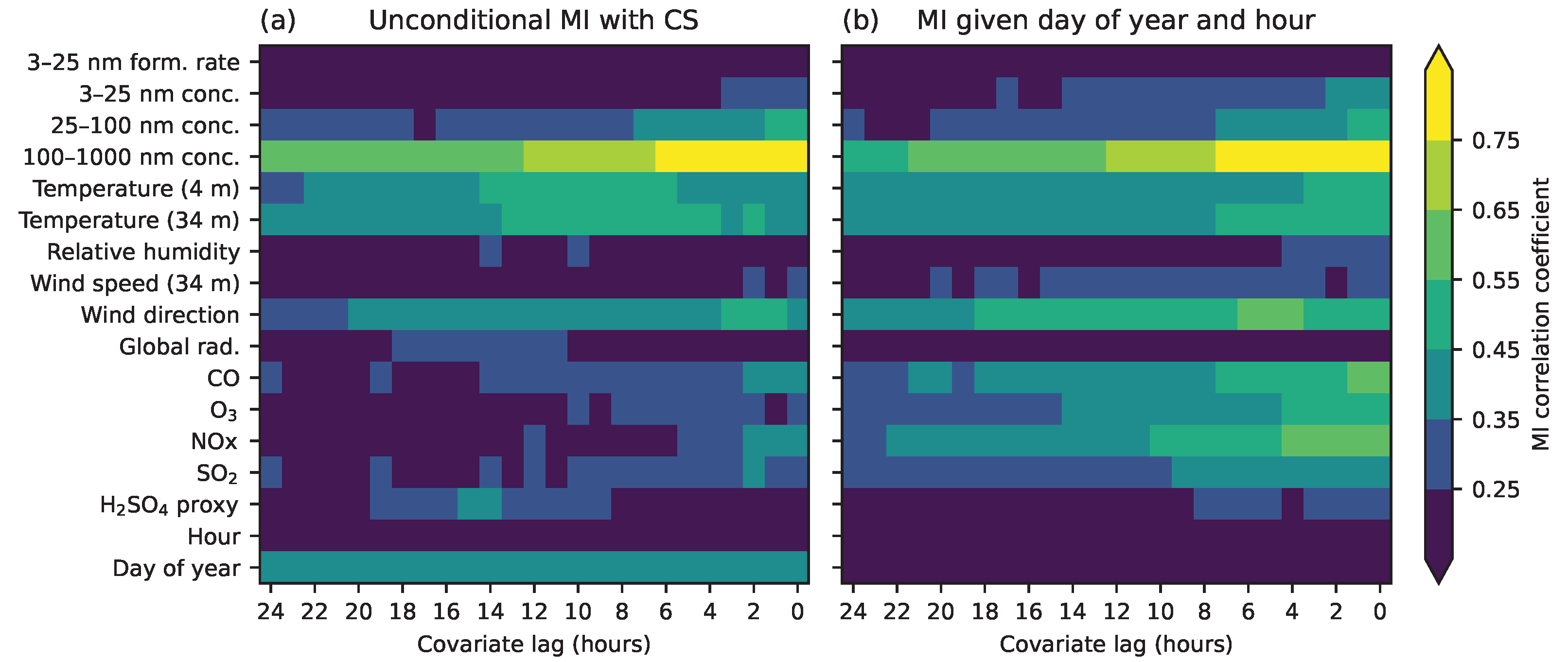
4.1. Removing Seasonal Dependency
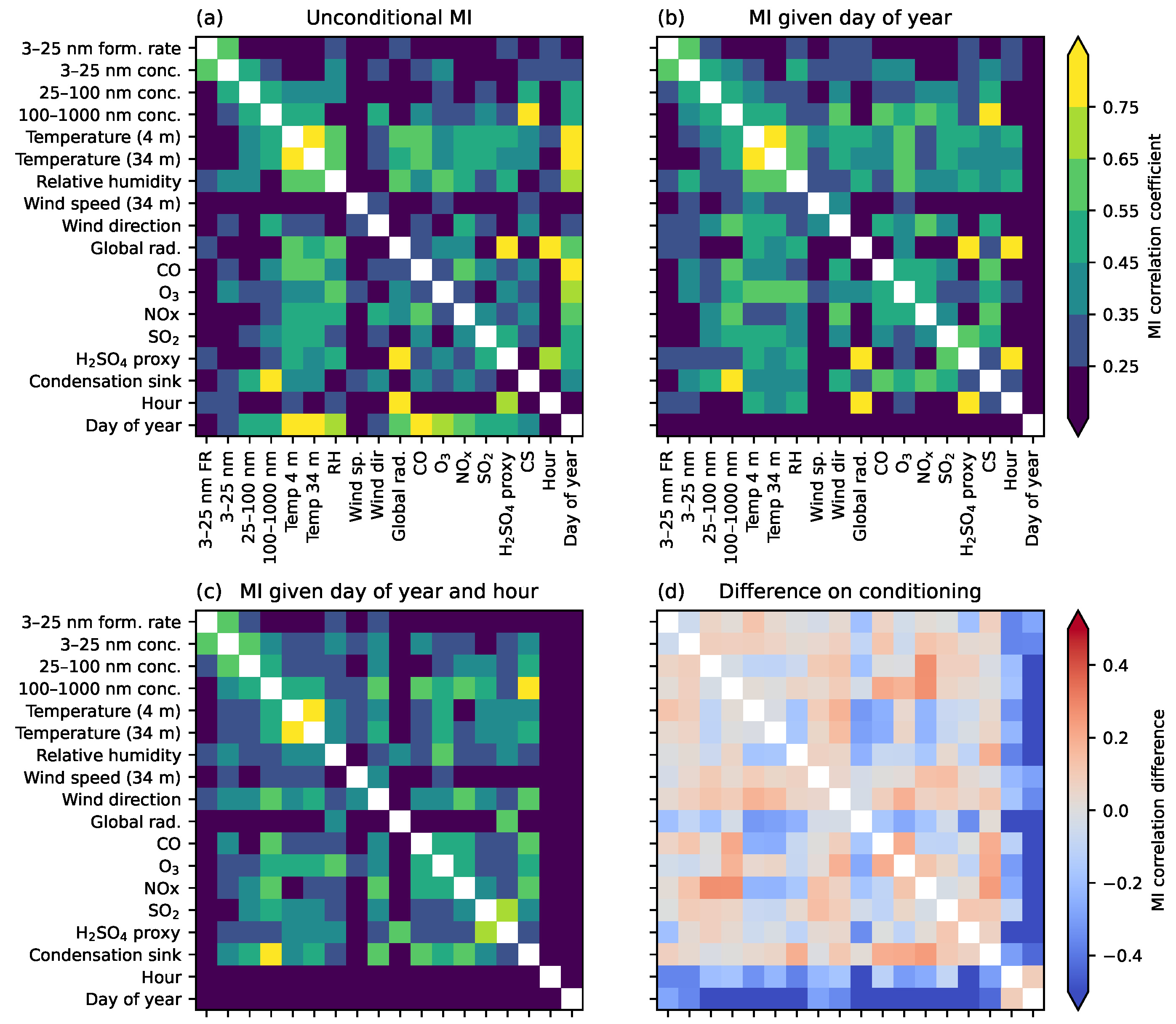
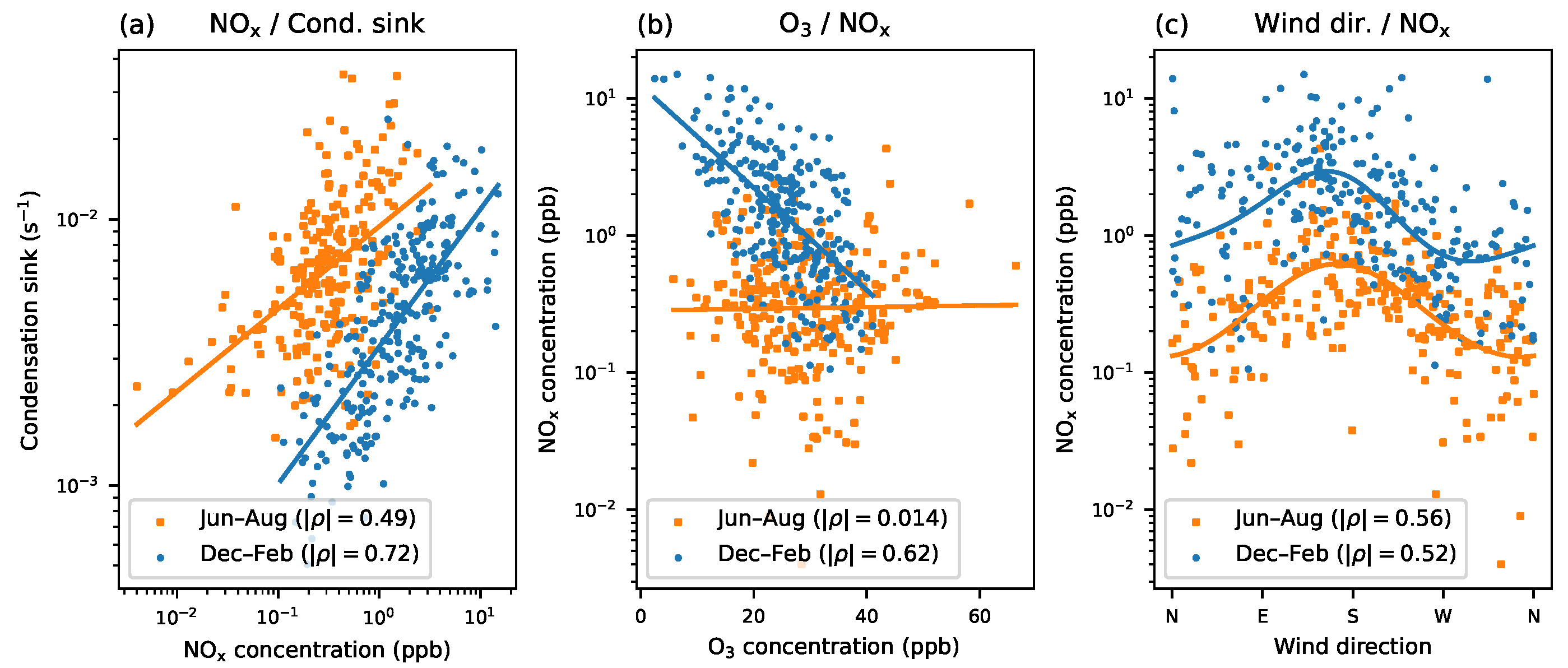
4.2. Discovering Associations across Many Variables
5. Conclusions
- 1.
- After the usual data quality checking, preprocess variables to have roughly symmetric histograms. Select a suitable subset of autocorrelated data.
- 2.
- Estimate pairwise MI between all variables, as in Figure 7.
- 3.
- Use conditional MI to investigate common factors such as seasonal cycles.
- 4.
- Estimate time dependencies with the variables of interest, as in Figure 9.
- 5.
- Draw scatter plots and manually explore the reduced set of the most interesting variables.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hari, P.; Kulmala, M. Station for Measuring Ecosystem–Atmosphere Relations (SMEAR II). Boreal Environ. Res. 2005, 10, 315–322. [Google Scholar]
- Kulmala, M.; Nieminen, T.; Nikandrova, A.; Lehtipalo, K.; Manninen, H.E.; Kajos, M.K.; Kolari, P.; Lauri, A.; Petäjä, T.; Krejci, R.; et al. CO2-induced terrestrial climate feedback mechanism: From carbon sink to aerosol source and back. Boreal Environ. Res. 2014, 19, 122–131. [Google Scholar]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pluim, J.; Maintz, J.; Viergever, M. Mutual-information-based registration of medical images: A survey. IEEE Trans. Med. Imaging 2003, 22, 986–1004. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Dada, L.; Alghamdi, M.A.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Hussein, T. Mutual information input selector and probabilistic machine learning utilisation for air pollution proxies. Appl. Sci. 2019, 9, 4475. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Zhang, H.; Tian, T. Development of stock correlation networks using mutual information and financial big data. PLoS ONE 2018, 13, e0195941. [Google Scholar] [CrossRef]
- Basso, K.; Margolin, A.A.; Stolovitzky, G.; Klein, U.; Dalla-Favera, R.; Califano, A. Reverse engineering of regulatory networks in human B cells. Nat. Genet. 2005, 37, 382–390. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Paasonen, P.; Kerminen, V.M.; Junninen, H.; Kulmala, M.; Foster, A.S. Exploring non-linear associations between atmospheric new-particle formation and ambient variables: A mutual information approach. Atmos. Chem. Phys. 2018, 18, 12699–12714. [Google Scholar] [CrossRef] [Green Version]
- Laarne, P.; Zaidan, M.A.; Nieminen, T. ennemi: Non-linear correlation detection with mutual information. SoftwareX 2021, 14, 100686. [Google Scholar] [CrossRef]
- Ulpiani, G.; Ranzi, G.; Santamouris, M. Local synergies and antagonisms between meteorological factors and air pollution: A 15-year comprehensive study in the Sydney region. Sci. Total Environ. 2021, 788, 147783. [Google Scholar] [CrossRef]
- Ulpiani, G.; Nazarian, N.; Zhang, F.; Pettit, C.J. Towards a living lab for enhanced thermal comfort and air quality: Analyses of standard occupancy, weather extremes, and COVID-19 pandemic. Front. Environ. Sci. 2021, 9, 556. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ihara, S. Information Theory for Continuous Systems; World Scientific: Singapore, 1993. [Google Scholar]
- Linfoot, E.H. An informational measure of correlation. Inf. Control 1957, 1, 85–89. [Google Scholar] [CrossRef] [Green Version]
- Granger, C.; Lin, J.L. Using the mutual information coefficient to identify lags in nonlinear models. J. Time Ser. Anal. 1994, 15, 371–384. [Google Scholar] [CrossRef]
- Frenzel, S.; Pompe, B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett. 2007, 99, 204101. [Google Scholar] [CrossRef] [PubMed]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Moon, Y.I.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318–2321. [Google Scholar] [CrossRef]
- Ross, B.C. Mutual information between discrete and continuous data sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [Green Version]
- Dada, L.; Paasonen, P.; Nieminen, T.; Buenrostro Mazon, S.; Kontkanen, J.; Peräkylä, O.; Lehtipalo, K.; Hussein, T.; Petäjä, T.; Kerminen, V.M.; et al. Long-term analysis of clear-sky new particle formation events and nonevents in Hyytiälä. Atmos. Chem. Phys. 2017, 17, 6227–6241. [Google Scholar] [CrossRef] [Green Version]
- Kulmala, M.; Petäjä, T.; Nieminen, T.; Sipilä, M.; Manninen, H.E.; Lehtipalo, K.; Dal Maso, M.; Aalto, P.P.; Junninen, H.; Paasonen, P.; et al. Measurement of the nucleation of atmospheric aerosol particles. Nat. Protoc. 2012, 7, 1651–1667. [Google Scholar] [CrossRef]
- Dada, L.; Ylivinkka, I.; Baalbaki, R.; Li, C.; Guo, Y.; Yan, C.; Yao, L.; Sarnela, N.; Jokinen, T.; Daellenbach, K.R.; et al. Sources and sinks driving sulfuric acid concentrations in contrasting environments: Implications on proxy calculations. Atmos. Chem. Phys. 2020, 20, 11747–11766. [Google Scholar] [CrossRef]
- Riuttanen, L.; Hulkkonen, M.; Dal Maso, M.; Junninen, H.; Kulmala, M. Trajectory analysis of atmospheric transport of fine particles, SO2, NOx and O3 to the SMEAR II station in Finland in 1996–2008. Atmos. Chem. Phys. 2013, 13, 2153–2164. [Google Scholar] [CrossRef] [Green Version]
- Lehtinen, K.E.J.; Korhonen, H.; Dal Maso, M.; Kulmala, M. On the concept of condensation sink diameter. Boreal Environ. Res. 2003, 8, 405–411. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laarne, P.; Amnell, E.; Zaidan, M.A.; Mikkonen, S.; Nieminen, T. Exploring Non-Linear Dependencies in Atmospheric Data with Mutual Information. Atmosphere 2022, 13, 1046. https://doi.org/10.3390/atmos13071046
Laarne P, Amnell E, Zaidan MA, Mikkonen S, Nieminen T. Exploring Non-Linear Dependencies in Atmospheric Data with Mutual Information. Atmosphere. 2022; 13(7):1046. https://doi.org/10.3390/atmos13071046
Chicago/Turabian StyleLaarne, Petri, Emil Amnell, Martha Arbayani Zaidan, Santtu Mikkonen, and Tuomo Nieminen. 2022. "Exploring Non-Linear Dependencies in Atmospheric Data with Mutual Information" Atmosphere 13, no. 7: 1046. https://doi.org/10.3390/atmos13071046
APA StyleLaarne, P., Amnell, E., Zaidan, M. A., Mikkonen, S., & Nieminen, T. (2022). Exploring Non-Linear Dependencies in Atmospheric Data with Mutual Information. Atmosphere, 13(7), 1046. https://doi.org/10.3390/atmos13071046






