Evidence for Intensification in Meteorological Drought since the 1950s and Recent Dryness–Wetness Forecasting in China
Abstract
:1. Introduction
2. Study Area and Data Sources
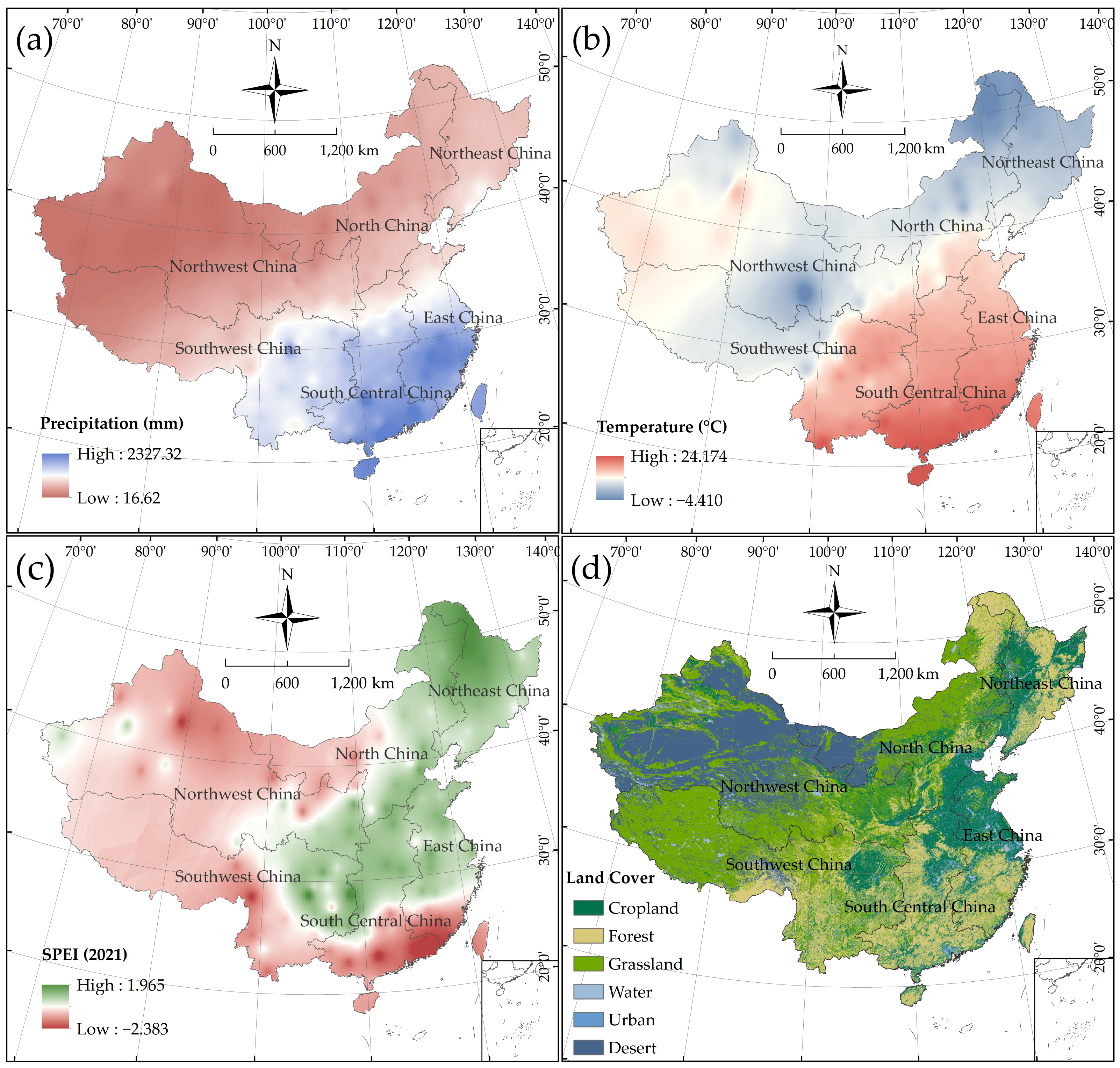
2.1. Study Domain
2.2. Data Sources
3. Methodology
3.1. Standardized Precipitation Evapotranspiration Index
- (1)
- Calculating monthly potential evapotranspiration (PET) applying the Thornthwaite method [94].where T is the monthly mean temperature (°C); I is a heat index calculated for the whole year; m is a coefficient depending on I; and K is a correction coefficient defined based on the latitude and month.
- (2)
- Estimating the monthly water deficit by the difference between precipitation (P) and PET.where refers to the amount of water deficit for the month i; represents the precipitation for the month i; and represents the reference evaporation values for the month i.
- (3)
- Constructing water profit and loss accumulation series at different timescales .where is the accumulated water deficit in the jth month of the ith year in the kth month scale; and is the water deficit in the jth month of the ith year.
- (4)
- Normalizing the difference of the climatic water balance as a log-logistic probability distribution. The probability density function can be expressed as follows:where , , and are parameters representing scale, shape, and origin. The D values are in the range of . Hence, the probability distribution function can be expressed as follows:where , , and can be obtained by the L-moment method as:where () is the factorial function and , , are the weighted matrix of the original data series and can be computed as:where N denotes the number of months.
- (5)
- The data sequence is subjected to a standardized normal distribution transformation to obtain the SPEI value at the corresponding timescale.
3.2. Modified Mann–Kendall Test
3.3. Theil–Sen Median Method
3.4. Pettitt Test
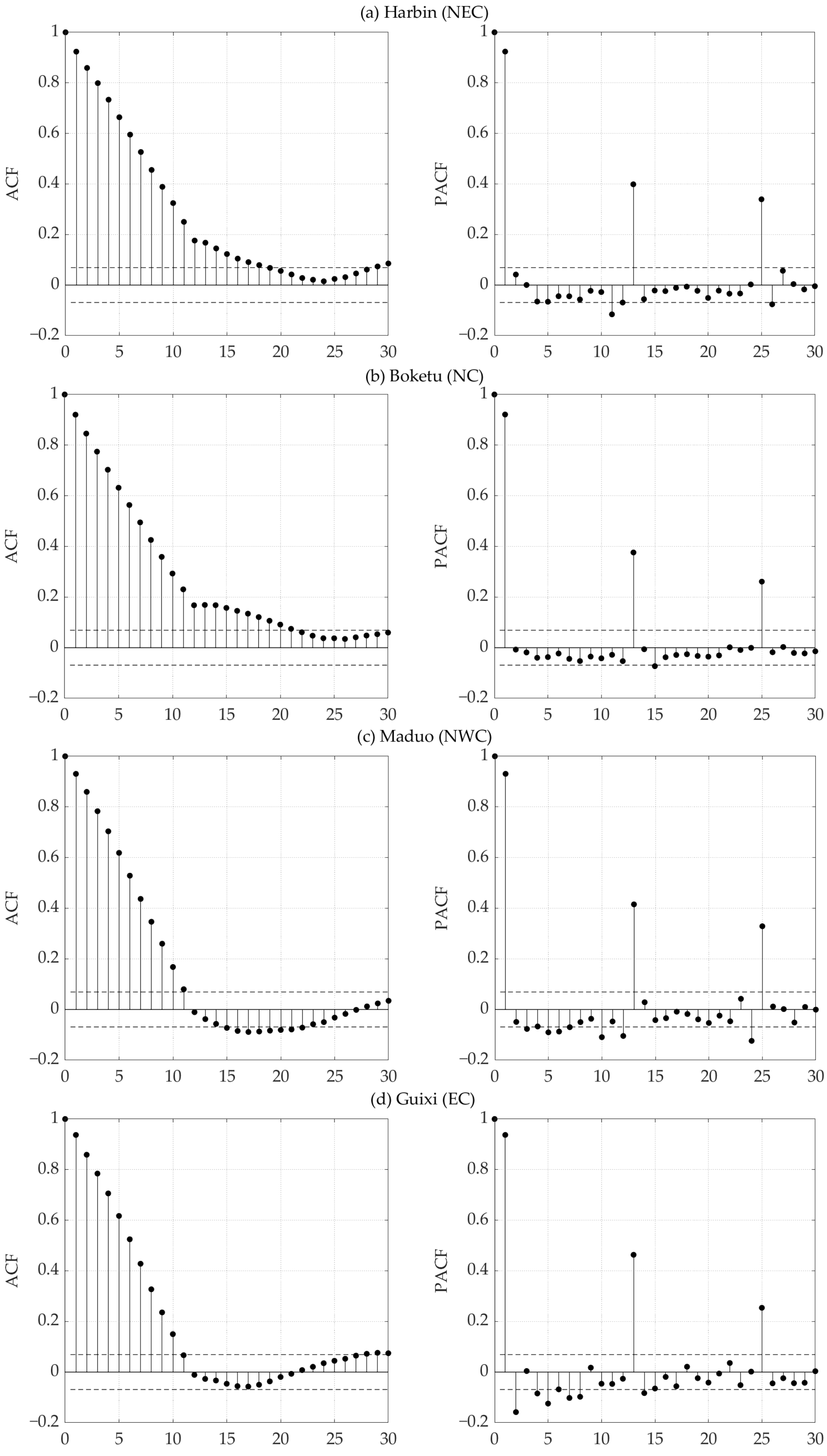
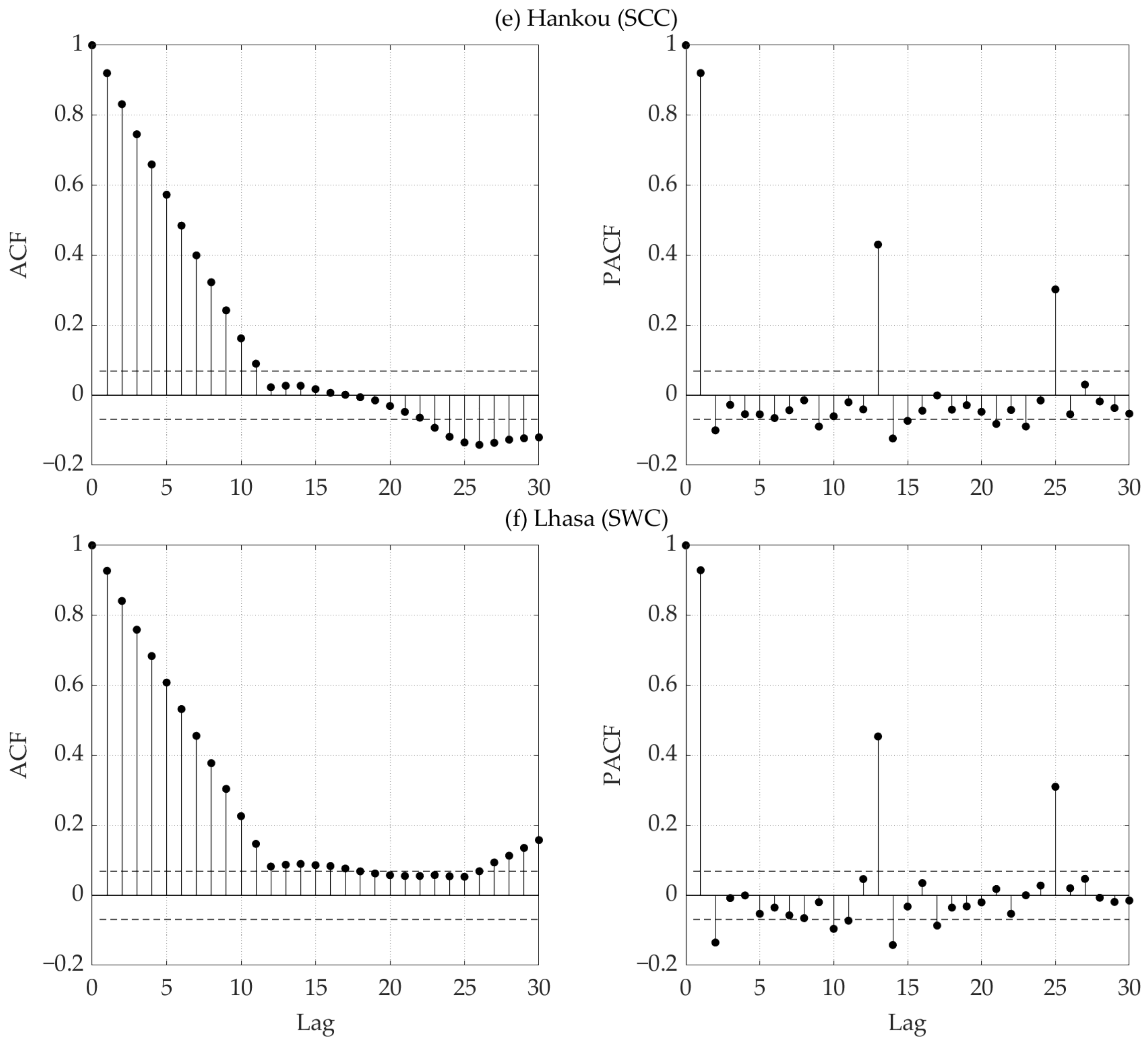
3.5. Autoregressive Integrated Moving Average Model
3.6. Autoregressive Integrated Moving Average Modeling Procedure
3.6.1. Model Identification
3.6.2. Parameter Estimation
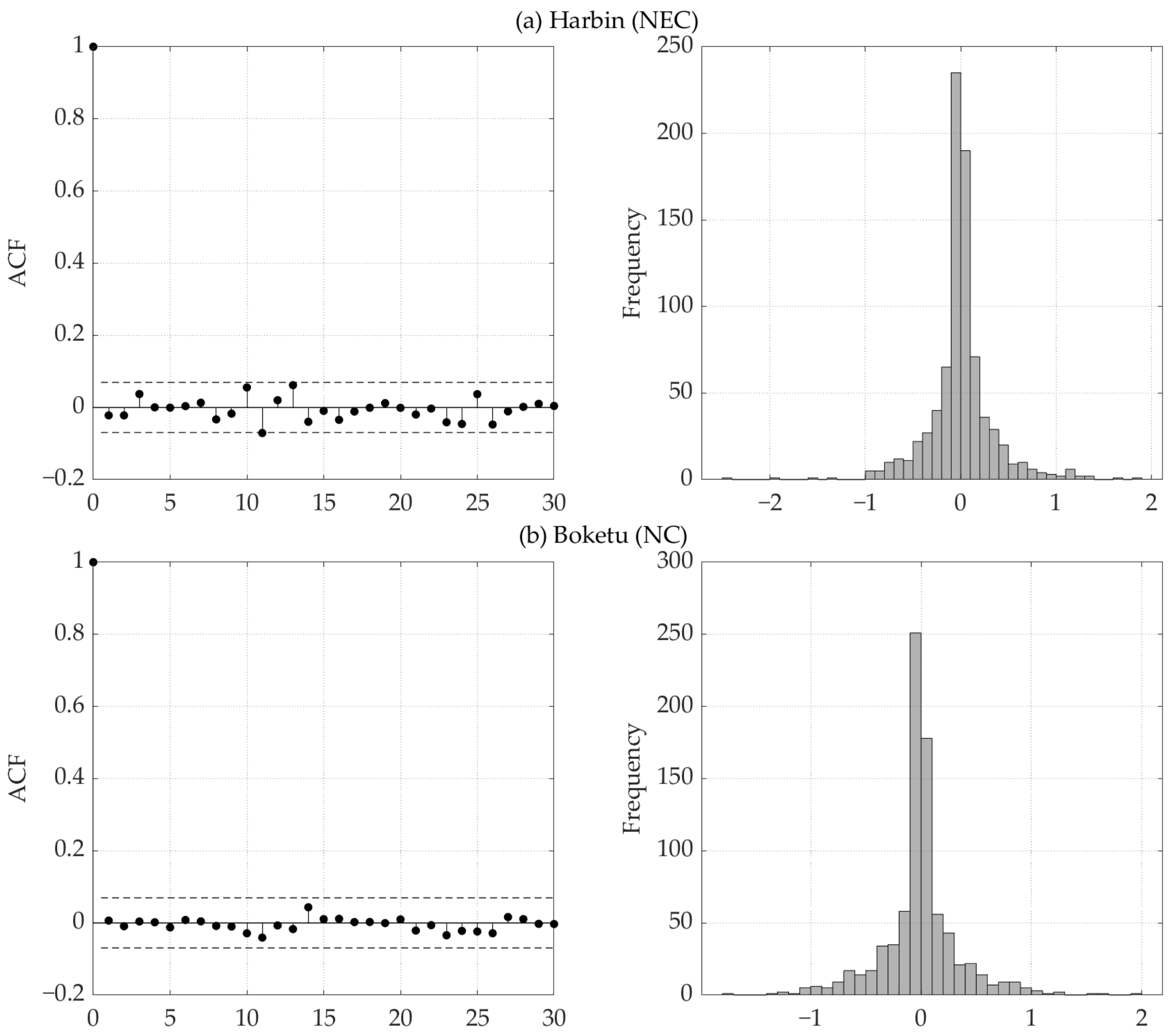
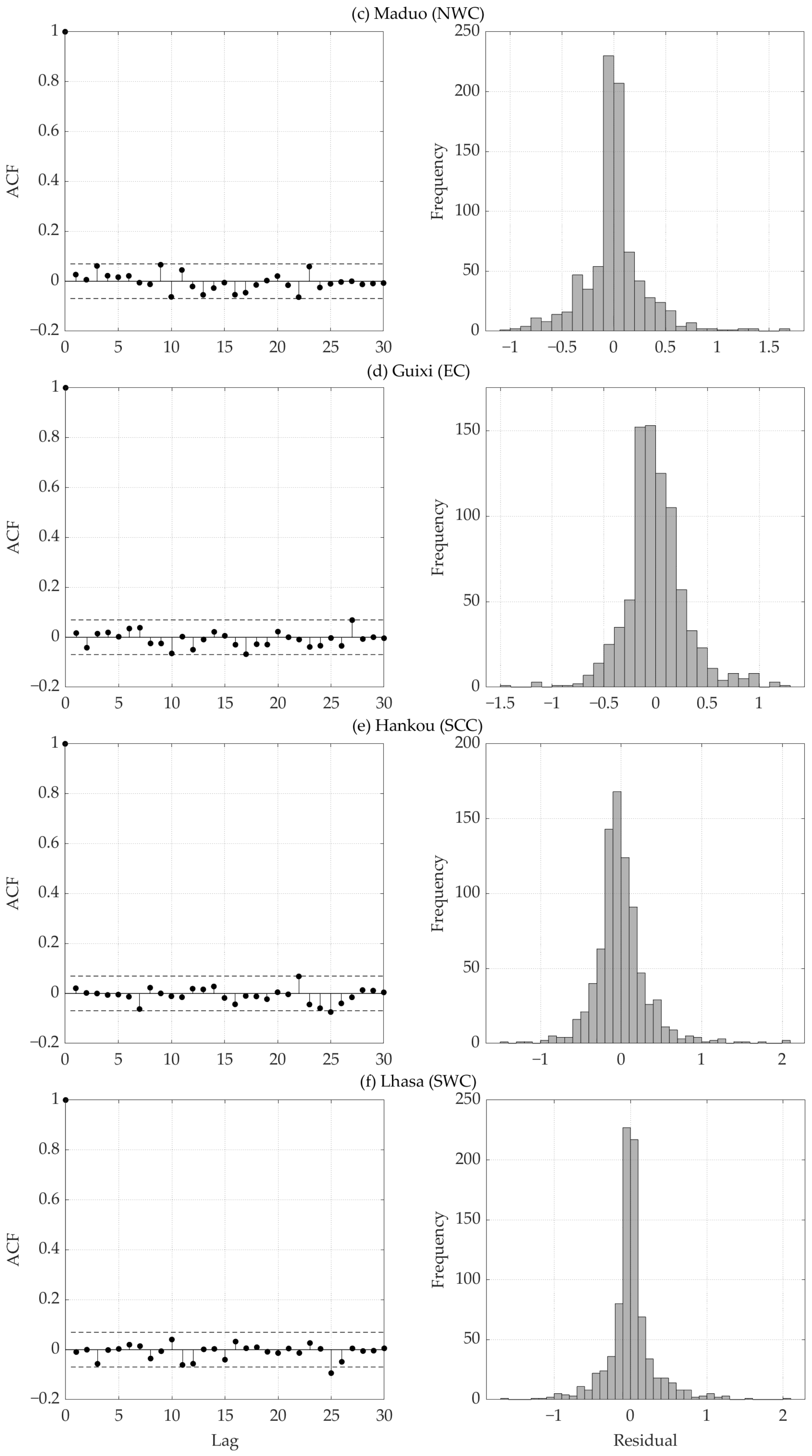
3.6.3. Diagnostic Checking
4. Results
4.1. Temporal Trends in Regional Dry–Wet Variation over China
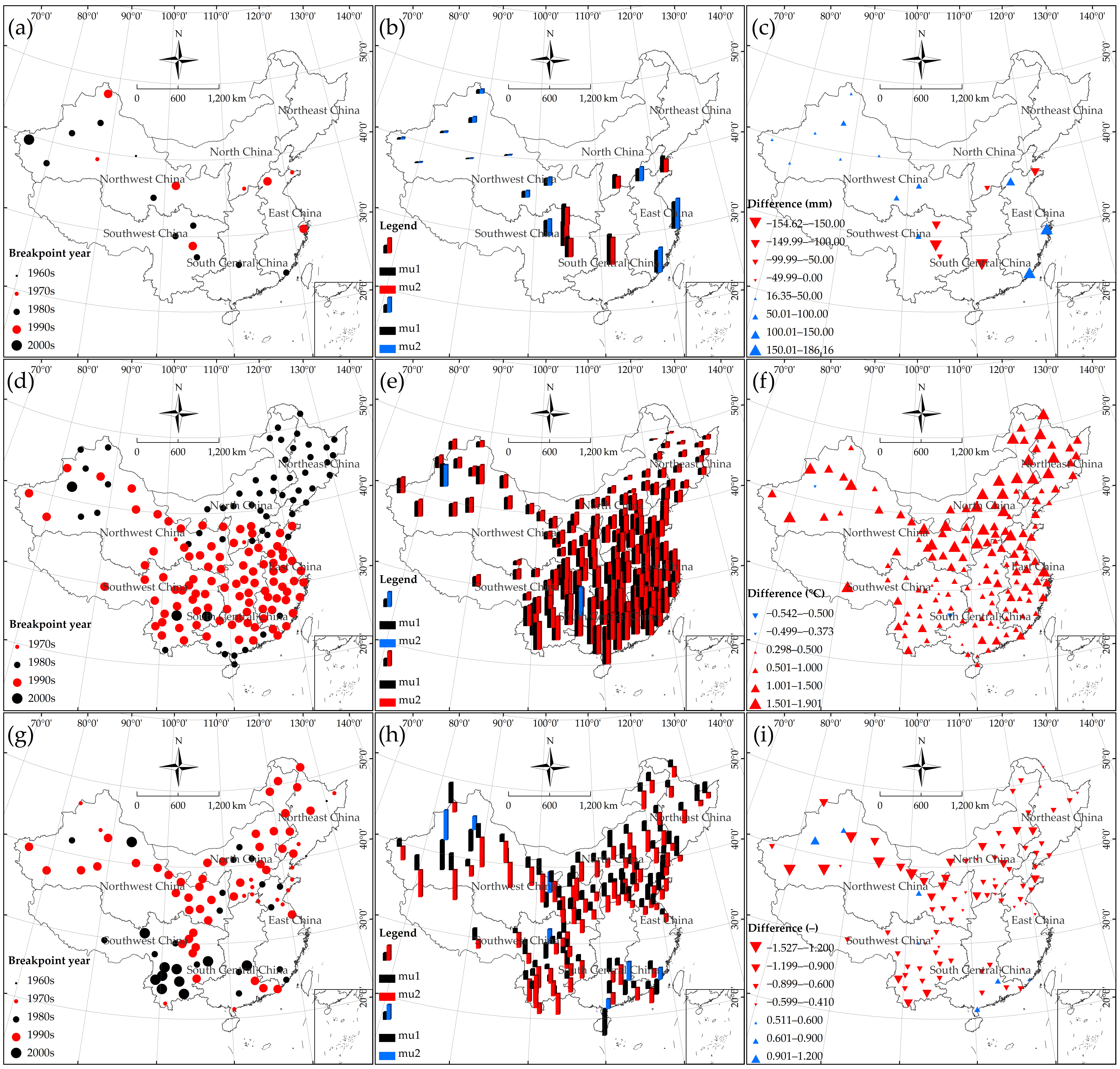
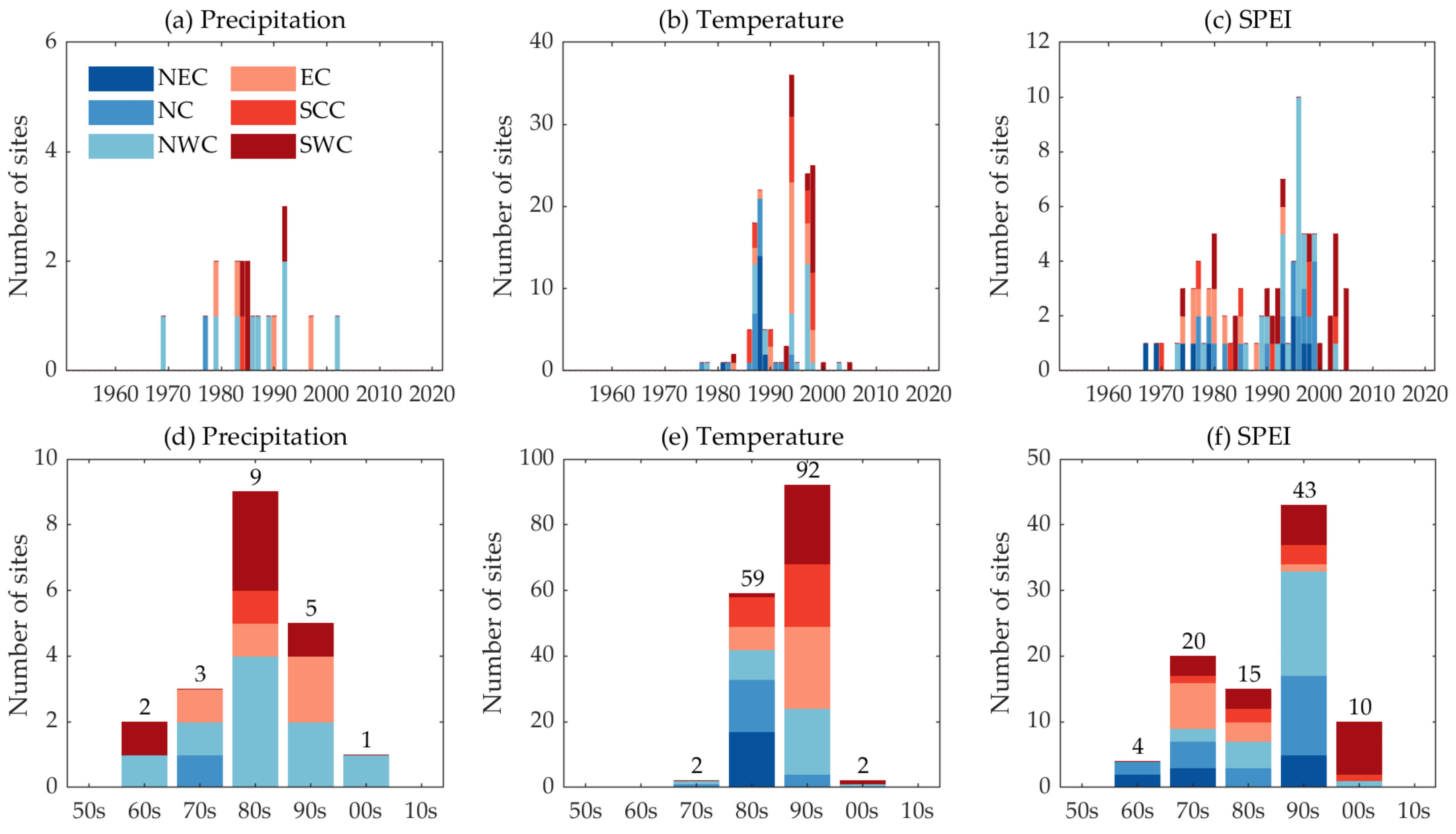
4.2. Abrupt Characteristic of Regional Dry–Wet Variation over China
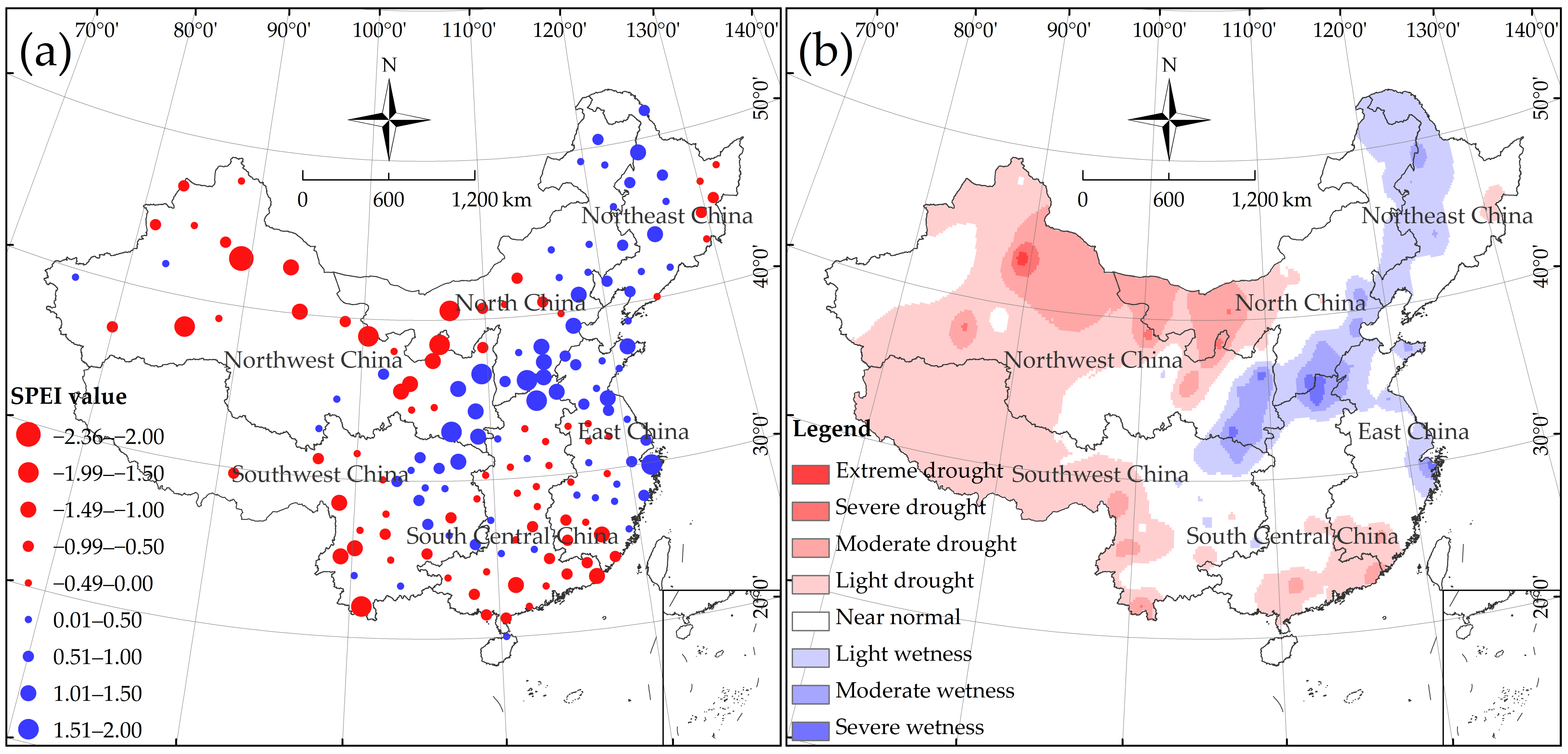
4.3. Spatial Variations in Wetting and Drying Trends over Mainland China
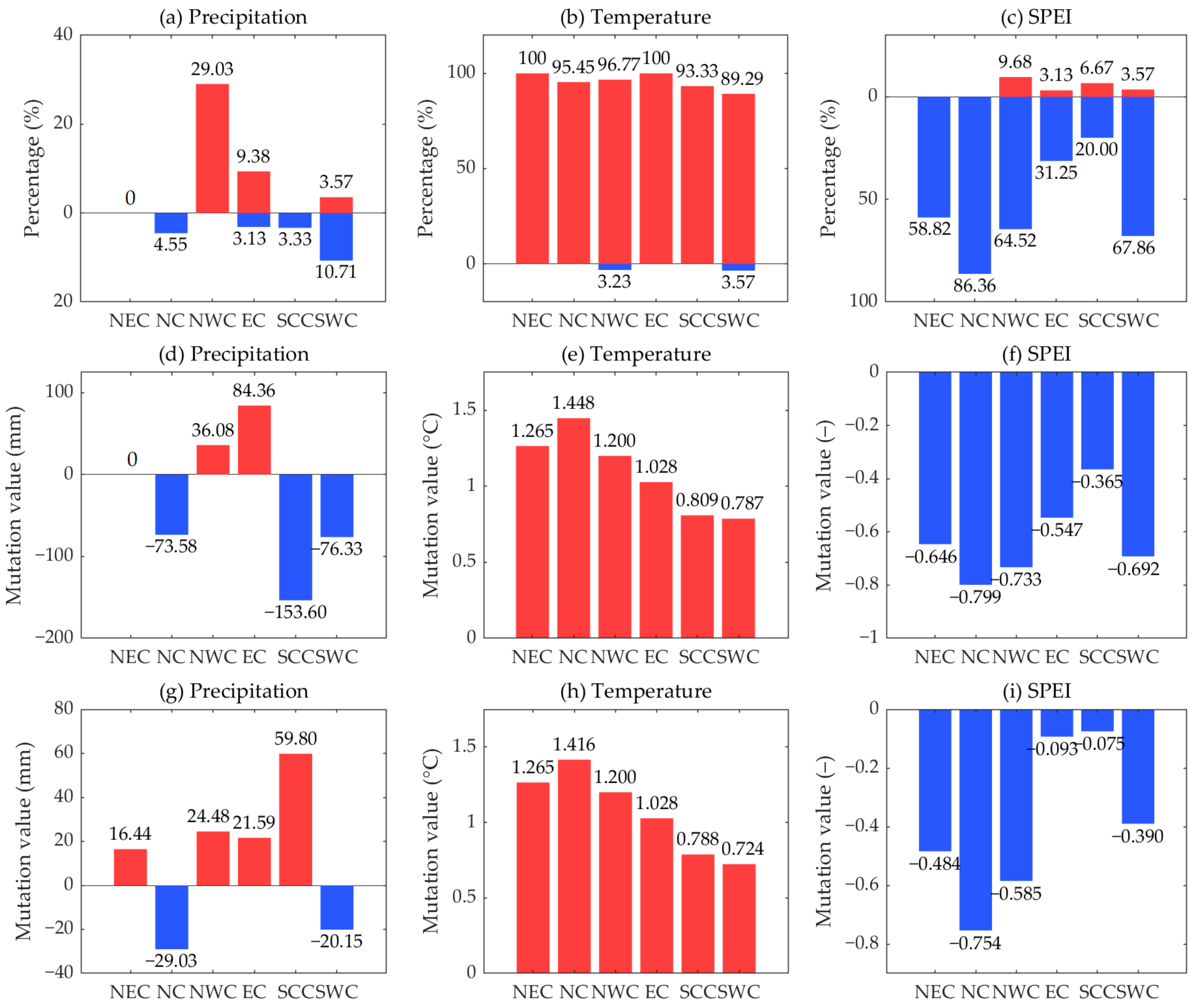
4.4. Spatio-Temporal Structure of Dry–Wet Transition over Mainland China

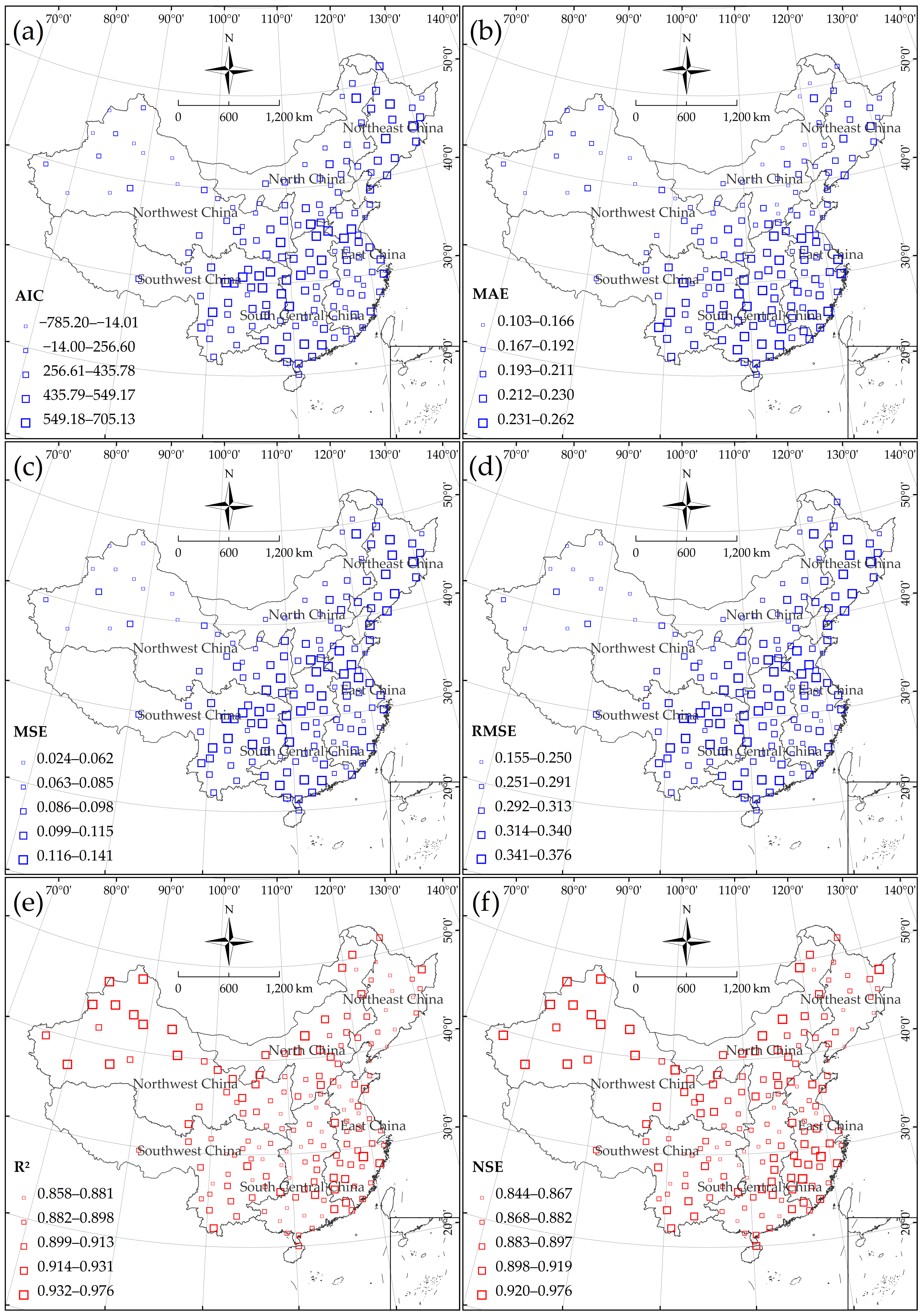
4.5. Forecasting of Recent Meteorological Droughts over China and Its Uncertainty
5. Discussion
5.1. Influence of Drought Index Selection on Dry–Wet Variations
5.2. Climatological Attribution of Regional Dry–Wet Variations over China
5.3. Development of Drought Forecasting Models
6. Conclusions and Recommendations
6.1. Conclusions
- (i)
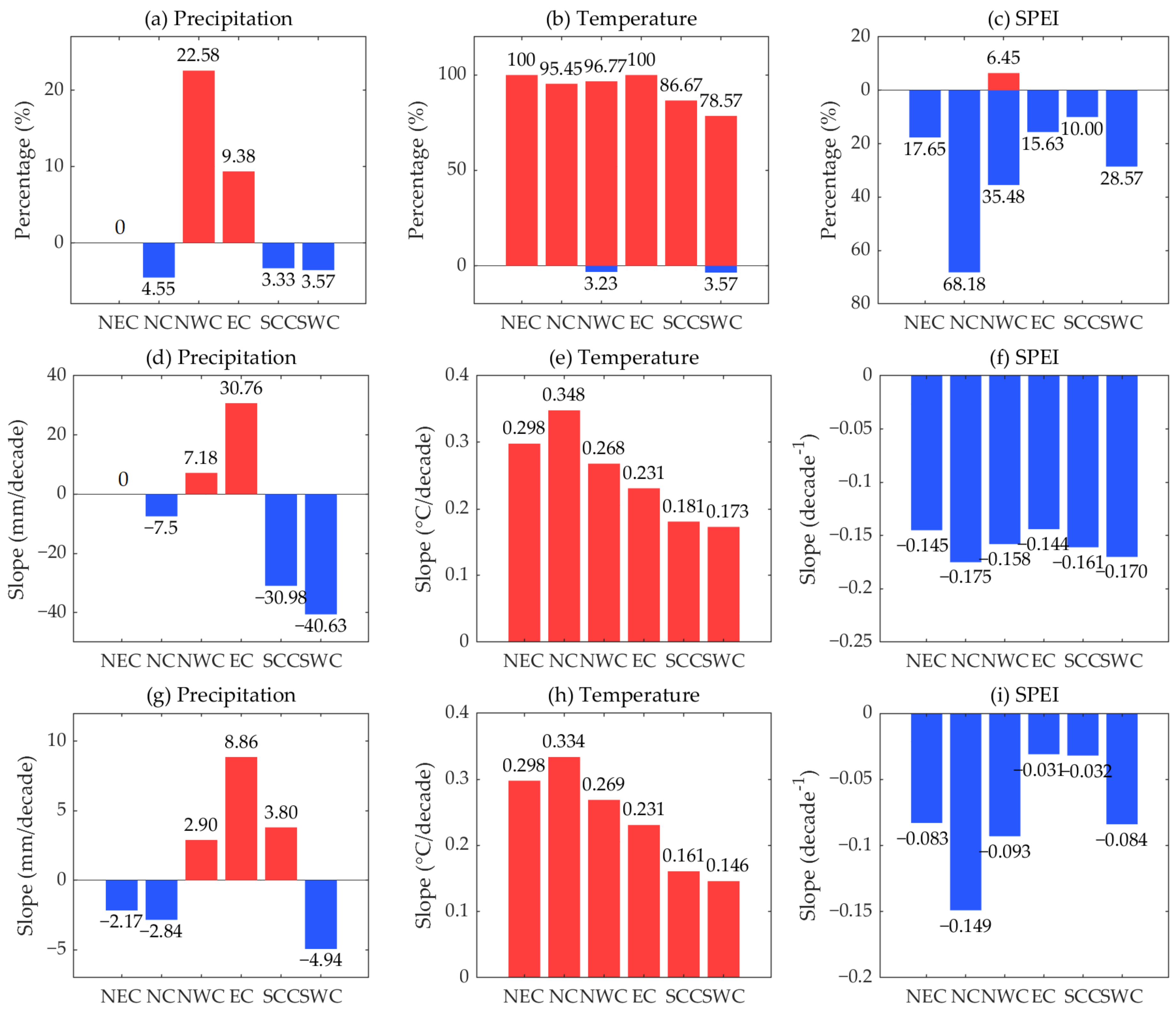
- The MMK test showed the interannual variation characteristics of intensified meteorological droughts in China. The SPEI showed an alternation from positive to negative anomalies since the 1950s, indicating that the six regions have experienced drying trends during the last 71 years, among which the NC region showed the most pronounced interdecadal drying trend, with a significant (p < 0.05) decreasing trend of the SPEI at the majority (68.18%) of the NC sites, i.e., an increase in dryness. In general, the intensified trend of the drying level in China from intense to weak was in the order of NC, NWC, SWC, NEC, SCC, and EC.
- (ii)
- The annual precipitation in most of China did not show significant abrupt changes since the 1950s, except for precipitation means in parts of NWC showing a movement from negative to positive anomalies. The mean air temperature at nearly all sites experienced a significant change-point during the 1980s/1990s, showing an abrupt alternation from cold to warm periods. The air temperature in NEC changed significantly in the late 1980s (1988); the breakpoint in air temperature at most of the NWC sites occurred in 1997; the year 1994 was the break year from the cold period to the warm period in EC. The break pattern of the SPEI showed a large temporal heterogeneity compared to the climate factors controlling for dry–wet variability (precipitation and temperature). The SPEI in NWC experienced a shift from positive to negative anomalies around 1996, indicating an inflection point in the dryness–wetness pattern.
- (iii)
- A non-significant step-change in precipitation and a significant positive jump in temperature at all stations (100%) in NEC resulted in a significant negative anomaly experienced by the SPEI over most (58.82%) of the NEC sites. The combined effect of decreasing precipitation (−29.03 mm) and significantly increasing temperature (1.416 °C) in NC resulted in a significant shift from wet to dry in most (86.36%) of the NC sites, causing the SPEI means to experience a negative offset of −0.799. The combined effect of significant positive anomalies in temperature (96.77%) and significant positive anomalies in precipitation (29.03%) can explain the significant negative offset in the SPEI means over most (64.52%) of NWC. The dry–wet change at the regional scale showed a high spatial heterogeneity, especially for EC and SCC. The weak increase in EC precipitation (21.59 mm) combined with a significant increase in EC temperature (1.028 °C) led to an alternation in the climate towards dryness (SPEI offset of −0.093) and spatial variability in regional dry–wet variation. A majority (93.33%) of the SCC sites experienced a significant transition from negative to positive temperature anomalies (0.809 °C); the precipitation variability in SCC had spatial heterogeneity, which may be the main reason for the spatial heterogeneity of the dry–wet change in the region. For SWC, the combination of an overall negative deviation in precipitation (−20.15 mm) and a significant positive deviation in air temperature (0.724 °C) resulted in a climate shift from wetness to dryness over most (67.86%) of the SWC sites (SPEI offset of −0.390). Overall, the SPEI at most sites (55–90%) in NC, NWC, NEC, and SWC experienced significant negative alternations since the 1950s, with mean offsets of approximately −0.80–−0.60, implying a significant drying tendency in these regions and a serious drought-induced environmental challenge.
- (iv)
- The general trend of annual precipitation was non-significant in China, yet the spatial variation had obvious regional characteristics. A significant (p < 0.01) upward trend was exhibited in precipitation in most of NWC; the precipitation in NC and SWC mainly showed a non-significant downward trend; there was no significant trend in NEC precipitation. The significant uptrend of precipitation was mainly concentrated to the west of 100° E; the rising magnitude of precipitation was higher in Eastern China near 30° N, with a changing rate of 20–40 mm/decade. The trend magnitude of 0.15–0.50 °C/decade in mean annual temperature was shown in most of China. Each of these regions has experienced a significant (p < 0.01) warming since the 1950s. The upward magnitude in temperature in the northern part of 30° N was noticeably higher than that in the southern part of 30° N, with trend slopes of 0.30–0.50 °C/decade and 0.15–0.30 °C/decade, respectively. A latitudinal distribution exists in the China/Northern Hemisphere air temperature response to climate warming, with a higher upward magnitude shown in temperature at high latitudes.
- (v)
- The climate in China is tending towards a drying regime; however, the drought evolution has a large spatial variability at the regional scale. The climate in NEC, NC, NWC, and SWC experienced a significant (p < 0.05) drying trend, while the dry–wet change in EC and SCC showed high spatial heterogeneity. EC and SCC surrounding 30° N have experienced a non-significant (p > 0.05) wetting trend since the 1950s. Geographically, the drought trends were statistically significant in Northern and Southern China, bounded by 30° N, with changing rates of −0.30–−0.20/decade and −0.20–−0.10/decade, respectively. This study reported the consistency of the spatial distribution of variations in precipitation and the SPEI along 30° N latitude. A weak upward trend in the SPEI, i.e., an increase in wetness, was shown in Eastern China surrounding 30° N, with a trend slope of 0.003–0.10/decade. This is closely related to the increase in precipitation in these areas (mainly in EC and SCC).
- (vi)
- Precipitation in parts of NWC and EC had a significant shift from negative anomalies to positive anomalies, and that in the eastern part of SWC and the south-central part of SCC experienced significant negative anomalies. The significant change-point in temperature occurred across 40–50° N (NEC and northern NC) of Eastern China in the 1980s; the area spanning 20–40° N (south of 40° N) showed a significant break in temperature in the 1990s. The temperature means’ offset was approximately 0.50–1.5 °C in SWC and SCC (south of 30° N), while that reached 1.50–1.90 °C in NEC, NC, NWC, and EC (north of 30° N). On average, the response of the climate in Northern China (mainly in NEC and NC) to climate warming had already emerged as early as the 1980s. These responses were earlier and more intense than those south of 40° N latitude (in the 1990s).
- (vii)
- The homogeneity test further corroborated the extensive drying tendency in China. The movement of the SPEI means indicated that the drought level is increasing at almost sites except for a part of Southeastern China (EC and SCC). The areas north and south of 30° N experienced a climate shift from wet to dry in the 1990s and 2000s, respectively. The dry–wet anomalies first appeared in the northern part of Eastern China (NEC and NC) and then migrated southward to affect Southern China (SCC). In terms of climate change, a significant positive anomaly in air temperature was experienced by almost sites in China. The significant increase in the mean temperature since 1980s/1990s may highly explain the significantly intensified drought status in NEC, NC, NWC, and SWC. Northern and Southwestern China experienced a significant (p < 0.05) increase in the drought level since the 1950s, which is strongly associated with significant warming over recent decades.
- (viii)
- Drought forecasting indicates that severe drought areas are distributed in NWC, the western part of NC, the western part of SWC, and the southern part of SCC in the near future. The climate is expected to show a wetness status in NEC, the southeastern part of NC, and the eastern part of EC. The susceptible areas for extreme weather events migrated to the northeast relative to the dry–wet condition in the past (2021). In view of the dry–wet pattern, the SPEI-indicated drought gravity center moved northward (western part of NC), and the wetness gravity center moved northeastward (30–40° N; 105–115° E). Compared to 2021, the drought severity will continue to increase in the next year in NWC and the western part of NC. The intensity of recent droughts in the western part of SWC and the southern part of SCC may be mitigated to some degree. Overall, NWC, the western part of NC, and the western part of SWC (20–50° N; 80–105° E) will continue to face severe challenges from droughts in the near term.
- (ix)
- The SARIMA models for NWC can better characterize the drought behavior in the area. The developed SARIMA models have the second-best capability to describe the drought evolution in NC. The forecasting of dry–wet conditions for the northern part of China can be considered more robust. The error metrics of the forecasting model showed a latitudinal distribution; this distribution corresponds to a general increase (decrease) in errors with decreasing (increasing) latitude in the Northern Hemisphere. This means that the SARIMA model may have a better ability to forecast the dry–wet variation at high-latitude than at low-latitude areas.
6.2. Limitations and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Number | Station | ID | Longitude (° E) | Latitude (° N) | Precip (mm) | Temp (°C) | Region |
|---|---|---|---|---|---|---|---|
| 1 | Changchun | 54,161 | 125.22 | 43.90 | 598.01 | 5.689 | NEC |
| 2 | Chaoyang | 54,324 | 120.45 | 41.55 | 477.28 | 9.095 | NEC |
| 3 | Dalian | 54,662 | 121.63 | 38.90 | 624.54 | 10.906 | NEC |
| 4 | Dandong | 54,497 | 124.33 | 40.05 | 997.15 | 8.962 | NEC |
| 5 | Funjin | 50,788 | 131.98 | 47.23 | 529.65 | 3.027 | NEC |
| 6 | Harbin | 50,953 | 126.77 | 45.75 | 539.54 | 4.376 | NEC |
| 7 | Hailun | 50,756 | 126.97 | 47.43 | 561.56 | 1.976 | NEC |
| 8 | Huma | 50,353 | 126.65 | 51.72 | 476.00 | −1.084 | NEC |
| 9 | Jiamusi | 50,873 | 130.17 | 46.49 | 556.73 | 3.567 | NEC |
| 10 | Jixi | 50,978 | 130.95 | 45.28 | 554.08 | 4.179 | NEC |
| 11 | Mudanjiang | 54,094 | 129.60 | 44.57 | 555.92 | 4.243 | NEC |
| 12 | Nenjiang | 50,557 | 125.23 | 49.17 | 492.37 | 0.408 | NEC |
| 13 | Qiqihar | 50,745 | 123.92 | 47.38 | 443.94 | 3.923 | NEC |
| 14 | Shenyang | 54,342 | 123.43 | 41.77 | 706.45 | 8.280 | NEC |
| 15 | Tonghua | 54,363 | 125.90 | 41.68 | 879.73 | 5.621 | NEC |
| 16 | Yanji | 54,292 | 129.47 | 42.88 | 533.75 | 5.454 | NEC |
| 17 | Yingkou | 54,471 | 122.20 | 40.67 | 650.96 | 9.491 | NEC |
| 18 | Baotou | 53,446 | 109.85 | 40.66 | 303.32 | 7.233 | NC |
| 19 | Beijing | 54,511 | 116.28 | 39.93 | 587.59 | 12.421 | NC |
| 20 | Boketu | 50,632 | 121.92 | 48.77 | 484.06 | −0.399 | NC |
| 21 | Changzhi | 53,882 | 113.04 | 36.03 | 587.06 | 9.720 | NC |
| 22 | Chengde | 54,423 | 117.93 | 40.97 | 534.04 | 8.979 | NC |
| 23 | Chifeng | 54,218 | 118.97 | 42.27 | 366.34 | 7.353 | NC |
| 24 | Duolun | 54,208 | 116.47 | 42.18 | 382.52 | 2.367 | NC |
| 25 | Hailar | 50,527 | 119.75 | 49.22 | 351.59 | −1.101 | NC |
| 26 | Hohhot | 53,463 | 111.68 | 40.82 | 409.03 | 6.690 | NC |
| 27 | Lindong | 54,027 | 119.40 | 43.98 | 376.04 | 5.566 | NC |
| 28 | Linfen | 53,868 | 111.32 | 36.05 | 486.85 | 12.874 | NC |
| 29 | Shanba | 53,420 | 107.10 | 40.58 | 136.86 | 7.613 | NC |
| 30 | Shijiazhuang | 53,698 | 114.42 | 38.03 | 546.08 | 13.562 | NC |
| 31 | Taiyuan | 53,772 | 112.55 | 37.78 | 442.18 | 10.127 | NC |
| 32 | Tianjin | 54,527 | 117.17 | 39.10 | 547.85 | 12.746 | NC |
| 33 | Tongliao | 54,135 | 122.27 | 43.60 | 388.54 | 6.752 | NC |
| 34 | Tulihe | 50,434 | 121.70 | 50.45 | 452.06 | −4.445 | NC |
| 35 | Ulanhot | 50,838 | 122.05 | 46.08 | 428.00 | 5.051 | NC |
| 36 | Xilinhot | 54,102 | 116.07 | 43.95 | 282.97 | 2.536 | NC |
| 37 | Xingtai | 53,798 | 114.50 | 37.07 | 538.79 | 13.840 | NC |
| 38 | Zhangjiakou | 54,401 | 114.88 | 40.78 | 406.28 | 8.559 | NC |
| 39 | Zhurihe | 53,276 | 112.90 | 42.40 | 215.27 | 5.117 | NC |
| 40 | Altay | 51,076 | 88.08 | 47.73 | 200.99 | 4.492 | NWC |
| 41 | Ankang | 57,245 | 109.03 | 32.72 | 825.44 | 15.835 | NWC |
| 42 | Dunhuang | 52,418 | 94.68 | 40.15 | 40.00 | 9.823 | NWC |
| 43 | Hami | 52,203 | 93.52 | 42.82 | 39.21 | 10.153 | NWC |
| 44 | Hanzhong | 57,127 | 107.03 | 33.07 | 871.83 | 14.691 | NWC |
| 45 | Hotan | 51,828 | 79.93 | 37.13 | 41.07 | 12.832 | NWC |
| 46 | Jiuquan | 52,533 | 98.48 | 39.77 | 90.11 | 7.665 | NWC |
| 47 | Jumo | 51,855 | 85.55 | 38.15 | 24.76 | 10.659 | NWC |
| 48 | Kashgar | 51,709 | 75.98 | 39.47 | 73.38 | 12.093 | NWC |
| 49 | Kuqa | 51,644 | 82.95 | 41.72 | 72.99 | 11.261 | NWC |
| 50 | Lanzhou | 52,889 | 103.88 | 36.05 | 315.27 | 9.949 | NWC |
| 51 | Linxia | 52,984 | 103.18 | 35.58 | 505.08 | 7.234 | NWC |
| 52 | Maduo | 56,033 | 98.22 | 34.92 | 328.01 | −3.500 | NWC |
| 53 | Minxian | 56,093 | 104.01 | 34.43 | 582.44 | 6.087 | NWC |
| 54 | Ruoqiang | 51,777 | 88.17 | 39.03 | 28.30 | 11.771 | NWC |
| 55 | Tacheng | 51,133 | 83.00 | 46.73 | 294.25 | 7.044 | NWC |
| 56 | Tianshui | 57,006 | 105.75 | 34.58 | 520.15 | 11.194 | NWC |
| 57 | Turpan | 51,573 | 89.20 | 42.93 | 16.56 | 14.826 | NWC |
| 58 | Urumqi | 51,463 | 87.62 | 43.78 | 273.37 | 7.092 | NWC |
| 59 | Wusu | 51,346 | 84.66 | 44.43 | 173.49 | 8.037 | NWC |
| 60 | Wuwei | 52,679 | 102.55 | 38.05 | 168.63 | 8.271 | NWC |
| 61 | Xi’an | 57,036 | 108.93 | 34.30 | 585.27 | 13.828 | NWC |
| 62 | Xifengzhen | 53,923 | 107.63 | 35.73 | 556.55 | 8.983 | NWC |
| 63 | Xining | 52,866 | 101.77 | 36.62 | 394.39 | 5.905 | NWC |
| 64 | Yan’an | 56,287 | 103.00 | 29.98 | 1716.06 | 16.387 | NWC |
| 65 | Yinchuan | 53,614 | 106.22 | 38.48 | 195.03 | 9.273 | NWC |
| 66 | Yining | 51,431 | 81.33 | 43.95 | 281.58 | 9.170 | NWC |
| 67 | Yulin | 53,646 | 109.70 | 38.23 | 416.76 | 8.592 | NWC |
| 68 | Yushu | 56,029 | 97.02 | 33.02 | 487.38 | 3.356 | NWC |
| 69 | Zhangye | 52,652 | 100.43 | 38.93 | 129.49 | 7.565 | NWC |
| 70 | Zhongning | 53.905 | 105.67 | 37.48 | 212.44 | 9.798 | NWC |
| 71 | Anqing | 58,424 | 117.05 | 30.53 | 1441.04 | 16.883 | EC |
| 72 | Dezhou | 54,714 | 116.22 | 37.29 | 562.48 | 13.402 | EC |
| 73 | Dongtai | 58,251 | 120.32 | 32.87 | 1073.08 | 14.887 | EC |
| 74 | Fenggu | 58,221 | 117.37 | 32.95 | 936.25 | 15.509 | EC |
| 75 | Fuyang | 58,203 | 115.83 | 32.93 | 922.32 | 15.295 | EC |
| 76 | Fuzhou | 58,847 | 119.28 | 26.08 | 1394.79 | 20.054 | EC |
| 77 | Ganzhou | 57,993 | 114.95 | 25.85 | 1439.06 | 19.597 | EC |
| 78 | Guangchang | 58,813 | 116.33 | 26.85 | 1734.93 | 18.391 | EC |
| 79 | Guixi | 58,626 | 117.21 | 28.30 | 1885.21 | 18.482 | EC |
| 80 | Hangzhou | 58,457 | 120.17 | 30.23 | 1457.10 | 16.767 | EC |
| 81 | Hefei | 58,321 | 117.23 | 31.87 | 1018.25 | 16.044 | EC |
| 82 | Heze | 54,906 | 115.26 | 35.15 | 653.66 | 14.077 | EC |
| 83 | Ji’an | 57,799 | 114.97 | 27.12 | 1534.61 | 18.640 | EC |
| 84 | Ji’nan | 54,823 | 116.98 | 36.68 | 674.93 | 14.116 | EC |
| 85 | Jiujiang | 58,502 | 115.59 | 29.45 | 1439.21 | 17.294 | EC |
| 86 | Linxi | 54,938 | 118.35 | 35.05 | 861.83 | 13.716 | EC |
| 87 | Nanchang | 58,606 | 115.92 | 28.60 | 1627.59 | 17.934 | EC |
| 88 | Nanjing | 58,238 | 118.80 | 32.00 | 1082.52 | 15.773 | EC |
| 89 | Ningbo | 58,562 | 121.56 | 29.86 | 1455.87 | 16.863 | EC |
| 90 | Pucheng | 58,731 | 118.53 | 27.92 | 1770.87 | 17.631 | EC |
| 91 | Qingdao | 54,857 | 120.33 | 36.07 | 709.93 | 12.660 | EC |
| 92 | Qingjiang | 58,144 | 119.03 | 33.60 | 956.24 | 14.508 | EC |
| 93 | Shanghai | 58,367 | 121.46 | 31.41 | 1186.32 | 16.434 | EC |
| 94 | Tunxi | 58,531 | 118.28 | 29.71 | 1733.85 | 16.630 | EC |
| 95 | Weifang | 54,843 | 119.08 | 36.70 | 622.58 | 12.750 | EC |
| 96 | Wenzhou | 58,659 | 120.67 | 28.02 | 1740.76 | 18.344 | EC |
| 97 | Xiamen | 59,134 | 118.08 | 24.48 | 1227.10 | 20.880 | EC |
| 98 | Xinpu | 58,044 | 119.10 | 34.36 | 908.61 | 14.315 | EC |
| 99 | Xuzhou | 58,028 | 117.22 | 34.19 | 853.83 | 14.602 | EC |
| 100 | Yantai | 54,765 | 121.26 | 37.36 | 664.92 | 12.750 | EC |
| 101 | Yaxian | 58,633 | 118.87 | 28.97 | 1695.83 | 17.560 | EC |
| 102 | Yongan | 58,921 | 117.35 | 25.97 | 1556.41 | 19.545 | EC |
| 103 | Anyang | 53,898 | 114.37 | 36.12 | 592.06 | 13.995 | SCC |
| 104 | Baise | 59,211 | 106.60 | 23.90 | 1091.86 | 22.173 | SCC |
| 105 | Beihai | 59,644 | 109.10 | 21.48 | 1739.30 | 22.888 | SCC |
| 106 | Binxian | 57,980 | 112.59 | 25.45 | 1509.89 | 17.939 | SCC |
| 107 | Changde | 57,662 | 111.68 | 29.05 | 1353.52 | 17.075 | SCC |
| 108 | Changsha | 57,679 | 113.04 | 28.12 | 1436.25 | 17.456 | SCC |
| 109 | Enshi | 57,447 | 109.47 | 30.28 | 1436.99 | 16.412 | SCC |
| 110 | Guangzhou | 59,288 | 113.19 | 23.08 | 1697.06 | 22.373 | SCC |
| 111 | Guilin | 57,957 | 110.30 | 25.33 | 1906.61 | 19.122 | SCC |
| 112 | Haikou | 59,758 | 110.35 | 20.03 | 1729.58 | 24.201 | SCC |
| 113 | Hankou | 57,494 | 114.13 | 30.62 | 1271.56 | 16.776 | SCC |
| 114 | Hengyang | 57,872 | 112.60 | 26.90 | 1326.32 | 18.273 | SCC |
| 115 | Heyuan | 59,293 | 114.68 | 23.73 | 1905.24 | 21.568 | SCC |
| 116 | Lingling | 57,865 | 111.36 | 26.14 | 1347.94 | 18.107 | SCC |
| 117 | Liuzhou | 59,044 | 109.23 | 24.22 | 1453.90 | 20.359 | SCC |
| 118 | Meixian | 59,117 | 116.12 | 24.30 | 1473.32 | 21.499 | SCC |
| 119 | Nanning | 59,431 | 108.35 | 22.82 | 1295.65 | 21.736 | SCC |
| 120 | Nanyang | 57,178 | 112.58 | 33.03 | 797.66 | 15.113 | SCC |
| 121 | Qujiang | 59,082 | 113.58 | 24.80 | 1594.82 | 20.427 | SCC |
| 122 | Shantou | 59,316 | 116.68 | 23.40 | 1560.61 | 21.876 | SCC |
| 123 | Wuzhou | 59266 | 111.18 | 23.29 | 1461.49 | 21.420 | SCC |
| 124 | Xinyang | 57,297 | 114.05 | 32.13 | 1099.06 | 15.473 | SCC |
| 125 | Yangjiang | 59,663 | 111.97 | 21.87 | 2331.82 | 22.553 | SCC |
| 126 | Yichang | 57,461 | 111.30 | 30.70 | 1157.32 | 16.951 | SCC |
| 127 | Yueyang | 57,584 | 113.08 | 29.38 | 1336.52 | 17.334 | SCC |
| 128 | Yunxian | 57,253 | 110.49 | 32.51 | 807.30 | 15.787 | SCC |
| 129 | Zhengzhou | 57,083 | 113.65 | 34.72 | 650.75 | 14.733 | SCC |
| 130 | Zhenjiang | 59,658 | 110.40 | 21.22 | 1628.90 | 23.307 | SCC |
| 131 | Zhijiang | 57,745 | 109.68 | 27.45 | 1262.01 | 16.689 | SCC |
| 132 | Zhongxiang | 57,378 | 112.57 | 31.17 | 971.28 | 16.301 | SCC |
| 133 | Baoshan | 56,748 | 99.22 | 25.13 | 968.48 | 16.172 | SWC |
| 134 | Bijie | 57,707 | 105.23 | 27.30 | 913.80 | 13.007 | SWC |
| 135 | Changdu | 56,137 | 97.17 | 31.15 | 482.00 | 7.763 | SWC |
| 136 | Chengdu | 56,294 | 104.02 | 30.67 | 920.37 | 16.310 | SWC |
| 137 | Chongqing | 57,516 | 106.48 | 29.52 | 1113.27 | 18.368 | SWC |
| 138 | Dali | 56,751 | 100.18 | 25.70 | 1044.01 | 15.165 | SWC |
| 139 | Daxian | 57,328 | 107.50 | 31.20 | 1195.92 | 17.356 | SWC |
| 140 | Deqin | 56,444 | 98.90 | 28.50 | 641.92 | 5.618 | SWC |
| 141 | Ganzi | 56,146 | 100.00 | 31.62 | 653.25 | 5.932 | SWC |
| 142 | Guiyang | 57,816 | 106.72 | 26.58 | 1139.85 | 15.069 | SWC |
| 143 | Huili | 56,671 | 102.25 | 26.65 | 1136.38 | 15.391 | SWC |
| 144 | Jinghong | 56,959 | 100.80 | 22.02 | 1163.76 | 22.361 | SWC |
| 145 | Kangding | 56,374 | 101.97 | 30.05 | 837.37 | 7.301 | SWC |
| 146 | Kunming | 56,778 | 102.68 | 25.02 | 992.92 | 15.256 | SWC |
| 147 | Lhasa | 55,591 | 91.13 | 29.67 | 452.63 | 8.235 | SWC |
| 148 | Lijiang | 56,651 | 100.47 | 26.83 | 961.82 | 12.962 | SWC |
| 149 | Lincang | 56,951 | 100.22 | 23.95 | 1140.59 | 17.602 | SWC |
| 150 | Mengzi | 56,985 | 103.38 | 23.38 | 828.93 | 18.914 | SWC |
| 151 | Mianyang | 56,196 | 104.68 | 31.47 | 915.82 | 16.578 | SWC |
| 152 | Nanchong | 57,411 | 106.08 | 30.80 | 1025.30 | 17.548 | SWC |
| 153 | Neijiang | 57,504 | 105.05 | 29.58 | 1019.54 | 17.660 | SWC |
| 154 | Rongjiang | 57,932 | 108.53 | 25.97 | 1214.32 | 18.372 | SWC |
| 155 | Xichang | 56,571 | 102.27 | 27.90 | 1013.48 | 17.172 | SWC |
| 156 | Xingren | 57,902 | 105.18 | 25.43 | 1300.31 | 15.463 | SWC |
| 157 | Ya’an | 53,845 | 109.50 | 36.60 | 550.54 | 9.906 | SWC |
| 158 | Yibin | 56,492 | 104.60 | 28.80 | 1099.62 | 18.039 | SWC |
| 159 | Youyang | 57,633 | 108.77 | 28.83 | 1365.54 | 14.888 | SWC |
| 160 | Zunyi | 57,713 | 106.88 | 27.70 | 1115.94 | 15.136 | SWC |
| Number | Station | Model | AIC | BIC | HQIC | Ljung-Box (Q) | Region |
|---|---|---|---|---|---|---|---|
| 1 | Changchun | SARIMA (1,0,1)(2,1,2) | 621.981 | 655.023 | 634.653 | 29.10 | NEC |
| 2 | Chaoyang | SARIMA (1,0,0)(2,1,2) | 431.521 | 459.842 | 442.383 | 29.96 | NEC |
| 3 | Dalian | SARIMA (1,0,1)(2,1,2) | 456.720 | 489.761 | 469.391 | 27.38 | NEC |
| 4 | Dandong | SARIMA (1,0,0)(1,1,2) | 547.965 | 571.566 | 557.016 | 31.37 | NEC |
| 5 | Funjin | SARIMA (2,0,0)(0,1,2) | 169.358 | 192.959 | 178.409 | 22.51 | NEC |
| 6 | Harbin | SARIMA (0,1,1)(1,1,2) | 533.707 | 557.302 | 542.756 | 22.24 | NEC |
| 7 | Hailun | SARIMA (1,0,0)(2,1,2) | 597.840 | 626.161 | 608.701 | 25.09 | NEC |
| 8 | Huma | SARIMA (2,0,0)(2,1,2) | 440.195 | 473.237 | 452.867 | 37.77 | NEC |
| 9 | Jiamusi | SARIMA (1,0,0)(2,1,2) | 435.626 | 463.947 | 446.488 | 14.71 | NEC |
| 10 | Jixi | SARIMA (1,0,0)(0,1,2) | 477.986 | 496.867 | 485.227 | 33.91 | NEC |
| 11 | Mudanjiang | SARIMA (1,0,1)(2,1,2) | 587.223 | 620.265 | 599.895 | 38.37 | NEC |
| 12 | Nenjiang | SARIMA (1,0,0)(0,1,2) | 535.165 | 554.046 | 542.406 | 47.51 | NEC |
| 13 | Qiqihar | SARIMA (2,0,0)(2,1,2) | 520.517 | 553.559 | 533.189 | 25.79 | NEC |
| 14 | Shenyang | SARIMA (0,1,0)(1,1,2) | 449.001 | 467.877 | 456.241 | 46.02 | NEC |
| 15 | Tonghua | SARIMA (1,0,0)(2,1,2) | 473.205 | 501.527 | 484.067 | 27.16 | NEC |
| 16 | Yanji | SARIMA (2,0,0)(1,1,2) | 549.178 | 577.499 | 560.039 | 23.06 | NEC |
| 17 | Yingkou | SARIMA (0,1,0)(1,1,2) | 435.780 | 454.656 | 443.020 | 19.06 | NEC |
| 18 | Baotou | SARIMA (1,1,0)(2,1,2) | 292.482 | 320.797 | 303.342 | 61.91 | NC |
| 19 | Beijing | SARIMA (0,1,0)(2,1,2) | 129.048 | 152.643 | 138.098 | 46.06 | NC |
| 20 | Boketu | SARIMA (1,0,1)(1,1,2) | 644.768 | 673.089 | 655.629 | 16.74 | NC |
| 21 | Changzhi | SARIMA (1,1,1)(0,1,2) | 600.729 | 624.325 | 609.779 | 26.18 | NC |
| 22 | Chengde | SARIMA (1,0,0)(0,1,2) | 433.676 | 452.557 | 440.917 | 35.16 | NC |
| 23 | Chifeng | SARIMA (1,0,1)(1,1,2) | 400.237 | 428.558 | 411.098 | 35.78 | NC |
| 24 | Duolun | SARIMA (0,1,0)(1,1,2) | 532.723 | 551.599 | 539.963 | 32.74 | NC |
| 25 | Hailar | SARIMA (0,1,2)(2,0,2) | 165.695 | 198.829 | 178.394 | 46.54 | NC |
| 26 | Hohhot | SARIMA (2,0,0)(0,1,2) | 211.490 | 235.091 | 220.542 | 46.25 | NC |
| 27 | Lindong | SARIMA (0,1,1)(2,1,2) | 359.136 | 387.450 | 369.995 | 36.64 | NC |
| 28 | Linfen | SARIMA (1,1,2)(0,1,2) | 424.671 | 452.985 | 435.530 | 25.23 | NC |
| 29 | Shanba | SARIMA (0,1,1)(2,1,2) | 335.478 | 363.792 | 346.337 | 27.82 | NC |
| 30 | Shijiazhuang | SARIMA (1,1,1)(1,1,2) | 323.969 | 352.283 | 334.828 | 35.18 | NC |
| 31 | Taiyuan | SARIMA (0,1,0)(0,1,2) | 472.380 | 486.537 | 477.810 | 42.60 | NC |
| 32 | Tianjin | SARIMA (1,1,0)(0,1,2) | 356.438 | 375.314 | 363.677 | 20.98 | NC |
| 33 | Tongliao | SARIMA (1,0,0)(0,1,2) | 402.889 | 421.770 | 410.130 | 23.42 | NC |
| 34 | Tulihe | SARIMA (1,0,0)(0,1,2) | 355.057 | 373.938 | 362.298 | 50.08 | NC |
| 35 | Ulanhot | SARIMA (1,0,1)(1,1,2) | 306.226 | 334.547 | 317.087 | 42.50 | NC |
| 36 | Xilinhot | SARIMA (0,1,1)(1,1,2) | 188.149 | 211.744 | 197.199 | 44.12 | NC |
| 37 | Xingtai | SARIMA (0,1,0)(1,1,2) | 217.899 | 236.775 | 225.139 | 33.94 | NC |
| 38 | Zhangjiakou | SARIMA (1,0,0)(2,1,2) | 297.810 | 326.132 | 308.672 | 36.88 | NC |
| 39 | Zhurihe | SARIMA (1,1,0)(0,1,2) | 127.377 | 146.253 | 134.616 | 61.00 | NC |
| 40 | Altay | SARIMA (2,0,0)(0,1,2) | 18.939 | 42.540 | 27.990 | 36.80 | NWC |
| 41 | Ankang | SARIMA (1,0,1)(0,0,2) | 528.951 | 552.624 | 538.023 | 23.41 | NWC |
| 42 | Dunhuang | SARIMA (1,1,0)(0,1,2) | −83.947 | −65.071 | −76.708 | 28.67 | NWC |
| 43 | Hami | SARIMA (0,1,2)(0,1,2) | −148.044 | −124.449 | −138.995 | 33.85 | NWC |
| 44 | Hanzhong | SARIMA (0,1,0)(0,1,2) | 472.149 | 486.307 | 477.579 | 48.34 | NWC |
| 45 | Hotan | SARIMA (1,1,1)(1,1,2) | −221.809 | −193.495 | −210.950 | 47.15 | NWC |
| 46 | Jiuquan | SARIMA (0,1,0)(0,1,2) | 351.778 | 365.935 | 357.208 | 42.35 | NWC |
| 47 | Jumo | SARIMA (2,1,1)(0,1,2) | −125.400 | −97.086 | −114.541 | 35.50 | NWC |
| 48 | Kashgar | SARIMA (2,0,2)(0,1,2) | 135.528 | 168.570 | 148.200 | 38.31 | NWC |
| 49 | Kuqa | SARIMA (0,1,0)(1,1,2) | 231.600 | 250.476 | 238.839 | 30.86 | NWC |
| 50 | Lanzhou | SARIMA (1,1,0)(2,1,2) | 221.810 | 250.124 | 232.670 | 21.70 | NWC |
| 51 | Linxia | SARIMA (2,0,0)(1,1,2) | 449.237 | 477.559 | 460.099 | 32.39 | NWC |
| 52 | Maduo | SARIMA (1,0,0)(1,1,2) | 373.421 | 397.022 | 382.472 | 34.58 | NWC |
| 53 | Minxian | SARIMA (1,0,1)(0,1,2) | 379.968 | 403.569 | 389.019 | 51.76 | NWC |
| 54 | Ruoqiang | SARIMA (1,0,0)(0,1,2) | 380.921 | 399.802 | 388.162 | 34.80 | NWC |
| 55 | Tacheng | SARIMA (1,1,0)(2,1,2) | −14.007 | 14.307 | −3.147 | 35.18 | NWC |
| 56 | Tianshui | SARIMA (0,1,2)(0,1,2) | 302.799 | 326.394 | 311.849 | 30.16 | NWC |
| 57 | Turpan | SARIMA (1,1,2)(1,1,2) | −785.200 | −752.167 | −772.531 | 24.32 | NWC |
| 58 | Urumqi | SARIMA (1,0,2)(1,1,2) | −43.637 | −10.595 | −30.965 | 30.70 | NWC |
| 59 | Wusu | SARIMA (1,0,2)(0,1,2) | 69.821 | 98.142 | 80.683 | 31.68 | NWC |
| 60 | Wuwei | SARIMA (1,0,0)(1,1,2) | 235.515 | 259.116 | 244.566 | 22.44 | NWC |
| 61 | Xi’an | SARIMA (1,1,1)(1,1,2) | 573.485 | 601.799 | 584.344 | 30.98 | NWC |
| 62 | Xifengzhen | SARIMA (2,1,2)(1,1,2) | 530.024 | 567.776 | 544.503 | 25.61 | NWC |
| 63 | Xining | SARIMA (1,2,1)(0,1,2) | 408.636 | 432.225 | 417.683 | 48.23 | NWC |
| 64 | Yan’an | SARIMA (1,1,1)(0,1,2) | 518.387 | 541.982 | 527.437 | 32.82 | NWC |
| 65 | Yinchuan | SARIMA (1,1,2)(2,1,2) | 246.672 | 284.424 | 261.151 | 30.92 | NWC |
| 66 | Yining | SARIMA (1,1,0)(0,0,1) | −31.523 | −17.322 | −26.080 | 55.93 | NWC |
| 67 | Yulin | SARIMA (1,0,1)(1,1,2) | 401.833 | 430.154 | 412.694 | 16.50 | NWC |
| 68 | Yushu | SARIMA (1,0,0)(1,1,2) | 341.645 | 365.246 | 350.696 | 31.00 | NWC |
| 69 | Zhangye | SARIMA (0,1,0)(0,1,2) | 55.954 | 70.111 | 61.384 | 39.29 | NWC |
| 70 | Zhongning | SARIMA (2,1,0)(1,1,2) | 256.604 | 284.918 | 267.463 | 35.41 | NWC |
| 71 | Anqing | SARIMA (2,0,0)(1,0,2) | 381.552 | 409.960 | 392.439 | 47.86 | EC |
| 72 | Dezhou | SARIMA (1,0,1)(0,1,2) | 294.138 | 317.739 | 303.190 | 28.28 | EC |
| 73 | Dongtai | SARIMA (2,0,1)(2,1,2) | 451.032 | 488.794 | 465.514 | 22.89 | EC |
| 74 | Fenggu | SARIMA (1,0,0)(0,1,2) | 434.095 | 452.976 | 441.336 | 40.50 | EC |
| 75 | Fuyang | SARIMA (1,0,1)(0,0,1) | 250.557 | 269.495 | 257.815 | 57.59 | EC |
| 76 | Fuzhou | SARIMA (1,0,0)(0,1,2) | 521.341 | 540.222 | 528.582 | 26.87 | EC |
| 77 | Ganzhou | SARIMA (1,1,0)(0,1,2) | 238.008 | 256.884 | 245.247 | 31.20 | EC |
| 78 | Guangchang | SARIMA (2,0,1)(0,1,2) | 210.874 | 239.196 | 221.736 | 40.06 | EC |
| 79 | Guixi | SARIMA (0,1,1)(2,1,2) | 336.065 | 364.379 | 346.924 | 41.50 | EC |
| 80 | Hangzhou | SARIMA (1,0,0)(1,0,2) | 358.610 | 382.283 | 367.682 | 29.26 | EC |
| 81 | Hefei | SARIMA (1,0,1)(0,0,1) | 523.982 | 542.920 | 531.240 | 35.99 | EC |
| 82 | Heze | SARIMA (1,1,0)(0,1,2) | 677.309 | 696.185 | 684.548 | 50.37 | EC |
| 83 | Ji’an | SARIMA (1,1,1)(0,1,2) | 289.690 | 313.285 | 298.740 | 24.96 | EC |
| 84 | Ji’nan | SARIMA (1,0,0)(0,1,2) | 433.945 | 452.826 | 441.186 | 22.42 | EC |
| 85 | Jiujiang | SARIMA (1,0,0)(0,1,2) | 327.546 | 346.427 | 334.787 | 40.33 | EC |
| 86 | Linxi | SARIMA (0,1,1)(0,1,2) | 613.011 | 631.887 | 620.250 | 27.73 | EC |
| 87 | Nanchang | SARIMA (1,0,2)(2,1,2) | 361.770 | 399.532 | 376.252 | 41.89 | EC |
| 88 | Nanjing | SARIMA (1,0,0)(0,0,1) | 352.993 | 367.197 | 358.437 | 40.91 | EC |
| 89 | Ningbo | SARIMA (1,0,0)(0,1,2) | 531.752 | 550.633 | 538.993 | 44.13 | EC |
| 90 | Pucheng | SARIMA (1,0,1)(0,1,2) | 397.672 | 421.273 | 406.723 | 45.44 | EC |
| 91 | Qingdao | SARIMA (2,0,0)(0,1,2) | 251.286 | 274.887 | 260.337 | 33.87 | EC |
| 92 | Qingjiang | SARIMA (1,0,0)(0,1,2) | 547.982 | 566.863 | 555.223 | 26.45 | EC |
| 93 | Shanghai | SARIMA (1,0,0)(0,1,2) | 503.774 | 522.655 | 511.015 | 26.40 | EC |
| 94 | Tunxi | SARIMA (2,0,0)(1,1,2) | 347.367 | 375.688 | 358.228 | 38.50 | EC |
| 95 | Weifang | SARIMA (2,1,1)(0,1,2) | 336.918 | 365.232 | 347.777 | 45.70 | EC |
| 96 | Wenzhou | SARIMA (1,0,0)(0,0,1) | 310.587 | 324.791 | 316.030 | 57.19 | EC |
| 97 | Xiamen | SARIMA (0,1,1)(0,1,2) | 367.123 | 385.999 | 374.363 | 43.67 | EC |
| 98 | Xinpu | SARIMA (1,0,2)(0,1,2) | 434.893 | 463.214 | 445.755 | 34.05 | EC |
| 99 | Xuzhou | SARIMA (0,1,0)(0,1,2) | 566.490 | 580.647 | 571.919 | 43.21 | EC |
| 100 | Yantai | SARIMA (0,1,0)(0,1,2) | 425.135 | 439.292 | 430.564 | 44.50 | EC |
| 101 | Yaxian | SARIMA (2,0,1)(1,0,2) | 80.523 | 113.665 | 93.224 | 38.11 | EC |
| 102 | Yongan | SARIMA (0,1,0)(0,1,2) | 514.180 | 528.337 | 519.609 | 37.92 | EC |
| 103 | Anyang | SARIMA (1,0,0)(0,1,2) | 505.245 | 524.126 | 512.486 | 23.25 | SCC |
| 104 | Baise | SARIMA (2,0,0)(0,1,2) | 466.903 | 490.504 | 475.955 | 43.50 | SCC |
| 105 | Beihai | SARIMA (1,0,0)(2,1,2) | 533.819 | 562.140 | 544.680 | 43.04 | SCC |
| 106 | Binxian | SARIMA (2,0,1)(0,0,1) | 251.754 | 275.427 | 260.827 | 32.04 | SCC |
| 107 | Changde | SARIMA (2,0,0)(0,1,2) | 461.957 | 485.558 | 471.008 | 24.01 | SCC |
| 108 | Changsha | SARIMA (1,0,0)(0,0,1) | 380.536 | 394.740 | 385.980 | 35.08 | SCC |
| 109 | Enshi | SARIMA (1,0,0)(0,1,2) | 619.585 | 638.466 | 626.826 | 32.11 | SCC |
| 110 | Guangzhou | SARIMA (1,0,0)(0,1,2) | 597.991 | 616.872 | 605.232 | 60.92 | SCC |
| 111 | Guilin | SARIMA (1,0,0)(2,0,1) | 403.833 | 427.506 | 412.905 | 41.76 | SCC |
| 112 | Haikou | SARIMA (0,1,2)(2,1,2) | 384.154 | 417.187 | 396.823 | 21.97 | SCC |
| 113 | Hankou | SARIMA (1,0,1)(0,1,2) | 485.309 | 508.910 | 494.360 | 28.26 | SCC |
| 114 | Hengyang | SARIMA (1,1,1)(2,0,1) | 404.758 | 433.158 | 415.643 | 33.29 | SCC |
| 115 | Heyuan | SARIMA (1,0,0)(2,0,1) | 319.169 | 342.842 | 328.242 | 39.49 | SCC |
| 116 | Lingling | SARIMA (1,1,0)(2,1,2) | 348.345 | 376.659 | 359.204 | 36.59 | SCC |
| 117 | Liuzhou | SARIMA (1,0,1)(1,1,2) | 540.351 | 568.672 | 551.212 | 39.28 | SCC |
| 118 | Meixian | SARIMA (1,0,1)(0,1,2) | 329.355 | 352.956 | 338.407 | 36.77 | SCC |
| 119 | Nanning | SARIMA (1,0,0)(0,1,2) | 628.703 | 647.584 | 635.944 | 40.12 | SCC |
| 120 | Nanyang | SARIMA (2,0,0)(0,1,2) | 510.283 | 533.884 | 519.334 | 25.41 | SCC |
| 121 | Qujiang | SARIMA (1,0,0)(0,1,2) | 473.493 | 492.374 | 480.734 | 45.92 | SCC |
| 122 | Shantou | SARIMA (2,1,2)(0,1,2) | 403.601 | 436.634 | 416.270 | 28.63 | SCC |
| 123 | Wuzhou | SARIMA (0,1,0)(2,1,2) | 559.181 | 582.776 | 568.231 | 30.61 | SCC |
| 124 | Xinyang | SARIMA (1,1,2)(1,1,2) | 583.954 | 616.987 | 596.623 | 43.47 | SCC |
| 125 | Yangjiang | SARIMA (2,0,0)(0,1,2) | 505.848 | 529.449 | 514.899 | 43.64 | SCC |
| 126 | Yichang | SARIMA (1,0,1)(0,1,2) | 561.646 | 585.247 | 570.697 | 44.96 | SCC |
| 127 | Yueyang | SARIMA (0,1,1)(2,0,2) | 332.295 | 360.695 | 343.180 | 44.49 | SCC |
| 128 | Yunxian | SARIMA (1,0,0)(1,1,2) | 507.678 | 531.279 | 516.729 | 37.92 | SCC |
| 129 | Zhengzhou | SARIMA (2,0,1)(1,1,2) | 646.528 | 679.570 | 659.200 | 27.79 | SCC |
| 130 | Zhenjiang | SARIMA (2,0,0)(0,1,2) | 510.773 | 534.374 | 519.825 | 43.15 | SCC |
| 131 | Zhijiang | SARIMA (1,0,0)(2,1,2) | 592.453 | 620.775 | 603.315 | 36.94 | SCC |
| 132 | Zhongxiang | SARIMA (1,0,1)(0,1,2) | 544.817 | 568.418 | 553.868 | 58.24 | SCC |
| 133 | Baoshan | SARIMA (1,1,1)(0,1,2) | 500.516 | 524.111 | 509.566 | 38.74 | SWC |
| 134 | Bijie | SARIMA (0,1,1)(2,1,2) | 548.958 | 577.273 | 559.818 | 20.34 | SWC |
| 135 | Changdu | SARIMA (1,0,0)(0,1,2) | 428.642 | 447.522 | 435.883 | 24.17 | SWC |
| 136 | Chengdu | SARIMA (1,1,1)(1,1,2) | 570.504 | 598.818 | 581.363 | 26.30 | SWC |
| 137 | Chongqing | SARIMA (1,0,0)(1,0,2) | 648.385 | 672.058 | 657.457 | 30.98 | SWC |
| 138 | Dali | SARIMA (1,0,0)(2,1,2) | 401.758 | 430.080 | 412.620 | 52.59 | SWC |
| 139 | Daxian | SARIMA (1,0,1)(0,0,1) | 587.484 | 606.423 | 594.742 | 37.64 | SWC |
| 140 | Deqin | SARIMA (0,1,2)(1,1,2) | 345.613 | 373.927 | 356.472 | 32.60 | SWC |
| 141 | Ganzi | SARIMA (1,0,0)(0,1,2) | 521.426 | 540.306 | 528.667 | 48.80 | SWC |
| 142 | Guiyang | SARIMA (1,0,0)(0,0,1) | 497.552 | 511.756 | 502.995 | 33.84 | SWC |
| 143 | Huili | SARIMA (1,0,1)(0,1,2) | 393.877 | 417.478 | 402.928 | 27.77 | SWC |
| 144 | Jinghong | SARIMA (1,1,1)(0,1,2) | 351.273 | 374.868 | 360.322 | 30.18 | SWC |
| 145 | Kangding | SARIMA (1,0,0)(2,1,2) | 705.131 | 733.453 | 715.993 | 44.52 | SWC |
| 146 | Kunming | SARIMA (1,0,2)(0,1,2) | 359.973 | 388.294 | 370.834 | 41.78 | SWC |
| 147 | Lhasa | SARIMA (0,1,1)(0,1,2) | 397.194 | 416.070 | 404.433 | 34.73 | SWC |
| 148 | Lijiang | SARIMA (1,0,2)(2,1,2) | 632.539 | 670.301 | 647.021 | 44.20 | SWC |
| 149 | Lincang | SARIMA (0,1,0)(1,1,2) | 423.164 | 442.040 | 430.404 | 42.62 | SWC |
| 150 | Mengzi | SARIMA (0,1,0)(0,1,2) | 386.124 | 400.281 | 391.554 | 45.43 | SWC |
| 151 | Mianyang | SARIMA (0,1,0)(0,1,2) | 516.308 | 530.465 | 521.738 | 44.81 | SWC |
| 152 | Nanchong | SARIMA (1,0,1)(1,1,2) | 603.111 | 631.432 | 613.972 | 30.48 | SWC |
| 153 | Neijiang | SARIMA (1,0,0)(2,1,2) | 476.277 | 504.599 | 487.139 | 33.89 | SWC |
| 154 | Rongjiang | SARIMA (1,0,2)(0,0,1) | 322.928 | 346.601 | 332.001 | 34.70 | SWC |
| 155 | Xichang | SARIMA (1,0,0)(1,1,2) | 511.369 | 534.970 | 520.420 | 35.36 | SWC |
| 156 | Xingren | SARIMA (1,0,0)(0,1,2) | 431.222 | 450.103 | 438.463 | 36.26 | SWC |
| 157 | Ya’an | SARIMA (0,1,0)(0,1,2) | 485.979 | 500.136 | 491.408 | 29.07 | SWC |
| 158 | Yibin | SARIMA (1,1,0)(2,1,2) | 238.126 | 266.440 | 248.985 | 25.18 | SWC |
| 159 | Youyang | SARIMA (1,0,0)(0,1,2) | 627.975 | 646.856 | 635.216 | 32.45 | SWC |
| 160 | Zunyi | SARIMA (2,1,2)(0,0,1) | 447.909 | 476.310 | 458.794 | 22.18 | SWC |
References
- IPCC. Summary for policymakers. climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridgem, UK, 2013. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridgem, UK, 2021. [Google Scholar]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Tang, H.; Wen, T.; Shi, P.; Qu, S.; Zhao, L.; Li, Q. Analysis of Characteristics of Hydrological and Meteorological Drought Evolution in Southwest China. Water 2021, 13, 1846. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Chen, Q.; Pu, X.; Xiang, L. Multi-models for SPI drought forecasting in the north of Haihe River Basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 2471–2481. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Wang, L.; Yang, M. Zonal Patterns of Meteorological Drought on the Yunnan-Guizhou Plateau, China. Front. Environ. Sci. 2021, 9, 722285. [Google Scholar] [CrossRef]
- Ding, Y.; Gong, X.; Xing, Z.; Cai, H.; Zhou, Z.; Zhang, D.; Sun, P.; Shi, H. Attribution of meteorological, hydrological and agricultural drought propagation in different climatic regions of China. Agric. Water Manag. 2021, 255, 106996. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.; Roderick, M. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, H.; Chen, J.; Fu, G.; Zhan, C.; Yang, H. Quantitative analysis of nonlinear climate change impact on drought based on the standardized precipitation and evapotranspiration index. Ecol. Indic. 2021, 121, 107107. [Google Scholar] [CrossRef]
- Zhao, N.; Chen, M. A Comprehensive Study of Spatiotemporal Variations in Temperature Extremes across China during 1960–2018. Sustainability 2021, 13, 3807. [Google Scholar] [CrossRef]
- Araneda-Cabrera, R.; Bermudez, M.; Puertas, J. Revealing the spatio-temporal characteristics of drought in Mozambique and their relationship with large-scale climate variability. J. Hydrol. Reg. Stud. 2021, 38, 100938. [Google Scholar] [CrossRef]
- Han, R.; Li, Z.; Li, Z.; Han, Y. Spatial–Temporal Assessment of Historical and Future Meteorological Droughts in China. Atmosphere 2021, 12, 787. [Google Scholar] [CrossRef]
- He, B.; Chang, J.; Wang, Y.; Wang, Y.; Zhou, S.; Chen, C. Spatio-temporal evolution and nonstationary characteristics of meteorological drought in inland arid areas. Ecol. Indic. 2021, 126, 107644. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Hayes, M.; Svoboda, M.; Heim, R. Are droughts becoming more frequent or severe in China based on the Standardized Precipitation Evapotranspiration Index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.; Tian, M.; Zhang, S.; Liu, J.; Zhu, D.; Li, D.; Chen, Y. Application of the ARIMA Models in Drought Forecasting Using the Standardized Precipitation Index. In Proceedings of the Computer and Computing Technologies in Agriculture VI, Zhangjiajie, China, 19–21 October 2013; pp. 352–358. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Wang, Y.; Li, Z.; Chang, J.; Guo, A.; Zhou, K. Characterizing spatio-temporal patterns of multi-scalar drought risk in Mainland China. Ecol. Indic. 2021, 131, 108189. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, Q.; Singh, V.; Shi, P.; Zheng, Y. Variations of dryness/wetness across China: Changing properties, drought risks, and causes. Glob. Planet. Chang. 2017, 155, 1–12. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Pan, T. Spatial and temporal patterns of drought hazard for China under different RCP scenarios in the 21st century. Int. J. Disaster Risk Reduct. 2021, 52, 101948. [Google Scholar] [CrossRef]
- Ma, D.; Deng, H.; Yin, Y.; Wu, S.; Zheng, D. Sensitivity of arid/humid patterns in China to future climate change under a high-emissions scenario. J. Geogr. Sci. 2019, 29, 29–48. [Google Scholar] [CrossRef] [Green Version]
- Min, S.; Zhang, X.; Zwiers, F.; Hegerl, G. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Zhang, Y.; Tong, L.; Li, X.; Li, J.; Sun, Z. Assessment of Spatial Agglomeration of Agricultural Drought Disaster in China from 1978 to 2016. Sci. Rep. 2019, 9, 14393. [Google Scholar] [CrossRef]
- Gong, X.; Du, S.; Li, F.; Ding, Y. Study on the Spatial and Temporal Characteristics of Mesoscale Drought in China under Future Climate Change Scenarios. Water 2021, 13, 2761. [Google Scholar] [CrossRef]
- Sun, S.; Du, W.; Song, Z.; Zhang, D.; Wu, X.; Chen, B.; Wu, Y. Response of Gross Primary Productivity to Drought Time-Scales Across China. J. Geophys. Res. Biogeosci. 2021, 126, e2020JG005953. [Google Scholar] [CrossRef]
- American Meteorological Society (AMS) Drought—An Information Statement. Available online: https://www.ametsoc.org/ams/index.cfm/about-ams/ams-statements/statements-of-the-ams-in-force/drought/ (accessed on 30 March 2022).
- Trenberth, K.; Dai, A.; van der Schrier, G.; Jones, P.; Barichivich, J.; Briffa, K.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Jiang, G.; Gu, X.; Zhao, D.; Xu, J.; Yang, C.; Wang, S.; Li, Y.; Li, B. The Study of Drought in Future Climate Scenarios in the Huang-Huai-Hai Region. Water 2021, 13, 3474. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Q.; Lu, H.; Wang, Z.; Zhang, K.; Wang, P. Future droughts in China using the standardized precipitation evapotranspiration index (SPEI) under multi-spatial scales. Nat. Hazards 2021, 109, 615–636. [Google Scholar] [CrossRef]
- Zhang, G.; Gan, T.; Su, X. Twenty-first century drought analysis across China under climate change. Clim. Dyn. 2021, 1–21. [Google Scholar] [CrossRef]
- Byakatonda, J.; Openy, G.; Sempewo, J.; Mucunguzi, D. Over a century evidence of historical and recent dryness/wetness in sub-humid areas: A Uganda, East African case. Meteorol. Appl. 2021, 28, e2028. [Google Scholar] [CrossRef]
- Tian, M.; Wang, P.; Khan, J. Drought Forecasting with Vegetation Temperature Condition Index Using ARIMA Models in the Guanzhong Plain. Remote Sens. 2016, 8, 690. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Chen, J.; Nie, T.; Dai, C. Spatial–temporal changes in meteorological and agricultural droughts in Northeast China: Change patterns, response relationships and causes. Nat. Hazards 2022, 110, 155–173. [Google Scholar] [CrossRef]
- Xu, H.; Wang, X.; Zhao, C.; Shan, S.; Guo, J. Seasonal and aridity influences on the relationships between drought indices and hydrological variables over China. Weather Clim. Extrem. 2021, 34, 100393. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Jiao, W.; Zeng, X.; Xing, X.; Zhang, L.; Yan, J.; Hong, Y. Drought monitoring based on a new combined remote sensing index across the transitional area between humid and arid regions in China. Atmos. Res. 2021, 264, 105850. [Google Scholar] [CrossRef]
- Ma, Z. The interdecadal trend and shift of dry/wet over the central part of North China and their relationship to the Pacific Decadal Oscillation (PDO). Chin. Sci. Bull. 2007, 52, 2130–2139. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, B.; Huang, H.; Zeng, J.; Wang, X.; Jiao, W. Spatiotemporal Characteristics of Drought in the North China Plain over the Past 58 Years. Atmosphere 2021, 12, 844. [Google Scholar] [CrossRef]
- El Kenawy, A.; Al Buloshi, A.; Al-Awadhi, T.; Al Nasiri, N.; Navarro-Serrano, F.; Alhatrushi, S.; Robaa, S.; Domínguez-Castro, F.; McCabe, M.; Schuwerack, P.; et al. Evidence for intensification of meteorological droughts in Oman over the past four decades. Atmos. Res. 2020, 246, 105126. [Google Scholar] [CrossRef]
- Sein, Z.; Zhi, X.; Ogou, F.; Nooni, I.; Lim Kam Sian, K.; Gnitou, G. Spatio-Temporal Analysis of Drought Variability in Myanmar Based on the Standardized Precipitation Evapotranspiration Index (SPEI) and Its Impact on Crop Production. Agronomy 2021, 11, 1691. [Google Scholar] [CrossRef]
- Ma, Z.; Fu, C. Some evidence of drying trend over Northern China from 1951 to 2004. Chin. Sci. Bull. 2006, 51, 2913–2925. [Google Scholar] [CrossRef]
- He, Y.; Ye, J.; Yang, X. Analysis of the spatio-temporal patterns of dry and wet conditions in the Huai River Basin using the standardized precipitation index. Atmos. Res. 2015, 166, 120–128. [Google Scholar] [CrossRef] [Green Version]
- Keyantash, J.; Dracup, J. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, Y.; Cao, L.; Wu, J.; Zhang, S.; Hu, C.; Zhujie, S. Characteristics of Dry-Wet Climate Change in China during the Past 60 Years and Its Trends Projection. Atmosphere 2022, 13, 275. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Beguería, S.; Lopez-Moreno, J. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.; Beguería, S.; Lopez-Moreno, J.; Angulo, M.; El Kenawy, A. A New Global 0.5° Gridded Dataset (1901–2006) of a Multiscalar Drought Index: Comparison with Current Drought Index Datasets Based on the Palmer Drought Severity Index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef] [Green Version]
- Mossad, A.; Alazba, A. Drought Forecasting Using Stochastic Models in a Hyper-Arid Climate. Atmosphere 2015, 6, 410–430. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Shah, S.; Uqaili, M.; Kumar, L.; Zafar, R. Forecasting of Drought: A Case Study of Water-Stressed Region of Pakistan. Atmosphere 2021, 12, 1248. [Google Scholar] [CrossRef]
- Baldi, M.; Zhou, S.; Sun, S.; Shi, W.; Wang, J.; Li, J.; Wang, G.; Lou, W. Spatiotemporal Differences in Dominants of Dryness/Wetness Changes in Southwest China. Adv. Meteorol. 2019, 2019, 2820769. [Google Scholar] [CrossRef]
- Chen, D.; Gao, G.; Xu, C.-Y.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Penman-Monteith estimates of reference ET in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- Ge, Q.; Liu, H.; Ma, X.; Zheng, J.; Hao, Z. Characteristics of temperature change in China over the last 2000 years and spatial patterns of dryness/wetness during cold and warm periods. Adv. Atmos. Sci. 2017, 34, 941–951. [Google Scholar] [CrossRef]
- Qian, C.; Zhou, T. Multidecadal Variability of North China Aridity and Its Relationship to PDO during 1900–2010. J. Clim. 2014, 27, 1210–1222. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Lei, H.; Yang, H.; Yang, D.; Cao, Y. Historical and future trends in wetting and drying in 291 catchments across China. Hydrol. Earth Syst. Sci. 2017, 21, 2233–2248. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Furtado, K.; Wu, P.; Zhou, T.; Chadwick, P.; Marzin, C.; Rostron, J.; Sexton, D. Increasing precipitation variability on daily-to-multiyear timescales in a warmer world. Sci. Adv. 2021, 7, eabf8021. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Yang, C.; Zhang, C.; Yu, H. A parametric multivariate drought index for drought monitoring and assessment under climate change. Agric. For. Meteorol. 2021, 310, 108657. [Google Scholar] [CrossRef]
- Li, Y.; Lu, H.; Yang, K.; Wang, W.; Tang, Q.; Khem, S.; Yang, F.; Huang, Y. Meteorological and hydrological droughts in Mekong River Basin and surrounding areas under climate change. J. Hydrol. Reg. Stud. 2021, 36, 100873. [Google Scholar] [CrossRef]
- Ari, G.; Bao, Y.; Asi, H.; Zhang, J.; Na, L.; Angge, L.; Bao, Y.; Han, A.; Dong, Z.; Tong, Z.; et al. Impact of global warming on meteorological drought: A case study of the Songliao Plain, China. Theor. Appl. Climatol. 2021, 146, 1315–1334. [Google Scholar] [CrossRef]
- Yang, Q.; Li, M.; Zheng, Z.; Ma, Z. Mapping future droughts under global warming across China: A combined multi-timescale meteorological drought index and SOM-Kmeans approach. Weather Clim. Extrem. 2021, 31, 100304. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Cui, H.; Chen, Q. Comparison of the Ability of ARIMA, WNN and SVM Models for Drought Forecasting in the Sanjiang Plain, China. Nat. Resour. Res. 2020, 29, 1447–1464. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Lu, G.; Liu, X.; Wang, Y.; Wang, D.; Liu, W.; Yue, P.; Zhu, B.; Duan, X. Climate Transition from Warm-Dry to Warm-Wet in Eastern Northwest China. Atmosphere 2021, 12, 548. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, C. Drought/wetting variations in a semiarid and sub-humid region of China. Theor. Appl. Climatol. 2020, 140, 1537–1548. [Google Scholar] [CrossRef]
- Xu, J.; Wang, D.; Qiu, X.; Zeng, Y.; Zhu, X.; Li, M.; He, Y.; Shi, G. Dominant factor of dry–wet change in China since 1960s. Int. J. Climatol. 2021, 41, 1039–1055. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.; Safeeq, M.; AghaKouchak, A.; Guan, K.; Funk, C. Temperature impacts on the water year 2014 drought in California. Geophys. Res. Lett. 2015, 42, 4384–4393. [Google Scholar] [CrossRef] [Green Version]
- Huntington, T. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Khapalova, E.; Jandhyala, V.; Fotopoulos, S.; Overland, J. Assessing Change-Points in Surface Air Temperature Over Alaska. Front. Environ. Sci. 2018, 6, 121. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Qian, W.; Zhu, Y. Climate Change in China from 1880 to 1998 and its Impact on the Environmental Condition. Clim. Chang. 2001, 50, 419–444. [Google Scholar] [CrossRef]
- Qian, W.; Hu, Q.; Zhu, Y.; Lee, D.-K. Centennial-scale dry–wet variations in East Asia. Clim. Dyn. 2003, 21, 77–89. [Google Scholar] [CrossRef]
- Yang, R.; Xing, B. Teleconnections of Large-Scale Climate Patterns to Regional Drought in Mid-Latitudes: A Case Study in Xinjiang, China. Atmosphere 2022, 13, 230. [Google Scholar] [CrossRef]
- Yang, R.; Xing, B. Spatio-Temporal Variability in Hydroclimate over the Upper Yangtze River Basin, China. Atmosphere 2022, 13, 317. [Google Scholar] [CrossRef]
- Li, M.; Ma, Z. Soil moisture-based study of the variability of dry–wet climate and climate zones in China. Chin. Sci. Bull. 2013, 58, 531–544. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Zhang, M.; Wang, S.; Che, C.; Ma, R.; Ma, Z. Changes in air temperature over China in response to the recent global warming hiatus. J. Geogr. Sci. 2019, 29, 496–516. [Google Scholar] [CrossRef] [Green Version]
- Song, J. Changes in dryness/wetness in China during the last 529 years. Int. J. Climatol. 2000, 20, 1003–1016. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, A.; Khalili, K.; Behmanesh, J.; Shirzad, A. Estimation of ARIMA model parameters for drought prediction using the genetic algorithm. Arab. J. Geosci. 2021, 14, 841. [Google Scholar] [CrossRef]
- Phan, T.; Nguyen, X. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red river. Adv. Water Resour. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Li, J.; Zhang, S.; Huang, L.; Zhang, T.; Feng, P. Drought prediction models driven by meteorological and remote sensing data in Guanzhong Area, China. Hydrol. Res. 2020, 51, 942–958. [Google Scholar] [CrossRef]
- Büyükşahin, Ü.; Ertekin, Ş. Improving forecasting accuracy of time series data using a new ARIMA-ANN hybrid method and empirical mode decomposition. Neurocomputing 2019, 361, 151–163. [Google Scholar] [CrossRef] [Green Version]
- Khodakhah, H.; Aghelpour, P.; Hamedi, Z. Comparing linear and nonlinear data-driven approaches in monthly river flow prediction, based on the models SARIMA, LSSVM, ANFIS, and GMDH. Environ. Sci. Pollut. Res. 2022, 29, 21935–21954. [Google Scholar] [CrossRef] [PubMed]
- Alquraish, M.; Ali. Abuhasel, K.; S. Alqahtani, A.; Khadr, M. SPI-Based Hybrid Hidden Markov–GA, ARIMA–GA, and ARIMA–GA–ANN Models for Meteorological Drought Forecasting. Sustainability 2021, 13, 12576. [Google Scholar] [CrossRef]
- Djerbouai, S.; Souag-Gamane, D. Drought Forecasting Using Neural Networks, Wavelet Neural Networks, and Stochastic Models: Case of the Algerois Basin in North Algeria. Water Resour. Manag. 2016, 30, 2445–2464. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Drought prediction based on SPI and SPEI with varying timescales using LSTM recurrent neural network. Soft Comput. 2019, 23, 8399–8412. [Google Scholar] [CrossRef]
- Musarat, M.; Alaloul, W.; Rabbani, M.; Ali, M.; Altaf, M.; Fediuk, R.; Vatin, N.; Klyuev, S.; Bukhari, H.; Sadiq, A.; et al. Kabul River Flow Prediction Using Automated ARIMA Forecasting: A Machine Learning Approach. Sustainability 2021, 13, 10720. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, X.; Xie, Z.; Wu, P.; Li, Y. Increasing flash droughts over China during the recent global warming hiatus. Sci. Rep. 2016, 6, 30571. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Islam, A.; Jiang, Y.; Shen, S. Attribution Analysis of Long-Term Trends of Aridity Index in the Huai River Basin, Eastern China. Sustainability 2020, 12, 1743. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Zhang, B.; Huang, H.; Wang, X.; Zeng, J.; Jiao, W.; Yao, R. Identification of Seasonal Sub-Regions of the Drought in the North China Plain. Water 2020, 12, 3447. [Google Scholar] [CrossRef]
- Zhang, H.; Song, J.; Wang, G.; Wu, X.; Li, J. Spatiotemporal characteristic and forecast of drought in northern Xinjiang, China. Ecol. Indic. 2021, 127, 1107712. [Google Scholar] [CrossRef]
- Wu, S.; Yan, X. Variations in droughts and wet spells and their influences in China: 1924–2013. Theor. Appl. Climatol. 2019, 135, 623–631. [Google Scholar] [CrossRef]
- Gong, Z.; Zhi, R.; Feng, G.; Zhang, Q. Dry/wet changes and their standing characteristics in China during the past 531 years. Acta Meteorol. Sin. 2011, 25, 142–155. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Zhou, J.; Zhou, L.; Xie, B.; Li, C. Monitoring drought dynamics in China using Optimized Meteorological Drought Index (OMDI) based on remote sensing data sets. J. Environ. Manag. 2021, 292, 112733. [Google Scholar] [CrossRef] [PubMed]
- Hoque, M.; Pradhan, B.; Ahmed, N.; Alamri, A. Drought Vulnerability Assessment Using Geospatial Techniques in Southern Queensland, Australia. Sensors 2021, 21, 6896. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, J.; Liu, R.; Ding, L. Influences of Climate Change and Human Activities on NDVI Changes in China. Remote Sens. 2021, 13, 4326. [Google Scholar] [CrossRef]
- Lei, X.; Wang, Z.; Lin, G.; Lai, C. Response of vegetation dynamics to drought at the eco-geographical region scale across China. Arab. J. Geosci. 2021, 14, 2649. [Google Scholar] [CrossRef]
- Wang, A.; Fu, J. Changes in Daily Climate Extremes of Observed Temperature and Precipitation in China. Atmos. Ocean. Sci. Lett. 2013, 6, 312–319. [Google Scholar] [CrossRef]
- Thornthwaite, C. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Yang, Q.; Li, M.; Zheng, Z.; Ma, Z. Regional applicability of seven meteorological drought indices in China. Sci. China Earth Sci. 2017, 60, 745–760. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Q.; Ding, Y.; Zhang, D. Application of a hybrid ARIMA-LSTM model based on the SPEI for drought forecasting. Environ. Sci. Pollut. Res. 2022, 29, 4128–4144. [Google Scholar] [CrossRef] [PubMed]
- Dikshit, A.; Pradhan, B.; Huete, A. An improved SPEI drought forecasting approach using the long short-term memory neural network. J. Environ. Manag. 2021, 283, 111979. [Google Scholar] [CrossRef]
- Ji, G.; Lai, Z.; Yan, D.; Wu, L.; Wang, Z. Spatiotemporal patterns of future meteorological drought in the Yellow River Basin based on SPEI under RCP scenarios. Int. J. Clim. Chang. Strateg. Manag. 2022, 14, 39–53. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin: London, UK; American Psychological Association: Washington, DC, USA, 1948. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Hamed, K.; Rao, A. A modified Mann–Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, R.; Wang, X.; Duan, L.; Liu, T.; Li, D. Long-term spatiotemporal variability in occurrences of wet and dry days across South Mongolian Plateau. Atmos. Res. 2021, 262, 105795. [Google Scholar] [CrossRef]
- Sen, P. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Cao, L.; Feng, R.; Pan, Y. Response of NDVI of Natural Vegetation to Climate Changes and Drought in China. Land 2021, 10, 966. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, B.; Peng, D.; Yu, L.; Lin, B.; Pan, Y.; Xie, Q. The trend towards a warmer and wetter climate observed in arid and semi-arid areas of northwest China from 1959 to 2019. Environ. Res. Commun. 2021, 3, 115011. [Google Scholar] [CrossRef]
- Pettitt, A. A Non-Parametric Approach to the Change-Point Problem. J. R. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Byakatonda, J.; Parida, B.; Kenabatho, P.; Moalafhi, D. Analysis of rainfall and temperature time series to detect long-term climatic trends and variability over semi-arid Botswana. J. Earth Syst. Sci. 2018, 127, 25. [Google Scholar] [CrossRef] [Green Version]
- Hipel, K.; McLeod, A. Time Series Modeling of Water Resources and Environmental Systems; Elsevier: London, UK, 1994. [Google Scholar]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: Ann Arbor, MI, USA, 1976. [Google Scholar]
- Wu, X.; Zhou, J.; Yu, H.; Liu, D.; Xie, K.; Chen, Y.; Hu, J.; Sun, H.; Xing, F. The Development of a Hybrid Wavelet-ARIMA-LSTM Model for Precipitation Amounts and Drought Analysis. Atmosphere 2021, 12, 74. [Google Scholar] [CrossRef]
- Khan, M.; Muhammad, N.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.; Araghinejad, S.; Azarnivand, A. Drought forecasting using data-driven methods and an evolutionary algorithm. Model. Earth Syst. Environ. 2017, 3, 1675–1689. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.; Reinsel, G.; Ljung, G. Time Series Analysis: Forecasting and Control; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Mishra, A.; Desai, V. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaption; Cambridge University Press: London, UK, 2012. [Google Scholar]
- NOAA. Climate Change: Global Temperature. Available online: https://www.climate.gov/news-features/understanding-climate/climate-change-global-temperature (accessed on 31 March 2022).
- Zhang, Q.; Zheng, Y.; Singh, V.; Luo, M.; Xie, Z. Summer extreme precipitation in Eastern China: Mechanisms and impacts. J. Geophys. Res. Atmos. 2017, 122, 2766–2778. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Lopez-Moreno, J.-I.; Beguería, S.; Lorenzo-Lacruz, J.; Sanchez-Lorenzo, A.; García-Ruiz, J.; Azorin-Molina, C.; Morán-Tejeda, E.; Revuelto, J.; Trigo, R.; et al. Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ. Res. Lett. 2014, 9, 044001. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, F.; Su, R.; Gao, C.; Xing, K. Response of carbon and water fluxes to dryness/wetness in China. Terr. Atmos. Ocean. Sci. 2021, 32, 53–67. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.; Peng, L. Drought evolution, severity and trends in Mainland China over 1961-2013. Sci. Total Environ. 2018, 616, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Allan, R.; Pereira, L.; Smith, M. Crop Evapotranspiration-Guidelines for Computing; Crop Water Requirements-FAO Irrigation and Drainage; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998; Volume 56. [Google Scholar]
- Huang, J.; Li, Y.; Fu, C.; Chen, F.; Fu, Q.; Dai, A.; Shinoda, M.; Ma, Z.; Guo, W.; Li, Z.; et al. Dryland climate change: Recent progress and challenges. Rev. Geophys. 2017, 55, 719–778. [Google Scholar] [CrossRef]
- Raible, C.; Bärenbold, O.; Gómez-Navarro, J. Drought indices revisited—Improving and testing of drought indices in a simulation of the last two millennia for Europe. Tellus A Dyn. Meteorol. Oceanogr. 2017, 69, 1287492. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Liu, Y.; Wang, W.; Singh, V.; Ren, L. A global perspective on the probability of propagation of drought: From meteorological to soil moisture. J. Hydrol. 2021, 603, 126907. [Google Scholar] [CrossRef]
- Zhang, X.; Hua, Y.; Feng, J.; Yan, D.; Liu, J.; Li, C.; Cheng, Y.; Ren, Q. The evolution characteristics of drought and the analysis of rainfall intensity probability during alternating dry–wet change in the haihe river basin. Appl. Ecol. Environ. Res. 2018, 16, 6395–6407. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q.; Rayburg, S. Climate change impacts on meteorological, agricultural and hydrological droughts in China. Glob. Planet. Chang. 2015, 126, 23–34. [Google Scholar] [CrossRef]
- Zhang, Q.; Kong, D.; Singh, V.P.; Shi, P. Response of vegetation to different time-scales drought across China: Spatiotemporal patterns, causes and implications. Glob. Planet. Chang. 2017, 152, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yu, R.; Zhai, P. More frequent and widespread persistent compound drought and heat event observed in China. Sci. Rep. 2020, 10, 14576. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Q.; Singh, V.P.; Liu, L. Transitional properties of droughts and related impacts of climate indices in the Pearl River basin, China. J. Hydrol. 2016, 534, 397–406. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D. The role of monitoring as a component of preparedness planning: Delivery of information and decision support tools. In Coping with Drought Risk in Agriculture and Water Supply Systems: Drought Management and Policy Development in the Mediterranean; Iglesias, C., Cancelliere, A., Cubillo, F., Garrote, L., Wilhite, D., Eds.; Springer Publishers: Dordrecht, The Nertherlands, 2009. [Google Scholar]
- Valipour, M.; Banihabib, M.; Behbahani, S. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Moeeni, H.; Bonakdari, H. Forecasting monthly inflow with extreme seasonal variation using the hybrid SARIMA-ANN model. Stoch. Environ. Res. Risk Assess. 2017, 31, 1997–2010. [Google Scholar] [CrossRef]
- Zheng, K.; Qin, W.; Du, X. Global Land Surface Dry/Wet Conditions Mining Based on Spatial-Temporal Association Rules. Earth Space Sci. 2021, 8, e01501. [Google Scholar] [CrossRef]
- Zhao, S.; Cong, D.; He, K.; Yang, H.; Qin, Z. Spatial-Temporal Variation of Drought in China from 1982 to 2010 Based on a modified Temperature Vegetation Drought Index (mTVDI). Sci. Rep. 2017, 7, 17473. [Google Scholar] [CrossRef]
- Qie, J.; Tian, Q.; Zhang, Y. Moisture changes over the past 467 years in the central Hexi Corridor, northWestern China. Dendrochronologia 2020, 63, 125725. [Google Scholar] [CrossRef]
- Li, L.; She, D.; Zheng, H.; Lin, P.; Yang, Z.-L. Elucidating Diverse Drought Characteristics from Two Meteorological Drought Indices (SPI and SPEI) in China. J. Hydrometeorol. 2020, 21, 1513–1530. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Z.; Liu, Y.; Band, L.; Wang, S.; Xu, H. Seasonal differences in future climate and streamflow variation in a watershed of Northern China. J. Hydrol. Reg. Stud. 2021, 38, 100959. [Google Scholar] [CrossRef]

| Categories | SPEI Values |
|---|---|
| Extreme wetness | >2.0 |
| Severe wetness | 1.5 to 2.0 |
| Moderate wetness | 1.0 to 1.5 |
| Light wetness | 0.5 to 1.0 |
| Near normal | −0.5 to 0.5 |
| Light drought | −1.0 to −0.5 |
| Moderate drought | −1.5 to −1.0 |
| Severe drought | −2.0 to −1.5 |
| Extreme drought | <−2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Xing, B. Evidence for Intensification in Meteorological Drought since the 1950s and Recent Dryness–Wetness Forecasting in China. Atmosphere 2022, 13, 745. https://doi.org/10.3390/atmos13050745
Yang R, Xing B. Evidence for Intensification in Meteorological Drought since the 1950s and Recent Dryness–Wetness Forecasting in China. Atmosphere. 2022; 13(5):745. https://doi.org/10.3390/atmos13050745
Chicago/Turabian StyleYang, Ruting, and Bing Xing. 2022. "Evidence for Intensification in Meteorological Drought since the 1950s and Recent Dryness–Wetness Forecasting in China" Atmosphere 13, no. 5: 745. https://doi.org/10.3390/atmos13050745
APA StyleYang, R., & Xing, B. (2022). Evidence for Intensification in Meteorological Drought since the 1950s and Recent Dryness–Wetness Forecasting in China. Atmosphere, 13(5), 745. https://doi.org/10.3390/atmos13050745






