Kolmogorov Complexity Analysis and Prediction Horizon of the Daily Erythemal Dose Time Series
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Complexity Measures
3. Results and Discussion
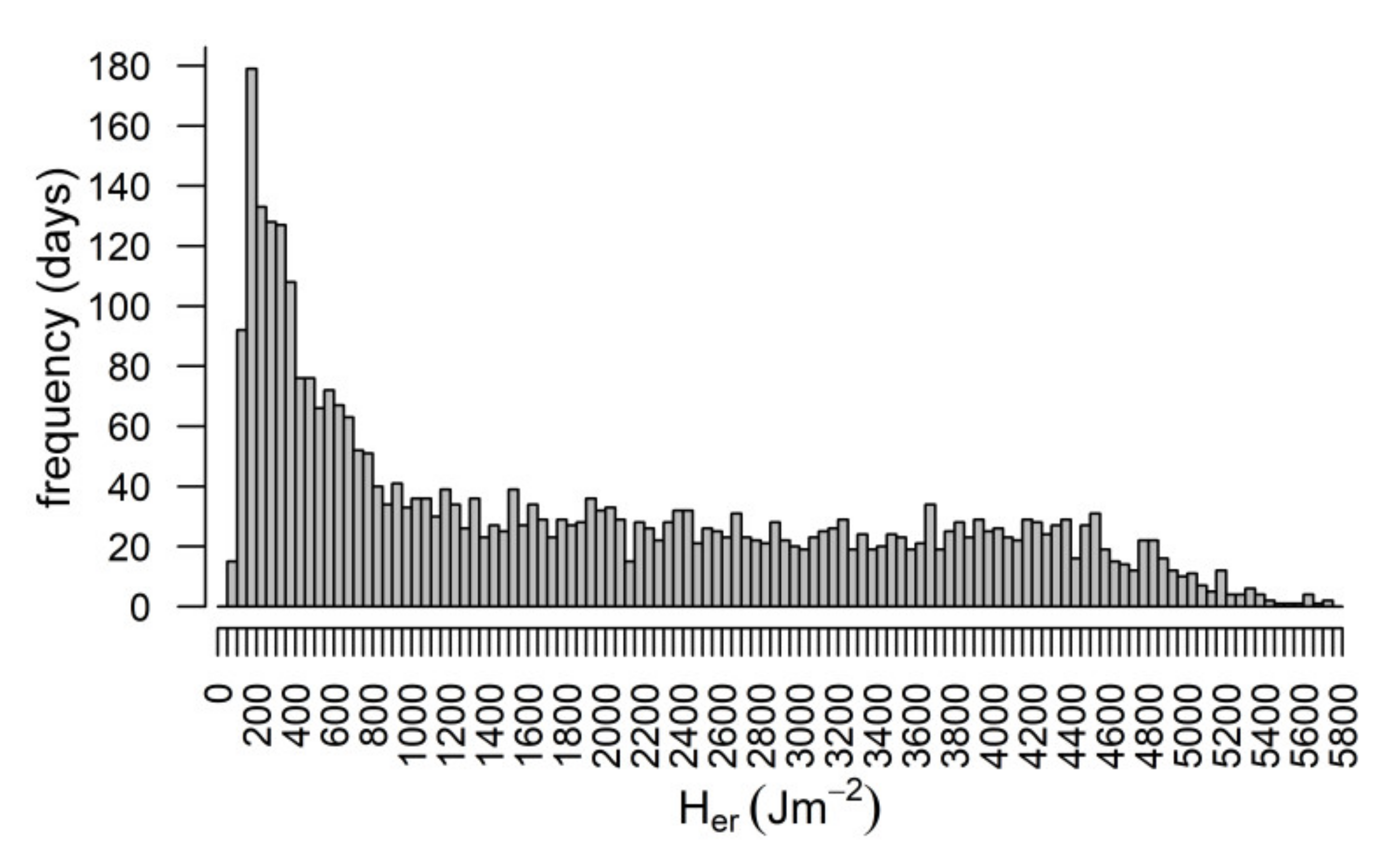
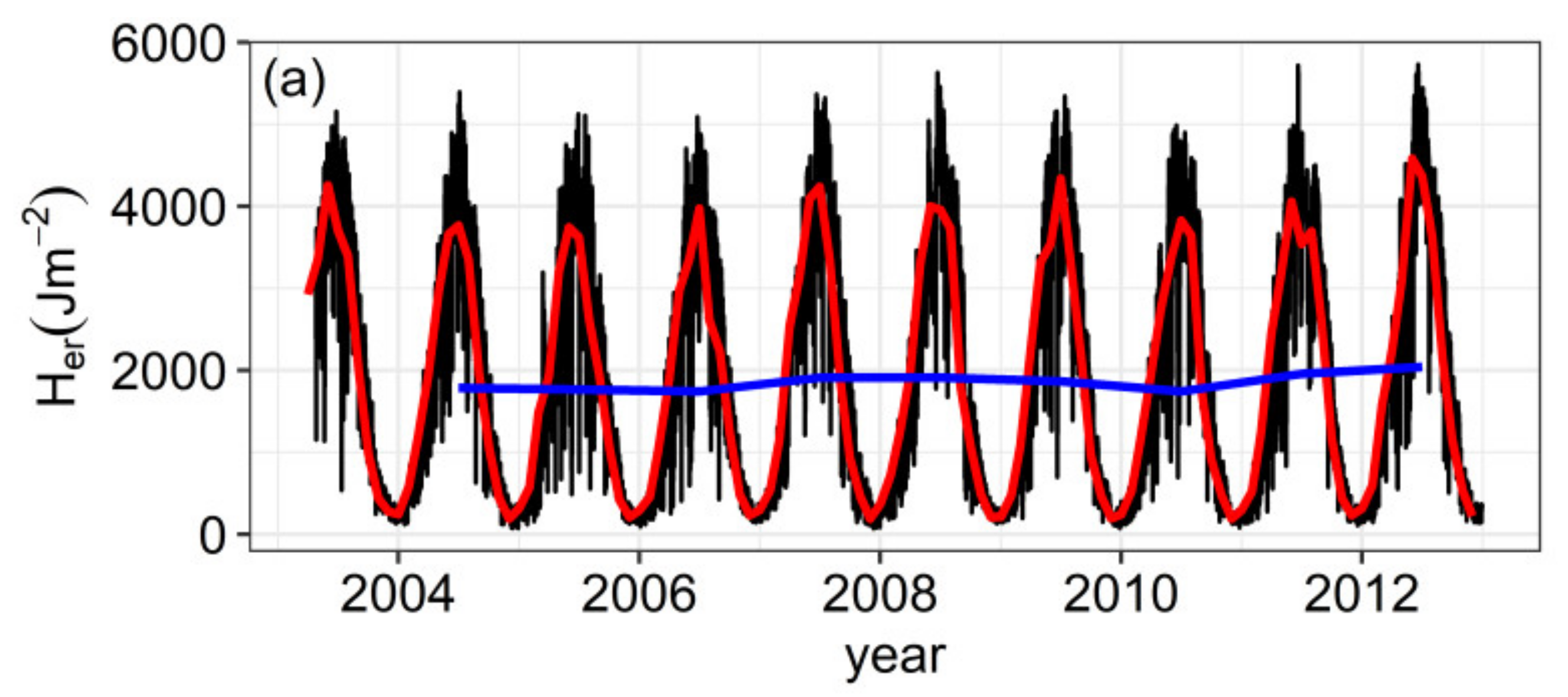
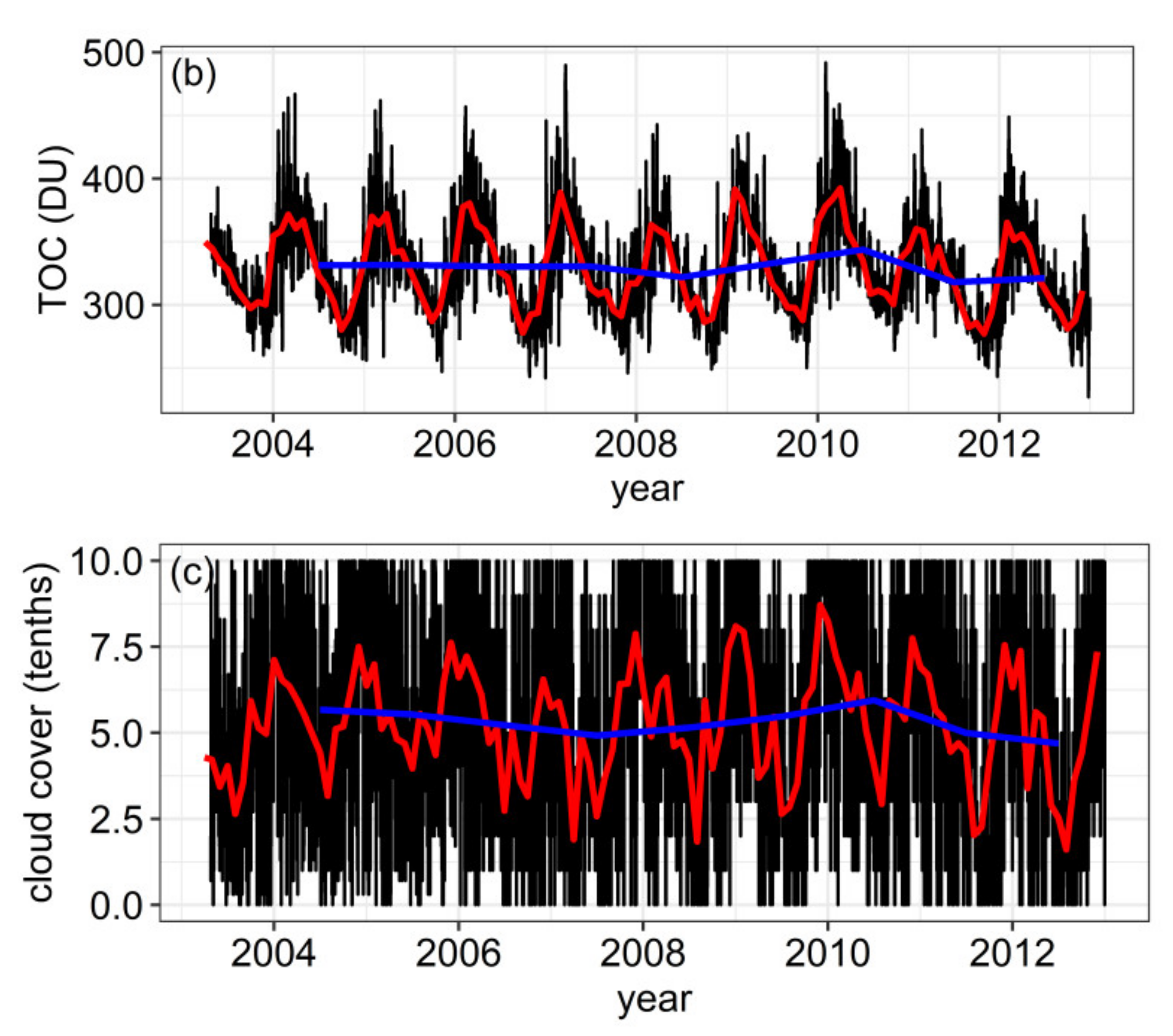
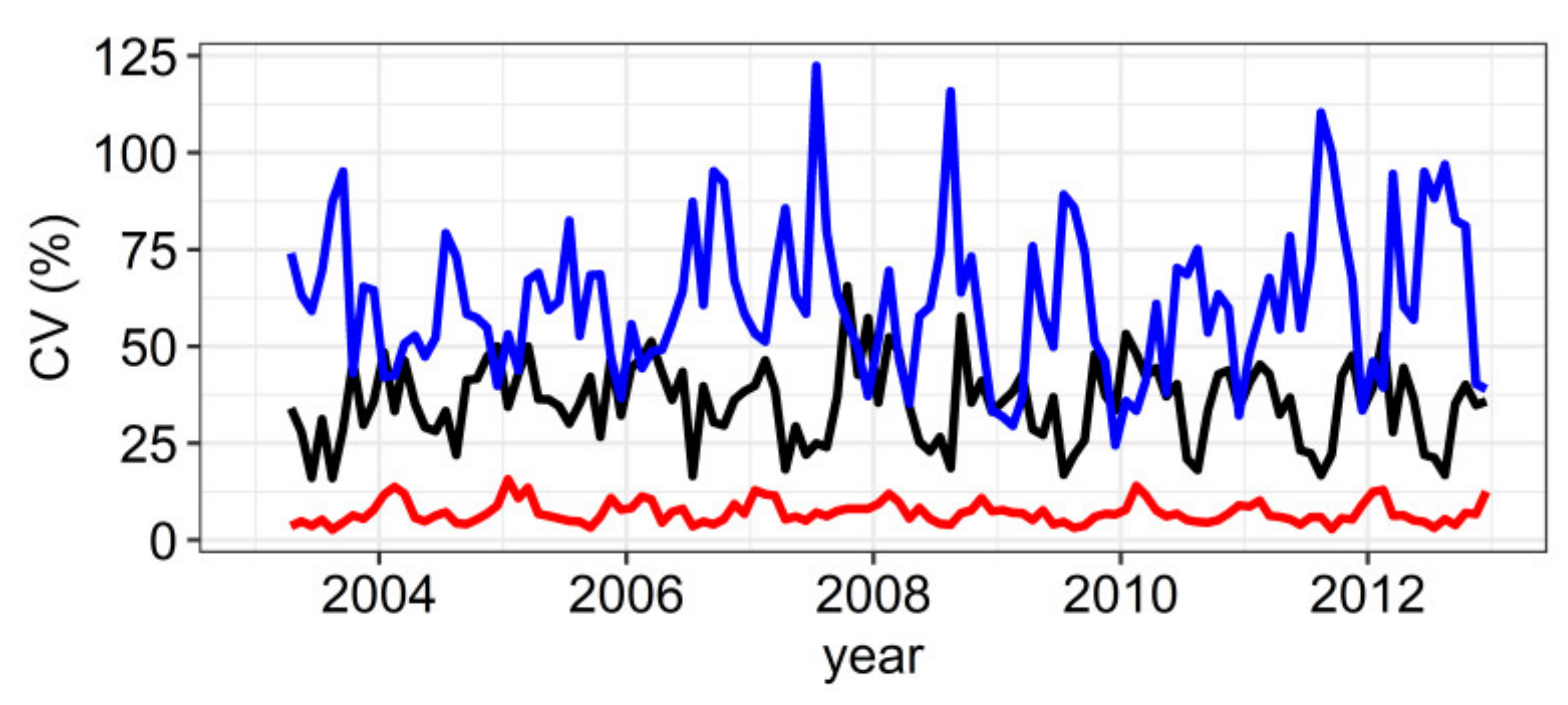
3.1. General Features of the Data
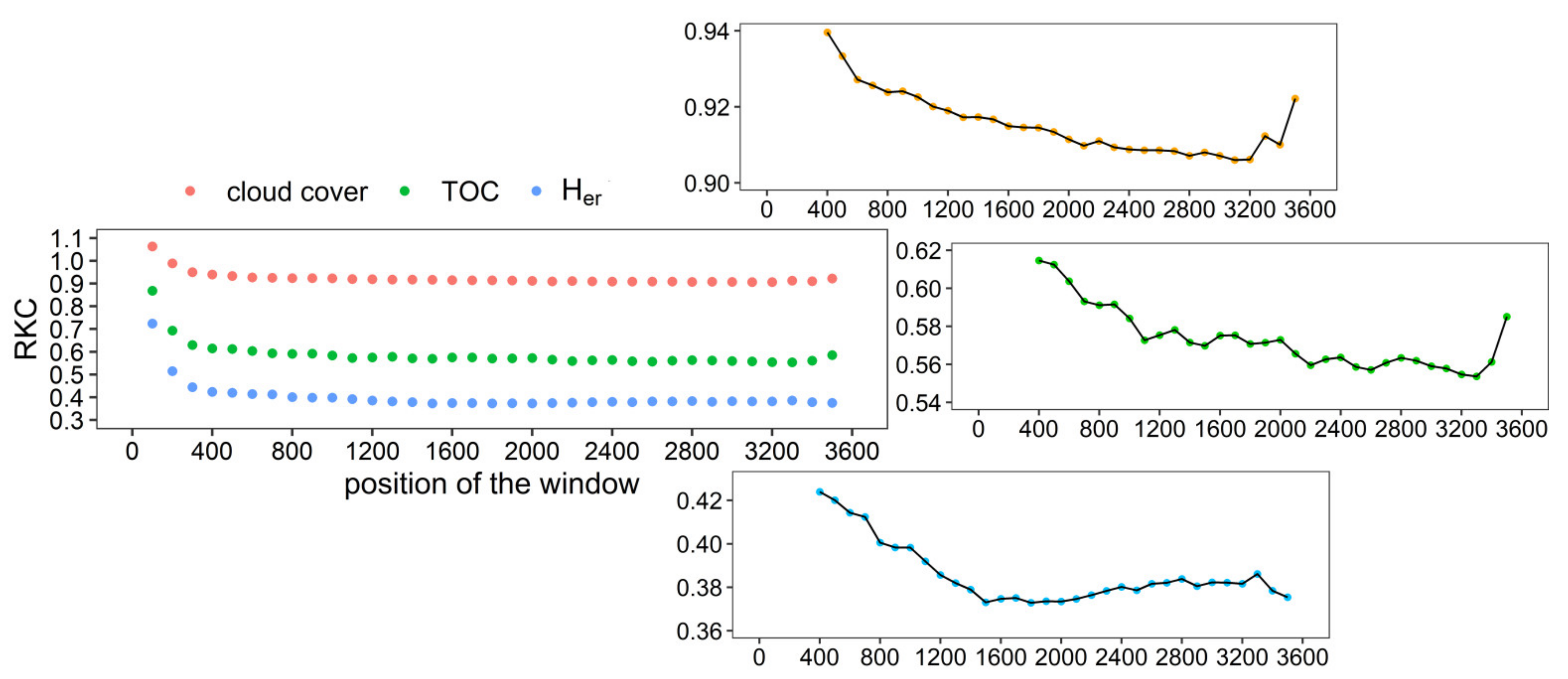
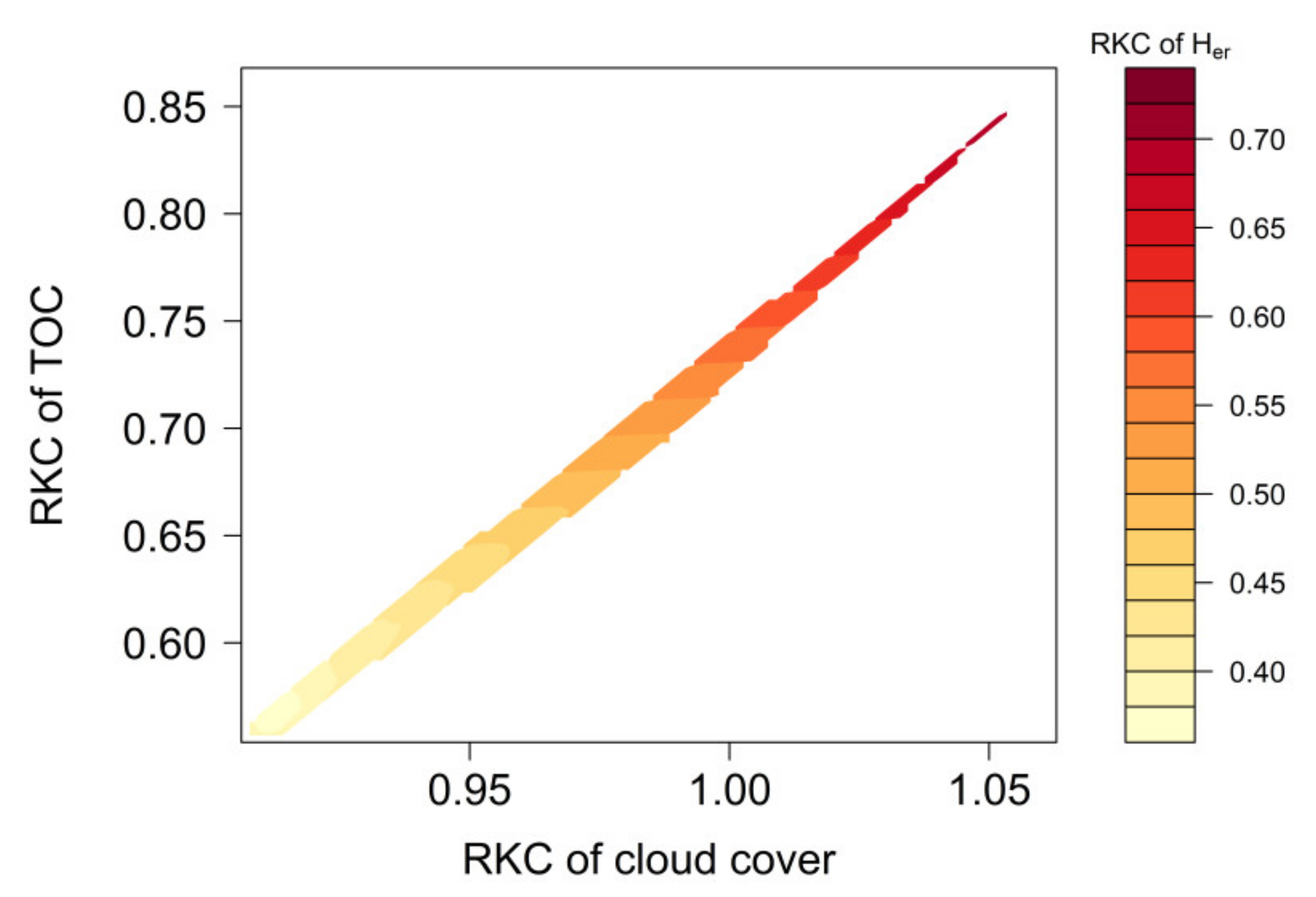
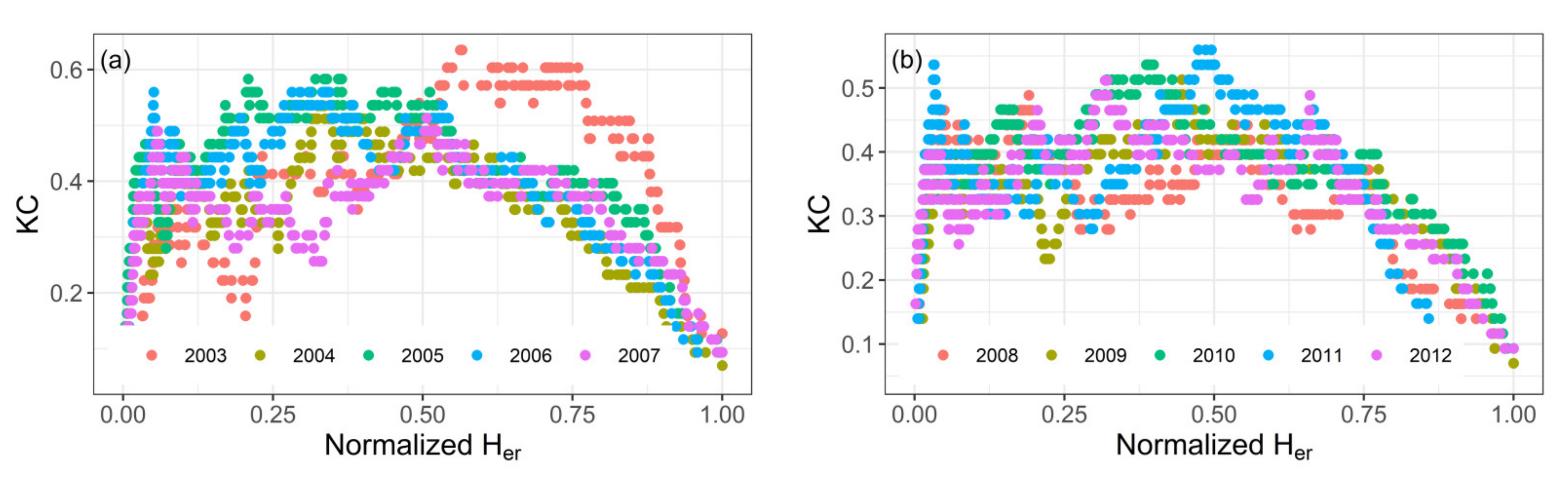
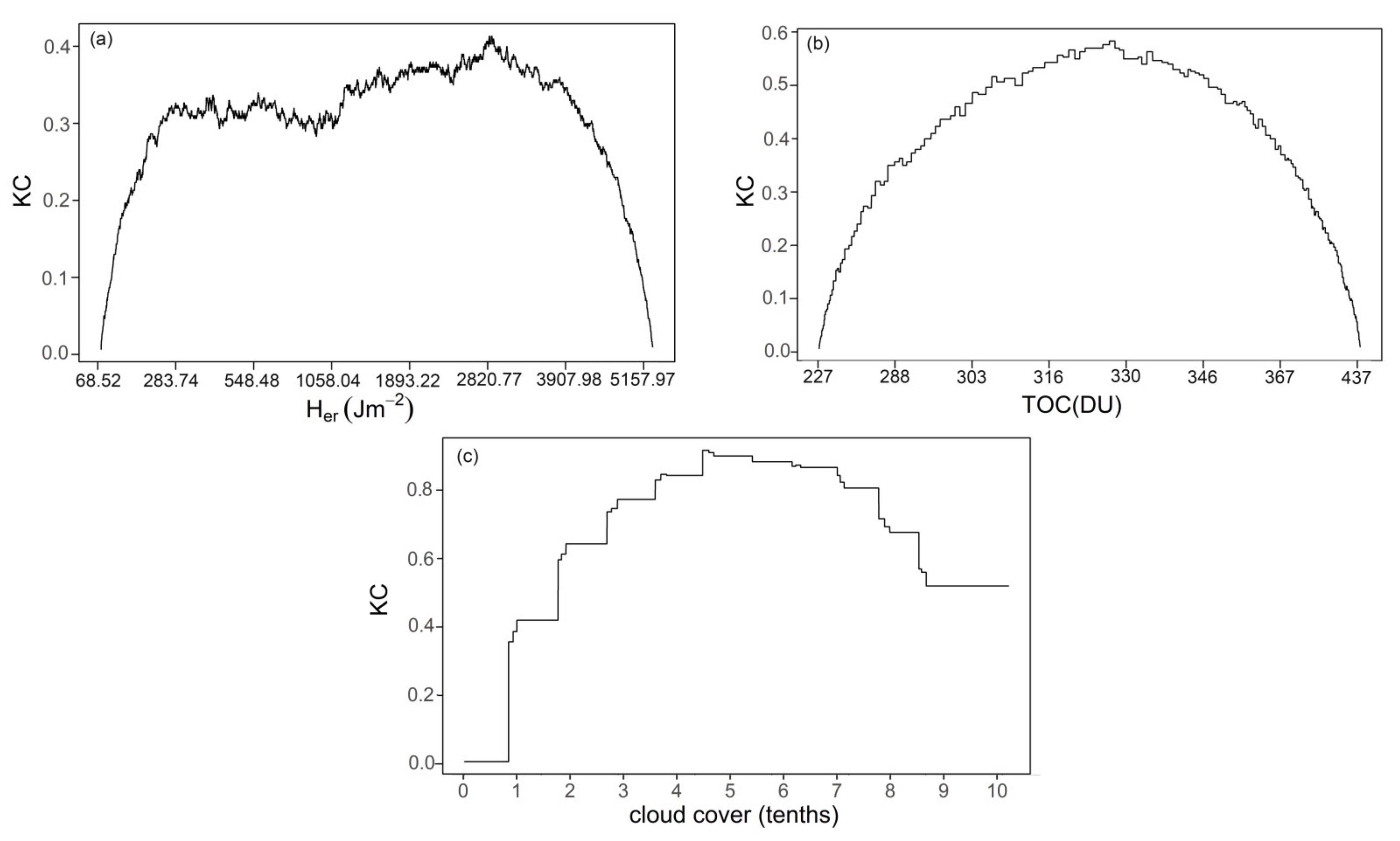
3.2. Kolmogorov Complexity and Kolmogorov Complexity Spectrum
3.3. Largest Lyapunov Exponent and Predictability of Daily
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- CIE International Lighting Vocabulary; Commission Internationale de l’Eclairage (International commission on Illumination): Vienna, Austria, 1987; Publication No. 17.4.
- Bukata, R.P.; Jerome, J.H.; Kondratyev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Kaurola, J.; Taalas, P.; Koskela, T.; Borkowski, J.; Josefsson, W. Long-term variations of UV-B doses at three stations in northern Europe. J. Geophys. Res. 2000, 105, 20813–20820. [Google Scholar] [CrossRef]
- Smedley, A.R.D.; Rimmer, J.S.; Moore, D.; Toumi, R.; Webb, A.R. Total ozone and surface UV trends in the United Kingdom: 1979–2008. Int. J. Climatol. 2012, 32, 338–346. [Google Scholar] [CrossRef]
- Petkov, B.; Vitale, V.; Di Carlo, P.; Mazzola, M.; Lupi, A.; Diémoz, H.; Fountoulakis, I.; Drofa, O.; Mastrangelo, D.; Casale, G.R.; et al. The 2020 Arctic ozone depletion and signs of its effect on the ozone column at lower latitudes. Bull. Atmos. Sci. Technol. 2021, 2, 8. [Google Scholar] [CrossRef]
- WMO Scientific Assessment of Ozone Depletion: 2018; Global Ozone Research and Monitoring Project—Report No. 58; World Meteorological Organization: Geneva, Switzerland, 1987.
- UNEP Environmental Effects and Interactions of Stratospheric Ozone Depletion, UV Radiation, and Climate Change: 2018 Assessment Report; Environmental Effects Assessment Panel (EEAP), United Nations Environment Programme (UNEP): Nairobi, Kenya, 2019.
- Eleftheratos, K.; Kazadzis, S.; Zerefos, C.S.; Tourpali, K.; Meleti, C.; Balis, D.; Zyrichidou, I.; Lakkala, K.; Feister, U.; Koskela, T.; et al. Ozone and Spectroradiometric UV Changes in the Past 20 Years over High Latitudes. Atmos.-Ocean 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Fountoulakis, I.; Bais, A.F.; Fragkos, K.; Meleti, C.; Tourpali, K.; Zempila, M.M. Short- and long-term variability of spectral solar UV irradiance at Thessaloniki, Greece: Effects of changes in aerosols, total ozone and clouds. Atmos. Chem. Phys. 2016, 16, 2493–2505. [Google Scholar] [CrossRef]
- Sanchez-Lorenzo, A.; Enriquez-Alonso, A.; Wild, M.; Trentmann, J.; Vicente-Serrano, S.M.; Sanchez-Romero, A.; Posselt, R.; Hakuba, M.Z. Trends in downward surface solar radiation from satellites and ground observations over Europe during 1983–2010. Rem. Sens. Environ. 2017, 189, 108–117. [Google Scholar] [CrossRef]
- Zerefos, C.S.; Tourpali, K.; Eleftheratos, K.; Kazadzis, S.; Meleti, C.; Feister, U.; Heikkilä, A. Evidence of a possible turning point in solar UV-B over Canada, Europe and Japan. Atmos. Chem. Phys. 2012, 12, 2469–2477. [Google Scholar] [CrossRef]
- De Bock, V.; De Backer, H.; Van Malderen, R.; Mangold, A.; Delcloo, A. Relations between erythemal UV dose, global solar radiation, total ozone column and aerosol optical depth at Uccle, Belgium. Atmos. Chem. Phys. 2014, 14, 12251–12270. [Google Scholar] [CrossRef]
- Bornman, J.F.; Barnes, P.W.; Robson, T.M.; Robinson, S.A.; Jansen, M.A.K.; Ballaré, C.L.; Flint, S.D. Linkages between stratospheric ozone, UV radiation and climate change and their implications for terrestrial ecosystems. Photochem. Photobiol. Sci. 2019, 18, 681–716. [Google Scholar] [CrossRef]
- Frey, L.; Bender, F.A.M.; Svensson, G. Cloud albedo changes in response to anthropogenic sulfate and non-sulfate aerosol forcings in CMIP5 models. Atmos. Chem. Phys. 2017, 17, 9145–9162. [Google Scholar] [CrossRef]
- Sabburg, J.; Wong, J. The effect of clouds on enhancing UVB irradiance at the earth’s surface: A one year study. Geophys. Res. Lett. 2000, 27, 3337–3340. [Google Scholar] [CrossRef]
- Arola, A.; Kazadzis, S.; Krotkov, N.; Bais, A.; Gröbner, J.; Herman, J.R. Assessment of TOMS UV bias due to absorbing aerosols. J. Geophys. Res. 2005, 110, D23211. [Google Scholar] [CrossRef]
- García, R.D.; Cachorro, V.E.; Cuevas, E.; Toledano, C.; Redondas, A.; Blumthaler, M.; Benounna, Y. Comparison of measured and modelled spectral UV irradiance at Izaña high mountain station: Estimation of the underlying effective albedo. Int. J. Climatol. 2016, 36, 377–388. [Google Scholar] [CrossRef]
- Blumthaler, M.; Ambach, W. Solar UV-B albedo of various surfaces. Photochem. Photobiol. 1988, 48, 85–88. [Google Scholar] [CrossRef]
- Krzyscin, J.W.; Eerme, K.; Janouch, M. Long-term variations of the UV-B radiation over Central Europe as derived from the reconstructed UV time series. Ann. Geophys. 2004, 22, 1473–1485. [Google Scholar] [CrossRef][Green Version]
- Fountoulakis, I.; Diémoz, H.; Siani, A.-M.; Laschewski, G.; Filippa, G.; Arola, A.; Bais, A.F.; De Backer, H.; Lakkala, K.; Webb, A.R.; et al. Solar UV Irradiance in a Changing Climate: Trends in Europe and the Significance of Spectral Monitoring in Italy. Environments 2020, 7, 1. [Google Scholar] [CrossRef]
- Fountoulakis, I.; Diémoz, H.; Siani, A.M.; Di Sarra, A.; Meloni, D.; Sferlazzo, D.M. Variability and trends in surface solar spectral ultraviolet irradiance in Italy: On the influence of geopotential height and lower-stratospheric ozone. Atmos. Chem. Phys. 2021, 21, 18689–18705. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Mihailovic, D.T.; Aksentijevic, A.; Mihailovic, A. Mapping regularities in the solar irradiance data using complementary complexity measures. Stoch. Environ. Res. Risk Assess. 2021, 35, 1257–1272. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Hitchcock, J.M.; Pavan, A.; Vinodchandran, N.V. Kolmogorov complexity in randomness extraction. ACM Trans. Comput. Theory 2011, 3, 1–12. [Google Scholar] [CrossRef]
- Mihailovic, D.T.; Mimic, G.; Nikolic-Djoric, E.; Arsenic, I. Novel measures based on the Kolmogorov complexity for use in complex system behavior studies and time series analysis. Open Phys. 2015, 13, 1–14. [Google Scholar] [CrossRef]
- Mihailović, D.; Malinović-Milićević, S.; Arsenić, I.; Dresković, N.; Bukosa, B. Kolmogorov complexity spectrum for use in analysis of of UV-B radiation time series. Mod. Phys. Lett. B 2013, 27, 1350194. [Google Scholar] [CrossRef]
- Bessafi, M.; Mihailović, D.T.; Malinović-Milićević, S.; Mihailović, A.; Jumaux, G.; Bonnardot, F.; Fanchette, Y.; Chabriat, J.-P. (Spatial and Temporal Non-Linear Dynamics Analysis and Predictability of Solar Radiation Time Series for La Reunion Island (France). Entropy 2018, 20, 946. [Google Scholar] [CrossRef]
- Mihailović, D.T.; Bessafi, M.; Marković, S.; Arsenic, I.; Malinović- Milićević, S.; Jeanty, P.; Delsaut, M.; Chabriat, J.-P.; Dresković, N.; Mihailović, A. Analysis of solar irradiation time series complexity and predictability by combining Kolmogorov measures and Hamming distance for La Reunion (France). Entropy 2018, 20, 570. [Google Scholar] [CrossRef]
- Bessafi, M.; Mihailovic, D.T.; Li, P.; Mihailovic, A.; Chabriat, J.-P. Algorithmic Probability Method Versus Kolmogorov Complexity with No-Threshold Encoding Scheme for Short Time Series: An Analysis of Day-To-Day Hourly Solar Radiation Time Series over Tropical Western Indian Ocean. Entropy 2019, 21, 552. [Google Scholar] [CrossRef]
- Beck, H.; Zimmermann, N.; McVicar, T.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- ISO/CIE 17166:2019 (E); CIE Erythema Reference Action Spectrum and Standard Erythema Dose. CIE Publications: Wien, Austria, 2019.
- WHO (World Health Organization). Global Solar UV Index: A Practical Guide; World Health Organization and International Commission on Non-Ionizing Radiation Protection; World Health Organization: Geneva, Switzerland, 2002. [Google Scholar]
- Vanicek, K.; Frei, T.; Litynska, Z.; Schmalwieser, A. UV-Index for the Public: A Guide for Publication and Interpretation of Solar UV Index Forecasts for the Public, Prepared by the Working Group 4 of the COST-713 Action “UVB forecasting” Report; European Union: Brussels, Belgium, 2000. [Google Scholar]
- Yankee Environmental Systems, Inc. UVB-1 UV Pyranometer, Installation and User Guide, 2000, version 2.0; Yankee Environmental Systems, Inc.: Turners Falls, MA, USA, 2000; 44p. [Google Scholar]
- CIE S007E-1998; CIE Erythema Reference Action Spectrum and Standard Erythema Dose. CIE Central Bureau: Vienna, Austria, 1998.
- Malinović-Milićević, S.; Mijatović, Z.; Stanojević, G.; Radovanović, M.M.; Popović, V. Health risks of extended exposure to low-level UV radiation—An analysis of ground-based and satellite-derived data. Sci. Total Environ. 2022, 831, 154899. [Google Scholar] [CrossRef]
- Malinović-Milićević, S.; Mijatović, Z.; Arsenić, I.; Podrašćanin, Z.; Firanj Sremac, A.; Radovanović, M.; Drešković, N. The importance of ground-based and satellite observations for monitoring and estimation of UV radiation in Novi Sad (Serbia). J. Geogr. Inst. Jovan Cvijic SASA 2020, 70, 57–70. [Google Scholar] [CrossRef]
- Diémoz, H.; Siani, A.M.; Casale, G.R.; di Sarra, A.; Serpillo, B.; Petkov, B.; Scaglione, S.; Bonino, A.; Facta, S.; Fedele, F.; et al. First national intercomparison of solar ultraviolet radiometers in Italy. Atmos. Meas. Tech. 2011, 4, 1689–1703. [Google Scholar] [CrossRef]
- Hülsen, G.; Gröbner, J. Characterization and calibration of ultraviolet broadband radiometers measuring erythemally weighted irradiance. Appl. Opt. 2007, 46, 5877. [Google Scholar] [CrossRef] [PubMed]
- Malinovic, S.; Mihailovic, D.T.; Kapor, D.; Mijatovic, Z.; Arsenic, I.D. NEOPLANTA: A Short Description of the First Serbian UV Index Model. J. Appl. Meteorol. Climatol. 2006, 45, 1171–1177. [Google Scholar] [CrossRef]
- Malinovic-Milicevic, S.; Mihailovic, D.T.; Radovanovic, M.M. Reconstruction of the erythemal UV radiation data in Novi Sad (Serbia) using the NEOPLANTA parametric model. Theor. Appl. Climatol. 2015, 12, 131–138. [Google Scholar] [CrossRef]
- Van der A, R.J.; Allaart, M.A.F.; Eskes, H.J. Extended and refined multi sensor reanalysis of total ozone for the period 1970–2012. Atmos. Meas. Tech. 2015, 8, 3021–3035. [Google Scholar] [CrossRef]
- Van der A, R.J.; Allaart, M.A.F.; Eskes, H.J. Multi-Sensor Reanalysis (MSR) of Total Ozone, Version 2. Dataset; Royal Netherlands Meteorological Institute (KNMI): De Bilt, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991; p. 748. [Google Scholar]
- Li, M.; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 1997. [Google Scholar]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.; Principe, J.C. Analysis of biomedical signals by the Lempel-Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar] [CrossRef]
- Adami, C. What is complexity? Bioessays. 2002, 24, 1085–1094. [Google Scholar] [CrossRef]
- Boeing, G. Visual analysis of nonlinear dynamical systems: Chaos, fractals, self-similarity and the limits of prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Liu, H.-F.; Dai, Z.-H.; Li, W.-F.; Gong, X.; Yu, Y.-H. Noise robust estimates of the largest Lyapunov exponent. Phys. Lett. A 2005, 341, 119–127. [Google Scholar] [CrossRef]
- Mihailović, D.T.; Nikolić-Dorić, E.; Arsenić, I.; Malinović-Milićević, S.; Singh, V.P.; Stošić, T.; Stošić, B. Analysis of daily streamflow complexity by Kolmogorov measures and Lyapunov exponent. Physica A 2019, 525, 290–303. [Google Scholar] [CrossRef]
- Frison, T.W.; Abarbanel, H.D.I. Ocean gravity waves: A nonlinear analysis of observations. J. Geophys. Res. 1997, 102, 1051–1059. [Google Scholar] [CrossRef]
- Gutierrez, R.J.; Boehmke, B.C.; Bauer, K.W.; Saie, C.M.; Bihl, T.J. anomalyDetection: Implementation of augmented network log anomaly detection procedures. R J. 2017, 9, 354–365. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]


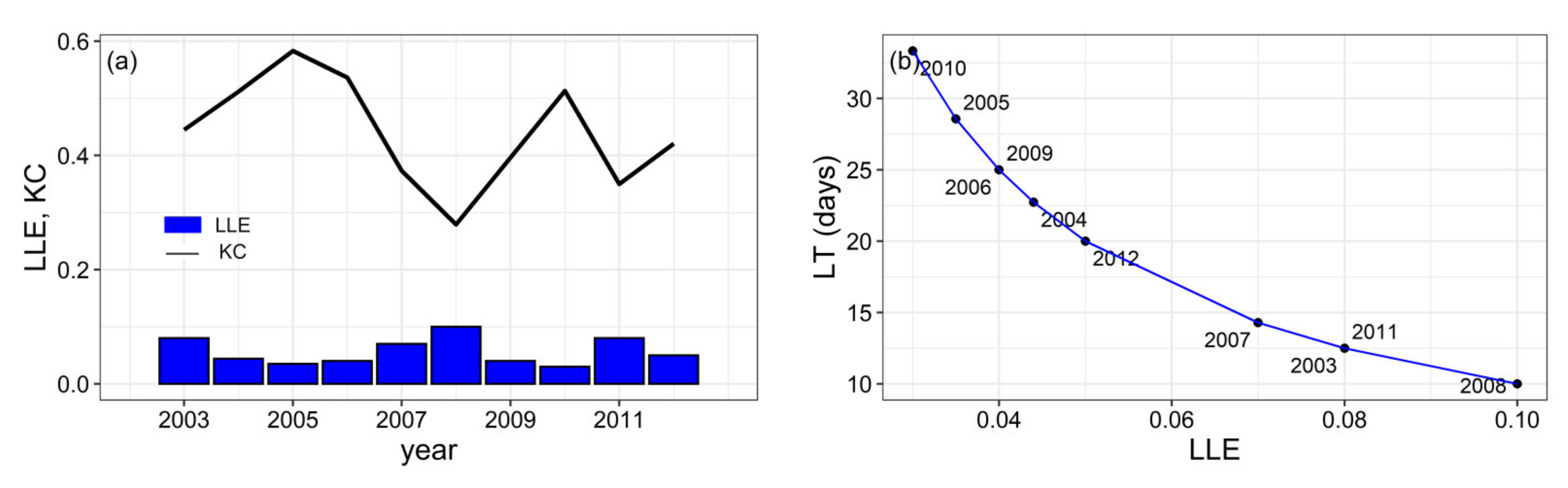
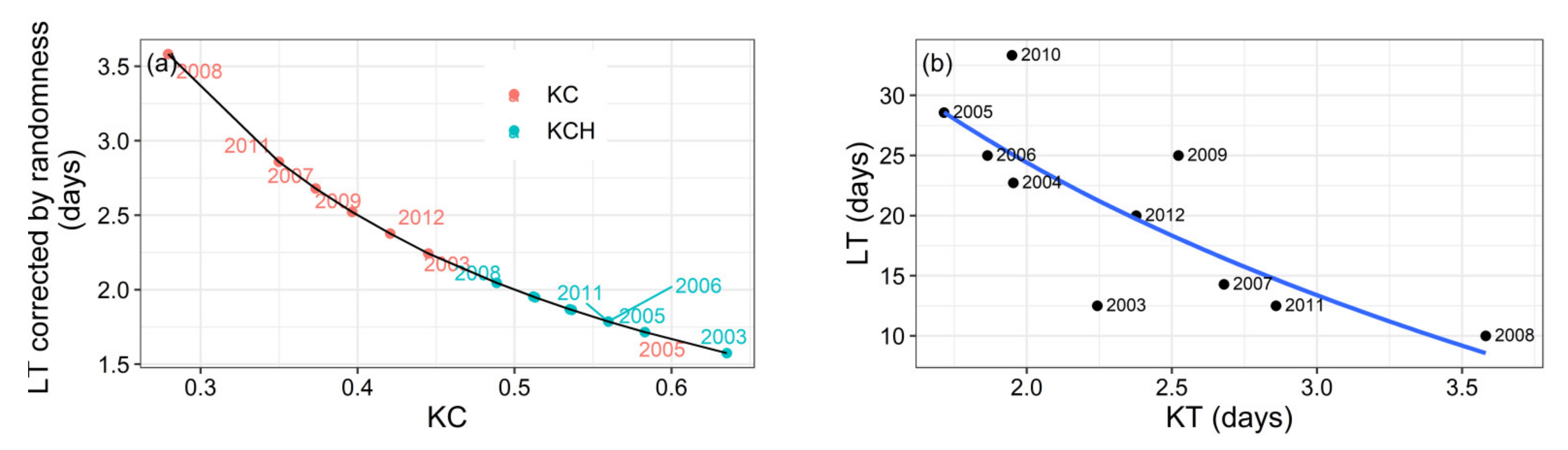
| Year | Kolmogorov Complexity (KC) | ||
|---|---|---|---|
| TOC | Cloud Cover | ||
| 2003 | 0.445 | 0.572 | 1.048 |
| 2004 | 0.512 | 0.558 | 0.954 |
| 2005 | 0.583 | 0.676 | 0.933 |
| 2006 | 0.536 | 0.676 | 0.956 |
| 2007 | 0.373 | 0.723 | 0.909 |
| 2008 | 0.279 | 0.605 | 0.907 |
| 2009 | 0.396 | 0.560 | 0.886 |
| 2010 | 0.420 | 0.630 | 0.933 |
| 2011 | 0.350 | 0.560 | 0.863 |
| 2012 | 0.421 | 0.745 | 0.861 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malinović-Milićević, S.; Mihailović, A.; Mihailović, D.T. Kolmogorov Complexity Analysis and Prediction Horizon of the Daily Erythemal Dose Time Series. Atmosphere 2022, 13, 746. https://doi.org/10.3390/atmos13050746
Malinović-Milićević S, Mihailović A, Mihailović DT. Kolmogorov Complexity Analysis and Prediction Horizon of the Daily Erythemal Dose Time Series. Atmosphere. 2022; 13(5):746. https://doi.org/10.3390/atmos13050746
Chicago/Turabian StyleMalinović-Milićević, Slavica, Anja Mihailović, and Dragutin T. Mihailović. 2022. "Kolmogorov Complexity Analysis and Prediction Horizon of the Daily Erythemal Dose Time Series" Atmosphere 13, no. 5: 746. https://doi.org/10.3390/atmos13050746
APA StyleMalinović-Milićević, S., Mihailović, A., & Mihailović, D. T. (2022). Kolmogorov Complexity Analysis and Prediction Horizon of the Daily Erythemal Dose Time Series. Atmosphere, 13(5), 746. https://doi.org/10.3390/atmos13050746







