Abstract
An assessment and prediction of PM2.5 for a port city of eastern peninsular India is presented. Fifteen machine learning (ML) regression models were trained, tested and implemented to predict the PM2.5 concentration. The predicting ability of regression models was validated using air pollutants and meteorological parameters as input variables collected from sites located at Visakhapatnam, a port city on the eastern side of peninsular India, for the assessment period 2018–2019. Highly correlated air pollutants and meteorological parameters with PM2.5 concentration were evaluated and presented during the period under study. It was found that the CatBoost regression model outperformed all other employed regression models in predicting PM2.5 concentration with an R2 score (coefficient of determination) of 0.81, median absolute error (MedAE) of 6.95 µg/m3, mean absolute percentage error (MAPE) of 0.29, root mean square error (RMSE) of 11.42 µg/m3 and mean absolute error (MAE) of 9.07 µg/m3. High PM2.5 concentration prediction results in contrast to Indian standards were also presented. In depth seasonal assessments of PM2.5 concentration were presented, to show variance in PM2.5 concentration during dominant seasons.
1. Introduction
The World Health Organization (WHO) has reported that 9 out of 10 people breathe air containing high levels of pollutants, and it is also estimated that air pollution is responsible for approximately 7 million deaths every year [1]. The burden of ill-health is not equally distributed, as approximately two-thirds of deaths occur in the developing countries of Asia. Air pollution in Asian countries is mainly due to increasing trends in economic and social development. In India, rapidly increasing industrialization, urbanization, and demand for transportation influence air pollution in many Indian cities [2]. The major health impacts of air pollutant PM2.5 are shown in Figure 1, which indicates that PM2.5 is the main air pollutant responsible for the most significant health problems viz. impacts on the central nervous system, breathing problems, chronic obstructive pulmonary disease, lung cancer, cardiovascular diseases, impacts on the reproductive system, etc., [3,4]. Therefore, it is of utmost importance to determine and forecast the PM2.5 concentration with more reliable and better forecasting models.
Figure 1.
Health impacts of air pollution.
Many studies have reported on pollutant forecasting models using ML approaches because it is very difficult to estimate originator pollutants with varying environmental conditions by traditional methods. ML approaches are capable of determining the causes of high pollutants, along with better forecasting of the increase and decrease in pollutants in the environment. Forecasting can help regulatory agencies or the government to control emission levels of pollutants such as nitric oxide (NO), nitrogen dioxide (NO2), nitrogen oxides (NOx), ammonia (NH3), sulphur dioxide (SO2), carbon monoxide (CO), benzene (C6H6), toluene (C7H8), etc., and alert residents to avoid outdoor activity, especially patients with respiratory problems.
ML approaches are based on data collected through various sensors located in different parts of the city. ML algorithms have advanced over the past few years, and their prediction is based on the quality of the data collection, i.e., data required for training the models. In our study, we considered the data collected at Visakhapatnam, a port city on the eastern side of peninsular India, for the assessment period 2018–2019.
This paper is organized as follows: Section 2 provides information about the literature review; Section 3 introduces the study area, methods of data collection, and descriptions of data and the machine learning regression model. Section 4 describes performance measurement indicators. Section 5 describes the results related to Visakhapatnam’s three predominant seasons and a comparison of prediction results of fifteen ML regression models. Section 6 presents the conclusion of the proposed work.
2. Literature Review
A number of studies have reported the implementation of ML approaches for urban air pollution, including PM2.5 concentration in recent years. Masood and Ahmad [5] presented a comparison of support vector machine (SVM) and artificial neural network (ANN) for the prediction of anthropogenic fine particulate matter (or PM2.5) for Delhi, based on various meteorological and pollutant parameters corresponding to a 2 year period from 2016 to 2018. ANN provided faster prediction and better accuracy, compared with SVM. Deters et al. [6] carried out research on the prediction of PM2.5 with the help of ML regression models considering selected meteorological parameters, and reported a high correlation between estimated data and real data. Moisan et al. [7] compared the performances of a dynamic multiple equation (DME) model in forecasting PM2.5 concentrations, with an ANN model and an ARIMAX model. They concluded that, although ANN in very few instances showed more significant and accurate results than the DME model, the overall performance of the DME model was slightly better than the ANN. Jiang et al. [8] reported the prediction of PM2.5 with the help of a long short-term memory (LSTM) model, with better accuracy. Suleiman et al. [9] compared three air quality control strategies, including SVM, ANN and boosted regression trees (BRT) for forecasting PM2.5 and PM10 concentrations in the roadside environment. They found that regression models with neural networks had better prediction performance, compared with SVM. A regression model which used extra trees regression and AdaBoost, for further boosting, was proposed for estimating PM2.5 for Delhi by Kumar S. et al. [10]. Regression and statistical methods were proposed by Chandu and Dasari [11] to study the causal relationship between PM2.5 and gaseous pollutants for the city of Visakhapatnam, but no forecasting model was proposed.
We chose Visakhapatnam, a port city of east peninsular India, which is surrounded on three sides by mountains and the Bay of Bengal on the fourth. This city is studded with major industries, including Hindustan Petroleum Corporation Limited (HPCL), Hindustan Zinc Limited (HZL), Bharat Heavy Plates and Vessels (BHPV), Hindustan Polymers Limited (HPL), Visakhapatnam Steel Plant (SP), Coastal Chemicals (CC), Andhra Cement Company (ACC) and Simhadri Thermal Power Corporation (STPC) [11]. Approximately 200 ancillary industries operate to supplement these main industries thereby causing air pollution, hence air quality research becomes a priority.
There are many ML regression-based models available in the literature; of these, fifteen ML regression models (presented in Section 3.3) were tested and implemented to predict the PM2.5 concentrations for Visakhapatnam. Among them, gradient boosting models (CatBoost, XGBoost and LightGBM) and voting regression models provided significant prediction results. Overall, the CatBoost model (that utilizes oblivious decision trees as the base learner) as proposed by Yandex Company [12] resulted in excellent prediction performance. The CatBoost model was able to archive comparable results, as obtained by other state of the art regression models such as RNN–LSTM [13], multivariate linear regression model [14] and LSTM [15]. Prediction accuracy of these regression models was validated using air pollutants (NO, NO2, NOx, NH3, SO2, CO, C6H6, C7H8) and meteorological parameters (relative humidity (RH), wind speed (WS), wind direction (WD), solar radiation (SR) and barometric pressure (BP), and temperature) as input variables.
This research work is different from previously reported studies on PM2.5, in multiple ways. In this study, in-depth seasonal and yearly variations in PM2.5 concentration were analyzed for two years. Fifteen machine learning methods were analyzed for optimal performance, compared with only two to three methods in most other studies, offering a more robust analysis for comparing models for real world implementation [6,7,8,9,10].
The main highlights of this manuscript are:
- (1)
- Analysis of the concentration of PM2.5 and air pollutants in the air of the eastern peninsular port city of India, on yearly and seasonal bases;
- (2)
- Evaluation of the correlation between PM2.5 concentration, air pollutants and meteorological parameters for the port city of Visakhapatnam;
- (3)
- Observation of the CatBoost prediction model as the most efficient prediction model for assessing and predicting the concentration of PM2.5 in the air;
- (4)
- Analysis of high PM2.5 concentration prediction results for the period under observation.
3. Materials and Methods
3.1. Study Area
Figure 2 shows the area under observation and wind rose diagram of the observation period. The study area, Visakhapatnam, a port city on the eastern side of peninsular India, with latitude 17°42′15″ N and longitude 83°17′52″ E, is located in the Indian state of Andhra Pradesh. The monitoring station for data collection was set up by the Andhra Pradesh Pollution Control Board (APPCB) [16]. Visakhapatnam is the largest city of Andhra Pradesh and the second largest east coast city in India, lying between the coast of the Bay of Bengal and the Eastern Ghats. According to the 2011 Indian census, Visakhapatnam had a population of 1,728,128 with a population density of 18,480/km2 [17].

Figure 2.
Location of port city Visakhapatnam (courtesy: google maps), and wind rose diagram (2018–2019) of study area.
Visakhapatnam observes tropical wet and dry climates during the year, with three dominant seasons: a summer season from March to June, a monsoon season from July to September, and a winter season from October to February. Though the summer extends from March to June, the maximum temperature is observed mainly in the month of May. The monsoon season extends from July to September, where an annual average rainfall of 44.05 inches was witnessed [18]. During winter, the minimum temperature is observed mainly in the month of January. The annual mean temperature of the city varies from 24.7 to 30.6 °C and observes an RH in the range of 68–80% [18].
During the period of observation, wind in the city blew with a mean speed of 2.32 m/sec in the direction of southwest (213.80 degrees, mean direction). The wind rose diagram in Figure 2 (based on a 24 h mean value) represents the direction of the wind, speed of wind and wind frequency of the location under observation for 2018–2019. The extent of the spoke determines the frequency of wind blowing in a specific direction. It is noted that the current PM2.5 concentration in Visakhapatnam air is 8 times above the WHO annual air quality guideline value [2]. Due to the extreme variation in climatic conditions and a very high concentration of PM2.5, there is a need to analyze ambient air quality, in addition to the impact of climatic factors, on the air quality of the city.
3.2. Data Description
In the present work, the data for air pollutants and PM2.5 concentration in the air, along with meteorological parameters, were collected for two consecutive years 2018–2019. Visakhapatnam has nine monitoring stations located at Industrial Estate Marripalem, Parawada, GVMC, Raitu Bajar, Police Barracks, Pedagantyada Gajuwada, Naval Area, Seethammadhara and Ganapuram Area, to measure the air quality index of the city. The original readings of air pollutant concentration and meteorological parameters were provided by the Central Pollution Control Board (CPCB) website [2] and APPCB [16] on 30 min, 1 h, 4 h, 8 h, 24 h and annual bases. For the present study, 24 h mean values of concentration of air pollutants and meteorological parameters were noted and utilized as prime variables for our prediction models. The raw dataset contained the record of air pollutants and meteorological parameters for 730 days. Of these days, the records for 32 days (19 days in 2018, and 13 days in 2019) were completely missed (either due to power failure, device failure or other reasons). After removing the 32 days, approximately 5% to 6% of values were further missed due to various parameters. The missing values were imputed using K-Nearest Neighbour (KNN) imputation method, and the values were imputed using the mean value from the n nearest neighbors. The value with k = 1, using the heterogeneous euclidean overlap metric (HEOM) distance, was chosen for the missing imputation for the presented dataset. After carefully processing, and missing value imputation, the observational record of air pollutants and meteorological parameters for 698 days was considered for our PM2.5 concentration analysis. The statistical descriptions of primary variables considered for analysis are presented in Table 1. For the period under observation, the city observed mean PM2.5 concentration of 48.63 µg/m3 with standard deviation of 30.05 µg/m3. Similarly, Table 1 shows the mean, standard deviation, minimum and maximum values of air pollutants and meteorological parameters.

Table 1.
Statistical description of air pollutants and meteorological parameters for the assessment period 2018–2019.
3.3. Machine Learning Model Description
For the prediction of PM2.5 concentration, 15 regression models, namely, voting regression (VR) [19], CatBoost regression (CB) [20], LightGBM regression (LGBM) [21], XGBoost regression (XGB) [22], LASSO least angle regression (LR-LA) [23], random forest regression (RF) [24], multi-layer perceptron regression (MLP) [25], LASSO regression (LAR) [26], partial least square regression (PLS) [27], quantile regression (QR) [28], multi-task ElasticNet (MTE) [29], ridge regression (RR) [30], Bayesian ridge regression (BRR) [31], KNN regression (KNN) [32] and linear regression (LR) [33] were trained and tested using data collected for the years 2018–19. The notion behind the consideration of 15 regression models was that the models broadly cover different regression approaches, thus offering more robust results. The broad regression approaches for models under consideration were:
- (a)
- Gradient boosting decision tree regression models: LGBM, XGB and CB;
- (b)
- Ensemble regression models: VR and RF (tree-based bagging ensemble technique);
- (c)
- Penalized regression models: LR–LA (lasso model with least-angle regression algorithm), LAR (lasso regularization technique to derive the coefficients exactly to zero), MTE (regularize multi-tasking using lasso and ridge norms) and RR (regularization technique to derive weights nearer to the origin);
- (d)
- Linear regression models: LR (using linear equation, i.e., linear relation of inputs and single target), BRR (linear regression using probability distribution) and;
- (e)
- Miscellaneous regression models: MLP (supervised neural network model), PLS (covariance-based statistical approach), QR (evaluates the median or other quantiles of target variable conditional on feature variables) and KNN (k-nearest neighbors algorithm).
However, despite predicting efficient results, regression models have their advantages and limitations. Table 2 presents the pros and cons of the proposed regression models for prediction of PM2.5 concentration.

Table 2.
Pros and cons of presented regression models.
3.4. CatBoost (Based on Gradient Boosting Algorithm) Model Description
Gradient boosting is a significant and effective machine learning technology implemented to deal with noisy, diverse features and complex correlated information. Using iteration, the technique amalgamates weak machine learning models with the aid of gradient descent in function space [34]. A gradient boosting based CB model was proposed by Yandex Company and the model utilizes oblivious decision trees as the base learner [12]. The decision trees are implemented for regression. Each tree indicates division of feature space and output value. Decision rule/splitting criteria are used during division of trees. Individual splitting criteria resembles a pair having a feature indicator , and threshold value . On implementing the decision rule/splitting criteria, a set of feature vectors can be disjointed into two subsets of and , so that for every , we have:
After implementing decision rule/splitting criteria to disjoint sets , we obtain disjoint sets . For a specified collection of sets and the target variable , the decision rule/splitting criteria can be given as:
where functions to estimate the optimality of the splitting criteria/decision rule and the collection with respect to the target variable . For an oblivious decision tree, can be defined as:
where is the target variable score with respect to the sample . In contrast to other regression models, the CB model has following advantages:
- (a)
- Categorical features: The model is capable of handling categorical features. In conventional gradient boosting decision tree-based algorithms, categorial features are replaced by their mean label value. If mean values are used to characterize features, then it will give rise to an effect of conditional shift [35]. However, in CB, an approach known as greedy target statistics is employed, and the model inculcates prior values to greedy target statistics. The employed technique reduces overfitting with minimum information loss;
- (b)
- Combining features: CB implements a greedy way to amalgamate all of the multiple categorical features and their combinations by the current tree during the formation of the new split. All the splits in the decision tree are considered as categories with two disjoint values and are employed during amalgamation;
- (c)
- The CB models are fast scorers. They are based on oblivious decision trees which are balanced and less inclined to overfitting.
4. Performance Measurement Indicators
Evaluation matrices for verification of high PM2.5 concentration: The National Ambient Air Quality Standards (NAAQS) [36] were developed by the Central Pollution Control Board, Ministry of Environment and Forests (Government of India), to regulate pollutant emissions into the air. According to the standards, a mean 24 h PM2.5 concentration of 60 µg/m3 was classified as higher concentration. For evaluating the high PM2.5 concentration, the following evaluation parameters were used: hit rate (HR), false alarm rate (FAR), threat score or critical success index (CSI), and true skill statistics (TSS). These parameters were evaluated using the contingency table shown in Table 3, and are presented in Table 4. The parameters were defined in terms of “Hit”, “Miss”, “False Alarm” and “Correct Rejection”. The terms “Hit” and “Correct Rejection” were possible cases when the prediction was accurate, and “False Alarm” and “Miss” were possible cases when the prediction was not accurate. The classification accuracy of the forecasting model was assumed to be good if “Hit” and “Correct Rejection” cases were predominant, with very low cases of “False Alarm” and “Miss”.

Table 3.
Contingency table.

Table 4.
Performance measurement indicators for regression prediction model validation and verification of high concentration.
Evaluation matrices for ML regression models: The prediction performance of regression models has been evaluated in terms of R2 Score, also known as “coefficient of determination”, MedAE, MAPE, RMSE, and MAE. Table 4 provides the performance measurement indicators utilized to validate the proposed prediction model.
5. Analysis of Results
In this section, we report a comprehensive analysis of the results, which comprises Section 5.1, Section 5.2, Section 5.3 and Section 5.4. Section 5.1 presents the correlation of PM2.5 concentration with air pollutants and meteorological parameters. Seasonal variation in PM2.5 concentration, along with other parameters, is presented in Section 5.2. PM2.5 concentration prediction using machine learning based regression models is reported in Section 5.3, and Section 5.4 presents an evaluation of the results for verification of higher concentration.
5.1. Correlation of PM2.5 Concentration with Air Pollutants and Meteorological Parameters
To statistically explore the relation between the concentration of PM2.5 with concentration of air pollutants and meteorological parameters, the correlation coefficients were calculated using Pearson’s correlation method, and are presented in Table 5. The Pearson’s correlation coefficient for two variables x and y can be evaluated as:
where and are the values of ith sample of variables x and y, respectively. and are the mean values of the variables x and y, respectively.

Table 5.
Correlation of PM2.5 with air pollutants and meteorological parameters.
Positive and negative correlations between the concentration of PM2.5 with the concentration of air pollutants and meteorological parameters were observed.
The air pollutants CO, NO2 and NOx formed a strong correlation with PM2.5 concentration. Among the meteorological parameters, WS, BP, and RH attained significant correlation with PM2.5 concentration. The air pollutant C7H8 showed a very low correlation value with PM2.5 concentration, which may have occurred due to fewer C7H8 emission sources in the city. An increment or decrement in the concentration of air pollutant stipulated a direct impact on the increment or decrement of PM2.5 concentration. All the meteorological parameters except BP and temperature exhibited a negative correlation with PM2.5 concentration. The meteorological parameter temperature marked a very low value of Pearson’s coefficient, which was probably due to insignificant variation in mean temperature values during the major seasons. The city observed an approximate mean temperature of 29 °C during the major seasons. It was noticed that WS reported a strong negative correlation with PM2.5 concentration.
5.2. Seasonal and Annual Behaviour of PM2.5 Concentration with Air Pollutants and Meteorological Parameters
An in-depth analysis of seasonal and annual behavior of PM2.5 concentration is presented in Section 5.2.1 and Section 5.2.2.
5.2.1. Seasonal Behavior of PM2.5 Concentration with Air Pollutants and Meteorological Parameters
For assessing the seasonal impact of air pollutants and meteorological parameters on PM2.5 concentration, a detailed statistical analysis is presented in Table 6. It was comprehended that the air pollutant concentration reported significant seasonal variations. A rise in PM2.5 concentration during December–February, and decrease from March–August, was observed for the study period. The seasonal variations in PM2.5 and air pollutant concentration were primarily due to the varying speed and direction of the wind, seasonal variation in SR, and lack of precipitation in winter which reduces surface vertical mixing and can lead to limited dilution and dispersion [37].

Table 6.
Seasonal behavior of PM2.5 concentration, air pollutants and meteorological parameters during summer season (sum.), winter season (win.) and monsoon season (mon.).
It was found that the air pollutant and PM2.5 concentration exhibit maximum variation in the winter season. The maximum value of PM2.5 concentration recorded during the winter season was 202.52 µg/m3, which was 106.62 µg/m3 and 130.68 µg/m3 higher than the maximum observed PM2.5 concentration during summer and monsoon season, respectively. The monsoon season observed marginally greater mean and median values of PM2.5 concentration (34.39 µg/m3 and 33.61 µg/m3, respectively) in contrast to the summer season. However, the summer season observed significant PM2.5 concentration variation (24 h) in contrast with the monsoon season, and observed higher minimum and maximum PM2.5 concentration. The summer season observed a mean PM2.5 concentration of 33.64 µg/m3 (standard deviation = 14.21 µg/m3) with minimum and maximum PM2.5 concentration of 9.09 µg/m3 and 95.90 µg/m3, respectively. Due to precipitation in the monsoon season, the air pollutant level dipped and led to a low concentration of air pollutants and PM2.5 concentration in the air.
During the winter season, a higher air pollutant concentration was noticed. The maximum values observed for air pollutants CO, NO2 and C6H6 were 2.18 mg/m3, 131.53 µg/m3 and 11.69 µg/m3, respectively. Due to an increase in the concentration of CO and oxides of nitrogen, a rise in PM2.5 concentration was observed. The rise in air pollutant concentration was probably due to the slow WS and temperature inversion effect in the winter season. As a result, the air pollutants and PM2.5 particles were trapped near the earth’s surface which, in turn, increased the PM2.5 concentration [38,39].
A substantial variation in PM2.5 concentration (24 h) was observed during the summer season, and a variation from 9.09 µg/m3 to 95.90 µg/m3 in PM2.5 concentration was reported during the period of observation. The season reported high SR (mean value = 167.18 W/m2; standard deviation = 56.02 W/m2) and high WS (mean value = 2.79 m/s; standard deviation = 0.73 m/s). Because of the high SR acquired by the earth’s near-surface atmosphere, the near-surface temperature increased, promoting upward movement, eventually diffusing PM2.5 concentration. In addition to higher SR, the high WS and high precipitation diluted the air pollutant concentration at the surface and caused a significant decrease in air pollutants and PM2.5 concentration during the summer season [38,39].
It was noted that the air pollutant SO2 concentration showed inadequate seasonal variability and remained approximately constant throughout the year. This was possibly due to SO2 emission sources (sulphur-containing fuels such as oil, coal and diesel) which constantly emit SO2 pollutants in the city. The primary sources of CO, SO2 and nitrate aerosols for the city are presumed to be power generation plants, engines in vehicles and ships, ship-yard industries and steel plants. The key source of C6H6 emission in the city is probably due to the presence of heavy chemical and petroleum industries, as C6H6 is a natural element of petrol and crude oil and is produced as a by-product during the oil refining process. In addition to major industries, the city is surrounded by many small and medium-size industries which add to the concentration of air pollutants. Though heavy, medium and small industries contribute to increasing air pollution, the city has the advantage of sea breezes, by which most of the air pollutant emissions are disseminated to sea and the impact of air pollutants on air quality is reduced. However, a relatively constant NH3 concentration was observed during the assessment period, which was probably due to the continuous emission of ammonia gases from industrial processes and vehicular emissions.
It was found that the city experiences greater humidity during the monsoon season, i.e., from 63.06% to 85.23%, with a mean humidity of 74.68%, whereas a mean humidity of 70% and 71.89% was observed by the city in the winter and summer seasons, respectively. As noted from Table 4, the metrological parameter ‘humidity’ exhibits a negative correlation with PM2.5 concentration. In the highly humid season, raindrops influence gaseous air pollutants by the phenomenon of absorption and collision. The phenomenon leads to wet decomposition and reduces the PM2.5 concentration [40,41].
As observed from the wind rose diagram (Figure 3) and from Table 6, slow and the infrequent wind blows during the winter season. To present a detailed analysis of WD, the wind rose diagram is plotted in sixteen directions from N to NNE (counterclockwise). The concentric circles in the wind rose diagram represent the probability percentage of wind blow, and are labeled with percentages increasing outward. As shown in Figure 3, the probability percentage concentric rings are placed at 5% intervals. For analysis, the WS is divided into nine bins and the bins are differentiated, with colors ranging from red to brown. The length of spoke around the circle is related to the frequency of time that the wind blows from a particular direction. The dominant wind directions during the winter season were found to be in the SSE and S directions, with a small secondary lobe in the SSW direction, and with minor lobes in the SW and SE directions, indicating less frequent wind blow in these minor lobe directions. The winter season observed a mean WS of 1.85 m/s, and approximately 65% of the time the wind blew in the direction of SSW to SSE (230–305 degrees). During the season, only 1–2% of infrequent high-speed winds (greater than 4.47 m/s) were observed. Approximately 20–25% of the time the wind blew at a speed of 2.47 m/s to 2.97 m/s. During the remaining time, the wind blew at a speed of less than 1.47 m/s. The summer and monsoon seasons observed frequent and high-speed winds during the period of observation, and the wind blew mainly in a southwest direction (primarily in direction of 180–250 degrees). During the monsoon season, approximately 40–45% of the time the wind blew with a speed greater than 3.18 m/s, and approximately 8–10% of the time the wind blew with a speed of 4.23 m/s to 4.75 m/s. However, infrequent WS greater than 4.75 m/s blew for approximately 1–2% of the entire season. Similar high-speed winds were observed for the summer season, with a SSW prominent wind direction. For the summer and monsoon seasons, the high-speed winds swept the air pollutants away from the city, hence, a low concentration of PM2.5 was observed during these months.
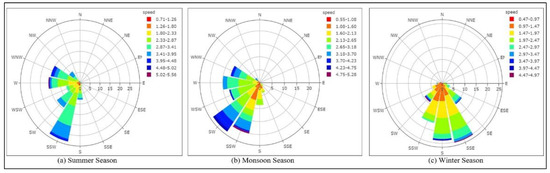
Figure 3.
Wind rose diagram for summer, monsoon and winter seasons.
5.2.2. Annual Behavior of PM2.5 Concentration, Air Pollutants and Meteorological Parameters
Annual variation in PM2.5 concentration, air pollutant and meteorological parameters for 2018 and 2019 are presented in Table 7. As observed, a minor increase in PM2.5 concentration was observed for 2018, and mean PM2.5 concentration values of 49.97 µg/m3 and 47.32 µg/m3 were noted for 2018 and 2019, respectively. A substantial variation in CO and NO concentration was observed for 2018 and 2019. A rise of 0.15 mg/m3 in mean value of CO emission was observed during 2019. However, the maximum value of CO emission (2.18 mg/m3) was noted in 2018. An inconsiderable variation in the mean concentrations of NO2, C6H6, and NOx was observed during the entire period.

Table 7.
Statistical description of PM2.5 concentrations, air pollutants and meteorological parameters for the assessment year 2018–2019.
A minor variation of 1.58 µg/m3 to 1.83 µg/m3 in the mean concentration of SO2 and NO was noted between 2018 and2019. As observed, the period under study observed approximately continuous mean temperature. During the period of observation, the city observed a mean temperature of approximately 29℃ with approximately the same median temperature in 2018–2019. In contrast to 2018, slightly stronger winds (mean speed of 2.40 m/s) blew during 2019, and the city observed maximal WS during the months of April–July. During the period of observation, the wind blew in the mean direction of 234.25 degrees to 193.71 degrees, and a change in wind direction was noticed in the months of November–January. A small variation of 3.33 mmHg in mean BP was observed for 2018–2019, and approximately the same values of minimum and maximum BP were noted for the period under study. However, variations in BP were noted for 2019. A high SR was observed in 2018 compared with 2019, and a mean SR of 143.01 W/m2 in 2018 was noted in contrast to 131.87 W/m2 for 2019. Higher peak values of SR were noted for 2018 in contrast to 2019. Due to the cumulative effect of variation in air pollutant concentration and meteorological parameters, continuous variable PM2.5 concentration was observed for the period 2018–2019.
5.3. Machine Learning-Based PM2.5 Concentration Estimation
In the present study, the performance of the machine learning based regression models, employed to estimate PM2.5 concentration in the air, were validated using data related to eight air pollutants and six meteorological parameters collected for the year 2018–2019 for Visakhapatnam. The air pollutants and meteorological parameters were utilized as independent input variables to train 15 distinct machine learning regression models to predict PM2.5 concentration. The model parameters were tuned using a grid search optimization technique. The dataset was divided into training and test datasets with a ratio of 80–20%, namely, 80% of observations were used to train the model and 20% of observations were sed to test the model. In our proposed methodology, the dataset was randomly categorized into a training dataset and a test dataset. The experiments were simulated using Python 3.8 open-source software on an IBM PC with Intel Core i-7–6700 CPU @ 3.40 GHz processor supported with 8 GB RAM. Table 8 presents the performance matrices of 15 regression models for the prediction of PM2.5 concentration. It was observed that the VR and gradient boosting regression models (CB, LGBM and XGB) showed notable performance, in contrast to other presented regression models.

Table 8.
PM 2.5 concentration prediction performance analysis using various regression models.
5.3.1. Performance of Regression Models
From Table 8, it was noted that the gradient boosting and VR models achieved a notable R2 score (0.71 to 0.81). The higher R2 score signified that the dataset values were well fitted in the model. Furthermore, the gradient boosting and VR prediction models achieved low error scores in terms of RMSE (11.42 µg/m3 to 14.03 µg/m3) and MAE (9.09 µg/m3 to 10.34 µg/m3). The CB prediction model outperformed RMSE, MAE, MAPE and MedAE, in terms of R2 score. The model yielded an R2 score of 0.81, RMSE of 11.42 µg/m3, MAPE of 0.29, and an MAE of 9.07 µg/m3. The prediction performance of the LGBM model was found to have deteriorated in contrast to the CB which predicted the results with an R2 score of 0.76, RMSE of 12.94 µg/m3, MAPE of 0.29 and MAE of 9.85 µg/m3. Comparable accuracies were observed for VR and XGB models. However, the models showed lower prediction performance against CB and LGBM regression models.
As observed, in addition to high R2, the CB regression predicted the PM2.5 concentration with minimum error amongst all the presented models. It was found that the CB model attained minimum MedAE (6.95 µg/m3) and MAPE (0.29) errors, revealing that the model was robust to the outliers presented in the dataset. Very low performance was observed for QR and KNN regression models. Low-performance scores in terms of R2 and high errors attained by these models indicated their inefficacy to fit the dataset values for predicting PM2.5 concentration. However, the RF model showed slightly improved performance in comparison to the KNN model. Least prediction performance was observed for the QR model, with low R2 scores (0.47) and unfavorable high error in terms of RMSE (19.18 µg/m3), MAE (14.21 µg/m3), MedAE (10.33 µg/m3) and MAPE (0.46).
The MLP regression model showed marked performance degradation for predicting the PM2.5 concentration. MLP predicted the results with an R2 score of 0.69, RMSE of 14.65 µg/m3, MAE of 11.12 µg/m3 and median absolute error of 8.96 µg/m3. All the penalized regularization regression models (LA-LSR, LAR, MTE, RR and BRR) and the LR model attained comparable prediction performance, with an approximate R2 score of 0.57, and RMSE and MAE in the proximity of 17 µg/m3 and 13 µg/m3, respectively. The models attained a median absolute error of approximately 8.75 µg/m3.
It was observed that the penalized–regularization model showed enhanced prediction performance in contrast to MLP, and diminished performance in comparison to voting and gradient boosting models. Comparative prediction performance with slightly increased MedAE was noted for the PLS prediction model.
Figure 4 and Figure 5 present the regression plots and residual error plots for the test dataset. Figure 4 shows the regression plots mapped between observed and predicted PM2.5 concentrations. As observed from Figure 4, compared with other models, the data points for CB model were highly concentrated on the ‘fitting line’ in the regression curve, indicating that the values were well fitted in the model. A low concentration of data points was observed on the ‘fitting line’ for LGBM, XGB and VR regression models, indicating that the values were not well fitted to the models.

Figure 4.
Regression plots of test dataset using VR, XGB, LGBM and CB prediction models.
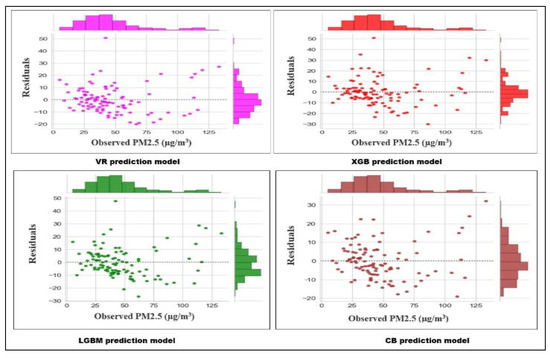
Figure 5.
Residual plots of test dataset using VR, XGB, LGBM and CB prediction models.
Figure 5 presents the residual error plots with their histograms showing residuals of the regression models evaluated for the test dataset. The results report that for XGB and VR regression models, the residuals and histogram peaks reside at around 0 to −20, yielding negatively biased results. It indicates that the model’s prediction was too high, and that the models probably predict higher PM2.5 concentration than compared with observed PM2.5 concentration. The LGBM model shows satisfactory improvement having a random and dispersed distribution of residual. However, the model observes low negatively biased residual error, and the results turn out to be slightly negative, biased with a moderate difference between predicted and observed PM2.5 concentrations. Amongst all the fifteen implemented models, the CB model shows significant prediction performance with minimum residual error. As observed from the residual error plot Figure 5, the model is least biased to positive and negative residuals and shows random residual distribution. The residual error in CB lies in the range of −20 to 30, with maximum residual present in the range of −10 to 10.
Time series and scatter plot between true and predicted PM2.5 concentrations for the test datasets are presented in Figure 6. As marked in Figure 6a, the models show adequate prediction performance and, as compared with other models, the CB model relatively follows the true PM2.5 concentration. The scatter plot presented in Figure 6b shows that in contrast to VR, XGB and LGBM models, the CB model predicts PM2.5 concentration in the proximity of observed/true PM2.5 concentration at maximum instants of time. For the CB regression model, Figure 5 and Figure 6 show fine agreement between the observed/true and predicted PM2.5 concentrations.
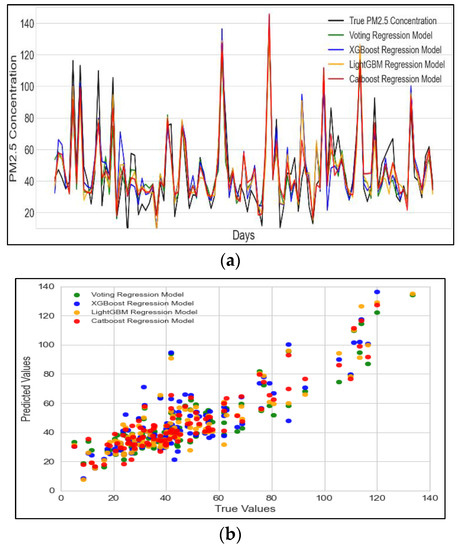
Figure 6.
(a) Time series plot of true and predicted PM2.5 concentration for the test dataset using different regression models. (b) Scatter plot between true and predicted PM2.5 concentration on the test dataset using VR, XGB, LGBM and CB models.
5.3.2. Impact of Input Variables (Air Pollutant Concentration and Meteorological Parameters) on the CB Model
To interpret the CB model, the impact of feature variables (air pollutants and meteorological parameters) on PM2.5 concentrations were evaluated, and are presented in Figure 7. The influence of feature variables was measured using Shapley additive explanations (SHAP) values [42].

Figure 7.
Impact of air pollutants and meteorological parameters on the CB regression model.
The SHAP framework defines the prediction in terms of a linear combination of binary variables that are used to describe whether an input feature is present in the model or not. The framework defines results in terms of Shapley values. Shapley (SHAP) values define the feature importance and impact of features on the prediction model by considering three required properties: (a) local accuracy, (b) missingness, and (c) consistency [42]. The y-axis points to the input variables indicating their impact on the model. The input variables on the y-axis are arranged according to their importance. The values on the x-axis indicate SHAP values, and points on the plot indicate Shapley values of input variables for the instances. The color gradient (blue to red) indicates variable importance from low to high. The higher the SHAP value, the higher is the variable’s impact on the model. As shown in Figure 7, variables NH3, BP, CO and NO2 significantly influenced the predicted PM2.5 concentration with positive correlation, i.e., the predicted value increased with the high feature values of NH3, BP, CO and NO2, and conversely, predicted value decreased with the lower feature values of NH3, BP, CO and NO2.
However, the variables SO2, NOx, and C6H6 also positively influenced the predicted results but had less impact on the prediction result. The variables WS, WD, SR, temperature, C7H8 and RH influenced the predicted PM2.5 concentration with negative correlation, i.e., higher values of WS, WD, SR, temperature, C7H8 and RH tended to decrease the predicted value, and vice versa.
5.4. Evaluation of High PM2.5 Concentration
During the period of observation, the city was exposed in 2019 to a higher value of PM2.5 concentration compared with 2018. Among the three dominant seasons of the city, the winter season observed a maximum number of days with higher PM2.5 concentration than NAAQS standards. The NAAQS standards classify a mean of 24 h PM2.5 concentration of 60 µg/m3 as higher concentration. However, the summer and monsoon seasons observed very few days of PM2.5 concentration greater than NAAQS standards.
Table 9 presents the prediction results for high PM2.5 concentration using the CB regression model for the period of observation. The high concentration prediction performance was evaluated using HR, FAR, CSI, TSS and OR measurement indices. The results for high concentration were evaluated on the test dataset. The results showed that the model achieved a high Hit rate of 0.85 for measuring accurate predictions and achieved a low score of 0.02 for false alarms.

Table 9.
Evaluation of predictions for high PM2.5 concentration using CB model on the test dataset.
The model also achieved high CSI and TSS scores, indicating the model’s excellent performance and its ability to correctly classify between “Yes” and “No” cases. Moreover, the CSI represented the model’s sensitivity to correct forecasts of high concentration, and the high value obtained by the CSI indicated that the high concentration cases of PM2.5 were generally predicted correctly.
It was found that, for the period under observation, the winter season encountered 166 days with PM2.5 concentrations greater than the standards set by NAAQS. Approximately 55–60% of days during the winter season witnessed higher PM2.5 concentration than the prescribed NAAQS standards. In contrast, approximately 4–5% of days witnessed higher PM2.5 concentration than the prescribed NAAQS standard in the summer and winter season. For approximately more than 90 days of the winter and monsoon seasons, the city was under the impact of higher C6H6 concentration than the prescribed standards.
6. Conclusions
In the present study, fifteen machine learning models were presented for analysis and prediction of PM2.5 concentration based on time series data. This study provided detailed insight into the air pollutants and meteorological parameters contributing to PM2.5. We targeted the statistical behavior of 24 h average air pollutant and PM2.5 concentrations along with meteorological parameters observed at the eastern coastal city of Visakhapatnam, India. Using Pearson’s correlation coefficient, the correlation of PM2.5 with air pollutants and meteorological parameters was determined. Seasonal behavior of air pollutants, PM2.5 concentration and metrological parameters were studied by extracting significant information from raw data collected from the Central Pollution Control Board and APPCB. It was deduced that the summer and monsoon seasons showed lower PM2.5 and air pollutant concentrations, compared with the winter season. The results revealed that the CB machine learning model is an efficient predictive model. For comparative analysis with other prediction models, we used R2 score, RMSE, MAE, and MedAE as MAPE performance parameters. The performance of the CB model was not only better than traditional models, such as the linear regression model and MLP, but also better than voting and other boosting models such as XGBoost and LightGBM. The prediction of PM2.5 concentration is a challenging task, owing to changing metrological and pollutant concentration, yet an amount of credibility in prediction results can be attained using copious data. The present study was carried out for a small period and notable results were achieved, however, significant improvement in forecasting results can be expected by examining the information over a greater period and, in addition, considering nearby geographical locations.
Author Contributions
Conceptualization, N.K.; Data curation, M.S., S.S., V.J. and S.K.; Formal analysis, M.S., N.K., S.S., V.J., S.M., S.K. and P.K.; Investigation, N.K., S.S., V.J., S.M. and S.K.; Methodology, M.S. and S.M.; Resources, V.J.; Supervision, P.K., Visualization, P.K.; Writing—original draft, M.S. and N.K.; Writing—review & editing, M.S., N.K., S.S., S.K. and P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The dataset is publicly available at https://cpcb.nic.in (accessed on 5 October 2021) and https://pcb.ap.gov.in/UI/Home.aspx (accessed on 5 October 2021).
Acknowledgments
The authors acknowledge Ashok K. Goel, GZSCCET, MRSPTU, Bathinda, for his valuable suggestions in conducting the research and performance analysis. Additionally, Shallu Sharma and Sumit Kumar are immensely thankful to Pravat Mandal, Manesar, and Ashok Mittal of Lovely Professional University, Punjab, for their support during the execution of this work.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- WHO. 2 May 2018. Available online: https://www.who.int/news/item/02-05-2018-9-out-of-10-people-worldwide-breathe-polluted-air-but-more-countries-are-taking-action (accessed on 25 November 2021).
- Central Pollution Control Board, India. Available online: https://www.cpcb.nic.in/ (accessed on 5 October 2021).
- EEA. Healthy Environment, Healthy Lives. 2019. Available online: https://www.eea.europa.eu/ (accessed on 26 November 2021).
- EEA. Air Pollution: How It Affects Our Health. 2021. Available online: https://www.eea.europa.eu/ (accessed on 26 November 2021).
- Masood, A.; Ahmad, K. A model for particulate matter (PM2.5) prediction for Delhi based on machine learning approaches. Procedia Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Deters, J.K.; Zalakeviciute, R.; Gonzalez, M.; Rybarczyk, Y. Modeling PM2.5 Urban Pollution Using Machine Learning and Selected Meteorological Parameters. J. Electr. Comput. Eng. 2017, 2017, 5106045. [Google Scholar] [CrossRef] [Green Version]
- Moisan, S.; Herrera, R.; Clements, A. A dynamic multiple equation approach for forecasting PM2.5 pollution in Santiago, Chile. Int. J. Forecast. 2018, 34, 566–581. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Luo, Y.; Zhang, B. Prediction of PM2.5 Concentration Based on the LSTM-TSLightGBM Variable Weight Combination Model. Atmosphere 2021, 12, 1211. [Google Scholar] [CrossRef]
- Suleiman, A.; Tight, M.; Quinn, A. Applying machine learning methods in managing urban concentrations of traffic related particulate matter (PM10 and PM2.5). Atmos. Pollut. Res. 2019, 10, 134–144. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, S.; Singh, S.K. A machine learning-based model to estimate PM2.5 concentration levels in Delhi’s atmosphere. Heliyon 2020, 6, e05618. [Google Scholar] [CrossRef]
- Chandu, K.; Dasari, M. Variation in Concentrations of PM2.5 and PM10 during the Four Seasons at the Port City of Visakhapatnam, Andhra Pradesh, India. Nat. Environ. Pollut. Technol. 2020, 19, 1187–1193. [Google Scholar] [CrossRef]
- Ferov, M.; Modry, M. Enhancing lambdaMART using oblivious trees. arXiv 2016, arXiv:1609.05610. [Google Scholar]
- Rao, K.S.; Devi, G.L.; Ramesh, N. Air Quality Prediction in Visakhapatnam with LSTM based Recurrent Neural Networks. Int. J. Intell. Syst. Appl. 2019, 11, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Prasad, N.K.; Sarma, M.; Sasikala, P.; Raju, N.M.; Madhavi, N. Regression Model to Analyse Air Pollutants Over a Coastal Industrial Station Visakhapatnam (India). Int. J. Data Sci. 2020, 1, 107–113. [Google Scholar] [CrossRef]
- Devi Golagani, L.; Rao Kurapati, S. Modelling and Predicting Air Quality in Visakhapatnam using Amplified Recurrent Neural Networks. In Proceedings of the International Conference on Time Series and Forecasting, Universidad de Granada, Granada, Spain, 25–27 September 2019; Volume 1, pp. 472–482. [Google Scholar]
- Andhra Pradesh Pollution Control Board. Available online: https://pcb.ap.gov.in (accessed on 5 October 2021).
- Census-India (2012) Census of India. The Government of India, New Delhi. 2011. Available online: https://censusindia.gov.in/census.website/ (accessed on 28 November 2021).
- Indian Meteorological Department. Government of India. Available online: https://mausam.imd.gov.in/ (accessed on 23 October 2021).
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. Catboost: Unbiased boosting with categorical features. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31, pp. 6638–6648. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Avila, J.; Hauck, T. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S. Neural Networks and Learning Machines; Pearson: Upper Saddle River, NJ, USA, 2009; Volume 3. [Google Scholar]
- Tibshirani, R. Regression Analysis and Selection via the Lasso. R. Stat. Soc. Ser. 1996, 58, 267288. [Google Scholar]
- Abdi, H. Partial least square regression (PLS regression). In Encyclopedia of Measurement and Statistics; Salkind, N.J., Ed.; Sage: Thousand Oaks, CA, USA, 2007. [Google Scholar]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Liu, J.; Ji, S.; Ye, J. Multi-task feature learning via efficient l 2, 1-norm minimization. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence; AUAI Press: Arlington, VA, USA, 2009; pp. 339–348. [Google Scholar]
- Kidwell, J.S.; Brown, L.H. Ridge Regression as a Technique for Analyzing Models with Multicollinearity. J. Marriage Fam. 1982, 44, 287–299. [Google Scholar] [CrossRef]
- Bayesian Ridge Regression. Available online: https://scikit-learn.org/stable/modules/linear_model.html#bayesian-ridge-regression (accessed on 13 December 2021).
- Fehrmann, L.; Lehtonen, A.; Kleinn, C.; Tomppo, E. Comparison of linear and mixed-effect regression models and k-nearest neighbour approach for estimation of single-tree biomass. Can. J. For. Res. 2008, 38, 1–9. [Google Scholar] [CrossRef]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 329. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 6638–6648. [Google Scholar]
- Zhang, K.; Schölkopf, B.; Muandet, K.; Wang, Z. Domain adaptation under target and conditional shift. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 819–827. [Google Scholar]
- The Gazette of India, Part III–Section 4, NAAQS CPCB Notification. 2009. Available online: https://cpcb.nic.in/ (accessed on 17 December 2021).
- Tai, A.P.K.; Mickley, L.J.; Jacob, D.J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: Implications for the sensitivity of PM2.5 to climate change. Atmos. Environ. 2010, 44, 3976–3984. [Google Scholar] [CrossRef]
- Khillare, P.S.; Sarkar, S. Airborne inhalable metals in residential areas of Delhi, India: Distribution, source apportionment and health risks. Atmos. Pollut. Res. 2012, 3, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Tang, G.; Wang, Y.; Tie, X. Analysis of a long-term measurement of air pollutants (2007–2011) in North China Plain (NCP); Impact of emission reduction during the Beijing Olympic Games. Chemosphere 2016, 159, 647–658. [Google Scholar] [CrossRef]
- Jian, L.; Zhao, Y.; Zhu, Y.-P.; Zhang, M.-B.; Bertolatti, D. An application of ARIMA model to predict submicron particle concentrations from meteorological factors at a busy roadside in Hangzhou, China. Sci. Total Environ. 2012, 426, 336–345. [Google Scholar] [CrossRef]
- Wang, J.; Ogawa, S. Effects of Meteorological Conditions on PM2.5 Concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public Health 2015, 8, 9089–9101. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. Available online: https://arxiv.org/abs/1705.07874 (accessed on 20 December 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).