Statistical Analysis of PM10 Concentration in the Monterrey Metropolitan Area, Mexico (2010–2018)
Abstract
1. Introduction
2. Methodology
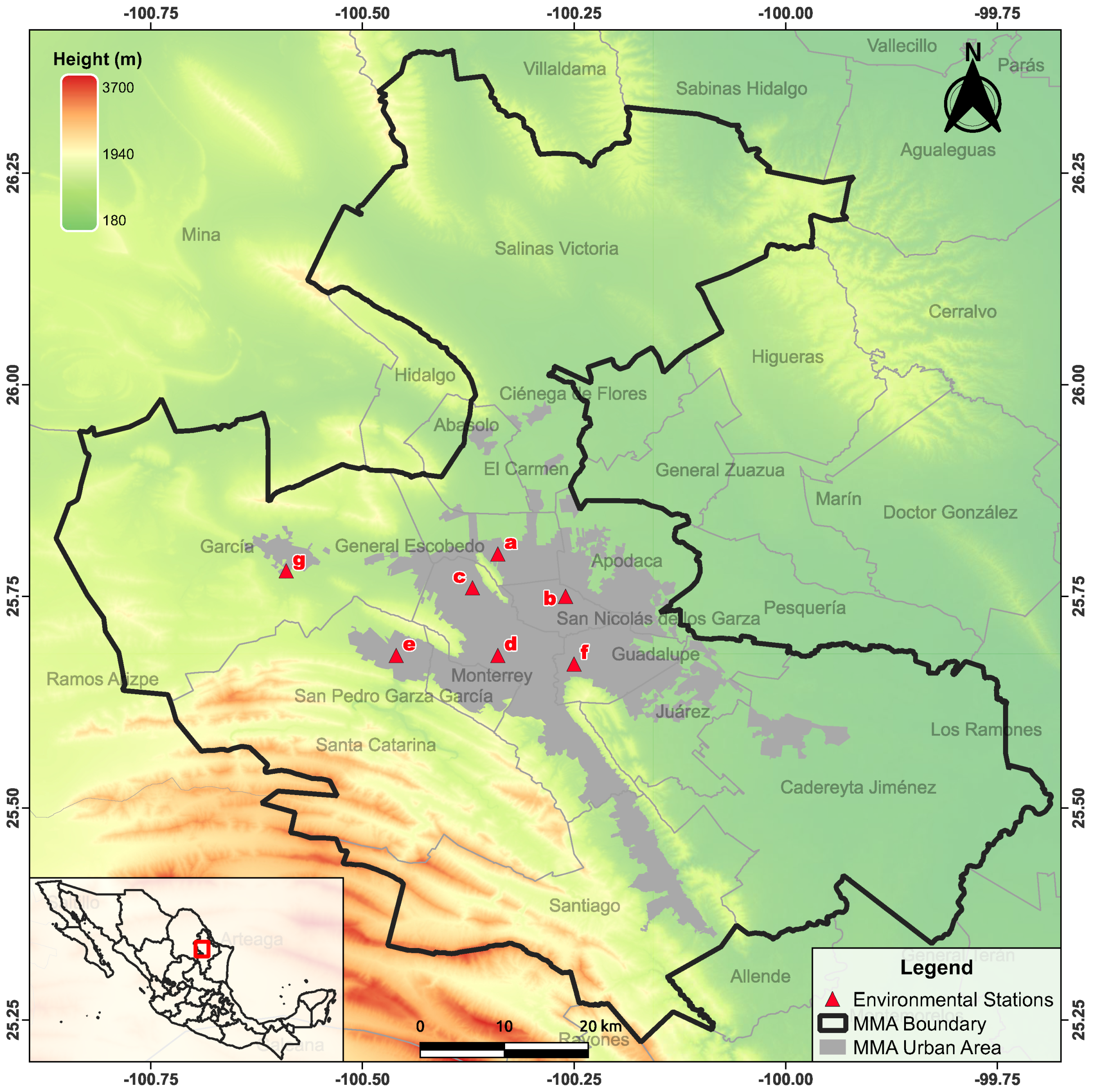
2.1. Data Acquisition and General Observations
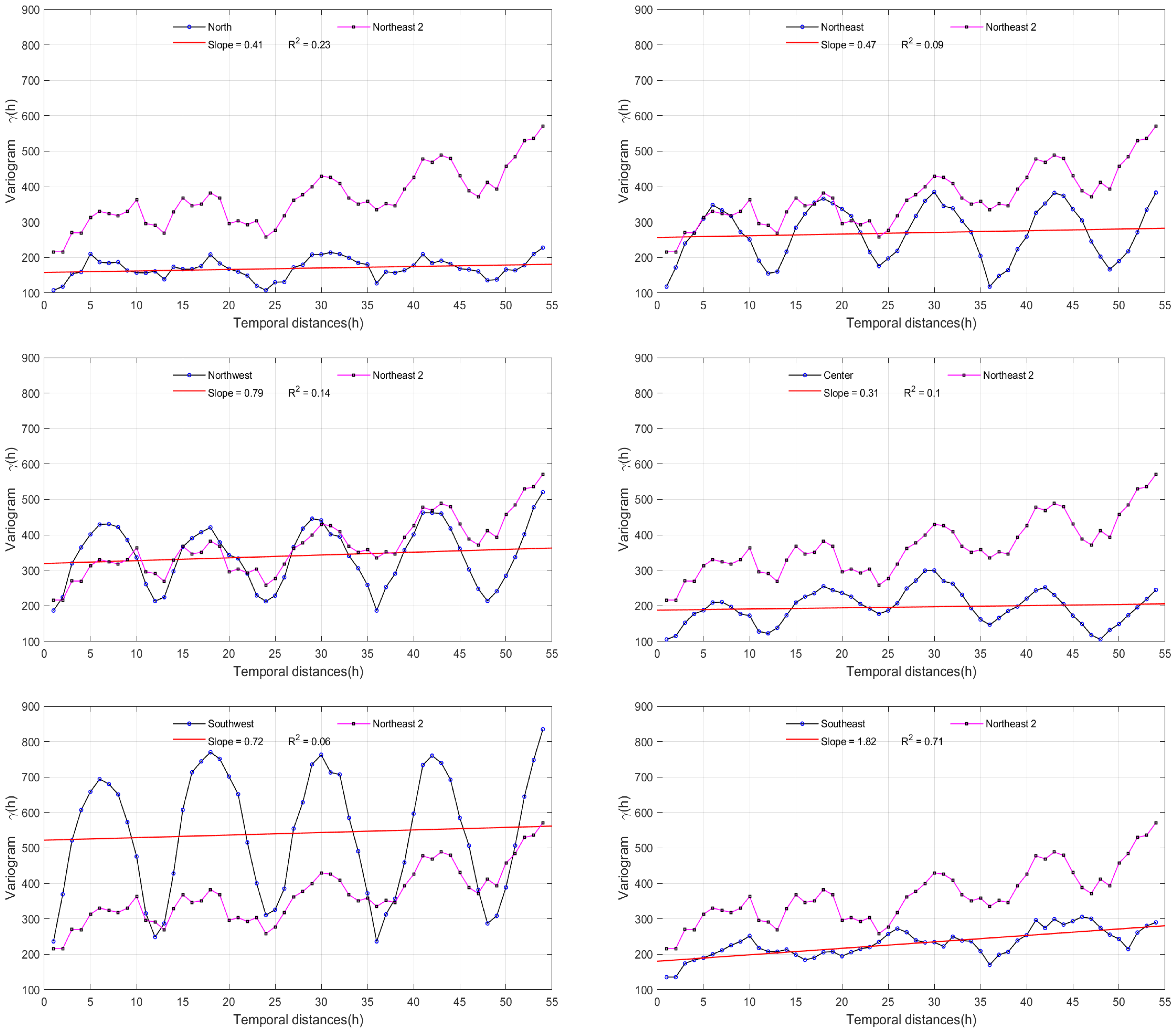
2.2. Experimental Semi-Variogram
2.3. Hurst Exponent
2.4. Higuchi Fractal Dimension (HFD)
3. Results
4. Discussion
4.1. Time Series and Semi-Variograms
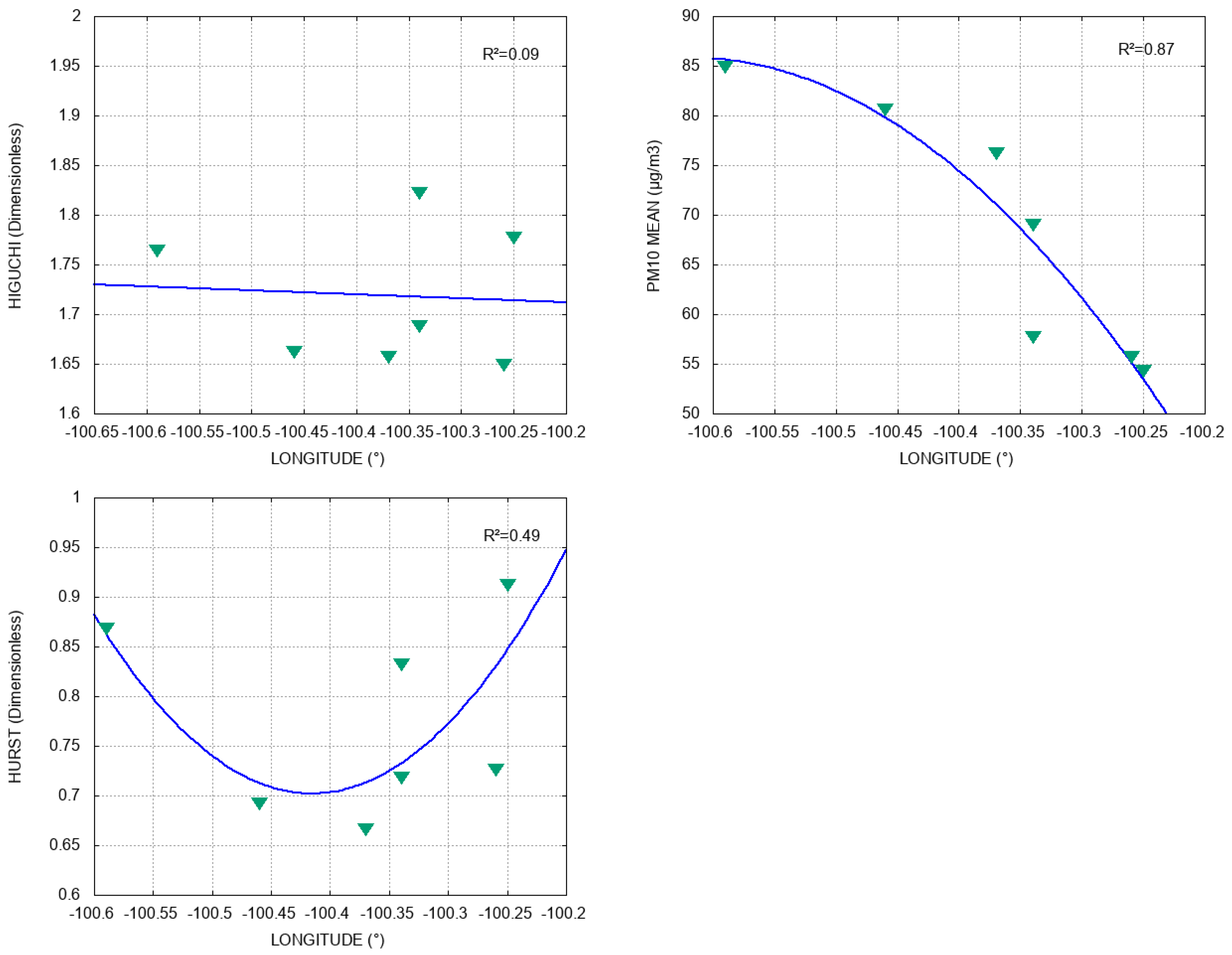
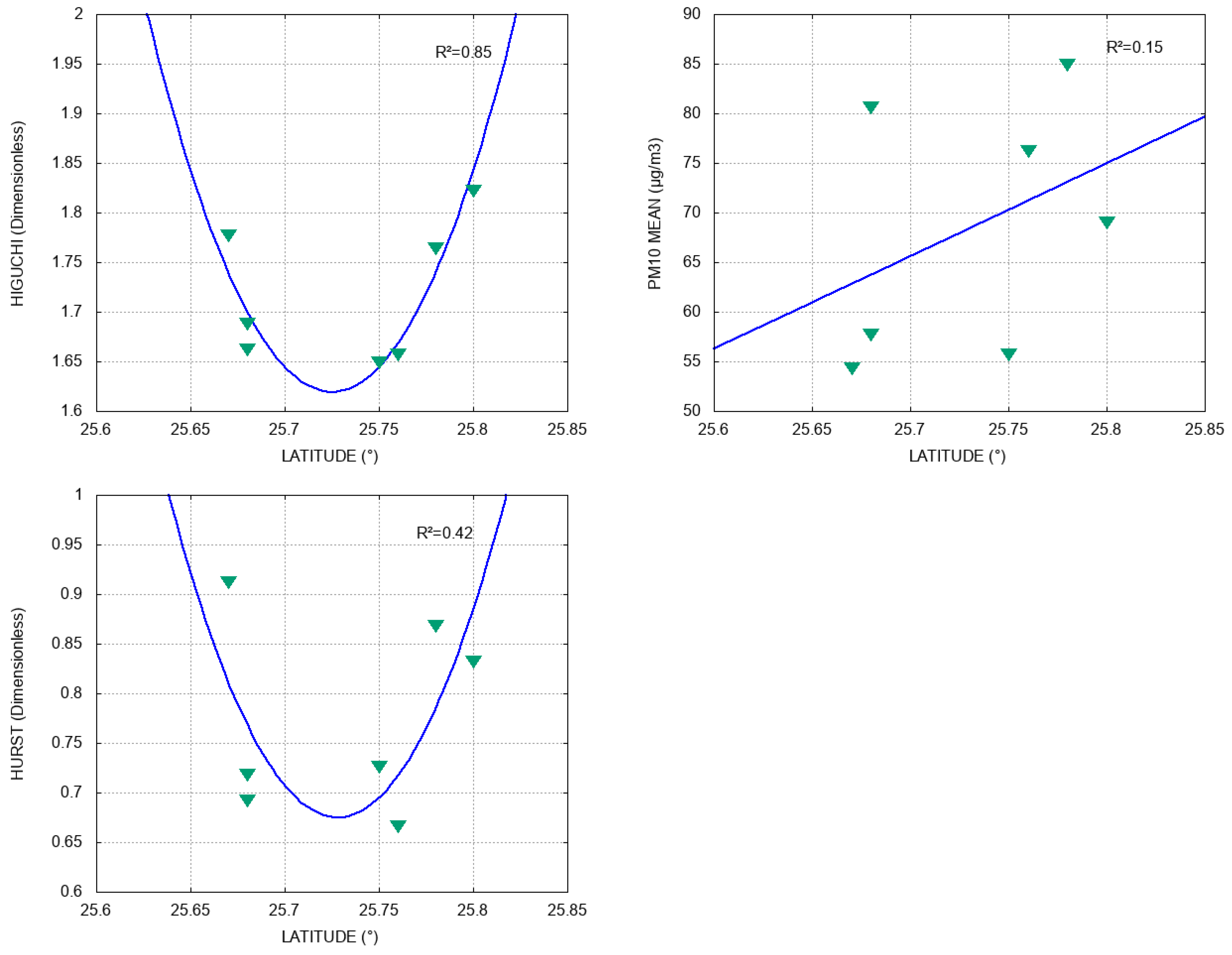
4.2. Fractal Exponents, PM10 Mean, and Geographic Parameters
5. Conclusions
- The annual cyclical behavior reported in previous studies was the same for the period studied, from 2010 to 2018, with greater pollution levels during the autumn-winter periods and lower levels during spring-summer periods;
- The PM10 concentration has been decreasing, which is promising for the people of the MMA in the near future. Nevertheless, half of the selected stations exceeded the AM limit during their most polluted period. Therefore, studying strategies to deal with pollution can help the authorities make decisions that protect the environment and the quality of life of MMA inhabitants;
- The highest values of average pollution are located in the western zone and the zone with the highest altitude in the MMA, which is probably a consequence of the main direction of wind flow, as well as geographical features. Consequently, we suggest a personalized alert system for the interior of the MMA so that the state government can issue policies and warn people from different areas of the metropolis according to the level of contamination presented by each zone;
- The persistence of the series, measured with and , is related in a quadratic way to the pollution mean. We did not find a correlation between these coefficients and altitude, but we found a strong correlation between and latitude, which is a significant result since latitude was not related to PM10 mean level;
- The use of the semi-variograms and fractal exponents and provided practical results in the time series analysis, which suggests that these techniques should continue to explored and that they should be complemented with other meteorological parameters for the corresponding authorities to take into account in their decision making.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alonso, E.; Martínez, W.; Rubio, J.C.; Velasco, F.; Chávez, H.L.; Ávalos, M.; Lara, C.; Cervantes, E. Calidad del Aire en Cuatro Ciudades de Michoacán, México: Su Efecto sobre Materiales de Construcción. Rev. Constr. 2007, 6, 66–74. [Google Scholar]
- Chan, C.K.; Yao, X. Air pollution in mega cities in China. Atmos. Environ. 2008, 42, 1–42. [Google Scholar] [CrossRef]
- Elliott, S.J.; Cole, D.C.; Krueger, P.; Voorberg, N.; Wakefield, S. The Power of Perception: Health Risk Attributed to Air Pollution in an Urban Industrial Neighbourhood. Risk Anal. 1999, 19, 621–634. [Google Scholar] [CrossRef] [PubMed]
- United States National Air Pollution Control Administration. Air Quality Criteria for Particulate Matter: Summary and Conclusions. 1969. Available online: https://files.eric.ed.gov/fulltext/ED070647.pdf (accessed on 30 December 2021).
- Secretaría de Salud. Norma Oficial Mexicana NOM-025-SSA1-2014, Salud ambiental. Valores límite Permisibles para la Concentración de Partículas Suspendidas PM10 y PM2.5 en el aire Ambiente y Criterios para su Evaluación. 2014. Available online: http://siga.jalisco.gob.mx/aire/normas/NOM-025-SSA1-2014.pdf (accessed on 30 December 2021).
- Santurtún Zarrabeitia, A. Contaminación Atmosférica, Tipos de Tiempo y Procesos Respiratorios en Santander y Zaragoza. Ph.D. Thesis, Universidad de Cantabria, Cantabria, Spain, 2014. [Google Scholar]
- Elvira, D.; Espinoza, P.; Claudia, I.; Molina, E. Contaminación del aire exterior Cuenca—Ecuador, 2009–2013. Posibles efectos en la salud. Rev. Fac. Cienc. Méd. Univ. Cuenca 2014, 32, 6–17. [Google Scholar]
- World Health Organization; Occupational and Environmental Health Team. Guías de Calidad del aire de la OMS Relativas al Material Particulado, el Ozono, el Dióxido de Nitrógeno y el dióXido de Azufre: Actualización Mundial 2005. 2006. Available online: https://apps.who.int/iris/handle/10665/69478 (accessed on 30 December 2021).
- Arreola Contreras, J.L.; González, G. Análisis espectral del viento y de partículas menores de 10 micrómetros (PM10) en el área metropolitana de Monterrey, México. Rev. Int. Contam. Ambient. 1999, 15, 95–102. [Google Scholar]
- Lee, C.K.; Ho, D.S.; Yu, C.C.; Wang, C.C. Fractal analysis of temporal variation of air pollutant concentration by box counting. Environ. Model. Softw. 2003, 18, 243–251. [Google Scholar] [CrossRef]
- Witt, A.; Malamud, B.D. Quantification of Long-Range Persistence in Geophysical Time Series: Conventional and Benchmark-Based Improvement Techniques. Surv. Geophys. 2013, 34, 541–651. [Google Scholar] [CrossRef]
- Gutiérrez-López, A.; Ramirez, A.I.; Lebel, T.; Santillán, O.; Fuentes, C. El variograma y el correlograma, dos estimadores de la variabilidad de mediciones hidrológicas. Rev. Fac. Ing. Univ. Antioq. 2011, 59, 193–202. [Google Scholar]
- Martínez, J.C. Aplicación del Modelaje Geoespacial en Geomática para Estimar los Niveles de Partículas Suspendidas PM10 en la Cuenca Atmosférica del Valle de México. Master’s Thesis, Centro de Investigación en Ciencias de Información Geoespacial, A.C., Mexico City, Mexico, 2011. [Google Scholar]
- Paez, M.; Gamerman, D.; de oliveira, V. Interpolation performance of a spatio-temporal model with spatially varying coefficients: Application to PM10 concentrations in Rio de Janeiro. Environ. Ecol. Stat. 2005, 12, 169–193. [Google Scholar] [CrossRef]
- Graeler, B.; Gerharz, L.; Pebesma, E. Spatio-Temporal Analysis and Interpolation of PM 10 Measurements in Europe. 2013. Technical Report. Available online: https://www.eionet.europa.eu/etcs/etc-atni/products/etc-atni-reports/etcacm_2012_8_spatio-temp_pm10analyses (accessed on 3 February 2022).
- Park, N.W. Time-Series Mapping of PM10 Concentration Using Multi-Gaussian Space-Time Kriging: A Case Study in the Seoul Metropolitan Area, Korea. Adv. Meteorol. 2016, 2016, 9452080. [Google Scholar] [CrossRef]
- Cabrera, J.B. A Geostatistical Method for the Analysis and Prediction of Air Quality Time Series: Application to the Aburrá Valley Region. Master’s Thesis, Technische Universität München, Munich, Germany, 2016. [Google Scholar]
- Gallardo, A. Geostadística. Ecosistemas 2007, 15. Available online: https://www.revistaecosistemas.net/index.php/ecosistemas/article/view/161 (accessed on 3 February 2022).
- Serna, J.M. Modelos Estadístico-Espaciales de Contaminantes del Aire en el Área Metropolitana de Monterrey. Master’s Thesis, Universidad Autónoma de Nuevo León, San Nicolás de los Garza, Mexico, 2020. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Some long-run properties of geophysical records. Water Resour. Res. 1969, 5, 321–340. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Meraz, M.; Rodriguez, E.; Femat, R.; Echeverria, J.; Alvarez-Ramirez, J. Statistical persistence of air pollutants (O3,SO2,NO2 and PM10) in Mexico City. Phys. A Stat. Mech. Its Appl. 2015, 427, 202–217. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Moustris, K.; Petraki, E.; Koulougliotis, D.; Cantzos, D. Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece. Environments 2019, 6, 29. [Google Scholar] [CrossRef]
- Krampah, F.; Amegbey, N.; Ndur, S.; Ziggah, Y.Y.; Hopke, P.K. Fractal Analysis and Interpretation of Temporal Patterns of TSP and PM10 Mass Concentration over Tarkwa, Ghana. Earth Syst. Environ. 2021, 5, 635–654. [Google Scholar] [CrossRef]
- Windsor, H.; Toumi, R. Scaling and persistence of UK pollution. Atmos. Environ. 2001, 35, 4545–4556. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W.; Kim, J. Multifractal detrended cross-correlation analysis between respiratory diseases and haze in South Korea. Chaos Solitons Fractals 2020, 135, 109781. [Google Scholar] [CrossRef]
- Rehman, S. Study of Saudi Arabian climatic conditions using Hurst exponent and climatic predictability index. Chaos Solitons Fractals 2009, 39, 499–509. [Google Scholar] [CrossRef]
- Rehman, S.; Siddiqi, A. Wavelet based hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Chaos Solitons Fractals 2009, 40, 1081–1090. [Google Scholar] [CrossRef]
- López-Lambraño, A.A.; Fuentes, C.; López-Ramos, A.A.; Mata-Ramírez, J.; López-Lambraño, M. Spatial and temporal Hurst exponent variability of rainfall series based on the climatological distribution in a semiarid region in Mexico. Atmósfera 2018, 31, 199–219. [Google Scholar] [CrossRef]
- Benavides-Bravo, F.G.; Martinez-Peon, D.; Benavides-Ríos, A.G.; Walle-García, O.; Soto-Villalobos, R.; Aguirre-López, M.A. A Climate-Mathematical Clustering of Rainfall Stations in the Río Bravo-San Juan Basin (Mexico) by Using the Higuchi Fractal Dimension and the Hurst Exponent. Mathematics 2021, 9, 2656. [Google Scholar] [CrossRef]
- Garza, G. Uncontrolled air pollution in Mexico City. Cities 1996, 13, 315–328. [Google Scholar] [CrossRef]
- Morales Hernández, J.C.; López Montes, A.L.; Frausto Martínez, O.; Cruz Romero, B.; González Mercado, C.L.; Carrillo González, F.M. Contaminación del aire en Puerto Vallarta, México. Bitácora Urbano Territ. 2021, 31. [Google Scholar] [CrossRef]
- Balderas-Mora, C.; Navarro-Parga, M.; Muñiz-Acuña, J.; Villarreal-Morales, C.; Gamboa-Quezada, R.; Castillo, A.R.; Ramírez-Lara, E.; López-Chuken, U.J. Estudio de la calidad microbiológica del aire en el Área Metropolitana de Monterrey NL México. Rev. Cienc. Farm. Biomed. 2020, 43–45. Available online: https://rcfb.uanl.mx/index.php/rcfb/article/view/308 (accessed on 5 February 2021).
- Audelo-Vucovich, E.; Vazquez-Cruz, C.; Beristain, F. Tendencia de la Dinámica No-Lineal en una Precontingencia Ambiental causada por Partículas en Suspensión. Inf. Tecnológica 2015, 26, 21–28. [Google Scholar] [CrossRef][Green Version]
- Dirección General de Gestión de la Calidad del Aire y Registro de Emisiones y Transferencia de Contaminantes. Informe de Evaluación Periodo 2008–2011. 2012. Techincal Report. Available online: https://www.gob.mx/cms/uploads/attachment/file/69344/Anexo_1_F_Informe_ProAire_Monterrey_E11.pdf (accessed on 3 February 2022).
- Vázquez Godina, E. Evaluación de la Política Pública Estatal para el Control de la Contaminación del aire en el área Metropolitana de Monterrey, Nuevo León 2008–2014. Ph.D. Thesis, Universidad Autónoma de Nuevo León, San Nicolás de los Garza, Mexico, 2018. [Google Scholar]
- González-Santiago, O.; Badillo-Castañeda, C.T.; Kahl, J.D.; Ramírez-Lara, E.; Balderas-Renteria, I. Temporal Analysis of PM10 in Metropolitan Monterrey, México. J. Air Waste Manag. Assoc. 2011, 61, 573–579. [Google Scholar] [CrossRef]
- Cubero, C. En 2018 Hubo 204 días Sobre la Norma de Calidad del aire en NL. 2019. Available online: https://www.milenio.com/politica/comunidad/2018-204-norma-calidad-aire-nl (accessed on 5 November 2021).
- Santos-Guzmán, J.; Madrigal-Ávila, C.; Hernández-Hernández, J.A.; Mejía-Velázquez, G.; Eraña-Rojas, I.E.; Elizondo-Montemayor, L.; Villela, L. Una década de monitoreo de plomo en sangre en niños escolares del área metropolitana de Monterrey, NL. Salud Pública México 2014, 56, 592–602. [Google Scholar] [CrossRef]
- Gasca-Sanchez, F.M.; Santos-Guzman, J.; Elizondo-Dueñaz, R.; Mejia-Velazquez, G.M.; Ruiz-Pacheco, C.; Reyes-Rodriguez, D.; Vazquez-Camacho, E.; Hernandez-Hernandez, J.A.; Lopez-Sanchez, R.d.C.; Ortiz-Lopez, R.; et al. Spatial Clusters of Children with Cleft Lip and Palate and Their Association with Polluted Zones in the Monterrey Metropolitan Area. Int. J. Environ. Res. Public Health 2019, 16, 2488. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, J.J.; Li, Z.; Gow, A.; Chung, K.F.; Hu, M.; Sun, Z.; Zeng, L.; Zhu, T.; Jia, G.; et al. Chronic exposure to air pollution particles increases the risk of obesity and metabolic syndrome: Findings from a natural experiment in Beijing. FASEB J. 2016, 30, 2115–2122. [Google Scholar] [CrossRef]
- Parasin, N.; Amnuaylojaroen, T.; Saokaew, S. Effect of Air Pollution on Obesity in Children: A Systematic Review and Meta-Analysis. Children 2021, 8, 327. [Google Scholar] [CrossRef] [PubMed]
- van Zelm, R.; Huijbregts, M.A.; den Hollander, H.A.; van Jaarsveld, H.A.; Sauter, F.J.; Struijs, J.; van Wijnen, H.J.; van de Meent, D. European characterization factors for human health damage of PM10 and ozone in life cycle impact assessment. Atmos. Environ. 2008, 42, 441–453. [Google Scholar] [CrossRef]
- Sistema Integral de Monitoreo Ambiental. Reportes Mensuales del Estado de la Calidad del Aire en el Área Metropolitana de Monterrey. Available online: http://aire.nl.gob.mx/rep_mensual.html (accessed on 4 October 2021).
- Secretaría de Medio Ambiente y Recursos Naturales. Norma Oficial Mexicana NOM-035-SEMARNAT-1993. 1993. Available online: https://www.profepa.gob.mx/innovaportal/file/1215/1/nom-035-semarnat-1993.pdf (accessed on 4 October 2021).
- Code of Federal Regulations. Title 40 Protection of Environment, Part 50, Appendix B. 1990. Available online: https://www.govinfo.gov/content/pkg/CFR-2021-title40-vol2/pdf/CFR-2021-title40-vol2-part50.pdf (accessed on 26 January 2022).
- World Health Organization. WHO Global Air Quality Guidelines: Particulate Matter (PM2.5 and PM10), Ozone, Nitrogen Dioxide, Sulfur Dioxide and Carbon Monoxide; World Health Organization: Geneva, Switzerland, 2021; p. xxi. 273p. [Google Scholar]
- Secretaria de Salud. Norma Oficial Mexicana NOM-025-SSA1-1993, Salud ambiental. Criterios para Evaluar la Calidad del aire Ambiente, con Respecto a Material Particulado. 1993. Available online: http://siga.jalisco.gob.mx/Assets/documentos/normatividad/ssa10253.htm#:~:text=Esta%20Norma%20Oficial%20Mexicana%20establece,micras%20en%20el%20aire%20ambiente.&text=Aplicable%20en%20todo%20el%20territorio,referente%20a%20la%20salud%20humana. (accessed on 3 February 2022).
- Benavides-Bravo, F.; Almaguer, F.; Soto-Villalobos, R.; Tercero-Gómez, V.; Morales-Castillo, J. Clustering of Rainfall Stations in RH-24 Mexico Region Using the Hurst Exponent in Semivariograms. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Marchant, B.; Lark, R. Estimating variogram uncertainty. Math. Geol. 2004, 36, 867–898. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Ardilla, E.; Luengas, D.; Moreno, J.F.T. Metodología en interpretación del coeficiente de Hurts. ODEON 2010, 5, 265–290. [Google Scholar]
- Wanliss, J.; Wanliss, G. Efficient Calculation of Fractal Properties via the Higuchi Method. Nonlinear Dyn. 2021. [Google Scholar] [CrossRef]
- Flores, L. Realizan Acciones para Frenar Contaminación en ZM de Monterrey. 2017. Available online: https://www.eleconomista.com.mx/estados/Realizan-acciones-para-frenar-contaminacion-en-ZM-de-Monterrey-20170807-0009.html (accessed on 3 February 2022).
- Benavides-Bravo, F.G.; Soto-Villalobos, R.; Cantú-González, J.R.; Aguirre-López, M.A.; Benavides-Ríos, A.G. A Quadratic-Exponential Model of Variogram Based on Knowing the Maximal Variability: Application to a Rainfall Time Series. Mathematics 2021, 9, 2466. [Google Scholar] [CrossRef]
- Sistema Integral de Monitoreo Ambiental. Reporte del Estado de la Calidad del Aire en el Área Metropolitana de Monterrey–Abril 2011. 2011. Available online: http://aire.nl.gob.mx/docs/reportes/mensuales/2011/04_Reporte_Abril_2011.pdf (accessed on 5 November 2021).
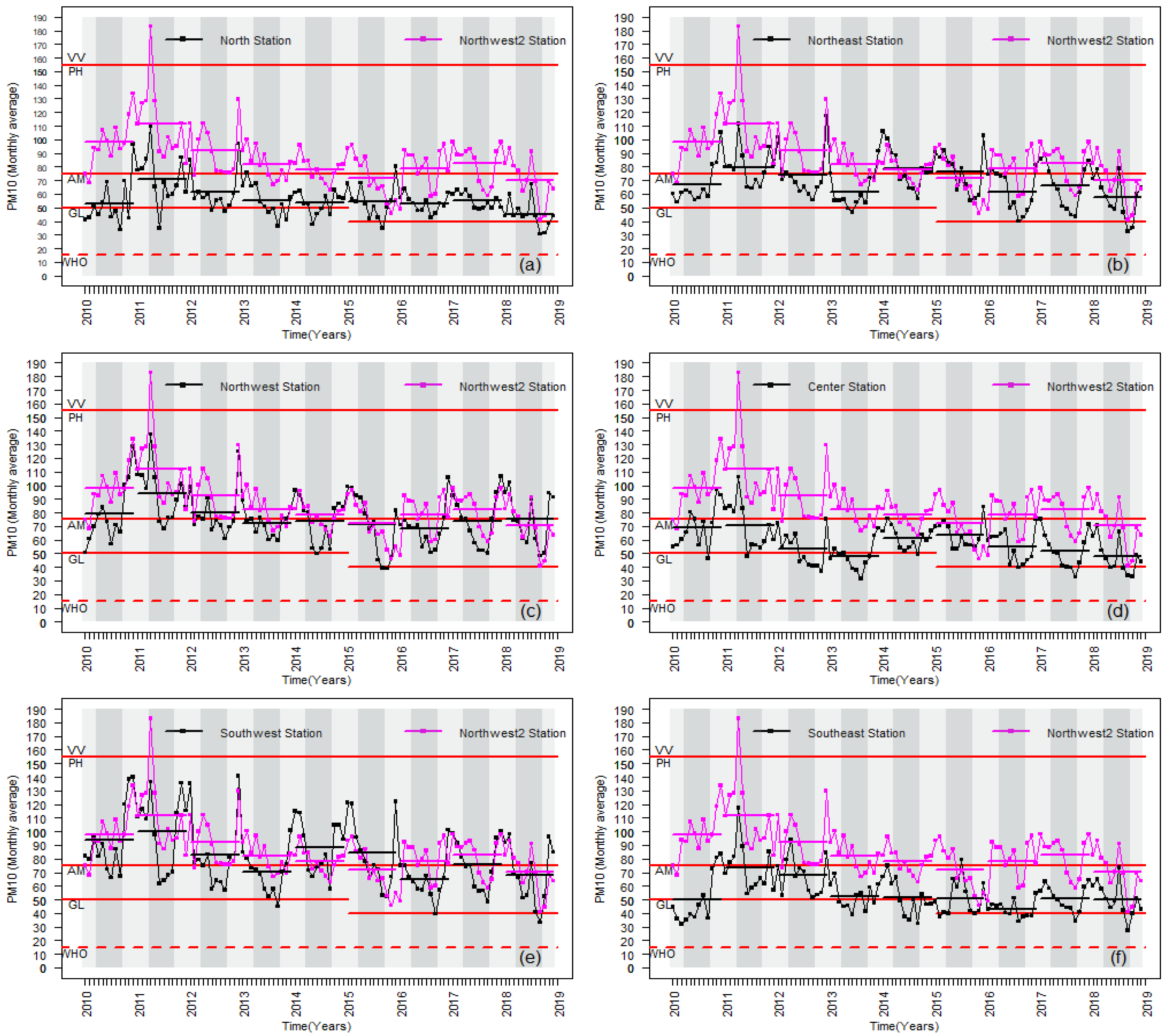


| Label | Air Quality | Health Risk | PM10 Interval (μg/m3) |
|---|---|---|---|
| GL | Good air quality | Low health risk | 0–40 |
| AM | Acceptable air quality | Moderate health risk | 40–75 |
| PH | Poor air quality | High health risk | 75–155 |
| VV | Very poor air quality | Very high health risk | 155–235 |
| WHO | Good air quality | Low health risk | 0–15 |
| Name | Latitude (°) | Longitude (°) | Altitude (m) | PM10 Mean (μg/m3) | Air Quality | Hurst | Higuchi |
|---|---|---|---|---|---|---|---|
| North | 25.80 | −100.34 | 528 | 56 | AM | 0.87 | 1.82 |
| Northeast | 25.75 | −100.26 | 476 | 69 | AM | 0.76 | 1.65 |
| Northwest | 25.76 | −100.37 | 571 | 76 | PH | 0.72 | 1.65 |
| Center | 25.68 | −100.34 | 560 | 58 | AM | 0.80 | 1.69 |
| Southwest | 25.68 | −100.46 | 694 | 81 | PH | 0.73 | 1.66 |
| Southeast | 25.67 | −100.25 | 492 | 55 | AM | 0.89 | 1.77 |
| Northwest2 | 25.78 | −100.59 | 716 | 85 | PH | 0.89 | 1.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguirre-López, M.A.; Rodríguez-González, M.A.; Soto-Villalobos, R.; Gómez-Sánchez, L.E.; Benavides-Ríos, Á.G.; Benavides-Bravo, F.G.; Walle-García, O.; Pamanés-Aguilar, M.G. Statistical Analysis of PM10 Concentration in the Monterrey Metropolitan Area, Mexico (2010–2018). Atmosphere 2022, 13, 297. https://doi.org/10.3390/atmos13020297
Aguirre-López MA, Rodríguez-González MA, Soto-Villalobos R, Gómez-Sánchez LE, Benavides-Ríos ÁG, Benavides-Bravo FG, Walle-García O, Pamanés-Aguilar MG. Statistical Analysis of PM10 Concentration in the Monterrey Metropolitan Area, Mexico (2010–2018). Atmosphere. 2022; 13(2):297. https://doi.org/10.3390/atmos13020297
Chicago/Turabian StyleAguirre-López, Mario A., Miguel Angel Rodríguez-González, Roberto Soto-Villalobos, Laura Elena Gómez-Sánchez, Ángela Gabriela Benavides-Ríos, Francisco Gerardo Benavides-Bravo, Otoniel Walle-García, and María Gricelda Pamanés-Aguilar. 2022. "Statistical Analysis of PM10 Concentration in the Monterrey Metropolitan Area, Mexico (2010–2018)" Atmosphere 13, no. 2: 297. https://doi.org/10.3390/atmos13020297
APA StyleAguirre-López, M. A., Rodríguez-González, M. A., Soto-Villalobos, R., Gómez-Sánchez, L. E., Benavides-Ríos, Á. G., Benavides-Bravo, F. G., Walle-García, O., & Pamanés-Aguilar, M. G. (2022). Statistical Analysis of PM10 Concentration in the Monterrey Metropolitan Area, Mexico (2010–2018). Atmosphere, 13(2), 297. https://doi.org/10.3390/atmos13020297







