Surface Layer Drag Coefficient at Different Radius Ranges in Tropical Cyclones
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Method
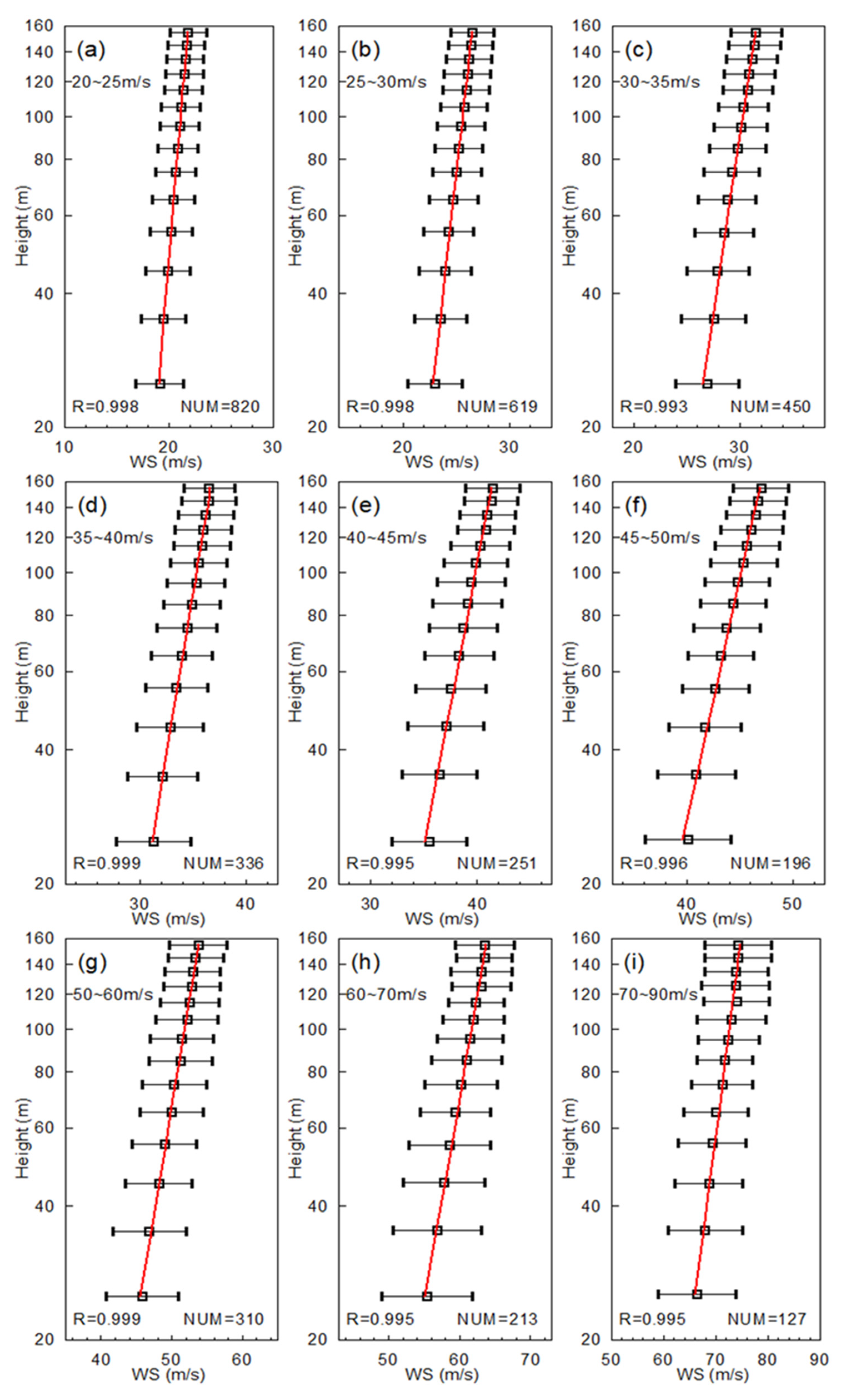
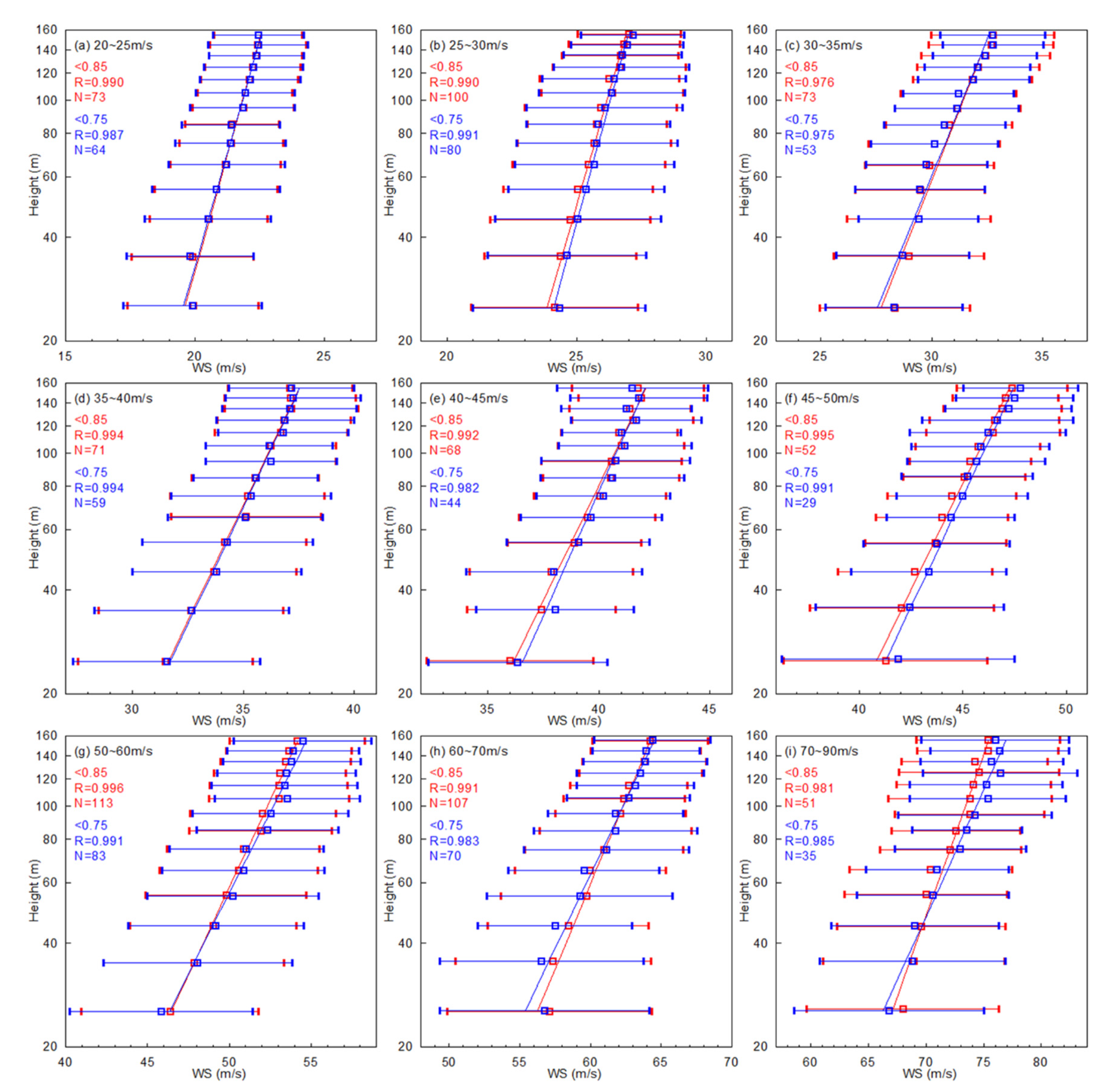
3. Results
4. Summary and Conclusions
- (1)
- From the range of R/RMW > 1.05 to that of R/RMW < 0.95, a systematic decrease of 5~25% in friction velocity is found for 7 out of the 9 MBL mean wind speed groups.
- (2)
- A clear feature of “roll-off” at about 35 m s−1 can be obtained for the ranges of either R/RMW > 1.05 or R/RMW < 1.05. However, in the ranges of R/RMW < 0.95, R/RMW < 0.85, and R/RMW < 0.75, the roll feature becomes vague, indicating the TC dynamics within and near the RMW play a role in affecting the flux-profile relationship.
- (3)
- When exceeds 40 m s−1, of R < 0.75RMW is significantly larger than that of R < 0.85RMW. This phenomenon is not caused by the extreme values in the relatively small sample size, and it is speculated to link with the TC dynamics (e.g., the large radial gradients of winds and the drastic vertical variation of the bulk Richardson number).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pielke, R.A., Jr.; Gratz, J.; Landsea, C.W.; Collins, D.; Saunders, M.A.; Musulin, R. Normalized hurricane damage in the United States: 1900–2005. Nat. Hazards Rev. 2008, 9, 29–42. [Google Scholar] [CrossRef]
- Schmidt, S.; Kemfert, C.; Höppe, P. The impact of socio-economics and climate change on tropical cyclone losses in the USA. Reg. Environ. Chang. 2010, 10, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wen, S.; Li, X.; Thomas, F.; Su, B.; Wang, R.; Jiang, T. Spatiotemporal distributions of influential tropical cyclones and associated economic losses in China in 1984–2015. Nat. Hazards 2016, 84, 2009–2030. [Google Scholar] [CrossRef]
- Wang, H.; Xu, M.; Onyejuruwa, A.; Wang, Y.; Wen, S.; Gao, A.E.; Li, Y. Tropical cyclone damages in Mainland China over 2005–2016: Losses analysis and implications. Environ. Dev. Sustain. 2019, 21, 3077–3092. [Google Scholar] [CrossRef]
- Zhang, J.A. Estimation of dissipative heating using low-level in situ aircraft observations in the hurricane boundary layer. J. Atmos. Sci. 2010, 67, 1853–1862. [Google Scholar] [CrossRef] [Green Version]
- Heng, J.; Wang, Y. Nonlinear response of a tropical cyclone vortex to prescribed eyewall heating with and without surface friction in TCM4: Implications for tropical cyclone intensification. J. Atmos. Sci. 2016, 73, 1315–1333. [Google Scholar] [CrossRef]
- Emanuel, K.A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics. J. Atmos. Sci. 1995, 52, 3969–3976. [Google Scholar] [CrossRef] [Green Version]
- Emanuel, K.A. Self-stratification of tropical cyclone outflow. Part II: Implications for storm intensification. J. Atmos. Sci. 2012, 69, 988–996. [Google Scholar] [CrossRef] [Green Version]
- Rogers, R.; Aberson, S.; Aksoy, A.; Annane, B.; Black, M.; Cione, J.; Dorst, N.; Dunion, J.; Gamache, J.; Goldenberg, S.; et al. NOAA’S Hurricane Intensity Forecasting Experiment: A Progress Report. Bull. Amer. Meteor. Soc. 2013, 94, 859–882. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, A.V.; Lukas, R.; Donelan, M.A.; Haus, B.K.; Ginis, I. The air-sea interface and surface stress under tropical cyclones. Sci. Rep. 2014, 4, 5306. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.B.; Saltzman, E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Jarosz, E.; Mitchell, D.A.; Wang, D.W.; Teague, W.J. Bottom-up determination of air-sea momentum exchange under a major tropical cyclone. Science 2007, 315, 1707–1709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bi, X.; Gao, Z.; Liu, Y.; Liu, F.; Song, Q.; Huang, J.; Huang, H.; Mao, W.; Liu, C. Observed drag coefficients in high winds in the near offshore of the South China Sea. J. Geophys. Res. Atmos. 2015, 120, 6444–6459. [Google Scholar] [CrossRef]
- Sanford, T.B.; Price, J.F.; Girton, J.B. Upper-ocean response to Hurricane Frances (2004) observed by profiling EM-APEX floats. J. Phys. Oceanogr. 2011, 41, 1041–1056. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res. 2012, 117, C09003. [Google Scholar] [CrossRef] [Green Version]
- Takagaki, N.; Komori, S.; Suzuki, N.; Iwano, K.; Kuramoto, T.; Shimada, S.; Kurose, R.; Takahashi, K. Strong correlation between the drag coefficient and the shape of the wind sea spectrum over a broad range of wind speeds. Geophys. Res. Lett. 2012, 39, L23604. [Google Scholar] [CrossRef] [Green Version]
- Potter, H.; Graber, H.C.; Williams, N.J.; Collins, C.O.; Ramos, R.J.; Drennan, W.M. In situ measurements of momentum fluxes in typhoons. J. Atmos. Sci. 2015, 72, 104–118. [Google Scholar] [CrossRef]
- Komori, S.; Iwano, K.; Takagaki, N.; Onishi, R.; Kurose, R.; Takahashi, K.; Suzuki, N. Laboratory measurements of heat transfer and drag coefficients at extremely high wind speeds. J. Phys. Oceanogr. 2018, 48, 959–974. [Google Scholar] [CrossRef]
- Hsu, J.Y.; Lien, R.C.; D’Asaro, E.A.; Sanford, T.B. Scaling of drag coefficients under five tropical cyclones. Geophys. Res. Lett. 2019, 46, 3349–3358. [Google Scholar] [CrossRef]
- Peng, W.; GAO, Z.; Li, Y.; Zhang, R.; Tong, B.; Wu, B.; He, Y. Testing drag coefficient approaches by using the buoy data collected in moderate to high wind under following, crossing and opposing swell conditions. J. Trop Meteor. 2019, 25, 336–343. [Google Scholar] [CrossRef]
- Gao, Z.; Peng, W.; Gao, C.Y.; Li, Y. Parabolic dependence of the drag coefficient on wind speed from aircraft eddy-covariance measurements over the tropical Eastern Pacific. Sci. Rep. 2020, 10, 1805. [Google Scholar] [CrossRef] [PubMed]
- Troitskaya, Y.I.; Sergeev, D.A.; Vdovin, M.; Kandaurov, A.; Ermakova, O.; Takagaki, N. Alaboratory study of the effect of surface waves on heat and momentum transfer at high wind speeds. J. Geophys. Res. Oceans 2020, 125, e2020JC016276. [Google Scholar] [CrossRef]
- Gao, Z.; Zhou, S.; Zhang, J.; Zeng, Z.; Bi, X. Parameterization of Sea Surface Drag Coefficient for All Wind Regimes Using 11 Aircraft Eddy-Covariance Measurement Databases. Atmosphere 2021, 12, 1485. [Google Scholar] [CrossRef]
- Aberson, S.D.; Franklin, J.L. Impact on hurricane track and intensity forecasts of GPS dropwindsonde observations from the first-season flights of the NOAA Gulfstream-IV jet aircraft. Bull. Amer. Meteor. Soc. 1999, 80, 421–428. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Young, K.; Hock, T.; Lauritsen, D.; Behringer, D.; Black, M.; Black, P.G.; Franklin, J.; Halverson, J.; Molinari, J.; et al. A Long-Term, High-Quality, High-Vertical-Resolution GPS Dropsonde Dataset for Hurricane and Other Studies. Bull. Amer. Meteor. Soc. 2015, 96, 961–973. [Google Scholar] [CrossRef] [Green Version]
- Richter, D.H.; Bohac, R.; Stern, D.P. An assessment of the flux profile method for determining air-sea momentum and enthalpy fluxes from dropsonde data in tropical cyclones. J. Atmos. Sci. 2016, 73, 2665–2682. [Google Scholar] [CrossRef]
- Richter, D.H.; Wainwright, C.; Stern, D.P.; Bryan, G.H.; Chavas, D. Potential Low Bias in High-Wind Drag Coefficient Inferred from Dropsonde Data in Hurricanes. J. Atmos. Sci. 2021, 78, 2339–2352. [Google Scholar] [CrossRef]
- Demuth, J.; DeMaria, M.; Knaff, J.A. Improvement of Advanced Microwave Sounding Unit tropical cyclone intensity and size estimation algorithms. J.J. Appl. Meteor.Meteor. Climatol. 2006, 45, 1573–1581. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D.; Powell, M.D.; Chen, Y. A hurricane boundary layer and wind field model for use in engineering applications. J.J. Appl. Meteor.Meteor. Climatol. 2009, 48, 381–405. [Google Scholar] [CrossRef]
- Powell, M.D. Final Report on the NOAA Joint Hurricane Testbed: Drag Coefficient Distribution and Wind Speed Dependence in Tropical Cyclones; NOAA/AOML: Miami, FL, USA, 2007. [Google Scholar]
- Jiang, W.; Wu, L.; Liu, Q. High-Wind Drag Coefficient Based on the Tropical Cyclone Simulated With the WRF-LES Framework. Front. Earth Sci. 2021, 9, 694314. [Google Scholar] [CrossRef]
- Byrne, D.; Zhang, J.A. Height-dependent transition from 3-D to 2-D turbulence in the hurricane boundary layer. Geophys. Res. Lett. 2013, 40, 1439–1442. [Google Scholar] [CrossRef]
- Kepert, J.; Wang, Y. The Dynamics of Boundary Layer Jets within the Tropical Cyclone Core. Part II: Nonlinear Enhancement. J. Atmos. Sci. 2001, 58, 2485–2501. [Google Scholar] [CrossRef]
- Bell, M.M.; Montgomery, M.T. Observed Structure, Evolution, and Potential Intensity of Category 5 Hurricane Isabel (2003) from 12 to 14 September. Mon. Wea. Rev. 2008, 136, 2023–2046. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Rogers, R.F.; Nolan, D.S.; Marks, F.D. On the Characteristic Height Scales of the Hurricane Boundary Layer. Mon. Wea. Rev. 2011, 139, 2523–2535. [Google Scholar] [CrossRef]
- Kepert, J.D. The dynamics of boundary layer jets within the tropical cyclone core. Part I: Linear theory. J. Atmos. Sci. 2001, 58, 2469–2484. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Drennan, W.M.; Black, P.G.; French, J.R. Turbulence Structure of the Hurricane Boundary Layer between the Outer Rainbands. J. Atmos. Sci. 2009, 66, 2455–2467. [Google Scholar] [CrossRef]
- Bryan, G.H.; Worsnop, R.P.; Lundquist, J.K.; Zhang, J.A. A simple method for simulating wind profiles in the boundary layer of tropical cyclones. Boundary-Layer Meteorl. 2017, 162, 475–502. [Google Scholar] [CrossRef] [Green Version]
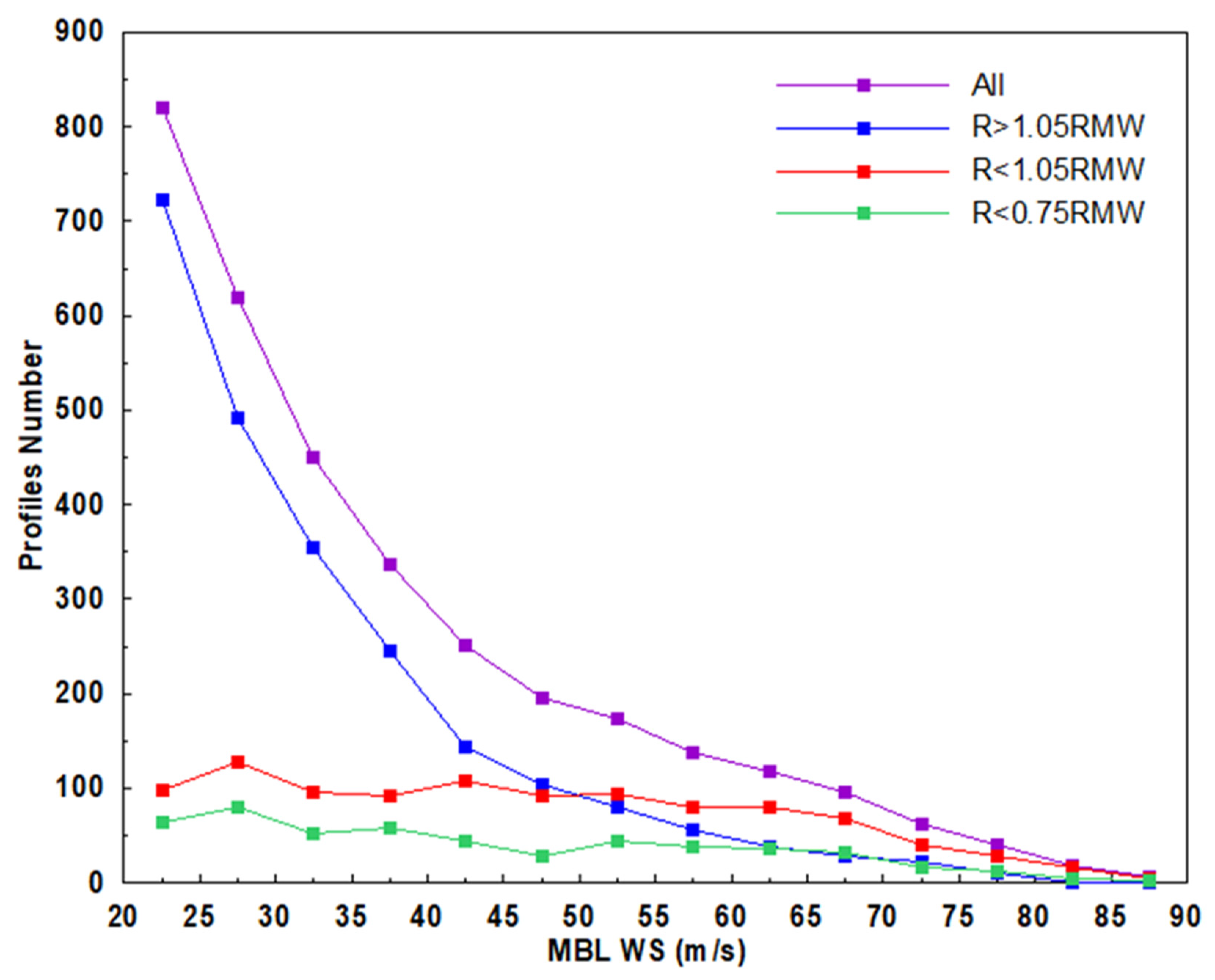



| MBL WS Group (Unit: m s−1) | R/RMW Range | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| All | >1.05 | <1.05 | <1.00 | <0.95 | <0.90 | <0.85 | <0.80 | <0.75 | |
| 20–25 | 820 | 722 | 98 | 92 | 85 | 77 | 73 | 70 | 64 |
| 25–30 | 619 | 491 | 128 | 117 | 113 | 107 | 100 | 88 | 80 |
| 30–35 | 450 | 355 | 95 | 92 | 87 | 83 | 73 | 64 | 53 |
| 35–40 | 336 | 245 | 91 | 86 | 79 | 76 | 71 | 67 | 59 |
| 40–45 | 251 | 143 | 108 | 92 | 82 | 75 | 68 | 57 | 44 |
| 45–50 | 196 | 104 | 92 | 84 | 74 | 65 | 52 | 39 | 29 |
| 50–60 | 310 | 135 | 175 | 160 | 144 | 128 | 113 | 96 | 83 |
| 60–70 | 213 | 67 | 146 | 139 | 127 | 117 | 107 | 87 | 70 |
| 70–90 | 127 | 35 | 92 | 79 | 70 | 61 | 51 | 41 | 35 |
| Sum | 3322 | 2297 | 1025 | 941 | 861 | 789 | 708 | 609 | 517 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, L.; Li, Y.; Gao, Z. Surface Layer Drag Coefficient at Different Radius Ranges in Tropical Cyclones. Atmosphere 2022, 13, 280. https://doi.org/10.3390/atmos13020280
Ye L, Li Y, Gao Z. Surface Layer Drag Coefficient at Different Radius Ranges in Tropical Cyclones. Atmosphere. 2022; 13(2):280. https://doi.org/10.3390/atmos13020280
Chicago/Turabian StyleYe, Lei, Yubin Li, and Zhiqiu Gao. 2022. "Surface Layer Drag Coefficient at Different Radius Ranges in Tropical Cyclones" Atmosphere 13, no. 2: 280. https://doi.org/10.3390/atmos13020280
APA StyleYe, L., Li, Y., & Gao, Z. (2022). Surface Layer Drag Coefficient at Different Radius Ranges in Tropical Cyclones. Atmosphere, 13(2), 280. https://doi.org/10.3390/atmos13020280








