Surface Gravity Wave Effect on Hurricane Energetics
Abstract
:1. Introduction
2. The Surface Wave Factor in the Energy Cycle of a Mature Tropical Cyclone
3. Wave Model and Experimental Design
3.1. The Wave Model
3.2. Experimental Design
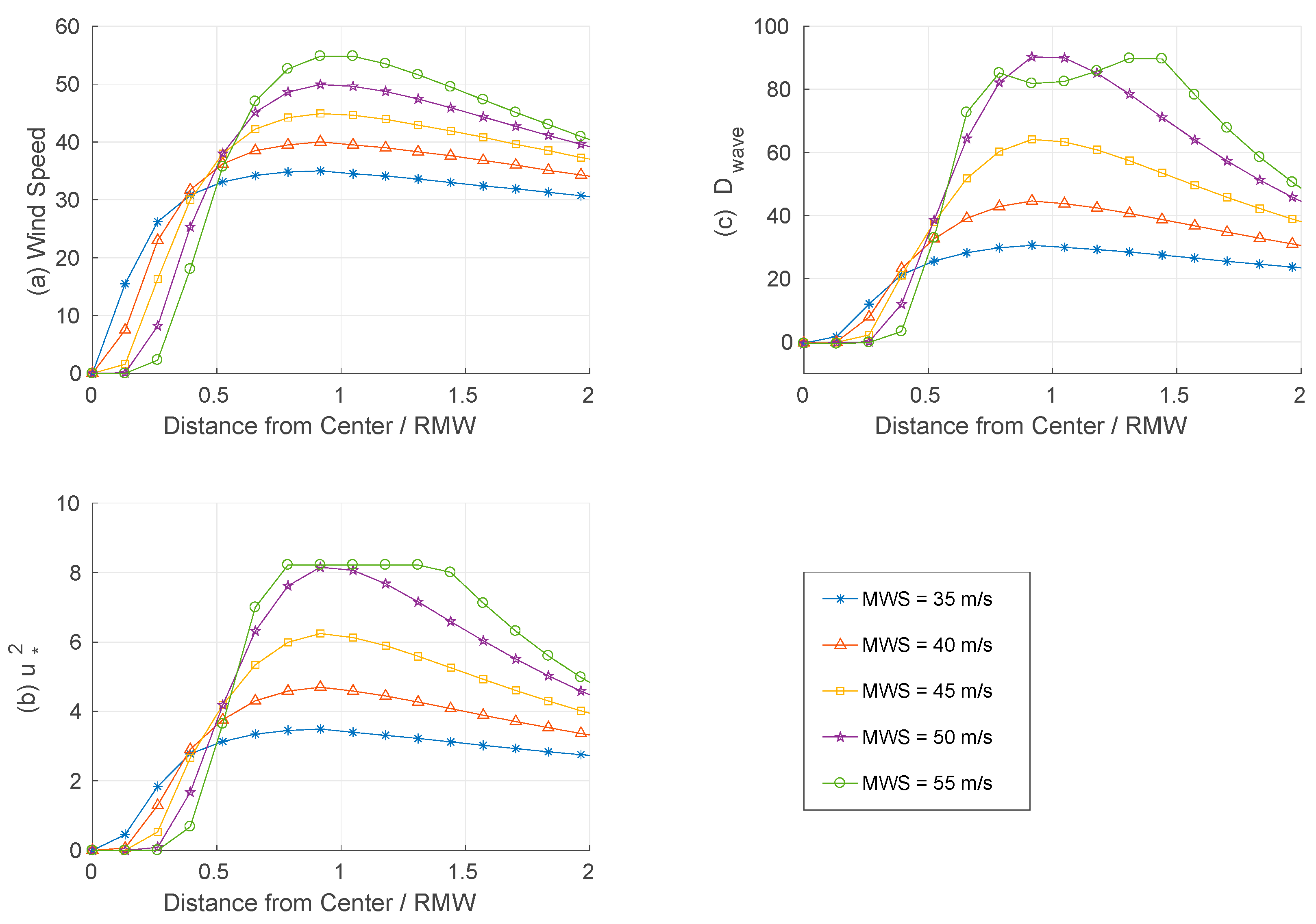
4. Results
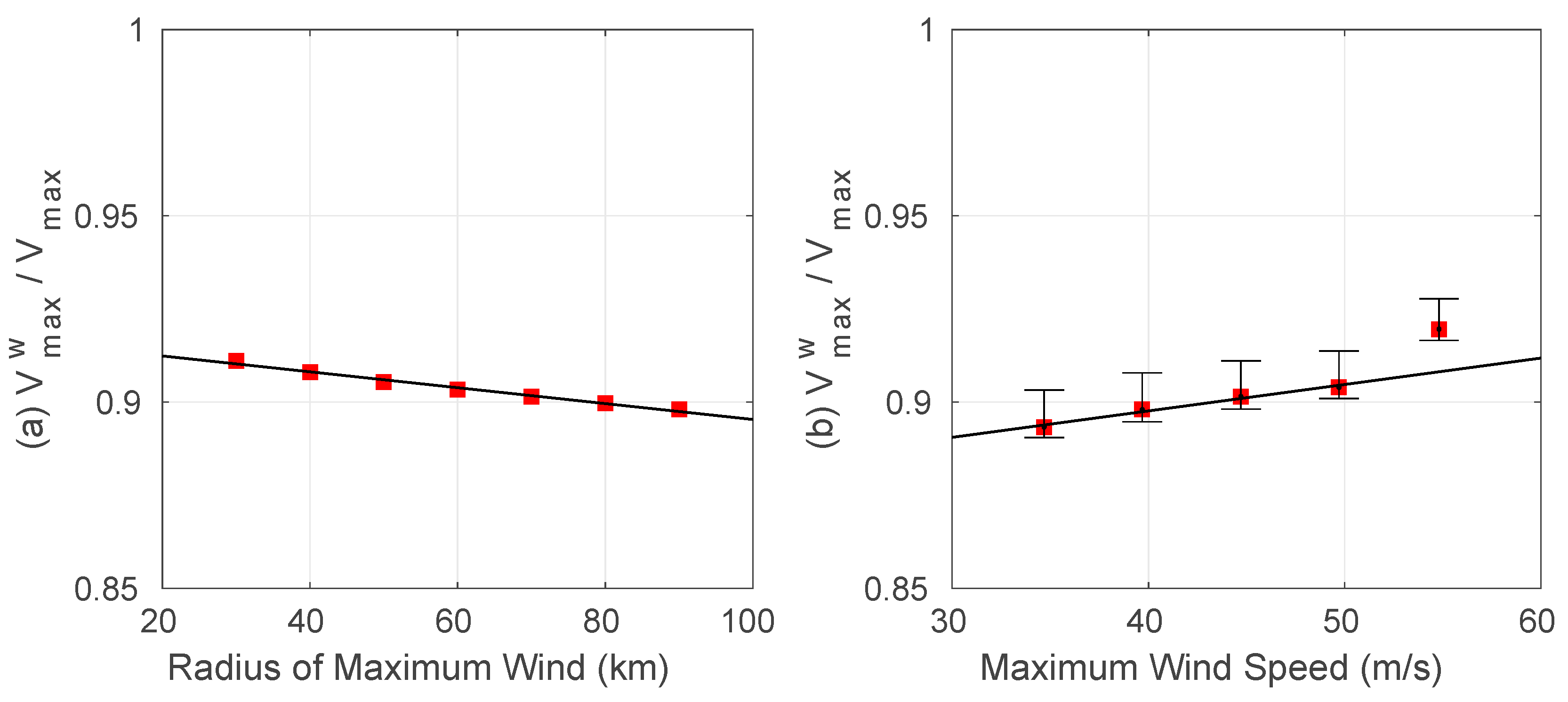
4.1. Variation of with Radius of Maximum Wind
4.2. Variation of with Maximum Wind Speed
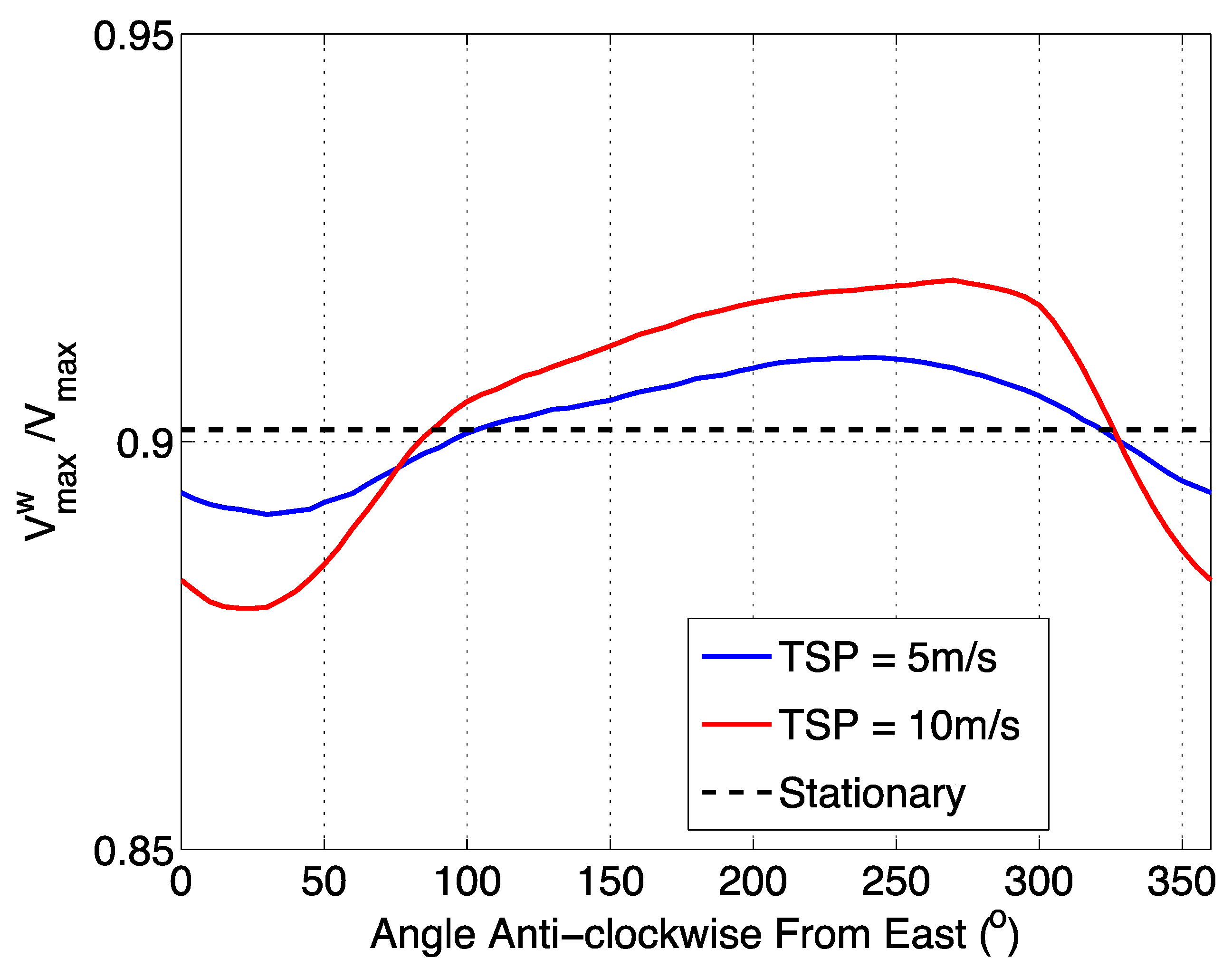
4.3. Moving Storm
5. Summary and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Emanuel, K. Tropical Cyclones. Annu. Rev. Earth Planet. Sci. 2003, 31, 75–104. [Google Scholar] [CrossRef]
- Riehl, H. A Model of Hurricane Formation. J. Appl. Phys. 1950, 21, 917–925. [Google Scholar] [CrossRef]
- Kleinschmidt, E., Jr. Gundlagen einer theorie des tropischen zyklonen. Arch. Meteorol. Geophys. Bioklimatol. Ser. A 1951, 4, 53–72. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I. J. Atmos. Sci. 1986, 42, 1062–1071. [Google Scholar] [CrossRef]
- Bister, M.; Emanuel, K.A. Dissipative heating and hurricane intensity. Meteorol. Atmos. Phys. 1998, 50, 233–240. [Google Scholar] [CrossRef]
- Emanuel, K. A Statistical Analysis of Tropical Cyclone Intensity. Mon. Weather Rev. 2000, 128, 1139–1152. [Google Scholar] [CrossRef]
- Andreas, E.L.; Emanuel, K.A. Effects of sea spray on tropical cyclone intensity. J. Atmos. Sci. 2001, 58, 3741–3751. [Google Scholar] [CrossRef] [Green Version]
- Drennan, W.M.; Donelan, M.A.; Terray, E.A.; Katsaros, K.B. Oceanic Turbulence Dissipation Measurements in SWADE. J. Phys. Oceanogr. 1996, 26, 808–815. [Google Scholar] [CrossRef] [Green Version]
- Terray, E.; Donelan, M.; Agrawal, Y.; Drennan, W.; Kahma, K.; Williams, A.; Hwang, P.; Kitaigorodskii, S. Estimates of Kinetic Energy Dissipation under Breaking Waves. J. Phys. Oceanogr. 1996, 26, 792–807. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Ginis, I.; Hara, T. Momentum Flux Budget across the Air–Sea Interface under Uniform and Tropical Cyclone Winds. J. Phys. Oceanogr. 2010, 40, 2221–2242. [Google Scholar] [CrossRef]
- Fan, Y.; Hwang, P. Kinetic energy flux budget across air-sea interface. Ocean Model. 2017, 120, 27–40. [Google Scholar] [CrossRef]
- Tolman, H.L. WAVEWATCHIII Development Group, 2014: User Manual and System Documentation of WAVEWATCH III version® 4.18. Available online: https://polar.ncep.noaa.gov/waves/wavewatch/manual.v4.18.pdf (accessed on 1 February 2022).
- Allard, R.; Rogers, E.; Martin, P.; Jensen, T.; Chu, P.; Campbell, T.; Dykes, J.; Smith, T.; Choi, J.; Gravois, U. The US navy coupled ocean-wave prediction system. Oceanography 2014, 27, 92–103. [Google Scholar] [CrossRef]
- Fan, Y.; Ginis, I.; Hara, T.; Wright, C.W.; Walsh, E.J. Numerical Simulations and Observations of Surface Wave Fields under an Extreme Tropical Cyclone. J. Phys. Oceanogr. 2009, 39, 2097–2116. [Google Scholar] [CrossRef]
- Fan, Y.; Rogers, W. Drag coefficient comparisons between observed and model simulated directional wave spectra under hurricane conditions. Ocean Model. 2016, 102, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Moon, I.-J.; Ginis, I.; Hara, T.; Tolman, H.L.; Wright, C.W.; Walsh, E.J. Numerical Simulation of Sea Surface Directional Wave Spectra under Hurricane Wind Forcing. J. Phys. Oceanogr. 2003, 33, 1680–1706. [Google Scholar] [CrossRef] [Green Version]
- Phadke, A.C.; Martino, C.D.; Cheung, K.F.; Houston, S.H. Modeling of tropical cyclone winds and waves for emergency management. Ocean Eng. 2003, 30, 553–578. [Google Scholar] [CrossRef]
- Xu, F.; Perrie, W.; Toulany, B.; Smith, P.C. Wind-generated waves in Hurricane Juan. Ocean Model. 2007, 16, 188–205. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Wea. Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Bidlot, J.-R.; Janssen, P.; Abdalla, S. A Revised Formulation of Ocean Wave Dissipation and Its Model Impact; ECMWF: Reading, UK, 2007; p. 27. [Google Scholar]
- Janssen, P.A.E.M. Quasi-linear theory of wind wave generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef] [Green Version]
- Janssen, P. The Interaction of Ocean Waves and Wind; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ardhuin, F.; Rogers, W.E.; Babanin, A.V.; Filipot, J.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.; Aouf, L.; et al. Semiempirical dissipation source functions for ocean waves. Part I: Definition, calibration, and validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef] [Green Version]
- Babanin, A.V. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rogers, W.E.; Babanin, A.V.; Wang, D.W. Observation-Consistent Input and Whitecapping Dissipation in a Model for Wind-Generated Surface Waves: Description and Simple Calculations. J. Atmos. Ocean. Tech. 2012, 29, 1329–1346. [Google Scholar] [CrossRef]
- Zieger, S.; Babanin, A.V.; Erick Rogers, W.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Model. 2015, 96, 2–25. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Babanin, A.; Fan, Y.; Zieger, S.; Guan, C.; Moon, I.-J. Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance. Ocean Model. 2017, 118, 73–93. [Google Scholar] [CrossRef]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.; Saltzman, E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef]
- Takagaki, N.; Komori, S.; Suzuki, N.; Iwano, K.; Kuramoto, T.; Shimada, S.; Kurose, R.; Takahashi, K. Strong correlation between the drag coefficient and the shape of the wind sea spectrum over a broad range of wind speeds. Geophys. Res. Lett. 2012, 39, L23604. [Google Scholar] [CrossRef] [Green Version]
- Takagaki, N.; Komori, S.; Suzuki, N. Estimation of friction velocity from the windwave spectrum at extremely high wind speeds. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016; Volume 35, p. 012009. [Google Scholar] [CrossRef] [Green Version]
- Takagaki, N.; Komori, S.; Suzuki, N.; Iwano, K.; Kurose, R. Mechanism of drag coefficient saturation at strong wind speeds. Geophys. Res. Lett. 2016, 43, 9829–9835. [Google Scholar] [CrossRef]
- Bidlot, J.-R.; Abdalla, S.; Janssen, P. A Revised Formulation for Ocean Wave Dissipation in CY25R1; ECMWF: Reading, UK, 2005; p. 35. [Google Scholar]
- Donelan, M.A.; Babanin, A.V.; Young, I.R.; Banner, M.L. Wave-follower field measurements of the wind-input spectral function. Part II: Parameterization of the wind input. J. Phys. Oceanogr. 2006, 36, 1672–1689. [Google Scholar] [CrossRef]

| Experiment | TSP (ms−1) | MWS (ms−1) | RMW (km) |
|---|---|---|---|
| A | 0 | 45 | 30, 40, 50, 60, 70, 80, 90 |
| B | 0 | 35, 40, 45, 50, 55 | 30 |
| 0 | 35, 40, 45, 50, 55 | 70 | |
| 0 | 35, 40, 45, 50, 55 | 90 | |
| C | 5, 10 | 45 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Yu, Z. Surface Gravity Wave Effect on Hurricane Energetics. Atmosphere 2022, 13, 279. https://doi.org/10.3390/atmos13020279
Fan Y, Yu Z. Surface Gravity Wave Effect on Hurricane Energetics. Atmosphere. 2022; 13(2):279. https://doi.org/10.3390/atmos13020279
Chicago/Turabian StyleFan, Yalin, and Zhitao Yu. 2022. "Surface Gravity Wave Effect on Hurricane Energetics" Atmosphere 13, no. 2: 279. https://doi.org/10.3390/atmos13020279
APA StyleFan, Y., & Yu, Z. (2022). Surface Gravity Wave Effect on Hurricane Energetics. Atmosphere, 13(2), 279. https://doi.org/10.3390/atmos13020279






