Influences of MJO on the Diurnal Variation and Associated Offshore Propagation of Rainfall near Western Coast of Sumatra
Abstract
1. Introduction
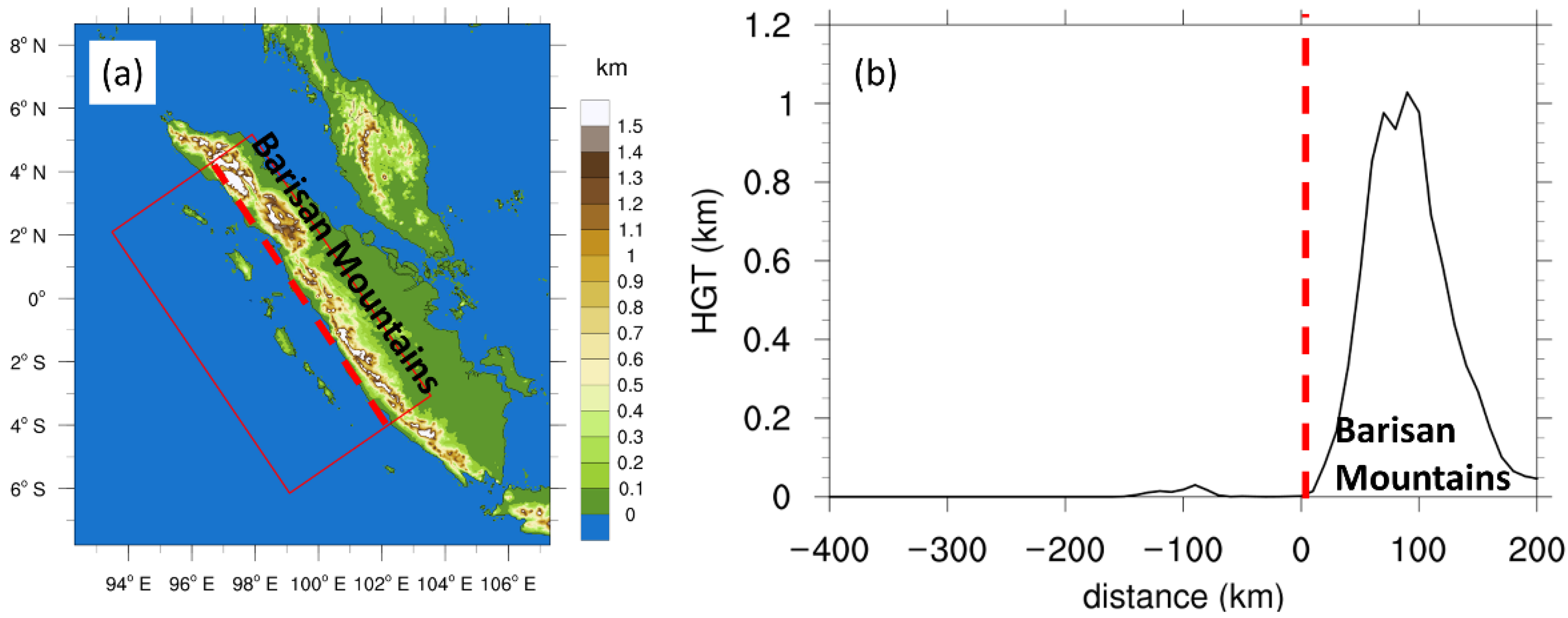
2. Data and Methodology
3. Results
3.1. Rainfall Variations Modulated by MJO
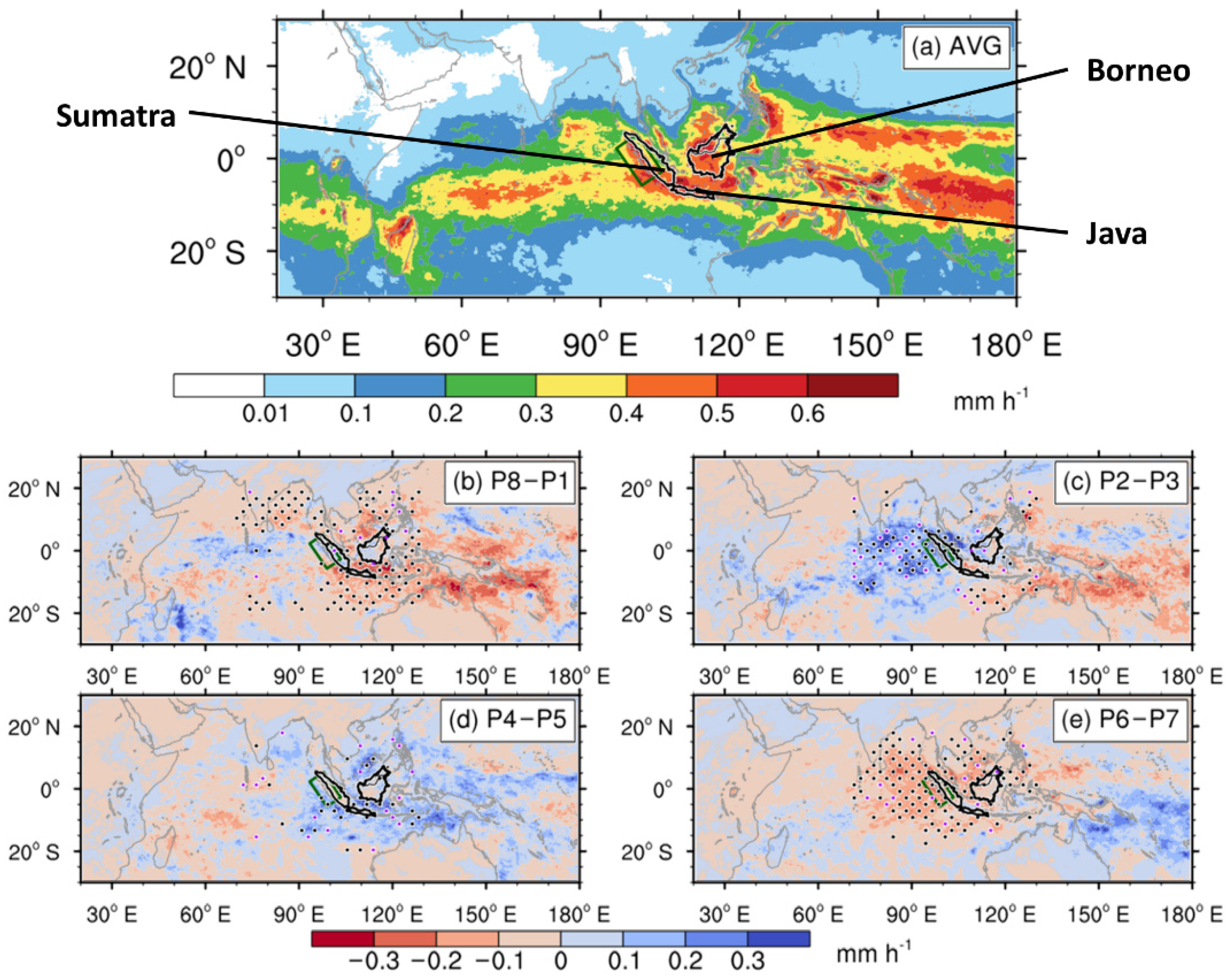
3.1.1. Spatial Distribution
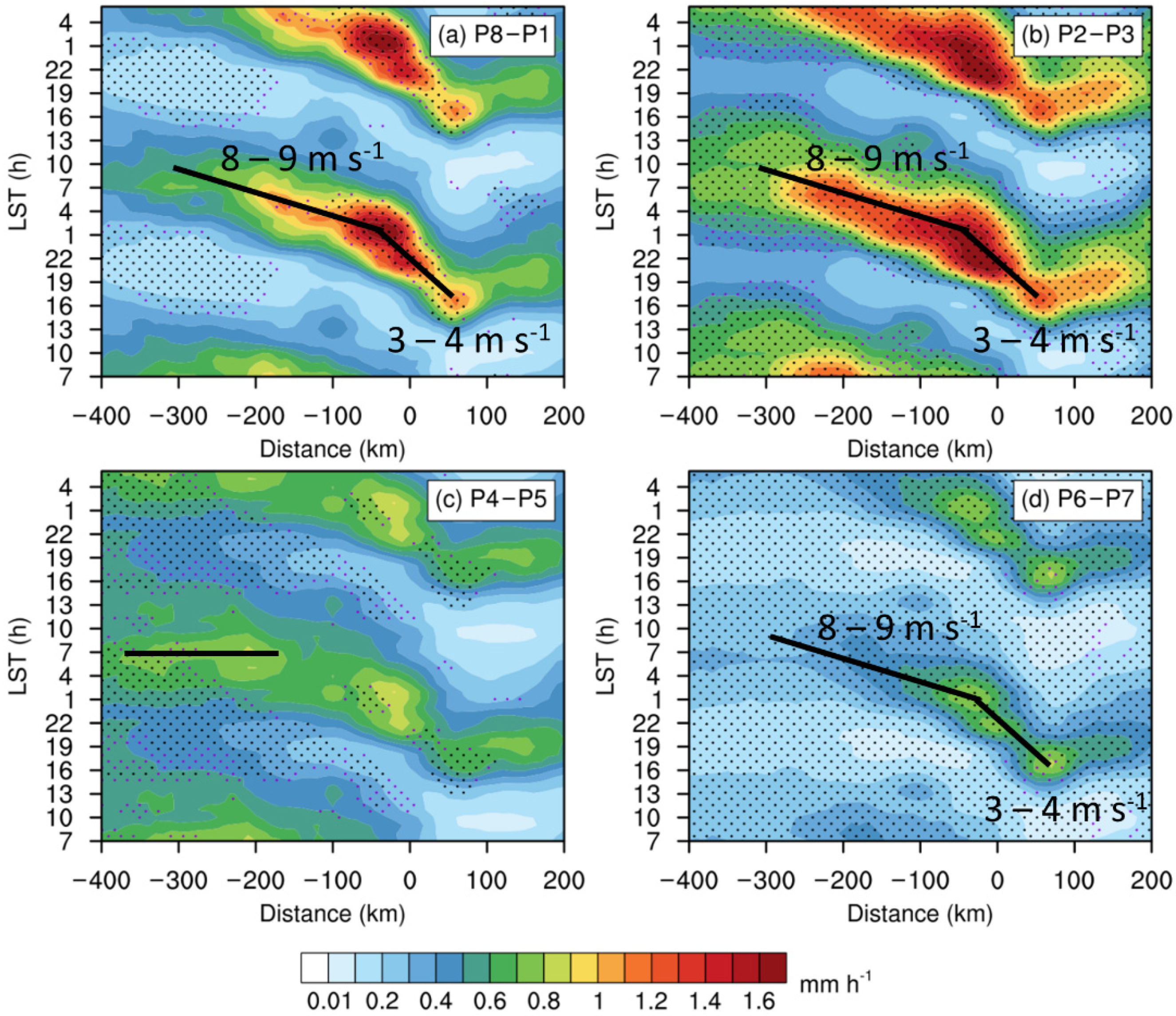
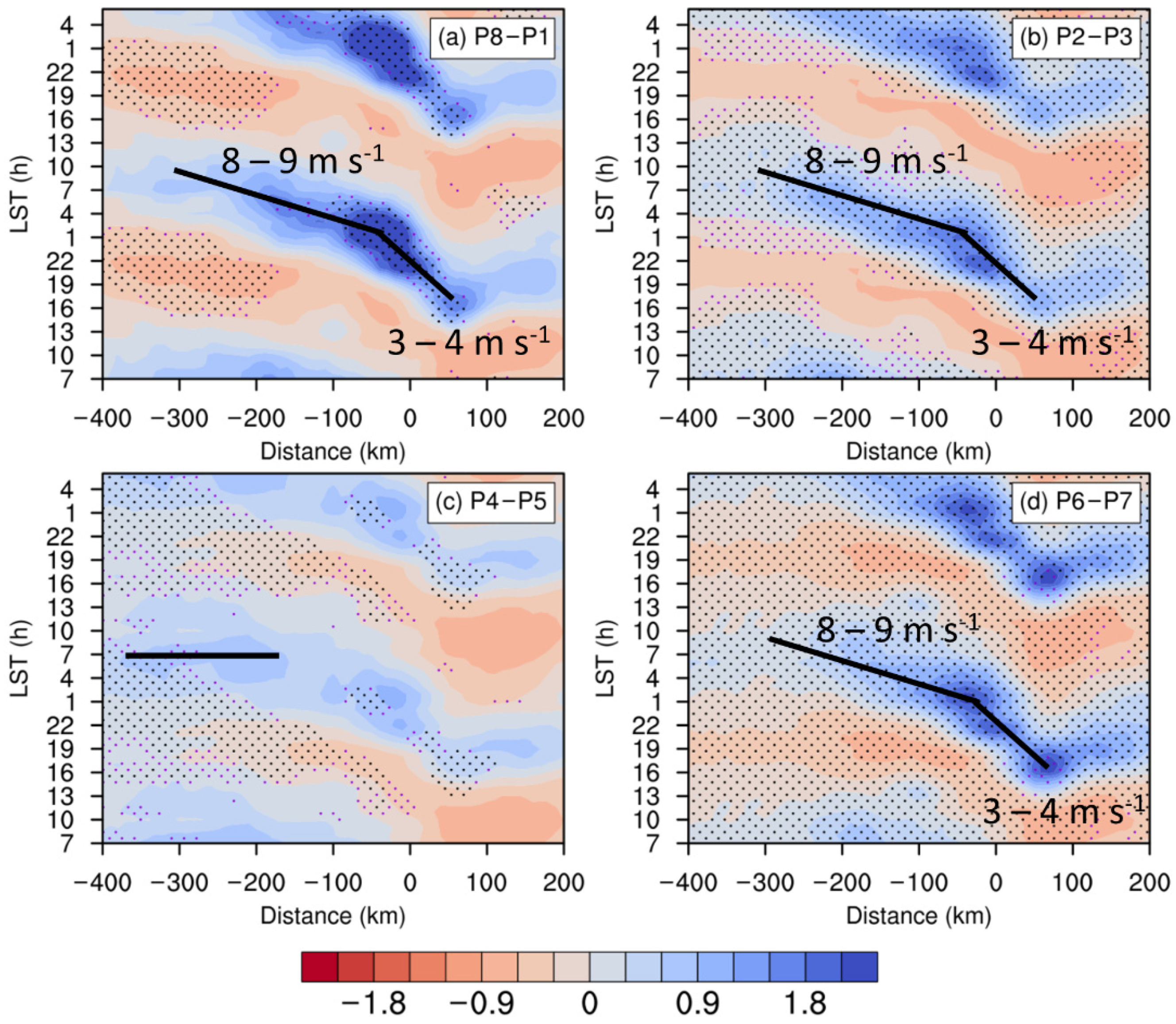
3.1.2. Diurnal Variation
3.2. Effect of Large-Scale Forcing
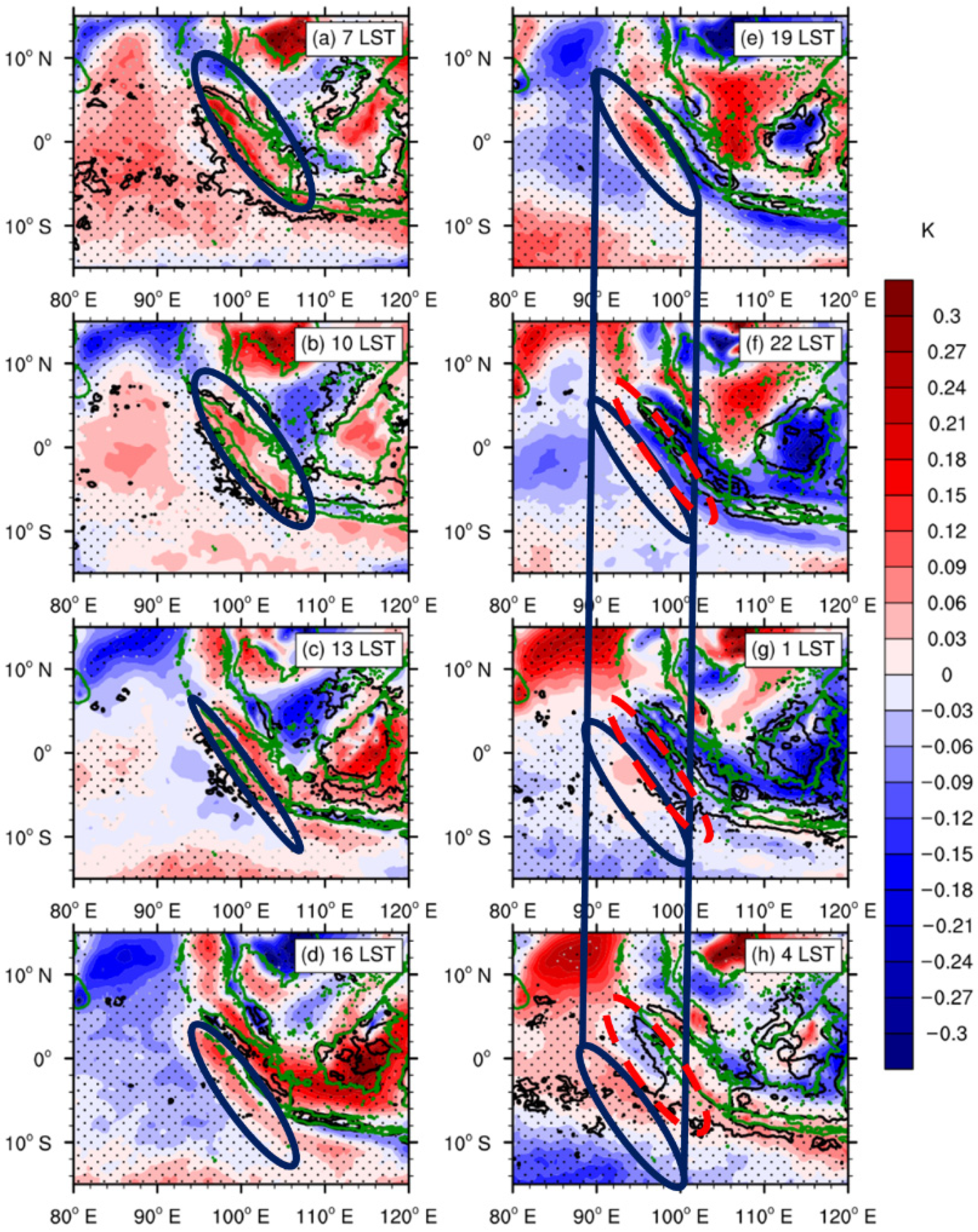
3.3. Effect of Local-Scale Land-Sea Circulation
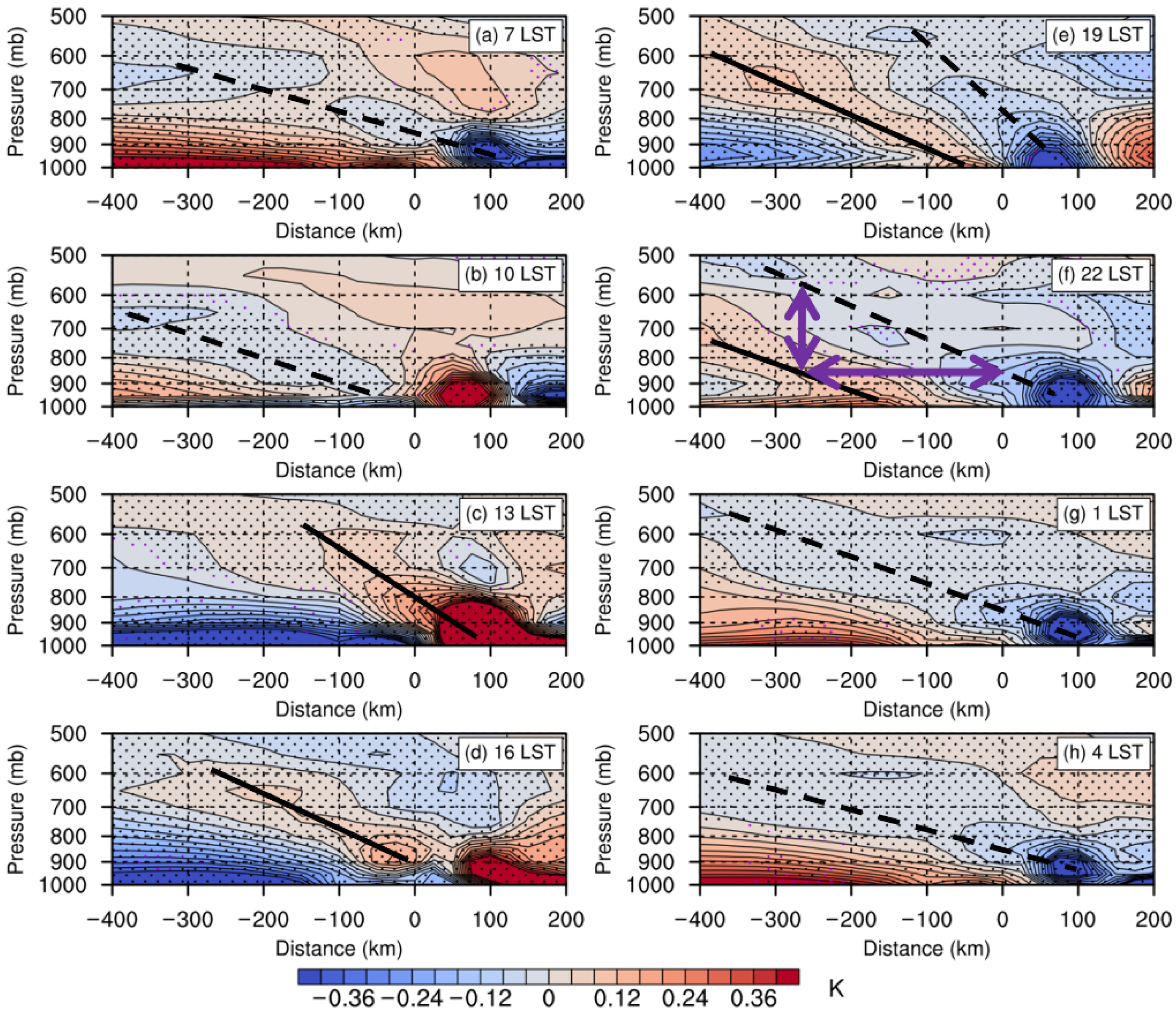
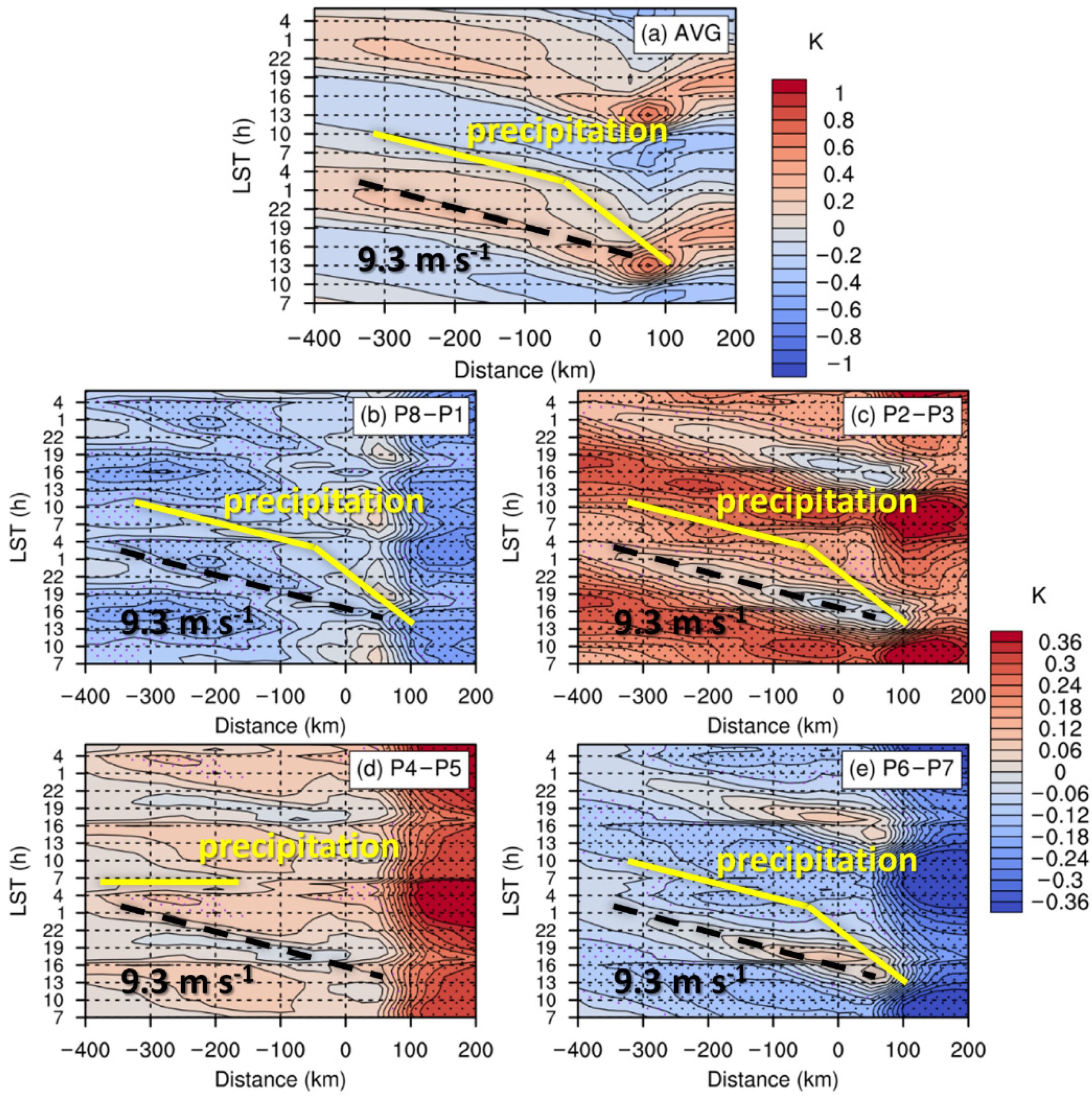
3.4. Diurnal Propagation Associated with Gravity Waves
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Madden, R.A.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.A.; Julian, P.R. Description of global-scale circulation cells in the tropics with a 40–50 day period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43, RG2003. [Google Scholar] [CrossRef]
- Jeong, J.-H.; Kim, B.-M.; Ho, C.-H.; Noh, Y.-H. Systematic variation in wintertime precipitation in East Asia by MJO-induced extratropical vertical motion. J. Clim. 2008, 21, 788–801. [Google Scholar] [CrossRef]
- Barrett, B.S.; Carrasco, J.F.; Testino, A.P. Madden–Julian oscillation (MJO) modulation of atmospheric circulation and Chilean winter precipitation. J. Clim. 2012, 25, 1678–1688. [Google Scholar] [CrossRef]
- Juliá, C.; Rahn, D.A.; Rutllant, J.A. Assessing the influence of the MJO on strong precipitation events in subtropical, semi-arid north-central Chile (30 S). J. Clim. 2012, 25, 7003–7013. [Google Scholar] [CrossRef]
- Zhou, S.; L’Heureux, M.; Weaver, S.; Kumar, A. A composite study of the MJO influence on the surface air temperature and precipitation over the continental United States. Clim. Dyn. 2012, 38, 1459–1471. [Google Scholar] [CrossRef]
- Zhang, C.; Ling, J. Barrier effect of the Indo-Pacific Maritime Continent on the MJO: Perspectives from tracking MJO precipitation. J. Clim. 2017, 30, 3439–3459. [Google Scholar] [CrossRef]
- Wang, B.; Rui, H. Synoptic climatology of transient tropical intraseasonal convection anomalies: 1975–1985. Meteorol. Atmos. Phys. 1990, 44, 43–61. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Michelsen, M.L.; Klein, S.A. Seasonal variations of tropical intraseasonal oscillations: A 20–25-day oscillation in the western Pacific. J. Atmos. Sci. 1992, 49, 1277–1289. [Google Scholar] [CrossRef][Green Version]
- Salby, M.L.; Hendon, H.H. Intraseasonal behavior of clouds, temperature, and motion in the tropics. J. Atmos. Sci. 1994, 51, 2207–2224. [Google Scholar] [CrossRef]
- Wu, C.-H.; Hsu, H.-H. Topographic influence on the MJO in the Maritime Continent. J. Clim. 2009, 22, 5433–5448. [Google Scholar] [CrossRef]
- Jia, X.; Chen, L.; Ren, F.; Li, C. Impacts of the MJO on winter rainfall and circulation in China. Adv. Atmos. Sci. 2011, 28, 521–533. [Google Scholar] [CrossRef]
- Mori, S.; Hamada, J.-I.; Hattori, M.; Wu, P.-M.; Katsumata, M.; Endo, N.; Ichiyanagi, K.; Hashiguchi, H.; Arbain, A.A.; Sulistyowati, R. Meridional march of diurnal rainfall over Jakarta, Indonesia, observed with a C-band Doppler radar: An overview of the HARIMAU2010 campaign. Prog. Earth Planet. Sci. 2018, 5, 47. [Google Scholar] [CrossRef]
- Katsumata, M.; Mori, S.; Hamada, J.-I.; Hattori, M.; Syamsudin, F.; Yamanaka, M.D. Diurnal cycle over a coastal area of the Maritime Continent as derived by special networked soundings over Jakarta during HARIMAU2010. Prog. Earth Planet. Sci. 2018, 5, 1–19. [Google Scholar] [CrossRef]
- Ramage, C.S. Role of a tropical “maritime continent” in the atmospheric circulation. Mon. Weather Rev. 1968, 96, 365–370. [Google Scholar] [CrossRef]
- Neale, R.; Slingo, J. The Maritime Continent and its role in the global climate: A GCM study. J. Clim. 2003, 16, 834–848. [Google Scholar] [CrossRef]
- Chang, C.; Harr, P.A.; Chen, H.-J. Synoptic disturbances over the equatorial South China Sea and western Maritime Continent during boreal winter. Mon. Weather Rev. 2005, 133, 489–503. [Google Scholar] [CrossRef]
- Lorenz, P.; Jacob, D. Influence of regional scale information on the global circulation: A two-way nesting climate simulation. Geophys. Res. Lett. 2005, 32, L18706. [Google Scholar] [CrossRef]
- Ando, K.; Syamsudin, F.; Ishihara, Y.; Pandoe, W.; Yamanaka, M.D.; Masumoto, Y.; Mizuno, K. Development of new international research laboratory for maritime-continent seas climate research and contributions to global surface moored buoy array. In Proceedings of the “OeanObs’ 09: Sustained Ocean Observations and Information for Society” Conference (Annex), Venice, Italy, 21–25 September 2009. [Google Scholar]
- Mori, S.; Jun-Ichi, H.; Tauhid, Y.I.; Yamanaka, M.D.; Okamoto, N.; Murata, F.; Sakurai, N.; Hashiguchi, H.; Sribimawati, T. Diurnal land–sea rainfall peak migration over Sumatera Island, Indonesian Maritime Continent, observed by TRMM satellite and intensive rawinsonde soundings. Mon. Weather Rev. 2004, 132, 2021–2039. [Google Scholar] [CrossRef]
- Love, B.S.; Matthews, A.J.; Lister, G.M. The diurnal cycle of precipitation over the Maritime Continent in a high-resolution atmospheric model. Q. J. R. Meteorol. Soc. 2011, 137, 934–947. [Google Scholar] [CrossRef]
- Vincent, C.L.; Lane, T.P. Evolution of the diurnal precipitation cycle with the passage of a Madden–Julian oscillation event through the Maritime Continent. Mon. Weather Rev. 2016, 144, 1983–2005. [Google Scholar] [CrossRef]
- Yokoi, S.; Mori, S.; Katsumata, M.; Geng, B.; Yasunaga, K.; Syamsudin, F.; Nurhayati; Yoneyama, K. Diurnal cycle of precipitation observed in the western coastal area of Sumatra Island: Offshore preconditioning by gravity waves. Mon. Weather Rev. 2017, 145, 3745–3761. [Google Scholar] [CrossRef]
- Yokoi, S.; Mori, S.; Syamsudin, F.; Haryoko, U.; Geng, B. Environmental conditions for nighttime offshore migration of precipitation area as revealed by in situ observation off Sumatra Island. Mon. Weather Rev. 2019, 147, 3391–3407. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Y. Tropical Rainfall Measuring Mission observation and regional model study of precipitation diurnal cycle in the New Guinean region. J. Geophys. Res. Atmos. 2006, 111, D17104. [Google Scholar] [CrossRef]
- Fujita, M.; Kimura, F.; Yoshizaki, M. Morning precipitation peak over the Strait of Malacca under a calm condition. Mon. Weather Rev. 2010, 138, 1474–1486. [Google Scholar] [CrossRef]
- Dipankar, A.; Webster, S.; Huang, X.-Y. Understanding biases in simulating the diurnal cycle of convection over the western coast of Sumatra: Comparison with pre-YMC observation campaign. Mon. Weather Rev. 2019, 147, 1615–1631. [Google Scholar] [CrossRef]
- Short, E.; Vincent, C.L.; Lane, T.P. Diurnal cycle of surface winds in the Maritime Continent observed through satellite scatterometry. Mon. Weather Rev. 2019, 147, 2023–2044. [Google Scholar] [CrossRef]
- Wu, P.; Hara, M.; Hamada, J.-i.; Yamanaka, M.D.; Kimura, F. Why a large amount of rain falls over the sea in the vicinity of western Sumatra Island during nighttime. J. Appl. Meteorol. Climatol. 2009, 48, 1345–1361. [Google Scholar] [CrossRef]
- Hassim, M.; Lane, T.; Grabowski, W. The diurnal cycle of rainfall over New Guinea in convection-permitting WRF simulations. Atmos. Chem. Phys. 2016, 16, 161–175. [Google Scholar] [CrossRef]
- Yulihastin, E.; Wahyu Hadi, T.; Sari Ningsih, N.; Ridho Syahputra, M. Early morning peaks in the diurnal cycle of precipitation over the northern coast of West Java and possible influencing factors. Ann. Geophys. 2020, 38, 231–242. [Google Scholar] [CrossRef]
- Johnson, R.H.; Rickenbach, T.M.; Rutledge, S.A.; Ciesielski, P.E.; Schubert, W.H. Trimodal characteristics of tropical convection. J. Clim. 1999, 12, 2397–2418. [Google Scholar] [CrossRef]
- Tian, B.; Waliser, D.E.; Fetzer, E.J. Modulation of the diurnal cycle of tropical deep convective clouds by the MJO. Geophys. Res. Lett. 2006, 33, L20704. [Google Scholar] [CrossRef]
- Ichikawa, H.; Yasunari, T. Propagating diurnal disturbances embedded in the Madden-Julian Oscillation. Geophys. Res. Lett. 2007, 34, L18811. [Google Scholar] [CrossRef]
- Vincent, C.L.; Lane, T.P. A 10-year austral summer climatology of observed and modeled intraseasonal, mesoscale, and diurnal variations over the Maritime Continent. J. Clim. 2017, 30, 3807–3828. [Google Scholar] [CrossRef]
- Seiki, A.; Yokoi, S.; Katsumata, M. The impact of diurnal precipitation over Sumatra Island, Indonesia, on synoptic disturbances and its relation to the Madden-Julian Oscillation. J. Meteorol. Soc. Jpn. Ser. II 2021, 99, 113–137. [Google Scholar] [CrossRef]
- Lubis, S.W.; Jacobi, C. The modulating influence of convectively coupled equatorial waves (CCEWs) on the variability of tropical precipitation. Int. J. Climatol. 2015, 35, 1465–1483. [Google Scholar] [CrossRef]
- Sakaeda, N.; Kiladis, G.; Dias, J. The diurnal cycle of rainfall and the convectively coupled equatorial waves over the Maritime Continent. J. Clim. 2020, 33, 3307–3331. [Google Scholar] [CrossRef]
- Ferrett, S.; Yang, G.Y.; Woolnough, S.J.; Methven, J.; Hodges, K.; Holloway, C.E. Linking extreme precipitation in Southeast Asia to equatorial waves. Q. J. R. Meteorol. Soc. 2020, 146, 665–684. [Google Scholar] [CrossRef]
- Peatman, S.C.; Schwendike, J.; Birch, C.E.; Marsham, J.H.; Matthews, A.J.; Yang, G.-Y. A Local-to-Large Scale View of Maritime Continent Rainfall: Control by ENSO, MJO, and Equatorial Waves. J. Clim. 2021, 34, 8933–8953. [Google Scholar] [CrossRef]
- Lubis, S.W.; Respati, M.R. Impacts of convectively coupled equatorial waves on rainfall extremes in Java, Indonesia. Int. J. Climatol. 2021, 41, 2418–2440. [Google Scholar] [CrossRef]
- Peatman, S.C.; Matthews, A.J.; Stevens, D.P. Propagation of the Madden–Julian Oscillation through the Maritime Continent and scale interaction with the diurnal cycle of precipitation. Q. J. R. Meteorol. Soc. 2014, 140, 814–825. [Google Scholar] [CrossRef]
- Birch, C.; Webster, S.; Peatman, S.; Parker, D.; Matthews, A.; Li, Y.; Hassim, M. Scale interactions between the MJO and the western Maritime Continent. J. Clim. 2016, 29, 2471–2492. [Google Scholar] [CrossRef]
- Rauniyar, S.P.; Walsh, K.J. Scale interaction of the diurnal cycle of rainfall over the Maritime Continent and Australia: Influence of the MJO. J. Clim. 2011, 24, 325–348. [Google Scholar] [CrossRef]
- Fujita, M.; Yoneyama, K.; Mori, S.; Nasuno, T.; Satoh, M. Diurnal convection peaks over the eastern Indian Ocean off Sumatra during different MJO phases. J. Meteorol. Soc. Jpn. Ser. II 2011, 89, 317–330. [Google Scholar] [CrossRef]
- Kamimera, H.; Mori, S.; Yamanaka, M.D.; Syamsudin, F. Modulation of diurnal rainfall cycle by the Madden-Julian Oscillation based on one-year continuous observations with a meteorological radar in west Sumatera. SOLA 2012, 8, 111–114. [Google Scholar] [CrossRef][Green Version]
- Harjupa, W.; Shimomai, T.; Hashiguchi, H.; Fujiyoshi, Y.; Kawashima, M. Differences in Mechanisms of Orographic Rainfall over West Sumatra (Case Study: 10 April and 23 April 2004). Jurnal Ilmu Fisika|Universitas Andalas 2021, 13, 8–17. [Google Scholar] [CrossRef]
- Xavier, P.; Rahmat, R.; Cheong, W.K.; Wallace, E. Influence of Madden-Julian Oscillation on Southeast Asia rainfall extremes: Observations and predictability. Geophys. Res. Lett. 2014, 41, 4406–4412. [Google Scholar] [CrossRef]
- Muhammad, F.R.; Lubis, S.W.; Setiawan, S. Impacts of the Madden–Julian oscillation on precipitation extremes in Indonesia. Int. J. Climatol. 2021, 41, 1970–1984. [Google Scholar] [CrossRef]
- Zhu, B.; Pu, Z.; Putra, A.W.; Gao, Z. Assimilating C-Band Radar Data for High-Resolution Simulations of Precipitation: Case Studies over Western Sumatra. Remote Sens. 2022, 14, 42. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Version 2015, 4, 26. [Google Scholar]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the morphing algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wheeler, M.C.; Hendon, H.H. An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon. Weather Rev. 2004, 132, 1917–1932. [Google Scholar] [CrossRef]
- Chen, S.S.; Houze, R.A., Jr. Diurnal variation and life-cycle of deep convective systems over the tropical Pacific warm pool. Q. J. R. Meteorol. Soc. 1997, 123, 357–388. [Google Scholar] [CrossRef]
- Sui, C.; Lau, K.; Takayabu, Y.; Short, D. Diurnal variations in tropical oceanic cumulus convection during TOGA COARE. J. Atmos. Sci. 1997, 54, 639–655. [Google Scholar] [CrossRef]
- Oh, J.-H.; Kim, K.-Y.; Lim, G.-H. Impact of MJO on the diurnal cycle of rainfall over the western Maritime Continent in the austral summer. Clim. Dyn. 2012, 38, 1167–1180. [Google Scholar] [CrossRef]
- Sakaeda, N.; Kiladis, G.; Dias, J. The diurnal cycle of tropical cloudiness and rainfall associated with the Madden–Julian oscillation. J. Clim. 2017, 30, 3999–4020. [Google Scholar] [CrossRef]
- Sakaeda, N.; Powell, S.W.; Dias, J.; Kiladis, G.N. The diurnal variability of precipitating cloud populations during DYNAMO. J. Atmos. Sci. 2018, 75, 1307–1326. [Google Scholar] [CrossRef]
- Wapler, K.; Lane, T.P. A case of offshore convective initiation by interacting land breezes near Darwin, Australia. Meteorol. Atmos. Phys. 2012, 115, 123–137. [Google Scholar] [CrossRef]
- Mapes, B.E.; Warner, T.T.; Xu, M. Diurnal patterns of rainfall in northwestern South America. Part III: Diurnal gravity waves and nocturnal convection offshore. Mon. Weather Rev. 2003, 131, 830–844. [Google Scholar] [CrossRef]
- Du, Y.; Rotunno, R. Thermally driven diurnally periodic wind signals off the east coast of China. J. Atmos. Sci. 2015, 72, 2806–2821. [Google Scholar] [CrossRef][Green Version]
- Du, Y.; Rotunno, R. Diurnal cycle of rainfall and winds near the south coast of China. J. Atmos. Sci. 2018, 75, 2065–2082. [Google Scholar] [CrossRef]
- Bai, H.; Deranadyan, G.; Schumacher, C.; Funk, A.; Epifanio, C.; Ali, A.; Endarwin; Radjab, F.; Adriyanto, R.; Nurhayati, N. Formation of Nocturnal Offshore Rainfall near the West Coast of Sumatra: Land Breeze or Gravity Wave? Mon. Weather Rev. 2021, 149, 715–731. [Google Scholar] [CrossRef]
- Ruppert, J.H.; Zhang, F. Diurnal forcing and phase locking of gravity waves in the Maritime Continent. J. Atmos. Sci. 2019, 76, 2815–2835. [Google Scholar] [CrossRef]
- Du, Y.; Rotunno, R.; Zhang, F. Impact of Vertical Wind Shear on Gravity Wave Propagation in the Land–Sea-Breeze Circulation at the Equator. J. Atmos. Sci. 2019, 76, 3247–3265. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, F. Banded convective activity associated with mesoscale gravity waves over southern China. J. Geophys. Res. Atmos. 2019, 124, 1912–1930. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, F.; Sun, Y.Q.; Wei, J.; Li, X. Practical and Intrinsic Predictability of Wave-Convection Coupled Bands Over Southern China. J. Geophys. Res. Atmos. 2021, 126, e2021JD034882. [Google Scholar] [CrossRef]

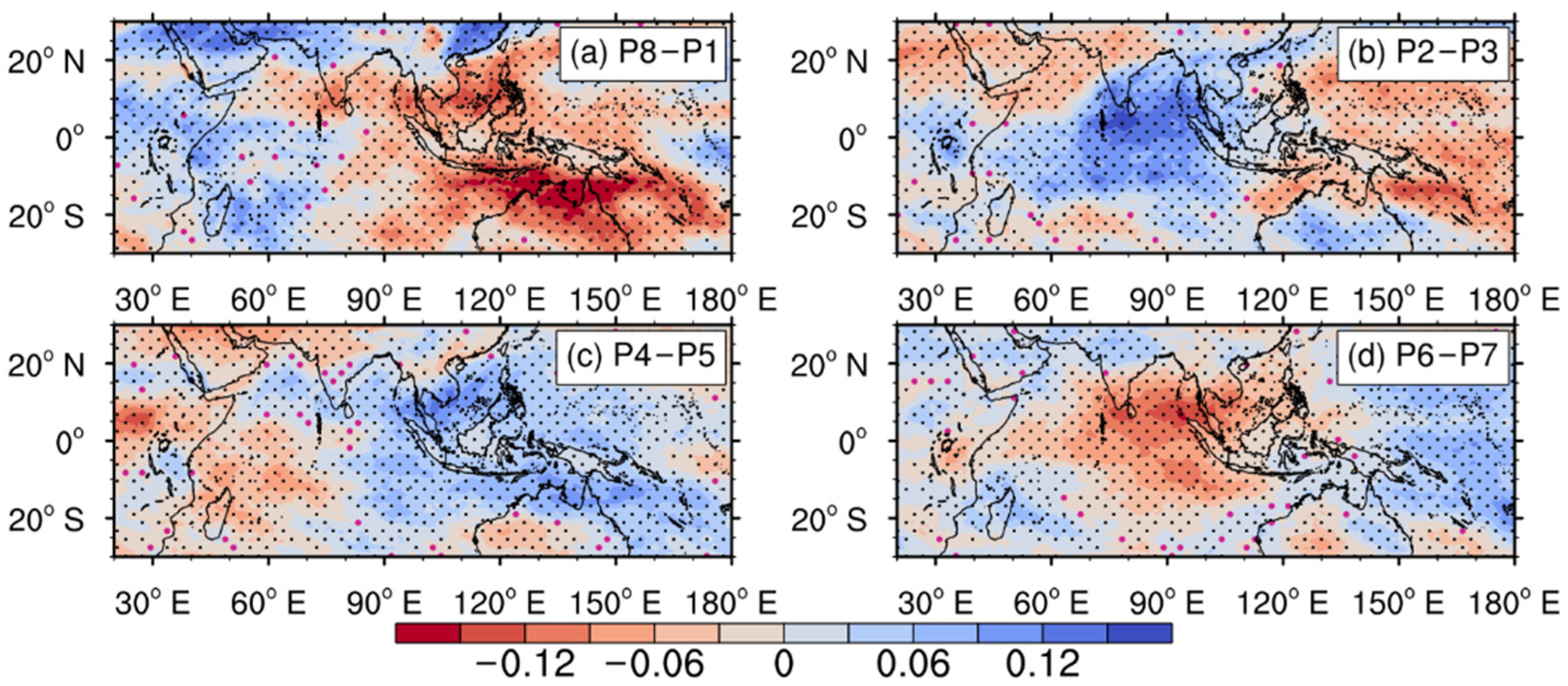
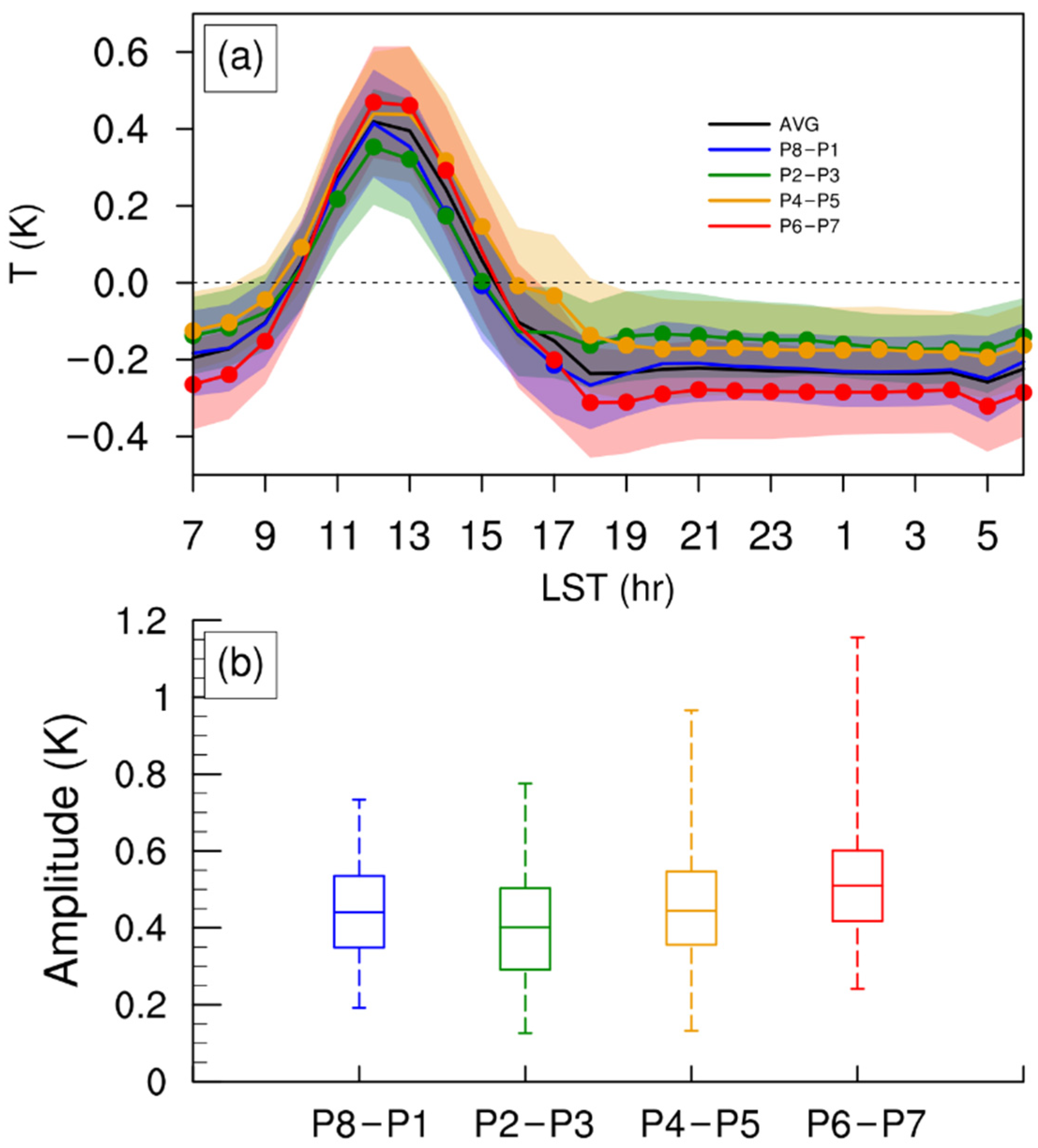
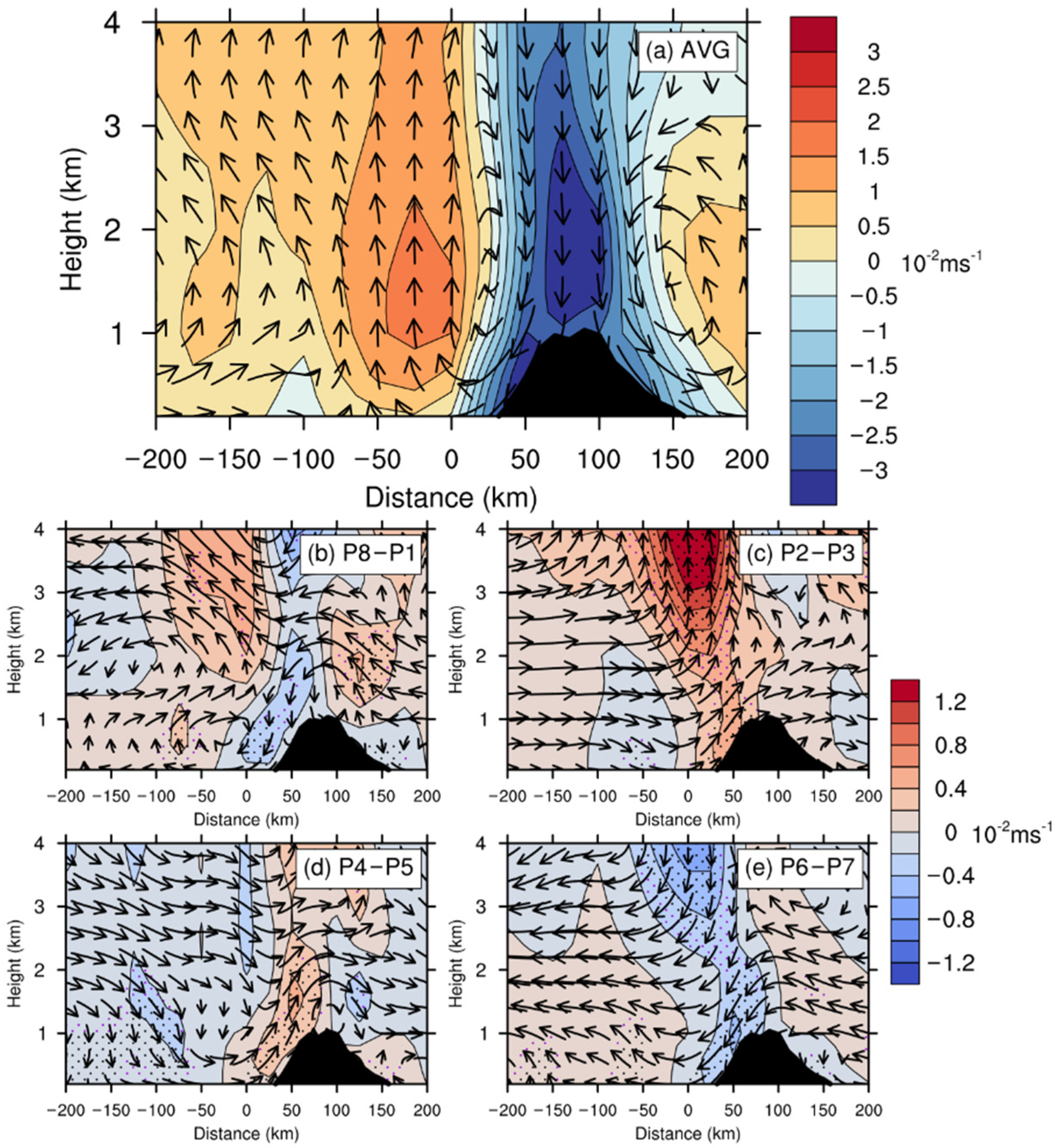
| P8–P1 | P2–P3 | P4–P5 | P6–P7 | |
|---|---|---|---|---|
| Ao | 0.599 | 0.648 | 0.248 | 0.266 |
| An | 0.896 | 0.799 | 0.491 | 0.762 |
| Ra | 0.668 | 0.812 | 0.505 | 0.349 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Du, Y.; Gao, Z. Influences of MJO on the Diurnal Variation and Associated Offshore Propagation of Rainfall near Western Coast of Sumatra. Atmosphere 2022, 13, 330. https://doi.org/10.3390/atmos13020330
Zhu B, Du Y, Gao Z. Influences of MJO on the Diurnal Variation and Associated Offshore Propagation of Rainfall near Western Coast of Sumatra. Atmosphere. 2022; 13(2):330. https://doi.org/10.3390/atmos13020330
Chicago/Turabian StyleZhu, Bojun, Yu Du, and Zhiqiu Gao. 2022. "Influences of MJO on the Diurnal Variation and Associated Offshore Propagation of Rainfall near Western Coast of Sumatra" Atmosphere 13, no. 2: 330. https://doi.org/10.3390/atmos13020330
APA StyleZhu, B., Du, Y., & Gao, Z. (2022). Influences of MJO on the Diurnal Variation and Associated Offshore Propagation of Rainfall near Western Coast of Sumatra. Atmosphere, 13(2), 330. https://doi.org/10.3390/atmos13020330







