Beam Quality Factor of Partially Coherent Airy Beam in Non-Kolmogorov Turbulence
Abstract
1. Introduction
2. Formulation
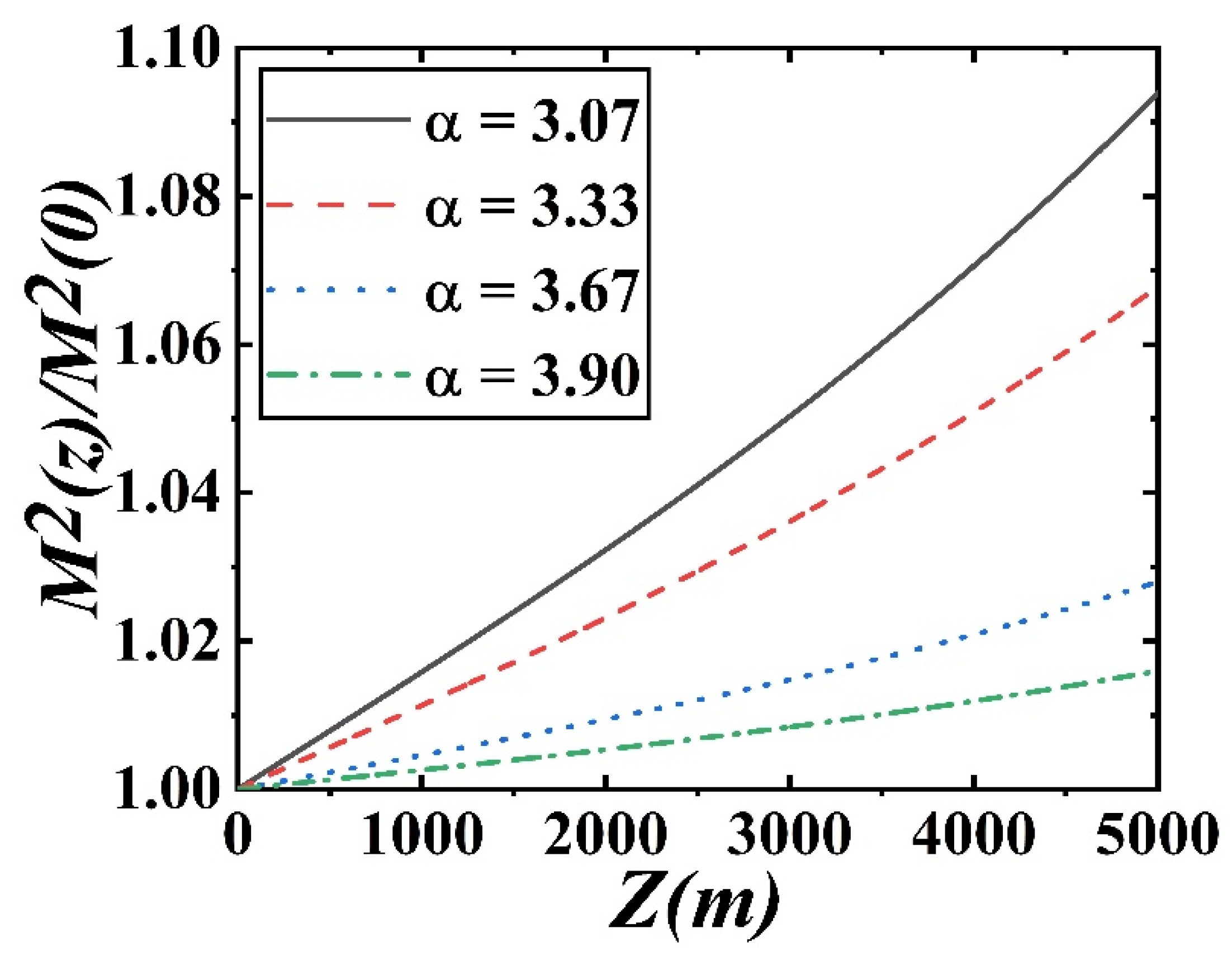
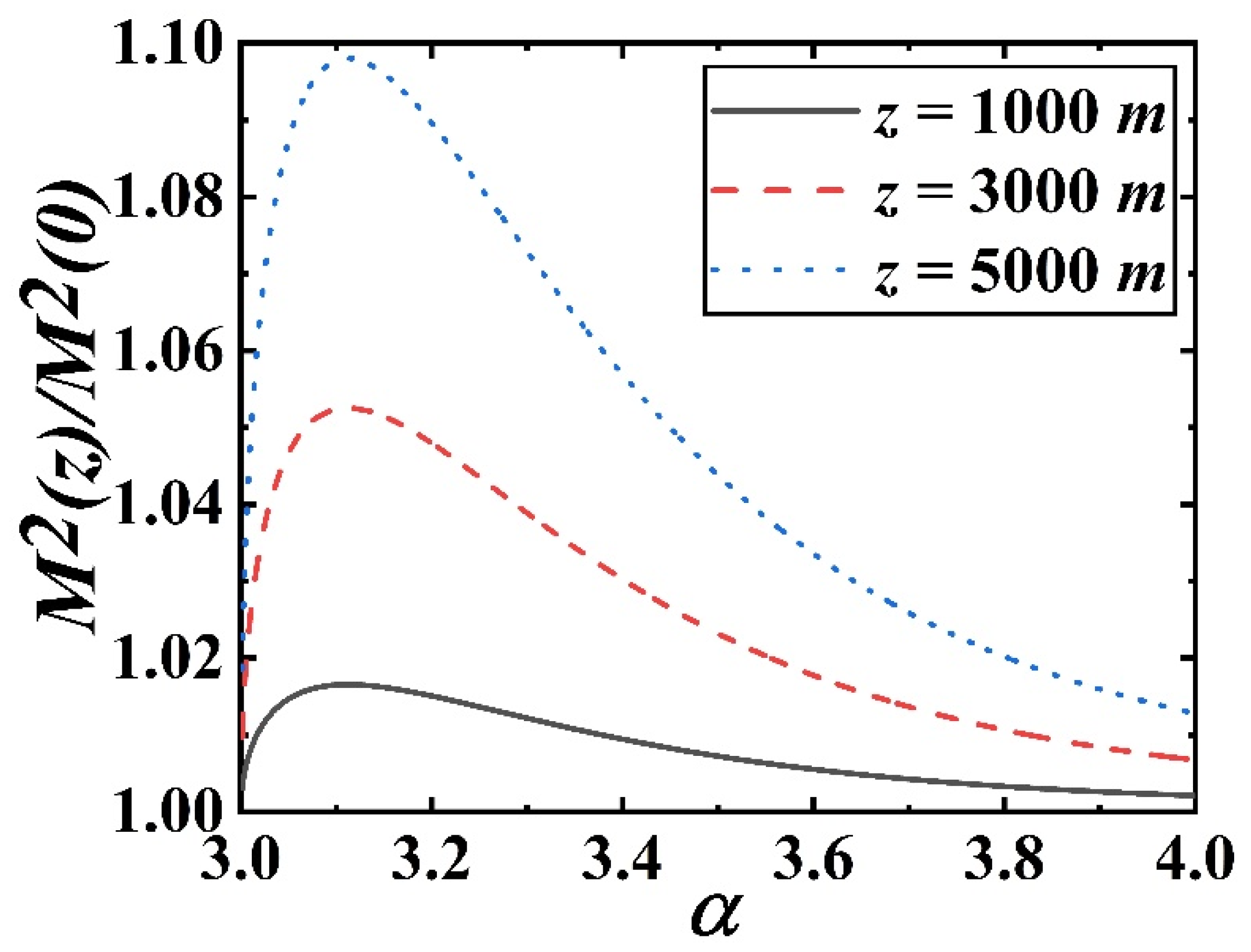
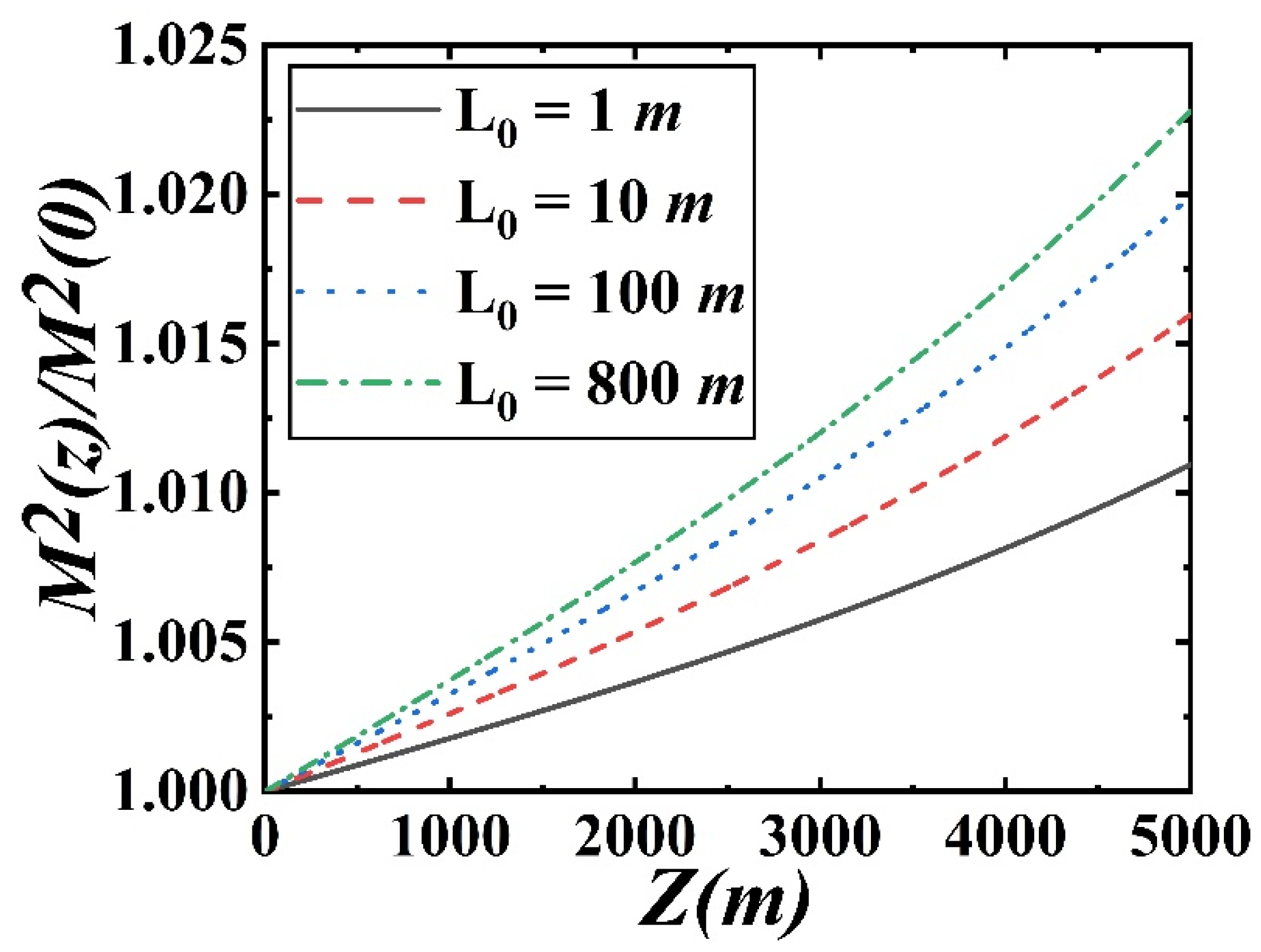
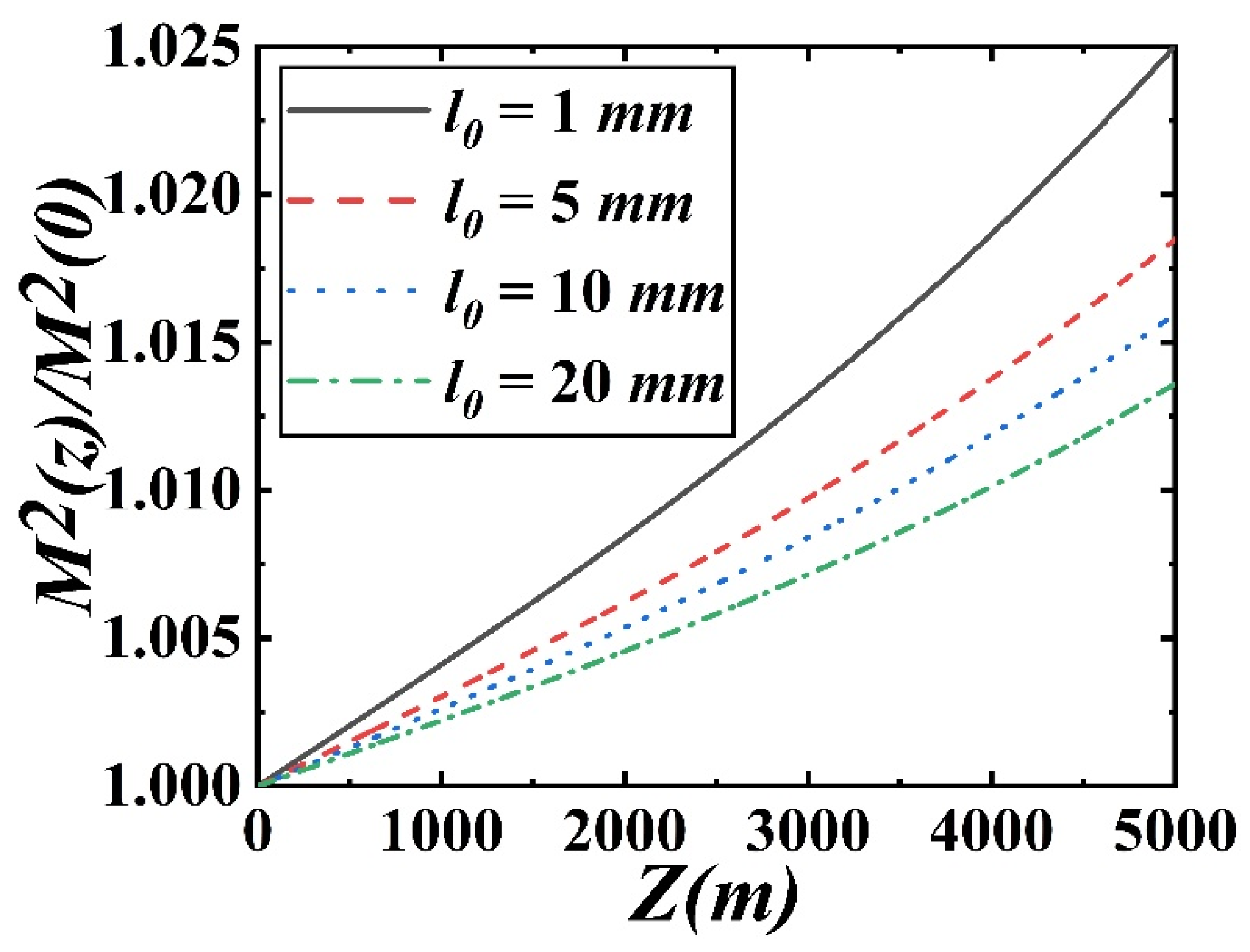
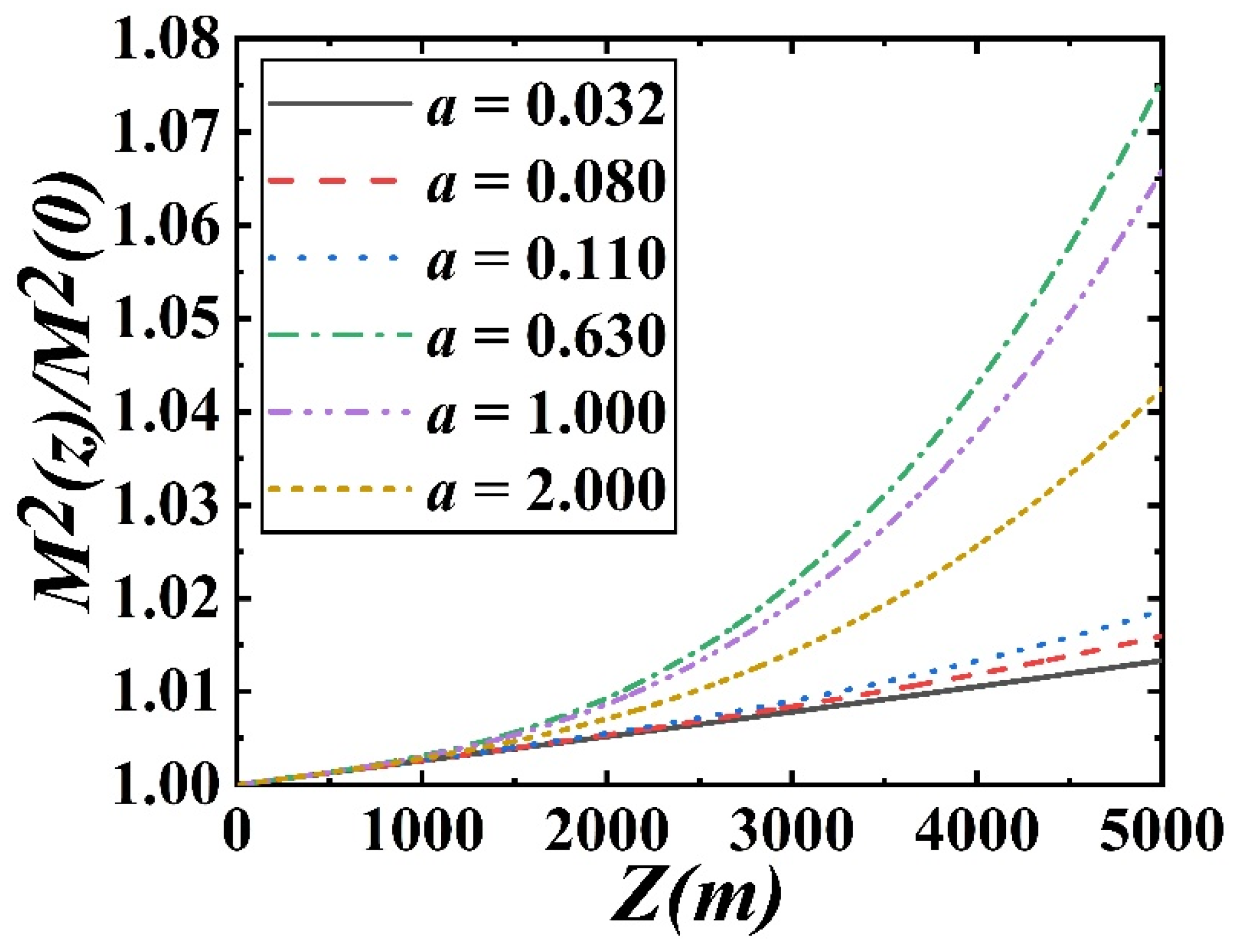
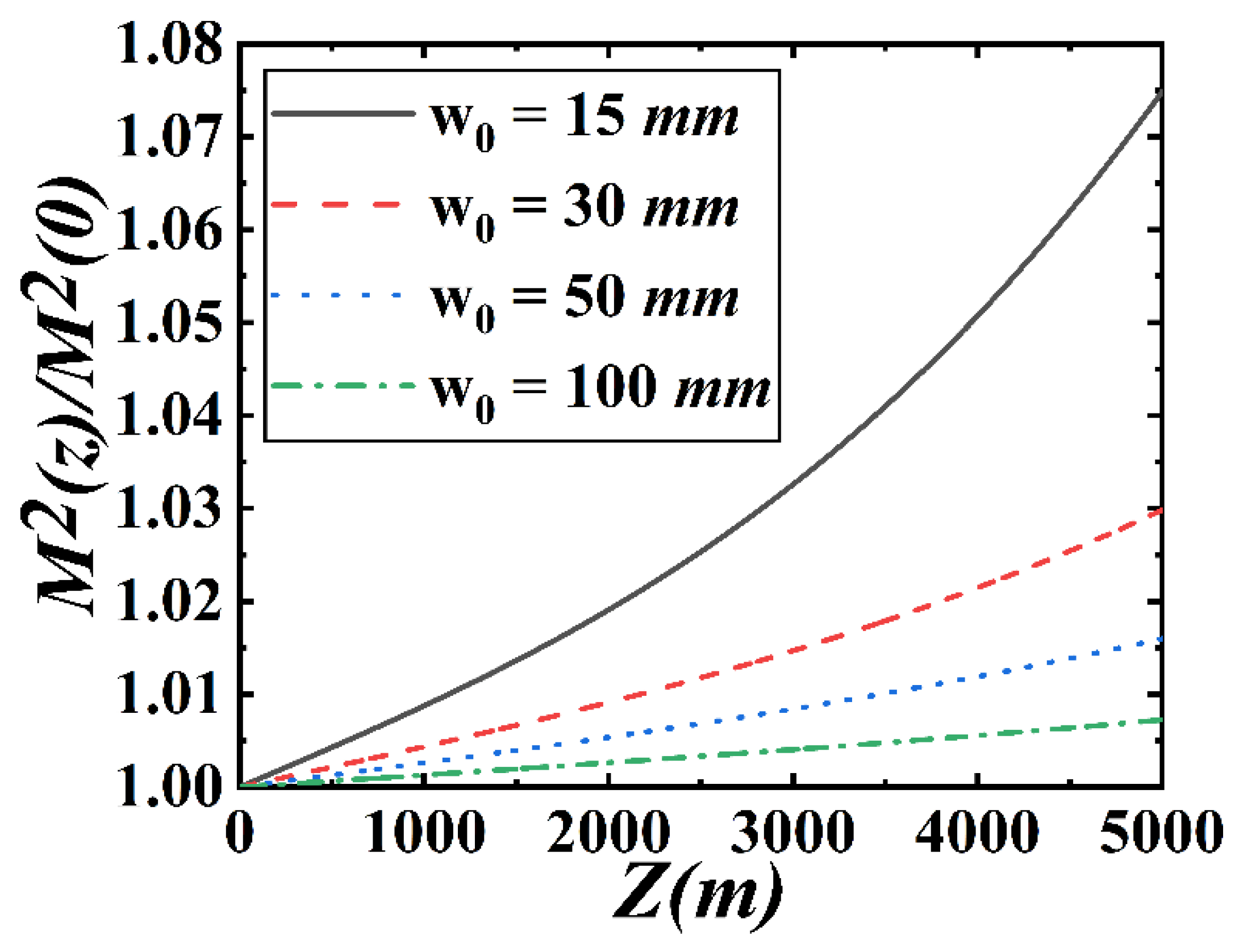
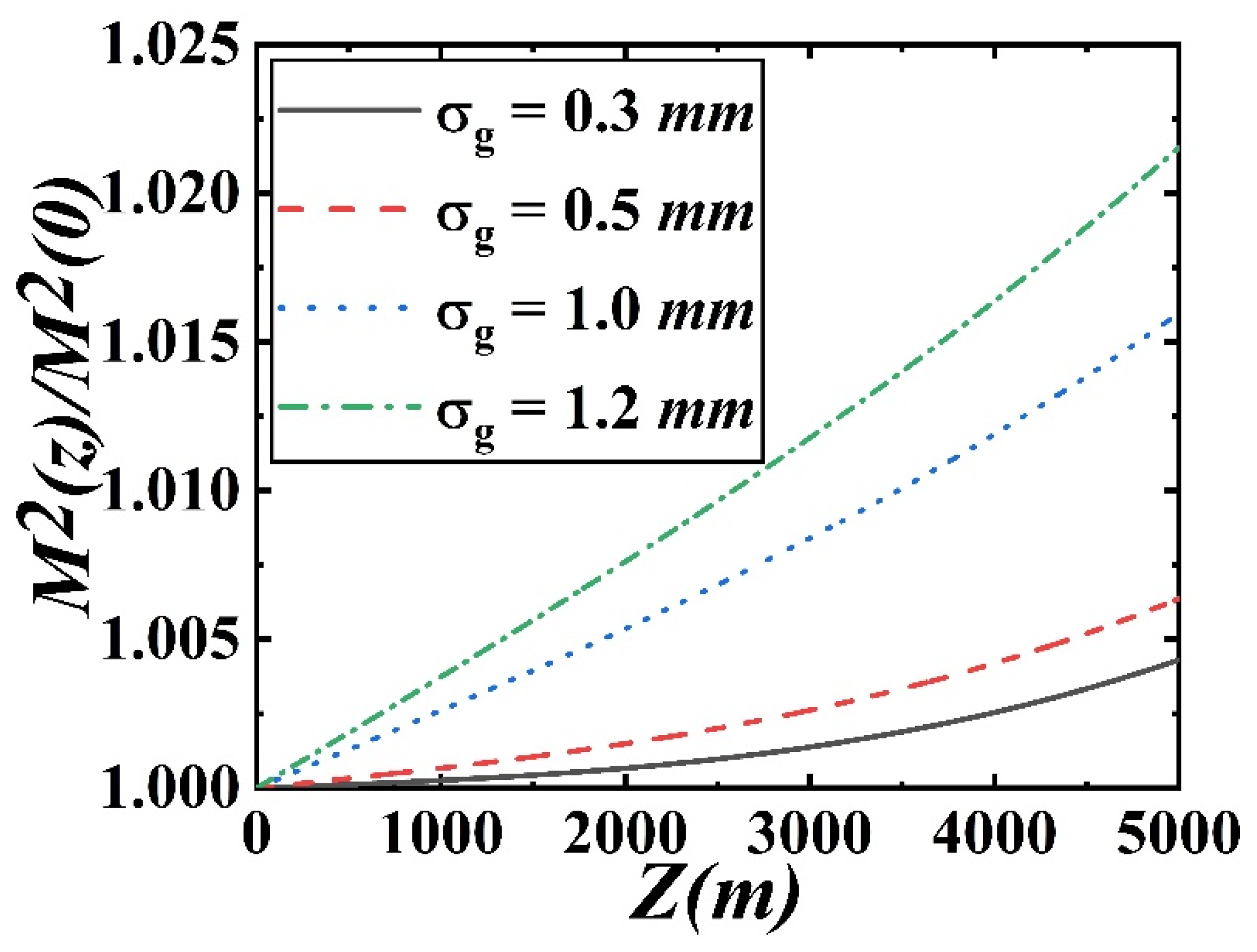
3. Numerical Results and Analysis
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Slusher, R.E. Laser technology. Rev. Mod. Phys. 1999, 71, S471–S479. [Google Scholar] [CrossRef]
- Strickland, D. Nobel Lecture: Generating high-intensity ultrashort optical pulses. Rev. Mod. Phys. 2019, 91, 030502. [Google Scholar] [CrossRef]
- Siegman, A.E. New developments in laser resonators. In Optical Resonators; SPIE: Bellingham, WA, USA, 1990; Volume 1224, pp. 2–14. [Google Scholar] [CrossRef]
- Gong, M.L.; Qiu, Y.; Huang, L.; Liu, Q.; Yan, P.; Zhang, H.T. Beam quality improvement by joint compensation of amplitude and phase. Opt. Lett. 2013, 38, 1101–1103. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, V.N. Strehl ratio for primary aberrations: Some analytical results for circular and annular pupils. J. Opt. Soc. Am. 1982, 72, 1258–1266. [Google Scholar] [CrossRef]
- Bélanger, P.A. Beam propagation and the ABCD ray matrices. Opt. Lett. 1991, 16, 196–198. [Google Scholar] [CrossRef]
- Zeng, X.; Hui, Z.; Zhang, M. M2 factor of controllable dark-hollow beams through a multi-apertured ABCD optical system. Appl. Opt. 2018, 57, 7667–7672. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, H.; Yuan, Z.; Yang, Y.; You, Y.; Wu, W.; He, B.; Zhou, J. Theoretical study of beam quality degradation caused by grating dispersion in a spectral beam combining system. In Seventh Symposium on Novel Photoelectronic Detection Technology and Applications; SPIE: Bellingham, WA, USA, 2021; Volume 11763, pp. 952–958. [Google Scholar]
- Ribbat, C.; Sellin, R.L.; Kaiander, I.; Hopfer, F.; Ledentsov, N.N.; Bimberg, D.; Kovsh, A.R.; Ustinov, V.M.; Zhukov, A.E.; Maximov, M. Complete suppression of filamentation and superior beam quality in quantum-dot lasers. Appl. Phys. Lett. 2003, 82, 952–954. [Google Scholar] [CrossRef]
- Riou, J.-F.; Guerin, W.; Le Coq, Y.; Fauquembergue, M.; Josse, V.; Bouyer, P.; Aspect, A. Beam Quality of a Nonideal Atom Laser. Phys. Rev. Lett. 2006, 96, 070404. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, W.; Yang, Z.; Wang, Y.; Zhao, W.; Li, X.; Wang, H.; Li, C.; Shen, D. High average power, strictly all-fiber supercontinuum source with good beam quality. Opt. Lett. 2011, 36, 2659–2661. [Google Scholar] [CrossRef]
- Hirose, K.; Liang, Y.; Kurosaka, Y.; Watanabe, A.; Sugiyama, T.; Noda, S. Watt-class high-power, high-beam-quality photonic-crystal lasers. Nat. Photon. 2014, 8, 406–411. [Google Scholar] [CrossRef]
- Bereczki, A.; Wetter, N.U. 100 W continuous linearly polarized, high beam quality output from standard side-pumped Nd:YAG laser modules. Opt. Laser Technol. 2017, 96, 271–275. [Google Scholar] [CrossRef]
- Chen, D.; Miao, Y.; Fu, H.; He, H.; Tong, J.; Dong, J. High-order cylindrical vector beams with tunable topological charge up to 14 directly generated from a microchip laser with high beam quality and high efficiency. APL Photon. 2019, 4, 106106. [Google Scholar] [CrossRef]
- Ma, P.; Miao, Y.; Liu, W.; Meng, D.; Zhou, P. Kilowatt-level ytterbium-Raman fiber amplifier with a narrow-linewidth and near-diffraction-limited beam quality. Opt. Lett. 2020, 45, 1974–1977. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.; Li, Z.; Wang, Z.; Chen, Z.; Xu, X. Research on a 4 × 1 fiber signal combiner with high beam quality at a power level of 12kW. Opt. Express 2021, 29, 26658–26668. [Google Scholar]
- Cai, Y. Model for an anomalous hollow beam and its paraxial propagation. Opt. Lett. 2007, 32, 3179–3181. [Google Scholar] [CrossRef]
- Zhou, G.; Feng, S.; Xu, Y.; Zhou, Y. Beam propagation factor and kurtosis parameter of hollow vortex Gaussian beams: An alternative method. J. Opt. Soc. Am. A 2019, 36, 1908–1916. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, T.; Wang, F.; Li, X.; Chen, R.; Zhou, Y.; Zhou, G. Realization and measurement of Airy transform of Gaussian vortex beams. Opt. Laser Technol. 2021, 143, 107334. [Google Scholar] [CrossRef]
- Dan, Y.; Zhang, B. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere. Opt. Express 2008, 16, 15563–15575. [Google Scholar] [CrossRef]
- Yuan, Y.; Cai, Y.; Qu, J.; Eyyuboğlu, H.T.; Baykal, Y.; Korotkova, O. M2-factor of coherent and partially coherent dark hollow beams propagating in turbulent atmosphere. Opt. Express 2009, 17, 17344–17356. [Google Scholar] [CrossRef]
- Cheng, F.; Cai, Y. Propagation factor of a truncated partially coherent flat-topped beam in turbulent atmosphere. Opt. Commun. 2011, 284, 30–37. [Google Scholar] [CrossRef]
- Yuan, Y.; Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y.; Chen, J. Propagation factor of partially coherent flat-topped beam array in free space and turbulent atmosphere. Opt. Lasers Eng. 2012, 50, 752–759. [Google Scholar] [CrossRef]
- Du, S.; Yuan, Y.; Liang, C.; Cai, Y. Second-order moments of a multi-Gaussian Schell-model beam in a turbulent atmosphere. Opt. Laser Technol. 2013, 50, 14–19. [Google Scholar] [CrossRef]
- Yu, J.; Chen, Y.; Liu, L.; Liu, X.; Cai, Y. Splitting and combining properties of an elegant Hermite-Gaussian correlated Schell-model beam in Kolmogorov and non-Kolmogorov turbulence. Opt. Express 2015, 23, 13467–13481. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Liu, L.; Jiang, Z.; Guo, J.; Wang, T. The effect of beam quality factor for the laser beam propagation through turbulence. Optik 2018, 156, 148–154. [Google Scholar] [CrossRef]
- Eckart, C.; Ferris, H.G. Equations of Motion of the Ocean and Atmosphere. Rev. Mod. Phys. 1956, 28, 48–52. [Google Scholar] [CrossRef]
- Peixoto, J.P.; Oort, A.H. Physics of climate. Rev. Mod. Phys. 1984, 56, 365–429. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 1998; pp. 47–50. [Google Scholar]
- Dayton, D.; Pierson, B.; Spielbusch, B.; Gonglewski, J. Atmospheric structure function measurements with a Shack-Hartmann wave-front sensor. Opt. Lett. 1992, 17, 1737–1739. [Google Scholar] [CrossRef]
- Golbraikh, E.; Moiseev, S. Different spectra formation in the presence of helical transfer. Phys. Lett. A 2002, 305, 173–175. [Google Scholar] [CrossRef]
- Rao, C.; Jiang, W.; Ling, N. Spatial and temporal characterization of phase fluctuations in non-Kolmogorov atmospheric turbulence. J. Mod. Opt. 2000, 47, 1111–1126. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, G.; Duan, Z.; He, D.; Gao, Z.; Wang, F. Spreading and M2-factor of elegant Hermite–Gaussian beams through non-Kolmogorov turbulence. J. Mod. Opt. 2011, 58, 912–917. [Google Scholar] [CrossRef]
- Chu, X. Evolution of beam quality and shape of hermite-gaussian beam in non-kolmogorov turbulence. Prog. Electromagn. Res. 2011, 120, 339–353. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, H.; Feng, H.; Du, Q.; Dan, Y. Propagation factors of standard and elegant Laguerre Gaussian beams in non-Kolmogorov turbulence. Optik 2016, 127, 10999–11008. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, Z.; Zhang, B. Propagation properties based on second-order moments for correlated combination partially coherent Hermite–Gaussian linear array beams in non-Kolmogorov turbulence. J. Mod. Opt. 2013, 60, 841–850. [Google Scholar] [CrossRef]
- Xu, H.; Cui, Z.; Qu, J.; Huang, W. Propagation properties of partially coherent higher-order cosh-Gaussian beam in non-Kolmogorov turbulence. Opt. Laser Technol. 2013, 50, 78–86. [Google Scholar] [CrossRef]
- Dan, Y.; Ai, Y.; Xu, Y. Propagation properties and turbulence distance of partially coherent Sinh-Gaussian beams in non-Kolmogorov atmospheric turbulence. Optik 2016, 127, 9320–9327. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, H.; Dan, Y.; Feng, H.; Wang, S. Beam wander and M2-factor of partially coherent electromagnetic hollow Gaussian beam propagating through non-Kolmogorov turbulence. J. Mod. Opt. 2015, 64, 844–854. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, Y.; Wang, X.; Dan, Y. Propagation factor and beam wander of electromagnetic Gaussian Schell-model array beams in non-Kolmogorov turbulence. OSA Contin. 2019, 2, 162–174. [Google Scholar] [CrossRef]
- Zhou, Y.; Yuan, Y.; Qu, J.; Huang, W. Propagation properties of Laguerre-Gaussian correlated Schell-model beam in non-Kolmogorov turbulence. Opt. Express 2016, 24, 10682–10693. [Google Scholar] [CrossRef]
- Liu, H.; Xia, J.; Hu, Z.; Lü, Y. Average intensity and propagation factors of the rectangular Laguerre–Gaussian correlated Schell-model beam propagating through non-Kolmogorov turbulence. J. Opt. 2018, 20, 105602. [Google Scholar] [CrossRef]
- Zhou, Z.-L.; Qu, J. Self-splitting and propagation factors of a superimposed Hermite-Gaussian correlated Schell-model beam in turbulent atmosphere. Results Phys. 2021, 28, 104609. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
- Chu, X. Evolution of an Airy beam in turbulence. Opt. Lett. 2011, 36, 2701–2703. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Chu, X. Beam wander of an Airy beam with a spiral phase. J. Opt. Soc. Am. A 2014, 31, 685–690. [Google Scholar] [CrossRef]
- Wen, W.; Chu, X. Beam wander of partially coherent Airy beams. J. Mod. Opt. 2014, 61, 379–384. [Google Scholar] [CrossRef]
- Wen, W.; Chu, X.; Cai, Y. Dependence of the beam wander of an airy beam on its kurtosis parameter in a turbulent atmosphere. Opt. Laser Technol. 2015, 68, 6–10. [Google Scholar] [CrossRef]
- Wen, W.; Jin, Y.; Hu, M.; Liu, X.; Cai, Y.; Zou, C.; Luo, M.; Zhou, L.; Chu, X. Beam wander of coherent and partially coherent Airy beam arrays in a turbulent atmosphere. Opt. Commun. 2018, 415, 48–55. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, L.; Zhang, Y. Spiral spectrum of Airy–Schell beams through non-Kolmogorov turbulence. Chin. Opt. Lett. 2016, 14, 042101. [Google Scholar] [CrossRef]
- Chen, R.-P.; Ying, C.-F. Beam propagation factor of an Airy beam. J. Opt. 2011, 13, 085704. [Google Scholar] [CrossRef]
- Dan, Y.; Zhang, B. Second moments of partially coherent beams in atmospheric turbulence. Opt. Lett. 2009, 34, 563–565. [Google Scholar] [CrossRef] [PubMed]
- Wen, W.; Mi, X.; Xiang, S. Quality factor of partially coherent Airy beams in a turbulent atmosphere. J. Opt. Soc. Am. A 2021, 38, 1612–1618. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, W.; Mi, X.; Chen, S. Beam Quality Factor of Partially Coherent Airy Beam in Non-Kolmogorov Turbulence. Atmosphere 2022, 13, 2061. https://doi.org/10.3390/atmos13122061
Wen W, Mi X, Chen S. Beam Quality Factor of Partially Coherent Airy Beam in Non-Kolmogorov Turbulence. Atmosphere. 2022; 13(12):2061. https://doi.org/10.3390/atmos13122061
Chicago/Turabian StyleWen, Wei, Xianwu Mi, and Sirui Chen. 2022. "Beam Quality Factor of Partially Coherent Airy Beam in Non-Kolmogorov Turbulence" Atmosphere 13, no. 12: 2061. https://doi.org/10.3390/atmos13122061
APA StyleWen, W., Mi, X., & Chen, S. (2022). Beam Quality Factor of Partially Coherent Airy Beam in Non-Kolmogorov Turbulence. Atmosphere, 13(12), 2061. https://doi.org/10.3390/atmos13122061




