A Comparison Study of Observed and the CMIP5 Modelled Precipitation over Iraq 1941–2005
Abstract
1. Introduction
2. Materials and Methods
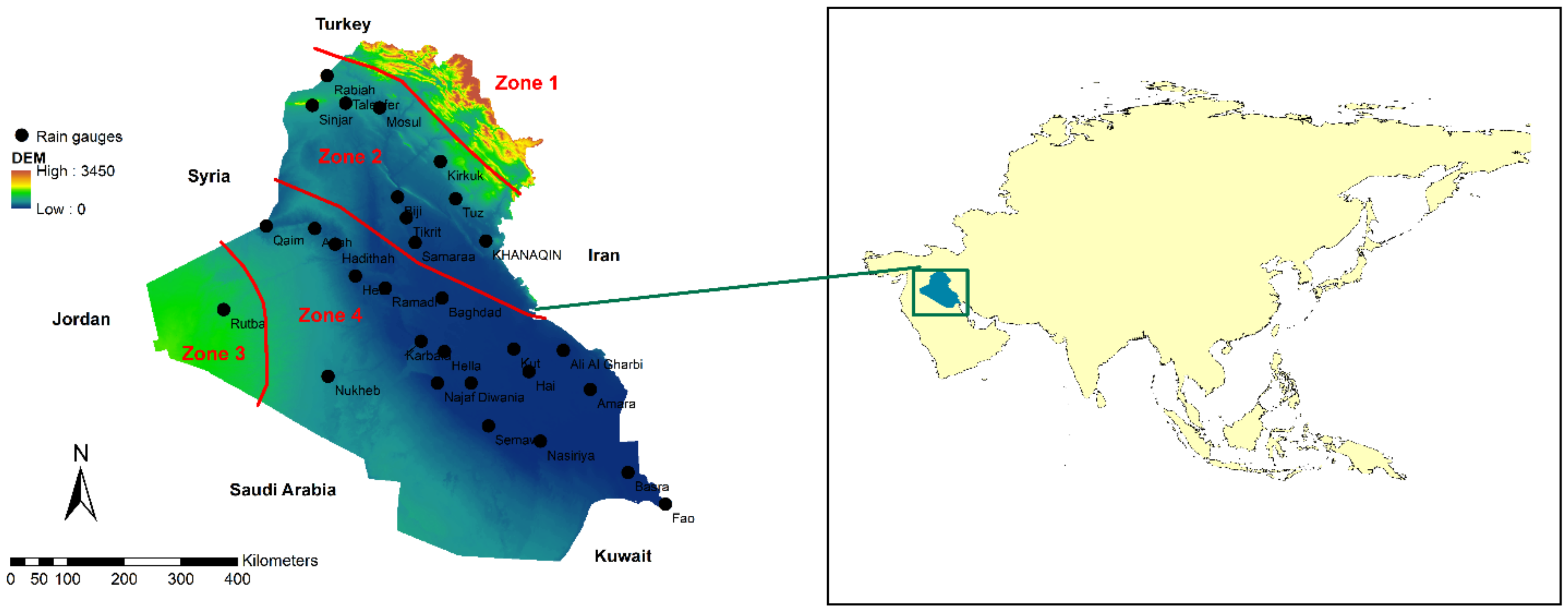
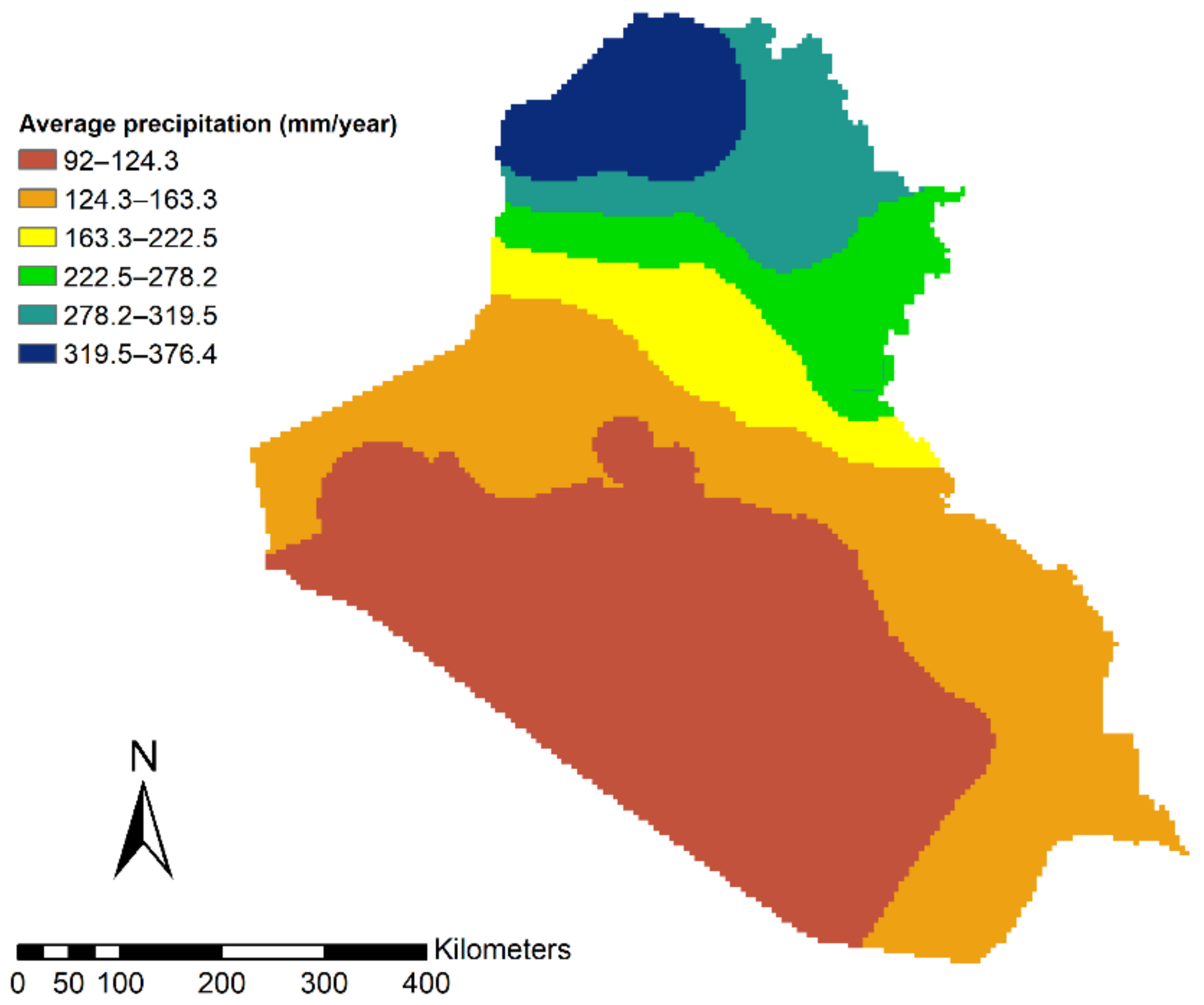
2.1. Study Area
- (1)
- Semi-arid and arid zones with a Mediterranean climate (zone 1 in Figure 1): The annual precipitation varies between 700 and 1000 mm and occurs between October and April. The country has cold and rainy winters, while summers are hot and dry; they are even torrid up to quite high altitudes. This zone mainly covers the north of the country. This is the only region in Iraq that receives a considerable amount of precipitation.
- (2)
- Steppes with winter rainfall of 200–400 mm annually (zone 2 in Figure 1): Summers are extremely hot, and winters are cold. In the cold season of the year, some depressions can pass that carry moderate precipitation.
- (3)
- The desert zone/northwest of Mesopotamia (zone 3 in Figure 1) has a high temperature in summer and less than 200 mm of yearly rainfall.
- (4)
- The irrigated area which covers the region between the Euphrates and Tigris rivers (zone 4 in Figure 1). This region has a desert or semi-desert climate, with mild winters and extremely hot summers.
2.2. Precipitation Data
- (1)
- Long-term experiments (century and longer); and
- (2)
- Near-term experiments (decadal prediction).
2.3. The Goodness-of-Fit Tests (GOFs)
- Mean error (ME), which can be calculated as follows:where is the observed rainfall at time t and is the simulated rainfall at time t.
- Mean absolute error (MAE):
- Root mean square error (RMSE), which can be calculated as:
- Correlation coefficient (r): This index measures the linear relationship between two time series with a range between −1 and 1, where −1 indicates a perfect negative correction, 0 no correlation at all and 1 a perfect positive correlation. It can be calculated as follows:
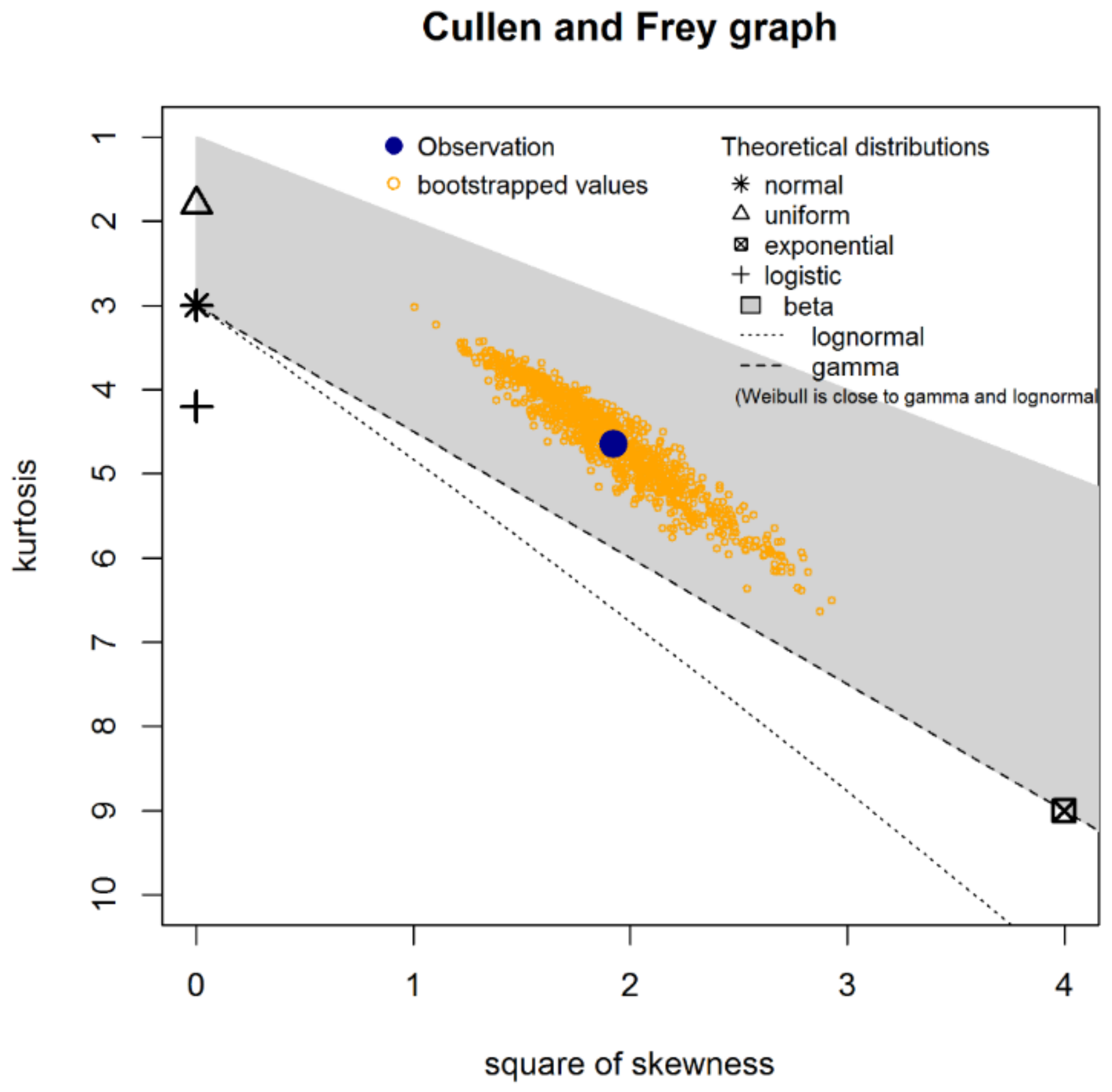
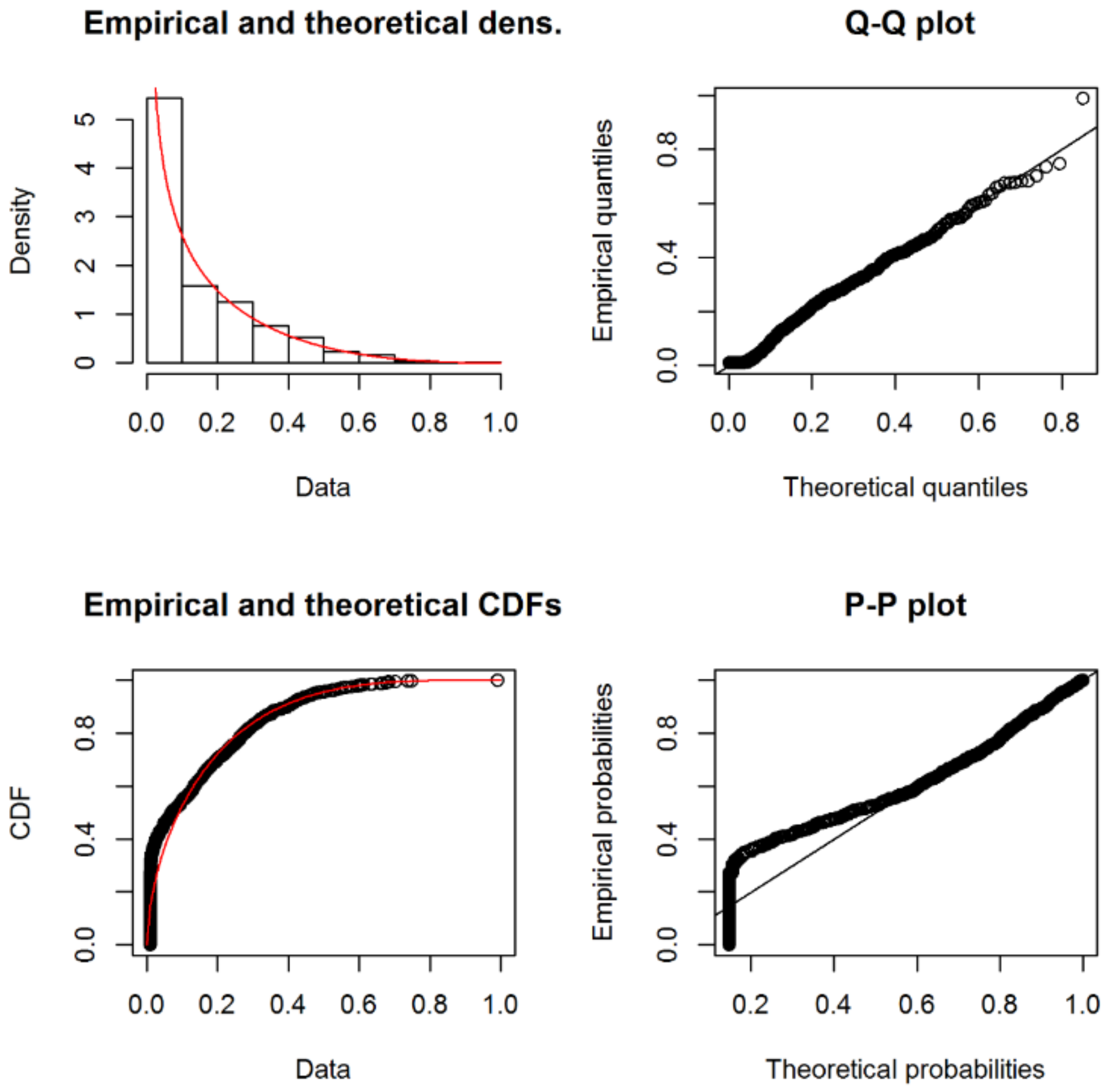
2.4. Fitting of Probability Distributions
- (1)
- To check if the two datasets are statistically consistent; and
- (2)
- To identify any changes in the probability distribution of simulated data for the future.
2.5. Bias Correction
2.6. Mann–Kendall Trend Test (MK)
- : is the number of data points;
- : is the number of tied groups for the month;
- : is the number of data in the group for the month.
3. Results
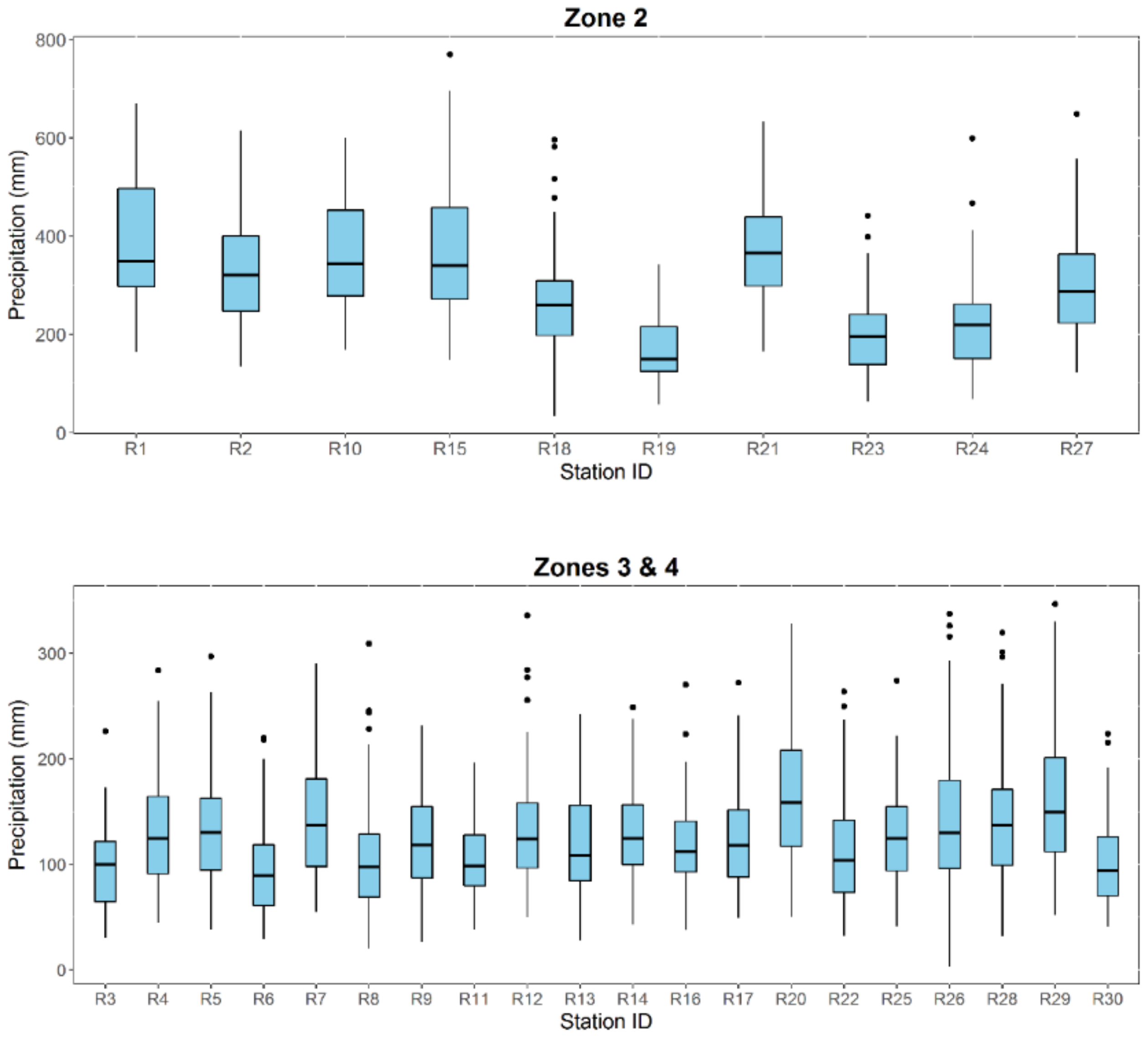
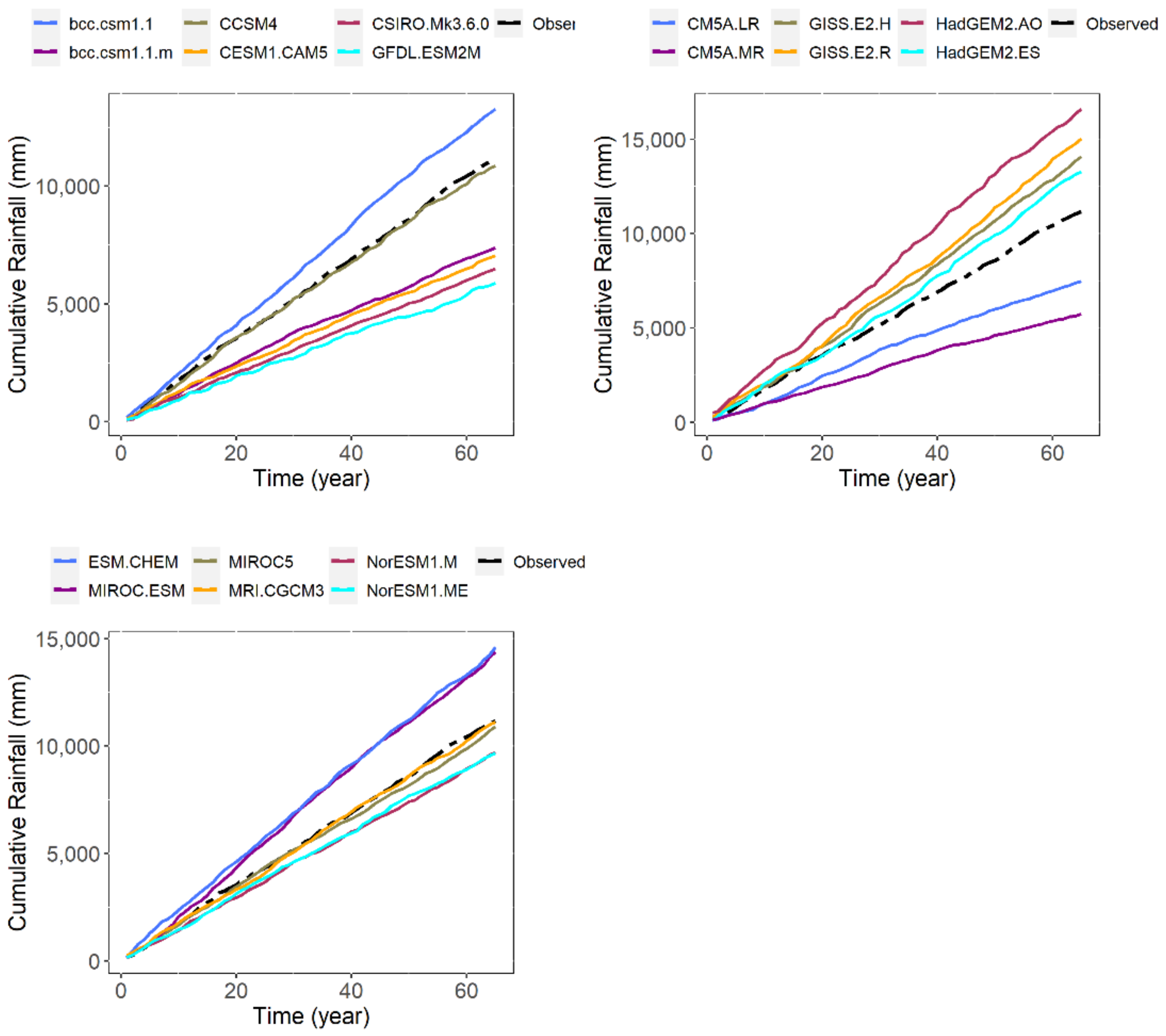
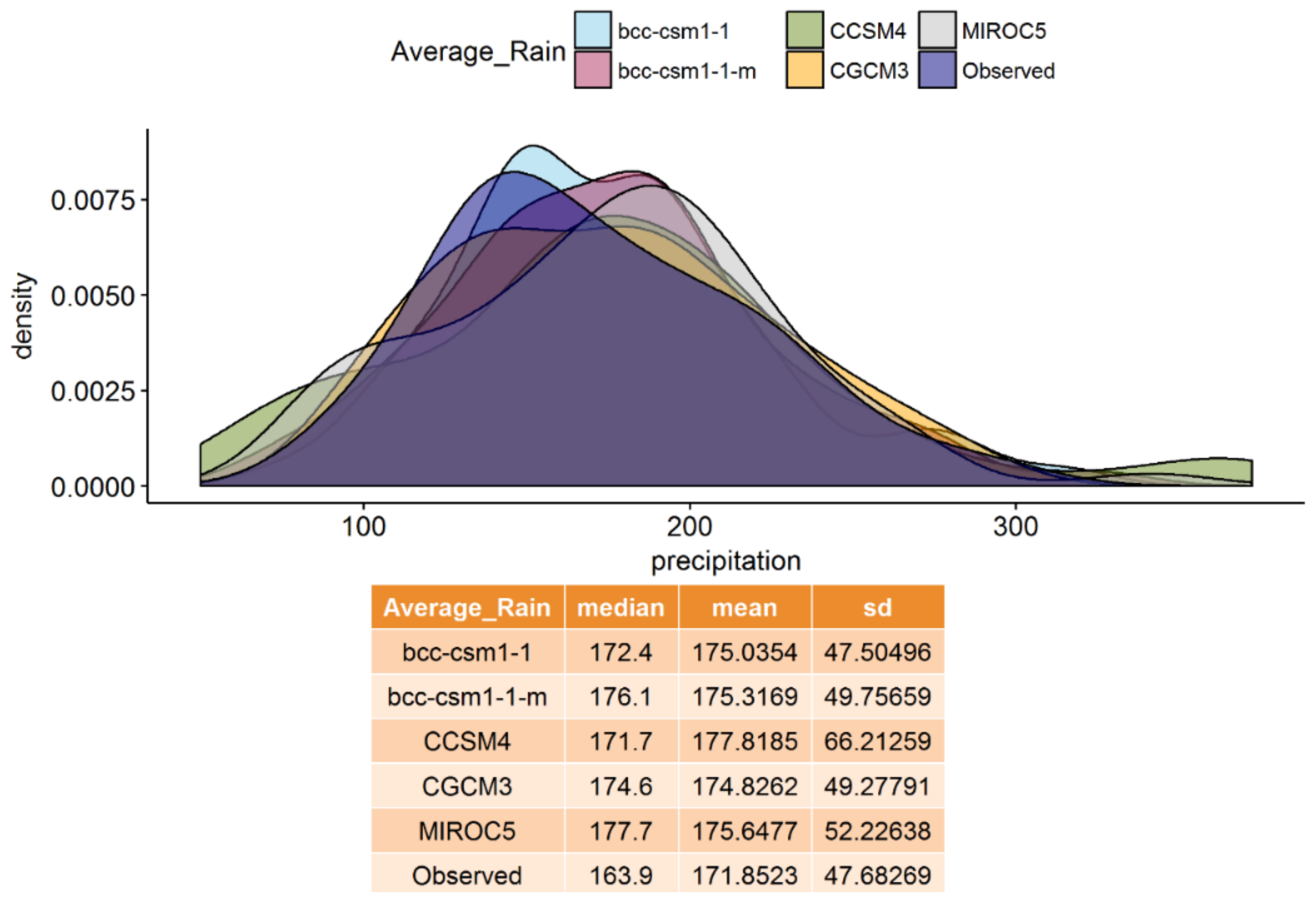
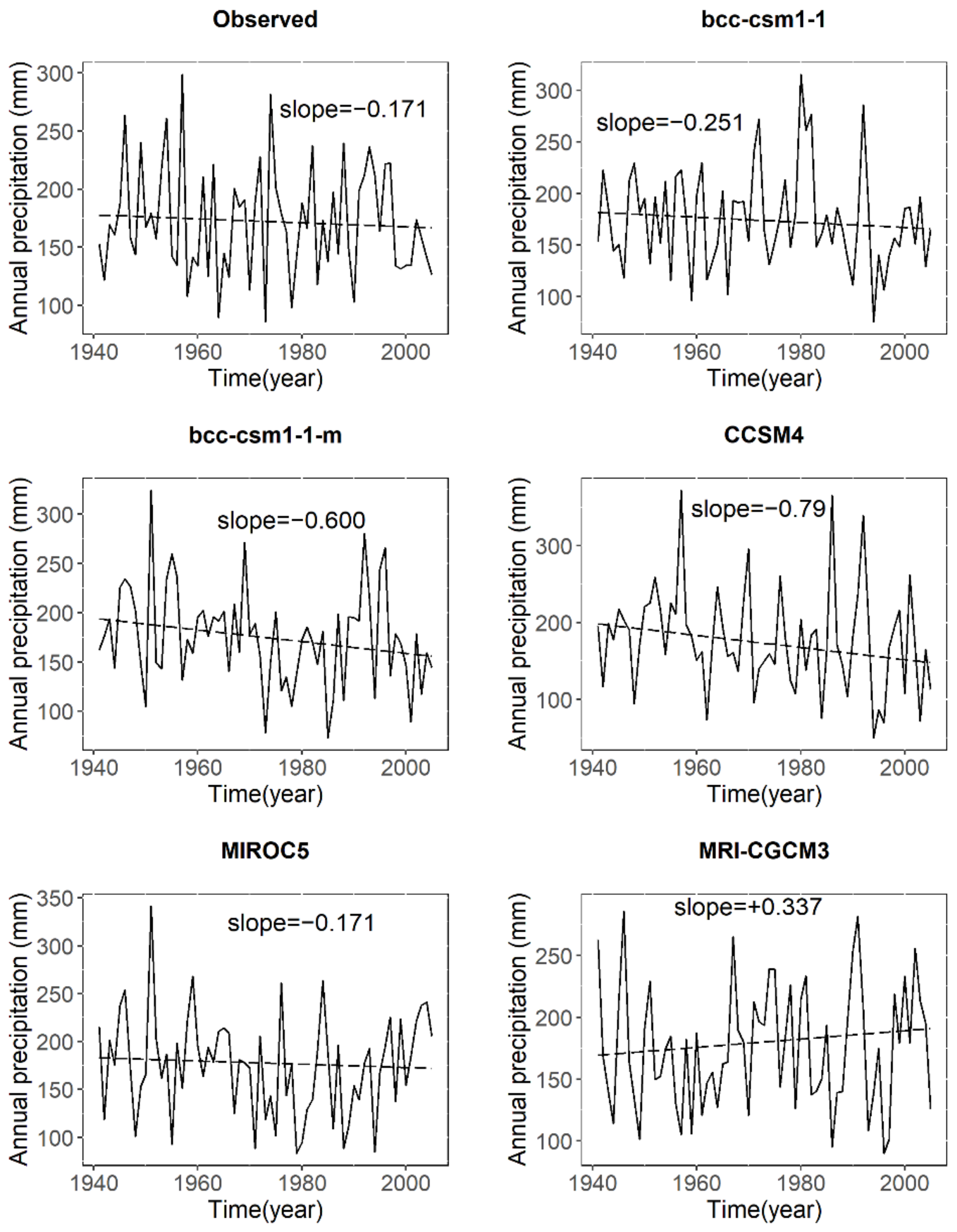
3.1. Statistical Comparison between Observed and Modelled Precipitation
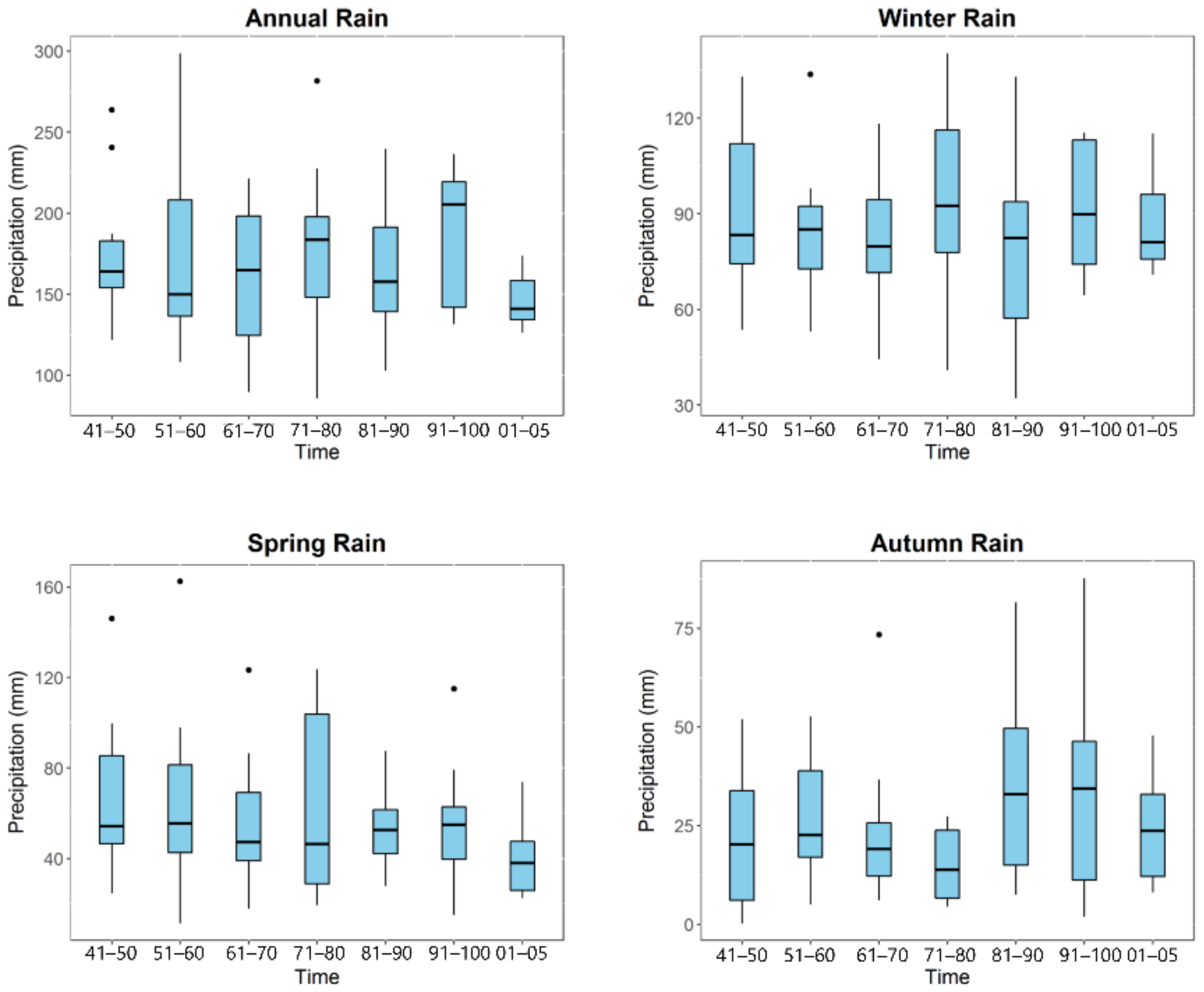
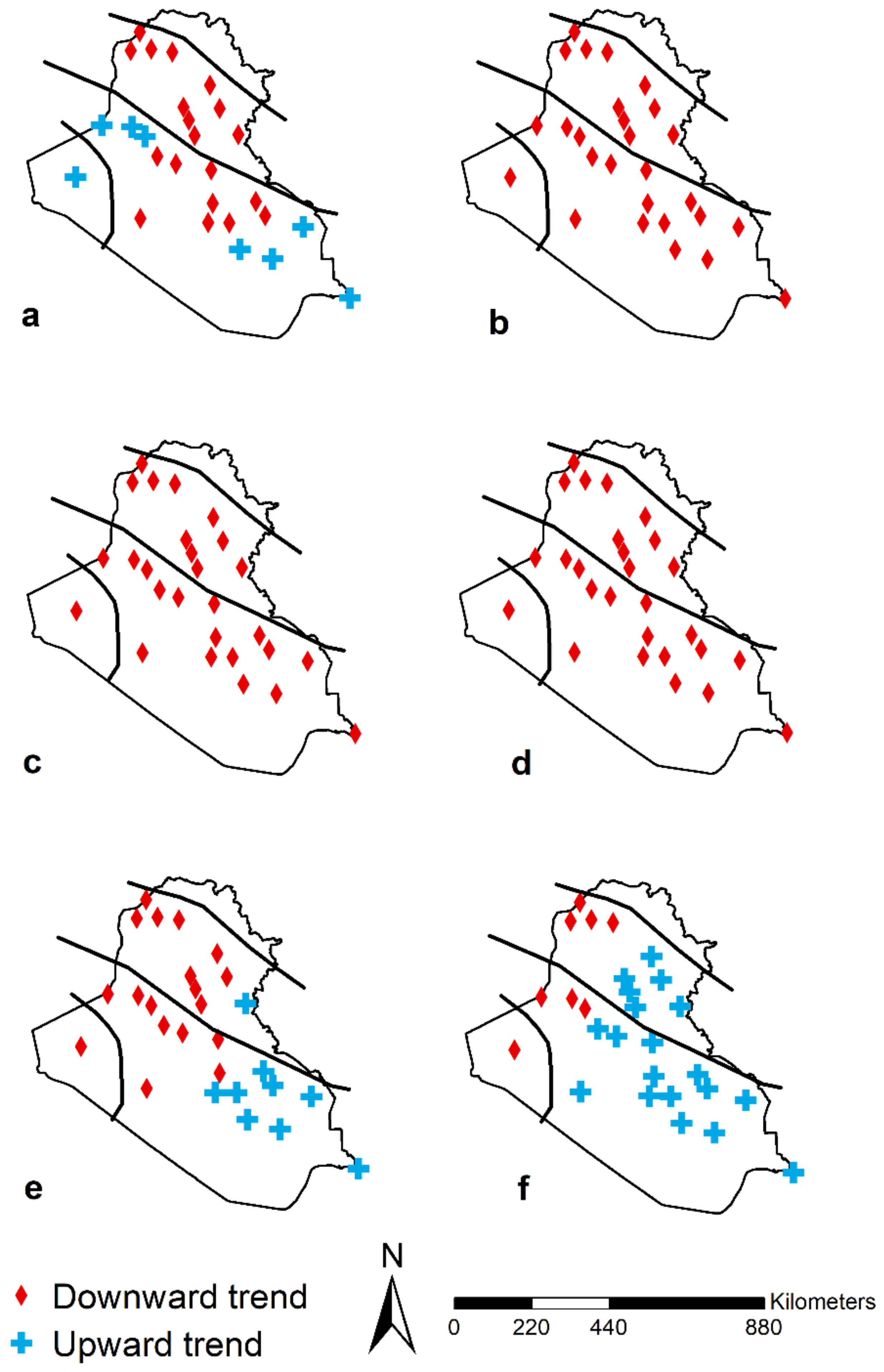
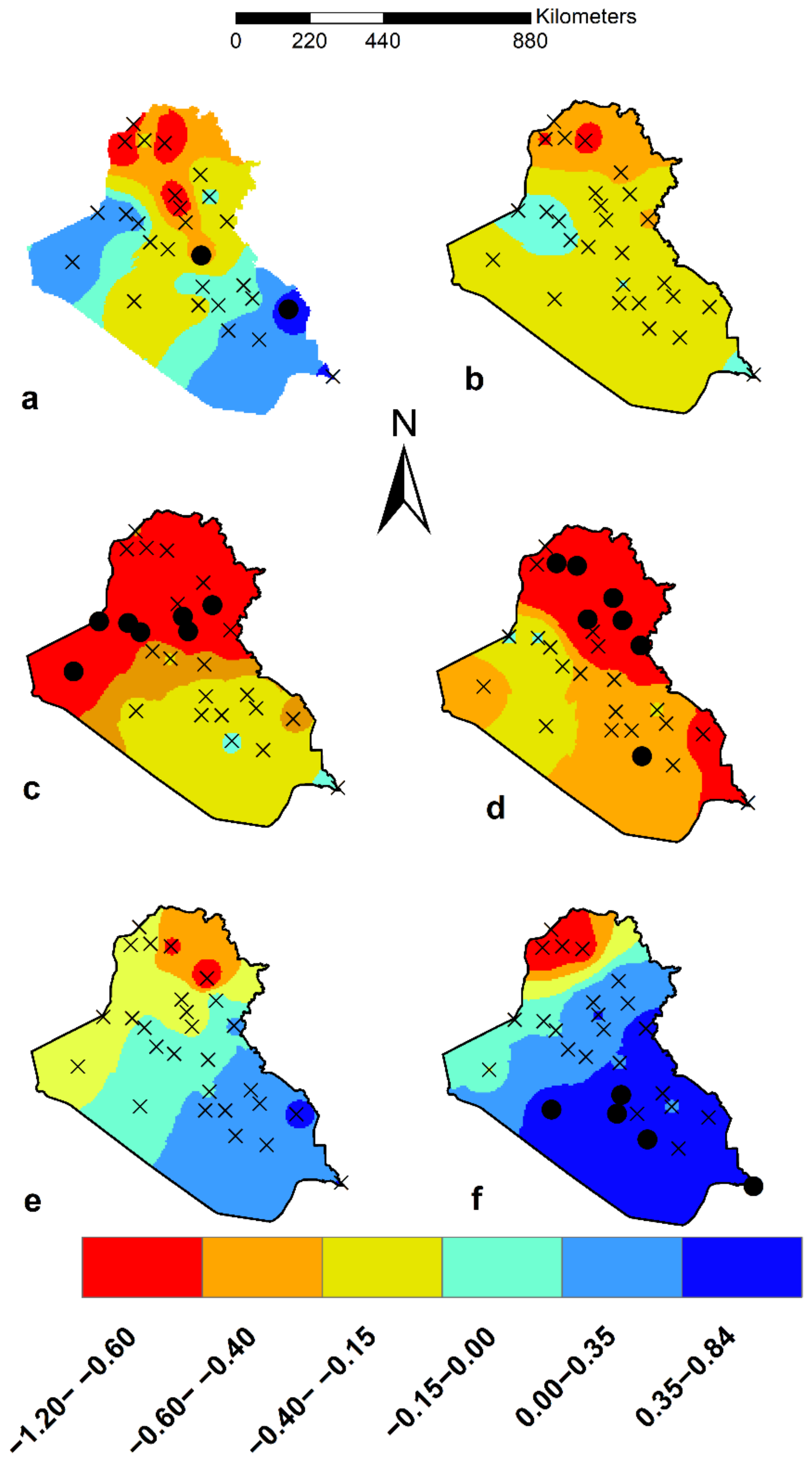
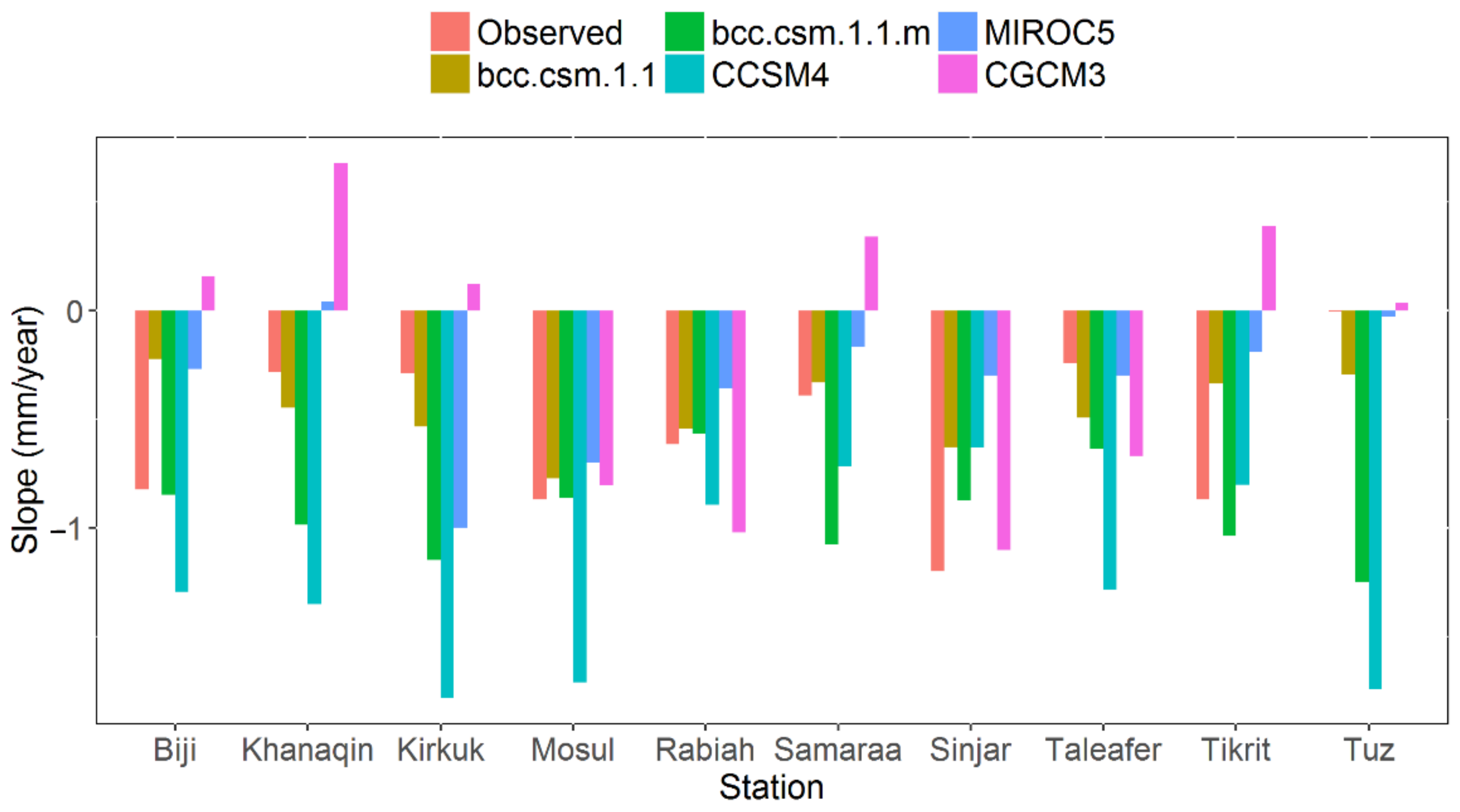
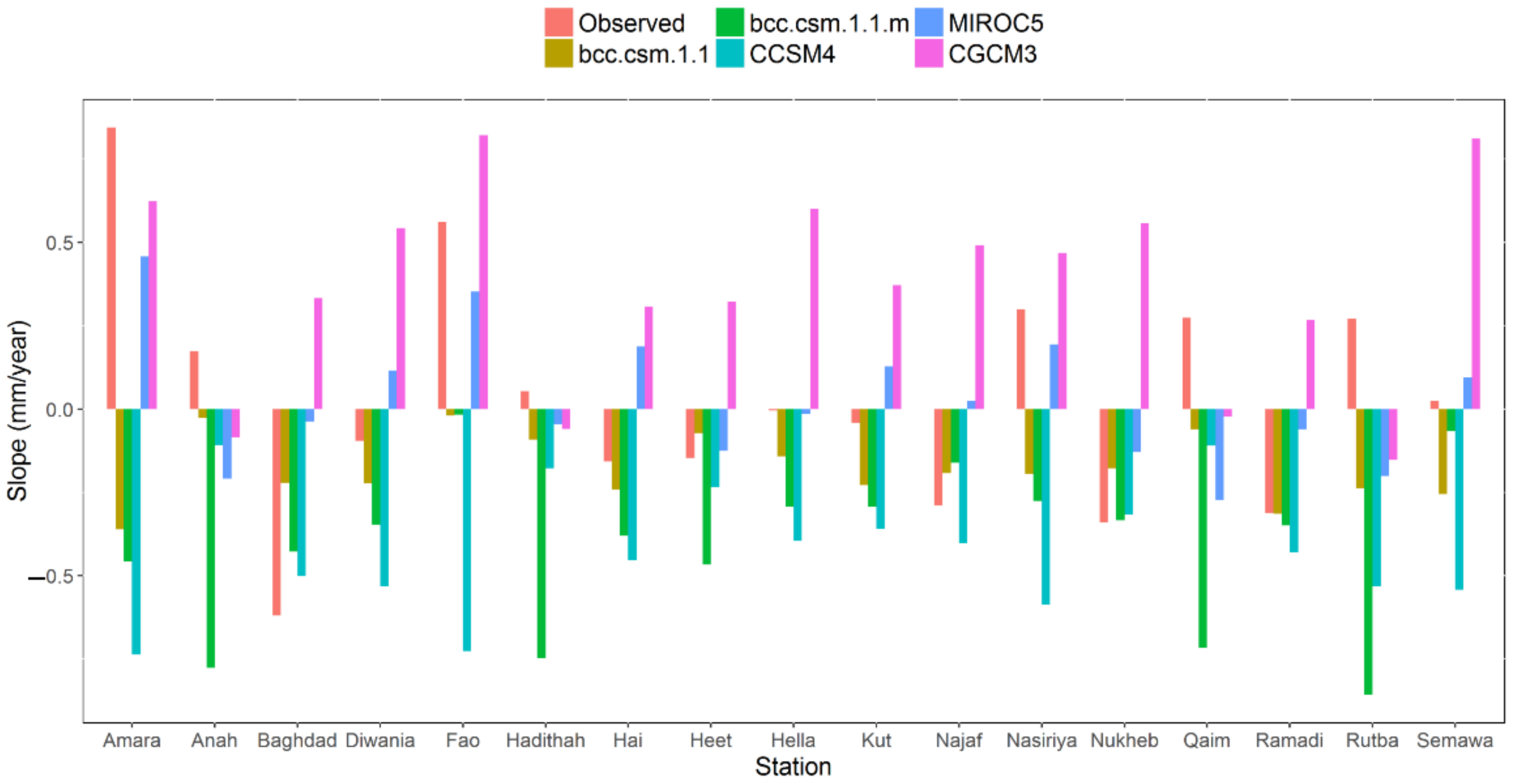
3.2. Trend Analysis of Precipitation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, P.; Jones, P.; Cao, L.; Yan, Z.; Zha, S.; Zhu, Y.; Yu, Y.; Tang, G. Trend of Surface Air Temperature in Eastern China and Associated Large-Scale Climate Variability over the Last 100 Years. J. Clim. 2014, 27, 4693–4703. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.; Riahi, K.; et al. The RCP Greenhouse Gas Concentrations and Their Extensions from 1765 to 2300. Clim. Change 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Jha, M.K. Hydrological Response Due to Projected Climate Variability in Haw River Watershed, North Carolina, USA. Hydrol. Sci. J. 2016, 61, 495–506. [Google Scholar] [CrossRef]
- Jin, X.; Sridhar, V. Impacts of Climate Change on Hydrology and Water Resources in the Boise and Spokane River Basins1. J. Am. Water Resour. Assoc. 2011, 48, 197–220. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Edwards, D.R. Long-term trend analysis of precipitation and air temperature for Kentucky, United States. Climate 2016, 4, 10. [Google Scholar] [CrossRef]
- Abdo, K.S.; Fiseha, B.M.; Rientjes, T.H.M.; Gieske, A.S.M.; Haile, A.T. Assessment of Climate Change Impacts on the Hydrology of Gilgel Abay Catchment in Lake Tana Basin, Ethiopia. Hydrol. Process. 2009, 23, 3661–3669. [Google Scholar] [CrossRef]
- New, M.; Todd, M.; Hulme, M.; Jones, P. Precipitation Measurements and Trends in the Twentieth Century. Int. J. Climatol. 2002, 21, 1889–1922. [Google Scholar] [CrossRef]
- Griggs, D.J.; Noguer, M. Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Weather 2006, 57, 267–269. [Google Scholar] [CrossRef]
- Xu, Z.; Takeuchi, K.; Ishidaira, H.; Li, J. Long-Term Trend Analysis for Precipitation in Asian Pacific FRIEND River Basins. Hydrol. Process. 2005, 19, 3517–3532. [Google Scholar] [CrossRef]
- Martinez, C.; Maleski, J.; Miller, M. Trends in Precipitation and Temperature in Florida, USA. J. Hydrol. 2012, 452, 259–281. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of Trend Detection Methods and Their Application to Detect Temperature Changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Tabari, H.; Somee, B.; Zadeh, M. Testing for Long-Term Trends in Climatic Variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Modarres, R.; Sarhadi, A. Rainfall Trends Analysis of Iran in the Last Half of the Twentieth Century. J. Geophys. Res. Atmos. 2009, 114, 1–9. [Google Scholar] [CrossRef]
- Palomino-Lemus, R.; Córdoba-Machado, S.; Gamiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. Summer precipitation projections over northwestern South America from CMIP5 models. Glob. Planet. Change 2015, 131, 11–23. [Google Scholar] [CrossRef]
- Sharmila, S.; Joseph, S.; Sahai, A.K.; Abhilash, S.; Chattopadhyay, R. Future projection of Indian summer monsoon variability under climate change scenario: An assessment from CMIP5 climate models. Glob. Planet. Change 2015, 124, 62–78. [Google Scholar] [CrossRef]
- Palizdan, N.; Falamarzi, Y.; Huang, Y.F.; Lee, T.S. Precipitation trend analysis using discrete wavelet transform at the Langat River Basin, Selangor, Malaysia. Stoch. Environ. Res. Risk Assess. 2017, 31, 853–877. [Google Scholar] [CrossRef]
- He, W.P.; Zhao, S.S.; Wu, Q.; Jiang, Y.D.; Wan, S. Simulating evaluation and projection of the climate zones over China by CMIP5 models. Clim. Dyn. 2019, 52, 2597–2612. [Google Scholar] [CrossRef]
- Dong, T.Y.; Dong, W.J.; Guo, Y.; Chou, J.M.; Yang, S.L.; Tian, D.; Yan, D.D. Future temperature changes over the critical Belt and Road region based on CMIP5 models. Adv. Clim. Change Res. 2018, 9, 57–65. [Google Scholar] [CrossRef]
- Lin, L.; Gettelman, A.; Xu, Y.; Wu, C.; Wang, Z.; Rosenbloom, N.; Bates, S.C.; Dong, W. CAM6 simulation of mean and extreme precipitation over Asia: Sensitivity to upgraded physical parameterizations and higher horizontal resolution. Geosci. Model Dev. 2019, 12, 3773–3793. [Google Scholar] [CrossRef]
- Tayler, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experimental design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Xu, W.; Zhou, T.; Wang, J.; Zhai, P.; Jones, P. Comparisons of time series of annual mean surface air temperature for China since the 1900s: Observations, model simulations, and extended reanalysis. Bull. Am. Meteorol. Soc. 2017, 98, 699–711. [Google Scholar] [CrossRef]
- Tian, D.; Guo, Y.; Dong, W. Future changes and uncertainties in temperature and precipitation over China based on CMIP5 models. Adv. Atmos. Sci. 2015, 32, 487–496. [Google Scholar] [CrossRef]
- Yang, S.; Feng, J.; Dong, W.; Chou, J. Analyses of extreme climate events over China based on CMIP5 historical and future simulations. Adv. Atmos. Sci. 2014, 31, 1209–1220. [Google Scholar] [CrossRef]
- Neumann, R.; Jung, G.; Laux, P.; Kunstmann, H. Climate trends of temperature, precipitation and river discharge in the Volta Basin of West Africa. Int. J. River Basin Manag. 2007, 5, 17–30. [Google Scholar] [CrossRef]
- Kunstmann, H.; Jung, G. Impact of regional climate change on water availability in the Volta basin of West Africa. IAHS Publ. 2005, 295, 75–85. [Google Scholar]
- Parry, M.L.; Canziani, O.; Palutikof, J.; Van der Linden, P.; Hanson, C. (Eds.) Climate Change 2007-Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Fourth Assessment Report of the IPCC (Vol. 4); Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Change, I.C. The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013; p. 1535. [Google Scholar]
- Deng, H.; Luo, Y.; Yao, Y.; Liu, C. Spring and summer precipitation changes from 1880 to 2011 and the future projections from CMIP5 models in the Yangtze River Basin, China. Quat. Int. 2013, 304, 95–106. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A.; Phillips, T.J. Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations. J. Geophys. Res. Atmos. 2014, 119, 1695–1707. [Google Scholar] [CrossRef]
- Nikiema, P.M.; Sylla, M.B.; Ogunjobi, K.; Kebe, I.; Gibba, P.; Giorgi, F. Multi-model CMIP5 and CORDEX simulations of historical summer temperature and precipitation variabilities over West Africa. Int. J. Climatol. 2017, 37, 2438–2450. [Google Scholar] [CrossRef]
- He, W.P.; Zhao, S.S. Assessment of the quality of NCEP-2 and CFSR reanalysis daily temperature in China based on long-range correlation. Clim. Dyn. 2018, 50, 493–505. [Google Scholar] [CrossRef]
- Yuan, N.; Ding, M.; Huang, Y.; Fu, Z.; Xoplaki, E.; Luterbacher, J. On the long-term climate memory in the surface air temperature records over Antarctica: A nonnegligible factor for trend evaluation. J. Clim. 2015, 28, 5922–5934. [Google Scholar] [CrossRef]
- FAO. Towards Sustainable Agricultural Development in Iraq. The Transition from Relief, Rehabilitation and Reconstruction to Development; Food Agricultural Organization: Rome, Italy, 2003. [Google Scholar]
- Ajaaj, A.A.; Mishra, A.K.; Khan, A.A. Comparison of BIAS Correction Techniques for GPCC Rainfall Data in Semi-Arid Climate. Stoch. Environ. Res. Risk Assess. 2016, 30, 1659–1675. [Google Scholar] [CrossRef]
- Cullen, A.C.; Frey, H.C. Probabilistic Techniques in Exposure Assessment: A Handbook for Dealing with Variability and Uncertainty in Models and Inputs; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R Package for Fitting Distributions. J. Stat. Softw. 2014, 64, 1–34. [Google Scholar]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Eden, J.; Widmann, M.; Grawe, D.; Rast, S. Skill, Correction, and Downscaling of GCM-Simulated Precipitation. J. Clim. 2012, 25, 3970–3984. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation Downscaling under Climate Change: Recent Developments to Bridge the Gap between Dynamical Models and the End User. Rev. Geophys. 2010, 48, 1–34. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis, 3; Confidence Regions for the Parameters of Polynomial Regression Equations; (SP 5a/50/R); Stichting Mathematisch Centrum, Statistische Afdeling: Amsterdam, The Netherlands, 1950; pp. 1–16. [Google Scholar]
- Marchetto, A. rkt: Mann–Kendall Test, Seasonal and Regional Kendall Tests; R Core Team: Vienna, Austria, 2021; p. 10. [Google Scholar]
| Station | Station ID | Lat. | Lon. | Altitude (m) | Station | Station ID | Lat. | Lon. | Altitude (m) |
|---|---|---|---|---|---|---|---|---|---|
| Sinjar | R1 | 36.32° | 41.83° | 583 | Diwaniya | R16 | 31.95° | 44.95° | 20 |
| Telaefer | R2 | 36.37° | 42.48° | 373 | Ramadi | R17 | 33.45° | 43.32° | 48 |
| Najaf | R3 | 31.95° | 44.32° | 53 | Tuz | R18 | 34.88° | 44.65° | 220 |
| Qaim | R4 | 34.38° | 41.02° | 178 | Samaraa | R19 | 34.18° | 43.88° | 75 |
| Anah | R5 | 34.37° | 41.95° | 175 | Amara | R20 | 31.83° | 47.17° | 9 |
| Nukheb | R6 | 32.03° | 42.28° | 305 | Mosul | R21 | 36.31° | 43.15° | 223 |
| Hai | R7 | 32.13° | 46.03° | 17 | Rutba | R22 | 33.03° | 40.28° | 222 |
| Semawa | R8 | 31.27° | 45.27° | 11 | Tikrit | R23 | 34.57° | 43.70° | 107 |
| Heet | R9 | 33.63° | 42.75° | 58 | Biji | R24 | 34.90° | 43.53° | 116 |
| Rabiah | R10 | 36.80° | 42.10° | 382 | Haditha | R25 | 34.13° | 42.35° | 108 |
| Hella | R11 | 32.45° | 44.45° | 27 | Fao | R26 | 29.98° | 48.50° | 1 |
| Baghdad | R12 | 33.30° | 44.40° | 32 | Khanaqin | R27 | 34.21° | 45.23° | 202 |
| Nasiriya | R13 | 31.02° | 46.23° | 5 | Basra | R28 | 30.50° | 47.83° | 2 |
| Kut | R14 | 32.49° | 45.75° | 21 | Ali AlGharbi | R29 | 32.46° | 46.68° | 13 |
| Kirkuk | R15 | 35.47° | 44.35° | 331 | Karbalaa | R30 | 32.61° | 44.01° | 29 |
| Model | Institution | Spatial Resolution (Lat. × Long.) |
|---|---|---|
| MRI-CGCM3 | Meteorological Research Institute, Japan (MRI) | 1.125° × 1.125° |
| MIROC5 | National Institute for Environmental Studies and Japan Agency for Marine-Earth Science and Technology (MIROC) | 1.4° × 1.4° |
| MIROC-ESM | 1.7° × 2.8° | |
| MIROC-ESM-CHEN | 1.7° × 2.8° | |
| CCSM4 | National Center for Atmospheric Research, USA (NCAR) | 0.94° × 1.25° |
| BCC-CSM1.1 | Beijing Climate Centre, China Meteorological Administration (BCC) | 2.7° × 2.8° |
| BCC-CSM1.1-m | 2.7° × 2.8° | |
| CSIRO-Mk3-6-0 | Commonwealth Scientific and Industrial Research Organization (CSIRO), Australia (CSIRO-QCCCE) | 1.86° × 1.87° |
| IPSL-CM5A-LR | Institute Pierre-Simon Laplace, France (IPSL) | 1.89° × 3.75° |
| IPSL-CM5A-MR | 1.26° × 2.5° | |
| HadGEM2-ES | Met Office Hadley Centre, UK (MOHC) | 1.25° × 1.875° |
| HadGEM2-AO | 1.25° × 1.875° | |
| GISS-E2-H | National Aeronautics and Space Administration Goddard Institute for Space Studies (NASA-GISS) | 2° × 2.5° |
| GISS-E2-R | 2° × 2.5° | |
| NorESM1-M | Norwegian Climate Centre (NCC) | 1.9° × 2.5° |
| NorESM1-ME | 1.9° × 2.5° | |
| GFDL-ESM2G | NOAA Geophysical Fluid Dynamics Laboratory, USA (NOAA-GFDL) | 2.5° × 2° |
| GFDL-ESM2M | 2.5° × 2° |
| Model | Fit Theoretical Distribution | MAE | R | ME | RMSE |
|---|---|---|---|---|---|
| bcc-csm1-1 | Beta | 12.8 | 0.38 | −2.7 | 19.36 |
| bcc-csm1-1-m | Beta | 9.98 | 0.48 | 4.86 | 16.54 |
| CCSM4 | Beta | 12.19 | 0.34 | 0.39 | 18.69 |
| CESM1-CAM5 | ---- | 12.02 | 0.25 | 5.28 | 18.89 |
| CSIRO-Mk3-6-0 | ---- | 10.34 | 0.41 | 6.01 | 17.41 |
| GFDL-ESM2M | ---- | 12.97 | 0.17 | 6.77 | 20.65 |
| GISS-E2-H | ---- | 13.49 | 0.38 | −3.75 | 19.75 |
| GISS-E2-R | Beta | 14.82 | 0.28 | −4.95 | 22.2 |
| HadGEM2-AO | ---- | 14.46 | 0.41 | −6.97 | 25.11 |
| HadGEM2-ES | ---- | 12.41 | 0.4 | −2.71 | 20.74 |
| IPSL-CM5A-LR | ---- | 10.82 | 0.39 | 4.75 | 18.27 |
| IPSL-CM5A-MR | ---- | 10.76 | 0.41 | 6.96 | 17.96 |
| MIROC5 | Beta | 11.49 | 0.42 | 0.35 | 16.96 |
| MIROC-ESM | Beta | 14.59 | 0.3 | −4.11 | 20.44 |
| MIROC-ESM-CHEM | Beta | 14.25 | 0.37 | −4.41 | 20.19 |
| MRI-CGCM3 | Beta | 12.35 | 0.33 | 0.07 | 18.8 |
| NorESM1-M | ---- | 12.03 | 0.3 | 1.87 | 18.39 |
| NorESM1-ME | ---- | 12.03 | 0.3 | 1.92 | 18.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, S.A.; Xuan, Y.; Al-Rammahi, A.H.; Addab, H.F. A Comparison Study of Observed and the CMIP5 Modelled Precipitation over Iraq 1941–2005. Atmosphere 2022, 13, 1869. https://doi.org/10.3390/atmos13111869
Abbas SA, Xuan Y, Al-Rammahi AH, Addab HF. A Comparison Study of Observed and the CMIP5 Modelled Precipitation over Iraq 1941–2005. Atmosphere. 2022; 13(11):1869. https://doi.org/10.3390/atmos13111869
Chicago/Turabian StyleAbbas, Salam A., Yunqing Xuan, Ali H. Al-Rammahi, and Haider F. Addab. 2022. "A Comparison Study of Observed and the CMIP5 Modelled Precipitation over Iraq 1941–2005" Atmosphere 13, no. 11: 1869. https://doi.org/10.3390/atmos13111869
APA StyleAbbas, S. A., Xuan, Y., Al-Rammahi, A. H., & Addab, H. F. (2022). A Comparison Study of Observed and the CMIP5 Modelled Precipitation over Iraq 1941–2005. Atmosphere, 13(11), 1869. https://doi.org/10.3390/atmos13111869








