Abstract
The effects of different modeling and solving approaches on the simulation of a steam ejector have been investigated with the computational fluid dynamics (CFD) technique. The four most frequently used and recommended turbulence models (standard k-ε, RNG k-ε, realizable k-ε and SST k-ω), two near-wall treatments (standard wall function and enhanced wall treatment), two solvers (pressure- and density-based solvers) and two spatial discretization schemes ( the second-order upwind scheme and the quadratic upstream interpolation for convective kinematics (QUICK) of the convection term have been tested and compared for a supersonic steam ejector under the same conditions as experimental data. In total, more than 185 cases of 17 different modeling and solving approaches have been carried out in this work. The simulation results from the pressure-based solver (PBS) are slightly closer to the experimental data than those from the density-based solver (DBS) and are thus utilized in the subsequent simulations. When a high-density mesh with y+ < 1 is used, the SST k-ω model can obtain the best predictions of the maximum entrainment ratio (ER) and an adequate prediction of the critical back pressure (CBP), while the realizable k-ε model with the enhanced wall treatment can obtain the best prediction of the CBP and an adequate prediction of the ER. When the standard wall function is used with the three k-ε models, the realizable k-ε model can obtain the best predictions of the maximum ER, and the three k-ε models can gain the same CBP value. For a steam ejector with recirculation inside the diffuser, the realizable k-ε model or the enhanced wall treatment is recommended for adoption in the modeling approach. When the spatial discretization scheme of the convection term changes from a second-order upwind scheme to a QUICK scheme, the effect can be ignored for the maximum ER calculation, while only the CBP value from the standard k-ε model with the standard wall function is reduced by 2.13%. The calculation deviation of the ER between the two schemes increases with the back pressure at the unchoked flow region, especially when the standard k-ε model is adopted. The realizable k-ε model with the two wall treatments and the SST k-ω model is recommended, while the standard k-ε is more sensitive to the near-wall treatment and the spatial discretization scheme and is not recommended for an ejector simulation.
1. Introduction
The continuous increase in energy consumption and the decrease in natural resources require a more efficient use of energy. The worldwide increase in air conditioning applications is one of the main reasons for today’s electricity consumption patterns [1] and necessitates more efficient refrigeration systems. Steam ejector refrigeration systems (SERSs) utilizing low-grade thermal energy to drive environmentally friendly refrigerants can be an attractive technology for the efficient use of available energy (e.g., solar energy, geothermal energy, industrial waste heat) [2,3]. These systems have many advantages, such as reliability, limited maintenance needs and low initial and operational costs [4]. Nevertheless, SERSs have not been able to penetrate the market due to their low coefficient of performance (COP) and severe degradation in performance when not operating under idealized design conditions [5].
SERS performance depends greatly on the behavior of the ejector, the heart of the overall system [6]. Two important parameters used to describe ejector performance are the entrainment ratio (ER) and the critical back pressure (CBP). The former is defined as the mass flow ratio of the secondary flow (ms) to the primary flow (mp), and the latter indicates the final pressure with the ejector working at its maximum capability. A well-designed ejector with high efficiency (efficiency here refers to the ratio of the increase of exergy of secondary flow to the decrease of exergy of primary flow) can improve the overall system performance and consequently make SERSs economically more attractive [6].
Numerous theoretical and experimental studies have been carried out over the last decades to understand not only the fundamentals but also ejector operation behavior considering a wide range of various geometries and operation parameters, leading to better ejector design and optimization. The reader can refer to the review of Tashtoush et al. [7] for a recent overview of theoretical and experimental works on ejectors. Most theoretical studies have relied on semi-empirical or lumped parameter models [5]. Given the small dimensions of ejectors and the need for thermal insulation, experimental studies are frequently limited to global measurements: mass flow rates, temperature and pressure at the inlets and the outlet and the ejector wall [8,9,10]. Only a few experimental works have focused on the shock wave structure using local methods with air as the working fluid [11,12,13,14]. However, both theoretical and experimental methods remain unable to comprehensively reproduce or describe the various flow phenomena (shock waves, mixing process, boundary layer, phase change, compressibility, supersonic flow, etc.) that take place inside an ejector [15,16].
For many years, the computational fluid dynamics (CFD) technique has proven to be the most reliable and efficient tool for flow analysis and ejector performance predictions. A number of CFD investigations have been carried out, and most of their modeling approaches can be characterized with common features such as the steady compressible flow hypothesis, the pressure inlet and outlet boundary with known operating pressures and temperatures, and the adiabatic ejector wall. However, there are differences in other numerical modeling and solving choices, e.g., turbulence models, near-wall region treatments, density- or pressure-based solvers, and spatial discretization schemes for the convective terms.
Bartosiewicz et al. [15] compared the performance of six RANS turbulence models, namely, the standard, realizable and RNG k–ε models (SKE, RKE and RNG, for short), the standard and SST k-ω models (SKW and SST, for short), and the Reynolds stress model (RSM), with a standard wall function when appropriate. For all equations, convective terms were discretized using a second-order upwind scheme. The RNG and SST models best predicted the shock phase, strength, and the mean line of pressure recovery. The validated model was used to reproduce different operation modes of a supersonic ejector [16].
Hemidi et al. [17] compared the SKE and SST models for supersonic air ejectors. The convection term was discretized with a second-order upwind scheme. Over the whole range of operating conditions, the overall deviation was below 10% for the SKE model, while the results for the SST model were in less agreement. In addition, Hemidi et al. [18], in the second part of their study, found that good predictions of the entrainment rate, even over a wide range of operating conditions, do not necessarily mean a good prediction of the local flow features.
Yang et al. [19] compared the operating curve of a 3D steam ejector simulated using the three k-ε models: the SKE, RKE and RNG models, with the standard wall function. The QUICK scheme was adopted for spatial discretization of the convection terms. A density-based implicit solver was used in the simulation. It was found that both ER and CBP were best predicted by the RKE model.
Ruangtrakoon et al. [20] investigated the effect of the primary nozzle geometries on the performance of an ejector. A density-based implicit solver was selected to solve the governing equations, and the convective terms were discretized with a second-order upwind scheme. The RKE model with the standard wall function and the SST model were chosen. The simulated results based on the SST model more closely corresponded to the experimental values than those based on the RKE model.
Gagan et al. [11] used the PIV technique for supersonic ejector flow visualization and compared it with numerical results obtained from the same six turbulence models used by Bartosiewicz et al. [15] with the standard wall function. The discretization scheme was set to a second-order upwind scheme. They recommended the SKE model.
Zhu and Jiang [14] investigated the entrainment performance and the shock wave structures in a 3D ejector. Four turbulence models were used: the SKE, RNG, RKE and SST models. The near-wall treatment for the three k-ε models used the standard wall function. The governing equations were solved using a pressure-based solver. A second-order upwind scheme was used to discretize the convective terms. The working fluid was N2 using the ideal gas relationship. The results showed that the RNG model agreed best with measurements for predictions of both the mass flow rate and shock wave structures.
Mazzelli et al. [21] investigated a rectangular cross-section ejector and compared four different turbulence models (SKE, RKE, SST, and stress-ω RSM model). A density-based solver was used for all calculations. The spatial discretization of both the conservation and turbulence equations was set to be a second-order upwind scheme. They found that the SST model performed the best, whereas ε-based models were more accurate at low motive pressures. The stress-ω RSM model showed predictions comparable to those of the SST model, but the model suffered from numerical stiffness and convergence issues that made its use inconvenient.
Croquer et al. [22,23] investigated an R134a ejector and compared the same four turbulence models used by Zhu and Jiang [14]. A pressure-based solver was used for all calculations. A second-order upwind scheme was used to discretize the convective terms of each equation except for the pressure equation. They concluded that the SST model showed the best performance.
Besagni et al. [24] compared seven turbulence models: Spalart-Allmaras and the six turbulence models used by Bartosiewicz et al. [15] and Gagan et al. [11]. The standard wall function, the non-equilibrium wall function and the enhanced wall treatment were used for the near-wall treatment sensitivity analysis. A density-based solver was applied. A second-order upwind scheme was used for the spatial discretization. It was found that the use of non-equilibrium wall function instead of standard wall function had little effect on the numerical results, and the differences between the standard wall function and the enhanced wall treatment were negligible in most cases. The SST model showed the best agreement for the ER evaluations and local flow phenomena.
Wang et al. [25] proposed an adaptive nozzle exit position ejector to enhance ejector performance by self-adjusting the position of the primary nozzle. The three k-ε models noted in Ref. [19] were used with a scalable wall function. A segregated implicit solver was adopted to solve the governing equations. A second-order upwind scheme was applied to discretize the convective terms. The maximum relative error of both the ER and CBP produced by the SKE model was closer to the experimental results than RKE or RNG in the cases tested.
Han et al. [26] studied the boundary layer separation inside the ejector, and four turbulence models used by Croquer et al. [22,23] and Zhu and Jiang [14] were tested and compared. A standard wall function and an enhanced wall treatment were applied to the near-wall treatment. The convection terms were discretized by a second-order upwind scheme. The SKE and RKE models with the enhanced wall treatment and the SST model were in good agreement with the experimental results. The average relative error of the RKE model with the enhanced wall treatment was the lowest.
However, all these works did not reach a consensus about the selection of numerical modeling approaches to investigate the flow and heat transfer in an ejector. Moreover, no particular attention was given to the influence of the solver or the numerical schemes on the predicted results [22]. In some cases, even if some experimental validations were performed, only the ER values were dealt with, and no local validations or the CBP was achieved. In fact, the modeling approaches showing good agreement with the ER value may not provide reasonable flow details or accurate CBP values.
Consequently, this work aims to determine the best modeling and solution approaches composed of appropriate turbulence models, near-wall treatments, solvers and spatial discretization schemes for steam ejector simulations by considering both global and local flow features. Four turbulence models (SKE, RKE, RNG and SST model, which are most frequently used and recommended), two near-wall treatments (standard wall function and enhanced wall treatment), two solvers (density- or pressure-based solvers) and two spatial discretization schemes (second-order upwind scheme and QUICK scheme) have been tested for a supersonic steam ejector and compared with the experimental data of the global quantities: the ER, and the CBP and the local quantities: wall static pressure [3].
2. Numerical Modeling
2.1. Geometry and Operating Conditions
A schematic view of an idealized process in a steam ejector is shown in Figure 1. A typical ejector mainly comprises four distinct parts: a primary nozzle, a mixing chamber, an ejector throat and a subsonic diffuser. High-pressure steam, known as the “primary fluid”, is expanded and accelerated by the primary nozzle and leaves the nozzle exit plane at a supersonic speed and a very low pressure. Subsequently, the secondary fluid at a lower pressure is entrained into the mixing chamber by the shear layer between the primary and secondary fluids and accelerated to sonic velocity. The two fluids are completely mixed at some location in the constant area duct (throat) and undergo a series of shock waves induced by the high pressure of the subsonic diffuser, resulting in a major compression effect and a sudden drop in velocity from supersonic to subsonic. The pressure is then further increased in the subsonic diffuser.
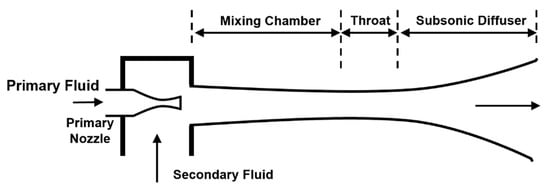
Figure 1.
Schematic of the idealized process in a steam ejector.
The geometry and operating conditions adopted in our simulation were based on the experimental setup developed by Sriveerakul et al. [3]. They experimentally tested nozzles and mixing chambers and throats with different structures to investigate the effect of geometry on ejector performance. As in the Yang et al. [19] study, nozzle No. 1, mixing chamber No. 1 and throat No. 3 were chosen, and the primary nozzle exit position was placed at 35 mm. The main geometrical characteristics of the ejector are listed in Table 1. The work conditions were a primary fluid saturated temperature Tp of 130 °C, a secondary fluid saturated temperature Ts of 10 °C and a back pressure Pb of 3–5.5 kPa.

Table 1.
Main geometrical parameters of the steam ejector.
2.2. Calculation Domain and Mesh Generation
Pianthong et al. [27] performed 3D numerical simulations for a supersonic steam ejector and found that there was no apparent 3D effect. An axisymmetric assumption for simplification is reasonable [28], and 2D axisymmetric calculations may be sufficient to investigate such flow configurations. The ejector structure used in this work is similar to that adopted in the Pianthong et al. [27] study; therefore, the model and mesh were created in a 2D domain with an axisymmetric solver.
Gambit version 2.4.6 was used to create the calculation domain and meshes of the model. The concentration of mesh density was focused on the areas where significant phenomena or high pressure/velocity gradients were expected, e.g., the mixing layer, boundary layer and structure transition. Six meshes were compared for a mesh independency study, and the final meshes were composed of approximately 59,840 and 192,375 quadrilateral elements for different simulation approaches (Table 2). The calculation domain and mesh system of the CFD model of the ejector are shown in Figure 2. The results of the mesh independence study are presented in Section 3.1.

Table 2.
Meshes for mesh independency.
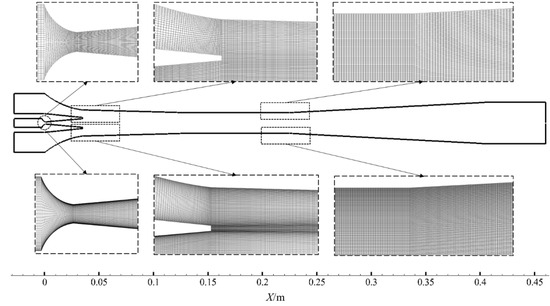
Figure 2.
Calculation domain and mesh details of the ejector: upper mesh for standard wall function (59,840 cells); lower mesh for enhanced wall treatment and SST turbulence model (192,375 cells).
2.3. Numerical Setting
2.3.1. Common Setting
The flow pattern inside a steam ejector is considered to be steady, compressible, and controlled by Reynolds averaging Navier-Stokes equations together with the continuity equation and energy equation. The equations are given as follows.
is the viscous dissipation and λ is the heat conductivity. The terms of and represent the Reynolds stresses and turbulent heat fluxes, respectively. These two terms need be modeled properly for a turbulent flow.
Pressure boundary conditions were applied on the inlets and outlet boundaries. Heat transfer through the walls was neglected due to the rapid mixing process. These are all common numerical settings used in ejector simulations. The CFD code ANSYS-Fluent 15.0 was employed in all the simulation works.
2.3.2. Solver
Selecting a solver is the first step in beginning a simulation, and many of the subsequent settings will correspond to the solver because each solver approach used to linearize and solve the discretized equations is different. In a density-based solver, the continuity equation is used to obtain the density field, while the pressure field is determined by the equation of state. On the other hand, in a pressure-based solver, the pressure field is extracted by solving the pressure or pressure correction equation obtained by manipulating the continuity and momentum equations. Both density- and pressure-based solvers are available in Fluent software. Historically, density-based solvers have been mainly used for high-speed compressible flows. However, both solvers have been recently extended and reformulated to solve for and operate under a wide range of flow conditions beyond their traditional or original intent [29]. Pressure-based solvers have demonstrated the capability to address highly compressible flows with shock waves in ejectors [14,22,23,30,31,32] and have usually provided more computational stability than density-based solvers. In this work, both solvers were used and compared. When the pressure-based solver was used in the simulation, the SIMPLE algorithm was employed to solve the pressure and velocity coupling.
2.3.3. Turbulence Model
Turbulence modeling is one of three key elements in CFD [33]. Very precise mathematical theories have evolved for the other two elements: grid generation and algorithm development, while far less precision has been achieved in turbulence modeling due to the complex behavior of turbulent flows. No single turbulence model is universally accepted as being suitable for all classes of problems. For the various flow phenomena (supersonic jet flow, shock wave, mixing layer, boundary layer under strong adverse pressure gradients, possible recirculation, etc.) that can occur inside an ejector, it is difficult to predict in advance which turbulence model is most suitable. It is usually necessary to judge the applicability and accuracy of a turbulence model by comparing it with the experimental data of global or local parameters.
Four turbulence models (SKE, RKE, RNG and SST models) have been frequently used to govern the turbulence characteristics and have been recommended by different authors [3,11,12,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] and adopted in this paper to test and compare their performances under different numerical settings. The four models belong to the Reynolds-averaged Navier-Stokes (RANS) turbulence models, and the Boussinesq hypothesis is used in each of them relating the Reynolds stresses to the mean velocity as,
where k is the turbulent kinetic energy and is the turbulent viscosity. Correspondingly, the turbulent heat fluxes can be modeled with the turbulent heat conductivity (λt) as given by,
where is the turbulence Prandtl number.
The Boussinesq hypothesis assumes that turbulent viscosity is an isotropic scalar quantity, which is not strictly true. However, the assumption works well for shear flows dominated by only one of the turbulent shear stresses covering many flows, such as wall boundary layers, mixing layers and jets. These flow phenomena can be found in the ejector flow; therefore, the four models are expected to be suitable for the turbulent flow simulation in an ejector.
The SKE model proposed by Launder and Spalding [34] was widely used in engneeing and developed many different variants. The SKE model is as follows.
where, the turbulent kinetic energy generation term is generated by average velocity gradient. The model constants have the default values , , , , .
The SKE model is a fully developed turbulence model for high Re flow. For the flow with low Re near the wall, the turbulence pulsation may be less than the influence of molecular viscosity. At this time, the use of SKE model may cause problems. Therefore, the calculation near the wall must be properly handled. The wall function method is usually used.
The SKE model can be well applied to most turbulent flow phenomena, but because it is assumed to be an isotropic scalar, it will produce some distortion when used in non-isotropic turbulence, such as strong swirl and curved wall flow. In view of this, many scholars have proposed corresponding correction schemes, such as RNG and RKE model.
Yakhot and Orzag [35] derived the RNG model from the instantaneous N-S equation by using the renormalization group theory. The model systematically removes the small-scale motion from the governing equation by reflecting the influence of small-scale motion in the large-scale motion and the modified viscosity term. The equations of RNG model are similar to that of the SKE model.
With , , , , .
Compared with the SKE model, the RNG model takes into account the time average strain rate of the mainstream, and takes into account the rotating and swirling flow by modifying the turbulent viscosity. Therefore, the model performs well in flows with high strain rate and large streamline bending. The RNG model is still a turbulence model established for fully developed high Re flow. The solution of near wall region also needs to be combined with wall function or other methods.
Shih et al. [36] thought that should not be a constant, but should be related to the strain rate in the flow field, so they proposed the RKE model. Its k equation is the same as that in the SKE model, but where is defined as,
with = 4.0, , , , , ,
The ε equation is also different from the SKE model.
with , , , , , .
Compared with the SKE model, the RKE model introduces the contents related to rotation and curvature in the calculation of turbulent viscosity, which can more accurately predict the expansion rate of flat and cylindrical jet. At the same time, it is easier to catch the boundary layer flow, flow separation and secondary flow with strong inverse pressure gradient than the SKE model. Therefore, the RKE model can more accurately calculate various flows including jet and mixed flow in free flow and boundary flow.
The shear stress transport model (SST) was developed by Menter [37] by efficiently integrating the robustness and accuracy of the standard k-ω model in the near wall region and the independence of k-ε model in the far field. SST model has a similar form to the standard k-ω model.
where the production of turbulence kinetic energy is different from in k-ε models.
Each of the constants is a blend of a k-ω (1) and k-ε model (2) constant, blended via:
where represents constant 1 and represents constant 2, F1 is blending function.
The SST model introduced an upper limit for the turbulent shear stress in boundary layers in order to avoid excessive shear-stress levels typically predicted with Boussinesq eddy-viscosity models. The eddy viscosity μt is defined as,
where S is the invariant measure of the strain rate and F2 is a second blending function. The SST model is considered to be more accurate and reliable for a wider class of flows (for example, adverse pressure gradient flows, airfoils, transonic shock waves) than the standard k-ω models.
These models are well known, and the reader can easily find related summaries of these turbulence models [34,35,36,37] and can refer to studies by Mazzelli et al. [21] or Croquer et al. [22], which include brief and complete summaries of the four turbulence models.
The three k-ε models were used as high-Reynolds turbulence models requiring a near-wall treatment, while the SST model was used as a low-Reynolds turbulence model requiring no near-wall treatment.
2.3.4. Near-Wall Treatment
An accurate representation of the flow in the near-wall region can determine successful predictions of wall-bounded turbulent flows. Traditionally, there are two approaches used to model the near-wall region: wall functions and near-wall models. Wall functions do not resolve the viscosity-affected inner region (viscous sublayer and buffer layer). Instead, semiempirical formulas are used to bridge the viscosity-affected near-wall region and the fully turbulent region. Near-wall models based on modifying the turbulence models enable the viscosity-affected region to be resolved with a mesh all the way to the wall, including the viscous sublayer. In the present study, two near-wall treatments, standard wall functions and enhanced wall treatments [29], were adopted and compared.
The standard wall function has been most widely used in steam ejector simulations and is defined in Equations (23) and (24):
where U+ and y+ are the dimensionless velocity and wall normal distance, κ is the von Kármán constant and E is the empirical constant (0.4187 and 9.793, respectively). When the standard wall function is used, the first near-wall node should be in the log-law layer for the best results, where 30 < y+ < 300, and Equation (24) is used; thus, less mesh is needed in the near-wall region. The first near-wall node should not be placed in the buffer layer, where 5 < y+ < 30.
U+ = y+; y+ < 5
In highly compressible flow, the temperature T+ distribution near the wall is obviously different from that in low subsonic flow due to the heating effect of viscous dissipation.
where is turbulent kinetic energy at the wall-adjacent cell centroid, is specific heat, is wall heat flux, is temperature at the wall-adjacent cell centroid, is temperature at the wall.
In the k-ε models, the k equation is solved in the whole domain including the wall-adjacent cells with at the wall, where n is the local coordinate normal to the wall. The ε at the wall-adjacent cells is computed on the basis of the local equilibrium hypothesis and computed from,
where is distance from the centroid of the wall-adjacent cell to the wall.
The enhanced wall treatment combines a two-layer model with enhanced wall functions and is identical to the two-layer model when the near-wall mesh is fine enough to be able to resolve the viscous sublayer (typically y+ ≅ 1). Hence, a much denser mesh is needed than the mesh for the standard wall function.
The SST model does not need a near-wall treatment because its mathematical structure already emphasizes the flow close to the wall. Conversely, the three k-ε models were applied with the two near-wall treatments. Therefore, in this study, a very fine mesh with y+ < 1 was used for the three k-ε models with the enhanced wall treatment and the SST model, while a medium mesh with 30 < y+ < 40 was used for the three k-ε models with the standard wall function. The enhanced wall treatment is actually equivalent to a two-layer model in this paper. Mesh sensitivity analysis was performed for the two near-wall treatments, respectively.
2.3.5. Fluid Property
Density was obtained using the ideal gas relationship, as widely used in References [3,14,38,39,40,41]. Other properties, such as specific heat, thermal conductivity and viscosity, were derived from real fluid thermodynamic properties of water vapor in IAPWS-IF97 by implementing a piecewise linear function of temperature into the Fluent code instead of assuming it to be constant, as in references [3,11,23,24,39].
2.3.6. Spatial Discretization Scheme
It is generally believed that as long as the spatial discretization scheme has second-order accuracy, false diffusion can be effectively suppressed; a sufficiently fine mesh can also obtain results with a certain accuracy with a lower order scheme, and at the same time, a higher order discretization scheme will consume more computing resources. Therefore, in the steam ejector simulation study, the second-order upwind scheme was mainly used, and less attention was given to whether the spatial discrete scheme has an impact and how dense the mesh needs to be so that it is not affected by the spatial discrete scheme. This work studied the influence of two different spatial discretization schemes on steam ejector simulation on the scale of commonly used meshes and sufficiently fine meshes to help select discrete schemes.
Two spatial discretization schemes, the second-order upwind scheme and the QUICK scheme, were adopted for the spatial discretization of the convection terms and the turbulence quantities. When the QUICK scheme was used, two nodes upstream and one node downstream were used for interpolation. Therefore, the QUICK scheme contains information on the flow direction and can reflect the transport characteristics. The QUICK scheme has third-order accuracy and is considered to be more precise. Consequently, the QUICK scheme requires more computing resources and introduces higher convergence difficulties. For the pressure equation, the PRESTO! scheme designed for flows involving steep pressure gradients was chosen.
2.3.7. Convergence Criteria
The calculation is considered to converge, and the iteration is finished when the following convergence criteria are met: (1) the residual terms are lower than 10−5 and stable; (2) the calculated mass flows of each face are stable, and the mass flow difference between the two inlet flows and the outlet flow of the ejector is less than 10−7 kg/s; and (3) the maximum velocity value at the ejector throat inlet is stable.
In total, 185 cases of 17 different modeling and solving approaches were examined in this work, as shown in Table 3.

Table 3.
Combinations of turbulence models and near-wall treatments(SKE, standard k-ε model; RNG, RNG k-ε model;RKE, realizable k-ε model; SST, SST k-ω model; SWF, standard wall function; EWT, enhanced wall treatment; 2ND, second-order upwind scheme; QUICK, quadratic upstream interpolation for convective kinematics; DBS, density-based solver; PBS, pressure-based solver).
3. Results
3.1. Mesh Sensitivity Analysis
Due to the different requirements of the near-wall treatments on the mesh, a mesh sensitivity analysis was performed. Six meshes of two sets were used to test and evaluate the mesh independence for the two near-wall treatments: Mesh01 (39,150 cells), Mesh02 (59,840 cells) and Mesh03 (72,060 cells) for the standard wall function, and Mesh04 (153,447 cells), Mesh05 (192,375 cells) and Mesh06 (394,300 cells) for the enhanced wall treatment and the SST model. The first three meshes were adjusted to place the first near-wall nodes of the nozzle wall in the region 30 < y+ < 40, while the first near-wall nodes of the ejector wall adjacent to the secondary fluid were adjusted to be in the region y+ < 1 because the secondary fluid was actually a low-Reynolds flow with a Reynolds number of approximately 1000 only, and the first near-wall nodes need to be several millimeters from the wall for y+ > 30, resulting in extremely sparse meshes. The first near-wall nodes of all walls of the latter three meshes were set in the region y+ < 1.
The former three meshes were tested under the RKE model with the standard wall function, while the latter three meshes were tested under the RKE model with the enhanced wall treatment. All six meshes were tested at a back pressure Pb = 3 kPa. The pressure-based solver was adopted to solve the governing equations with the QUICK scheme applied to discretize convective terms.
The Mach number (Ma) distributions of the central axis and the axial velocity (ut) at the throat inlet radius (Rt) were chosen to be compared for mesh independence, as shown in Figure 3. For the standard wall function, it can be seen that the trends of Ma, ut and ER of Mesh01, Mesh02 and Mesh03 are almost the same. For the enhanced wall treatment and the SST model, the trends of Ma, ut and ER of Mesh05 and Mesh06 are almost the same, while Mesh04 is slightly different. When the number of meshes is more than 39,150 and 153,447, Ma and ut and ER are approximated, and the fluctuation of the output parameters is the same. To reduce the computational costs and increase the calculation efficiency, the medium meshes Mesh02 (59,840 cells) and Mesh05 (192,375 cells) were selected (Figure 2). It is easy to see that these characteristic parameters were different with near-wall treatments. The reasons for this result will be discussed in Section 3.3.
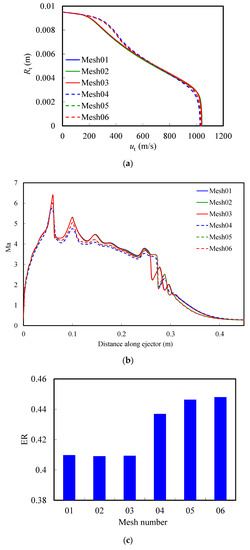
Figure 3.
Variation of characteristic parameters under different meshes: (a) Axial velocity distribution at the throat inlet, (b) Mach number distribution along the ejector centerline, (c) ER variation with mesh.
3.2. Influence of the Solver
The density-based solver (DBS) and pressure-based solver (PBS) were compared with the three k-ε models, while the spatial discretization scheme was unchanged as a second-order upwind scheme and near-wall treatment as a standard wall function, based on Mesh02 (59,840 cells). Therefore, six combinations were formed, and a total of 64 cases were calculated.
The experimental data (EXP) in Sriveerakul et al. [3] were used to validate the CFD results from modeling the ejectors used in their experiments under the same operating conditions. The error values of the simulation results and experimental data are defined as:
while the deviation values of the calculation results are defined as:
In this section, the reference simulation results are from the pressure-based solver.
Figure 4a depicts the ER comparison of the experiment and the three k–ε models under the two solvers and shows the similarity in the ejector performance characteristics as the back pressure of the ejector was varied. The ejector operating mode was divided into three parts distinguished by the CBP and the breakdown back pressure: the choked flow, the unchoked flow, and the reversed flow of secondary fluid [3]. In the choked flow region, when the back pressure was lower than the CBP, the secondary flow choking in the mixing chamber caused the ejector to entrain the same amount of the secondary flow. This kept the ER of the entire region constant. In the unchoked flow region, when the back pressure exceeded the CBP, there was no secondary flow choking. The entrained secondary flow changed, and the ER began to drop rapidly.
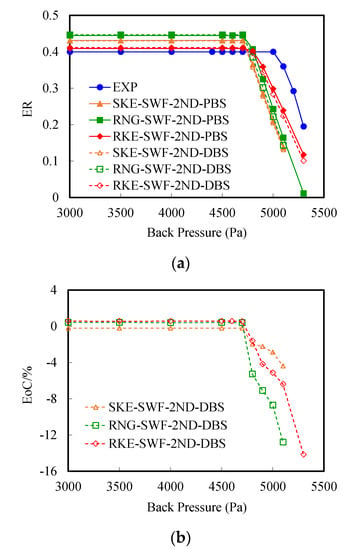
Figure 4.
Comparison of ejector performance from experimental data and CFD results utilizing different solvers: (a) Comparison of ejector performance, (b) Comparison of the EoC of ejector performance.
The EoC values remained stable in the choked flow region, and their absolute values increased with Pb in the unchoked flow region, as shown in Figure 4b. The ER values from the density-based solver were slightly higher than those from the pressure-based solver when the RKE or RNG model was adopted until the back pressure reached the CBP; then, the ER values from the density-based solver are becoming lower with Pb increasing than that from the pressure-based solver with all three k-ε models. As shown in Table 4, the EoC values of the maximum ER are in the range of −0.20% to 0.57%, and the CBP values are all the same.

Table 4.
Comparison of the ejector performance with different solvers and turbulence models.
Figure 5 illustrates the comparison between the wall static pressure distributions from the experimental and simulated results. The comparison was conducted when the ejector was operated at Pb =3.0 kPa in the choked flow region. The figure shows the similarity in the wall static pressure distributions along the ejector between the experimental and the simulated results. The two solvers produced wall static pressure values closer to each other as the ER and CBP in the cases were tested.
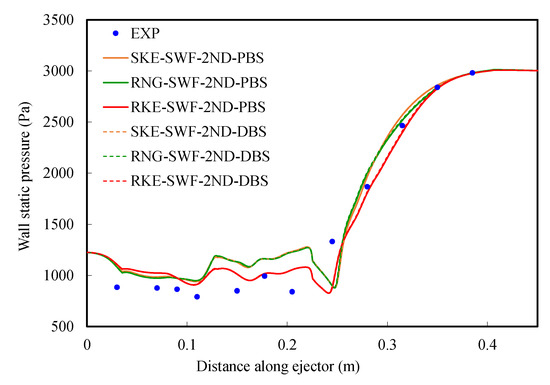
Figure 5.
Wall static pressure profile along the ejector at Pb = 3 kPa; effect of different turbulence models and solvers.
From the performance parameters and wall static pressure distribution results, there is almost no difference between the two solvers in the choked flow region, and there are significant differences only in the unchoked flow region. On the whole, the performance parameters from the pressure-based solver are slightly closer to the experimental data and the pressure-based solver has better calculation convergence. Therefore, it can be concluded that the results calculated by the pressure-based solver are more consistent with the experimental data, and the pressure-based solver should be utilized in the latter simulation.
3.3. Influence of the Turbulence Model and the Near-Wall Treatment
In this section, four turbulence models and two near-wall treatments were adopted and compared. The two near-wall treatments, the standard wall function and enhanced wall treatment, were adopted when the three k-ε models were chosen. The SST model was used as low-Reynolds-number model, and the meshes were the same as those used for the three k-ε models with the enhanced wall treatment. In total, seven combinations were formed, and two meshes with different y+ values were used, i.e., Mesh02 and Mesh05. The second-order upwind scheme was adopted for the spatial discretization of the convection terms. The pressure-based solver was adopted, and the SIMPLE algorithm was employed to couple the solving of pressure and velocity. In total, an additional 43 cases were calculated.
Figure 6 depicts the ER comparison of the experiment and the four turbulence models and shows the similarity in the ejector performance characteristics when the ejector’s back pressure was varied. In contrast with the k-ε models, the SST model provided a smooth transition. As shown in Table 5, taking the last simulation results of Mesh02 with the standard wall function as a reference, the EoC values of the maximum ER of the simulation results of Mesh05 were in a range of 9.07–11.26%, and the EoC values of the CBP values were 6.38%, meaning that both the maximum ER and the CBP values were higher when the enhanced wall treatment was adopted. The EoE values of the maximum ER were in a range of 5.63–21.57%, and the EoE values of the CBP values were in a range of −14.0% to 0, meaning that the maximum ER values were all higher than the experimental values.
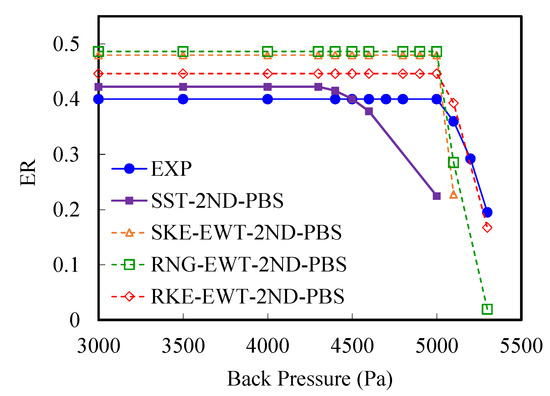
Figure 6.
Comparison of ejector performance from experimental data and CFD results utilizing different turbulence models.

Table 5.
Comparison of the ejector performance with different turbulence models.
Among the simulation results for Mesh05, the maximum ER value of the SST model was closest to the experimental value, with an EoE value of 5.63%, while the EoE value of the CBP was the largest (−14%). Among the three k-ε models, the maximum ER value of the RKE model was closest to the experimental data, and the CBP values were the same. The three k-ε models provided better predictions of the CBP than the SST model. However, the simulation results of Mesh02 showed that the maximum ER value of the RKE model with the standard wall function was closest to the experimental value with an EoE value of only 2.28%, while the EoE value of the CBP was −6.0%, as shown in Table 3. The three k-ε models provided the same predictions of the CBP with the two meshes and the two near-wall treatments. This implies that when a high-density mesh with y+ < 1 is used, the SST model can be applied to obtain the best predictions of the maximum ER, and this conclusion is the same as in References [11,20,23,24]. The RKE model with enhanced wall treatment can be adopted for the best prediction of the CBP and an adequate prediction of the maximum ER. When the standard wall function is used with a medium mesh, the RKE model can be applied to obtain the best predictions of the maximum ER among the three k-ε models, and this conclusion is the same as in References [19,20]. The RNG and SKE model with a standard wall function can be adopted for the prediction of the CBP and an adequate prediction of the maximum ER, while the RNG and SKE models with enhanced wall treatment can be adopted for the prediction of the CBP only.
Figure 7a illustrates the comparison between the wall static pressure distributions from the experimental and the simulated results of seven different modeling approaches at Pb =3.0 kPa. The wall static pressures of the RNG and SKE models almost overlapped before flowing into the diffuser, regardless of whether a standard wall function or enhanced wall treatment was used. The performance curves of the two turbulent models also had high similarity (Figure 4a and Figure 6). The wall static pressure of the RKE model was significantly different from the RNG and SKE and closer to the test data, whether the standard wall function or enhanced wall treatment was used. The performance curves of the RKE model were also closer to the test data. The wall static pressure of the SST model almost overlapped with that of the RKE model with SWF in the mixing chamber until X = 0.105 m and was closest to the experimental data before reaching the point at one third of the diffuser. Figure 7b depicts the variation of the EoE between the calculated and the test wall static pressure values along the flow direction under each modeling approach. On the whole, the calculated value of wall static pressure before the diffuser was higher than the test value, and it was lower than the test value near the diffuser entrance, after which the pressure gradually recovered, the calculated value and the test value gradually converged, and the EoE decreased. The EoE trends of the seven modeling approaches were similar in the throat, but after entering the diffuser, the SST model showed great differences. The EoE of the SST model was relatively uniform, and the range of the EoE was smaller than those of the other six modeling approaches.
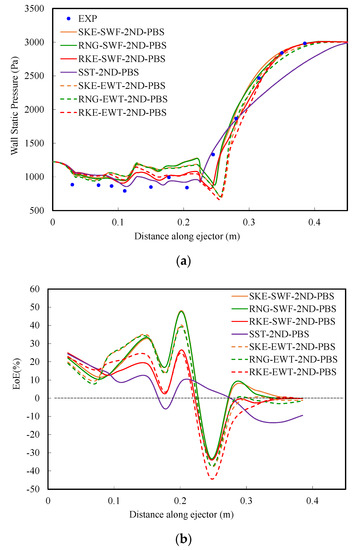
Figure 7.
Wall static pressure profile along the ejector at Pb = 3 kPa; effect of different turbulence models and near-wall treatments: (a) Comparison of ejector wall static pressure; (b) EoE comparison of ejector wall static pressure.
The calculation reliability of the seven modeling approaches was quantified and compared by calculating the root mean square (RMS) value of the EoE. As shown in Table 6, the RMS of the EoE value of the SST model was the smallest, followed by the RKE-SWF and RKE-EWT approaches. Although the SST model had larger errors in the diffuser, the overall error was small. The RKE model had the smallest RMS error among the three k-ε models. The static wall pressure can reflect the details of the flow field, so it can be considered that the SST model and the RKE model are more accurate for the calculation of the turbulent flow in a steam ejector.

Table 6.
RMS of EOE of wall static pressure (%).
Figure 8 shows the variation curves of the Mach number (Ma) along the ejector axis and the Mach number contours of the flow field under the seven modeling approaches. Figure 8a shows that all the modeling approaches could depict the first shock wave train at the nozzle exit, especially the positions of the first two shock waves being basically the same, and only the Mach number peak values were different. It should be noted that the SST model had small fluctuations in the Mach number trough rather than a smooth transition. After the flow entered the throat (X = 0.130–0.225), a third shock wave was generated, and the peak value and position of the modeling approaches were quite different. The Mach number of the SST model was basically stable in the throat, in contrast with the other six schemes showing a downward trend. After the mixed fluid entered the diffuser, a second shock wave train was generated under the action of the pressure gradient. The Mach number trends of the seven modeling approaches were different. Among them, the Mach wave of the SST model was gentler but had not yet reached stability, even at the exit of the diffuser (X = 0.405). Figure 8b shows that the main fluid continued to accelerate after leaving the nozzle, and obvious expansion waves appeared. Shock waves appeared under the restriction of the mixing layer between the two fluids. Then, the expansion waves and the shock waves alternately appeared, forming a “diamond wave” at the first shock train. As seen in Figure 7a, the pressure change in the mixing chamber was relatively stable, and it can be considered that the two fluids achieved constant-pressure mixing. There was no significant difference in the flow in the mixing chamber described by all modeling approaches, but the difference began to appear after the flow enters the diffuser. The flow under the six modeling approaches based on the k-ε model showed obvious spreading and then contraction after entering the diffuser, and there was a clear boundary in the high Mach number region meaning that the shock wave was stronger. In the diffuser calculated by the SST model, the high Mach number region was relatively long and narrow, and only slow contraction could be seen without spreading.
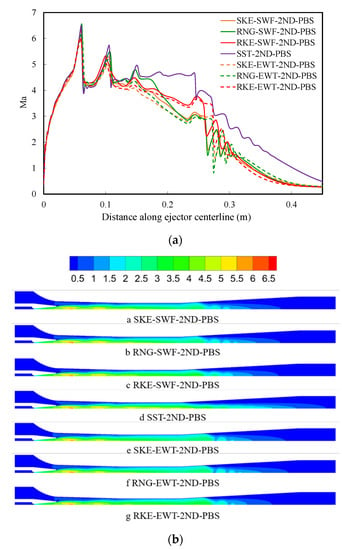
Figure 8.
Mach number distribution at Pb = 3 kPa: (a) Mach number along the ejector centerline, (b) Contours of the Mach number distribution: (a–g) show contours under the seven modeling approaches.
The pressure and Mach number variation in the diffuser of each modeling approach were quite different. To study the reason for this feature, the streamlines inside the diffuser were outlined. It can be seen that there was a recirculation region in the diffuser, as shown in Figure 9, and the size of the recirculation region calculated by each modeling approach was different. By extracting the wall shear stress distribution curve, the positions of the separation point and the reattachment point under each modeling approach were obtained, as shown in Figure 10, and the starting position and ending position of the recirculation can be judged. Viewed along the flow direction, the separation point occurred when the wall shear stress was equal to 0 for the first time, and the reattachment point occurred when it was equal to 0 again. When using the standard wall function, the separation point and reattachment point calculated by the RNG and SKE models basically coincided; while the separation point calculated by the RKE model was earlier, the reattachment point was later, and the recirculation region was obviously larger. When the enhanced wall treatment was used, the separation points of these three k-ε models were basically the same, and the reattachment points calculated by the RNG and SKE models were later than the RKE model, indicating that the effect of the enhanced wall treatment was greater than these three turbulence models for recirculation region prediction. Two recirculation cores were still visible in the recirculation zone calculated by the RKE model, and the recirculation was wider (in the radial direction). The standard wall function is considered to be unsuitable for large pressure gradients and boundary layer separation, while the enhanced wall treatment is usually recommended for these situations. At the same time, the SKE model is considered unsuitable for flows with large pressure gradients. The RKE model is considered to be more suitable for flows that include separated flows, boundary layers under strong reverse pressure gradients, and recirculation. These conclusions have also been verified here. With the enhancement by the enhanced wall treatment, the three k-ε models have improved the prediction ability of recirculation. Therefore, it is recommended to use the RKE model or the enhanced wall treatment for flows with recirculation in the steam ejector.

Figure 9.
Recirculation inside the diffuser at Pb = 3 kPa: (a–g) show streamlines under the seven modeling approaches. (a–g) show contours under the seven modeling approaches.
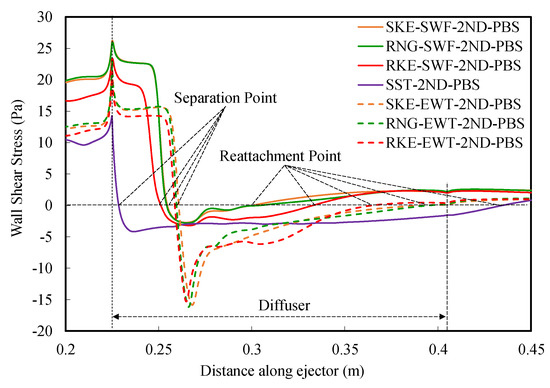
Figure 10.
Distribution of the ejector wall shear stress at Pb = 3 kPa.
Both the RKE and RNG models are improved variants of the k-ε model since the advantages and disadvantages of the SKE model are known. However, the RNG model does not show significant improvement over the SKE model in this steam ejector simulation, while the RKE model shows substantial improvements. This may be because the RNG and the SKE model have similar forms of transport equations for k and ε, while the RKE model contains a new formulation for the turbulent viscosity and a modified transport equation for ε, derived from an exact equation for the transport of the mean-square vorticity fluctuation [36]. Mainly due to the modeled dissipation equation, the SKE model and other k-ε models with the modeled equation for ε are found to predict the spreading rate in planar jets reasonably well, but the spreading rate for axisymmetric jets is unexpectedly poor, while the RKE model is found to predict the spreading rate for axisymmetric jets as well as that for planar jets. This reason may explain the superiority of the RKE model over the RNG and the SKE model for the simulation of a steam ejector with the flow dominated by axisymmetric jets.
The starting point for the development of the SST model was the need for the accurate prediction of aeronautic flows with strong adverse pressure gradients and separation [42]. Compared with the k-ε models, the SST model gains the largest recirculation region, the separation point is closer to the diffuser inlet, and the reattachment point even exceeds the diffuser and enters the outlet pipe. The SST model is considered to be suitable for the separated flow generated by the reverse pressure gradient, but in the current flow, there is interference from the second shock train and the confined wall, and the calculated flow spreading when entering the diffuser is obviously weak and cannot spread to the boundary in time to overcome the adverse pressure gradients. Therefore, the calculated recirculation is larger, and there is the possibility of overpredicting the recirculation and underpredicting the flow spreading rate. The existence of recirculation produces a large energy loss, so the back pressure that can be overcome is lower, and the obtained CBP value is also lower.
3.4. Influence of the Spatial Discretization Scheme
This section studies the influence of two different spatial discretization schemes for steam ejector simulation on the scale of commonly used meshes (such as Mesh02) and sufficiently fine meshes (such as Mesh05) to help choose discrete schemes. The aforementioned seven simulation schemes were changed from the second-order upwind scheme (2ND) to the QUICK scheme and recalculated, adding a total of 78 cases.
Figure 11 and Table 7 show the ejector performance calculation results under different modeling approaches and discretization schemes and use the calculation results of the second-order upwind scheme as a reference to show the EoC between the calculation results. When the back pressure was less than the CBP, the flow was in the choked flow region, and the calculated EoC value of the maximum ER value caused by the change of the upwind schemes on the two scale meshes was less than 1%. Except for the modeling approach based on the SKE model, the EoC of the other schemes was less than 0.11% and could be ignored. When using a regular-scale mesh, after the upwind scheme of the SKE-SWF approach was changed from 2ND to QUICK, the calculated CBP value was reduced from 4.7 kPa to 4.6 kPa, the EoC value was −2.13%, and the CBP values of the other modeling approaches remained unchanged.
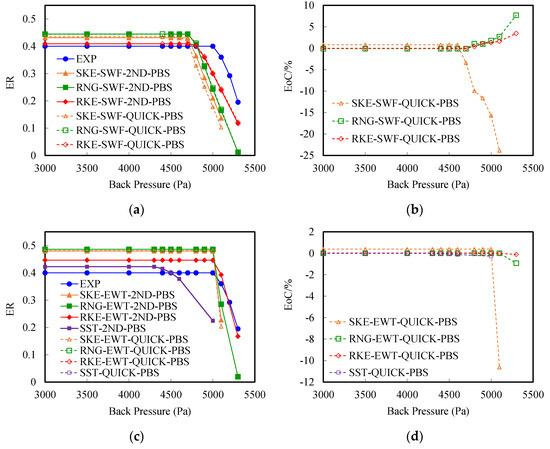
Figure 11.
Comparison of ejector performance from experimental data and CFD results utilizing different solvers: (a) Comparison of ejector performance, (b) EoC comparison of ejector performance, (c) Comparison of ejector performance, (d) EoC comparison of ejector performance.

Table 7.
Comparison of the ejector performance with different solvers and turbulence models.
When the back pressure was greater than the CBP, the flow was in the unchoked flow region, and as the back pressure increased, the EoC caused by the higher order upwind scheme increased. The changes in EoC when the SKE model was used were the most significant, while the changes in EoC when the RKE model and the SST model were used were weaker. The EoC value when using a regular-scale mesh was generally greater than that of a high-density mesh.
If the unchoked flow region was not considered during the design and operation, the performance parameters of the steam ejector mainly consisted of the maximum ER and the CBP. When using regular-scale meshes combined with a standard wall function, the three k-ε models were basically not affected by the special discrete scheme when calculating the maximum ER value. When only the SKE model was used to calculate the CBP value, it was more affected by the special discrete scheme. When the high-density mesh was combined with the enhanced wall treatment, the maximum ER value and CBP value calculated by all the modeling approaches were basically not affected by the special discrete scheme; that is, under the current mesh density, the difference between the 2ND and QUICK schemes could be ignored.
4. Conclusions
In this paper, we numerically studied the effects of different modeling and solving approaches on the simulation of a supersonic steam ejector. The numerical approaches were validated and compared against the experimental data of global quantities: the ER and the CBP and local quantities: wall static pressure. In particular, the four most frequently used and recommended turbulence models, two near-wall treatments, two solvers and two spatial discretization schemes of the convection term have been tested and compared. In total, more than 185 cases of 17 different modeling and solving approaches were carried out in this work, and several conclusions are obtained as follows:
- (1)
- In the choked flow region, the pressure- and density-based solvers have no significant difference for the global and local parameters, while in the unchoked flow region, the simulation results from the pressure-based solver are slightly closer to the experimental data than those of the density-based solver.
- (2)
- When a conventional density mesh is used with a standard wall function, the RKE model can obtain the best predictions of the maximum ER, and its RMS value of the wall static pressure error is the least among the three k-ε models, while they gain the same adequate CBP value with the spatial discretization scheme as the second-order upwind scheme. Hence, the RKE model with a standard wall function is recommended for a conventional density mesh.
- (3)
- When a high-density mesh with y+ < 1 is used, the SST model can obtain the best predictions of the maximum ER, and its RMS value of the wall static pressure error is lower than the three k-ε models with an adequate prediction of the CBP, while the RKE model with enhanced wall treatment can obtain the best prediction of the CBP and an adequate prediction of the ER. The SST model may overpredict the recirculation in an ejector. Hence, the RKE model with enhanced wall treatment is recommended for a high-density mesh, especially for a steam ejector with recirculation inside the diffuser.
- (4)
- The difference between the second-order upwind scheme and the QUICK scheme can be ignored for the maximum ER calculation, while the CBP value from the SKE model with the standard wall function is affected. Hence, the SKE model is more sensitive to the near-wall treatment and the spatial discretization scheme and is not recommended for the ejector simulation.
- (5)
- In the choked flow region, the location of the secondary shock process varies with the back pressure. The shock will move upstream into the ejector throat as the back pressure increases, but the mixing process is not disturbed, and the secondary flow remains choked. In the unchoked flow region, the secondary flow is not choked, and its flow rate decreases, resulting in a rapid drop of the ER as the back pressure increases. The shock moves upstream into the mixing chamber and disturbs the mixing between the primary and secondary fluids, increasing the complexity of the flow. That is why the numerical results for unchoked flow tend to be more susceptible to modeling or solving approaches than those for choked flow.
Author Contributions
Conceptualization, J.X. and Q.W.; methodology, L.C.; validation, W.K. and C.W.; writing—original draft preparation, X.Y.; writing—review and editing, L.Y. and H.J.; supervision, H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52076097 & U20A20303).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (52076097 & U20A20303).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| 2ND | second-order upwind scheme |
| CBP | critical back pressure (Pa) |
| COP | coefficient of performance |
| cp | specific heat (J/kg K) |
| D | diameter (mm) |
| DBS | density-based solver |
| ER | entrainment ratio |
| EoC | deviation values of calculation results, EoC = (simulation result/reference simulation result − 1) ···100 |
| EoE | error value of simulation result and experimental data, EoE = (simulation result/experimental data − 1) ···100 |
| EWT | enhanced wall treatment |
| EXP | experimental data |
| K | turbulence kinetic energy (m2/s2) |
| mp | primary flow rate (kg/s) |
| ms | secondary flow rate (kg/s) |
| Pb | back pressure (Pa) |
| PBS | pressure-based solver |
| RKE | realizable k-ε model |
| RMS | root mean square |
| RNG | RNG k-ε model |
| RSM | Reynolds Stress model |
| Rt | throat radius |
| SERS | steam ejector refrigeration system |
| SKE | standard k-ε model |
| SKW | standard k-ω model |
| SST | SST k-ω model |
| SWF | standard wall function |
| Tp | primary fluid saturated temperature, Tp = 130 °C |
| Ts | secondary fluid saturated temperature, Ts = 10 °C |
| u | streamwise velocity component (m/s) |
| u’, T’ | turbulence fluctuation terms(m/s, K) |
| ut | axial velocity at the throat inlet (m/s) |
| v | radial velocity component (m/s) |
| X | distance along ejector (m) |
| Greek | |
| α | thermal diffusivity (m2/s) |
| ε | turbulence dissipation rate (m2/s3) |
| λ | heat conductivity (W/m K) |
| μ | dynamic viscosity (kg/m s) |
| ρ | density (kg/m3) |
| ω | specific dissipation rate |
References
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Proposal and assessment of a novel geothermal combined cooling and power cycle based on Kalina and ejector refrigeration cycles. Appl. Therm. Eng. 2018, 130, 767–781. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Li, Y.; Wang, R.Z. Progress of mathematical modeling on ejectors. Renew. Sustain. Energy Rev. 2009, 13, 1760–1780. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. Ejectors: Applications in refrigeration technology. Renew. Sustain. Energy Rev. 2004, 8, 129–155. [Google Scholar] [CrossRef]
- Tashtoush, B.M.; Moh’d, A.A.-N.; Khasawneh, M.A. A comprehensive review of ejector design, performance, and applications. Appl. Energy 2019, 240, 138–172. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. An experimental investigation of a steam ejector refrigerator: The analysis of the pressure profile along the ejector. Appl. Therm. Eng. 2004, 24, 311–322. [Google Scholar] [CrossRef]
- Selvaraju, A.; Mani, A. Experimental investigation on R134a vapour ejector refrigeration system. Int. J. Refrig. 2006, 29, 1160–1166. [Google Scholar] [CrossRef]
- Mazzelli, F.; Milazzo, A. Performance analysis of a supersonic ejector cycle working with R245fa. Int. J. Refrig. 2015, 49, 79–92. [Google Scholar] [CrossRef]
- Gagan, J.; Smierciew, K.; Butrymowicz, D.; Karwacki, J. Comparative study of turbulence models in application to gas ejectors. Int. J. Therm. Sci. 2014, 78, 9–15. [Google Scholar] [CrossRef]
- Marynowski, T.; Desevaux, P.; Mercadier, Y. Experimental and numerical visualizations of condensation process in a supersonic ejector. J. Vis. 2009, 12, 251–258. [Google Scholar] [CrossRef]
- Bouhanguel, A.; Desevaux, P.; Gavignet, E. Flow visualization in supersonic ejectors using laser tomography techniques. Int. J. Refrig. 2011, 34, 1633–1640. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, P. Experimental and numerical investigation of the effect of shock wave characteristics on the ejector performance. Int. J. Refrig. 2014, 40, 31–42. [Google Scholar] [CrossRef]
- Bartosiewicz, Y.; Desevaux, P.; Aidoun, Z.; Mercadier, Y. CFD-Experiments Integration in the Evaluation of Six Turbulence Models for Supersonic Ejectors Modeling. Integrating CFD and Experiments Conference. Available online: https://www.semanticscholar.org/paper/CFD-Experiments-Integration-in-the-Evaluation-of-Bartosiewicz-Desevaux/7d1996f2a50ba5b270193f15a7025431f205baa8 (accessed on 7 November 2021).
- Bartosiewicz, Y.; Aidoun, Z.; Mercadier, Y. Numerical assessment of ejector operation for refrigeration applications based on CFD. Appl. Therm. Eng. 2006, 26, 604–612. [Google Scholar]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.-M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part I: Experimental validation of single-phase and two-phase operation. Appl. Therm. Eng. 2009, 29, 1523–1531. [Google Scholar]
- Hemidi, A.; Henry, F.; Leclaire, S.; Seynhaeve, J.-M.; Bartosiewicz, Y. CFD analysis of a supersonic air ejector. Part II: Relation between global operation and local flow features. Appl. Therm. Eng. 2009, 29, 2990–2998. [Google Scholar]
- Yang, X.; Long, X.; Yao, X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures. Int. J. Therm. Sci. 2012, 56, 95–106. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Thongtip, T.; Aphornratana, S.; Sriveerakul, T. CFD simulation on the effect of primary nozzle geometries for a steam ejector in refrigeration cycle. Int. J. Therm. Sci. 2013, 63, 133–145. [Google Scholar] [CrossRef]
- Mazzelli, F.; Little, A.B.; Garimella, S.; Bartosiewicz, Y. Computational and experimental analysis of supersonic air ejector: Turbulence modeling and assessment of 3D effects. Int. J. Heat Fluid Flow 2015, 56, 305–316. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 1: Numerical benchmark. Int. J. Refrig. 2016, 61, 140–152. [Google Scholar] [CrossRef]
- Croquer, S.; Poncet, S.; Aidoun, Z. Turbulence modeling of a single-phase R134a supersonic ejector. Part 2: Local flow structure and exergy analysis. Int. J. Refrig. 2016, 61, 153–165. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Computational fluid-dynamics modeling of supersonic ejectors: Screening of turbulence modeling approaches. Appl. Therm. Eng. 2017, 117, 122–144. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Wang, X.; Zhao, H. Design and numerical investigation of an adaptive nozzle exit position ejector in multi-effect distillation desalination system. Energy 2017, 140, 673–681. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Pianthong, K.; Seehanam, W.; Behnia, M.; Sriveerakul, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Convers. Manag. 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
- Varga, S.; Oliveira, A.C.; Diaconu, B. Numerical assessment of steam ejector efficiencies using CFD. Int. J. Refrig. 2009, 32, 1203–1211. [Google Scholar] [CrossRef]
- ANSYS FLUENT Theory Guide Release 15.0; ANSYS Inc.: Canonsburg, PA, USA, 2013; Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf (accessed on 7 November 2021).
- Dong, J.; Hu, Q.; Yu, M.; Han, Z.; Cui, W.; Liang, D.; Ma, H.; Pan, X. Numerical investigation on the influence of mixing chamber length on steam ejector performance. Appl. Therm. Eng. 2020, 174, 115204. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.Z. Investigation of entrainment behavior and characteristics of gas–liquid ejectors based on CFD simulation. Chem. Eng. Sci. 2011, 66, 405–416. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical modeling of two-phase supersonic ejectors for work-recovery applications. Int. J. Heat Mass Transf. 2012, 55, 5744–5753. [Google Scholar]
- Wilcox, D.C. Turbulence modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; p. 2. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: London, UK, 1972; p. 169. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Opgenorth, M.J.; Sederstrom, D.; McDermott, W.; Lengsfeld, C.S. Maximizing pressure recovery using lobed nozzles in a supersonic ejector. Appl. Therm. Eng. 2012, 37, 396–402. [Google Scholar] [CrossRef]
- Wu, H.; Liu, Z.; Han, B.; Li, Y. Numerical investigation of the influences of mixing chamber geometries on steam ejector performance. Desalination 2014, 353, 15–20. [Google Scholar] [CrossRef]
- Dong, J.; Yu, M.; Wang, W.; Song, H.; Li, C.; Pan, X. Experimental investigation on low-temperature thermal energy driven steam ejector refrigeration system for cooling application. Appl. Therm. Eng. 2017, 123, 167–176. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, H.; Zhang, C.; Wang, L.; Han, J. Optimization analysis of structure parameters of steam ejector based on CFD and orthogonal test. Energy 2018, 151, 79–93. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).