Abstract
This study investigates the sensitivity of the GNSSseg segmentation method to change in: GNSS data processing method, length of time series (17 to 25 years), auxiliary data used in the integrated water vapor (IWV) conversion, and reference time series used in the segmentation (ERA-Interim versus ERA5). Two GNSS data sets (IGS repro1 and CODE REPRO2015), representative of the first and second IGS reprocessing, were compared. Significant differences were found in the number and positions of detected change-points due to different a priori ZHD models, antenna/radome calibrations, and mapping functions. The more recent models used in the CODE solution have reduced noise and allow the segmentation to detect smaller offsets. Similarly, the more recent reanalysis ERA5 has reduced representativeness errors, improved quality compared to ERA-Interim, and achieves higher sensitivity of the segmentation. Only 45–50% of the detected change-points are similar between the two GNSS data sets or between the two reanalyses, compared to 70–80% when the length of the time series or the auxiliary data are changed. About 35% of the change-points are validated with respect to metadata. The uncertainty in the homogenized trends is estimated to be around 0.01–0.02 kg m year.
Keywords:
segmentation; homogenization; climate; GNSS; integrated water vapor; time series; trend; reanalysis 1. Introduction
Long records of observational data are essential to monitoring climate change and understanding the underlying climate processes [1,2]. However, long time series are often affected by inhomogeneities due to changes in instrumentation, in station location, in observation and processing methods, and/or in the measurement conditions around the station [3]. Inhomogeneities often take the form of abrupt changes, which are detrimental to estimating trends and multi-scale climate variability [4]. Various homogenization methods have been developed for the detection and correction of such change-points in the context of climate data analysis [1,2,5,6,7,8,9].
In this paper, we are interested in ground-based Global Navigation Satellite System (GNSS) integrated water vapor (IWV) measurements. GNSS measurements are qualified among the most accurate and continuous IWV measurements in all weather conditions but have only quite recently been considered for climate analysis [10,11,12,13]. Parracho et al. [14] was one among the first to analyze global IWV trends from more than 15 years of GNSS data and to confront them to the ECMWF reanalysis, ERA-Interim (ERAI), Dee et al. [15], and to the NASA/MERRA-2 reanalysis [16]. Significant differences were discovered in IWV trends between the two reanalyses and between the reanalyses and the GNSS data. On the one hand, this study pointed to the importance of the atmospheric model, the assimilation system, but also the quality and quantity of assimilated observations in reanalyses. On the other hand, inhomogeneities were also suspected in the GNSS data at several sites. Developing a homogenized GNSS IWV time series is of prime importance to estimate regional and global IWV trends and variability but also to verify climate models and reanalyses. This study investigates in more detail the homogeneity of the GNSS IWV data set used by Parracho et al. [14], as well as a more recently reprocessed GNSS data set. It also updates the previous results from Parracho et al. [14] and Bock and Parracho [17] with the new ECMWF reanalysis, named ERA5 [18].
The main causes of inhomogeneities in GNSS IWV time series are:
- Equipment changes (antenna, radome, and receiver). Each antenna/radome pair has a particular impact on the measurements, which is taken into account at the processing level with a specific calibration model (see Section 2). However, model imperfections, multipath and on-site electromagnetic coupling with the antenna’s environment, and equipment aging are responsible for small biases which can change over time. The quality of measurements also depends on the receivers. Modern receivers have more stable clocks, reduced cycle slips, and noise and are capable of observing satellites from new GNSS systems (GPS, GLONASS, etc.). Hence, changes in data quality/properties are expected, which can introduce offsets and possibly trends (e.g., when new satellites are introduced progressively). Changes in receiver settings, such as cutoff angle, are also known to produce abrupt changes in the mean IWV estimates [19].
- Changes in the environment near the receiver antenna can introduce multipath and obstructions that alter the measurements and cause inhomogeneities.
- Processing changes. The details of the data processing are known to impact the IWV estimates. The most important aspects and parameters are the tropospheric model (the mapping functions, the a priori hydrostatic model, the time-dependency), the antenna/radome calibration models, the elevation-dependent weighting, and the cutoff angle (see Section 2).
The first cause is well documented for International GNSS Service (IGS) stations and other scientific networks (ftp://igs.ign.fr/pub/igs/igscb/station/log/, accessed on 30 July 2021). Therefore, metadata can be used to check if change-points detected in the IWV time series can be explained by known equipment changes. The second cause is usually not well documented, but the analysis of the raw measurements and post-fit residuals can help to detect changes in the environment. The third cause is of a different nature as it depends on the analysis procedure and models, which are both the subject of active research in order to improve the accuracy and homogeneity of the GNSS products (see Section 2). However, not all biases and inhomogeneities can be corrected at the processing level, and further post-processing homogenization methods are needed.
Many different homogenization methods have been developed by climatologists. The heart of any homogenization method is the detection of change-points, the so-called segmentation method. Some segmentation methods use statistical tests [6,7], while others use a penalized likelihood approach [1,2,20]. The performance of both approaches are comparable, but, in general, the results depend on the data properties (nature of the background noise, presence of a periodic bias and/or a trend), the adopted model (parametric or non-parametric), and the search method (optimal or sub-optimal) [9,21].
Quarello [21] developed a segmentation method, called GNSSseg, especially devoted to detect changes in the mean of time series of IWV differences between GNSS and a reference and taking into account the presence of a periodic bias and a heterogeneous noise with a monthly variation. The method uses a penalized likelihood approach and is optimal in the sense that the estimation of the positions of the change-points is done using an efficient algorithm. The method proposes several penalty criteria, which aims to choose the number of change-points, with different sensitivities to the data properties (length of the time series, noise distribution, etc.). The use of several criteria can help to mitigate their limitations but requires special post-processing to make the final decision, either automatic or manual. The post-processing may also include outlier detection, validation with metadata when available, and manual inspection. The automatic version of the GNSSseg algorithm was evaluated in a benchmark exercise and compared to other existing segmentation methods where it was found to be one of the most efficient in detecting change-points in synthetic time series mimicking the GNSS minus ERAI IWV differences at the moderate complexity [22].
The general objective of this paper is to evaluate the sensitivity of segmentation results with the GNSSseg method (recently improved in terms of computational time and so-called GNSSfast method) and the subsequent trend estimates to various qualitative and quantitative properties of both GNSS and reference data. The study considers the particular cases of two different GNSS data sets (IGS repro1 and CODE REPRO2015) combined with two different reanalysis data sets, ERA-Interim [15] and ERA5 [18], which serve as references to compute to IWV differences used in the segmentation. IGS repro1 and CODE REPRO2015 are representative of the 1st and 2nd generation of IGS reprocessing products, and, as such, they are expected to be of different quality. They also cover different time periods. ERAI and ERA5 are the 4th and 5th generation reanalyses produced by ECMWF [18] and are also of different quality and spatial resolution.
The paper is organized as follows. In Section 2, we describe the characteristics of the two GNSS IWV data sets and discuss which factors in the data processing control the accuracy of the daily IWV estimates and their homogeneity in the long term. We also present the global homogenization and the trend estimation methods. In Section 3.1, we study the impact of data properties on the segmentation results. The following questions are specifically investigated: (1) What is the impact of the different data processing between IGS repro1 and CODE REPRO2015 on the segmentation results? (2) what is the impact of the time length on the segmentation results? (3) What is the impact of the reference data source (ERAI versus ERA5)? (4) What is the impact of the auxiliary data source used in the ZTD to IWV conversion (ERAI versus ERA5)? The segmentation results will be compared on the basis of several statistics: the number of detections before and after outlier screening, the number of outliers, and the number of validations/attributions after screening using metadata and nearby stations. In Section 3.2, the corrected time series are used to estimate linear trends, and the same questions as above are investigated for the trends. Finally, Section 4 concludes the paper and discusses the future work.
2. Materials and Methods
2.1. GNSS IWV Data
Before describing the characteristics of the two GNSS IWV data sets used in this study, we deem it is necessary to discuss which factors in the data production control the accuracy of the daily IWV estimates and their homogeneity in the long term. The raw GNSS measurements consist of code and carrier phase signals transmitted by GNSS satellites (GPS, GLONASS, etc.), which are measured by ground-based stations composed of an antenna and a multi-channel receiver [23]. The measurements collected from a global tracking network are analyzed in routine by several International GNSS Service (IGS) analysis centers who compute accurate satellite orbits and clock parameters (https://www.igs.org/acc/, accessed on 30 July 2021). These, as well as other parameters (Earth Rotation Parameters (ERPs) and satellite phase biases), are necessary for subsequent users to process accurate station positions and tropospheric delays for their own applications (e.g., geodesy, surveying, weather forecasting, etc.). Both the IGS and user data processing procedures rely on the use of various models to account for geophysical effects (solid Earth tides, ocean tides), atmospheric propagation effects through the ionosphere and the neutral atmosphere, and instrumental biases and variations induced by the transmitter and receiver antennas and electronics [24]. The propagation effect in the neutral atmosphere, so-called tropospheric delay, is traditionally decomposed into its hydrostatic and wet components in the zenith direction, which are mapped into the slant observation direction which their respective mapping functions, and a two-parameter horizontal gradient model [25]:
where is the Zenith Hydrostatic Delay (ZHD), mainly due to the contribution from dry air, is the Zenith Wet Delay (ZWD), due to water vapor molecules, is the horizontal gradient vector, is the unit vector pointing into the direction of the observed satellite, , , and are the respective mapping functions, and is the elevation angle.
During the GNSS data processing, is corrected a priori, while and G are estimated. The ZWD estimates can include some residual bias from incorrect a priori ZHD correction or a deficiency of the hydrostatic and wet mapping functions. The GNSS software traditionally provide the total Zenith Tropospheric Delay (ZTD), which is the sum of the a priori ZHD, , and estimated ZWD, :
The main parameter of interest for climate studies is the Integrated Water Vapor (IWV), i.e., the integral of the water vapor molecules at the zenith. The conversion of into operates, thus, in two steps [25]:
The accuracy of the IWV estimates is, thus, basically determined by the accuracy of the ZTD parameters derived from the GNSS data processing and the quality of the ZWD to IWV conversion procedure. For the purpose of retrieving , a more accurate estimate of is required than the one used a priori for the processing. It can be derived from the surface air pressure data, , available at the GNSS station [26]:
where is the dry air refractivity coefficient, is the dry air specific gas constant, is the surface air pressure, and is the mean acceleration due to gravity. The ZWD to IWV conversion factor is defined as a function of the weighted mean temperature [10]:
where and are refractivity coefficients for the water molecule, and is the specific gas constant for water vapor. The refractivity coefficients were taken from Bock [27]. The weighted mean temperature is defined by Bevis et al. [10]:
where and are the specific mass of water vapor and the air temperature, respectively, at height z above the surface. The integral is from the surface to the top of the atmosphere. It can be computed from a vertical profile of and given by a radiosonde climatology or an atmospheric model.
In this study, the auxiliary data, and , required for the conversion of the ZTD estimates into IWV are computed from a global atmospheric reanalysis. Using reanalysis data has several advantages: the data are available at any position and time on the globe, the pressure and temperature are well constrained by observations, making the reanalysis data the best estimate of the global atmospheric state at any position and time, and the assimilation system uses an efficient screening and bias correction procedure to reject suspect observational data and adjust bias changes associated to observational system changes (e.g., between older and new satellites). In this study, we will consider two different reanalyses: ERA-Interim [15] and ERA5 [18]. Details on the reanalyses are given in the subsection below. The and data are computed from 6-hourly pressure level data, as described in Reference [14] and the subsequent IWV estimates are aggregated into daily estimates, as described in Reference [17]. The interest of comparing two different reanalysis is that ERA5 is of superior quality due to the assimilation of more observations and of higher spatial resolution, i.e., providing more accurate pressure and temperature estimates in regions of steep topography. The accuracy of reanalysis estimates of and , as compared to other data sources, is further discussed in Bock [27] and Bock et al. [28].
The main factors conditioning the accuracy of the ZTD estimates at the GNSS data processing level are, by decreasing order, the hydrostatic and wet mapping functions, the a priori ZHD correction data, and the antenna phase center variation (PCV) models. Any bias in these data and models would map directly into the ZWD estimates. The mapping functions are the most important because they determine how the signals from the satellites at various elevations are mapped into the zenith direction (from a mathematical point of view, they represent the partial derivatives, or regressors, of the ZHD and ZWD parameters). Because the hydrostatic delay is corrected a priori, any bias in the a priori ZHD, or in the hydrostatic mapping function, will also map into the estimated ZWD [29]. Receiver antenna phase center variations also highly depend on the elevation angle and, to a lesser extent, on the azimuth angle. Before 2005, relative calibration models were used in the IGS network, which were progressively replaced with absolute calibrations [30]. The convention at IGS is to use a type-mean calibration, i.e., a mean calibration model determined from several calibrated antennas of the same type (producer and product) when available, and a specific variant for each antenna/radome combination. When no specific antenna/radome combination exists, the rule is to “adopt” the antenna calibration without radome. In addition, when the antenna calibration does not exist, the calibration is “copied” from a similar antenna (based on electronic and mechanic properties). The official antenna/radome calibrations are distributed by IGS in the form of ANTEX (Antenna Exchange Format) files, e.g., igs05.atx and igs08.atx, at the times when the IGS and CODE data sets used in this study were produced. Absolute calibrations from “Robot” and “Chamber” are the most accurate, while relative calibrations (type “field”) and relative converted to absolute (type “converted”) are the less accurate [31]. The impact of satellite and receiver antenna offsets (PCO) and PCVs on geodetic parameters have been mainly investigated for positioning purposes. The impact on ZTD estimates has not been much studied yet, although it is known that it would be tightly correlated with the vertical position component. One of the goals of this paper is, thus, to examine how the change from igs05.atx to igs08.atx impacts the accuracy and homogeneity of the GNSS IWV series and to which extent these differences are detected by our segmentation method. In addition to the aforementioned factors, there are other errors sources that can impact the accuracy of the ZTD estimates, such as multipath and ambiguity fixing errors, as well as satellite orbits and clock errors, and unmodeled and mis-modeled station displacements at sub-daily time scales (e.g., tides). However, these are minor errors sources for the purpose of our study here. For further details, see the study of Ning et al. [32]. Of main concern here are the sources of bias and the mechanisms through which these biases can change with time, i.e., translate into inhomogeneities.
In this study, we consider two different GNSS data sets, which are representative of two different generations of reprocessing products delivered by IGS (see Table 1). The first one, referred to as IGS repro1, was produced by JPL/NASA in 2010–2011 in precise point positioning (PPP) mode with GIPSY OASIS II software [33] as a special release of ZTD estimates. This data set used the reprocessed IGS orbits, clocks, and ERPs produced by JPL/NASA in the framework of the 1st reprocessing campaign organized by IGS. The reprocessed satellite products were generated for the period 1 January 1995 to 31 December 2007, but JPL completed the series until mid-2011 in a consistent way. In this study, we use the ZTD estimates until 31 December 2010 to have an integer number of years. According to the discussion above, the prominent features of the processing procedure are:

Table 1.
Processing strategies used by JPL/NASA to produce the IGS first reprocessed tropospheric data set (IGS repro1) and by the Center for Orbit Determination in Europe (CODE) to produce the CODE REPRO2015 reprocessed data set.
- Standard Temperature and Pressure (STP) model used for a priori ZHD correction [34],
- Global mapping function (GMF) for the hydrostatic and wet delays [35],
- IGS05 reference frame and igs05.atx absolute antenna PCO/PCV models
- 7° elevation cutoff angle, and
- uniform observation weighting.
It should be noted that, due to a flaw in the data file handling, the ZTD files for a number of stations are not available on the FTP repository, and older files were used instead, for which a major difference was the use of the older NMF hydrostatic and wet mapping functions [36].
The second GNSS data set, referred to as CODE REPRO2015, was processed by the Center for Orbit Determination in Europe (CODE) in 2015 [37] using the Bernese GNSS software [38] in network mode (double-differenced observations). This data set used the reprocessed IGS orbits, clocks, and ERPs produced by CODE in the framework of the 2nd reprocessing campaign organized by IGS. The reprocessed products cover the period from 1 January 1994 to 31 December 2014. For the purpose of this study, we completed the series with the operational CODE products until the end of 2018 [39]. However, the latter underwent a switch in the reference frame to IGS14 and in the antenna cnetwork alibration (double-differenced observations).model to igs14.atx, on 29 January 2017. This change was, thus, included in the metadata for the CODE solution.
The prominent features of the CODE processing procedure are:
- ECWMF grid estimates of a priori ZHD and ZWD distributed by Technical University of Vienna [40],
- Vienna mapping function (VMF1) for the hydrostatic and wet delays [40],
- IGb08 reference frame and igs08_1852.atx absolute antenna PCO/PCV models,
- 3° elevation cutoff angle,
- 1/cos(zenith) observation weighting, and
- GPS observations (1994–2001) and GPS + GLONASS (2002–2014).
According to the discussion above, we see that all the main factors conditioning the accuracy of the ZTD estimates are different between the two data sets. Not discussed above are the elevation cutoff angle and observation weighting, which contribute significantly to the sensitivity of ZTD estimates to the various elevation-dependent error sources (mapping functions, antenna PCO/PCV models, and multipath). The purpose of using a lower elevation cutoff angle in CODE is to include more observations, i.e., increase the precision of the estimated parameters. However, multipath is generally higher at low elevations. To mitigate it, the lower elevation observations are down-weighted. The JPL/NASA processing strategy was different as they used a 7° cutoff angle and no down-weighting. Possibly, this strategy might be more sensitive to multipath and anomalous propagation effects at low elevations.
The ZTD estimates from both data sets were screened for outliers following the methodology described in Bock [41] and Stepniak et al. [42], and converted to IWV using either ERA-Interim or ERA5 reanalysis. The 6-hourly IWV data were compared to the reanalysis IWV data and further screened for outliers (for each station, the IWV differences exceeding the median ± five standard deviations were removed). Afterward, the IWV values from GNSS and reanalysis, and the IWV differences between GNSS and reanalysis, were aggregated into daily and monthly estimates and made publicly available on the AERIS data center [43,44].
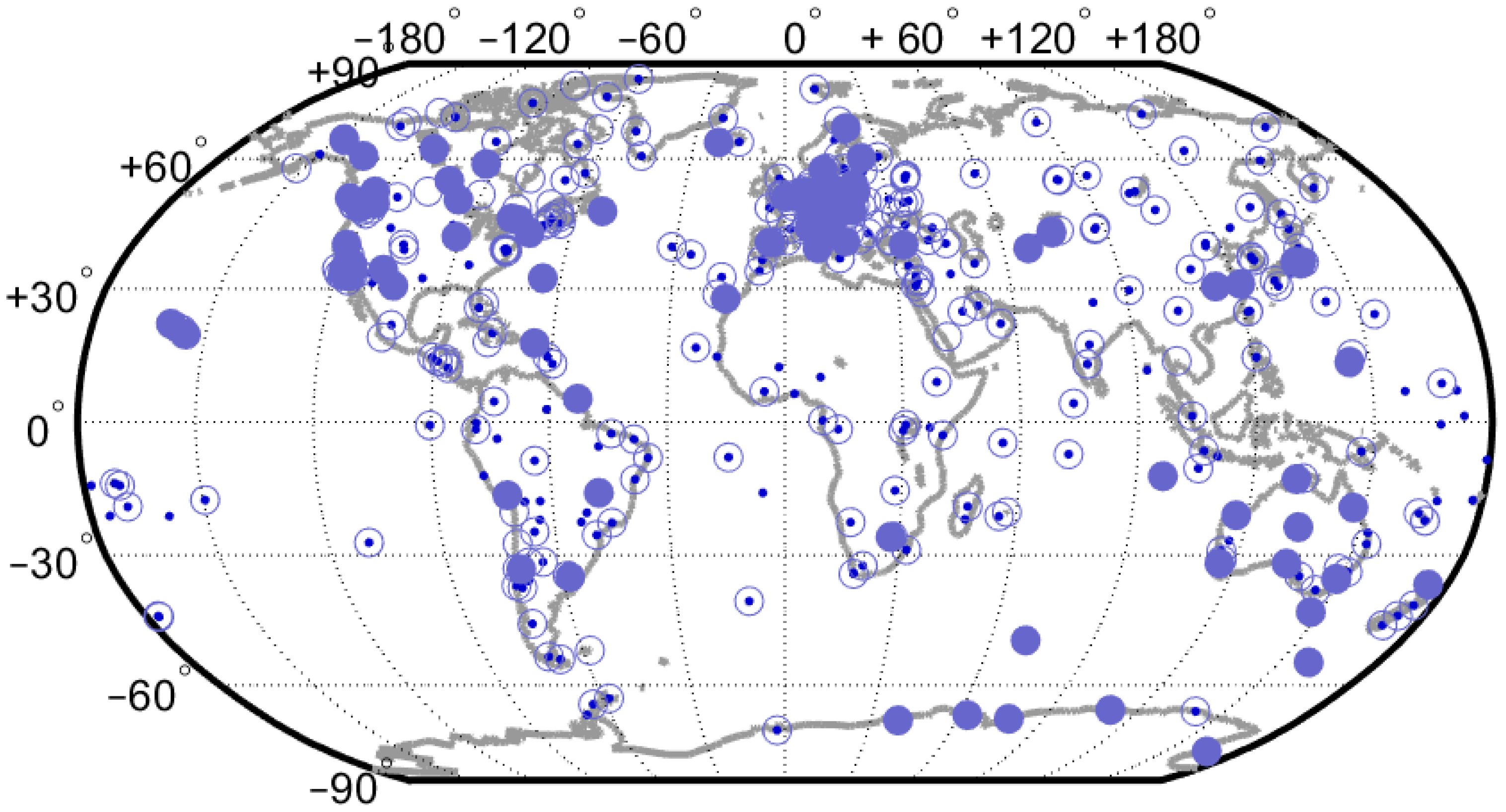
Figure 1 shows the location of the GNSS station available from the two data sets. In this study, we selected 81 common stations, for which the time series in both data sets covered a period of at least 15 years.
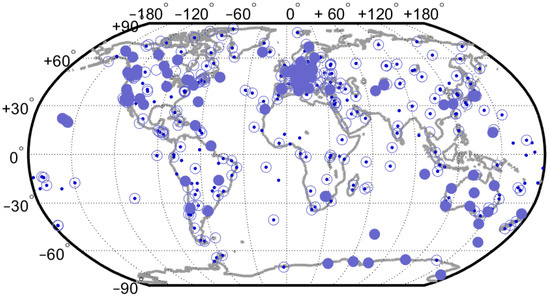
Figure 1.
Map of the GNSS stations available from the two reprocessed data sets: IGS repro1 (empty circles), CODE REPRO2015 (small dots), and the 81 common stations (full circles) used in this study.
2.2. Reference IWV Data
Our homogenization method operates on IWV differences between a GNSS series and a reference series. Because the IGS network is quite sparse, we cannot use a nearby station as is commonly done by climatologists (as in Venema et al. [9]). Instead, for every GNSS station, a series of IWV from each of the two reanalyses is derived, and daily IWV differences are formed, as explained above. In earlier studies, we found that ERA-Interim and GNSS IWV had significant representativeness differences in Antarctica and in regions of steep topography (Andes, Himalayas, etc.) or near the oceans [17]. In this study, we will investigate the impact of representativeness errors on the segmentation results by comparing the results from the two reanalyses. The spatial resolution of the reanalyses is 0.75° × 0.75° for ERA-Interim and 0.25° × 0.25° for ERA5. Reduced representativeness errors are, thus, expected from ERA5 data. Moreover, the IWV values computed from ERA5 are also expected to be of higher quality since this reanalysis used a more recent model and assimilation system, and assimilated a much larger number of observations, especially in recent years [18].
2.3. Homogenization Method
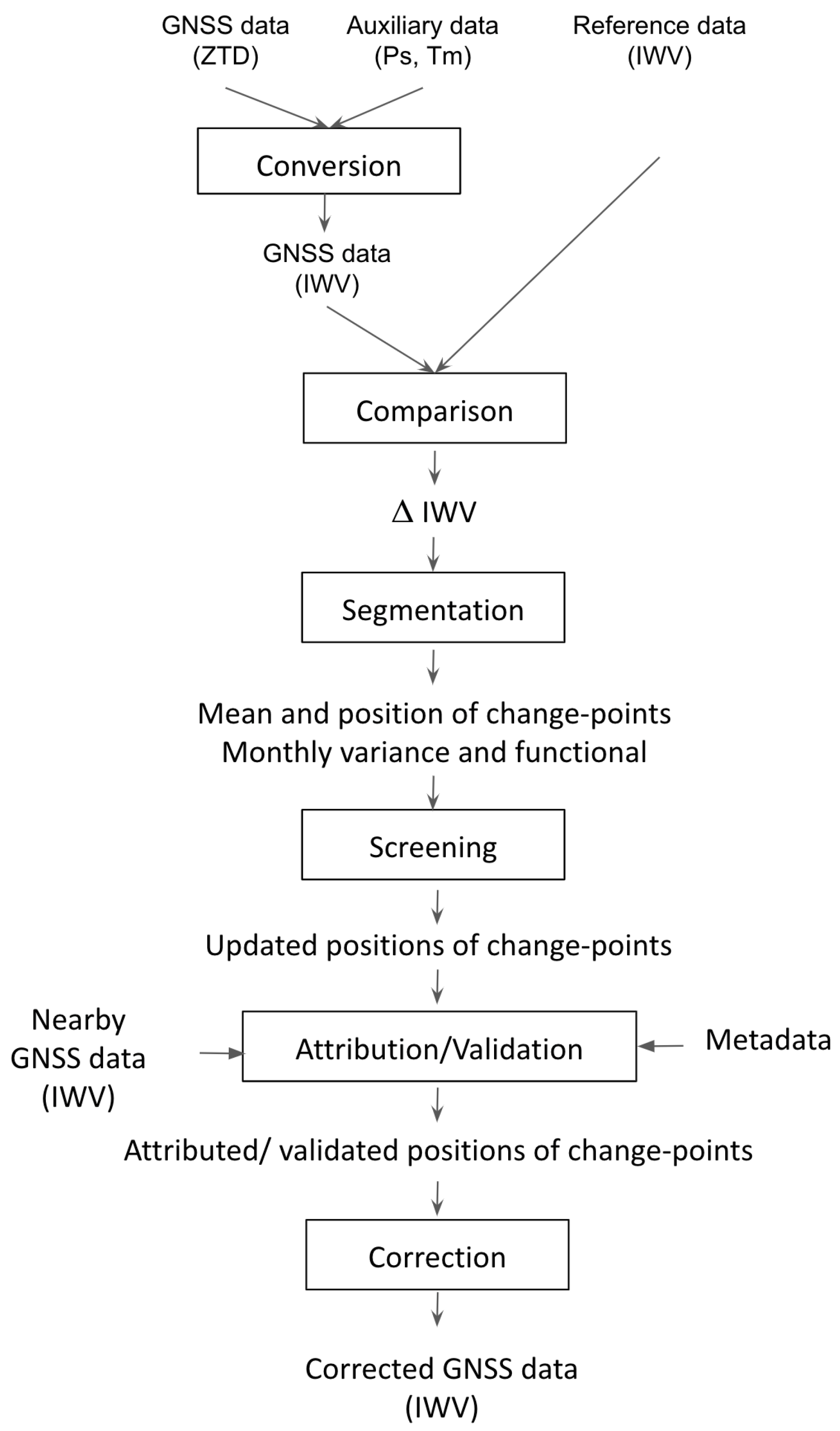
Figure 2 shows the data flow chart starting with the GNSS ZTD data and ending with the corrected IWV series. The first two steps (Conversion and Comparison) are described in the previous sub-section.
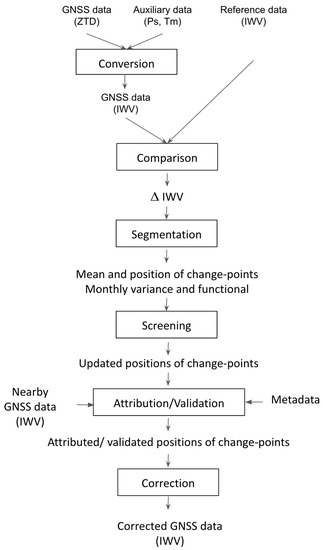
Figure 2.
Flowchart of the general homogenization procedure.
The third step is the segmentation, i.e., the detection of change-points in the mean of the IWV difference time series. Here, we use the fast version of the GNSSfast R package published by Quarello et al. [45]. This version is available on https://github.com/arq16/GNSSfast.git, accessed on 30 July 2021. The segmentation method estimates K, the number of segments, or the number of change-points K-1, the K means of the segments, and the K − 1 positions of the change-points, as well as a periodic bias function f and the monthly variance of the noise (also with annual periodicity), in a unified model for each IWV difference time series. It has been shown in a previous paper that modeling a periodic bias function and a heterogeneous noise helps to accommodate for the representativeness differences between the GNSS IWV data and the reanalysis IWV data (see Quarello [21]). The inference procedure is based on a penalized likelihood approach. Several penalty criteria are considered, but here we will present only the results for the so-called Birgé and Massart’s penalty based on the ‘dimension jump’ proposed by Birgé and Massart [46] and calibrated in Lebarbier [47]. In a previous study, the GNSSseg method was compared to other existing segmentation methods on the basis of a benchmark data set and was found to be one of the most efficient [22].
The noise in the IWV differences is generally not perfectly Gaussian and strong peaks can lead to spurious change-points. These false detections are checked and screened out by a special post-processing procedure, which is symbolized in Figure 2 by the Screening step. In this step, clusters of 2 or more nearby change-points are checked for a significant change in the mean before and after using a weighted t-test. In this study, we consider as a cluster all the change-points closer than 80 days (the value of 80 days was found as optimal based on a mixture model analysis). The change-points within a cluster are flagged as “outliers” in the following. If the change in the mean is not significant (at the level of 5%), all the change-points in the cluster are removed. If it is significant, the group of change-points is replaced with one change-point, and its position is taken as the mean of the positions.
With a relative segmentation approach, such as used here, climatologists often assume that the reference is homogeneous [9]. If the reference is not homogeneous, multiple comparisons are necessary to determine in a statistical way to which of the series each detected change-points belong to. This task is accomplished during the Attribution/Validation step. The attribution of a change-point to GNSS or reference is decided based on the comparison with nearby GNSS series, while the validation is referring to the comparison of the detected change-points with the GNSS metadata. For the attribution step, the idea is to use all the available stations in the GNSS data, as long as the time series covers a period of time encompassing the tested change-point. We tested the procedure with the CODE REPRO2015 data set, including all 434 stations, with a maximum distance of 200 km and a time window of ±six months around the change-points. Based on the available data, about 30% of the change-points from the selected 81 stations could be checked. This number is too small to apply this test in a systematic way to all the data sets used in this study. So, we decided not to include it in the general discussion but only for a few cases studies. Instead, we will only use the validation step with respect to the GNSS metadata with a window of ±62 days, as in Van Malderen et al. [22].
The last step is the correction of the GNSS time series for the changes in the mean based on the attributed/validated change-points. Here, we follow the approach of Van Malderen et al. [22] which consists in subtracting from the GNSS IWV series a piece-wise constant function constructed from the change in means of the GNSS-reference series, where the last segment is taken as a reference. The performance of the correction depends on all the previous steps.
2.4. Trend Estimation Method
Following Weatherhead et al. [48], we use a linear trend model:
where is the IWV time series, the linear trend function, a seasonal component which will be represented by a fourth order Fourier Series, , t is time in days since some reference date, days, and the noise which is assumed to be autoregressive of the order 1 (AR(1)), that is, , where the are independent random variables with zero mean and variance . The AR(1) noise is a good statistical representation of the day-to-day variability in the IWV time series around the mean seasonal cycle. The unknown parameters of this model are: , the mean IWV, the slope of the linear trend, the and coefficients of the Fourier Series, the autocorrelation of the noise, and the variance of the noise. We use a Generalized Least Squares (GLS) algorithm to estimate all the parameters and their formal errors.
3. Results
3.1. Segmentation Results
This section discusses the segmentation results and how they are impacted by four factors: (1) the GNSS data processing (IGS versus CODE), (2) the length of time series (short period, 1994–2010, and long period, 1994–2018), (3) the reference data set (ERAI versus ERA5), and (4) the auxiliary data used in the ZTD to IWV conversion (ERAI versus ERA5).
Table 2 summarizes the segmentation results for all four comparisons. Statistics are given for 81 common stations in both GNSS data sets. They include average data properties, such as the mean of the estimated monthly variances and the standard deviation of the estimated functional (stdf). The segmentation results are compared by means of the total number of detected change-points, both before and after the screening, the number of outliers, the number of metadata validations, and the number of similar detections.

Table 2.
Summary of pairwise comparisons of segmentation results from various data sets used in this work. The validation with respect to GNSS metadata and the similar detection statistics used a closeness window of ±62 days. (a) Segmentation is run over the full time series (1994–2018), but change-points are compared for the time-limited period (1994–2010). (b) This CODE data set uses auxiliary data from ERA5. (c) This CODE data set uses auxiliary data from ERAI.
3.1.1. Impact of GNSS Data Processing
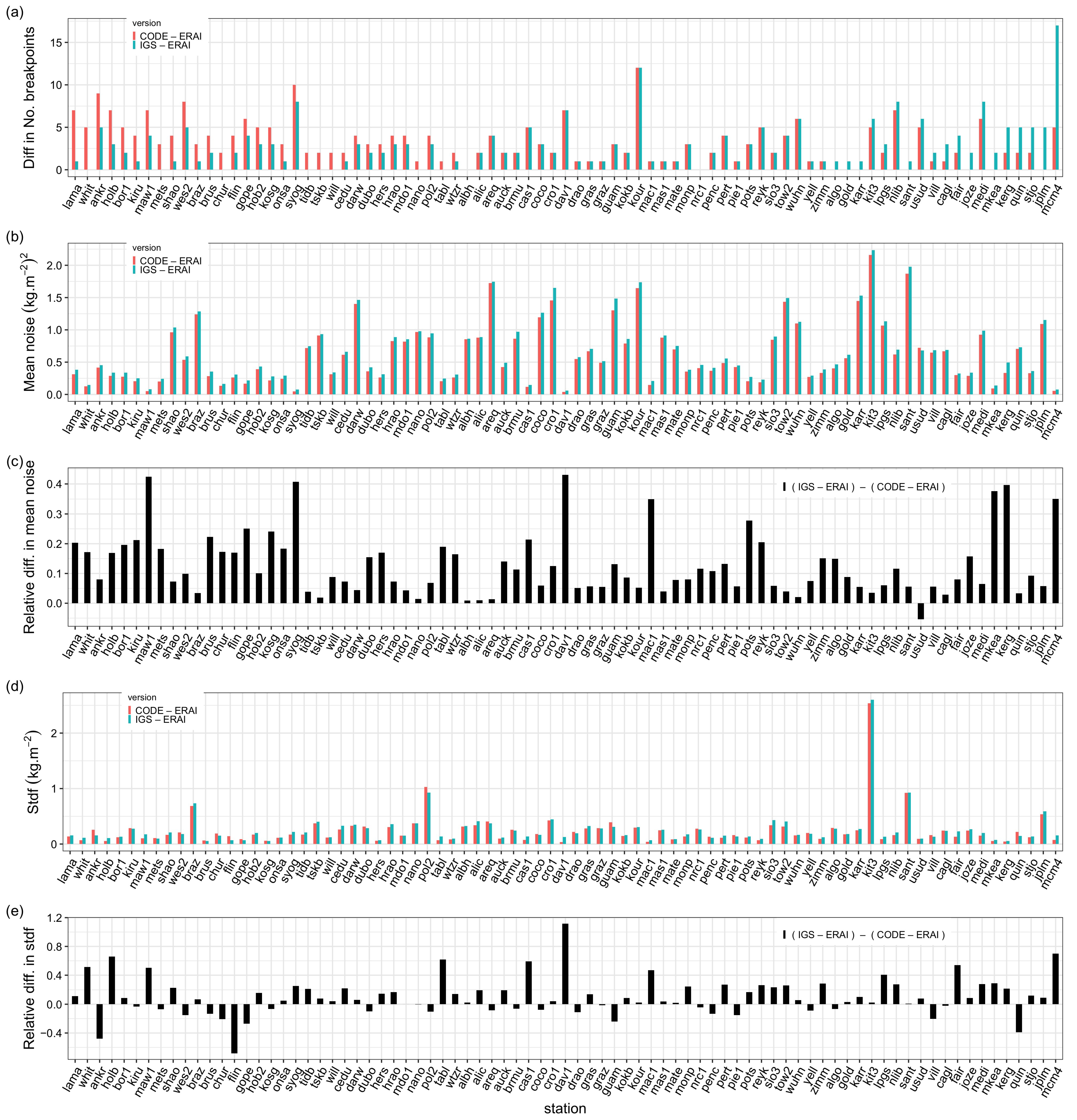
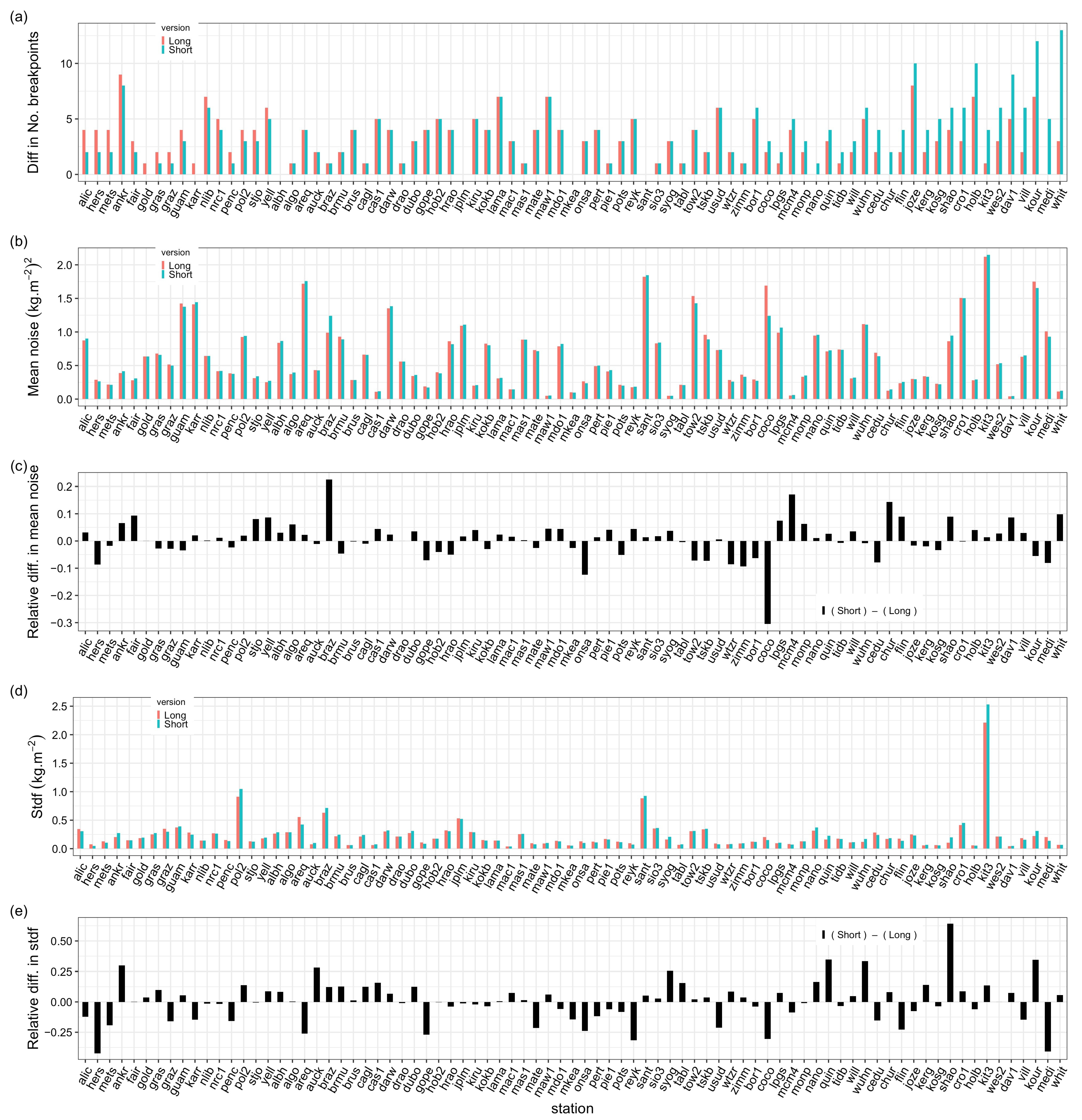
In comparison to CODE, IGS is noisier with respect to the reanalysis with about 10% higher monthly variances in the time-matched data on average (Table 2). Inspection of the monthly variances by station shows that the noise is systematically larger in the IGS data set for all stations except at USUD (Figure 3c). All the stations located in Antarctica (DAV1, MAW1, SYOG, MCM4, MAC1, CAS1) show a significantly larger relative monthly variance in the IGS data set, with a maximum of 43% at DAV1. We believe that the use of the VMF1 mapping function in the CODE solution makes a major difference as it accounts for the high-resolution (6-hourly) temporal variations in the atmospheric (dry and wet) layering, whereas the GMF used in the IGS solution only models a smooth seasonal variation. On the other hand, the stdf, which quantifies the magnitude of the periodic bias, does not show such a systematic difference, although CODE shows smaller values again on average. A majority of stations in the IGS data set have slightly larger stdf (54 stations, i.e., 67%, larger versus 27 stations, i.e., 33%, smaller). For a few stations, the difference in stdf is relatively big, exceeding ±50% (Figure 3d,e). The difference in stdf can be explained by the difference in mapping functions, a priori ZHD, and elevation cutoff angle. Specific cases are discussed below.
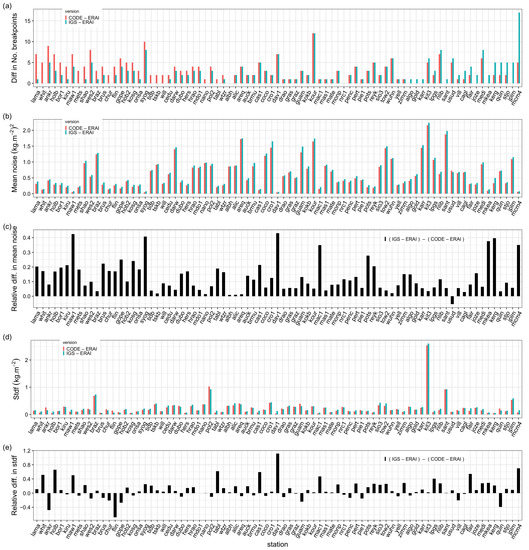
Figure 3.
Comparison of segmentation results from two different GNSS data sets, IGS repro1 (IGS), and CODE REPRO2015 (CODE), at 81 common stations: (a) number of detected change-points, (b) mean of the monthly variance, (c) relative difference in the mean of monthly variance (IGS − CODE), (d) standard deviation of the functional modeling the periodic bias (stdf), (e) relative difference in the standard deviation of the functional (IGS − CODE). All the parameters are estimated from time-matched series for the period 1995–2010. The relative differences are computed relative to the mean (IGS + CODE)/2.
The segmentation found more change-points in the CODE data set, both before and after the screening, compared to IGS, and slightly more outliers (38 versus 36). After screening, the validation percentages of the two data sets are very similar (28.9 and 29.9%). However, the number of similar change-points is relatively small (48.8%), indicating a strong dependence of the segmentation results on the GNSS processing method. There are several reasons that can explain the difference in the number, as well as the position, of change-points. Firstly, the segmentation is sensitive to the magnitude and stationarity of the noise. Since the noise is higher for the IGS data set, a number of small offsets are not detected there. Secondly, IGS includes mapping function changes in 2008 and 2009, which are not included in CODE. They lead to 15 extra-detections in IGS. Thirdly, the improved tropospheric model and updated antenna/radome calibrations used in the CODE processing are likely to reduce some mean biases and seasonal variations in addition to the reduced noise, which may lead to a difference in the number and positions of change-points (e.g., higher periodic biases in IGS may lead to extra change-points). To summarize, some of the data features may increase the number of change-points in IGS, while others may increase the number in CODE. Below, we examine a few special cases.
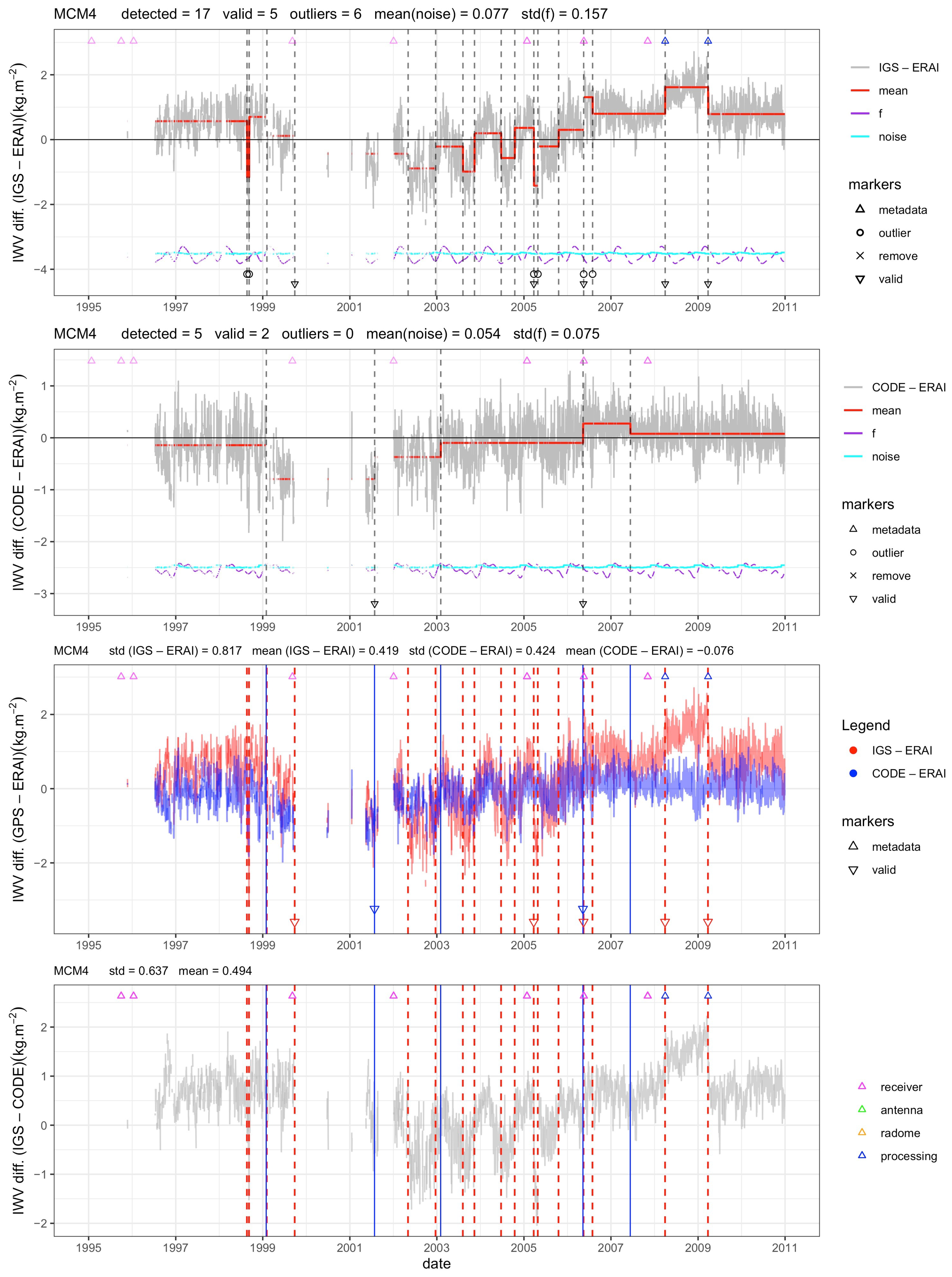
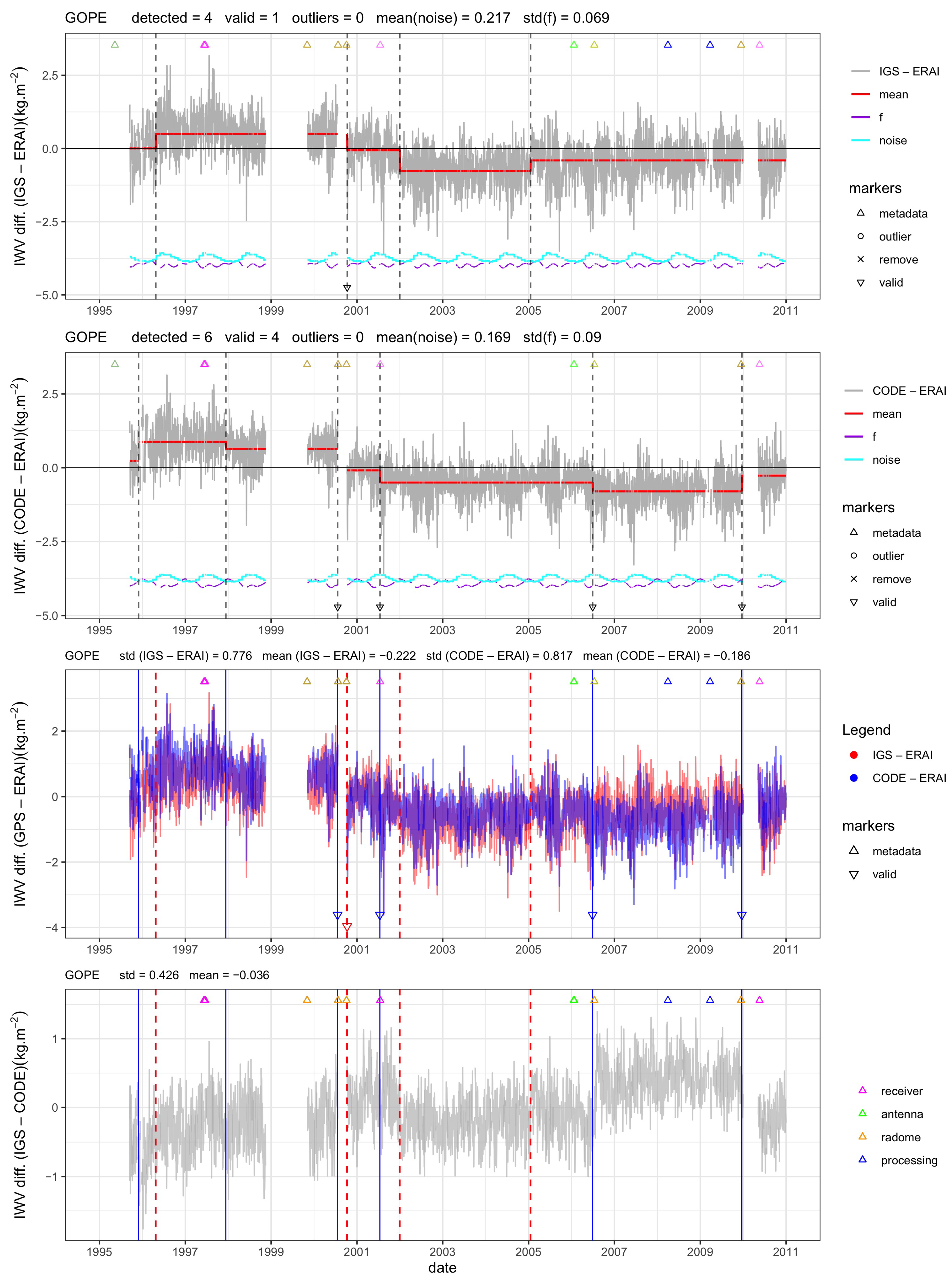
Figure 4 shows a pathological example (station MCMC4, McMurdo, Antarctica). For this station and all other stations in Antarctica, the difference in a priori ZHD leads to a reduced bias (mean and seasonal) in the CODE IWV estimates with respect to ERAI. The mean difference between CODE and IGS for MCM4 is about −0.5 kg m. Large oscillations are seen in both solutions during the period 2002–2006. These oscillations are believed to arise in the GNSS measurements due to snow intrusion between the antenna and radome as discussed by Koulali and Clarke [49]. Most of the stations in Antarctica show this feature for some periods. In the CODE solution, the oscillations are slightly smaller, which may be explained by the use of a lower cutoff angle which would mitigate the anomalous path delay variations partly. In the IGS series, these oscillations lead to several extra change-points, although they are not due to equipment changes and, thus, are not validated by the metadata. The mapping function change in 2008 (from GMF to NMF) and 2009 (from NMF to GMF) in IGS also leads to 2 additional change-points. As a consequence, the IGS series at MCM4 has 17 change-points, including 6 outliers due to high noise, whereas the CODE solution has only 5 change-points. The number of validations with respect to metadata are 5 and 2, for IGS and CODE, respectively, with one validated change-point in 2006 (due to a receiver change) similar in both cases.
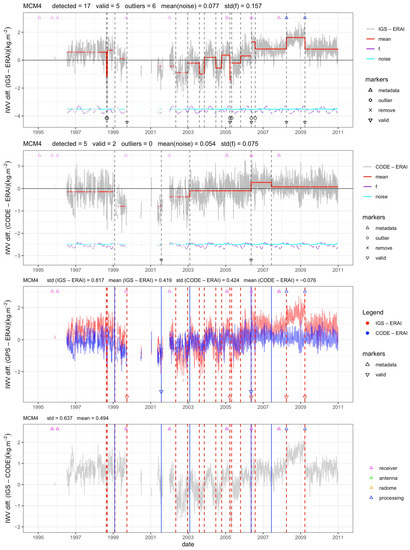
Figure 4.
Time series of IWV differences at station MCM4 (McMurdo, Ross Island, Antarctica). The two top plots show the results for IGS-ERAI and CODE-ERAI, with segmentation results superposed (the red line shows the weighted mean as estimated by the segmentation method, where the black dashed lines indicate the change-point positions, the cyan line is the estimated monthly mean variance, and the purple line is the estimated functional modeling the periodic bias). The validated change-points are indicated by a marker at the lower end of the black dashed line. The 3rd plot from the top shows the two IWV difference series and detected change-points for clarity of the comparison. The lower plot shows the difference, IGS-CODE, with change-points superposed. In all plots, the markers at the top indicate the equipment changes. The color code is given in the lower plot. The processing changes apply only to IGS.
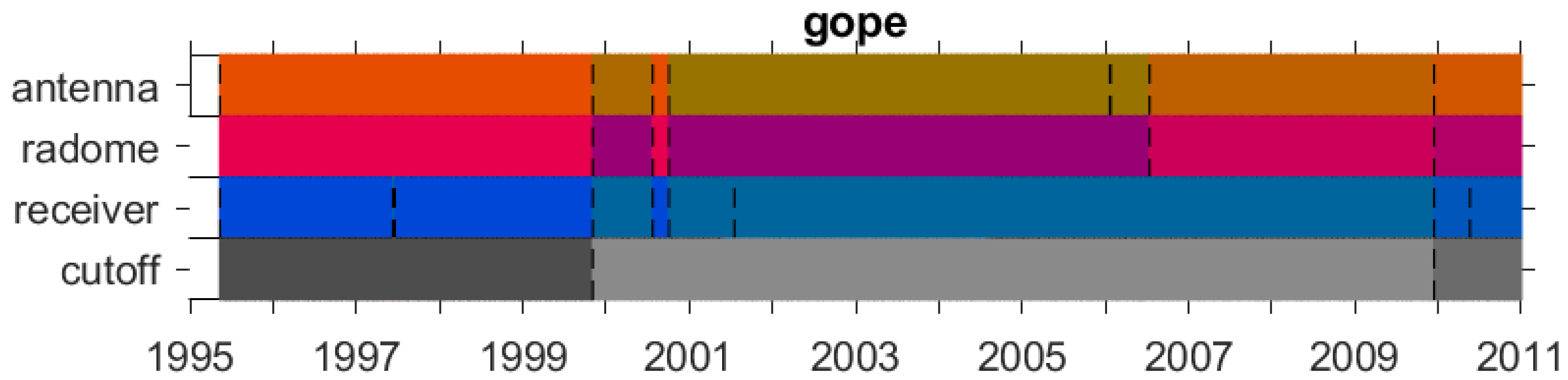
Next, we examine another example (station GOPE, Czech Republic), where the equipment changes have a strong and different impact on the CODE and IGS solutions. Over the study period (1995–2010), many changes occurred at this station. Figure 5 gives a visual description of these changes based on the IGS metadata, where each color represents a specific equipment type (producer and product), and the vertical dashed lines indicate a sub-type change (serial number or firmware for receivers). Five different antenna/radome types were used at this site: TRM14532.00/NONE (from 13 May 1995 to 4 November 1999 and from 24 July 2000 to 4 October 2000), ASH701073.3/SNOW (from 4 November 1999 to 24 July 2000), ASH701946.3/NONE (from 4 October 2000 to 14 July 2006), and TPSCR3_GGD/CONE (from 14 July 2006 to 14 December 2009), TPSCR.G3/TPSH (since 14 December 2009). Three different receiver types were used: TRIMBLE_4000SSE (from 13 May 1995 to 4 November 1999, and 24 July 2000 to 4 October 2000), ASHTECH_Z18 (from 4 November 1999 to 24 July 2000, and 4 October 2000 to 14 December 2009), and TPS_NETG3 (from 14 December 2009 to 8 August 2018). The figure shows that the same receivers were removed and reinstalled for some periods, as well as that they got several firmware updates (see the dashed vertical lines). The cutoff angle was also changed twice, going from 15 degrees to 5 degrees on 4 November 1999, and from 5 degrees down to 0 degree on 14 December 2009. The impact of these equipment and setting changes on the GPS-ERAI IWV differences is obvious from Figure 6. For example, there is a strong change in the mean IWV difference for both solutions before and after 4 October 2000. This change is detected (and validated) by the segmentation in both data sets. Before that date, CODE has 2 other change-points, while IGS has only one, although IGS shows similar changes in the mean to CODE but they are not detected. Neither of these change-points is explained by the metadata. After 4 October 2000, CODE has 3 more change-points, while IGS has only 2. All 3 are validated in the case of CODE, and none is validated in the case of IGS. However, the IGS detected change-points seem correct as they well represent the changes in the mean of that series. The difference in the number and positions of change-points between the IGS and CODE segmentation results is actually due to the difference in the two GNSS IWV data, as highlighted in the lower plot of Figure 6. This difference can be explained by the different antenna/radome calibration models used in the two GNSS processing. The most striking bias between the two series is for the period from 14 July 2006 to 14 December 2009 where the TPSCR3_GGD/CONE antenna/radome pair is used. In the igs05.atx calibration file used in the IGS solution, this calibration was of “Field” type (i.e., an older relative calibration dating back to April 2005), while the CODE solution used a more recent “Robot” type calibration (from April 2013). For all other antenna/radome types used at this station, both GNSS solutions used similar calibration types (“Robot” or “Copied”), although the CODE calibrations were more recent in all cases, which may explain the small residual biases between the two solutions. Another abrupt shift in the CODE−IGS series is observed on 1 January 2002 which coincides with the introduction of GLONASS observations in the CODE solution. A closer look reveals that, for some reason, the shift is merely in the IGS−ERAI series and that the CODE−ERAI series is, rather, drifting.
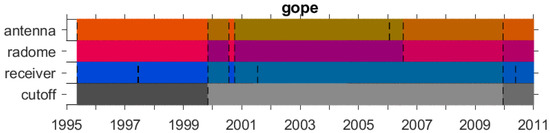
Figure 5.
Schematic view of the equipment changes that occurred at station GOPE (Ondrejov, Czech Republic) during the period 1995–2010. Each color symbolizes a different equipment type (producer and product). Vertical dashed lines show additional changes with the same type (serial number or firmware upgrade in the case of receivers). Information extracted from the IGS site logs (ftp://igs.ign.fr/pub/igs/igscb/station/log/, accessed on 30 July 2021).
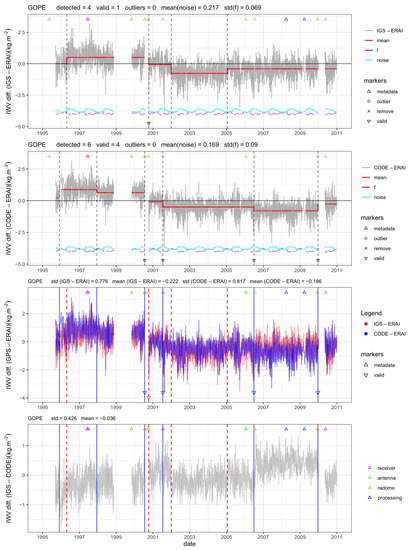
Figure 6.
Similar to Figure 4, but for station GOPE (Ondrejov, Czech Republic).
The GOPE example shows that antenna/radome changes at a site are likely to produce an abrupt shift in the mean IWV, even though calibration models are used during the data processing. Different calibration types and versions have different biases, leading to different inhomogeneities in the two reprocessed GNSS data sets analyzed in this work and to different segmentation results. Many such cases could be found by inspecting the time series and segmentation results. In some cases, receiver changes and observation cutoff angle changes also induce abrupt shifts of different amplitudes for the two data sets. This feature might be due to the use of different processing cutoff angles (3 degrees in CODE and 7 degrees in IGS). In other cases, we can see a small drift (below 0.5 kg m) between the two solutions, which might be due to the change in the number of satellites used in the processing, especially with the inclusion of GLONASS observations in the CODE solution starting from 2002, although not many GNSS stations were recording GLONASS data in the period from 2002 to 2010. Since the amplitude of such small drifts is generally small compared to the noise, it would not induce extra change-points in the segmentation; although this cannot be guaranteed for sure, it may impact the trend estimates.
3.1.2. Impact of the Length of Time Series
The impact of the length of time series is inspected from the comparison of CODE-ERAI segmentation results where the segmentation was run both on the full (1994–2018) series and on the series limited to 1994–2010. The change-points statistics (number of detections, outliers, and validations) reported in the second section of Table 2 are given for the common period (1994–2010).
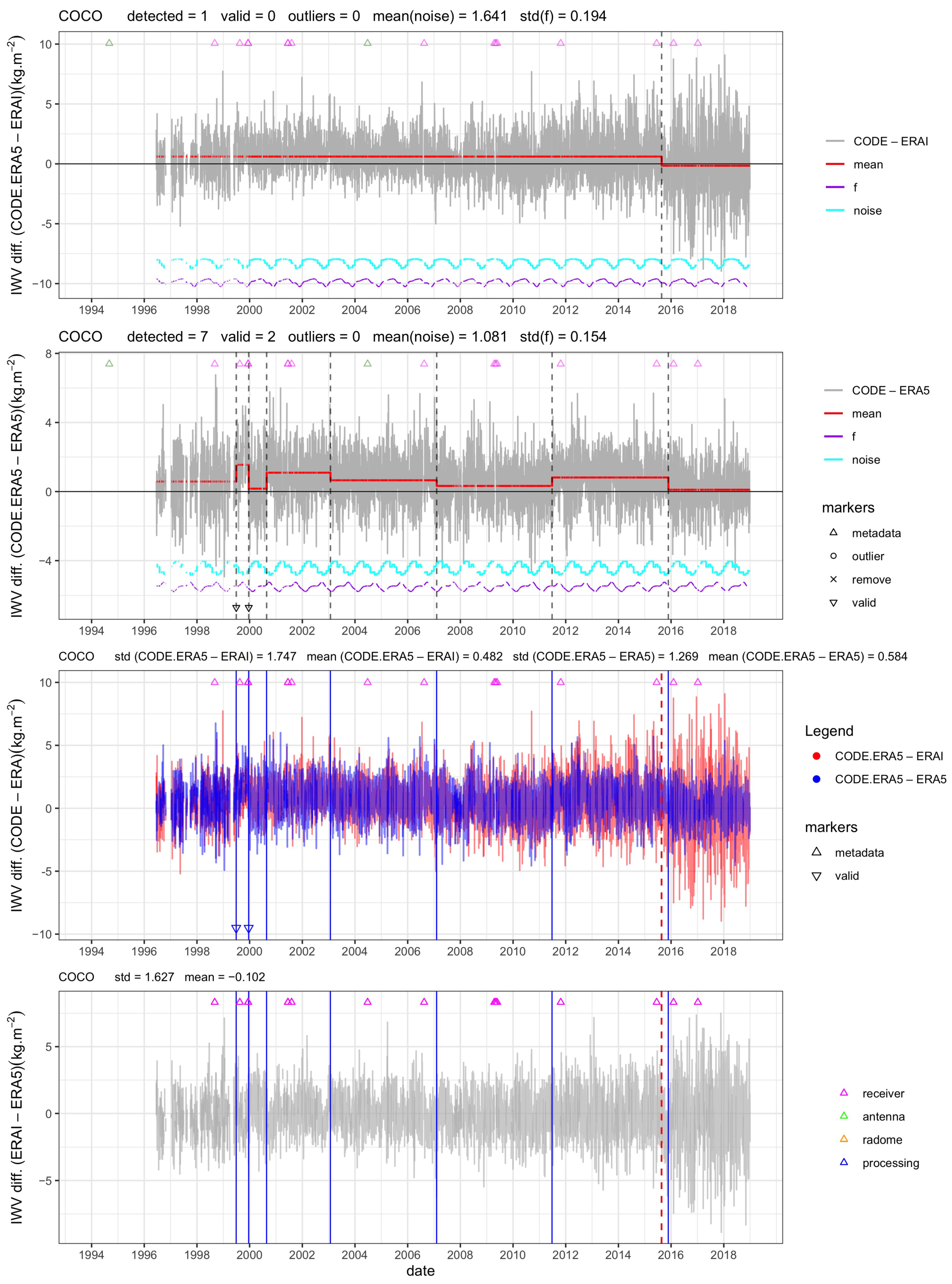
It can be deduced from Table 2 that the estimated monthly mean variance and the estimated stdf are nearly similar on average over all stations. However, inspecting individual stations shows that small differences exist (Figure 7b–e). Slightly more than half of the stations have smaller variance in the full series (57 versus 43%) and smaller stdf (52 versus 48%). This difference can be explained by the fact that the GNSS IWV estimates become more accurate with time; thus, the agreement with the reanalysis improves in the more recent years included in the full series. On the other hand, the cases where the noise is larger in the full time series may either be due to situations where the GNSS measurements get noisier, or the ERA-Interim reanalysis becomes less accurate with time. This is, for example, the case at station COCO where the monthly variance is 25% higher in the full series. The same situation is observed at many tropical stations, although the quality of the GNSS data has generally improved at these sites. We suspect that the problem is in the quality of the ERAI reanalysis, which may indeed have degraded in recent years due to the end of several satellite missions [18]. One obvious case is with station COCO discussed in the next sub-section.
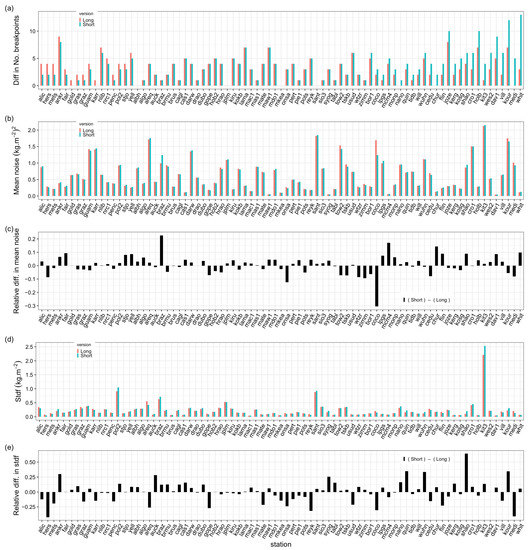
Figure 7.
Similar to Figure 3, but comparing segmentation results from two different lengths of the CODE data set (long time series, from 1994 to 2018, short time series, from 1994 to 2010). The mean noise and standard deviation of the functional (stdf) are representative of the full times series, but the number of breakpoints are counted in the common period only (1994–2010).
The number of change-points detected from the long time series in the common period is smaller than for the short time series, both before and after screening (Table 2). The same is found for the number of outliers, while the percentage of validations is consistently increased. These results indicate that, on average, the segmentation yields more accurate results with the long time series. The difference in the number of change-points can be understood from the fact that the penalty criterion is conservative and tends to choose a small number of change-points. For instance, the total number of change-points found from the long time series is 321 (not shown), i.e., not much larger than the total number for the short time series (296, as reported in Table 2). Because of this conservative property, the number and positions of the change-points in the two series cannot be expected to be the same at most stations. Figure 7 shows that 39 stations (48%) have the same number of change-points (although the positions may not be the same), 16 stations (20%) have a larger number in the long series, and 26 stations (32%) have a smaller number in the long series. Nevertheless, 80.8% of the change-points are similar (i.e., within ± 62 days).
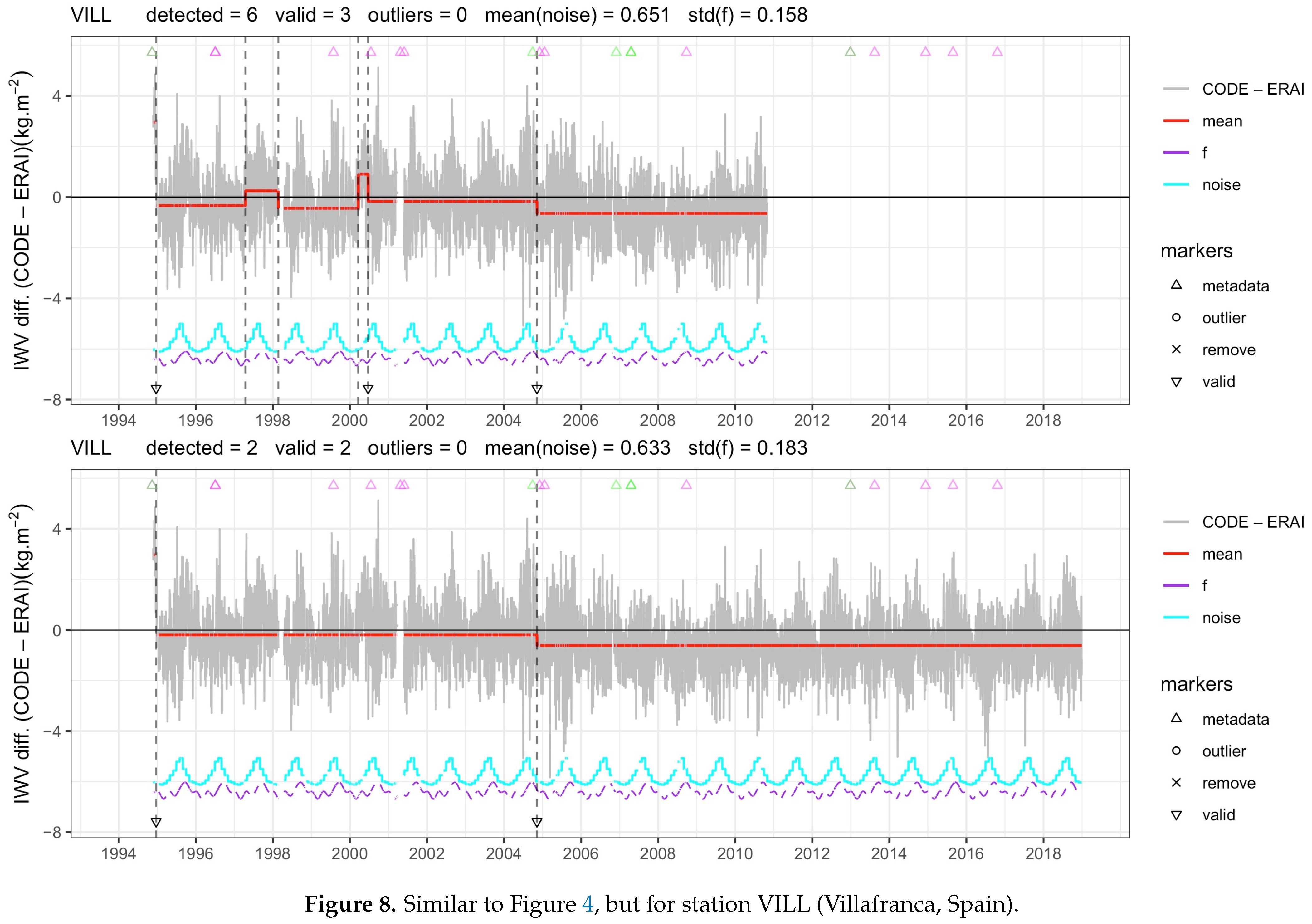
Figure 8 shows the example of station VILL (Villafranca, Spain), where the mean noise and stdf are very similar for the two-time series, but the segmentation results are quite different: 6 change-points are detected in the short time series and 2 in the long time series. Two change-points are similar in both series and are validated. The additional change-points found in the short time series capture short but significant variations in the mean. These change-points are not retained in the long time series because other such variations are seen all along in the long time series. The penalty criterion avoids selecting all those change-points, and the final optimal solution eventually has only one change-point. This solution seems more reasonable.
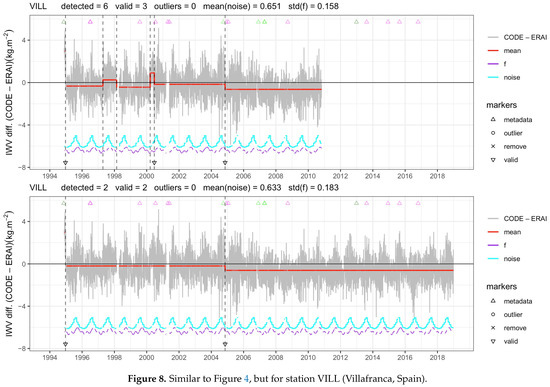
Figure 8.
Similar to Figure 4, but for station VILL (Villafranca, Spain).
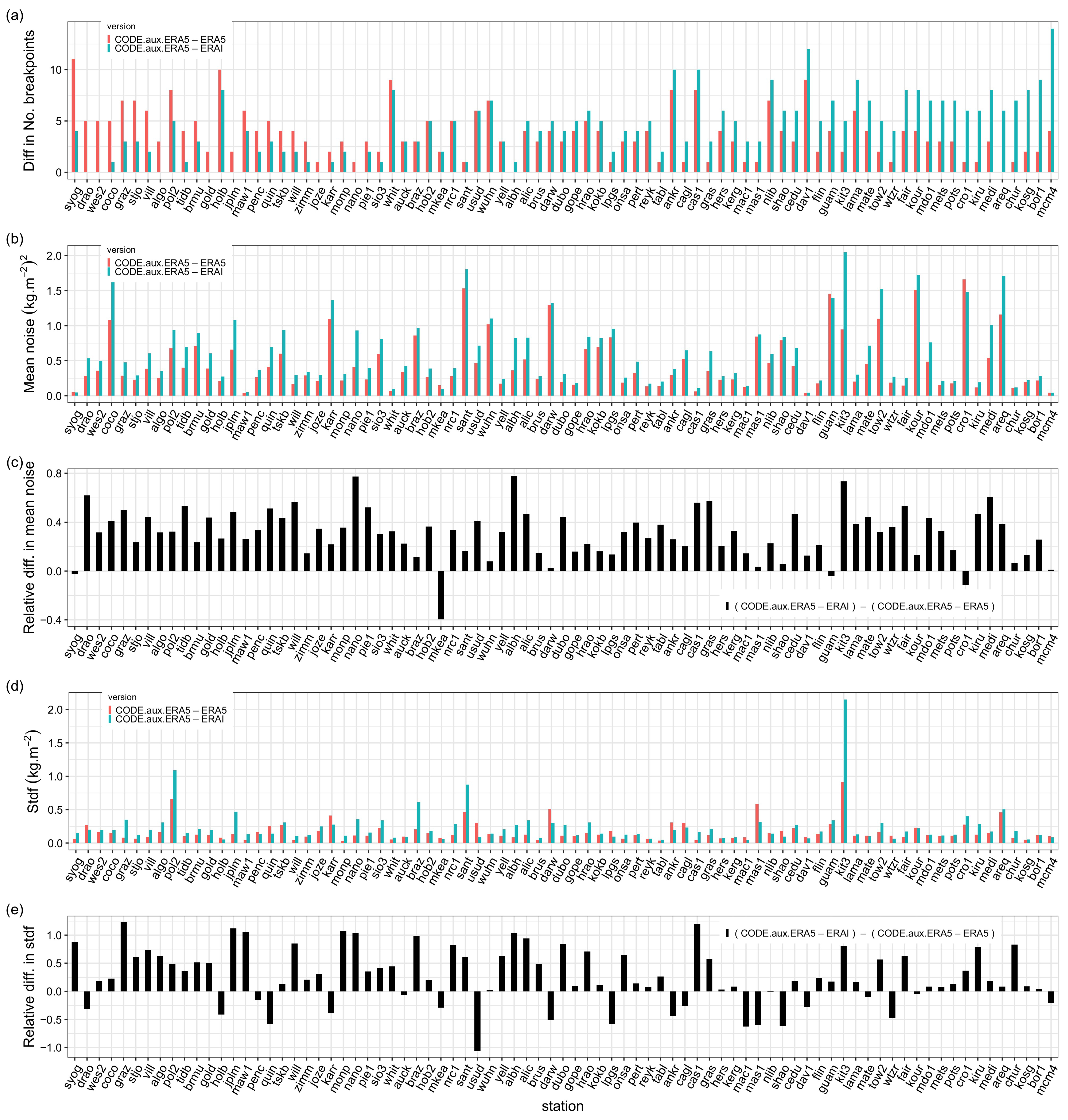
3.1.3. Impact of the Reference Data Set
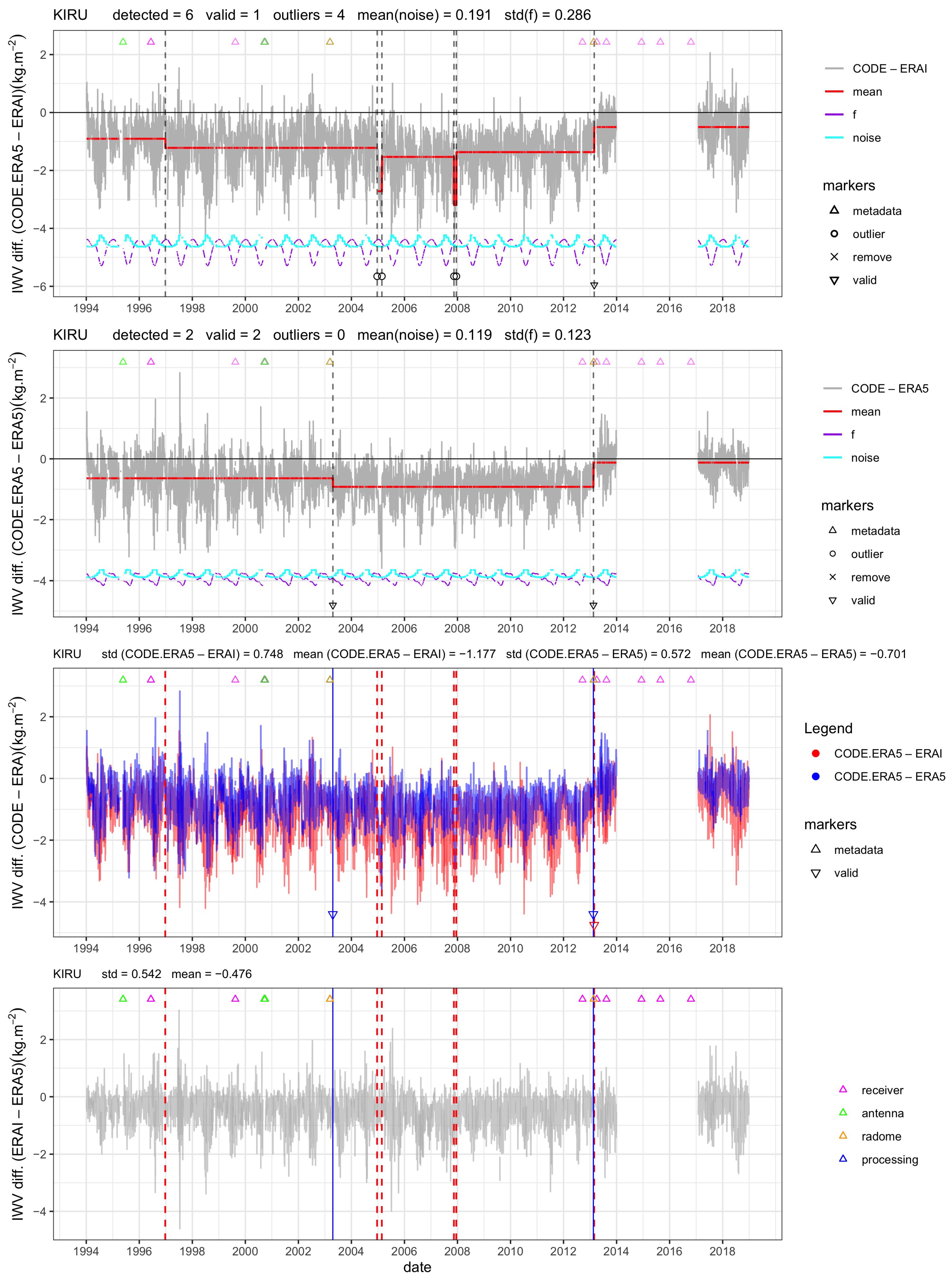
The third section of Table 2 summarizes the segmentation results when either ERAI or ERA5 is used as a reference, i.e., the segmentation is run for CODE-ERAI or CODE-ERA5 IWV differences, when the same auxiliary data is used in the GNSS ZTD to IWV conversion (here from ERA5). Globally, both the mean noise and the stdf with ERA5 are reduced by 25% compared to ERAI. Figure 9c,e show that the reduction in noise and stdf is observed at 95% and 75% of all stations, respectively. This difference can be explained by the lower representativeness error in ERA5 due to higher spatial resolution, as well as higher quality of the IWV temporal variations in this reanalysis, probably due to the assimilation of more satellite observations. Figure 10 shows the most striking case of increase in noise with time for ERAI. The impact on the segmentation results is quite significant. Only one change-point is detected in the more noisy series, while seven change-points are detected in the less noisy one. At many stations, there is also an excess noise in ERAI during the moist period of each year; see the example of station KIRU (Kiruna, Sweden) in Figure 11. At this station, the CODE-ERAI series has much larger seasonal variations in the noise and in the functional than CODE-ERA5. This leads to more change-points in more noisy series (6 versus 2) because of the sharp increase in the noise during some years, which is not well represented by the periodic bias and monthly variance. As a result, four outliers are detected in the CODE-ERAI segmentation results. In the CODE-ERA5, the two change-points are validated by the metadata, which is, again, better than in the CODE-ERAI results. Other examples with large changes in stdf are stations KIT3, POL2, and SANT (Figure 9d). These stations were also pointed as extreme cases of representativeness errors in ERAI by Bock and Parracho [17] due to steep orography.
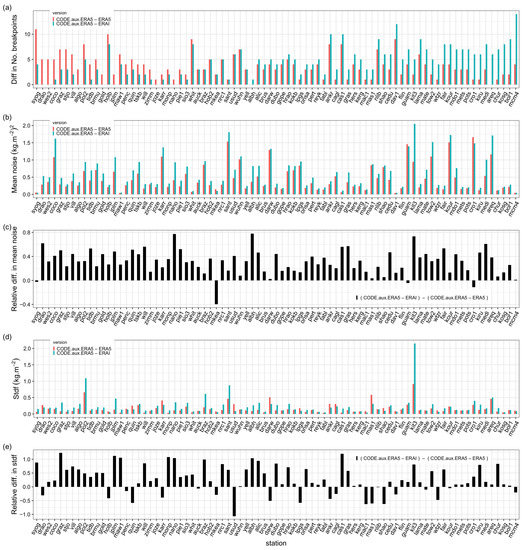
Figure 9.
Similar to Figure 3 but comparing the segmentation results using two different reference data sets, ERA-Interim (ERAI) and ERA5.
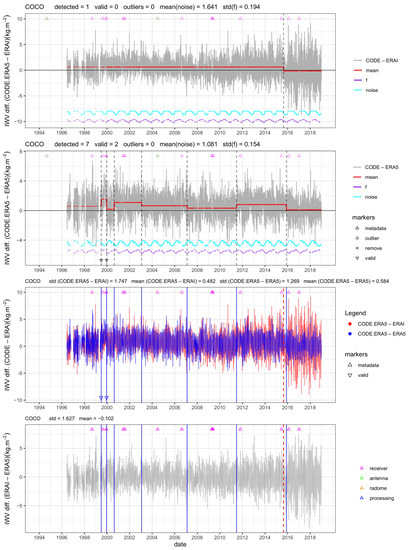
Figure 10.
Similar to Figure 4, but for station COCO (Cocos (Keeling) Island, Australia).
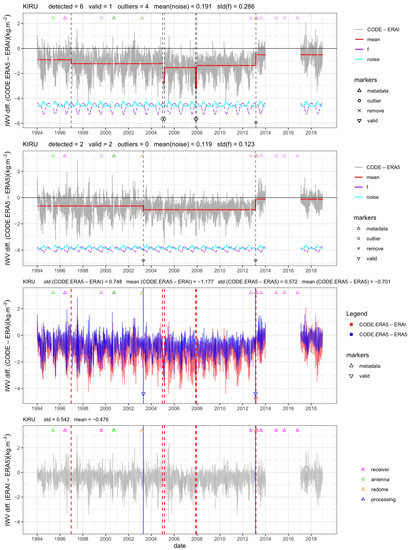
Figure 11.
Similar to Figure 4, but for station KIRU (Kiruna, Sweden).
From Table 2, we see that the total number of change-points is larger when ERA5 is used as a reference. This can be understood as the consequence of the general decrease of the noise and periodic bias with this reanalysis, as discussed in the case of station COCO above. When the noise is decreased, it is easier to detect a small offset in the time series. With the increase in the number of change-points, the number of outliers is increased, as well. However, after screening, the percentage of validations is higher with ERA5 as a reference. So, there is a clear benefit of using the more recent reanalysis as a reference.
Figure 9a shows that 37 stations (46%) in CODE-ERA5 have a higher number of change-points than CODE-ERAI, 29 stations (36%) have a smaller number, and 15 stations have a similar number. From Figure 9c,e, we see that MKEA (Mauna Kea volcano, Mauna Kea, USA) and USUD (Usuda, Japan) are two cases where the mean noise or stdf increased with ERA5 as a reference by 40% and 107%, respectively. Both stations are located in regions of steep topography where both reanalyses have significant representativeness errors compared to the GNSS observations. In the case of MKEA, the station is located at an altitude of 3729 m, whereas the altitudes of the surrounding grid points from both reanalyses are much lower. In the case of USUD, the situation is opposite, with the station is closer to the sea level than the surrounding grid points from the reanalyses.
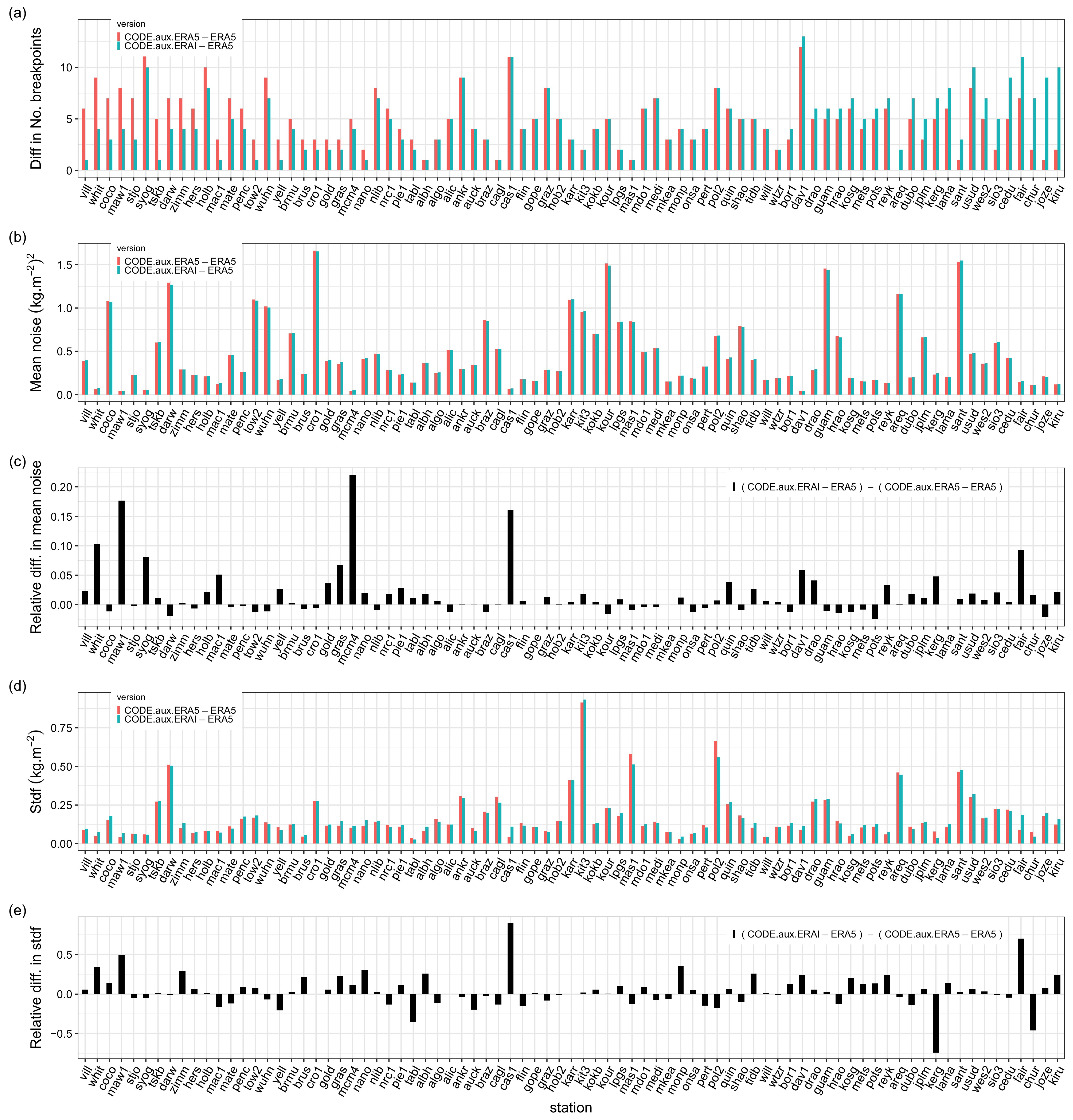
3.1.4. Impact of the Auxiliary Data Set
The auxiliary data used in the conversion of GNSS ZTD to IWV impacts the quality of the GNSS IWV data and may lead to different segmentation results in a similar way as the processing and reference data sets. Table 2 shows that on average the mean noise and stdf are the same, but the segmentation statistics are slightly different (number of change-points, outliers, and validations). Figure 12 shows that the noise and stdf results actually change for many stations. In general, the absolute values of the noise are very close, but the relative differences are not that small. At 60% of the stations, ERAI induces larger noise than ERA5, with values up to 10–20%, while, at 40% of the stations, ERA5 yields similar or higher mean noise in ERAI, but the relative increase there is small (2.5% at maximum). These results are consistent with the representativeness differences between the reanalyses discussed above, although the pressure and temperature data are much less subject to small-scale variations than IWV.
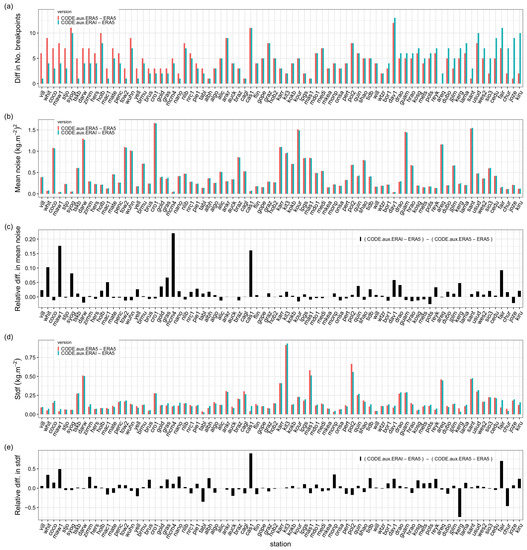
Figure 12.
Similar to Figure 3, but comparing segmentation results from GNSS data sets that used two different auxiliary data, from ERA-Interim (ERAI) and ERA5.
The results are similar for stdf (60% of the stations have a larger periodic bias with ERAI), but the relative difference can be much higher (up to ). This is because many stations are located in complex regions, such as the mountains and near the oceans. In some cases, ERA5 induces a larger periodic bias compared to the ERAI, for instance, at CHUR (Churchill, MB, Canada), KERG (Port aux Français, French Southern Territories), and TABL (Wrightwood, CA, USA).
Although the total number of change-points in the two data sets are very similar before and after screening (see Table 2), the number of change-points can be quite different from station to station (Figure 12a). The results with auxiliary data from ERAI show 18% more outliers than with ERA5. From this perspective, it is better to use ERA5. However, the percentage of similar change-points is still quite high (around 71%), which points to a moderate impact of the auxiliary data on the segmentation results in the end.
3.2. IWV Trend Estimates
3.2.1. Impact of GNSS and Reanalysis Data Set Properties on Trend Estimates
Table 3 summarizes the trend results obtained with the different GNSS data sets and the two reanalyses discussed in Section 3.1. The numbers report the mean and standard deviation of the trend estimates (in kg m year) over the 81 stations, as well as the number of significant trends at the 0.05 level (using a Student’s t-test), and the standard error in the trend estimate (). Following from Section 3.1, three-time periods, with lengths 16, 17, and 25 years, are presented, respectively.

Table 3.
Summary of IWV trends from various data sets used in this work. The number of stations with significant trends at level is given in brackets. (a) GNSS data converted with auxiliary data from ERAI and segmentation applied the CODE—ERA5 IWV difference. (b) GNSS data converted with auxiliary data from ERA5 and segmentation applied the CODE—ERAI IWV difference. (c) GNSS data converted with auxiliary data from ERA5 and segmentation applied the CODE—ERA5 IWV difference.
From the two reanalyses, we see that the mean trends are positive, indicating a net moistening, globally, with slightly different values between the three periods. This reminds us that the mean linear trends from different periods may not generally agree because they are strongly influenced by inter-annual to inter-decadal variability. However, the decrease in the standard deviation is noticeable from the shorter to the longer period (e.g., from 0.052 kg m year to 0.031 kg m year for the ERA5 data set), which indicates a decreasing influence of the inter-annual variability with time, as well as more consistent trend estimates from the global network with long time series. This decrease is also seen in the GNSS data sets, raw and corrected. It is also consistent with a decrease in the standard error with the longer time series, from 0.035 to 0.018 kg m year, and the subsequent increase in the number of significant trends, e.g., from 8 to 35 with ERA5. ERAI and ERA5 show different means and standard deviations in the short periods, which is not surprising according to the differences in the IWV time series extracted from the two reanalyses (see Section 3.1). The mean difference is negligible on the longer period, but the variability is slightly smaller in ERA5. The RMS difference amounts to 0.013 kg m year (not reported in Table 3), which indicates that there are substantial local differences in the trends from the two reanalyses. Note that the mean positive (moistening) IWV trend of 0.027 kg m year from the reanalyses (and also from the GNSS data) is fairly consistent with the prediction from Clausius-Clapeyron law of 7% IWV increase per 1 °C induced by the global increase in temperature of ∼1 °C over the past four decades, given a global mean IWV of 18 kg m [50].
Next, we examine the results for the two GNSS data sets, IGS and CODE, before and after homogenization, and their differences with respect to ERA5. In this section, we consider two different corrected (homogenized) data sets. In the first one, we use only the change-points validated from the metadata, while, in the second one, we use all the detected change-points. We will refer to these data sets as “partially corrected” and “fully corrected” data sets, respectively. Ideally, we could also consider a third version where only the change-points attributed to GNSS are included, but this is not possible here because no nearby stations are available in many cases (see the discussion in Section 2). The raw GNSS trends show quite a large difference in the mean (0.024 versus 0.018 kg m year) and a RMS difference of 0.016 kg m year (not reported Table 3). This difference is not unexpected given the differences in the data processing (Section 2) and the inhomogeneities they induce, as discussed from the segmentation results in Section 3.1. Especially, the inhomogeneities in the IGS data set due to the older antenna/radome calibration models may be a significant cause of uncertainty in the trends. The mean difference is reduced in both corrected data sets, although the RMS difference is not reduced in the partially corrected data set (0.019 kg m year), contrary to what one would expect after both data sets are homogenized. This result can be understood from the fact that the segmentation results of the IGS and CODE data sets are sometimes very different and the validated change-points may not coincide in both solutions (see Figure 4 and Figure 6). On the other hand, the IGS and CODE GNSS fully corrected data sets are much more consistent (RMS difference of 0.006 kg m year). The latter result gives good confidence that the segmentation method is able to detect all the significant change-points in either data set. However, we know that not all these change-points may come from the GNSS time series, but some of them may be due to inhomogeneities in the reference reanalysis (in this case, ERAI). As a consequence, the fully corrected GNSS trends will be very close to the trends from the segmentation reference data set in the end. In Table 3, we give the RMS difference between the GNSS data sets and ERA5 (which is taken as another reference, although not independent from ERAI). In general, the RMS differences between the fully corrected GNSS trends and ERA5 are significantly smaller than between the raw or the partially corrected trends and the ERA5 trends. We note also that the number of significant trends is drastically reduced for both corrected GNSS data sets (from 20 to 9 for IGS and from 18 to 9 for CODE). This indicates that a large portion of uncorrected stations had significant trends because of inhomogeneities in their time series.
The results from the CODE time-limited data set are quite similar, although the change in the mean trend is reduced between the uncorrected and the corrected series, and the agreement with ERA5, in the end, is improved. The number of significant trends is also higher than with the time-matched data sets. Recall that the main difference between this data set and the CODE time-matched is only one more year and fewer gaps, but these differences can have a sensible impact on the segmentation results and trend estimates.
The results from the long time series using either ERAI or ERA5 as auxiliary data or reference data for the segmentation are presented in the rightmost part of Table 3. The mean trends from the uncorrected GNSS data are slightly larger than the trends from the reanalyses (0.030–0.033 kg m year for GNSS compared to 0.027 kg m year for ERAI and ERA5). The corrected GNSS series achieve closer mean trends to the reanalyses, as well as reduced RMS differences. The smallest RMS difference with respect to ERA5 is found with the fully corrected GNSS data using ERA5 as a reference, which is to be expected (ERA5 is not independent in this case). In terms of variability, the partially corrected trends show slightly smaller standard deviation, i.e., smaller spatial variability, which suggests more homogeneous and consistent trends in the global network. The slightly higher variability in the fully corrected GNSS trends might be due to some inhomogeneities in the reference series (ERA5 or ERAI). This point is further discussed in the next sub-section. The impact of the segmentation reference (ERAI versus ERA5) on the corrected GNSS trends is small in terms of mean, but the RMS difference between the GNSS trends at individual stations amounts to 0.015 kg m year for the partially corrected series and 0.012 kg m year for the fully corrected series (not shown). The impact of the auxiliary data is significantly smaller, with a RMS difference between the trends using ERAI and ERA5 as auxiliary of 0.008 kg m year for the partially corrected series and 0.002 kg m year for the fully corrected series (not shown).
3.2.2. Impact of Homogenization on GNSS Trend Estimates
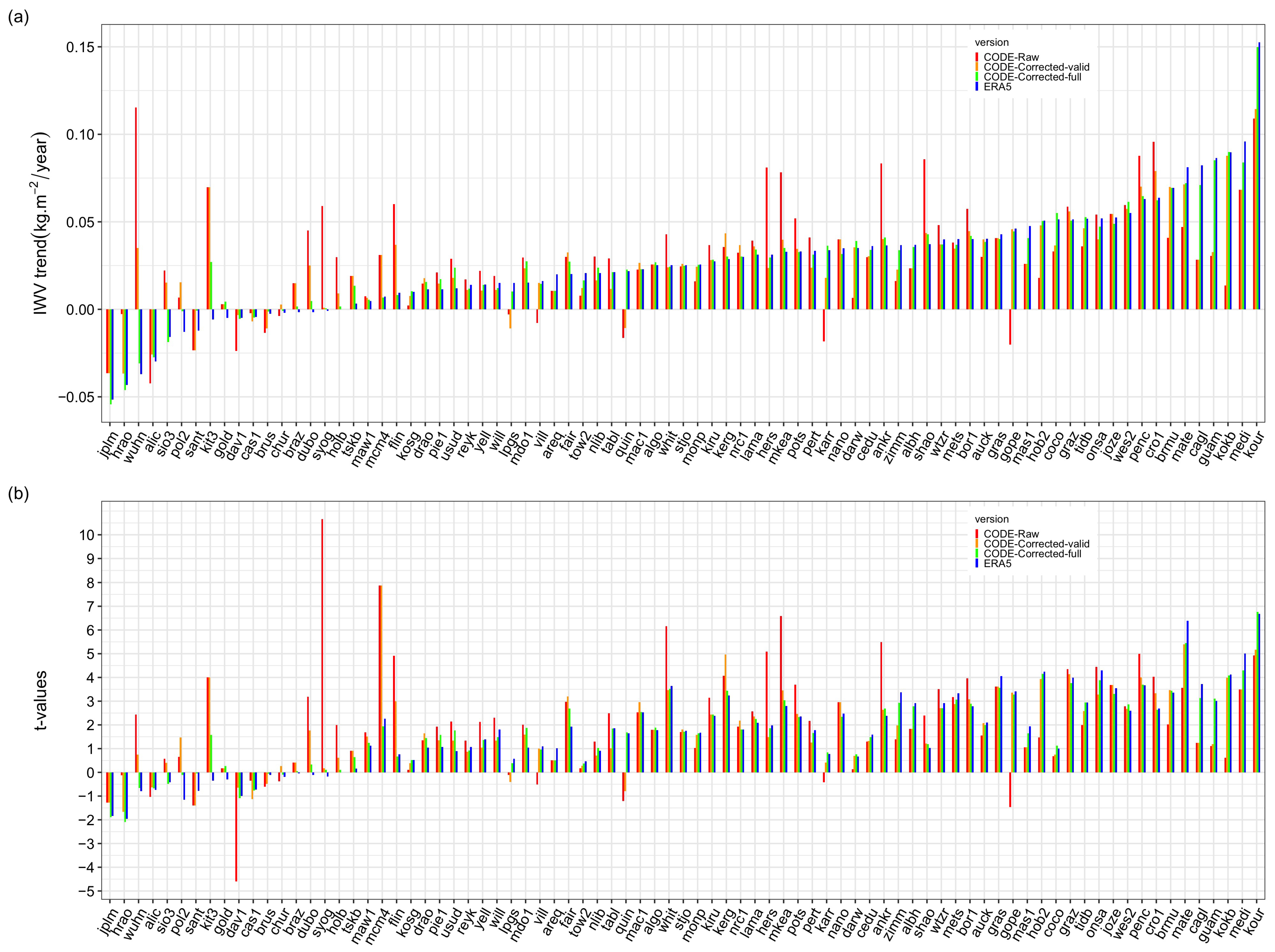
In this sub-section, we analyze in more details our ’best’ data set at hand, i.e., the long CODE GNSS series (1994–2018) using ERA5 as auxiliary data and reference for the segmentation. Figure 13a shows the IWV trend estimates for the GNSS data, uncorrected and corrected, and ERA5. A majority of the GNSS stations have positive trends (89% with the partially corrected data, 86% with the fully corrected data, versus 80% for the ERA5 data), consistent with the overall positive mean trend of 0.027 kg m year reported in Table 3. Among these, only of the corrected GNSS trends are significant at p = 0.05 (or t = 1.99, see Figure 13b), versus 49% with the uncorrected GNSS data, and 41% with ERA5. The largest positive trend is found for KOUR (Kourou, French Guiana), reaching a value of ∼0.110 kg m year (t = 5) for the uncorrected and partially corrected trends, and 0.150–0.153 kg m year (t ∼ 7) for the fully corrected GNSS data and ERA5. This station, as well as a few others in the Tropics (KOKB, GUAM, BRMU, CRO1, etc.), shows consistent and significant moistening over the past 2.5 decades. Strong moistening is also found at several Mediterranean stations (MEDI, CAGL, MATE), confirming the strong warming in this area [51]. A few stations show consistent drying from GNSS data (uncorrected and corrected) and ERA5, mostly in arid regions, such as JPLM (Pasadena, CA, USA), HRAO (Krugersdorp, South Africa), ALIC (Alice Springs, Australia), and SANT (Santiago, Chile).
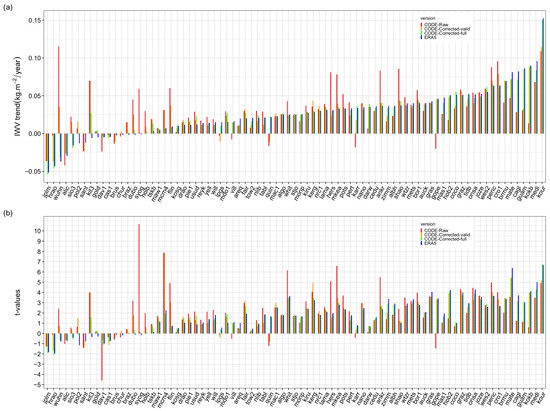
Figure 13.
Comparison of: (a) trend estimates kg m year, and (b) t-values from different uncorrected (raw) and corrected GNSS data (CODE with auxiliary ERA5 and reference ERA5) and ERA5 at 81 common stations.
A striking feature in Figure 13 is that many uncorrected GNSS trends are quite large, and significant, while the corrected trends are much smaller, and are, in some cases, insignificant. The trends of the partially corrected series are significantly different from the uncorrected trend (with a RMS difference of 0.022 kg m year), although they agree with each other better than with ERA5 (0.033 kg m year). On the other hand, the trends of the fully corrected GNSS data are much closer to ERA5 (with a RMS difference of 0.006 kg m year) than to the uncorrected trends (RMS difference of 0.031 kg m year). The RMS difference between the partially corrected and the fully corrected trends is 0.016 kg m year. It is actually expected that the corrected trends will tend to align with the reference data (in this case, ERA5). However, the partially corrected trends are relatively independent from the reference since only about 36.5% of the detected change-points are validated. It is also noticeable that the partial correction has a strong impact on the trends at many sites, such as a change in the sign (e.g., GOPE, KARR, VILL, etc.), a change from significant to insignificant (e.g., HERS, SHAO, SYOG, WUHN, etc.), or vice versa (GOPE, KOKB, TIDB, etc.). The trends of the fully corrected data get closer to ERA5.
Four cases will be discussed in more detail in the following, where the IWV trends change from significant to insignificant, or vice versa. The corresponding time series and change-points are shown in Figure 14.
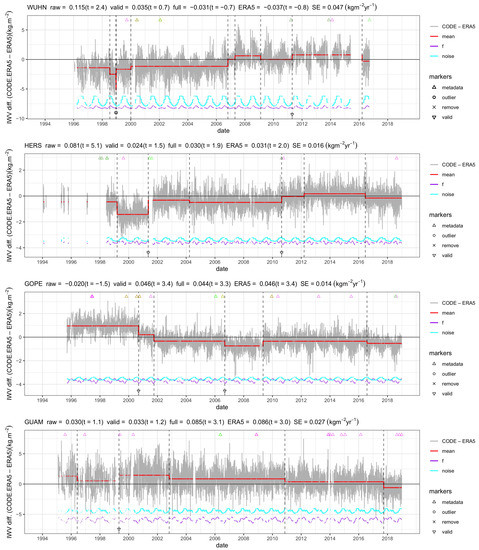
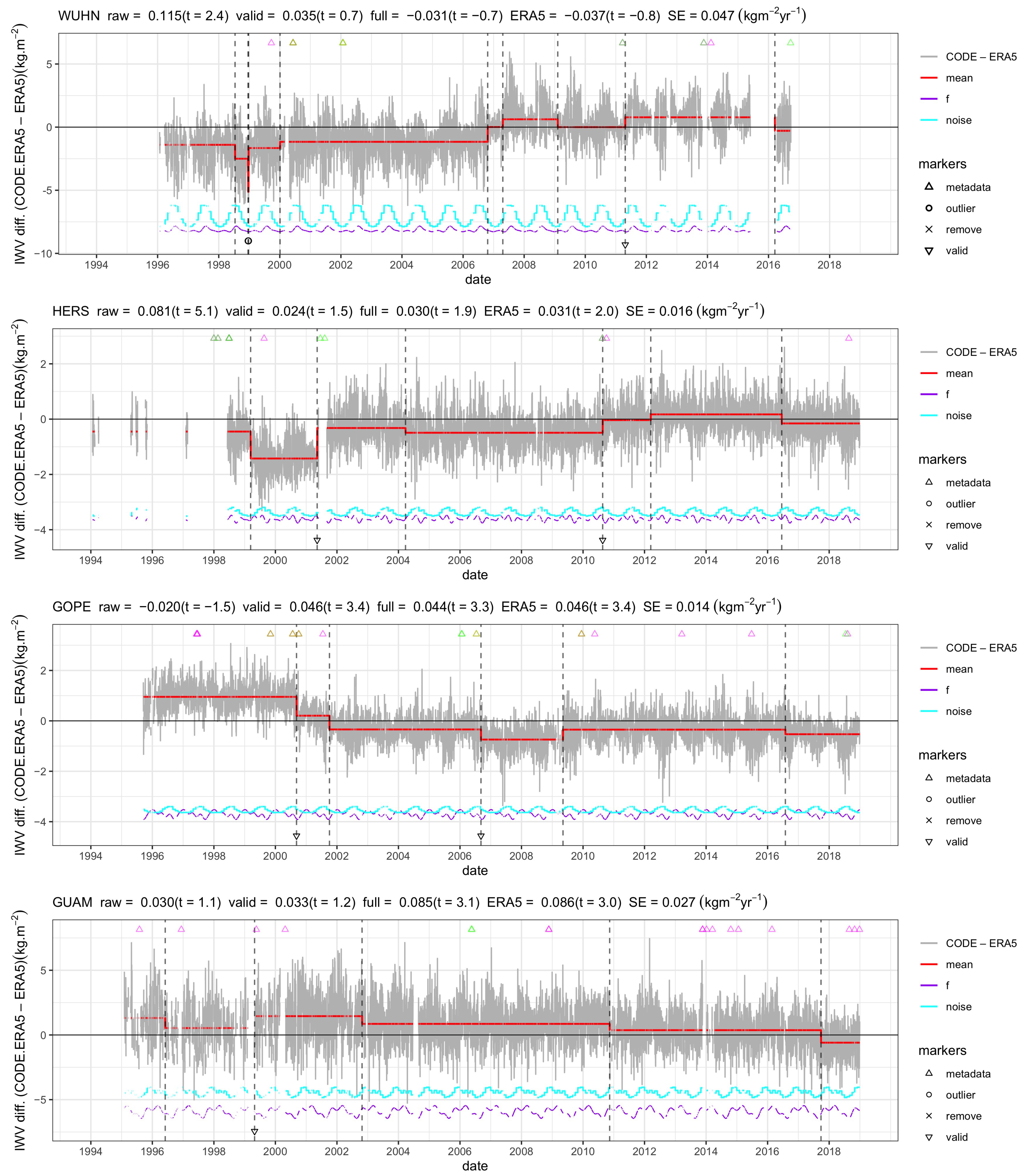
Figure 14.
Similar to the upper plot in Figure 4, but for different stations: HERS (Hailsham, United Kingdom), GOPE (Ondrejov, Czech Republic), KOKB (Waimea, United States), and GUAM (Dededo, Guam). The IWV differences are computed as GNSS - ERA5, where GNSS is converted using auxiliary data from ERA5, and the segmentation is run with ERA5 as a reference.
Firstly, we examine the case of station WUHN (Wuhan, China), where the uncorrected GNSS trend is positive and significant (0.115 kg m year, t = 2.44), while the fully corrected trend and the ERA5 trend are of opposite sign (−0.031 and −0.037 kg m year, respectively) but not significant (t = −0.65 and −0.79). At this site, the change in sign of the trend is suspected to arrive from a strong downward shift in the ERA5 time series, which was already commented by Parracho et al. [14] and attributed to a change in the radiosonde type in Wuhan in 2006 impacting the ERA-Interim reanalysis. Parracho et al. [14] also noticed an extended region of a negative trend in eastern China, in contradiction with the GNSS observations and the MERRA-2 reanalysis. A similar shift is actually detected in the nearby station SHAO (Sheshan, China), where the uncorrected GNSS trend of 0.086 kg m year is decreased to 0.043 kg m year in the fully corrected data. The ERA5 trend is even smaller (0.037 kg m year), although not negative. At both WUHN and SHAO, the GNSS trend changes from significant to insignificant after correction.
Secondly, let us examine the case of station HERS (Hailsham, UK). The segmentation detected six change-points, among which only two are validated with the metadata. Overall, the mean shifts are going upwards, meaning that the inhomogeneities induce a spurious positive trend in the GNSS series. The correction of the GNSS series for two validated change-points has a strong impact on the trend, decreasing it from 0.081 to 0.024 kg m year and from significant to insignificant (t-value from 5.1 to 1.5). Including the 4 additional change-points has a further, although small, effect, leading to a final GNSS trend of 0.030 kg m year, close to the ERA5 trend (0.031 kg m year). Two nearby stations (HERT and HRM1) could be used in the attribution step to confirm the two validated change-points but not the other ones. The other change-points could not be tested. The impact of the correction is substantial and seems justified at this station, with a final trend reduced by −0.051 kg m year, i.e., a factor of 2.7.
Next, we examine station GOPE (Ondrejov, Czech Republic), which has a strong significant trend after correction but insignificant before. GOPE is a special case, which has a negative trend in the raw data in contradiction was many surrounding stations in Europe, such as ZIMM (Switzerland), WTZR (Germany), and BOR1 (Poland), which have positive trends. This feature was already noticed by Parracho et al. [14] from the uncorrected IGS data set over the shorter period (1995–2010). Figure 14 shows that the mean shifts are going downwards, so inducing a negative trend in the GNSS series compared to ERA5. Two change-points are validated with the metadata. After correction of these change-points, the trend goes from a insignificant drying of −0.020 kg m year to a significant moistening of 0.046 kg m year. Three other change-points have a minor impact (the fully corrected trend is 0.044 kg m year) because the most important break in 2000 is validated. For this station, we could also test the attribution with several nearby stations collocated with station WTZR (distant by 162 km). The two validated change-points, as well as the one in 2001, could be attributed to GOPE.
The last example is station GUAM (Dededo, Guam), in the western tropical Pacific, which has a similar large trend in ERA5 to KOKB, another station in the Pacific Ocean. The trends are very different between the partially and fully corrected GNSS series at GUAM because only one change-point is validated, and it is located near the beginning of the series. The last three change-points have a strong impact on the GNSS correction, although their origin is questionable. Indeed, they are located quite far away from any known equipment change reported in the metadata. The last change-point (on 26 September 2017) could be checked in the attribution step with the nearby station GUUG (Mangilao, USA), located at a distance of 18 km from GUAM. Comparing the GNSS series at GUUG to the ERA5 series at GUAM revealed a significant change in mean on this date. From this result, we should attribute this change-point to the ERA5 series and not the GNSS series. At this site, thus, we also suspect the other unvalidated change-points to be due to ERA5. This assumption may be further checked by inspecting observation statistics from the assimilation system, but this is left for future work.
4. Conclusions
This study investigated the sensitivity of the segmentation method and the IWV trend estimates to different GNSS and reference data properties. It was shown that the GNSS processing methods and the reference data (ERAI versus ERA5) have the strongest impact on the segmentation results (i.e., number and positions of change-points), while the impact is weaker when the length of the time series (17 versus 25 years) or the auxiliary data (ERAI versus ERA5) are changed. Changing the latter two was shown to achieve 81% and 71% similar change-points, but only 45–49% when the GNSS data set or the reference was changed. These discrepancies in the results indicate that the segmentation is sensitive to small changes in the mean signal, in the noise, and in the periodic bias. These features are determined by several aspects of the GNSS processing procedure, especially: the a priori ZHD correction, the antenna/radome calibration model, the mapping functions, and the elevation cutoff angle. The more recent and more accurate ZHD correction, antenna/radome calibration model, and mapping functions used in the CODE reprocessing achieve smaller noise and periodic bias but, at the same time, lead to an increase in the number of detected change-points because the segmentation is able to detect smaller changes in the mean. The same is observed when the reference is changed from ERAI to ERA5. The reduction in the noise and periodic bias in ERA5 is partly due to the better spatial resolution and partly to the more recent atmospheric model and assimilation of more observations. In terms of the percentage of validation of the detected change-points with respect to the GNSS metadata, the length of the time series has the strongest impact. The average percentage is ∼30% with the short time series (16 or 17 years), while it rises to 34–36% with the long time series (25 years), for a window of ±62 days. This difference might be due to the particular penalty function that we used here [46,47]. The penalty function might be calibrated differently to achieve a better balance between the probability of detection and the probability of false detection to our particular data [6].
This study also points to the strong impact of the inhomogeneity correction on the estimated trends. When only the change-points validated with the metadata are used, the impact of the correction is substantial on the global mean trend, on the dispersion, and on the RMS difference with respect to ERA5. When all the detected change-points are used, the mean and dispersion are again modified, but to a lesser extent, and the RMS difference with ERA5 is further reduced. The latter feature is expected when ERA5 or ERAI are used as a reference in the segmentation, especially since a few change-points may be due to the reanalyses (e.g., suspected at stations WUHN, GUAM). The uncertainty in the estimated trends from the use of the different reprocessed GNSS data sets or reference reanalysis in the segmentation is about 0.015–0.019 kg m year (RMS difference between the tested pairs of data sets) when only the validated change-points are used and 0.002 to 0.012 kg m year when all the change-points are used. The auxiliary data has a marginal impact on the trends. The longer time series (25 years) provides higher accuracy in the trend estimates, with a mean standard error of 0.018 kg m year and a dispersion of ∼0.03 kg m year throughout the global network. The homogenized GNSS trends and both reanalyses agree in the global mean IWV trend estimate of 0.027 kg m year, which indicates a global moistening over the past 2.5 decades at a rate close to the 7% per degree of warming predicted by Clausius Clapeyron equation [50].
The main limitation of our current homogenization method is the attribution step (Figure 2), which could not be used to check all the change-points because of the lack of nearby stations. In future work, we plan to include reprocessed GNSS data from additional stations in regions where dense networks are available (e.g., Europe, USA, Japan, etc.). Some limitations of the current segmentation method were highlighted, as well, especially the dependence on the length of the time series, which may be mitigated by careful calibration of the penalty function. The segmentation method is also sensitive to the long-term variations in the noise and bias, which are not specifically modeled here (we assume both are periodic with a fundamental period of 1 year). At some sites, strong inter-annual or decadal variations in the noise and/or bias were captured by the segmentation. These spurious change-points need to the detected and removed, unless the long-term variations are reduced, e.g., from the use of a better reference data set, such as a nearby GNSS station, rather than a reanalysis.
Finally, this study also helped to better understand the performance and limitations of the GNSS data processing procedures. This knowledge can be helpful in the future to reprocess the GNSS data and produce better “homogenized” daily IWV time series at the processing level.
Author Contributions
E.L., O.B. and K.N.N. developed the statistical conceptualization methods of the work. Data and climatological aspects were dealt with by O.B., and computational issues were handled by O.B. and K.N.N., all shared in the writing of the manuscript. A.Q. developed the segmentation method and R package used in this study. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the CNRS program LEFE/INSU through the project VEGAN.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The daily IWV data set based on the IGS repro1 ZTD data (120 stations, period 1995–2010) is available from https://dx.doi.org/10.14768/06337394-73a9-407c-9997-0e380dac5591, accessed on 30 July 2021 [43]. The daily IWV data set based on the CODE REPRO2015 ZTD data (436 stations, period 1994–2018) is available from https://dx.doi.org/10.25326/18, accessed on 30 July 2021 [44].
Acknowledgments
The authors are grateful to AERIS, the French data and service center for atmosphere, for providing the ERA-Interim and ERA5 reanalysis data, and hosting the GNSS IWV data sets. The contribution of the fourth author has been conducted as part of the project Labex MME-DII (ANR11-LBX-0023- 01) and within the FP2M federation (CNRS FR 2036).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CODE | Center for Orbit Determination in Europe |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| ERP | Earth Rotation Parameter |
| ERAI | ECMWF reanalysis Interim |
| ERA5 | ECMWF reanalysis v5 |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GMF | Global Mapping Function |
| IGS | International GNSS Service |
| IWV | Integrated water vapor |
| JPL/NASA | NASA’s Jet Propulsion Laboratory |
| NMF | Neill Mapping Function |
| PC0 | Phase Center Offset |
| PCV | Phase Center Variation |
| PWV | Precipitable Water Vapor |
| VMF | Vienna Mapping Function |
| ZHD | Zenith Hydrostatic Delay |
| ZTD | Zenith Tropospheric Delay |
| ZWD | Zenith Wet Delay |
References
- Caussinus, H.; Mestre, O. Detection and correction of artificial shifts in climate series. J. R. Stat. Soc. Ser. C Appl. Stat. 2004, 53, 405–425. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, J.; Wang, X.L.; Lund, R.; Lu, Q.Q. A Review and Comparison of Changepoint Detection Techniques for Climate Data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Jones, P.D.; Raper, S.C.B.; Bradley, R.S.; Diaz, H.F.; Kellyo, P.M.; Wigley, T.M.L. Northern Hemisphere Surface Air Temperature Variations: 1851–1984. J. Clim. Appl. Meteorol. 1986, 25, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Easterling, D.; Peterson, T. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Climatol. 1995, 15, 369–377. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. A J. R. Meteorol. Soc. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N. Detection of Undocumented Changepoints Using Multiple Test Statistics and Composite Reference Series. J. Clim. 2005, 18, 4271–4286. [Google Scholar] [CrossRef]
- Szentimrey, T. Development of MASH homogenization procedure for daily data. In Proceedings of the Fifth Seminar for Homogenization and Quality Control in Climatological Databases, WCDMP-No. 71, Budapest, Hungary, 29 May–2 June 2008; pp. 123–130. [Google Scholar]
- Costa, A.C.; Soares, A. Homogenization of Climate Data: Review and New Perspectives Using Geostatistics. Math. Geosci. 2009, 41, 291–305. [Google Scholar] [CrossRef]
- Venema, V.K.C.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertacnik, G.; Szentimrey, T.; Stepanek, P.; Zahradnicek, P.; et al. Benchmarking homogenization algorithms for monthly data. Clim. Past 2012, 8, 89–115. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Bussinger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Bourcy, T.; David, L.; Goutail, F.; Hoareau, C.; Keckhut, P.; Legain, D.; Pazmino, A.; Pelon, J.; et al. Accuracy assessment of water vapour measurements from in situ and remote sensing techniques during the DEMEVAP 2011 campaign at OHP. Atmos. Meas. Tech. 2013, 6, 2777–2802. [Google Scholar] [CrossRef] [Green Version]
- Van Malderen, R.; Brenot, H.; Pottiaux, E.; Beirle, S.; Hermans, C.; De Maziere, M.; Wagner, T.; De Backer, H.; Bruyninx, C. A multi-site intercomparison of integrated water vapour observations for climate change analysis. Atmos. Meas. Tech. 2014, 7, 2487–2512. [Google Scholar] [CrossRef] [Green Version]
- Ning, T.; Wickert, J.; Deng, Z.; Heise, S.; Dick, G.; Vey, S.; Schöne, T. Homogenized Time Series of the Atmospheric Water Vapor Content Obtained from the GNSS Reprocessed Data. J. Clim. 2016, 29, 2443–2456. [Google Scholar] [CrossRef]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV trends and variability in atmospheric reanalyses and GPS observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
- Bock, O.; Parracho, A. Consistency and representativeness of integrated water vapour from ground-based GPS observations and ERA-Interim reanalysis. Atmos. Chem. Phys. 2019, 19, 9453–9468. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2046. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Fritsche, M.; Rülke, A.; Steigenberger, P.; Rothacher, M. On the homogeneity and interpretation of precipitable water time series derived from global GPS observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Domonkos, P. Adapted Caussinus-Mestre Algorithm for Networks of Temperature series (ACMANT). Int. J. Geosci. 2011, 2, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Quarello, A. Development of New Homogenisation Methods for GNSS Atmospheric Data. Application to the Analysis of Climate Trends and Variability. Ph.D. Thesis, Sorbonne Universite, Paris, France, 2020. [Google Scholar]
- Van Malderen, R.; Pottiaux, E.; Klos, A.; Domonkos, P.; Elias, M.; Ning, T.; Bock, O.; Guijarro, J.; Alshawaf, F.; Hoseini, M.; et al. Homogenizing GPS Integrated Water Vapor Time Series: Benchmarking Break Detection Methods on Synthetic Data Sets. Earth Space Sci. 2020, 7, e2020EA001121. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS 2010 Conventions; Technical Report; IERS: Frankfurt-am-Main, Germany, 2010. [Google Scholar]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Bock, O. Standardization of ZTD screening and IWV conversion. In Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Jones, J., Guerova, G., Douša, J., Dick, G., de Haan, S., Pottiaux, E., Bock, O., Pacione, R., van Malderen, R., Eds.; Springer International Publishing AG: Cham, Switzerland, 2020; Chapter 5; pp. 314–324. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Flamant, C.; Doerflinger, E.; Jansen, F.; Fages, R.; Bony, S.; Schnitt, S. Integrated water vapour observations in the Caribbean arc from a network of ground-based GNSS receivers during EUREC4A. Earth Syst. Sci. Data 2021, 13, 2407–2436. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2015, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Ning, T.; Wang, J.; Elgered, G.; Dick, G.; Wickert, J.; Bradke, M.; Sommer, M.; Querel, R.; Smale, D. The uncertainty of the atmospheric integrated water vapour estimated from GNSS observations. Atmos. Meas. Tech. 2016, 9, 79–92. [Google Scholar] [CrossRef] [Green Version]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Byun, S.H.; Bar-Sever, Y.E. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod. 2009, 83, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Niell, A.E.; Tregoning, P.; Schuh, H. The Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Susnik, A.; Dach, R.; Villiger, A.; Maier, A.; Arnold, D.; Schaer, S.; Jäggi, A. CODE Reprocessing Product Series. 2016. Available online: https://boris.unibe.ch/80011/ (accessed on 25 August 2021). [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; User Manual. 2015. Available online: https://boris.unibe.ch/72297/ (accessed on 8 May 2012). [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Orliac, E.; Prange, L.; Susnik, A.; Villiger, A.; Jäggi, A. CODE Final Product Series for the IGS; 2018. Available online: https://boris.unibe.ch/119490/ (accessed on 25 August 2021). [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 11, 2406. [Google Scholar] [CrossRef]
- Bock, O.; Pacione, R.; Ahmed, F.; Araszkiewicz, A.; Bałdysz, Z.; Balidakis, K.; Barroso, C.; Bastin, S.; Beirle, S.; Berckmans, J.; et al. Use of GNSS Tropospheric Products for Climate Monitoring (Working Group 3). In Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate; Jones, J., Guerova, G., Douša, J., Dick, G., de Haan, S., Pottiaux, E., Bock, O., Pacione, R., van Malderen, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 267–402. [Google Scholar]
- Stepniak, K.; Bock, O.; Wielgosz, P. Reduction of ZTD outliers through improved GNSS data processing and screening strategies. Atmos. Meas. Tech. 2018, 11, 1347–1361. [Google Scholar] [CrossRef] [Green Version]
- Bock, O. GPS Data: Daily and Monthly Reprocessed IWV Data from 120 Global GPS Stations, Version 1.2. 2016. Available online: https://observations.ipsl.fr/espri/metadata/global_gps_iwv_v1.2.html/ (accessed on 25 August 2021). [CrossRef]
- Bock, O. Global GNSS IWV Data at 436 Stations over the 1994–2018 Period. 2019. Available online: https://www.aeris-data.fr/metadata/metadata/?5829bd3d-4593-4e66-bce2-c8c6311360af (accessed on 25 August 2012). [CrossRef]
- Quarello, A.; Bock, O.; Lebarbier, E. A new segmentation method for the homogenisation of GNSS-derived IWV time-series. arXiv 2020, arXiv:2005.04683. [Google Scholar]
- Birgé, L.; Massart, P. Gaussian model selection. J. Eur. Math. Soc. 2001, 3, 203–268. [Google Scholar] [CrossRef] [Green Version]
- Lebarbier, E. Detecting Multiple Change-Points in the Mean of Gaussian Process by Model Selection. Signal Process. 2005, 85, 717–736. [Google Scholar] [CrossRef] [Green Version]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Meng, X.; Choi, D.; Cheang, W.; Keller, T.; DeLuisi, J.; Wuebbles, D.J.; Kerr, J.B.; et al. Factors affecting the detection of trends: Statistical considerations and applications to environmental data. J. Geophys. Res. Atmos. 1998, 103, 17149–17161. [Google Scholar] [CrossRef]
- Koulali, A.; Clarke, P.J. Effect of antenna snow intrusion on vertical GPS position time series in Antarctica. J. Geod. 2020, 94. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Stanitski, D.M.; Gobron, N.; Willett, K.M. Global Climate [in “State of the Climate in 2019”]. Bull. Am. Meteorol. Soc. 2020, 101, S9–S127. [Google Scholar] [CrossRef]
- Ulbrich, U.; Lionello, P.; Belušić, D.; Jacobeit, J.; Knippertz, P.; Kuglitsch, F.G.; Leckebusch, G.C.; Luterbacher, J.; Maugeri, M.; Maheras, P.; et al. 5—Climate of the Mediterranean: Synoptic Patterns, Temperature, Precipitation, Winds, and Their Extremes. In The Climate of the Mediterranean Region; Lionello, P., Ed.; Elsevier: Oxford, UK, 2012; pp. 301–346. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).