Abstract
The removal of non-climatic biases, so-called inhomogeneities, from long climatic records needs sophistically developed statistical methods. One principle is that the differences between a candidate series and its neighbor series are usually analyzed instead of the candidate series directly, in order to neutralize the possible impacts of regionally common natural climate variation on the detection of inhomogeneities. In most homogenization methods, two main kinds of time series comparisons are applied, i.e., composite reference series or pairwise comparisons. In composite reference series, the inhomogeneities of neighbor series are attenuated by averaging the individual series, and the accuracy of homogenization can be improved by the iterative improvement of composite reference series. By contrast, pairwise comparisons have the advantage that coincidental inhomogeneities affecting several station series in a similar way can be identified with higher certainty than with composite reference series. In addition, homogenization with pairwise comparisons tends to facilitate the most accurate regional trend estimations. A new time series comparison method is presented here, which combines the use of pairwise comparisons and composite reference series in a way that their advantages are unified. This time series comparison method is embedded into the Applied Caussinus-Mestre Algorithm for homogenizing Networks of climatic Time series (ACMANT) homogenization method, and tested in large, commonly available monthly temperature test datasets. Further favorable characteristics of ACMANT are also discussed.
1. Introduction
Records of instrumental climatic observations are an important source of understanding about climate change and climate variability, and the use of observed climatic data is involved directly or indirectly in almost all kinds of climatological and applied climatological research. However, the temporal and spatial comparability of observed climatic data is generally affected by varying technical conditions of the observations. Any piece of observed data (x) and also their time series can be divided to three components: (i) climate signal (u) of the area represented by the observing station, (ii) station effect (v) specific to the conditions and performance of observations at the observing site, (iii) fast changing local weather effects (ε), and generally none of these three components is zero. Equation (1) presents the relation of these components to the vectors of time series of station s.
While the climate signal is often similar for relatively large geographical areas, the station effect is often characterized by a certain temporal constancy. Finally, the weather effects appear as noise due to their fast and irregular spatio-temporal variation.
In climatology, the purpose of time series homogenization is to detect and remove the station effect from the observed data, as homogenized data characterize the true climatic variations better than raw climate observations. The principal tool of the separation of station effects is the comparison of nearby time series. As the climate signal is approximately the same for nearby stations, the difference (ratio) between a candidate series and its neighbor series will show the station effect of the candidate series for climatic elements with typically additive (multiplicative) inhomogeneities. This homogenization is referred to as relative homogenization, and the difference or ratio series as relative time series (T), while the rarer case when a candidate series is homogenized without neighbor series is absolute homogenization. Although written documents of technical changes (so-called metadata) can be utilized in homogenization, the principal tools are statistical procedures. A relative homogenization method has at least three parts: (i) time series comparison, (ii) detection of inhomogeneities, iii) correction of time series (by removing inhomogeneities). Optionally, a homogenization procedure may include additional steps like outlier filtering, iterative removal of inhomogeneities, infilling data gaps, etc. In this study, we focus on the statistical tools of time series comparison and inhomogeneity detection in relative homogenization methods, and present some methodological novelties. The next section (Section 2) includes a brief description of the state of the art of time series comparison and inhomogeneity detection methods. The novel approach of combined time series comparison included in the forthcoming version of the Applied Caussinus-Mestre Algorithm for homogenizing Networks of climatic Time series (ACMANT) homogenization method is presented in Section 3 after a brief presentation of ACMANT. Section 4 shows some efficiency tests proving the benefit of the newly applied methodology, and concluding remarks close the study in Section 5.
2. State of the Art of Time Series Comparison and Inhomogeneity Detection in the Homogenization of Climatic Time Series
2.1. Comparison of Time Series
One initial idea of relative homogenization is that if we find a perfectly homogeneous reference time series representing the same climate as the candidate series, the difference of the candidate and reference series will directly show the station effect of the candidate series. However, neighbor series are generally neither perfectly homogeneous nor represent exactly the same climate as the candidate series. Although in dense observing networks the climatic differences between neighbor series can be favorably small, the selection of fairly homogeneous reference series seems impossible before homogenization. Usually, one of the two following tools is used to treat this problem: (i) construction of composite reference series with averaging of several neighbor series of the candidate series; (ii) pairwise comparison of the candidate series with several neighbor series, and the statistical evaluation of the results of individual comparisons. Here, we briefly discuss the advantages and drawbacks of both tools.
- (i)
- Composite reference series. In starting a homogenization, the candidate series and its neighbor series all may include inhomogeneities. The purpose of using composite reference series is to reduce the effects of inhomogeneities of the neighbor series by averaging the series and their inhomogeneities. Peterson and Easterling [1] suggested the use of weighted averages where the weights are the squared spatial correlations of the first difference series (i.e., series of increments between adjacent values).
In Equation (2), G and F denote candidate series and its reference series, respectively, Gs denotes the neighbor series s of candidate series G, while ws stands for the weight belonging to series Gs.
To reduce potential errors due to possible large inhomogeneities in neighbor series, homogenization with composite reference series is often performed in iterative steps where the roles of candidate series and reference series change during the iteration [2,3,4]. This technique may provide favorably high accuracy of homogenized data of individual time series, but it treats two problems less effectively: (a) in iterative procedures, the temporal evolution of individual series becomes more and more similar, but the convergence of the iteration might fail to find the true temporal variation of the climate signal, and this might result in relatively large errors in area average trends; (b) when a notable portion of time series is affected by similar inhomogeneities, both the averaging of neighbor series and the mentioned iterations have reduced efficiency in the inhomogeneity removal. In the efficiency tests of the Spanish MULTITEST project [5], the results of the Climatol homogenization method [6] represented all these attributes of composite reference series use with iterative removal of inhomogeneities well. Note that the generally good results for individual time series and lower accuracy for area mean characteristics may seem a contradiction, which, however, is only a seeming contradiction. Absolute errors are generally much smaller for area mean characteristics than for individual time series, hence the homogeneity of individual time series may improve in spite of a low efficiency in improving the area mean accuracy. The relatively large errors for area mean characteristics are an important issue, as climate science expects the most accurate assessments for climatic zones, rather than for individual time series.
- (ii)
- Pairwise comparisons. In a pairwise comparison, the differences between the candidate series and its neighbor series are examined one by one. When an inhomogeneity appears similarly in each relative time series, it belongs to the candidate series, while when an inhomogeneity appears only in the comparison with one neighbor series, then this belongs to the neighbor series. This seems to be easy, but when the signal-to-noise ratio (SNR) is low (e.g., for multiple inhomogeneities, for unusual local weather anomalies, etc.), inhomogeneities do not seem to be significant in a few or many of the relative time series, or they appear with imprecise timings, which may complicate the correct evaluation of the inhomogeneity detection results of individual time series comparisons. Therefore, the evaluation of pairwise comparisons is often performed manually, preferably together with metadata use [7,8,9]. Menne and Williams [10] constructed an automatic homogenization method with pairwise comparisons, the Pairwise Homogenization Algorithm (PHA), and this has been applied to some large global or regional datasets [11,12,13]. Ref. [5] reported that PHA provides one of the most accurate regional mean trends among the tested homogenization methods, except for low SNR datasets. However, the homogenization accuracy for individual station series is notably lower with PHA than with some other tested methods. Note that PHA does not include iterations for removing inhomogeneities of neighbor series before their use for a candidate series.
From the test results of Climatol and PHA methods, we may conclude that pairwise comparisons favor the accurate detection of regional mean trends, while the reconstruction of local climate variability is more accurate with the use of composite reference series. Obviously, considering only the results of two homogenization methods is a simplification, as the homogenization accuracy depends on all segments of the homogenization, and even the details of composite reference series use or pairwise comparisons are varied according to homogenization methods. For instance, to determine the group of neighbor series being used in the homogenization of a given candidate series, often a threshold spatial correlation is applied, but alternatively a maximum geographical distance [14] or a predefined number of the closest neighbor series [2,6] can be applied. Sometimes the iterative improvement of composite reference series is omitted, but the most inhomogeneous neighbor series are excluded [15]. The weights of neighbor series of a composite reference series may be identical or set by the inverse distance from the candidate series [3], by the squared spatial correlation between the candidate series and its neighbor series [1] or by ordinary kriging [16]. Furthermore, in some homogenization methods, the comparison between candidate and neighbor series notably differs from the two methods discussed here [17,18].
The efficiency tests of the European project COST ES0601 (“HOME”) [19] found much lower efficiency of the PHA method than MULTITEST [5], and the PRODIGE method [20] was notably more accurate than PHA both for individual and network mean time series, although PRODIGE includes an iterative removal of inhomogeneities. The large differences between the HOME results and MULTITEST results may be due to three reasons: (a) the HOME benchmark is relatively small, its surrogate temperature section consists of only 15 networks and, in addition, nine of the 15 networks are small, comprising only five time series in each. (b) Later versions of PHA might be more accurate than the version tested by HOME. (c) PRODIGE is a very effective homogenization method for its appropriately selected mathematical tools considering all of the time series comparison, inhomogeneity detection and bias correction methods, as well as for the well-designed structure of the homogenization [20].
In any case, the excellence of PRODIGE inspired the generation of new methods during and just after HOME, using the basic tools of PRODIGE and adding new features for the automation of the method, for improving user-friendliness, and/or for achieving further improvements in the homogenization accuracy. These methods are the interactive HOMER [21], the automatic AHOPS [22] and HOMOP [23], and the ACMANT versions published to date are also automatic.
Despite possible doubts on the diversity of homogenization methods, the differences between the advantages of composite reference series use and those of pairwise comparisons are robust based on both theoretical arguments and experimental results. This indicates the difficulty of constructing homogenization methods with near optimal efficiency both for area average and local climate variability.
2.2. Detection of Inhomogeneities
The statistical detection of inhomogeneities has a century-long history, and likely this part of the time series homogenization is the most widely and most exhaustively studied area. This brief review of detection methods is limited to the ones performed within relative homogenization and which treat inhomogeneities affecting the correct comparability of section means of time series. The most common and most frequently examined type of inhomogeneities is the sudden change in the section mean values (referred to as a break) at a certain point of the time series, as most kinds of technical changes (e.g., station relocation, changes in the instrumentation, observers, etc.) result in such breaks.
A large number of inhomogeneity detection methods have been developed, and they can be grouped in various ways. Here, we group the methods according to the (i) approach to detect different kinds of inhomogeneities (i.e., breaks or gradually changing biases); (ii) use of parameters estimated from the sample; (iii) solutions for multiple structures of inhomogeneities.
- (i)
- Detection of different kinds of inhomogeneities
Most inhomogeneity detection methods detect breaks only, and not only because the most frequent form of inhomogeneity is a break. An issue with the methods detecting both breaks and linearly changing biases [24,25] is that two consecutive breaks with the same sign shifts can easily be mixed up with trend-like inhomogeneities. On the other hand, gradually changing biases can be fairly (although not perfectly) approached with breaks. Efficiency tests show that the homogenization accuracy with methods detecting both breaks and trend-like inhomogeneities tends to be slightly lower than with the best break detection methods. For instance, the standard normal homogeneity test (SNHT) has two main versions, i.e., the earlier version [26] detects breaks only, while the later version [24] detects both breaks and shifts. Both versions were tested in eight datasets of varied properties [27] and the homogenization accuracy turned out to be slightly but consequently higher with the early version. In the continuation of this short review, we consider methods detecting breaks only.
- (ii)
- Use of parameters estimated from the sample
Parameters estimated from the noisy and inhomogeneous time series hold estimation errors which might worsen the homogenization accuracy. It might seem to be obvious that for detecting breaks of the section mean values, section mean values and nothing else should be estimated from the sample. However, the true picture is more complex. There exist (a) non-parametric methods, (b) methods using estimated section mean values and estimated standard deviation from the entire time series, (c) methods using more than one estimated parameter per section of time series.
- (a)
- Non-parametric methods [28] have the advantages that their results are not affected by possible asymmetries of the probability distribution, and are relatively insensitive to possible occurrences of outlier values. However, the homogenization accuracy tends to be slightly lower with them than with the best break detection methods [27,29], due to the reduced information provided by them (i.e., they do not calculate shift size).
- (b)
- In the ideal case, section mean values are estimated from the sample, but other estimated parameters (when necessary) are estimated from the whole time series. Such methods are the sequential t-test with identical standard deviation on both sides of a break [30], tests of accumulated anomalies [31,32] and a few versions of maximum likelihood methods, e.g., SNHT. By definition, a maximum likelihood method searches the time point where the probability of break occurrence is maximal, and tests show that the best performing break detection methods belong to this group. Note, however, that the manual break detection is the easiest with the visual examination of accumulated anomalies, hence the latter can be the most advantageous when low SNR and metadata favor manual break detection. The SNHT break detection method is one of the most widely used and also one of the best performing methods (note that with SNHT one can refer either to the whole homogenization method or to its break detection method, and here we discuss strictly only the break detection segment of SNHT). Before using SNHT, time series (T) must be normalized by extracting their average and dividing the values by the empirical standard deviation. Then, at any point j of T, the SNHT statistic (SSNHT) is calculated by Equation (3):
The length of time series is n, and the upper stroke denotes the section average. The presence of a break is most probable where SSNHT is the highest.
- (c)
- Sometimes both the section means and section standard deviations are estimated from the sample, based on the reasoning that, at break points, often not only the mean changes, but also other properties of the probability distribution. Such changes affect the correct break detection even when only the breaks of the section means are searched. Although this reasoning is theoretically correct, the potential benefit of including the changes of standard deviation in the calculations might be completely lost and even overcompensated by the estimation errors which are generally larger for empirical standard deviations than for averages. These methods are usually never subjected to method comparison tests on large datasets, as their use is more complicated and computationally time consuming in comparison with other methods. I do not recommend their use, in spite of their seeming mathematical elegance.
A slightly different issue is when a break detection method compares statistical characteristics not directly related to section means. The best known representatives of this group are the two phase regression methods, in which linear trends are fitted to the values of the examined sections in order to find breaks of the section means [33,34]. Although breaks can be detected with fair efficiency by such methods, I do not know of any clear indication why any of them should be preferred to the methods of group (b).
- (iii)
- Solutions for multiple structures of inhomogeneities
Climatic time series often include more than one break. Some methods can detect multiple structures of inhomogeneities simultaneously, they are referred to as multiple break methods, while many others detect only one break at a given step, and thus they need a hierarchic algorithm to find multiple break structures.
Regarding multiple break methods, MASH [18] includes a multiple t-test for the simultaneous detection of breaks, while PRODIGE and the related method family includes the optimal step function fitting (known also as optimal segmentation). The variety of multiple break methods is small, with the mentioned two methods their description is almost complete. The variety is wider if we consider that step function fittings are performed with slightly differing details in different methods.
A step function with K steps splits the time series to K + 1 constant sections. This model approaches the true properties of a relative time series including K breaks and low noise well, but note that the model still functions adequately when the estimated break number and break positions are not perfect, or when not all the inhomogeneities are breaks. We introduce the concepts of internal distance (I) for differences of values from the relevant section mean, and external distance (E) for differences of section means from the mean of the whole time series.
For a given K, the step positions with minimum internal variance provide the best fitting step function.
In Equation (6), y1, y2, … yK are the positions of breaks, y0 = 0, yK+1 = n.
During the performance of a homogenization procedure, the optimal number of steps is generally unknown. In PRODIGE and HOMER, the semi-empirical Caussinus–Lyazrhi criterion (C-L criterion) [35] is used for setting K. In the expression determining the C-L statistic (q), the first expression monotonously decreases with increasing K, but this decrease may be balanced or overbalanced by the penalty term P which increases with increasing K. Finally, K facilitating the minimal q according to Equations (7) and (8) is selected.
ACMANT applies the C-L criterion with a slight modification in the penalty term [36], more precisely, in ACMANT the exact form of penalty term varies according to the phases of the homogenization procedure. A further variation in the application within ACMANT is that, sometimes, synchronous break positions of two variables are searched with fitting two step functions to the examined two variables (Section 3.1).
Step function fitting is sometimes applied with other formulas than the C-L criterion to set K [29,37], and the step function model is sometimes modified by adding trend and seasonally changing components [38]. The efficiencies of these method versions need further tests.
There exist experiments [39,40] with multiple break detection methods using other and more complex models than the step function fitting, but their description is skipped here, because they seem to use too many parameter estimations from the inhomogeneous sample, and we have already discussed the related issues. Finally, we mention the joint detection [41]. This method detects multiple breaks synchronously for a whole network comprising sufficiently correlated time series. The method was developed by a group of European statisticians and they recommended it to climate data homogenization. However, this method is not a relative homogenization tool, and it was built into HOMER [21] by mistake.
Around the starting of the new millennium, the superiority of multiple break methods in comparison with hierarchic break detection techniques was a widely accepted thesis, particularly in Europe. However, Menne and Williams [42] reported that single break detection methods embedded into an appropriately designed hierarchic algorithm can be fully competitive with multiple break methods. Later tests with sophistically developed large test datasets [27,29,43] proved that hierarchic break detections with the cutting algorithm [34] often approach the performance of the best multiple break methods. In detail, the accuracy of linear trend estimations is often the best with step function fitting (for this kind of method comparison test, break detections are supplied with a uniform bias removal algorithm), despite that the detected break number and break positions are generally less accurate with step function fitting than with some other methods. The relatively high uncertainty of break numbers and break positions with step function fitting was examined by [44], and it seems an inherent feature of the method.
The differences between residual root mean squared errors (RMSEs) and residual trend biases after homogenization are usually small when only the break detection segments are different in homogenization [27,29,43], although a few break detection methods give notably poorer results for particular errors or weaknesses. It is important to note that the inclusion of a cutting algorithm is indispensable for the use of any single break detection method. The majority of the widely used homogenization methods of the recent decade include single break detection methods, namely PHA, Climatol and the penalized t-test [45] and penalized F-test [46] of the RHtests package. All these methods include the cutting algorithm, and thus the efficiency differences found by MULTITEST have principally other sources than the break detection parts of the methods.
3. ACMANT and Its Development with the Combined Time Series Comparison
In this section, the ACMANT homogenization method is presented, and its relation to the other members of the PRODIGE method family is briefly described (Section 3.1). Then, a summary of the MULTITEST results is shown (Section 3.2), since those results inspired the latest development, the inclusion of combined time series comparison in ACMANT (Section 3.3). Finally, some more information is provided about the forthcoming ACMANT version (ACMANTv5, Section 3.4).
3.1. Presentation of ACMANT
The development of ACMANT started during the HOME project using the break detection and correction segments of PRODIGE. The first ACMANT version [47] was prepared only for the homogenization of monthly temperature series. Its development has been continuous since then, and the last published version of (ACMANTv4) [36] can be used for the homogenization of temperature, precipitation amount, relative humidity, sunshine duration, radiation, wind speed and atmospheric pressure, either on daily or monthly scales.
The ACMANT development is based on three main sources: (i) earlier knowledge; (ii) own innovative ideas; (iii) tests with benchmark datasets. Now ACMANT is a highly accurate, user-friendly method, and easily applicable to the homogenization of large datasets.
- (i)
- Adaptation of earlier knowledge in ACMANT
The most important earlier work is the PRODIGE homogenization method [20]. Both its break detection method (step function fitting with the C-L criterion) and correction method (joint calculation of correction terms with the ANOVA correction model) are built into ACMANT. Further examples are the adaptation of the use of composite reference series [1], optimal weighting of neighbor series in time series comparisons [16] and the downscaling of correction terms from monthly to daily values [48]. Note that the break detection and bias correction parts are common for all members of the PRODIGE-based method family (i.e., HOMER, AHOPS, HOMOP and ACMANT), apart from small differences in technical details.
The ANOVA correction model is an important tool for effective homogenization, this has both theoretical and practical evidence [49]. According to my knowledge, it is used only in the methods developed from PRODIGE. In the common ANOVA model, the climate signal is considered identical for the time series homogenized together [20,36], while a more developed version takes into account spatial climatic variations. The latter version is referred to as weighted ANOVA, and its use was suggested first by Szentimrey [16]. However, the weighted ANOVA model is applied only in ACMANT. In the ANOVA correction model, every change of the station effects is presumed to be a break, and the break positions (js,1, js,2 ... js,Ks) are presumed to be known for each series s of the network. Then, the estimated climate signal (U’) and station effect (V’) under the condition of zero noise (ε ≡ 0) can be calculated for each time series by the equation system (9) and (10), and these provide the optimal estimations of U and V of Equation (1).
In Equations (9) and (10), G denotes candidate series, y time unit, l length of homogeneous section, and w weight. Equation (9) must be applied to each time unit (y), and Equation (10) for each homogeneous section of each series (s). In the common ANOVA model w ≡ 1, while in the optimally weighted ANOVA, the weights are determined by ordinary kriging. However, the calculations with the weighted ANOVA model are time consuming, therefore in ACMANT a simpler weighting, i.e., the squared spatial correlations, is applied.
- (ii)
- Own innovative ideas
- Bias sizes of temperature, relative humidity, sunshine duration and radiation often have semi-sinusoid annual cycles, since the impacts of technical changes are often closely connected to the natural solar radiation. As the natural annual cycle of radiation can be fairly approached with a sinusoid curve in middle and high latitudes, the use of the model of a sinusoid annual cycle with modes in the solstices is advantageous for the estimation of the intra-annual variation of the station effect. This idea is used in the elaboration of both the break detection and bias correction methods for the relevant homogenization tasks. Regarding the break detection part, the solution is the bivariate detection for annual means (variable A) and summer–winter differences (variable B). Annual values (y) of B are defined by the weighted average of monthly mean temperatures where the weights (w) are specific for calendar months (m):
For summer months: w5 = w6 = w7 = 1, w8 = 0.5
For winter months: w1 = w11 = w12 = −1, w2 = −0.5
For the other months: w3 = w4 = w9 = w10 = 0
Then, the bivariate detection with step function fitting to A and B can be written by similar formulas to Equations (6) and (7).
In Equations (12) and (13), p is an empirical constant, and P’ differs from P of Equation (8) only by a further empirical constant varying according to the phase of the homogenization procedure [36].
Regarding the bias corrections, the correction terms are calculated by the ANOVA correction model independently for variables A and B, then a coefficient of sinusoid annual cycle is applied to the station effect of B, with which the parts of monthly and daily correction terms relating to the annual cycle of station effect are calculated.
Note again that the use of the bivariate model (both its break detection and correction parts) must be restricted to the relevant geographical regions and climatic variables.
- Bivariate detection for breaks of precipitation total where the year can be divided into a rainy season and snowy season—Technical problems with snow amount measurement differ from those of the liquid precipitation measurement, therefore in the ideal case rain and snow amounts should be homogenized separately. However, precipitation total time series usually include the data without separations according to precipitation form. This issue is treated by separating the year into a rainy season and a snowy season (where applicable), and applying a bivariate homogenization similar to the one for radiation-dependent inhomogeneities. More details about the precipitation homogenization with ACMANT have been described [36,50].
- Detection and correction of short-term platform-shaped inhomogeneities—Temporally existing technical problems or observation errors may result in temporal, platform-shaped changes in the temporal evolution of the station effect [43,51]. Therefore, a specific break detection segment is included in ACMANT for the removal of biases of 1–28 months in duration. Naturally, only relatively large biases can be detected with sufficient certainty for such short periods, therefore such inhomogeneities are referred also to as outlier periods. Note that the special treatment of such biases is needed in ACMANT, because the time span between two consecutive breaks is at least 3 years in the principal break detection segment of ACMANT.
- The principal break detection is performed on time series of annual resolution, and initially, the minimum time span between two consecutive breaks is three years. In subsequent steps, break positions are refined by using monthly data and also on daily scales in case of daily data homogenization. In such refinements, subsections supposed to include only one break are examined, thus the calculations are relatively simple, and the whole break detection procedure is relatively fast. Final break positions may include consecutive breaks much closer than 3 years both for the break position refinements and for the independently detected short-term, platform-shaped inhomogeneities. However, there appears to be a potential weakness, i.e., when several large breaks occur within a short section, this detection algorithm may be inaccurate. Note, however, that such accumulation of breaks with sufficient SNR for their accurate detection is rare. The most important benefit of the ACMANT break detection scheme is not the saving of computation time, but the reduction in parameter estimations from the inhomogeneous sample: when breaks are searched in data of daily resolution, the consideration of seasonal cycle and autocorrelation is indispensable [38,52].
- Ensemble homogenization—In time series homogenization, the estimated adjustment terms for bias removal often have considerable uncertainty, which may originate from break detection uncertainties or adjustment term calculation uncertainties. The core idea of ensemble homogenization in ACMANT is that uncertainty ranges are monitored by the repeated execution of some homogenization steps with slightly differing conditions. With using the average of the uncertainty range in the final corrections, the probability of committing large errors decreases, and the homogenization accuracy generally increases. Based on experiments (not shown), when ensemble estimations are made in an intermediate phase of the homogenization procedure, the optimum adjustment terms are usually smaller than the average of the uncertainty range, since the choice of slightly lowered adjustment terms reduces the risk of error accumulations by the subsequent steps of the homogenization procedure. Note that the idea of ensemble homogenization is not fully new in ACMANT. In MASH [18], the adjustment terms of a given iteration step are calculated as the minimum of several distinct estimations based on the use of varied relative time series. However, ACMANT is the first method in which the ensemble of this kind of operation is named ensemble homogenization.
- (iii)
- Tests with benchmark datasets.
ACMANT is a complex homogenization procedure, and to check its correct operation and efficiency, its operation is frequently checked during its development. To check the correctness and accuracy of the homogenization, I use the homogeneous benchmark datasets developed by earlier projects [19,53], and introduce varied sets of inhomogeneities to them. Readers can find more about this aspect of the ACMANT development in [54,55].
3.2. Homogenization Accuracy According to MULTITEST
The Spanish MULTITEST project (2015–2017) was dedicated to testing automatic monthly homogenization algorithms on large test datasets of varied climatic and inhomogeneity properties. The MULTITEST research group could test only fully automatic methods with openly accessible executive files. Although the project was announced to the international scientific community, we could test only nine versions of five homogenization methods (ACMANT, Climatol, MASH, PHA, RHtests). In addition, an automatic version of HOMER was tested, which included the joint segmentation segment (the problem with this segment was revealed later).
For the accuracy of homogenization results in individual time series, the RMSE of monthly and annual values and the mean absolute bias of linear trends were calculated, while the accuracy of network mean values were evaluated by the network mean linear trend biases and annual RMSE. We found that the automatic HOMER was the only method for which the homogenization accuracy depends on the climate signal, i.e., for datasets with flat climatic trends the HOMER results were good or even excellent, while for datasets with enhanced climatic trends the HOMER results were poor. For this reason, we excluded HOMER from the publication [5], and thus ACMANT remained the only tested method including the ANOVA correction model.
In [5], the results for 12 temperature test datasets are published. Considering the 12 datasets and five efficiency measures mentioned, 60 pieces of data are compared for the tested methods, and generally a notable and statistically significant advantage of ACMANTv4 is shown by them. In detailed, ACMANT was significantly more accurate than any other method in 35 cases (58.3%), still the most accurate but with an insignificant advantage against some other methods in 17 cases (28.3%), slightly less accurate than at least one other method, but with insignificant disadvantage in seven cases (11.7%) and significantly less accurate than at least one other method in one case (1.7%), the latter occurred with the network mean trend bias and in comparison with the PHA results. Note that the mean systematic trend bias for whole datasets was also monitored, and for this characteristic, PHA was more accurate than ACMANT, but the difference between them was not statistically significant.
Naturally, with the inclusion of more homogenization methods or using other test datasets, such statistics may change considerably. In this study, we focus on the exceptional case of the MULTITEST results where PHA was significantly more accurate than ACMANTv4. This occurred when half of the time series of a test dataset included semi-synchronous breaks within a short period. Further tests (not shown) revealed that the advantage of PHA occurs for datasets with synchronous or semi-synchronous breaks, and in the case of high SNR synchronous breaks, its advantage may also appear in other efficiency measures than the network mean trend bias.
The adequate treatment of semi-synchronous breaks is an important issue, as they truly occur for organized technical changes like the worldwide automation of meteorological instruments around the end of the last century. Such changes might seriously affect the accuracy of climate trend estimations. In fact, even with the best statistical homogenization methods, only a portion of such biases can be removed, and in the correct treatment of semi-synchronous breaks, both the selection of homogenization method and the use of metadata are important.
3.3. Break Detection with Combined Time Series Comparison
The break detection with combined time series comparison is planned to be included in the first homogenization cycle of ACMANTv5. This break detection method consists of two steps: in step 1, a pairwise comparison is performed, while in step 2 composite reference series are used. No adjustment is applied between step 1 and step 2, but the detected breaks of step 1 are considered obligatory break positions in the break detection of step 2. The idea behind this combination is that SNR is generally lower in pairwise comparisons than with using composite reference series, therefore, once a break has been detected in step 1, it must remain a detected break in step 2. Furthermore, semi-synchronous breaks can be detected more effectively with pairwise comparisons than with using composite reference series contaminated by similar inhomogeneities to the one of the candidate series, therefore the detected semi-synchronous breaks of step 1 must be inserted as known break positions before the detection with composite reference series.
In both step 1 and step 2, the optimal step function fitting is applied on time series of annual resolution, and with the same parameterization of the C-L criterion as in the first homogenization cycle of ACMANTv4. In this phase of the homogenization, the coefficient in the penalty term (which is 2.0 in the original formula, see Equation (8)) is 3.92 (2.8) in univariate (bivariate) detection. These elevated coefficients show that in the first homogenization cycle of ACMANT, only relatively large breaks are searched, otherwise the false alarm rate would be too high.
In the development of the break detection with combined time series comparison, a critical point was to decide if the step function fitting of the earlier ACMANT versions can be kept or should be changed to SNHT detection at least at the pairwise comparison step. This problem arose because the break detection uncertainty is generally lower with SNHT detection than with step function fitting (as was discussed in Section 2.2), and the efficiency of break detection with pairwise comparisons is especially sensitive to the uncertainty of estimated break positions. However, in the present solution of the detection with pairwise comparison, the step function fitting method is applied in a way that alternative break positions are jointly considered when pieces of the break detection results show high uncertainty, and with this innovation the evaluation of the pieces of the detection results is made similar to ensemble procedures.
The uncertainty of the detection result for an individual relative time series is defined as high when there exist at least two break numbers (K1 and K2) for which the absolute difference of C-L statistics (q1 and q2) is smaller than d (Equation (14)).
In Equation (14), p stands for the coefficient of the penalty term of the C-L criterion. In other words, the uncertainty is defined as high when there exist at least two C-L statistics closer to each other than half of the increment of the penalty term for two consecutive K. In such cases, the break positions detected by differing K give alternative break positions. The alternative break positions are generally considered with varied weights according to the differences in C-L statistics from qopt (Equation (7)), but the weights are constant for breaks belonging to a given K of a given relative time series. Equation (15) shows the calculation of preliminary weights (h’), which are normalized to h by Equation (16) in order to facilitate a total weight of detected breaks independent from the number of alternative solutions (J).
Applying these formulas, the weights of detected breaks are identical to 1 when no significant uncertainty is found, while they vary between 0 and 1 in the reverse case. In the evaluation of the pieces of the detection results for relative time series, breaks with positions falling into adjacent years are considered concordant, but each piece of the results is considered only once (i.e., to one break of one candidate series). From this point, the evaluation of the detected breaks by the pairwise comparison is the same as in the PHA method [10]. In ACMANT, the minimum number of concordant breaks is 2.1 to validate a break position in the candidate series.
Turning to step 2, a difference in comparison with ACMANTv4 is that no ensemble homogenization is applied in the break detection with composite reference series of this homogenization cycle, i.e., in the detection with combined time series comparison only one composite reference series is constructed using all the appropriate neighbor series for it. Neighbor series are uniformly weighted in this phase of the homogenization, and the other details of the relative time series construction are the same as in ACMANTv4.
3.4. ACMANTv5
ACMANTv5 is the forthcoming version of the ACMANT homogenization package. One difference in comparison with the previous version will be that the break detection of the first homogenization cycle will be changed to break detection with combined time series comparison. A further planned change is that the new version will have an interactive option. The software will offer a fully automatic version (optionally), and default solutions in the interactive mode where certain kinds of user interventions will be allowed. The planned possibilities of user intervention are as follows:
- Subnetworks (when generated automatically) can be edited,
- Default minimum threshold of spatial correlation (0.4) can be altered,
- List of detected breaks of the first homogenization cycle will be editable,
- User may introduce metadata, which will be considered in the pairwise homogenization step as a detection result with weight = 1 by an imaginary relative time series.
The ACMANTv5 software package will be released in the last quarter of 2021.
4. Efficiency of ACMANTv5
The automatic version of the ACMANTv5 monthly temperature homogenization program has been tested. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show a comparison between the accuracy of ACMANTv4 and ACMANTv5 using the 12 temperature test datasets and five efficiency measures of [5]. Following [5], synthetic (surrogated) test datasets are denoted by Y1…Y6 (U1…U6) in each figure. The individual test datasets differ in the forms, frequency and magnitude distribution of the inserted inhomogeneities. For the comparisons between ACMANTv4 and ACMANTv5, the mean normalized changes (Z) in the residual errors of homogenization results are calculated.
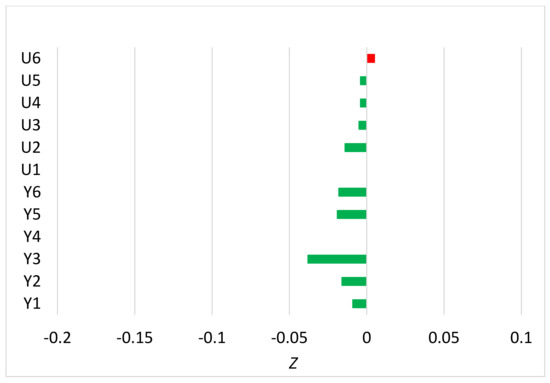
Figure 1.
Mean normalized difference of monthly root mean squared errors (RMSEs) between ACMANTv5 and ACMANTv4. Negative values (green bars) mean improvement, positive values (red bar) mean worsening. Y (U) denotes synthetic (surrogated) test datasets.
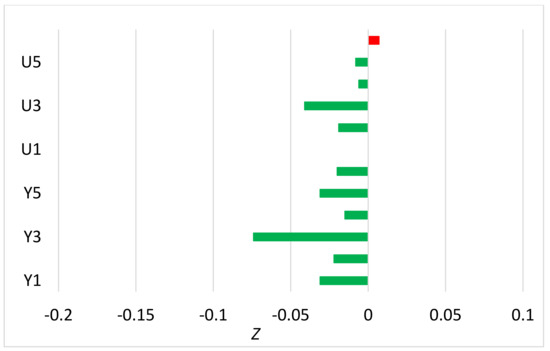
Figure 2.
The same as Figure 1, but for the annual RMSE of individual series.
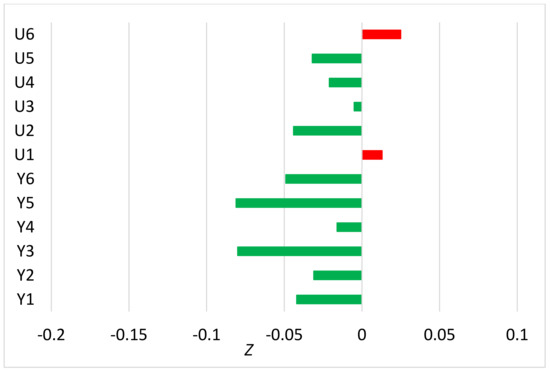
Figure 3.
The same as Figure 1, but for the mean absolute trend bias of individual series.
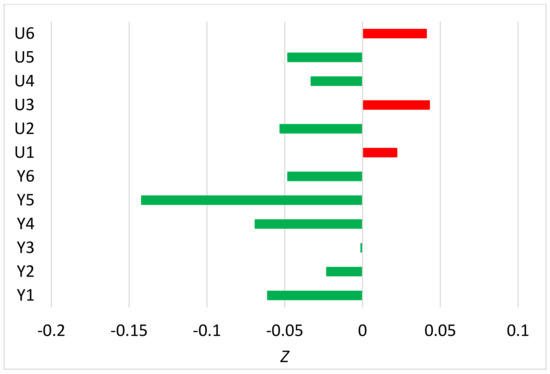
Figure 4.
The same as Figure 1, but for the mean absolute network mean trend bias.
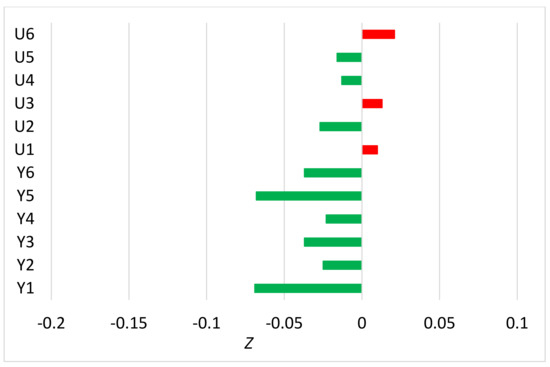
Figure 5.
The same as Figure 1, but for the network mean annual RMSE.
In Equation (17), E4 and E5 denote the mean residual errors with ACMANTv4 and ACMANTv5, respectively. When the mean residual error is smaller with ACMANTv5 than with ACMANTv4, Z is between 0 and −1, while it is positive in the reverse case. Figure 1 and Figure 2 show that monthly and annual RMSE are mostly smaller with ACMANTv5 than with ACMANTv4, but the improvement is usually smaller than 5%.
The differences between ACMANTv5 and ACMANTv4 residual errors are generally larger for the trend biases of individual time series (Figure 3) than for RMSEs, and even larger for the network mean trend biases (Figure 4), and again the errors with ACMANTv5 are generally smaller than with ACMANTv4.
Note that the larger differences for trend biases than for RMSEs may be due to the larger sampling errors for the former efficiency measures, at least partly. Most of the test datasets include no more than 100 networks, and due to the exponential distribution of homogenization errors, this sample size is insufficient for the accurate calculation of mean network mean trend bias. In any case, the largest improvement (14%) when using ACMANTv5 instead of ACMANTv4 is seen for the network mean trend bias of dataset Y5 where the large ratio of semi-synchronous breaks caused the relatively low accuracy of ACMANT in the tests of [5]. Regarding the network mean RMSE (Figure 5), the relations between ACMANTv5 and ACMANTv4 are similar to the ones in Figure 4, except that the scattering of Z according to test datasets is lower.
Further experiments (not shown) indicate that ACMANTv5 is consequently more accurate than ACMANTv4 for datasets with significant network mean trend errors caused by non-concerted beaks, although the improvement is notably smaller than for dataset Y5. Among the 12 datasets shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, Y6, U2 and U5 belong to this group. In the other cases, when network mean trend errors are generally small, the accuracies of ACMANTv5 and ACMANTv4 seem to be the same.
5. Concluding Remarks
This paper reports about the most recent developments of the ACMANT homogenization method. According to available method comparison test results, ACMANT is the most accurate homogenization method for a wide range of homogenization tasks when both the accuracy of area mean values and the accuracy of individual time series are considered important.
The inclusion of appropriate statistical tools and the meticulous attention to the details in the whole method development process further elevate the probability that ACMANT is the best method or at least one of the best homogenization methods. Note that further comparative tests are needed to know more about the efficiencies of currently available homogenization methods, as the homogenization accuracy with any homogenization method highly depends on dataset properties.
The combined time series comparison discussed in this study improves the homogenization accuracy when the data include synchronous or semi-synchronous breaks. The forthcoming version ACMANTv5 will include this new module, and users will have the option to intervene in the homogenization with ACMANT when they judge certain interventions to be beneficial.
I hope that ACMANT will become a useful tool for more accurate climate trend and climate variability estimations and for achieving improved results in applied climatology research.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Peterson, T.C.; Easterling, D.R. Creation of homogeneous composite climatological reference series. Int. J. Climatol. 1994, 14, 671–679. [Google Scholar] [CrossRef]
- Moberg, A.; Alexandersson, H. Homogenization of Swedish temperature data. II: Homogenized gridded air temperature compared with a subset of global gridded air temperature since 1861. Int. J. Climatol. 1997, 17, 35–54. [Google Scholar] [CrossRef]
- Azorin-Molina, C.; Vicente-Serrano, S.M.; McVicar, T.R.; Jerez, S.; Sanchez-Lorenzo, A.; López-Moreno, J.-I.; Revuelto, J.; Trigo, R.M.; Lopez-Bustins, J.A.; Espírito-Santo, F. Homogenization and assessment of observed near-surface wind speed trends over Spain and Portugal, 1961–2011. J. Clim. 2014, 27, 3692–3712. [Google Scholar] [CrossRef]
- Yosef, Y.; Aguilar, E.; Pinhas, A. Detecting and adjusting artificial biases of long-term temperature records in Israel. Int. J. Climatol. 2018, 38, 3273–3289. [Google Scholar] [CrossRef]
- Domonkos, P.; Guijarro, J.A.; Venema, V.; Brunet, M.; Sigró, J. Efficiency of time series homogenization: Method comparison with 12 monthly temperature test datasets. J. Clim. 2021, 34, 2877–2891. [Google Scholar] [CrossRef]
- Guijarro, J.A. Homogenization of Climatic Series with Climatol. 2018. Available online: http://www.climatol.eu/homog_climatol-en.pdf (accessed on 2 September 2021).
- Kuglitsch, F.G.; Toreti, A.; Xoplaki, E.; Della-Marta, P.M.; Luterbacher, J.; Wanner, H. Homogenization of daily maximum temperature series in the Mediterranean. J. Geophys. Res. 2009, 114, D15108. [Google Scholar] [CrossRef] [Green Version]
- Brunetti, M.; Caloiero, T.; Coscarelli, R.; Gullà, G.; Nanni, T.; Simolo, C. Precipitation variability and change in the Calabria region (Italy) from a high resolution daily dataset. Int. J. Climatol. 2012, 32, 57–73. [Google Scholar] [CrossRef]
- Mamara, A.; Argiriou, A.A.; Anadranistakis, M. Detection and correction of inhomogeneities in Greek climate temperature series. Int. J. Climatol. 2014, 34, 3024–3043. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N. Homogenization of temperature series via pairwise comparisons. J. Clim. 2009, 22, 1700–1717. [Google Scholar] [CrossRef] [Green Version]
- Trewin, B. A daily homogenized temperature data set for Australia. Int. J. Climatol. 2013, 33, 1510–1529. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Willett, K.M.; Morice, C.P.; Parker, D.E. Pairwise homogeneity assessment of HadISD. Clim. Past 2014, 10, 1501–1522. [Google Scholar] [CrossRef] [Green Version]
- Menne, M.J.; Williams, C.N.; Gleason, B.E.; Rennie, J.J.; Lawrimore, J.H. The global historical climatology network monthly temperature dataset, version 4. J. Clim. 2018, 31, 9835–9854. [Google Scholar] [CrossRef]
- Vertačnik, G.; Dolinar, M.; Bertalanič, R.; Klančar, M.; Dvoršek, D.; Nadbath, M. Ensemble homogenization of Slovenian monthly air temperature series. Int. J. Climatol. 2015, 35, 4015–4026. [Google Scholar] [CrossRef]
- Begert, M.; Schlegel, T.; Kirchhofer, W. Homogeneous temperature and precipitation series of Switzerland from 1864 to 2000. Int. J. Climatol. 2005, 25, 65–80. [Google Scholar] [CrossRef]
- Szentimrey, T. Methodological questions of series comparison. In Proceedings of the Sixth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 26–30 May 2008; WCDMP-No. 76. Lakatos, M., Szentimrey, T., Bihari, Z., Szalai, S., Eds.; WMO: Geneva, Switzerland, 2010; pp. 1–7. [Google Scholar]
- Maronna, R.; Yohai, V.J. A bivariate test for the detection of a systematic change in mean. J. Am. Stat. Assoc. 1978, 73, 640–645. [Google Scholar] [CrossRef]
- Szentimrey, T. Multiple analysis of series for homogenization (MASH). In Proceedings of the Second Seminar for Homogenization of Surface Climatological Data, Budapest, Hungary, 9–13 November 1998; WCDMP-41. Szalai, S., Szentimrey, T., Szinell, C., Eds.; WMO: Geneva, Switzerland, 1999; pp. 27–46. [Google Scholar]
- Venema, V.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertačnik, G.; Szentimrey, T.; Štěpánek, P.; Zahradníček, P.; et al. Benchmarking monthly homogenization algorithms. Clim. Past 2012, 8, 89–115. [Google Scholar] [CrossRef] [Green Version]
- Caussinus, H.; Mestre, O. Detection and correction of artificial shifts in climate series. J. R. Stat. Soc. Ser. C Appl. Stat. 2004, 53, 405–425. [Google Scholar] [CrossRef]
- Mestre, O.; Domonkos, P.; Picard, F.; Auer, I.; Robin, S.; Lebarbier, E.; Böhm, R.; Aguilar, E.; Guijarro, J.A.; Vertačnik, G.; et al. HOMER: Homogenization software in R—Methods and applications. Időjárás Quart. J. Hung. Met. Serv. 2013, 117, 47–67. [Google Scholar]
- Rustemeier, E.; Kapala, A.; Meyer-Christoffer, A.; Finger, P.; Schneider, U.; Venema, V.; Ziese, M.; Simmer, C.; Becker, A. AHOPS Europe—A gridded precipitation data set from European homogenized time series. In Proceedings of the Ninth Seminar for Homogenization and Quality Control in Climatological Databases; Szentimrey, T., Lakatos, M., Hoffmann, L., Eds.; WCDMP-85; WMO: Geneva, Switzerland, 2017; pp. 88–101. [Google Scholar]
- Chimani, B.; Venema, V.; Lexer, A.; Andre, K.; Auer, I.; Nemec, J. Inter-comparison of methods to homogenize daily relative humidity. Int. J. Climatol. 2018, 38, 3106–3122. [Google Scholar] [CrossRef]
- Alexandersson, H.; Moberg, A. Homogenization of Swedish temperature data. Part I: Homogeneity test for linear trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar] [CrossRef]
- Vincent, L.A. A technique for the identification of inhomogeneities in Canadian temperature series. J. Clim. 1998, 11, 1094–1104. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Domonkos, P. Efficiencies of inhomogeneity-detection algorithms: Comparison of different detection methods and efficiency measures. J. Climatol. 2013, 2013, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Van Malderen, R.; Pottiaux, E.; Klos, A.; Domonkos, P.; Elias, M.; Ning, T.; Bock, O.; Guijarro, J.; Alshawaf, F.; Hoseini, M.; et al. Homogenizing GPS integrated vapor time series: Benchmarking break detection methods on synthetic datasets. Earth Space Sci. 2020, 7, e2020EA001121. [Google Scholar] [CrossRef] [Green Version]
- Ducré-Robitaille, J.-F.; Vincent, L.A.; Boulet, G. Comparison of techniques for detection of discontinuities in temperature series. Int. J. Climatol. 2003, 23, 1087–1101. [Google Scholar] [CrossRef]
- Craddock, J.M. Methods of comparing annual rainfall records for climatic purposes. Weather 1979, 34, 332–346. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Solow, A. Testing for climatic change: An application of the two-phase regression model. J. Clim. Appl. Meteorol. 1987, 26, 1401–1405. [Google Scholar] [CrossRef] [Green Version]
- Easterling, D.R.; Peterson, T.C. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Climatol. 1995, 15, 369–377. [Google Scholar] [CrossRef]
- Caussinus, H.; Lyazrhi, F. Choosing a linear model with a random number of change-points and outliers. Ann. Inst. Stat. Math. 1997, 49, 761–775. [Google Scholar] [CrossRef]
- Domonkos, P. ACMANTv4: Scientific Content and Operation of the Software; 71p. Available online: https://github.com/dpeterfree/ACMANT (accessed on 2 September 2021).
- Li, S.; Lund, R. Multiple changepoint detection via genetic algorithms. J. Clim. 2012, 25, 674–686. [Google Scholar] [CrossRef]
- Hewaarachchi, A.P.; Li, Y.; Lund, R.; Rennie, J. Homogenization of daily temperature data. J. Clim. 2017, 30, 985–999. [Google Scholar] [CrossRef]
- Toreti, A.; Kuglitsch, F.G.; Xoplaki, E.; Luterbacher, J. A novel approach for the detection of inhomogeneities affecting climate time series. J. Appl. Meteorol. Climatol. 2012, 51, 317–326. [Google Scholar] [CrossRef]
- Schwaller, L.; Robin, S. Exact Bayesian inference for off-line change-point detection in tree-structured graphical models. arXiv 2016, arXiv:1603.07871 [stat.ML]. [Google Scholar] [CrossRef]
- Picard, F.; Lebarbier, E.; Hoebeke, M.; Rigaill, G.; Thiam, B.; Robin, S. Joint segmentation, calling and normalization of multiple CGH profiles. Biostatistics 2011, 12, 413–428. [Google Scholar] [CrossRef] [Green Version]
- Menne, M.J.; Williams, C.N. Detection of undocumented changepoints using multiple test statistics and composite reference series. J. Clim. 2005, 18, 4271–4286. [Google Scholar] [CrossRef]
- Domonkos, P. Efficiency evaluation for detecting inhomogeneities by objective homogenisation methods. Theor. Appl. Climatol. 2011, 105, 455–467. [Google Scholar] [CrossRef]
- Coll, J.; Domonkos, P.; Guijarro, J.; Curley, M.; Rustemeier, E.; Aguilar, E.; Walsh, S.; Sweeney, J. Application of homogenization methods for Ireland's monthly precipitation records: Comparison of break detection results. Int. J. Climatol. 2020, 40, 6169–6188. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Wen, Q.H.; Wu, Y. Penalized maximal t test for detecting undocumented mean change in climate data series. J. Appl. Meteor. Climatol. 2007, 46, 916–931. [Google Scholar] [CrossRef]
- Wang, X.L. Penalized maximal F test for detecting undocumented mean shift without trend change. J. Atmos. Oceanic Technol. 2008, 25, 368–384. [Google Scholar] [CrossRef]
- Domonkos, P. Adapted Caussinus-Mestre algorithm for networks of temperature series (ACMANT). Int. J. Geosci. 2011, 2, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Vincent, L.A.; Zhang, X.; Bonsal, B.R.; Hogg, W.D. Homogenization of daily temperatures over Canada. J. Clim. 2002, 15, 1322–1334. [Google Scholar] [CrossRef]
- Lindau, R.; Venema, V. On the reduction of trend errors by the ANOVA joint correction scheme used in homogenization of climate station records. Int. J. Climatol. 2018, 38, 5255–5271. [Google Scholar] [CrossRef] [Green Version]
- Domonkos, P. Homogenization of precipitation time series with ACMANT. Theor. Appl. Climatol. 2015, 122, 303–314. [Google Scholar] [CrossRef]
- Rienzner, M.; Gandolfi, C. A composite statistical method for the detection of multiple undocumented abrupt changes in the mean value within a time series. Int. J. Climatol. 2011, 31, 742–755. [Google Scholar] [CrossRef]
- Lund, R.; Wang, X.L.; Lu, Q.Q.; Reeves, J.; Gallagher, C.; Feng, Y. Changepoint detection in periodic and autocorrelated time series. J. Clim. 2007, 20, 5178–5190. [Google Scholar] [CrossRef] [Green Version]
- Killick, R.E. Benchmarking the Performance of Homogenisation Algorithms on Daily Temperature Data. Ph.D. Thesis, University of Exeter, Exeter, UK, 2016. Available online: http://hdl.handle.net/10871/23095 (accessed on 2 September 2021).
- Domonkos, P.; Coll, J. Homogenisation of temperature and precipitation time series with ACMANT3: Method description and efficiency tests. Int. J. Climatol. 2017, 37, 1910–1921. [Google Scholar] [CrossRef] [Green Version]
- Domonkos, P.; Coll, J. Time series homogenisation of large observational datasets: The impact of the number of partner series on the efficiency. Clim. Res. 2017, 74, 31–42. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).