A Statistical Analysis of Daily Snow Depth Trends in North America

Abstract

Several attempts to assess regional snow depth trends have been previously made. These studies estimate trends by applying various statistical methods to snow depths, new snowfalls, or their climatological proxies such as snow water equivalents. In most of these studies, inhomogeneities (changepoints) were not accounted for in the analysis. Changepoint features can dramatically influence trend inferences from climate time series. The purpose of this paper is to present a detailed statistical methodology to estimate trends of a time series of daily snow depths that account for changepoint features. The methods are illustrated in the analysis of a daily snow depth data set from North America.

1. Introduction

Snow is a viable proxy through which one may study climate change, as the associated modifications to precipitation and temperature patterns are believed to be strongest during the cold season in the mid and high latitudes where snowfall is prominent [1,2,3,4,5]. The rate at which climate is changing in polar regions is thought to exceed the rate at which natural systems can adapt [6]. Global climate models indicate that snow cover changes will considerably impact the cryopsheric portion of the water budget [7,8,9]. Snow is a vital environmental and geophysical quantity and is sensitive to climate change since its magnitude and extent depend on both temperature and precipitation [10,11,12].

Snow depth is the measured (or estimated) depth of a snow pack at a location, and takes into account the accumulation, ablation, and evolution of a snow pack. Therefore, snow depth should not be confused with snow cover (presence/absence) or new snowfall. Satellite data over the Northern Hemisphere suggest that snow cover has lessened since the mid-1980s [6,13,14,15,16,17,18]. Snow depth analyses complement snow cover change studies, providing further information on hydrological resources, surface energy, soil processes, and ecological systems [12,19]. Trend estimates in snow depths [12,13,20,21] and new snowfall [22,23,24,25] over various portions of the United States and Canada have been previously computed and related to climate variability [8,18,26,27,28].

When assessing long-term trends in snow depths, one should consider the temporal homogeneity of the data ([21,23,29,30]). Snow depth series often have discontinuities induced by changes in measuring location, equipment, or methods. These discontinuities—the so-called changepoints (breakpoints)—are crucial in constructing a realistic trend estimate at any one location ([21,24,30]). We do not attempt to attribute causes to any identified changepoints—they could be due to climate shifts, measuring changes, station moves, etc.; see [29] for additional discussion.

Perhaps the paramount contribution here lies with methods to handle the changepoint effects. Our methods apply equally well to snowfall and snow cover trend estimation. In this work, an unknown number of changepoints are modeled as mean level shifts at unknown points in time, for each gridded snow depth series.

Ref. [30] lists four difficulties in estimation of daily snow depth trends:

• Snow is seasonal, mostly absent during the summer months at all but Arctic or high alpine locations.
• Daily snow depths are highly correlated in time: tomorrow’s snow depth depends on today’s snow depth. Statistical inferences that ignore correlation will yield artificially high levels of confidence.
• Snow depths cannot be negative—this “zero modified support set issue" or hard boundary must be addressed.
• One should allow for changepoints in trend analyses; as we will see, they are of critical importance.

This is the first study to address all four points above in a regional assessment of snow depth trends.

Previous snow trend studies have used various methods to obtain trends. Some studies use trend estimates obtained by minimizing a sum of squared deviations ([12,20]); however, homogenization issues are not considered there. Ref. [24] quality control their data for inhomogeneities via expert opinion; however, their methods involve a target minus reference series approach, which are difficult to use here since our gridded series may aggregate many series over each grid cell. Other studies ([8,18,28,29]) use the methods in [31], where a non-parametric regression analysis is performed on yearly maximal new snowfall amounts using Kendall’s tau statistic ([32]). While Kendall’s tau statistic can be made to accommodate the serial correlation in snow depth data ([31]), it is non-trivial to do such; moreover, these methods cannot handle changepoint features. Ref. [7] address changepoints by merging distinct station records via the standard normal homogeneity test (SNHT) in [33]. The SNHT is a single changepoint test and may not describe multiple changepoint scenarios well ([34]).

Ref. [29] note that the data used here contain many undocumented changepoints. In general, the snow depth data are replete with changepoints; indeed, the Napoleon series studied in [30] contained 18 documented breakpoints from 1 January 1900 to 31 December 2003.

Estimation of multiple changepoint times via genetic algorithms (GA) has become increasingly popular in climate homogenization pursuits ([35,36]). Here, a GA is applied to the snow depth series at each grid to estimate changepoint times. These changepoints are subsequently used in a stochastic storage model. The storage model approach used here was introduced in [30] and stems from queueing theory. Snow is a natural storage phenomena: the snow depth today is the snow depth yesterday, plus any new snow that has fallen, minus any ablation or compaction. Ref. [37] also use storage models to describe daily snow depths, but do not allow for trends, melting in the fall and winter, or snow increases during spring ablation. In addition to trend estimates, computation of trend standard errors is also considered.

Results are demonstrated by applying our methods to a snow depth data set previously constructed and analyzed in [12,28,29]. This article does not focus on how to assess the suitability of one data set over another, but rather how to get an accurate trend estimate from given data. The papers perhaps most relevant to this study are perhaps [38], which develop additional statistical issues of the methods, and [39], which also studies trends in snow depth time series with periodic aspects considered.

The rest of the study proceeds as follows. A description of the data and study period is presented in Section 2. Section 3 describes our changepoint estimation techniques. Section 4 discusses the stochastic storage model used to compute trend standard errors. Section 5 presents results and concluding remarks.

2. The Data

The development of the gridded data set used in this study is now summarized. The creation of $1^{\circ }\times 1^{\circ }$ daily snow depth grids from station level data from 1900–2000 is discussed by Dyer and Mote (2006), although only data from 1960–2000 were analyzed there. Kluver et al. (2016) update the creation and validation procedures introduced in Dyer and Mote (2006), and extend the time record to 1900–2009. A brief review of the data is now discussed; the interested reader is referred to [12,22,29], for additional detail.

The grids considered in the data examined here extend from ${25}^{\circ }$ N to ${71}^{\circ }$ N latitude and from ${53}^{\circ }$ W to ${168}^{\circ }$ W longitude. Station data are interpolated to $1^{\circ }\times 1^{\circ }$ grids via the Spheremap spatial interpretation program in [29,40] report station density and found that the number of stations in a grid cell reporting snow depths varies widely with time (see Figure 1 of [29]), with a large increase in the number of reporting stations beginning in 1948 due to the full digitization of Cooperative Observer Program (COOP) station network data. A depiction of station density by grid is given in Figure 3 of [29].

Ref. [29] caution against using pre-1948 data in estimating trends, since station density is sparse before this time. As such, our study will commence in the summer of 1947 and finish in summer 2009 to permit work with “winter centered years” defined below. Observations during the latter half of 2009 will be omitted to accommodate the Section 3 and Section 4 methods.

Although [12] study snow trends on the entirety of North America from 1960–2000, a period in which stations are claimed (without numerical quantification) to be more evenly dispersed, we restrict this study to the largest contiguous grid set reporting at least 20 winter seasons of station observations, subject to the following constraint: the northern most grid in the study region, at each longitude, is set to be the northernmost cell containing at least 20 winter seasons with one or more reporting stations during 1948–2009. Concessions are made to make this region contiguous; this essentially excludes only a few isolated Arctic grids with good data. Our study region will be evident in our graphics.

Ref. [29] admit that the data contain various undocumented inhomogeneities in space and time due to differences in station recording procedures, reaffirming the importance of changepoints. After estimating the changepoint times, they are used in a stochastic storage model to help gauge uncertainty in the estimated trends. The storage model easily accommodates changepoint features.

3. Changepoint Methods

This section discusses our multiple changepoint detection methods. This is tantamount to data homogenization. The methods are illustrated with a snow depth series from a cell centered at latitude 44.5${}^{\circ }$ N, Longitude 115.5${}^{\circ }$ W, located near Warm Lake in the Boise National Forest in Central Idaho.

Genetic algorithms (GAs) have been successfully used in recent climate homogenization studies ([34,35]). GAs use principles of genetic selection and mutation to intelligently search for the best possible (as defined below) changepoint configuration. Although trends in daily depths are our focus, changepoints in yearly average snow depth series are first estimated. Homogenization for daily series is significantly more involved because of the long series lengths encountered ([36]). Any changepoint detected in the yearly series is assigned to the first day of the corresponding gridwinter centered year.

Let ${\left\{X_t\right\}}_{t=1}^N$ denote the snow depth series at a fixed grid for days $t=1,\dots ,N$. Winter centered years (WCYs) are analyzed here. The starting observation for any WCY is 1 July; 30 June of the subsequent calendar year is the last day. WCYs prevent a single winter season from straddling two distinct years. To have 1948 commence our study, $t=1$ will correspond to 1 July 1947; $t=N=22,265$ corresponds to 30 June 2009, the study end date. Leap year data are handled by deleting the 30 June observation within the calendar year on which 29 February occurs—this has virtually no impact on results. There are $n=61$ years in our study. For a periodic notation with time, we write time t as $t=dT+\nu$ where $d\in \{0,\dots ,n-1\}$ is the WCY and $\nu \in \{1,\dots ,T=365\}$ represents the day within the WCY.

At a given grid, define $Y_d=\#{\left(\mathcal{W}\right)}^{-1}{\sum }_{\nu \in \mathcal{W}}{X}_{dT+\nu }$ as the average winter snow depth for WCY $d\in \{0,\dots ,n-1\}$, where $\#\left(A\right)$ is the number of elements in the set A and $\mathcal{W}$ denotes the snow season for this grid. The snow season is considered to start on the first day in the Fall/Winter on which snow is present on at least 35 percent of the WCY years in the study; the last day of the WCY is the latest day in the Winter/Spring on which at least 35 percent of the WCY years report snow. The 35 percent proportion is somewhat arbitrary, but is chosen as it is high enough for accurate inferences to be made based on the minimum number of days with snow cover without being overly selective. For the grid centered near Warm Lake, Idaho, the snow season spans 25 October to 21 May inclusive, a length of 218 days.

We now describe our changepoint detection methods. Due to averaging (the central limit theorem), $Y_d$ is approximately normally distributed. Hence, the changepoint techniques for normal data from [34] apply. Trend components must be included in the changepoint detection methodology to avoid identifying spurious changepoints caused by the presence of non-zero trends ([41]). Our basic model for the yearly average snow depths ${\left\{Y_d\right\}}_{d=0}^{n-1}$ is the time series regression of form

$$Y_d=\alpha +\gamma d+{\mu }_d+{ϵ}_d.$$

(1)

Here, $\alpha$ models the grid’s average daily snow depth (less any trend), $\gamma$ is a linear trend parameter, ${\mu }_d$ is a changepoint effect described further below, and ${\left\{{ϵ}_d\right\}}_{d=0}^{n-1}$ is a zero-mean first order autoregressive (AR(1)) error process that induces temporal correlation into the yearly averages. The AR(1) errors obey ${ϵ}_d=\varphi {ϵ}_{d-1}+Z_d$, where $\left\{Z_d\right\}$ is a zero-mean white noise process with variance ${\sigma }^2$, and $\varphi \in (-1,1)$ is the correlation between consecutive years of average snow depths. The changepoint effect ${\mu }_d$, with k mean shifts at times ${\tau }_1<{\tau }_2<\cdots <{\tau }_k$, respectively, is

$${\mu }_d=\left\{\begin{array}{cc}{\Delta }_0=0,& {\tau }_0<d<{\tau }_1\\ {\Delta }_1,& {\tau }_1\le d<{\tau }_2\\ ⋮& ⋮\\ {\Delta }_k,& {\tau }_k\le d<{\tau }_{k+1}\end{array}\right.,$$

where ${\tau }_0=0$ and ${\tau }_{k+1}=n+1$ by convention. Here, ${\Delta }_{\ell }$ is interpreted as the changepoint effect of the ℓth regime, measured relative to the first regime (${\Delta }_{\ell }-{\Delta }_{\ell -1}$ is the shift magnitude since the last regime).

This model contains the regression parameters $\alpha ,\gamma ,{\Delta }_1,\dots ,{\Delta }_k$, the changepoint parameters k, ${\tau }_1,{\tau }_2,\dots ,{\tau }_k,{\tau }_{k+1}$ and the time series parameters $\varphi$ and ${\sigma }^2$. For a given configuration of k changepoints occurring at the times ${\tau }_1,\dots ,{\tau }_k$, the regression parameters are estimated using standard linear regression methods; Yule–Walker estimators are fitted to linear regression residuals to estimate the time series parameters $\varphi$ and ${\sigma }^2$. ([42] provide details).

Estimation of the best changepoint configuration of a time series is a statistical model selection problem. Popular model selection criteria include the Akaike Information Criterion (AIC), the Bayesian Information (BIC), and Minimum Description Lengths (MDLs). To date, MDL methods have produced superior empirical results ([43,44]). MDL methods minimize an objective function of form $\mathrm{MDL}=-ln\left(L_{\mathrm{opt}}\right)+P$ over all possible changepoint configurations. Here, $-ln\left(L_{\mathrm{opt}}\right)$ is an optimal model likelihood given the number of changepoints k and their locations ${\tau }_1,\dots ,{\tau }_k$, and P, which depends on the number of changepoints and their location times, is a penalty term to prevent overfitting. Unlike AIC and BIC penalties, MDL penalties depend on where the changepoints lie. The MDL penalty is more than a multiple of the number of changepoints, penalizing closely spaced changepoint times more than sparsely spaced changepoints.

The Innovations form of the multivariate Gaussian likelihood is used:

$$L(\varphi ,\sigma ,\alpha ,\gamma ;k,{\Delta }_1,\dots ,{\Delta }_k)={\left(2\pi \right)}^{-\frac{N}{2}}{\left(\prod _{t=0}^{N-1}{v}_t\right)}^{-\frac{1}{2}}exp\left(-\frac{1}{2}\sum _{t=1}^N\frac{{(Y_t-{\widehat{Y}}_t)}^2}{v_{t-1}}\right).$$

(2)

Here, ${\widehat{Y}}_t$ is the one-step-ahead predictor of $Y_t$ and $v_t=E\left[{(Y_{t+1}-{\widehat{Y}}_{t+1})}^2\right]$ is its mean squared prediction error. For an AR(1) series, ${\widehat{Y}}_t={\widehat{m}}_t+\widehat{\varphi }(Y_{t-1}-{\widehat{m}}_{t-1})$, where ${\widehat{m}}_t=\widehat{\alpha }+\widehat{\gamma }d+{\widehat{\mu }}_d$, and $v_t={\widehat{\sigma }}^2$. Parameter estimates for $\varphi$ and $\sigma$ are calculated from the Yule–Walker equations involving the sample variance and lag one autocorrelation of ${\left\{{\widehat{ϵ}}_d\right\}}_{d=0}^{n-1}$. Substituting the estimators of $\varphi ,\sigma ,\alpha ,\gamma ;k,{\Delta }_1,\dots ,{\Delta }_k$ into (2) gives $ln\left(L_{\mathrm{opt}}\right)$ for the changepoint configuration with k changepoints at locations ${\tau }_1,\dots ,{\tau }_k$.

The penalty term for the changepoint configuration is that in [35]. When $k>0$,

$$P=P(k;{\tau }_1,\dots ,{\tau }_k)=\frac{1}{2}\sum _{\ell =1}^{k+1}log({\tau }_{\ell }-{\tau }_{\ell -1})+\sum _{\ell =2}^{k}log\left({\tau }_{\ell }\right)+{log}_2\left(k\right);$$

when $k=0$, the penalty vanishes from the model ($P=0$). The best changepoint model is estimated as the one that minimizes the MDL score. As an exhaustive search for changepoint configuration(s) requires evaluation of $2^n$ MDL scores, an arduous task even on the world’s fastest computers for even moderately large n. Here, a GA was devised to perform the minimization. GAs have recently been employed for multiple changepoint detection in climate data ([34,35,44]). See [45] for more on genetic algorithms.

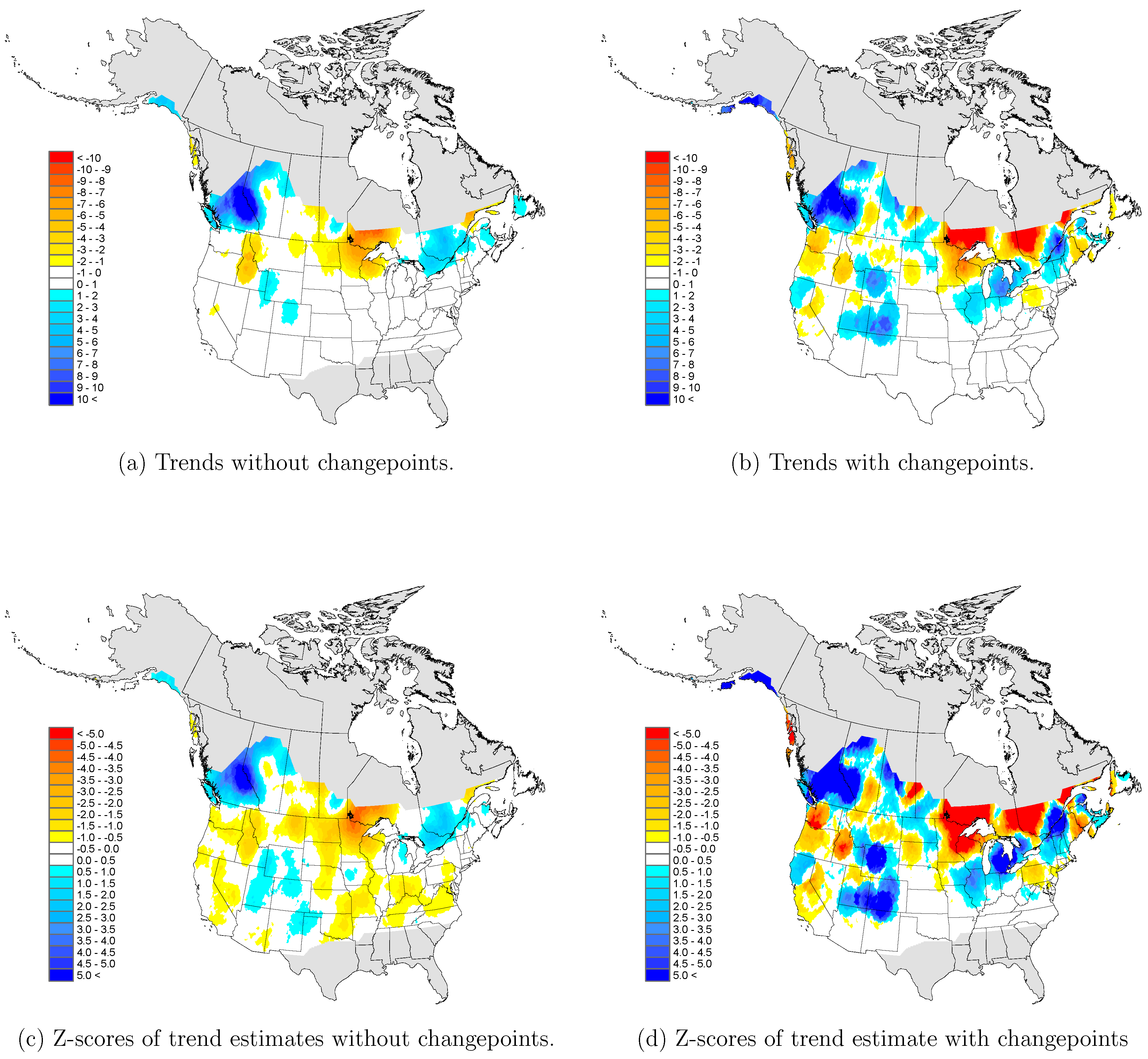
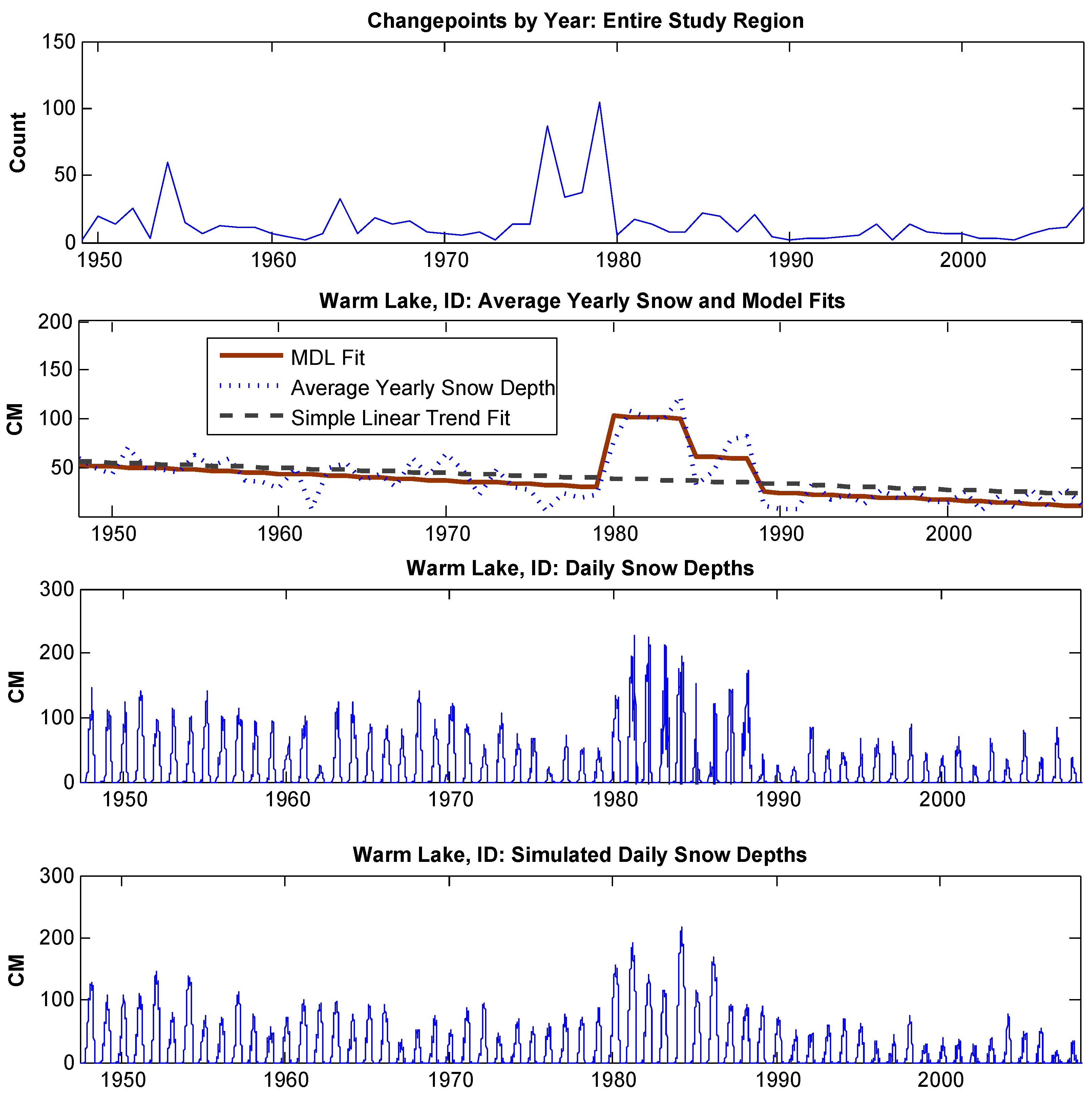
Panel 1 of Figure 2 depicts the number of changepoints estimated by year for our 1217 grid study region. Three peaks are seen in 1953, 1974, and 1978 respectively. As an example, when these methods are applied to the Warm Lake, Idaho grid, changepoints are declared on 1 July of 1979, 1984, and 1988. Panel 1 of Figure 2 graphically depicts the MDL and a simple linear regression fit to ${\left\{Y_d\right\}}_{d=0}^{n-1}$. For this grid, the slope of the MDL regression structure is more negative than that for the simple linear trend when changepoints are ignored; more particulars about this example are given later.

4. The Storage Model

Ref. [30] introduce a storage model to estimate trends in daily snow depths in the presence of changepoints. This model was fitted to a time series from Napoleon, North Dakota.

For each fixed grid, estimates of the number of mean shifts k and their times ${\tau }_1,\dots ,{\tau }_k$ are now in place. Our model for the daily snow depths is based on the storage equation

$$X_t=max\{X_{t-1}+C_t,0\},$$

where $C_t$ quantifies the random change in the snow pack from day $t-1$ to day t. The max term prevents the snow depths from becoming negative. Here, the depth change $C_t$ is assumed statistically independent of $X_1,\dots ,X_{t-1}$.

We posit that $m_t:=E\left[C_t\right]$ has a periodic component, possibly multiple changepoints, and a linear trend. The variance $Var\left(C_t\right)=w_t^2$ is assumed periodic with period $T=365$. For computational convenience, $C_t$ is assumed normally distributed: $C_t\sim N(m_t,w_t^2)$; other distributions can be easily used if desired. Specifically, $m_t$ is parameterized at time $t=nT+\nu$ as

$$m_t=P_{\nu }\left[A+Bcos\left(\frac{2\pi (\nu -\zeta )}{T}\right)+{\delta }_t+\gamma t\right],$$

(3)

where the mean shifts are parametrized as in the last section:

$${\widehat{\delta }}_t=\left\{\begin{array}{cc}0,\hfill & t\in \{1,\dots ,\widehat{{\tau }_1}T-1\}\hfill \\ {\Delta }_1,\hfill & t\in \{{\widehat{\tau }}_{1}T,\dots ,{\widehat{\tau }}_{2}T-1\}\hfill \\ ⋮\hfill & ⋮\hfill \\ {\Delta }_{\widehat{k}},\hfill & t\in \{{\widehat{\tau }}_{\widehat{k}}T,\dots ,dn\}\hfill \end{array}\right..$$

The term $P_{\nu }$ is a zero/one indicator that is unity only when $\nu \in \mathcal{W}$.

To estimate the storage model parameters (this is not the same task as estimating changepoint numbers and locations), we minimize the weighted sum of squared one-step-ahead prediction errors

$$S\left(\mathbf{\theta }\right)=\sum _{d=0}^{n-1}\sum _{\nu =1}^T\frac{{(X_{dT+\nu }-{\widehat{X}}_{dT+\nu })}^2}{w_{\nu }^2}.$$

Here, $\mathbf{\theta }={(A,B,\zeta ,\gamma ,{\Delta }_1,\dots ,{\Delta }_k)}^{\prime }$ is a vector containing all model parameters and ${\widehat{X}}_t:=E_{\mathbf{\theta }}\left[X_{t+1}\right|X_t]$ is the one-step-ahead prediction, calculated in Woody et al. (2009) as

$$E_{\mathbf{\theta }}\left[X_{t+1}\right|X_t]=\left[X_t+m_{t+1}\right]\left[1-\Phi \left(\frac{-X_t-m_{t+1}}{w_{t+1}}\right)\right]+w_{t+1}\varphi \left(\frac{X_t+m_{t+1}}{w_{t+1}}\right),$$

(4)

where $\Phi (·)$ and $\varphi \left(x\right)=e^{-x^2/2}/\sqrt{2\pi }$ are the cumulative distribution and density functions, respectively, of a standard normal random variable. Because snow is seasonal, weighted least squares is used. Here, the weight $w_{\nu }$ is set to $\mathrm{Var}\left(Z_{\nu }\right)$. To estimate $w_{\nu }$, first calculate a point estimate of the mean change from day $\nu -1$ to day $\nu$ via ${\widehat{e}}_{\nu }=n^{-1}{\sum }_{d=0}^{n-1}(X_{dT+\nu }-X_{dT+\nu -1})$. The estimate of $w_{\nu }$ is then simply a multiple of the sample standard deviation:

$${\widehat{w}}_{\nu }^2=n^{-1}\sum _{d=0}^{n-1}{(X_{dT+\nu }-X_{dT+\nu -1}-{\widehat{e}}_{\nu })}^2.$$

We smooth these daily variances via the Matlab function “cfit” before using them to minimize variability.

Some minor quality control is applied to the daily snow depths before trend inference is conducted. Following [46], if the day to day change in snow depths during season $\nu$ is more than four standard deviations from the mean daily change for season $\nu$, ${\widehat{e}}_{\nu }$, then the data for that day is flagged and considered missing.

While the parameter $\gamma$ controls the trend and is the object of our study, it is not easily interpretable within the storage equation. For example, because of the maximum in the storage equation, $\widehat{\gamma }=50$ does not imply a depth change of 50 units per time. A quantity that does have interpretable units of depth change per time is the linear trend statistic in the presence of changepoints:

$$\widehat{\beta }=\frac{{\sum }_{r=1}^{k+1}{\sum }_{n\in {\mathcal{H}}_r}{\sum }_{\nu =1}^T\left(X_{nT+\nu }-{\overline{X}}_r\left(\nu \right)\right)\left(nT+\nu -{\overline{t}}_r\left(\nu \right)\right)}{{\sum }_{r=0}^k{\sum }_{n\in {\mathcal{H}}_r}{\sum }_{\nu =1}^T{\left(nT+\nu -{\overline{t}}_r\left(\nu \right)\right)}^2},$$

(5)

where ${\mathcal{H}}_r=\{t:{\tau }_{r-1}\le t<{\tau }_r\}$ denote the set of times the series experienced the r-th regime, $r\in \{0,1,\dots ,k\}$, and ${\overline{X}}_r\left(\nu \right)$ and ${\overline{t}}_r\left(\nu \right)$ denotes the average snow depth and time, respectively, for day $\nu$ in regime r. See [47] or [48] for more on this statistic. In this context, $\widehat{\beta }$ estimates the mean change in the snow depth per time (scaled to cm per century below). To obtain standard errors for $\widehat{\beta }$, we simply simulate 1000 independent realizations of the storage model with parameters as estimated from the data for each grid, and then compute the sample mean and standard deviations of the 1000 trend estimates in (5). Simulation is used because explicit forms for storage equation means do not exist.

At Warm Lake, three changepoints are estimated, and occur on 1 July 1979, 1 July 1984, and 1 July 1988. Parameter estimates for $m_t$ in Equation (3) are $\widehat{A}=-0.8772$, $\widehat{B}=1.9843$, $\widehat{\zeta }=181.0640$, $\widehat{\gamma }=-0.9813$, ${\widehat{\Delta }}_1=0.9709$, ${\widehat{\Delta }}_2=0.5225$, and ${\widehat{\Delta }}_3=0.0034$. The negative $\widehat{\gamma }$ implies overall declining snow depths; the positive ${\widehat{\Delta }}_1$ entails an abrupt shift to a snowier era from 1 July 1979–30 June 1984. This is followed by a modest drop in snow depths from 1 July 1984–29 June 1988, and finally another decrease in depths from 1 July 1988 onwards. The thousand simulations of the storage model with these parameters report an average trend of $\widehat{\beta }=-42.81$ cm/century, with a standard error of $12.64$ cm/century. This yields a z-score of $-3.3869$ when testing the null hypothesis that $\beta =0$ (a one-sided p-value of $3.5344\times {10}^{-04}$). The daily snow depths from 1 July 1948 to 30 June 2009 are depicted in Panel 3 of Figure 2. A simulation of the daily snow depths using the parameter estimates from the storage model fit reported above is shown in Panel 4 of Figure 2 and depicts a reasonable likeness to the raw data in Panel 3, including the estimated mean level shifts (simulation is another use of the storage model).

In contrast, if changepoints are ignored, parameter estimates are $\widehat{A}=-0.7728$, $\widehat{B}=1.8748$, $\widehat{\zeta }=179.9746$, and $\widehat{\gamma }=-0.6544$. The thousand simulations of the storage model with these parameters report an average trend statistic of $\widehat{\beta }=-30.1848$ cm/century, with a standard error of $5.6673$ cm/century. This yields a z-score of $-5.3261$ when testing that $\beta =0$ (a one-sided p-value of $5.0172\times {10}^{-8}$). Overall, snow depths are inferred to be decreasing at Warm Lake, more so when changepoints are taken into account.

5. Results

North American results are described for two cases: (1) when changepoints were ignored and (2) when changepoints were included. The study area contained 6613 grids in total; however, only 1217 grids in the study region experienced a winter season as defined above or have data that met our quality constraints. The average number of changepoints over these 1217 grids was 0.7198 with a standard error of 0.8975. More specifically, 664 (54.56%) of the grids were changepoint free, 272 grids (22.35%) had only one changepoint, 241 grids (19.80%) had two changepoints, 38 grids (03.12%) had three changepoints, and 2 (0.16%) had four changepoints (the maximum number detected).

More grids reported negative depth trends than positive depth trends, regardless of whether or not changepoints were considered. When changepoints were ignored, 469 grids (38.54%) reported positive depth trends and 748 grids (61.47%) reported negative depth trends. When changepoints were taken into account, 537 grids (44.12%) reported positive snow depth trends and 680 grids (55.88%) reported negative snow depth trends.

The magnitude of the estimated trends was a different story: the average grid trend was 0.3212 cm/century without changepoints, with a standard error of 4.6585, and 0.1519 cm/century, with a standard error of 9.1046, when changepoints were included. Overall, the addition of changepoints reduced the average depth trend.

The mean trend of grids with positive trends when changepoints were ignored was 2.7735 cm/century; the mean trend for grids with decreasing trends when changepoints were ignored was −0.8551 cm/century. In contrast, the mean trend for grids reporting increasing trends was 4.9067 cm/century when changepoints were taken into account; the mean trend for decreasing grids was −4.9698 cm/century when changepoints were taken into account. The magnitude of the trends was substantially larger when changepoints were considered.

6. Conclusions

The top two panels of Figure 1 show trends, in cm/century, with and without changepoints. The bottom two panels of Figure 1 depict smoothed z-scores from the trends. The z-scores are computed assuming a null hypothesis that the trend is zero, with the trend $\widehat{\beta }$ at each station derived by dividing the trend by the standard error of the trend estimate.

Some spatial patterns are evident in the Figure 1 depth trends and z-scores. We will explain our interpretation of the z-score maps; interpretation of the raw trends proceeds similarly. Increasing depth trends are evident in the Southern and Northern Rocky Mountains, regardless of whether changepoints are considered. Much of the rest of the study area, particularly the US Midwest and plains states and Canadian provinces, are seeing declining snow depths. One area where inferences change when changepoints are neglected/accounted lies near the Southeastern Ontario and Southwestern Quebec border. In conclusion, the authors believe changepoint considerations to be of critical importance when performing trend inference in a time series of snow depths.